e1 Zvi Bodie 投資學 v10
8.5 指數模型在組合管理中的實際應用
本節討論的基調錶明在投資組合管理實際運用中指數模型是受歡迎的。從馬科維茨模型轉到指數模型是一個重要的決定,因而第一個問題就是指數模型比馬科維茨全協方差模型差嗎?
8.5.1 指數模型比全協方差模型差嗎
這個問題類似一般關於簡約模型的價值問題。做一個類比,我們通過在迴歸方程中增加解釋變量來考查這個問題。我們知道增加解釋變量在大多數情況下會增加R2,不會使R2下降。但是這不一定就意味著它是一個更好的迴歸方程(注:調整後的R2可能會下降,增加的變量並沒有足夠的解釋力量來彌補額外的自由度。)。一個更好的標準是看回歸方程的預測能力。一個值得注意的問題是增加一個有利於對樣本內解釋能力的變量是否有利於樣本外的預測精確性。增加變量可能增加顯著性,但同時對預測精確性是不利的。換句話說,包含自變量不多的簡約模型常常有優越性。預測因變量的值依賴兩個因素:係數估計的精確性和自變量預測的精度。當我們增加變量時,這兩個精確性都會受損。
用完全分散化的馬科維茨模型或多指數模型來代替單指數模型時,這個問題也會出現。增加一個指數需要預測該指數組合的風險溢價和各證券對新指數的β值。與單指數模型相比,馬科維茨模型在資產協方差結構上更靈活。但如果不能在任何置信度下估計協方差,這個優勢是不現實的。運用全協方差矩陣需要估計數以千計的風險值,即使在原理上馬科維茨模型更好,但是太多的估計誤差累計對投資組合的影響可能導致其實際上劣於單指數模型推導出來的投資組合。
相比全協方差模型潛在的優越性,單指數模型框架的實際好處非常明顯。它的另一個決定性優點是分解了宏觀分析和證券分析。
8.5.2 行業指數模型
無疑,指數模型吸引了行家的關注。因為它接近有效,為證券分析提供了一個方便的基準。
一個沒有證券特別消息或內部信息的投資經理會認為證券的α值為0。按照式(8-9)將預測這個證券的風險溢價等於βiRM。如果就總收益預測重新表述,則:

一個預測市場指數收益E(rM)並觀測無風險短期國債收益率rf的投資經理能運用這個模型決定任何證券的基準期望收益。β係數、市場風險σ2M、公司特有風險σ2(e)都可以從歷史證券特徵線中估計得到,也就是說從證券超額收益對市場指數超額收益的迴歸中得到。
很多地方可以得到這些迴歸結果,或稱“β指引”,表8-6是一個例子。它一般使用標準普爾500指數作為市場組合的代理,運用最近60個月的觀測值去計算迴歸參數,並在迴歸中使用總收益而非超額收益。在這種方法下,他們的估計用一個變形的指數模型:

而不是:

為了理解這個變形的影響,把式(8-27)變為:
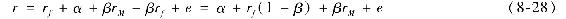
比較式(8-26)和式(8-28),會看到如果在樣本期rf是一個常數,這兩個公式有相同的自變量rM和殘差e,因此兩個迴歸方程中的斜率係數是相同的。(注:實際上,rf是隨時間變化的,然而,rf的變動和股票市場變動相比太小,對於β估計微不足道。)
表8-6 市場敏感度統計數據:2004~2008年60個月的股票總收益對標準普爾500指數收益
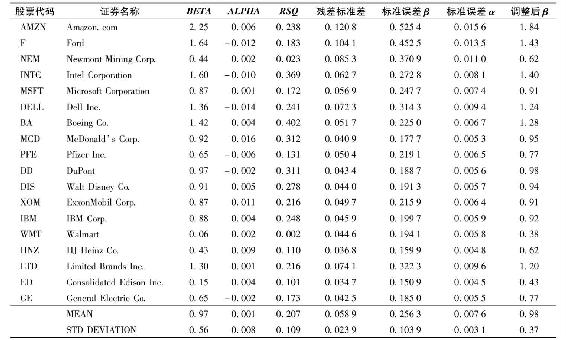
資料來源:Compiled from CRSP(University of Chicago)database.
表8-6中的β刻畫的截距項α實際上是α+rf(1-β)的估計量。如果要保證這一計算過程合理,則需要保證rf(1-β)在以月度計算的基礎上非常小,且相對於股票收益率的波動而言可以忽略不計。但注意到β≠1,當式(8-27)中使用超額收益率時,式(8-26)的迴歸截距並不等於指數模型的α。
切記這些α值是事後的估計值,並不是說可以事前預測出這些α值。事實上,證券分析博弈本質上是在事前預測α值。一個好的組合做多未來α值為正的股票,做空未來α值為負的股票,這樣才會打敗市場。
概念檢查8-4
表8-6迴歸中Intel指數模型每月的α是多少?假定這一期間短期國債月均收益率為0.2%。
表8-6的其他數據和討論惠普時所用的表8-3基本相同。回憶R2,這裡看到對於大多數公司R2低於0.5,意味著股票的公司特有風險超過系統風險,也說明分散化的重要性。
殘差標準差一列是迴歸殘差的標準差,或稱迴歸的標準誤差,就像Excel,“β指引”也包含α、β估計的標準誤差,便於評估估計的準確性。注意到α的標準誤差偏大。
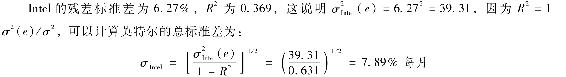
這是英特爾樣本期的月度標準差,所以年化後標準差為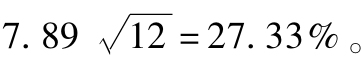
最後一列稱作調整後β,調整β值的動機是:在整個期間,平均而言股票的β值似乎有向1變動的趨勢。對這種現象的一個解釋來自直覺。企業通常生產特定產品提供特定服務。通過採用不同的方法,一個新的公司可能和老公司相比有很多不一樣的地方,比如從技術到管理風格。然而隨著公司的成長,一個公司通常會分散化經營,首先是擴大到其他相似產品,後來進行更多樣化的經營。當公司變得越來越傳統,它開始與經濟中的其他成分越來越相似。因此β值有向1變動的趨勢。
另一種統計解釋是:我們知道所有證券的平均β值等於1,因此在估計一個證券的β值之前,最好的預測就是其β值等於1。當在一個特定樣本期間估計β值時,保留了一些樣本誤差,β值和1差距越大,存在估計誤差的可能性越大,隨後則更容易趨向於1。
樣本期間,β係數的估計是我們最好的猜測。然而,給定β值向1的變化趨勢,未來β係數的預測應當順勢調整。
表8-6簡單地調整了β估值。[1]方法是取樣本β估計值和1進行加權:

【例8-1】調整β
表8-6中的60個月間,Intel的β是1.6,因此它的調整β是1.4,向1前進了1/3。
沒有Intel的更多信息,如果我們估計市場指數收益為10%,短期國債為4%,從“β指引”中我們得到:
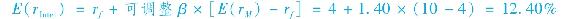
樣本期迴歸α值為-1%。因為Intelβ大於1,所以指數模型估計的α更大一些。如同式(8-28),需要減去(1-β)rf才能得到指數模型的α。在任何情況下,α的標準差為0.81%,α的估值遠小於標準差的2倍,所以無法拒絕α為0的原假設。
8.5.3 預測β
調整後的β可以用來理解歷史數據估計的β值不是未來β的最好估計:β有向1移動的趨勢,這意味著我們可能要為β構建一個預測模型。
一個簡單方法是收集在不同期β的數據,然後估計迴歸方程:

得到a和b的估計值,就能運用該公式來預測未來的β值

然而,何必限制用這麼簡單的方法去預測β值,而不研究其他財務變量在預測β值方面的有效性呢?比如,如果相信公司規模和負債比率是β值的兩個決定因素,把式(8-30)擴充為:
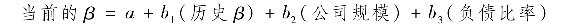
現在利用a、b1、b2和b3的估計值來預測未來的β值。
該方法被羅森伯格和蓋伊[2]使用,他們發現下列變量有助於預測β。
(1)收入變量
(2)現金流變量
(3)每股收益增長率
(4)市值(公司規模)
(5)股息收益
(6)資產負債比率
概念檢查8-5
比較表8-7中前5個和後4個行業,哪些特徵決定了調整因素?
羅森伯格和蓋伊也發現通過控制一個公司的財務特徵值,行業類型有助於預測β。例如,他們發現金礦開採行業的平均β值比單獨使用財務特徵預測得到的估值低0.827。這並不奇怪,對金礦開採行業-0.827的β值調整反映出金價和市場收益是相反變動的。
表8-7 行業β和調整因素

華爾街實戰8-1描述了有關α的賭局。
華爾街實戰8-1 關於α的賭局
對於相信有效市場的人來說,最近交易所交易基金(ETF)數量的增長可以看作是個勝利。ETF是追蹤某一特定指數的證券組合,它通常要收取一定百分比的管理費。它們允許投資者以低成本的方式投資於一個涵蓋國際權益市場、政府和公司債市場,以及商品市場等廣泛的投資組合。
但隨著ETF的資產和指數基金的增長,行業中的另一個部門卻發展得更加迅猛。精算公司Watson Wyatt估計包含對衝基金和私募投資等的“另類投資”(alternative investment)在2005年增長了20%,為1.26萬億美元。進行這項投資的人要支付更高額的管理費並期望獲得一個更好的收益。一個增長最快的資產類別——對衝基金的基金,收取的管理費最高。
為什麼人們要支付高昂的管理費呢?部分原因是投資者已經可以區分市場收益率、β(系統性)風險和經理人績效(以α來度量)。“為什麼不對β和α分開定價呢?”Hendenrson全球投資者(一個基金管理公司)的Arno Kitts問道。“β是一種商品而α則是一種技術。”
沒有一家公司擅長所有的投資領域。這導致了一種“核心和衛星”的模式,在這種模式下,資產的一部分投資於盯住某種指數的投資組合,而另一部分則交給某些領域的投資專家。但這樣也會造成一些問題。獨立經理人之間的關係相對簡單,然而要研究和監督專業投資者的行為就很困難了。這將導致中間人的產生,即經理的經理(傳統的機構業務中)和基金的基金(在對衝基金行業),從而提高管理費用。
管理費用的存在也許暗示著投資者能夠預先識別老練的基金經理人。但是,研究表明這是非常困難的。而且,即便投資者能識別有能力的經理人,這些超額的業績也將反映在管理費的提高中。“一個不成比例的α收益將給經理人而非客戶。”Schroders的資產經理人Alan Brown說道。
在任何情況下,投資者都很有可能去追尋α收益,即使存在如ETF和盯住基金等更便宜的另類投資。華信惠悅諮詢公司(Watson Wyatt)的Craig Baker說道,雖然不是每個人都能找到超過市場收益的投資機會,但找到這些機會的那些人將具有先行優勢。只要這樣一種信條存在,經理人就能收取高額的管理費。
資料來源:The Economist,September 14,2006.Copyright©The Economist Newspaper Limited,London.
8.5.4 指數模型和跟蹤證券組合
假設投資經理相信自己找到了低估的組合。他的證券分析團隊估計了這一組合超額收益的指數模型方程(用標準普爾500指數)並得到以下估值:

因此,組合的α值為4%,β值為1.4。這個經理相信其證券分析的質量,但是擔心近期大市的業績。如果購買該組合而市場整體下滑的話,投資依然有可能虧損,即使組合的價值相對被低估。他想要一個可以利用其證券分析但又獨立於市場的組合。
為了這個目的,可以建立一個跟蹤證券組合(tracking portfolio,T),組合P的跟蹤證券組合是為了配對組合P收益中的系統部分。核心理念是以這個組合去跟蹤組合P收益中對市場敏感的部分。這意味著跟蹤組合要有和P一樣的β值,但是非系統風險越小越好。這一過程也稱為β捕捉。
投資組合P的跟蹤組合將有一個標準普爾500指數的槓桿頭寸,目的是使得它的β值達到1.4。因此,T包含1.4權重的標準普爾500指數和-0.4權重的短期國庫券。因為T由標準普爾500指數和短期國庫券構建,因此其α值為0。
現在考慮購買投資組合P,但同時通過做空跟蹤組合T來消除系統風險,組合T消除了投資組合P多頭頭寸的系統性風險敞口:整個組合頭寸是市場中性的。因此,即使市場表現不好,這一組合也不會受影響。但是組合P的α值保持不變。最終組合C,每美元的超額收益為:
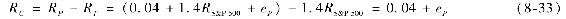
這一組合仍然是有風險的(殘差風險eP),但是系統性風險被消除了,而且如果P是合理分散化的,其系統性風險也會很小。從而實現了目標:投資經理鎖定4%的α,但消除了系統性風險敞口。這一分離尋求α和選擇系統性風險敞口的過程稱為α搬運。
這一“多頭-空頭策略”是很多對衝基金的行為特徵。對衝基金經理找到被低估的證券並試圖進行純賭博。他們對衝掉所有外在的風險,只是對察覺到的α下注。跟蹤組合是對衝不需要的風險敞口時常用的方法。對衝基金經理使用指數迴歸的方法或其他更復雜的變形來創建跟蹤組合,這是對衝策略的核心。
[1] 更復雜的方法見Oldrich A.Vasicek,“A Note on Using Cross-Sectional Information in Bayesian Estimation of Security Betas,”Journal of Finance 28(1973),pp 1233-39。
[2] Barr Rosenberg and J.Guy,“Prediction of Beta from Investment Fundamentals,Parts 1 and 2,”Financial Analysts Journal,May-June and July-August 1976.