e1 Zvi Bodie 投資學 v10
8.4 組合構造與單指數模型
在這一部分，我們考察指數模型在組合構造中的意義。我們會看到這一模型有很多優點，不僅在參數估計方面，而且能運用在簡化分析和組織分散上。[1]
8.4.1 α和證券分析
單指數模型最重要的優點或許是它為宏觀和證券分析提供了框架，這對最優組合的效率至關重要。馬科維茨模型要求估計每個證券的風險溢價。期望收益的估計取決於對宏觀和公司的預測。但是如果不同的分析師對一個大型的機構（比如共同基金）證券進行分析，一個可能的結果是宏觀預測上出現矛盾，而宏觀預測影響證券的收益預期。此外，在證券分析中關於市場指數的收益和風險基本假設並不明顯。
單指數模型的分析框架分離這兩種收益波動的來源，減少不同分析師分析的差異。我們可以寫出單指數模型框架輸入數據的準備步驟。
（1）宏觀經濟分析，用於估計市場指數的風險和溢價。
（2）統計分析，用於估計β係數和殘差的方差σ2（ei）。
（3）投資經理用市場指數風險溢價和證券β係數的估計值來建立證券的期望收益，這不需要相關的證券分析。市場驅動的期望收益以證券都受影響的信息為條件，而不基於證券分析獲取單個公司的信息。市場驅動的期望收益可以作為一個基準。
（4）準確的證券特有收益的預測（證券α）從各種證券估值模型得到，因此，α值反映了證券分析中發現的私人信息帶來的增量風險溢價。
在式（8-9）中，單個證券的風險溢價中與證券分析無關的部分為βiE（RM）。也就是說，風險溢價僅來自證券追隨市場指數的趨勢。任何超過這一基準的期望收益（證券α）都產生自非市場因素。
證券分析的最終結果為一列α值。估計β係數的統計方法是標準化的。因此，我們不希望不同分析師的輸入數據有太大差別。相反，宏觀和證券分析有更大的發揮空間，分析師在這方面彼此角逐。運用指數模型解決由市場因素導致的溢價，組合管理者便能確信宏觀分析師針對市場指數風險溢價的估計值，證券分析師應用一致的市場分析來獲得α值。
在組合構造中，α並不只是期望收益的一部分這麼簡單。它是告知我們某一個證券是高估還是低估的核心變量。考慮一隻股票，已經獲得α值和β值，我們可以輕易地找到擁有相同β的其他證券。因此，真正決定一個證券是否有投資吸引力的是它的α值。事實上，一個由+α值的證券獲得一個溢價，若該溢價高於跟蹤市場指數波動趨勢，則該證券是被低估的，一個被動投資者會在其投資組合中提高該證券的權重。相反，在其他條件一定時，-α的證券則被高估，其投資權重要相應下調，如果允許的話，較理想的策略是賣空該證券。
8.4.2 指數組合作為投資資產
單指數模型的有效邊界圖與第7章馬科維茨模型的程序非常相似。在這裡，指數模型能夠使輸入列表更加簡化，而且，組合最優化顯示出單指數模型的另一優勢，即簡單、直觀地顯現出最優風險投資組合。在這種情形下，討論最優化的機制之前，首先考慮指數組合在最優組合中的角色。
假設一個投資公司的章程限制其僅能投資標準普爾500指數中的股票。在這種情況下，標準普爾500指數涵蓋了宏觀經濟對該投資公司持有的大公司股票的影響。假設公司的投資範圍只涵蓋可投資空間的一部分子集，如果組合僅限於這些可投資產品，投資經理可能要擔心其投資的分散化程度有限了。
應對分散化不足的簡單方法是直接把標準普爾500指數作為一個投資資產。從式（8-8）和式（8-9）來看，如果我們把標準普爾500指數看作市場指數，那麼它的β值為1，沒有公司特有風險，α值為0，即其期望收益中不包括非市場風險溢價部分。式（8-10）顯示任一證券i和指數的協方差為βiα2M。為了區別標準普爾500指數與公司投資的n只股票，把標準普爾500指數命名為第n+1種資產。我們可以將標準普爾500指數看作當投資經理不進行證券分析時投資的一種消極資產組合。如果投資經理願意進行證券研究，那麼他可能會構造包含該指數的積極組合，得到更好的收益風險權衡。
8.4.3 單指數模型的輸入數據
如果投資經理打算構造一個組合，包括n家積極研究的公司和一個消極的指數組合，則輸入數據為：
（1）標準普爾500指數的風險溢價。
（2）標準普爾500指數的標準差估計值。
（3）n套如下估計值：①β係數估計值；②個股殘差的方差；③證券的α值（個股的α值估計值，連同標準普爾500指數的風險溢價，以及個股的β決定了個股的期望收益）。
8.4.4 單指數模型的最優風險組合
單指數模型讓人們可以直接求解最優風險組合並看出該解的屬性。首先，我們可以肯定，沿著馬科維茨模型的思路，很容易構建最優化過程並畫出在這一框架下的有效邊界。
運用估計的α和β係數，加上指數組合的風險溢價，應用式（8-9）能得到n+1個期望收益值。運用β係數的估計值和殘差方差以及指數組合的方差，應用式（8-10）則可以建立協方差矩陣。給定風險溢價和協方差矩陣，可以像第7章描述的一樣實施最優程序。
我們可以在第8.2節的基礎上進一步描述分散化是如何在單指數框架下發揮作用的。等權重組合的α、β和殘差方差都是單個證券相應參數的簡單平均值，而且，這個結論並不侷限於等權重組合中，只須把簡單平均方法改為加權平均方法即可。具體地：
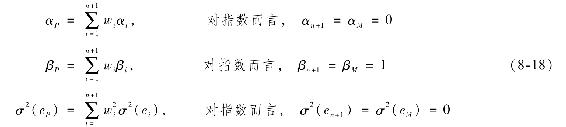
目標是通過組合權重的選擇來最大化組合的夏普比率。得到組合的夏普比率為：
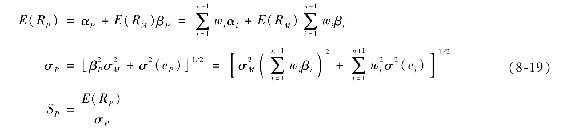
這時，和標準的馬科維茨程序一樣，我們可以採用Excel的最優化程序來最大化夏普比率。然而，這並不是必須的，因為最優組合能用指數模型得到。同時，最優組合的解讓人們瞭解證券分析組合構建中證券分析的用處。我們並不會給出每個代數步驟，而是給出我們的結論以及優化步驟的解釋。
在深入研究結果之前，首先解釋該模型表達的基本風險收益權衡。如果只對分散化感興趣，將只持有市場指數。證券分析給我們去尋找非零α值證券的機會並選擇不同的持有頭寸。這種不同頭寸的成本是對分散化的背離，換句話說，承擔了不必要的公司特有風險。這個模型顯示最優化風險投資組合是在尋找α和偏離有效分散化之間的權衡。
最優風險組合被證明是由兩個組合構成的：①積極組合，稱之為A，由n個分析過的證券組成（之所以稱為積極組合，是因為通過積極的證券分析後構建的組合）；②市場指數組合，這是第n+1種資產，目的是為了分散化，稱之為消極組合並標記為組合M。
首先假定積極組合的β值為1，在這種情況下，在積極組合中的最優權重相當於比率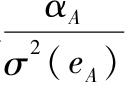
。這個比率平衡了積極組合的貢獻（α值）以及它對組合方差（殘差方差）的貢獻。類似地，指數組合的權重相當於
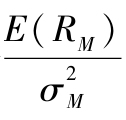因此，積極組合的初始頭寸（如果β等於1）為：
接著，考慮積極組合真實β值情況對該頭寸進行修正。對於任何水平的σ2A，積極組合的β值越高，積極組合與消極組合之間的相關性越大。這意味著積極組合帶來較少的分散化好處，在投資組合中的頭寸也應該更小。相應地，積極組合的頭寸應增加。積極組合頭寸的準確調整如下（注：經過代數計算，可以看出β等於指數模型和積極組合的相關係數與SD（指數）/SD（積極組合）的乘積。如果βA=1，相關係數大於式（8-20）隱含的相關係數，所以指數的分散化價值更小，這就要求如式（8-21）的調整。）：
注意，當βA=1時，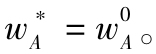
8.4.5 信息比率
式（8-20）和式（8-21）得到積極組合的最優頭寸，投資於積極組合的權重為w*A，投資於指數組合的權重為1-w*A。我們可以計算其期望收益、標準差和夏普比率。最優化組合的夏普比率會超過指數組合。它們之間的精確關係為：
式（8-22）表明積極組合（當持有最優權重時）對整個風險投資組合夏普比率的貢獻取決於它的α值和殘差標準差的比率。這個重要的比率稱為信息比率（information ratio）。該比率度量當積極組合權重過高或過低時，通過證券分析可以獲得的額外收益與公司特有風險的比值。因此式（8-22）表明要最大化夏普比率，必須最大化積極組合的信息比率。
如果投資於每個證券的相對比例為αi/σ2（ei），此時積極組合的信息比率將實現最大化。調整這個比率，使得所有積極組合中證券的頭寸相加等於w*A，即每個證券權重為：
運用這組權重，可以得到每個證券對積極組合信息比率的貢獻依賴於它們各自的信息比率，即
這個模型揭示了在有效利用證券分析中信息比率的核心角色作用。某一證券的加入對組合的正面貢獻是增加了非市場風險溢價，證券加入對組合的負面影響則是公司特有風險帶來組合方差的增加。
與α不同，市場部分（系統性）的風險溢價為βiE（RM），被單個證券不可分散的（市場）風險β2iσ2M拖累。兩者都受相同的β值的影響。這對任何證券來說都一樣，因為任何具有相同β值的證券對風險和收益兩者都有相同的平衡貢獻。換句話說，證券的β既不是罪臣也不是功臣。它是一個同時影響證券風險和風險溢價的因素。因此我們關注積極組合的整體β值，而不是關注單個證券的β值。
從式（8-23）可以看出，如果一個證券的α為負，則該證券在最優風險投資組合中應為空頭頭寸。如果禁止賣空，一個具有負α值的證券將從最優化程序中剔除掉，權重為零。隨著α非零的證券數量的增加，積極組合本身更好地分散化，在整個風險組合中積極組合的權重也會增加，相應地，消極指數組合權重將降低。
最後注意，當且僅當所有α值為零時，指數組合是一個有效的投資組合，這一點很直觀。除非證券分析找到一個α值非零的證券，否則包含這個證券的積極組合將使得這個組合投資吸引力降低。除了其系統風險之外，雖然會獲得市場風險溢價，但這個證券會通過公司特定風險增加組合的方差。然而，α值為零時，公司特有風險無法通過非市場風險溢價得到補償。因此，如果所有證券有零α值，那麼積極組合的最優權重為零，指數組合的權重為1。然而，當證券分析找到證券具有非市場風險溢價即α非零時，指數組合就不再有效了。
8.4.6 最優化過程總結
一旦證券分析完成，證券和市場指數參數的指數模型估計值確定，可以總結最優風險組合的構造程序如下。
（1）計算積極組合中每個證券的原始頭寸：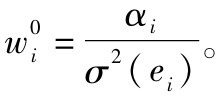
（2）調整這些原始權重，使組合權重和為1，即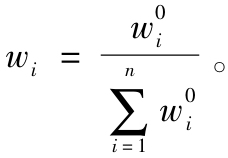
（3）計算積極組合的α值：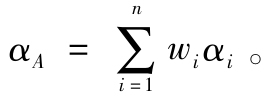
（4）計算積極組合的殘差：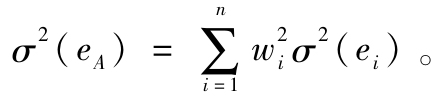
（5）計算積極組合的原始頭寸：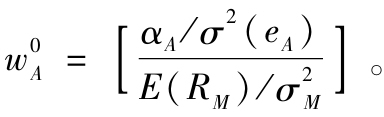
（6）計算積極組合的β值：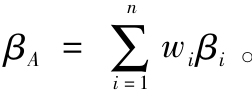
（7）調整積極組合的原始頭寸：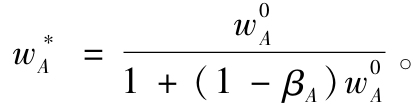
（8）此時最優風險組合的權重：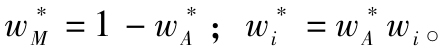
（9）計算最優風險組合的風險溢價。根據指數組合的風險溢價和積極組合的α值，得出最優風險組合的風險溢價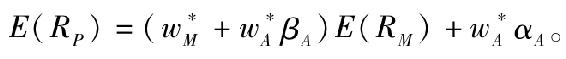
注意由於指數投資組合的β值為1，則風險組合的β值為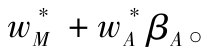
（10）運用指數組合的方差和積極組合的殘差計算最優風險組合的方差：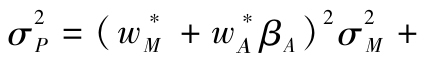
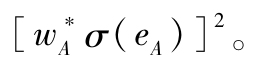
8.4.7 實例
可以通過用標準普爾500指數和在第8.3節討論風險參數的6只股票構建最優投資組合來演示指數模型的應用。
這個例子只包含了6只股票，從三個行業中選擇三對公司的目的是能夠產生相對高的殘差相關性。這對該指數模型是個嚴格的檢驗，因為當進行協方差矩陣估計時，該模型忽略殘差之間的相關性。因此，比較從指數模型得到的結果和具有所有特徵的馬科維茨模型得到結果之間的差異，有一定的研究意義。
風險溢價預測 表8-4中子表4包含每隻股票的α和風險溢價的估計值。在實際投資過程中，這些α值本來是投資公司最重要的產品。但統計量在這裡只扮演一個小角色，在這個領域，宏觀分析和證券分析最重要。在這個例子中，只是用示範數值來演示組合構建的過程和可能產生的結果。你可能會奇怪為什麼選擇這麼小的示範α估計值，理由是即使證券分析揭示定價明顯錯誤的股票，即大的α值，這些預測在相當大程度上也受到估計誤差的影響。在第27章會討論調整實際預測值的重要過程。
最優風險組合 表8-4中子表5展示了最優風險投資組合的計算。遵循了第8.4節所示的基本程序。在這個例子中允許賣空。注意到積極組合中（第52行）每個證券都有和α值相同的標記。在允許賣空的情況下，積極組合中的頭寸都相當大（如英國石油的頭寸是0.7349）。這是一個激進型組合，組合的α值2.22%比其組合中任何單個證券的α估計值要大得多。然而這種激進型組合也會導致一個較大的殘差平方和（0.0404，相應的殘差標準差為20%）。因此，積極組合的配置權重降低了，最終到一個適度值（0.1718，C57單元格）。再次強調了在最優化投資組合時分散化觀點是優先考慮的。
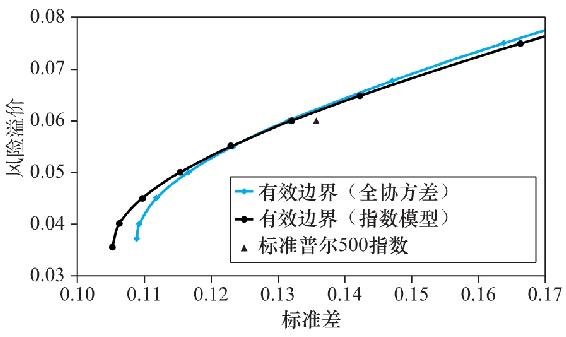
圖8-5 指數模型與全協方差模型的有效邊界
最優風險投資組合的風險溢價是6.48%，標準差是14.22%，夏普比率是0.46（見J58~J61單元格）。通過比較，指數組合的夏普比率是0.44（見B61單元格），這個比率與最優風險投資組合的夏普比率非常接近。這一小的改善是運用適度的預測值的結果。在第11章市場有效性和第12章業績評估中，用實例說明這些結果在共同基金公司中運用很普遍。當然，一些投資組合管理者能夠也確實構建了業績更好的投資組合。
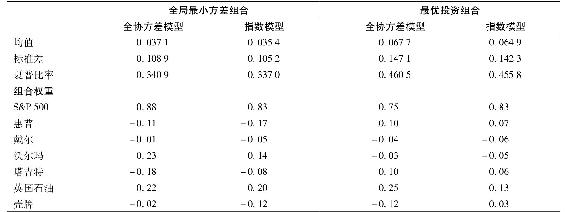
在這裡一個有趣的問題延伸是用指數模型得到的結論是否劣於用全協方差模型（馬科維茨模型）得到的結論？圖8-5展示了用樣本數據採取兩個模型得到的有效邊界，發現它們之間的差別非常小。表8-5比較了整體最小方差組合G與用這兩個模型得出的最優風險投資組合構成的組合的期望業績。這兩個組合明顯不同的地方僅在於只考慮方差的最小方差組合。沿有效邊界向上移動，要求的期望收益排除了協方差不同帶來的影響，投資組合在業績上變得越來越相似。
表8-5 指數模型和全協方差模型對比
[1] 用指數模型來建立最優風險組合由Jack Treynor和Fischer Black提出，“How to Use Security Analysis to Improve Portfolio Selection，”Journal of Business，January 1973。