BUSINESS BOOKS

8.3　估計單指數模型

以單因素模型理論為基礎，我們這裡提供一個綜合性例子，首先估計迴歸方程式（8-8），然後估計證券收益的協方差矩陣。

為了敘述方便，下面分析六大美國公司：標準普爾500指數中信息技術板塊的惠普（HP）和戴爾（Dell），零售板塊的塔吉特（Target）和沃爾瑪（Walmart），能源板塊的英國石油（BP）和皇家荷蘭殼牌公司。

我們觀察這6只股票、標準普爾500指數和短期國庫券在5年中的月收益率（即60個觀察值）。首先計算7個風險資產的超額收益，然後通過惠普的準備過程示範整個輸入數據表。本章後面講述如何建立最優風險組合。

8.3.1　惠普的證券特徵線

將指數模型迴歸方程式（8-8）運用於惠普公司即為：

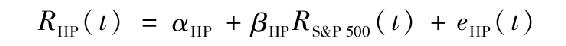
上式描述了惠普公司的超額收益率與用標準普爾500指數收益率來代表的經濟狀況變化之間的線性關係。迴歸估計結果描述的是一條截距為α_HP、斜率為β_HP的直線，稱做惠普的證券特徵線（security characteristic line，SCL）。

圖8-2顯示了惠普和標準普爾500指數60個月的超額收益率，圖中顯示惠普的收益與指數的收益一般是同向變動的，但其波動幅度更大。事實上，標準普爾500指數年化超額收益的標準差為13.58%，而惠普為38.17%。惠普公司收益的波動幅度比指數大，這意味著其敏感度大於市場平均值，即β大於1.0。

圖8-3的散點圖更清楚地描述了惠普和標準普爾500指數收益率之間的關係。如圖所示，迴歸線穿過散點，每個散點和迴歸線的垂直距離就是對應每個t值惠普收益率的殘差e_HP（t）。圖8-2和圖8-3中的收益率不是年化的，散點圖顯示，惠普的月收益率波動幅度超過±30%，而標準普爾500指數的收益只在-11%~8.5%波動。迴歸分析的結果如表8-3所示。

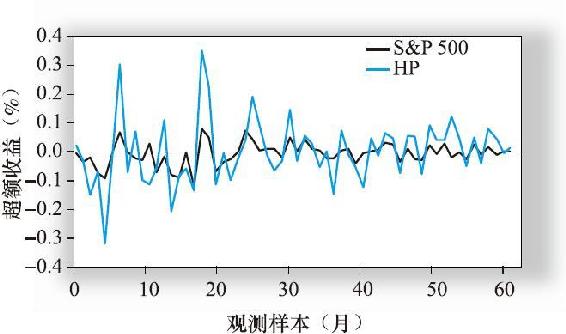
圖8-2　S&P 500和HP的超額收益

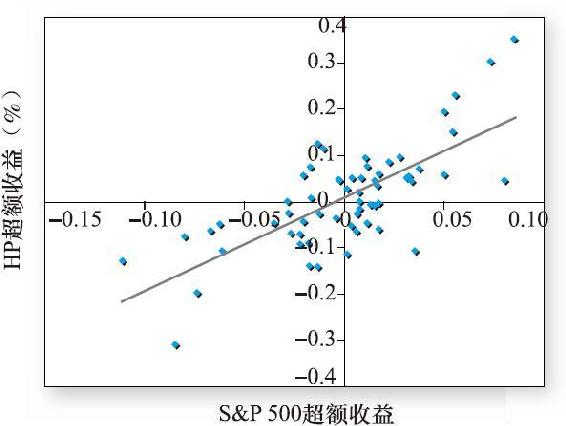
圖8-3　S&P 500和HP的超額收益

8.3.2　惠普證券特徵線的解釋力

先考慮表8-3，我們看到惠普和標準普爾500指數的相關性很高，達到0.7238，說明惠普經常隨著標準普爾500指數的波動而同向變動。R²為0.5239，說明標準普爾500指數的方差可以解釋惠普方差的52%左右。調整後的R²稍小於原來的R²，修正了因使用α和β估計值而非真實值所產生的偏差。（注：一般來說，調整後的R²通過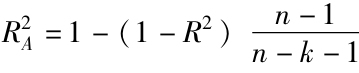推導，其中k為自變量的個數（此處為1），因為截距項導致額外一個自由度的缺失。）當有60個觀測樣本時，這一偏差很小，為殘差的平方，對這一點我們要做更深入的討論。這是一個衡量由公司特有因素引起的股票與指數平均關係變動的指標，且該指標基於樣本內數據。另一個更嚴格的檢驗是分析樣本各期限的收益率，並檢驗自變量（標準普爾500指數的收益）的預測能力。樣本外數據的迴歸預測值與實際值之間的關係通常會大大低於樣本內數據的相關性。

表8-3　Excel輸出，惠普證券特徵線的迴歸統計

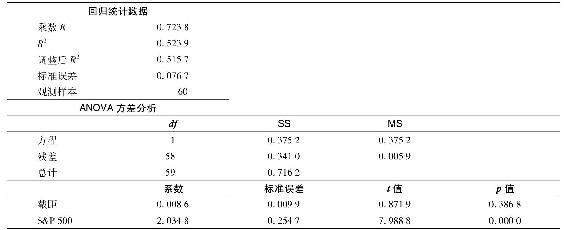
8.3.3　方差分析

表8-3的第二欄顯示了證券特徵線的方差分析結果。其中，迴歸平方和（SS）0.3752表示因變量（惠普收益率）方差中能夠被自變量（標準普爾500收益率）解釋的那一部分，該值等於β²_HPσ²_S&P500。MS這一列為殘差項（0.0059），表示惠普收益率中無法被自變量解釋的部分，即獨立於市場指數的那一部分，該值的平方根就是第一欄中報告的迴歸方程的標準誤差（SE）0.0767。如果將總的迴歸平方和（SS）0.7162除以59，就可以得出因變量方差的估計值，即每月0.012，相當於11%的月標準差，如果換算成年度值，（注：當月度數據轉化成年化度量時，平均收益和方差均被乘以12。如果方差是乘以12，則標準差要乘以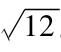。）就可得年標準差38.17%。注意到，R²等於被解釋的SS除以總SS。

注：

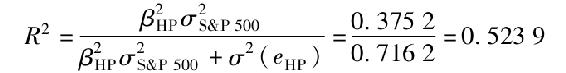
等價地，R²等於1減方差中不能被市場收益解釋的部分，即1減公司特定風險和總風險的比率，對於惠普公司而言，即

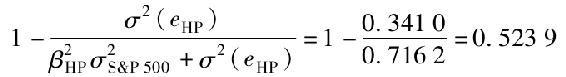
8.3.4　α估計

下面移到表8-3最下方一欄，截距（0.0086）是對惠普公司樣本期α的估計。儘管從經濟意義上來看這個值已經足夠大（年化後達10.32%），但在統計上是不顯著的。後面幾個統計量可以驗證這一點，第一個統計量是估計的標準誤差（0.0099），這一統計量衡量了估計的誤差，如果標準誤差大，那麼可能的估計誤差也相應大。

注：殘差的標準誤差和α估計值的標準誤差關係為：

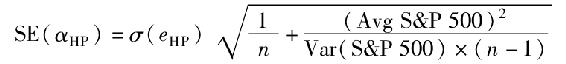
該欄中的t統計量是迴歸係數與其標準誤差之比，等於估計值大於0的標準誤差值，因此可以用來評估真實值等於0而非估計值的概率。^[1]直覺告訴我們，如果真實值為0，那麼估計值就不會偏離太遠，因此t值越大，真實值等於0的概率越低。

就α而言，我們感興趣的是對除去市場變化影響的惠普平均淨收益。假如惠普收益的非市場成分被定義為特定時期內實際收益減去市場變化引起的收益，這也被稱為公司特有收益，縮寫為R_fs，即

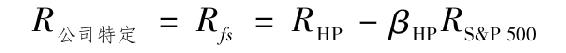
如果R_fs服從均值為0的正態分佈，其估計值與其標準誤差之比服從t分佈。從t分佈表中可以查到在估計值和估計誤差為正的條件下真實α值為0甚至更低的概率。這一概率被稱為顯著性水平，或如表8-3所示的概率p值。傳統的統計顯著性閥值為5%，一般要求t值高於2.0。迴歸結果顯示惠普α的t值為0.8719，意味著該估值並不顯著。也就是說，在某一置信水平下，不能拒絕真實α值等於0的原假設。p值（0.3868）表示如果真實α值為0，那麼得到0.0086的可能性為0.3868，即存在一定的可能性。綜上分析可以得到以下結論：R_fs的樣本平均值太低以至於不能拒絕真實值為0的原假設。

但是，即使α值在樣本內的經濟意義和統計意義上均顯著，我們仍不確定將α值作為未來的預測值。大量的經驗數據顯示5年內α值不會維持不變，即某一樣本期間的估計值與下一期間的估計值之間沒有實質的聯繫。換句話說，當市場處於穩定期時迴歸方程估計得到的α值所代表的證券平均收益率不能用來預測未來公司的業績，即證券分析很難的原因。過去不一定預測未來。本書的第11章講述市場有效性時將闡述這一問題。

8.3.5　β估計

表8-3的迴歸輸出結果表明惠普的β估計為2.0348，是標準普爾500指數的兩倍多。這麼高的敏感性對科技股票而言是正常的。估計的標準差為0.2547。

注：

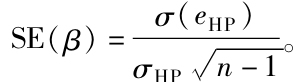
該β值和標準差產生一個很大的t值（7.9888），p值幾乎為0。我們可以大膽地拒絕惠普真實β值為0的原假設。更有趣的是，t統計量也可以檢驗惠普的β值比市場的平均β值大的原假設。這一t值會度量β的估計值偏離假設值1的誤差，且足夠大到產生統計顯著性。

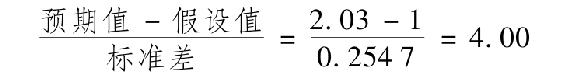
然而，有一點需要牢記，精確並不是我們所追求的目標。例如，如果要在95%的顯著水平下構建一個包括真實β值的置信區間，就應該以估計值為中心，加減約2倍標準差，這樣就形成了一個範圍較大的區間（1.43~2.53）。

8.3.6　公司特有風險

惠普殘差的月度標準差為7.67%，年化後為26.6%。這個數字很大，考慮到惠普本來就很高的系統性風險。系統性風險的標準差為β×σ（S&P 500）=2.03×13.58=27.57%，注意到惠普的公司特有風險和系統性風險一樣大，而這對於單隻股票來說非常常見。

8.3.7　相關性和協方差矩陣

圖8-4描繪了選自標準普爾500指數各板塊中一對規模相同的股票的超額收益率。我們看到IT行業是波動性最大的，其次是零售板塊，最後是能源板塊。

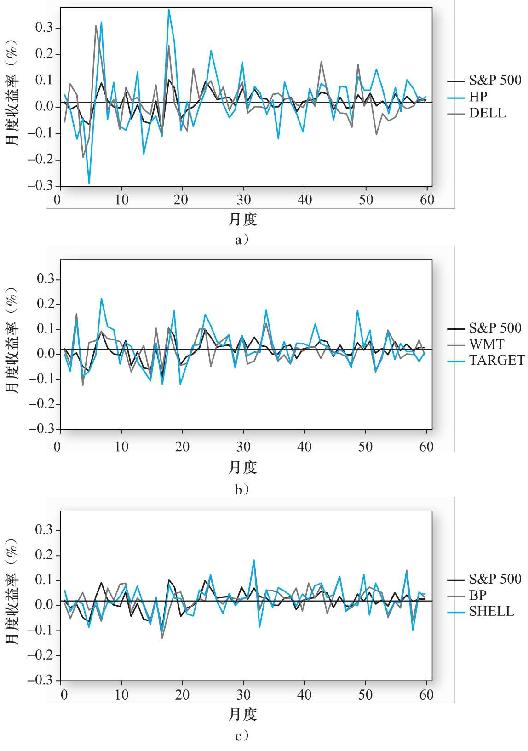
圖8-4　組合資產的超額收益

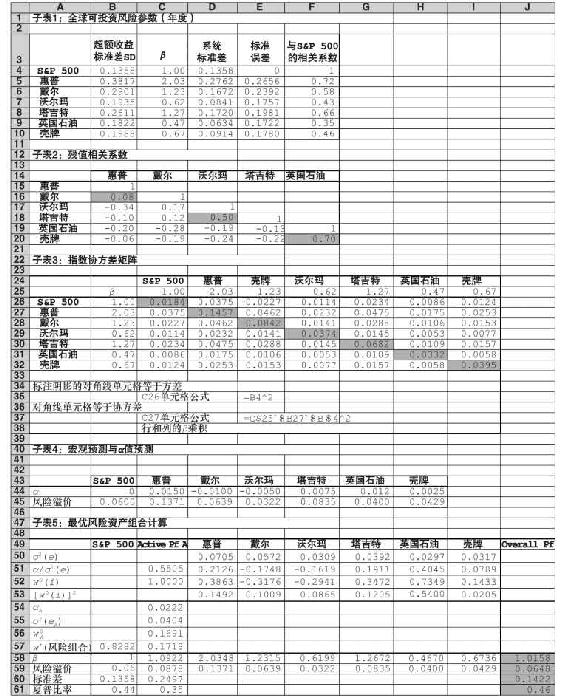
表8-4的子表1顯示了標準普爾500指數和六種證券風險參數的估計值，從殘差的高標準差這一項就可以看出分散化的重要性。這些證券均具有很高的公司特有風險。集中於這些證券的投資組合具有過分高的波動性和較低的夏普比率。

子表2顯示證券對標準普爾500指數的迴歸超額收益殘差的相關性矩陣。陰影部分顯示同一板塊股票的相關性。兩隻石油股票之間相關性高達0.7，這和指數模型所有殘差不相關的假設相矛盾。當然，這麼高的相關係數是因為所選的配對公司來自同一行業。跨行業的相關性一般會小很多。對行業指數殘差相關性的實證估計值更符合指數模型。實際上，這一樣本中部分股票殘差間的相關性為負。當然，相關性也受統計樣本誤差的影響。

子表3給出了單指數模型由式（8-10）所得的協方差，標準普爾500指數和單個股票的方差位於矩陣對角線上。單個股票的方差估計為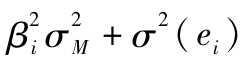，非對角線上為協方差，值為。

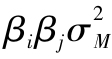表　8-4

[1] t統計量建立在收益正態分佈的假設上。總的來說，如果我們通過計算偏離假設值與標準誤差比值來估計一個正態分佈變量，得到的結果服從t分佈。觀測值很大時，t分佈近似正態分佈。