e1 Zvi Bodie 投資學 v10
8.2 單指數模型
使單因素模型具備可操作性的一個方法是將標準普爾500這類股票指數的收益率視為共同宏觀經濟因素的有效代理指標。這一方法推導出和單因素模型相似的等式，稱為單指數模型（single-index model），因為它使用市場指數來代表共同經濟因素。
8.2.1 單指數模型的迴歸方程
標準普爾500指數是一個股票組合，其價格和收益率易於觀察。我們有足夠的歷史數據來估計系統性風險。用M表示市場指數，其超額收益率為RM=rM-rf，標準差為σM。因為指數模型是線性的，我們可以用單變量線性迴歸來估計一個證券對市場指數的敏感性係數。我們讓證券超額收益率Ri=ri-rf對RM迴歸，數據採用歷史樣本Ri（t）和RM（t）配對，t表示觀察樣本的日期（比如特定月的超額收益）。[1]迴歸方程（regression equation）是：
這一方程的截距α是當市場指數超額收益為0時該證券的期望超額收益率，斜率βi是證券對指數的敏感性，即每當市場指數上漲或下跌1%時證券i收益的漲跌幅。ei均值為0，是t時刻公司層面收益率的衝擊，也稱為殘值（residual）。
8.2.2 期望收益與β的關係
因為E（ei）=0，將式（8-8）中的收益率取期望值，得到單指數模型的收益-β關係：
式（8-9）中的第二項說明證券的風險溢價來自指數風險溢價，市場風險溢價成了證券的敏感係數。我們之所以稱其為系統性風險溢價，是因為它源自整個市場的風險溢價，代表整個經濟系統的狀況。
風險溢價的剩餘部分是α，為非市場溢價。比如，如果你認為證券被低估，期望收益更高，則α更高。接著，我們會看到當證券價格處於均衡時，這類機會將在競爭中消失，α也會趨於0。但是現在先假設每個證券分析師對α的估計都不同。如果投資經理認為可以比其他分析師做得更好，那麼他們會自信能找到α非零的證券。
用指數模型分解單個證券風險溢價為市場和非市場兩部分，極大地簡化了投資公司宏觀經濟和證券分析工作。
8.2.3 單指數模型的風險和協方差
馬科維茨模型的一個問題是所需估計參數的龐大數量，但是指數模型大大減少了需要估計的參數。式（8-8）分別得到每個證券系統和公司層面的風險，以及任意一對證券間的協方差。方差和協方差都由證券的β和市場指數決定。
式（8-9）和式（8-10）意味著單指數模型估計所需的參數只包含單個證券的α、β和σ（e）、市場指數的風險溢價和方差。
概念檢查8-1
以下數據描繪了一個由三隻股票組成的金融市場，滿足單指數模型。
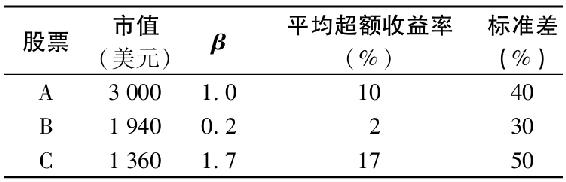
市場指數組合的標準差為25%，請問：
a.市場指數投資組合的平均超額收益率為多少？
b.股票A與股票B間的協方差是多少？
c.股票B與指數之間的協方差是多少？
d.將股票B的方差分解為市場和公司兩部分。
8.2.4 單因素模型的估計值
單因素模型的結果如表8-2所示。
表 8-2
該模型需要的變量包括：
·n個超額收益估計值，αi
·n個敏感係數估計值，βi
·n個公司特有方差的估計值，σ2（ei）
·1個市場溢價估計值，E（RM）
·1個宏觀經濟因素方差的估計值，σ2M
這（3n+2）個估計值便是單指數模型所需的數據。對於一個50只證券的組合，我們需要152個估計值而非馬科維茨模型要求的1325個估計值。對於紐約股票交易所的所有上市股票，約3000只，我們需要9002個估計值而不是450萬個。
顯而易見，指數模型為什麼進行了如此有用的簡化。在一個有成千上萬證券的市場上，馬科維茨模型需要天文數字的估計值，而指數模型只需要馬科維茨模型估計值的一小部分。
指數模型的另一個常被忽略但同樣重要的優勢是，指數模型的簡化對證券分析專業化非常重要。如果每對證券間的協方差需要直接計算，那麼分析師就無法實現專業化。比如，如果一組分析師專業分析電腦產業而另一組分析汽車製造業，那麼誰擁有足夠的專業背景來估計IBM和GM的協方差呢？然而，指數模型給出了計算協方差更容易的方法。證券間的協方差都來自一個共同因素的影響，即市場指數收益，而且可以應用式（8-8）迴歸估計得到。
但是從指數模型假設條件得出的簡化方法並不是沒有成本的。指數模型的成本來自其對資產不確定性結構上的限制。將風險簡單地二分為宏觀和微觀兩個部分，過於簡化了真實世界的不確定性並忽略了股票收益依賴性的重要來源。比如，二分法忽略了行業的事件，這些事件影響該行業中很多公司，但是不對宏觀經濟造成影響。
最後也很重要的一點是，設想單指數模型是完全準確的，唯獨兩隻股票——英國石油和殼牌的殘差項是相關的。指數模型會忽略這一相關關係（假設它為零），但馬科維茨算法會在組合方差最小化時自動考慮到該相關性（實際上包括每一對證券的相關性）。如果我們的證券總量較小，兩種模型得到的最優組合會顯著不同。馬科維茨得到的組合，英國石油和殼牌的權重會較小，得到的組合方差更低，因為兩隻股票相關性降低了分散化的價值。相反，當相關性為負時，指數模型會低估分散化潛在的價值。
因此，當殘差項相關的股票有較大的α值，而且佔整個投資組合較大的比例時，單指數模型推導出的最優組合可能會明顯次於馬科維茨模型。如果很多股票殘差項都有相關性，那麼額外包含了捕捉證券間風險因素的多指數模型可能更適用於組合的分析和構造。本章中我們會介紹相關殘差項的影響，多指數模型會在隨後的章節中介紹。
概念檢查8-2
假設用指數模型估計的股票A和B的超額收益如下：
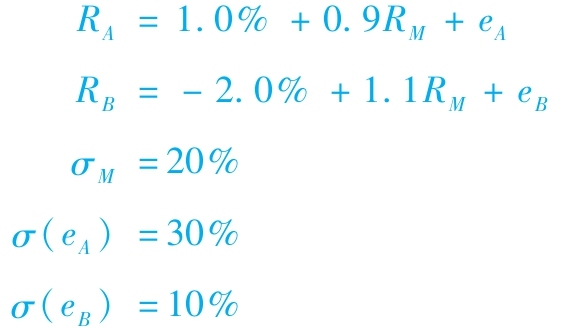
求每隻股票的標準差和它們之間的協方差。
8.2.5 指數模型和分散化
由夏普首次提出的指數模型[2]同樣為投資組合分散化提供了新的視角。假設我們選擇等權重n個證券構成的組合，每個證券的超額收益率為：
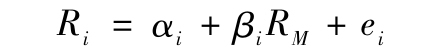
類似地，組合的超額收益為：
當組合中股票的數量增加時，非市場因素帶來的組合風險越來越小，這部分風險通過分散化逐漸被消除。然而，無論公司數量如何上升，市場風險仍然存在。
為了理解這一結果，注意這一等權重組合的超額收益為：
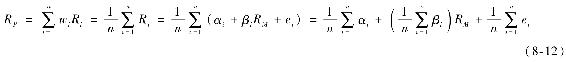
比較式（8-11）和式（8-12），我們看到組合對市場敏感度為：
為βi的平均值。組合的非市場收益為：
為α的平均值，加上零均值變量：
為公司部分的平均值。因此組合方差為：
組合方差的系統性風險部分為β2Pσ2M，取決於每個證券的敏感係數。這部分風險取決於組合β和σ2M，無論組合如何分散化，都保持不變。不論持有多少股票，它們對市場的風險敞口都會反映在組合的系統風險中。[3]
相對地，組合方差的非系統性風險為σ2（eP），來自公司層面的ei。因為這些ei是獨立的，期望值為0，所以可以說當更多的股票被加到投資組合中，公司層面風險會被消除，降低了非市場風險。這類風險因此稱為可分散的。為了更清晰地看這一問題，檢驗等權重組合的方差，其公司部分為：
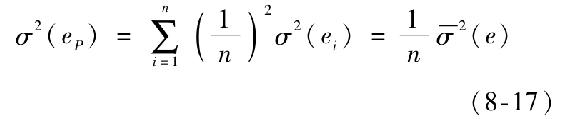
其中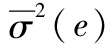
為公司的平均方差。因為該平均值獨立於n，當n變大時，σ2（eP）趨於0。
總之，隨著分散化程度增加，投資組合的總方差就會接近系統風險，定義為市場因素的方差乘以投資組合敏感性係數的平方β2P，圖8-1說明了這一現象。
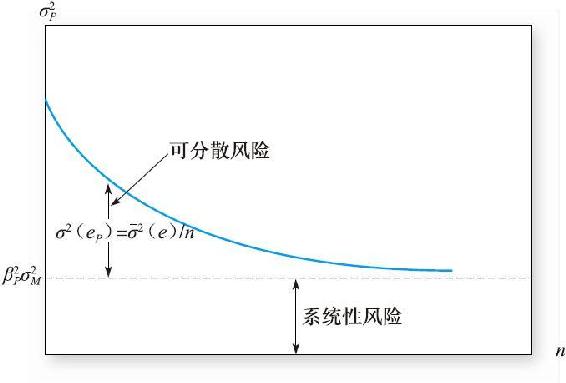
圖8-1 單因素經濟中β係數為βP等權重組合方差
圖8-1顯示當組合中包含越來越多的證券時，組合方差因為公司風險的分散化而下降。然而，分散化的效果是有限的，即使n很大，由於共同或市場因素引起的風險仍然存在，無法被分散化。
實證分析驗證了這一分析。圖7-2說明了組合分散化對投資組合標準差的影響，這些實證結果類似於圖8-1現實的理論圖形。
概念檢查8-3
回到概念檢查8-2，假如構建一個由題中的A、B股票組成的等權重投資組合，該組合的非系統標準差為多少？
[1] 實際操作中經常使用和式（8-8）相似的“修正”指數模型，使用總收益而非超額收益，尤其使用日數據時，因為短期國庫券的日收益率為0.01%，所以超額收益和總收益幾乎相等。
[2] William F.Sharpe，“A Simplified Model of Portfolio Analysis，”Management Science，January 1963.
[3] 當然，我們也可以構造零系統風險的組合。通過將-β和+β的資產混合。我們討論的意義是，大部分證券β值為正，意味著由很多這些證券構成完全分散化的組合，其系統性風險也會為正。