e1 Zvi Bodie 投資學 v10
8.1 單因素證券市場
8.1.1 馬科維茨模型的輸入數據
組合選擇的成功依賴於輸入數據的質量,即證券期望收益率和協方差矩陣的估計。長期來看,有效組合會超過輸入劣質數據得到的組合。
假設你的證券分析師要全面分析50只股票,這意味著輸入數據如下:

這一任務令人生畏,更別說50只證券構成的組合依然相對較小。n=100時,估計值增加到5150。若n=3000,約為紐約證券交易所股票的數量,我們需要估計450萬個以上的值。
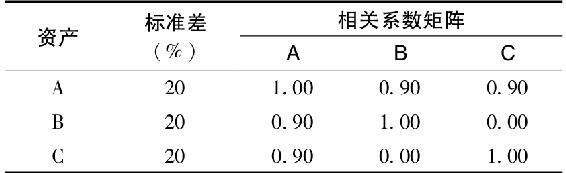
應用馬科維茨模型進行組合最優化的另一難題在於相關係數的估計誤差會導致無意義的結果,這是因為部分相關係數相互衝突,如表8-1所示[1]。
假設你構造的組合資產A、B、C的權重分別為-1、1、1,經過計算你會得到組合方差為-200%。而方差值必須是非負的,因此我們確信相關係數的估計值相互衝突。當然,真實的相關係數矩陣一定是相互一致的[2],但是我們並不知道相關係數真實值,而估計值總是不準確的。不幸的是,相關係數矩陣的相互衝突與否並非一眼就能看出,所以亟待尋找更簡單的模型。
引用一個簡化描述證券風險來源方式的模型讓我們可以使用更少且具有一致性的風險參數和風險溢價的估計值。因為受共同經濟因素影響,證券間協方差為正,這種簡化才得以面世。一些常見的經濟因素包括商業週期、利率、自然資源成本等。這些變量未預期的變化會導致整個股票市場收益率未預期的變化。通過將這種不確定性分解為系統性和公司層面的來源,我們大大簡化了協方差和相關係數的估計。
表 8-1
8.1.2 收益的正態分佈和系統性風險
我們總是可以將任何證券i的收益率分解為期望收益率和非期望部分之和:

ei的均值為0,標準差為σi,它描述了證券收益的不確定性。
當相關的證券收益率可以用正態分佈來很好地近似時,我們稱其服從聯合正態分佈。這一假設意味著,任何時間證券收益受一個或多個變量共同決定,如果一個以上的變量導致證券服從正態分佈,那麼這種收益被稱為服從多元正態分佈。我們先從簡單的單因素證券市場開始,擴展在後續章節會具體介紹。
假設引起所有公司的證券收益變化的因素是一些影響所有公司的宏觀經濟變量m,那麼可以將不確定性分解為經濟整體的不確定性(用m表示)和特定公司的不確定性(用ei表示)此時,我們將式(8-1)改寫為:

用宏觀經濟因素m度量未預期的宏觀突發事件。因此,它的均值為0,標準差為σm。相反,ei只衡量特定公司的突發事件。注意到m沒有下標是因為m影響所有公司。最重要的是,m和ei是不相關的,因為ei是公司層面的,和影響整個經濟的宏觀因素獨立。於是ri的方差來自兩個獨立的部分——系統的和公司的。因此:

經濟因素m產生證券間的相關性,因為所有證券都會對同一宏觀經濟新聞有所反應,但是公司層面的事件,假設中認為在公司之間是無相關性的。因為m與ei不相關,所以兩隻證券i和j的協方差為:
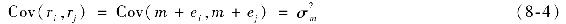
此外,一些證券對經濟衝擊比其他證券更為敏感。例如,汽車公司對經濟條件的反應比製藥公司要劇烈得多。所以可以加一個對宏觀經濟條件的敏感性係數。因此,如果定義希臘字母βi為公司i的敏感性係數,那麼改變式(8-2)得到單因素模型(single-factor model):

式(8-5)表明證券i的系統性風險由其βi係數決定。週期性公司對市場的敏感性更高,所以系統性風險就更大。證券i的系統性風險為β2iσ2m,總風險為:

任意兩證券間協方差為
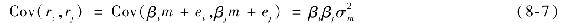
就系統性風險和市場暴露而言,這一公式表示公司間存在近似替代關係,β值相等的公司,其市場風險也相同。
到目前為止,我們只使用了證券收益聯合正態分佈的統計意義。僅證券收益的正態性就保證了組合收益也是正態的,且證券收益和共同宏觀因素之間存在線性關係。這大大簡化了組合分析。然而,統計分析並未識別共同宏觀因素,也未能確定該因素在長期投資中如何作用。儘管如此,共同因素、單個證券的方差以及證券間的協方差在長期中變化非常緩慢(通過實證可以證明)。現在我們需要尋找一個變量來代表共同因素,這一變量必須可以觀察,易於估計其波動性和單個證券對其的敏感度。
[1] 感謝西北大學凱洛格管理學院的Andrew Kaplin、Ravi Jagannathan提供本例。
[2] 數學上,一個相關矩陣不能產生負的投資組合方差的性質,被稱為正定性。