e1 Zvi Bodie 投資學 v10
附錄7B 投資組合統計量回顧
本附錄將基於由兩個資產組成投資組合的情形進行分析。表示為資產D和資產E(也可以認為是股票和債券),但是在附錄中所使用的風險和收益參數並不一定與7.2節中使用的一致。
7B.1 期望收益
我們使用的“期望值”和“平均值”概念之間沒有差異。在這個分析中將存在n種狀態,狀態i的收益率是r(i),概率是P(i),期望收益是:

如果你想使每種狀態的收益率增加Δ,那麼收益率的平均值將增加Δ。如果你在每一種狀態的收益率乘以w,新的均值將是原來的w倍。
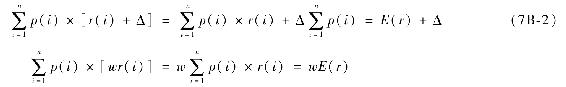
【例7B-1】期望收益率
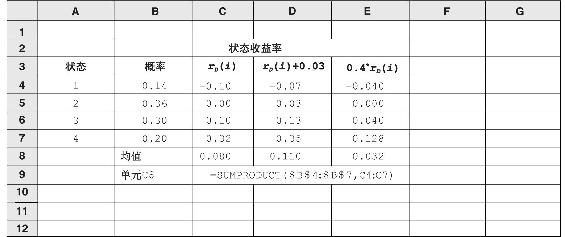
表7B-1的C列列出了各種債券情形下的收益率。在D列給每一個狀態收益率加上3%,E列將每一收益率乘以0.4。這個表說明了知何計算C、D和E列的期望收益率。明顯可以看出,D列增加了3%,E列都乘以了0.4。
表7B-1 債券的狀態分析
現在來構建一個投資組合,受一定的投資預算約束,w(D)為投資於債券的比例,w(E)為投資於股票的比例。每一種狀態的投資組合收益率和它的期望收益率已由式(7B-3)確定:
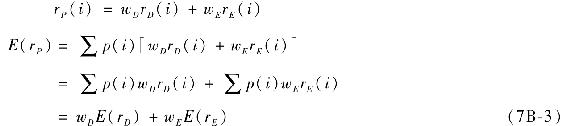
在每種狀態下的組合收益率是各構成部分收益率的加權平均值。權重是投資於這些資產的投資比例,即投資組合權重。投資組合的期望收益率是資產平均收益率的加權平均。
【例7B-2】投資組合收益率
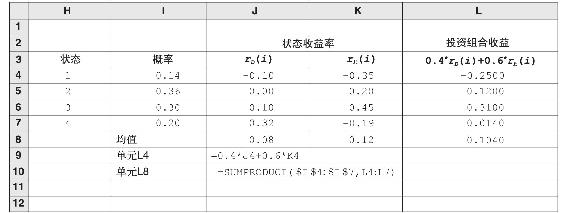
表7B-2列出了股票和債券的收益率。假定權益部分的權重為0.6,而債權的權重為0.4,每種狀態下投資組合的收益率如L列所示。使用SUMPRODUCT函數,即用每一種狀態的收益率乘以每一種狀態的概率,然後求和,即在單元格L8得出了投資組合的期望收益率0.104。
表7B-2 債券和股票的狀態分析
7B.2 方差和標準差
假設在某種狀態下資產的期望收益率的方差和標準差可以由下式給出[1]
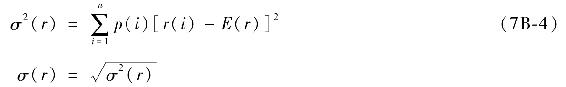
注意到方差項是平方項,而標準差是方差開方後的值,與原來的收益相比有同樣的單位,因此它作為衡量收益波動性的工具更簡便有效。
給每種狀態的收益率加上一個固定的值Δ,相應的收益率均值也增加了Δ。因此,每一種狀態相對於收益率均值的偏差並不受影響,方差和標準差都沒有受影響。相反,當你給每一種狀態乘以w,方差值則等於原來的方差乘以w2(即w乘以標準差)
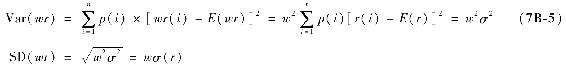
Excel中並沒有直接的方法可以算出情境分析的收益率方差和標準差。裡面的STDEV和VAR函數是用於時間序列分析的。我們需要計算殘差的加權平方值,而為了避免計算每個收益率偏離均值殘差的平方列,可以通過用兩項的差來計算方差,以簡化問題。
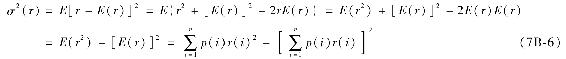
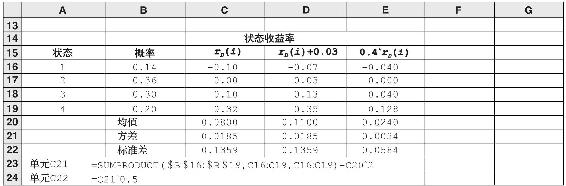
【例7B-3】在Excel中計算風險資產的方差
可以在式(7B-6)中用SUMPRODUCT函數計算第一個表達式E(r2)。例如,在表7B-3中,C21單元格中E(r2)是通過使用該函數,用各狀態的概率乘以資產收益率再乘以資產收益率。接著再減去[E(r)](注意到在單元格C21中減去C20的平方),即得到方差。
表7B-3 債券的狀態分析
投資組合收益率的方差並不像計算均值那樣簡單。投資組合的方差不是資產方差的加權平均值。任何情形下,投資組合收益率相對於其收益率均值的偏差可由式(7B-7)得出:
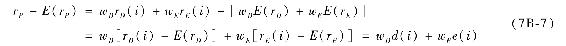
其中小寫d和e代表與預期值的偏差
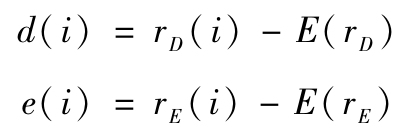
於是組合的方差可以表示為
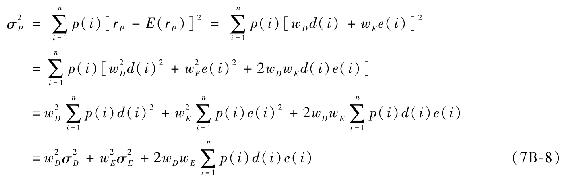
式(7B-8)表示一個投資組合的方差是各種資產方差的加權和(注意權重是各種投資組合權重的平方)以及下面將要提到的協方差部分。
注意到d(i)e(i)是兩種資產收益在每種狀態下相對於均值的偏差乘積,它的加權期望叫協方差,表示為Cov(rD,rE),兩個資產的協方差對投資組合的方差有很大影響。
7B.3 協方差
兩個變量的協方差等於
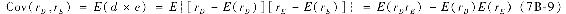
協方差是量化兩個變量之間的方差的一種很好的方法。可以通過一個例子簡單地知道它的運用。
假設對錶7B-4中給出的股票和債券有3種狀態。狀態1:債券價格下跌(負的偏差)而股票價格上漲(正的偏差)。狀態3:債券價格上升但是股票價格下降。當比率朝相反的方向變化時,如這個例子中,偏差的乘積為負。相反,如果比率朝相同的方向發展,乘積的符號則為正。乘積的大小表明某種狀態中相反或同向的程度。加權平均值反映了變量在幾種狀態中協變的平均趨勢。表格的最後一行,可以看到協方差是-80(H6格)。
表7B-4 股票和債券的三種狀態

假設在某狀態中股票的運動方向與債券的方向相同。具體來說,轉換第1種狀態和第3種狀態對股票收益的預測,使股票收益在第1種狀態中為-10%,在第3種狀態中為30%。這樣,在這兩個狀態中最終值仍然相等,但是符號為正,即協方差為正,為80,反映了兩個資產回報趨勢相繼變化。如果狀態收益的水平發生變化,協方差的強度也會變化,通過偏差的乘積大小反映出來。協方差大小的變化反映了偏差的變化和協方差的強度。
如果不存在同向運動,因為正的乘數剛好等於負的乘數,協方差為零。而且,其中一項資產是無風險的,它的協方差與任何風險資產的協方差都為零,因為它對於均值的偏差為零。
利用式(7B-9)最後一行的公式通過Excel來計算協方差會很簡單。第一部分E(rD×rE)可以通過Excel的SUMPRODUCT函數來計算。注意,給每個收益率加Δ不會改變協方差,因為對均值的偏差仍然沒有改變。但是如果對其中一個變量乘以一個固定的數,協方差將會隨著這個數的變化而變化。兩個變量都乘以一個數則等於協方差與這兩個數的乘積:
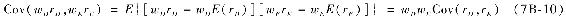
式(7B-10)的兩倍實際上加上式(7B-8)的最後一項,所以投資組合方差是每項資產方差的加權之和再加上協方差的兩倍乘以wDwE。
像方差一樣,協方差單位也是平方項,但是開方時,因為協方差可能為負數,如表7B-4所示,在這種情況下,可以把協方差表示為兩個變量的標準差乘以兩個變量的相關係數。
7B.4 相關係數
相關係數定義如下

相關係數一定落在[-1,1]區間中。這個結論可以通過下面的論證得到。怎樣的兩個變量會有最大程度的同向運動?邏輯上來說,變量自己與自己有最大程度的共同運動,下面來證明。
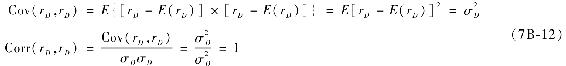
相似地,相關係數的最小值為-1。(讀者自己證明。)
相關係數一個最重要的特點是它不會因為變量增加和增倍而變化。假設債權的收益率為rD,將它乘以一個常數wD,然後加上一個固定值Δ。它與權益的相關係數沒有受到影響:
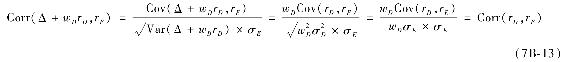
因為相關係數對收益率之間的關係給人感覺更加直觀,所以有時候把協方差表示為相關係數的形式:

【例7B-4】計算協方差和相關係數
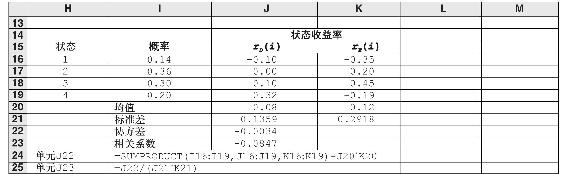
表7B-5列示了股票和債券的協方差和相關係數,所用的是其他例子中相同的情境分析方法。協方差的計算運用式(7B-9),通過SUMPRODUCT函數得出,如單元格J22所示,從中提出E(rD)×E(rE),相關係數的計算見單元格J23,等於協方差除以各項資產標準差的乘積。
表7B-5 股票和債券的情境分析
7B.5 投資組合方差
見式(7B-8)和式(7B-10),兩項資產組成的投資組合方差是各項資產的方差乘以投資組合權重的平方之和,再加上兩項資產收益率的相關係數和標準差以及投資組合權重的乘積的兩倍:
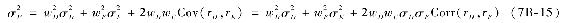
【例7B-5】計算投資組合方差
投資組合方差的計算見表7B-6。在此計算投資組合標準差有兩種方法:第1種方法是通過投資組合的收益率情境分析(見單元格E35);第2種方法是使用式(7B-15)的第1行(見單元格E36)。這兩種方法得到的結果相同,也可以試著運用上式第2行相關係數來計算投資組合方差。
表7B-6 股票和債券的情境分析
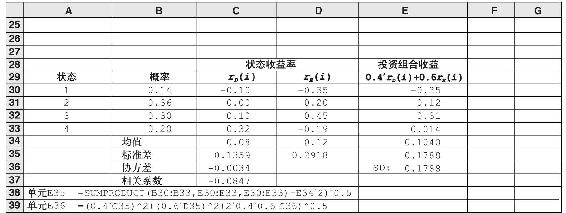
假設其中一項資產E被一種貨幣市場工具——一種無風險資產所替代,則E的方差為零,同時E和D的協方差也為零。在那種情況下,如式(7B-15)所示,投資組合標準偏差等於wDσD,換句話說,當把風險投資組合與無風險資產組合,投資組合的標準差就等於風險投資組合的標準差乘以其權重。上述結論在第6章中被廣泛運用。
[1] 資產收益率方差並不是唯一用來衡量波動性特徵值的統計量,絕對偏差常用來替代偏差的平方,所以有時絕對偏差值(MAD)也用來度量波動性。方差作為較好衡量波動性的特徵值有幾個原因,一是絕對值在數學上更加難處理;二是偏差平方給予較大偏差更大的權重;三是當資產收益服從正態分佈時,均值和方差兩個特徵值能夠完全描述收益分佈。