BUSINESS BOOKS

附錄7A　電子表格模型

有很多軟件包可以用來計算有效邊界，現在瞭解使用微軟Excel計算有效邊界的方法。Excel遠非最好的工具，它受到要處理的資產數量的限制，但它通過簡單的投資組合優化工具能說明許多複雜軟件包的機理，我們發現，運用Excel計算有效邊界相當簡單。

運用馬科維茨投資組合優化程序來實際說明國際的分散化投資。假設投資經理為美國客戶服務，他在2006年想要投資下一年度的風險資產組合，包括美國大公司股票和6個發達國家資本市場：日本、德國、英國、法國、加拿大和澳大利亞。首先描述一下輸入項：風險溢價預測和協方差矩陣。接著，介紹Excel的Solver功能。最後展示經理解決這一問題的方法。

7A.1　協方差矩陣

為獲得最近的風險參數，經理整理了2001~2005年最近60個月的月均收益率和同一時期的短期國庫券利率。

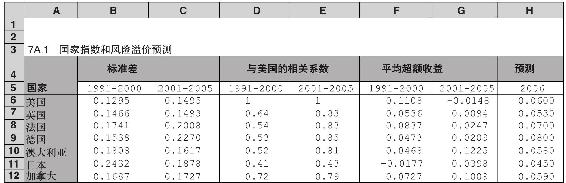
超額收益率的標準差顯示在表7A-1（C列）中，範圍14.95%（美國大公司股票）~22.7%（德國）。為觀察這些參數怎樣隨時間變化。1991~2000年的標準差顯示在B列中。此外，計算出上述兩個時期6個國外市場上的大公司股票與美國大公司股票的相關係數。這裡可以看出，與全球化的趨勢一致，近一時期來這種相關性越來越高。

表　7A-1

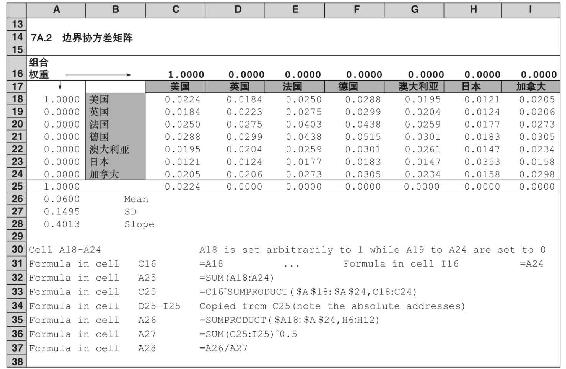
協方差矩陣顯示在表7A-2中，它是通過使用Excel中的“工具欄”菜單“Data Analysis”對話框中的COVARIANCE功能，來實現對7個國家的60種收益形成的排列。由於Excel軟件的自由度偏差缺陷，協方差矩陣不能準確統計預測，因此，矩陣裡的每個元素的都乘以60/59來消除偏差。

表　7A-2

7A.2　期望收益率

由超額收益率估計風險參數（協方差矩陣）是一項簡單的技術工作，而估計風險溢價（預期超額收益）則是一件麻煩的工作。在第5章討論過，估計期望收益使用歷史數據是不可靠的，例如，正如F列和G列顯示的，2001~2005年（單元格G6）美國大公司股票平均期望收益為負，更一般地，1991~2000年與2001~2005年兩個時期的平均收益差距很大。

在這一例子中，只將經理預測的未來收益描述在H列。在第8章中，將建立一個框架使預測過程更為清晰。

7A.3　邊界協方差矩陣和組合方差

表7A-2的協方差矩陣的旁邊是組合權重，如7.2節和表7-2解釋的那樣。其值在協方差矩陣的左邊，單元格A18~A24，由優化程序選出。現在，任意對美國輸入1.0，對其他國家輸入0。位於協方差矩陣上方的A16~I16單元格中的值必須等於左邊列中的權重，以使它們隨列權重的改變而改變，列權重的改變由Excel Solver來控制。單元格A25加上列權重並用來使優化程序控制組合權重和為1.0。

位於協方差矩陣下方的單元格C25~I25，用於計算任意設置的權重的組合方差。每一單元格累積同列上單元格的組合方差的貢獻、可用SUMPRODUCT的功能完成這一任務。例如，33行顯示了運用公式得到單元格C25中的值。

表7A-3的方框中是風險溢價的約束值。

表　7A-3

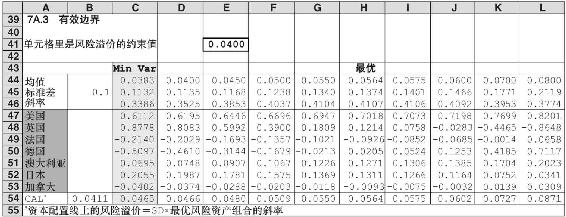
最後，協方差矩陣下方的左邊列A26~A28顯示了從邊界協方差矩陣計算得出的投資組合統計。A26是投資組合風險溢價，其公式在35行，為投資組合權重乘上表7A-1預測列（H6~H12）。下面的單元格A27為投資組合標準差。

方差由邊界協方差矩陣下方的單元格C25~I25相加得出。A27由C25~I25之和開平方得出。最後一個統計值在A28中，為投資組合的夏普比率，也就是資本配置線的斜率，資本配置線穿過由列權重所組成的投資組合（A28的值等於A26/A27）。最優的風險組合會使夏普比率最大。

7A.4　運用Excel Solver

Excel的Solver是一個界面友好、功能強大的優化問題計算工具。它有3個部分：目標函數、決策變量和約束條件。圖7A-1展示了Solver的3張圖片。現在的討論涉及圖7A-1a。

上面的對話框中要求你選擇目標函數的目標單元格，也就是你想要優化的變量。在圖7A-1a中，目標單元格是A27——投資組合的標準差。目標單元格下面，你可以選擇你的目標，最大化、最小化或設置你的目標函數等於特定的值。這裡選擇最小化投資組合的標準差。

接下來的對話框包含決策變量。Solver能改變這些單元以最優化目標單元格中的目標函數。在此，輸入單元格A18~A24，人們選擇投資組合的權重來使組合波動最小。

Solver底部的對話框包括一些約束條件。投資組合優化中必須滿足的一條是“可行性約束”，即投資組合權重之和為1。進入約束條件框中，設定A25（權重之和）為1.0。

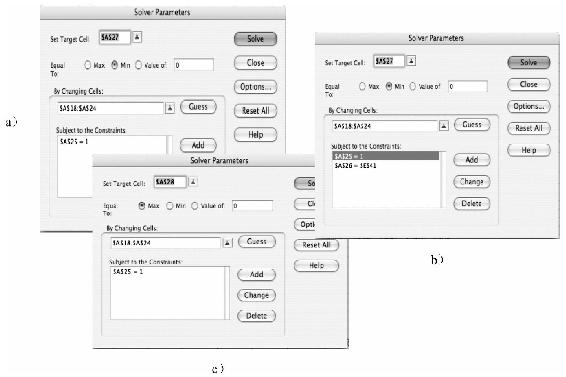
圖7A-1　Solver對話框

7A.5　找出最小方差組合

開始就確認全局最小方差組合（G）是有效的，這樣就提供了部分有效邊界的起點。一旦你如圖7A-1a所示輸入了目標單元格、決策變量單元格和可行性約束條件，你就可以點擊“solve”，Solver就能得出組合G。複製組合統計數字和權重到輸出表7A-3。表7A-3中的C列顯示出由輸入得出的最小標準差（SD）是11.32%。注意組合G的SD明顯低於最低的單一指數的SD，通過組合G的風險溢價（3.83%），開始用更大的風險溢價建立有效邊界。

7A.6　畫出風險組合的有效邊界

決定所需的風險溢價（指向有效邊界），進而使用這一風險溢價來畫出有效邊界圖形。在組合G的邊界上多取些點是有益的，因為邊界在這一區域曲率最大。從輸入中選取值最大的點的風險溢價為有效（這裡為8%德國）。通過以下方法你能找到所有有效邊界。

（1）在Solver輸入約束條件如下：A26（組合風險溢價）必須等於E41中的值，如圖7A-1b所示。E41用於改變所需的風險溢價和產生不同的邊界上不同的點。

（2）對於前沿上其餘點，可通過在E41中輸入不同的風險溢價來獲得，要求Solver再次運算得到。

（3）複製Solver每次在（2）中給你的解答到表7A-3，表中集合了有效邊界上的點。下一步，改變E41重複第2步。

7A.7　找出有效邊界上的最優風險組合

有了有效邊界之後，尋找邊界上夏普比率（如報酬-波動性比率）最高的組合。這個組合是有效邊界和資本配置線的切點。為了找到它，只需改變Solver中的兩項。第一更改A27~A28目標單元格的值、組合的夏普比率，並使這一單元格中值最大。接著，解除上次你使用Solver設定的風險溢價的約束條件。這時，Solver操作如圖7A-1c所示。

現在Solver得出了最優風險組合。複製最優風險組合的統計數據和它們的權重至表7A-3，為了得到一張清晰的圖，將優化組合列入表7A-3，以使表中所有組合的風險溢價從組合G的3.83%穩定增長至8%。

以C45~I45中數據（水平或X軸為標準差）和C44~I44中數據（垂直或Y軸為組合風險溢價）做出有效邊界。這一結果見圖7A-2。

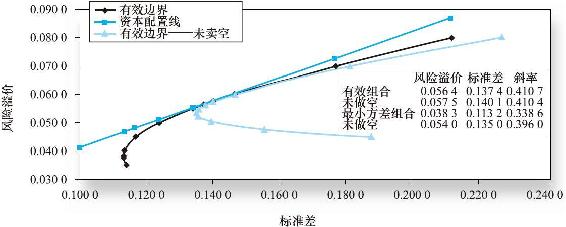
圖　7A-2

7A.8　最優的資本配置線

在圖7A-2有效邊界圖中添加已確認的最優風險組合的資本配置邊界線是很有指導意義的。這一資本配置線的斜率與最優風險組合的夏普比率相等。因此，在表7A-3的下面加了一行，單元格內輸入每一列的投資組合的標準差與單元格H46中的最優風險組合夏普比率的乘積，這就得到了沿著資本配置線有效邊界的每一個投資組合的風險溢價。接著又在圖中加入一組數據，以單元格中B45~I45中的標準差為X軸，而B54~I54中的元素作為Y軸。資本配置線如圖7A-2所示。

7A.9　最優風險組合和賣空約束

藉助於投資經理所使用的輸入表，最優風險投資組合要求持有法國和加拿大股票的空頭頭寸（如表7A-3的H列所示）。在許多情況下，投資組合管理者被禁止持有空頭頭寸。如果是這樣的話，需要修正投資計劃。

為了完成這個任務，重複這個練習，但是做了一下改變。加入了下面的約束條件：在投資組合所有列中的元素，A18~A24，必須大於或等於零。你可以在你的工作表中嘗試找出有賣空約束的有效邊界。限制邊界曲線如圖7A-2所示。