e1 Zvi Bodie 投資學 v10
概念檢查答案
7-1 a.第一項為wD×wD×σ2D,因為這是矩陣對角上的元素σ2D,列上的項wD和行上的項wD的乘積,用這種方法對協方差矩陣的每一項進行運算,就得到w2Dσ2D+wDwECov(rE,rD)+wEwDCov(rD,rE)+w2Eσ2E,和式(7-3)相同,因為Cov(rE,rD)=Cov(rD,rE)。
b.協方差矩陣如下
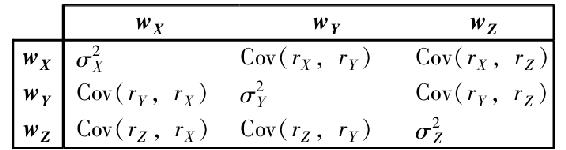
組合方差由這9項構成
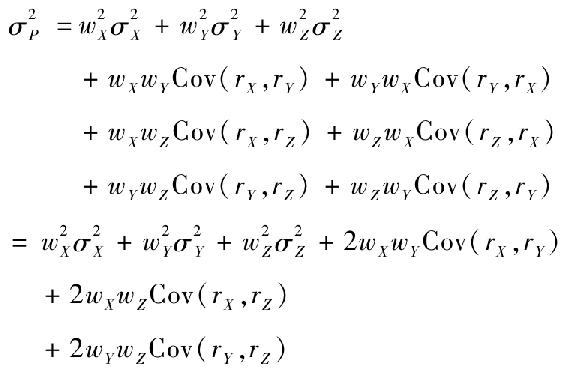
7-2 可行集的參數為E(rD)=8%,E(rE)=13%,σD=12%,σE=20%,從標準差和相關係數我們得到協方差矩陣:

總體最小方差組合為:
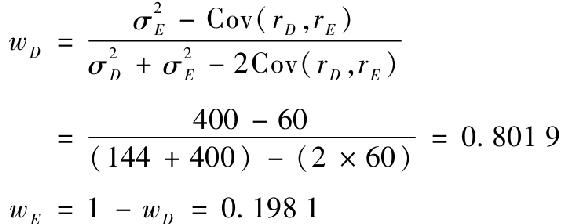
期望收益和標準差為
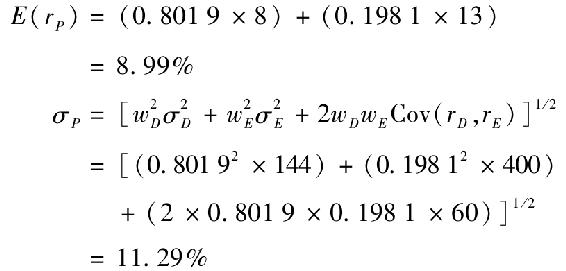
對於其他投資組合,wD將從0.1增至0.9,相應的wE從0.9降至0.1。將這些投資組合代入期望收益與標準差的計算中,注意在wD或wE為1時,就代表單獨持有該股票,所得期望收益與標準差即為該股票自身的值,於是得到下表。
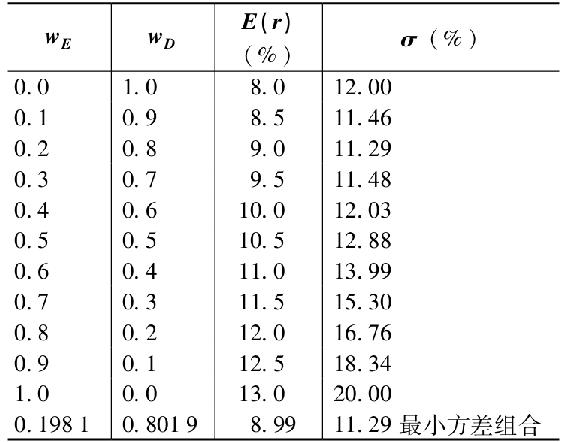
這樣就可以畫出圖形。
7-3 a.股票和風險債券基金的期望收益與方差計算與題2相似,這裡就不再表示。在給出A部分的圖解時要注意這些計算。另外,基金之間的協方差為
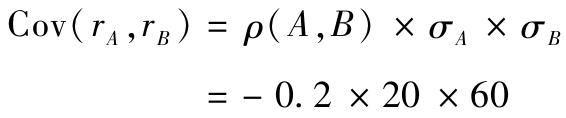
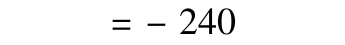
b.最優風險組合的權重為
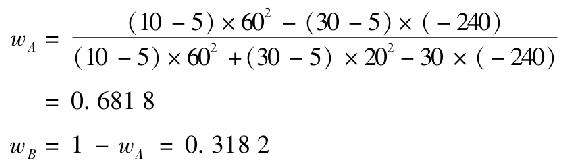

注意到,這裡最優風險組合的標準差小於股票A,同時投資組合P並不是整體最小方差投資組合,整體最小方差投資組合的權重為
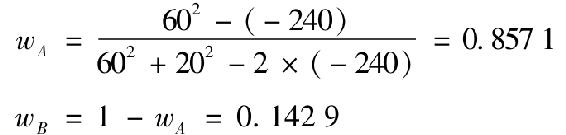
標準差為
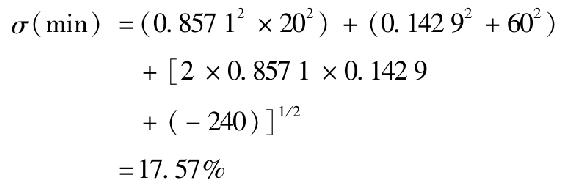
c.資本配置是無風險收益點與最優風險組合的連線,它代表短期國庫券與最優風險投資組合之間的所有有效組合,資本配置線的斜率為
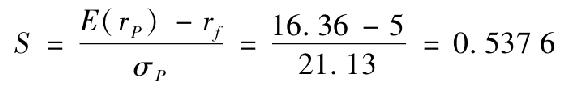
d.在給定風險厭惡係數A的條件下投資者願意投資到最優風險投資組合的比例為
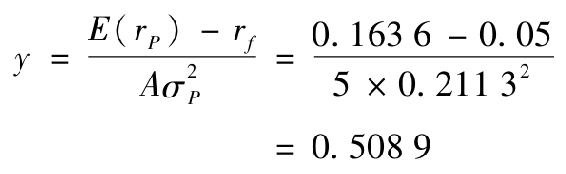
這意味著風險厭惡係數A=5的投資者願意在這個最優風險投資組合中投入50.89%的財產,由於AB兩種股票在投資組合中的比例分別為68.18%和31.82%,這個投資者分別投資於這兩種股票的比例為34.7%和16.19%。

7-4 有效邊界來源於投資經理對各種投資收益的預測和對風險即協方差矩陣的估計。預測本身並不能決定結果,選擇樂觀估計的經理人就意味著碰上好的形勢時會得到更大的收益,而在情況惡劣時的損失也會更大。能準確預測的管理人能得到好的回報,投資者看到資產管理人做出的曲線(預測)時,所要做的應該是瞭解其預測準確性的記錄,從而選擇預測準確的管理者。這樣進行投資組合的選擇,從長遠來看將會更加出色。
7-5 本題的有關參數為E(r)=15%,σ=60%,所有股票相關係數0.5。
a.投資組合的期望收益與投資組合規模無關,因為所有證券具有相同的期望收益。當n=25種股票時,投資組合的標準差為
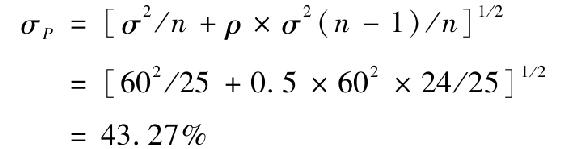
b.因為所有股票是同質的,因此有效投資組合是等權重的,要得到標準差為43%的投資組合,需要解出n:
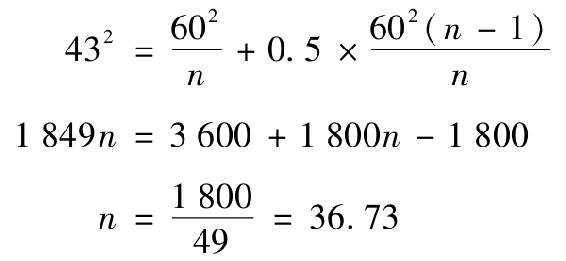
所以至少要37只股票的組合才能達到這一目標。
c.當n變得非常大時,等權重有效投資組合的方差將減少,剩下的方差來自股票間的協方差:
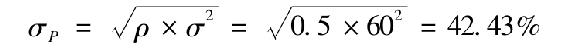
n=25時,得到非系統風險為0.84%,即25只股票的投資組合的非系統風險為0.84%;當n=37時,投資組合的標準差為43%,非系統統風險為0.57%。
d.如果無風險利率為10%,那麼不論投資組合規模為多大,風險溢價為15%-10%=5%,充分分散的投資組合的標準差為42.43%,資本配置的斜率為S=5/42.43=0.1178。