BUSINESS BOOKS

7.4　馬科維茨資產組合選擇模型

7.4.1　證券選擇

組合構造問題可以歸納為多個風險資產和一個無風險資產的情況。在兩風險資產的例子中，該問題有三步。首先，確認可行集的風險收益權衡；然後，通過計算使資本配置線斜率最大的各資產權重確認最優風險組合。最後，確認最合適的投資組合，由無風險資產和最優風險組合構成。

第一步是決定投資者面臨的風險收益機會，由風險資產的最小方差邊界（minimum-variance frontier）給出。這條邊界線是在給定組合期望收益下方差最低的組合點描成的曲線。給定期望收益、方差和協方差數據，所描成的曲線如圖7-10所示。

注意到所有單個資產都在該邊界的右方，至少當存在賣空機制時是這樣的^[1]。這說明由單個資產構成的風險組合不是最有效的。分散化投資可以提升期望收益降低風險。

所有最小方差邊界上最小方差組合上方的點提供最優的風險和收益，因此可以作為最優組合，這一部分稱為風險資產有效邊界（efficient frontier of risky assets）。對於最小方差點下方的組合，其正上方就存在具有相同標準差但期望收益更高的組合。因此最小方差組合下部的點是非有效的。

第二步是包含無風險資產的最優化。與之前一樣，我們尋找報酬-波動性比率最高的資本配置線，如圖7-11所示。

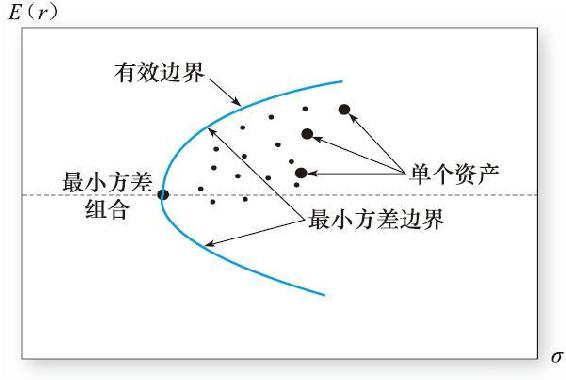
圖7-10　風險資產的最小方差邊界

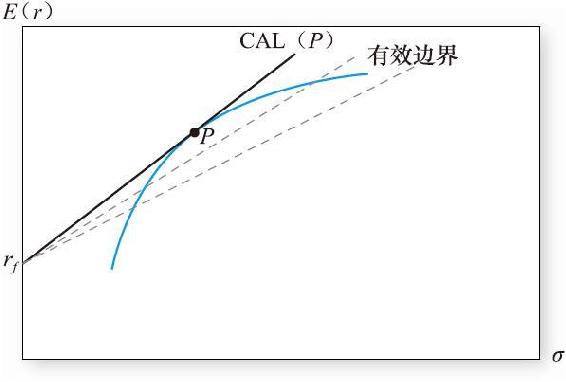
圖7-11　風險資產有效邊界和最優資本配置線

這條資本配置線優於其他資本配置線，與有效邊界相切，切點是最優風險組合P。

最後一步是投資者在最優風險資產P和短期國庫券之間選擇合適的比例構成最終組合，如圖7-8所示。

現在我們考慮構造組合每一步的細節。在第一步中，風險收益分析，投資經理需要每個證券的期望收益率和標準差、證券間協方差矩陣的估計值。投資經理現在有E（r_i）和n×n的協方差矩陣，矩陣對角線上是n個σ²_i，其餘是n²-n=n（n-1）個協方差值，且關於對角線對稱，所以有n（n-1）/2個數值需要估計。如果我們在50只證券中進行組合管理，則需要估計50個期望收益值，50個標準差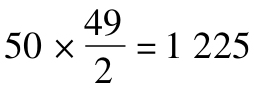，個協方差。這一任務很艱鉅。

一旦這些估計完成，任意風險組合（各資產權重為w_i）的期望收益和方差都可以通過協方矩陣或通過下列的式（7-2）、式（7-3）延伸公式計算得到：

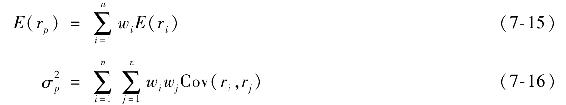
之前我們提到分散化的理念有很長的歷史了。“不要把雞蛋放在一個籃子裡”這句話早在現代金融理論出現之前就已存在。直到1952年，哈里·馬科維茨^[2]正式發表了包含分散化原理的資產組合選擇模型，為他贏得了1990年的諾貝爾經濟學獎。他的模型就是組合管理的第一步：確認有效的組合集，即風險資產有效邊界。

風險資產組合邊界背後的核心原理是，對於任意風險水平，我們只關注期望收益率最高的組合，或者說，邊界是給定期望收益風險最小的組合集。

確實，計算風險組合有效集的兩種方法是等價的。可以考慮表示這一過程的圖解，圖7-12顯示了最小方差邊界。

圖7-12所示是一個最小方差程序的算法，橫向為每一個期望收益水平，我們尋找方差最小的組合，用方形標記該點，或者豎向每一個方差水平，我們尋找期望收益率最高的組合，用圓形標記該點，都可以得到圖7-12所示的最小方差邊界的基本形狀，然後去掉下面虛線部分，因為它是非有效的。

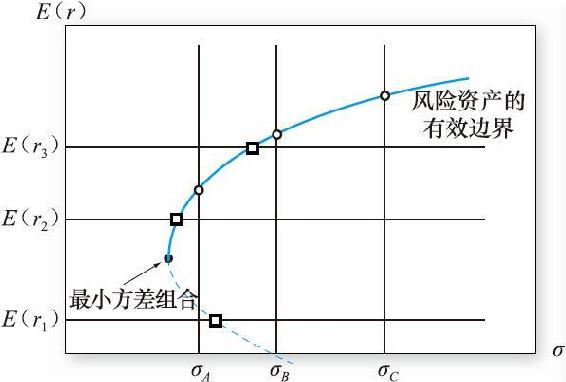
圖7-12　有效投資組合集

這一步完成之後，我們就得到了一系列有效組合，因為最優程序的解包含組合的內部權重w_i，期望收益率E（r_P）和標準差σ_P。這些數據隨後進入最優化程序中。

現在我們回過頭來看一下，到目前為止投資經理都做了什麼。證券分析師分析得到的估計值轉化為一列期望收益值和一個協方差矩陣，這些估計值被稱為數據輸入表，進入最優化程序中。

在進行第二步選擇最優風險資產之前，先考慮一個實際問題。一些客戶可能會受到約束，比如賣空限制。對於這類客戶，投資經理需要在尋找有效組合的程序中排除資產頭寸為負的情形。此時有效組合可能是單個證券，比如擁有最高期望收益率的證券也會是前沿邊界組合之一，因為無法通過賣空機制用多個證券構造期望收益率相同風險卻較低的組合。

約束條件不僅僅包含賣空的限制，客戶還會要求最低的股利收益率，此時就需要各證券的股利收益率數據，並加一個約束語句來保證所有證券的預期股利收益率高於設想的某個值。

投資經理可以調整有效邊界來滿足客戶不同的要求。當然，附加額外要求後的報酬-波動性比率只會次於無額外要求的情形。所以，客戶在附加投資的額外要求時應該考慮到這些非法律要求的限制所帶來的成本。

另一種約束條件是從政治或道德上排除在某一特定產業或特定國家的投資。這種投資稱為社會責任投資，必須承擔降低報酬-波動性比率的成本，這一成本可以看作對隱含理由做的貢獻了。

Excel應用：兩證券模型

下列表單可以用來計算一個包含兩風險資產的投資組合的收益率和風險。模型計算了在不同資產權重下投資組合的收益率和風險。相應的圖像會自動生成。這個模型允許你設定一個目標收益率然後計算無風險資產和最優風險投資的一個最優組合。表單中所使用的兩證券收益數據來源於表7-1。這張表單可以點擊如下網址查看www.mhhe.com/bkm。

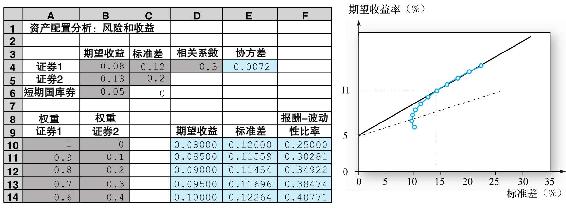
問題

1.假定你的目標期望回報率是11%。

a.該期望收益率下最低波動性組合是哪個？

b.這一組合的標準差是多少？

c.組合的構成是什麼樣的？

7.4.2　資本配置和分離特性

已經有了有效邊界，可以進行第二步引入無風險資產。圖7-13顯示了有效邊界和三條資本配置線。和之前一樣，把資本配置線向上旋轉直到與有效邊界相切，切點為最優風險組合P，且該資本配置線的報酬-波動性比率最大。這時投資經理的任務已經完成，組合P是投資經理為客戶找到的最優風險組合。

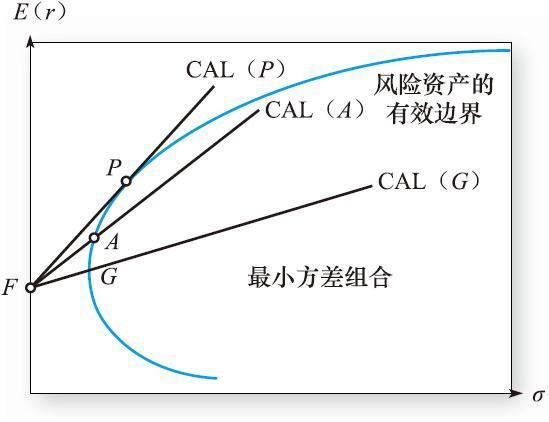
圖7-13　有效集組合和資本配置線

Excel應用：最優資產組合

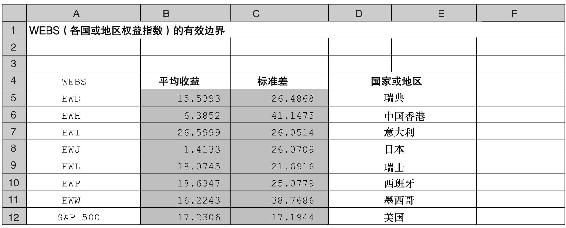
一個刻畫最優資產組合的表單模型可以登錄網站www.mhhe.com/bkm找到。它包含了一個和這一節內容類似的模板。這一模型可以用來計算在存在賣空和無賣空限制的情況下，給定目標收益水平下的最優證券組合。每一組輸入都將生成相應的有效邊界的圖像。我們網站上的例子利用了這個模型和幾個國家及地區的權益指數（稱為WEBS證券）。

最令人驚歎的結論是投資經理會向所有客戶提供風險組合P，無論客戶的風險厭惡程度如何^[3]。客戶不同的風險厭惡程度通過在資本配置線上選擇不同的點來實現。相比之下更加厭惡風險的客戶會在無風險資產和最優風險組合P之間更多投資於無風險資產。

另外一種尋找最優風險組合的方法是通過一開始就引入無風險利率。這種方法下，我們編寫計算表的程序來優化組合P的夏普比率。這裡值得一提的原因是可以免去畫有效邊界而直接找出CAL斜率最大的組合。計算表程序最大化夏普比率完全不受預期收益或方差限制（僅需要受制於組合的權重之和為1）。圖7-13顯示的問題解決方案是找出使CAL斜率（夏普比率）最大的組合，不需要考慮預期收益或標準差。預期收益和標準差可以通過計算組合權重和式（7-15）、式（7-16）很容易得到。

這個方法不能直接給出整個最小方差邊界，不過這個缺點可以通過尋找以下兩個組合來彌補：第一個我們熟悉的最小方差組合，即圖7-12中的G。組合G是通過不管預期收益如何的情況下最小化方差得到，參見圖7-13。組合G的預期收益較無風險利率大（即風險溢價為正）。

另外一個組合，我們在後文中將詳細介紹，最小方差邊界上的非有效組合，它與最優風險組合的協方差（相關係數）為零。我們稱該組合Z。一旦確定了組合P，我們通過數據表程序解出與P的協方差為零的最小化標準差組合。在後續章節中，我們再回過頭討論這個組合。

邊界組合的一個重要特性是，最小方差邊界上的任何兩個組合構造出的組合依然在邊界上，它處在邊界上的位置取決於組合的權重。因此組合P加組合G或Z可以得到整個效率邊界。

這一結果稱為分離特性（separation property），闡明組合決策問題可以分為兩個獨立的步驟^[4]。第一步是決定最優風險組合，這是完全技術性的工作。給定投資經理所有證券的數據，最優風險組合對所有客戶就是一樣的。然而，第二步整個投資組合在無風險短期國庫券和最優風險組合間的配置，取決於個人的偏好。在這裡客戶是決策者。

這裡關鍵的問題是：投資經理為所有客戶提供的最優風險組合都是組合P，換句話說，不同風險厭惡程度的投資者會滿足於由兩個共同基金構成的市場：一個基金在貨幣市場進行無風險投資，一個持有資本配置線與有效邊界切點上的最優風險組合P，這一結果使得職業投資管理更有效率且成本也更低。一家投資管理公司服務於更多的客戶而管理成本增加得很少。

但是在實際中，不同的投資經理對證券估計的數據是不一樣的，因此會得到不同的有效邊界，提供不同的“最優”組合。這種偏差來自證券分析的差異。值得一提的是通俗的GIGO（garbage in-garbage out）原則也可以應用於證券分析。如果證券分析質量很差，那麼被動的市場指數基金生成的資本配置線都會優於由低質量證券分析生成的資本配置線。

概念檢查7-4

假設有兩個投資經理分別為兩家投資管理公司工作。每家公司都僱用了一批證券分析師準備馬科維茨算法的輸入數據。所有工作完成後，經理A得到的有效邊界優於經理B，所謂優於是指A的最優風險投資組合位於B的左上方，這樣所有投資者都願意在經理A的資本配置線上進行投資。

a.造成這一現象的原因有哪些？

b.造成這一現象是因為A比B強嗎？

c.造成這一現象是因為A的計算機高級嗎？

d.如果你正為客戶提出建議，你會建議他們把資金轉移到位於左上方的投資組合嗎？

當一個數據輸入表採用證券最近的收益率來表示其真實的期望收益率時，將會使得到的有效邊界失去意義。

考慮一個年均標準差為50%的股票，如果用它10年平均來估計收益，估計的標準差將達到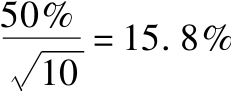，這一平均基本無法代表來年的期望收益^[5]。在第25章中，我們將給出一個例子，說明用歷史平均的數據可能會得到更高的夏普比率，從而使有效邊界更加樂觀。

正如我們看到的，不同客戶的最優風險組合也因其各自的約束條件而不同，比如股利收益約束、稅收因素和其他客戶偏好。即使如此，這部分分析說明一定數量的組合就可以滿足大量的投資者，這是共同基金行業的理論基礎。

最優化技術是組合構造問題中最容易的部分，基金經理間真正的競爭在於證券分析精確性上的角逐。這種分析和合理的解釋是組合構造的藝術。^[6]

7.4.3　分散化的威力

7.1節介紹了分散化的理念，但是由於系統風險的存在，分散化帶來的益處存在限制。有了前面的工具，我們可以重新考慮這一問題，同時深入窺探分散化的威力。

回憶式（7-16），組合的方差為

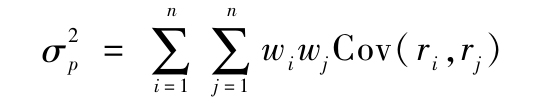
考慮最簡單的分散化策略，組合中每一資產都是等權重的，即w_i=1/n，這時式（7-16）可寫作（將i=j的情況從連加符號中移出，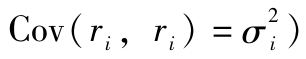

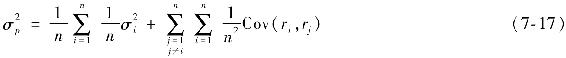
定義平均方差和平均協方差為

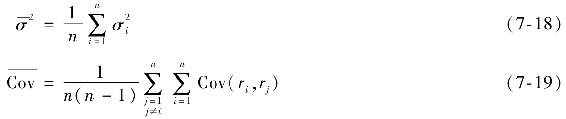
得出組合的方差為

現在檢驗分散化的效果。當證券之間的平均協方差為零時，即所有風險都是公司特有的，由式（7-20）可知組合方差在n變大時趨近於零。因此，當證券間收益不相關時，分散化降低組合風險的威力是無窮的。

然而，更重要的是，經濟層面的風險因素使股票收益存在正相關性。在這種情況下，當組合高度分散化後，組合方差為正。當n變大時，儘管公司特有的風險最終被消除了，但是等號右邊第二部分趨於Cov。因此分散化組合不可消除的風險取決於不同證券間收益率的協方差，這反過來就是經濟中系統性因素的顯現。

為了進一步考察系統風險和各證券間相關性的關係，簡單假設所有證券的標準差都為σ，證券間相關係數都為ρ，協方差為ρσ²，此時式（7-20）化為

證券間相關性的影響這時就很明顯了。當ρ=0時，我們得到保險原理，組合方差在n變大時趨於零。然而，當ρ>0時，組合方差為正。實際上，當ρ=1時，不論n如何，組合方差等於σ²，說明分散化沒有意義。在完全相關的情況下，所有風險都是系統的。更一般的情況，當n增大，系統性風險保持為ρσ²。

表7-4給出了證券數量擴大時ρ=0，ρ=0.4兩種情況下的組合標準差。其中令σ=50%。正如我們預想的，組合風險在ρ=0.4時更大。更令人吃驚的是，相關係數為正時，組合風險隨著證券數量上升而下降的速度相對慢很多，因為證券間的相關性限制了分散化的空間。

表7-4　相關性和無相關性的證券等權重構造組合的風險減少

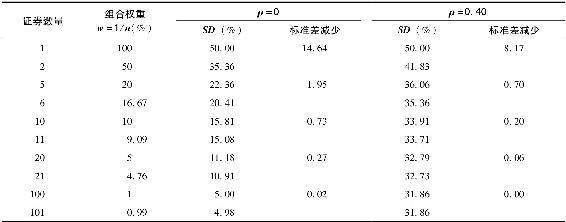
注意到對100個證券構成的組合，彼此不相關的情況下標準差為5%，和零標準差還有一段距離。當ρ=0.40，標準差很高，達到31.86%，非常接近於不可分散的系統性風險，為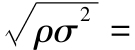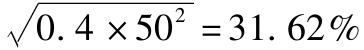，說明進一步分散化也沒什麼意義了。

上面計算中最重要的一點是：當我們持有分散化組合時，某一證券對於整個組合風險的貢獻取決於該證券和其他證券之間的協方差，並非該證券的方差。在第9章我們將會看到，這意味著風險溢價也取決於協方差而非收益的變動。

概念檢查7-5

假設風險證券包括很多股票，分佈均為E（r）=15%，σ=60%，相關係數統一為0.5。

a.25只股票等權重構成的組合的收益分佈是什麼？

b.要構造標準差不超過43%的組合，至少需要多少隻股票？

c.系統性風險是多少？

d.如果短期國庫券存在，收益率10%，資本配置線的斜率是多少？

7.4.4　資產配置和證券選擇

如同之前看到的，證券選擇和資產配置理論是一樣的。這兩步都需要構造有效邊界，並在有效邊界上選擇一個最優組合。既然這樣，是否還有必要區分資產配置和證券選擇呢？

有三個因素需要考慮。首先，出於儲蓄的天性和對利益的追求，社會對專業投資管理的需求呈迅速上升態勢。其次，金融市場和各類金融工具的繁榮使得專業投資管理的收益超過一般的業餘投資者。最後，投資分析有巨大的規模效益。最終的結果是有競爭力的投資公司隨著行業的發展擴大其規模，組織管理的效率也變得非常關鍵。

一個大型的投資公司很可能既投資於國內也投資於國際市場，其資產範圍更廣，每種資產都需要相應的專家。因此，每一資產類組合的管理不再集中，一步最優化所有證券也顯得不太可能，即使理論上可以實現。

實踐中總是獨立地最優化每類資產中的證券選擇，同時，高一級的管理會更新各資產類的最優情況並調整完善資產組合的投資權重。

7.4.5　最優組合和非正態收益

此前使用的組合最優化技術是建立在收益正態分佈的假設下的。然而，收益率可能的非正態性要求我們關注諸如在險價值、預期損失這類強調最壞情況損失的風險度量方法。

在第6章中我們提到在肥尾分佈下需要重新考慮資本配置，因為此時在險價值和預期損失值會很高。特別地，當預測到較高的在險價值和預期損失值時，我們應當適當減少風險組合的配置。當我們選擇最優風險組合時，分散化對在險價值和預期損失也是有影響的，只不過，這種情況下分散化的效果很難用正態分佈情形的方法來展現。

目前，估計在險價值和預期損失一個實用的方法是自舉法（拔靴法）（見5.9節）。我們從一個組合的資產收益歷史數據開始，計算組合收益看成從組合中資產歷史收益中抽取一次，可以計算無窮多的隨機組合的收益。這種方法計算的5萬個收益就足夠估計出在險價值和預期損失。此時我們可以比較最優風險組合和其他組合的在險價值與預期損失，如果某個組合的值比最優組合低的話，我們可能會傾向於這一組合。

[1] 當存在賣空機制時，最高期望收益的證券會在有效邊界上，因為該證券是獲得該期望收益的唯一方式。當賣空機制存在時，這種收益可以通過賣空低收益、買進高收益的證券來獲得這種最高收益，但是風險卻較低。

[2] Harry Markowitz，“Portfolio Selection，”Journal of Finance，March 1952.

[3] 附加額外約束條件的客戶，會得到另一個的最優組合，會次於無附加約束條件時得到的組合。

[4] 由James Tobin首次發現，“Liquidity Preference as Behavior toward Risk”，Review of Economic Statistics 25（Feb 1958 pp.65-86）

[5] 而且無法通過觀察更高頻的收益率來避免這一問題，在第5章中我們指出用樣本平均估計期望收益的精確性取決於樣本時期，而非樣本期內觀察頻率。

[6] 你可以在Wealthcare Capital Management白皮書中找到一些有意思的關於實際操作中有效分散化問題的討論，網址：http://www.finance ware.com/ruminations/WP Efficiency Deficiency.pdf.或www.mhhe.com/bkm的在線學習中心上可以找到該內容。