BUSINESS BOOKS

7.2　兩個風險資產的組合

在上一部分我們考查了多個證券等權重構造組合的分散化問題，現在是研究有效分散化的時候了，給定任何期望收益我們可以構造最低風險的風險資產組合。

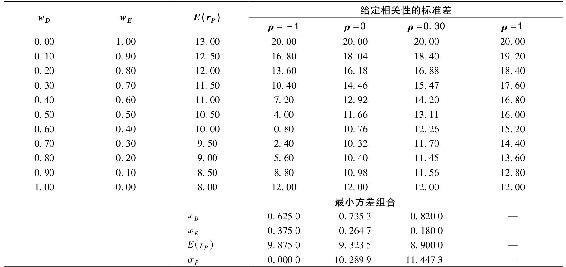
兩個風險資產構成的組合相對容易分析，其原理也可應用於多個資產組合。所以我們討論兩個資產（一個專門投資長期債券的基金D，一個專門投資股票的基金E）構成的資產配置。表7-1列出了這兩個基金的收益分佈。

投資於債券基金的比例定義為w_D，剩餘的1-w_D，定義為w_E，投資於股票基金。這個組合的收益率r_p是^[1]

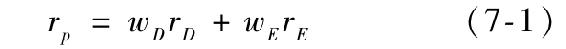
表7-1　兩個共同基金的描述性統計

r_D和r_E分別是債券基金和股票基金的收益率。

組合的期望收益是兩種證券期望收益的加權平均值，權重分別為其投資的比例

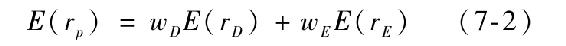
方差是

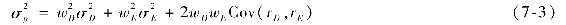
可以看出組合的方差並不像期望收益率，並不是兩個基金方差的加權平均。為了更好地理解組合方差，回想一個變量和它自己的協方差就是這個變量的方差

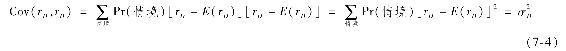
因此，組合方差的另一種表達方式為

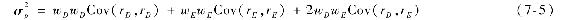
組合方差就是協方差的加權值，權重為協方差內一對資產在組合中權重的乘積。

表7-2展示如何用數據表計算組合的方差。表7-2a分別給出了兩隻基金收益的協方差矩陣。

表7-2　組合方差的計算

根據基金佔投資組合權重形成的協方差矩陣，不同權重比例標註在矩陣的外沿，即第一行和列。投資組合方差等於協方差矩陣中的每個元素與不同行列對應的權重交乘，再將各項相加，便得到了公式7.5給出的投資組合方差。

表7-2b展示了這一計算過程，即交乘協方差矩陣：每個協方差同時乘以行和列中的外圍權重。表7-2b最後一欄將所有協方差項進行加總，得到了與投資組合方差方程7.5一樣的計算結果。

計算過程中，由於協方差矩陣是關於對角線對稱的，即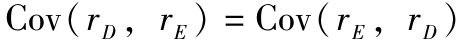，因此，每個協方差項出現兩次。

交乘協方差矩陣可應用於多項資產組合方差的計算。表格方式以簡單的實現這一計算過程。概念檢查1要求你嘗試計算三項資產組合的方差。通過這個練習來考察你對這個概念是否深刻理解。

式（7-3）揭示瞭如果協方差為負，那麼組合的方差會降低。但即使協方差為正，組合標準差仍然低於兩個證券標準差的加權平均，除非兩個證券是完全正相關的。

概念檢查7-1

a.驗證上面協方差計算方法和式（7-3）是一致的。

b.考慮三個基金X、Y和Z，權重為w_X、w_Y和w_Z。證明組合方差是

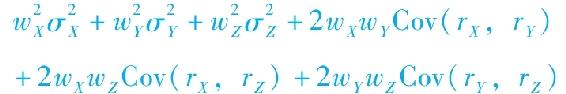
為了證明這一點，注意到協方差可由相關係數ρ_DE計算得到

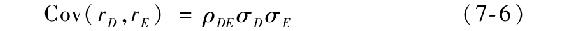
因此

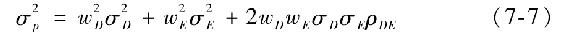
其他不變，當ρ_DE高時組合方差就高。當兩個資產完全正相關，即ρ_DE=1時，等號右邊可化簡為

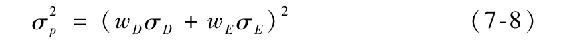
或

因此，組合標準差就是兩個收益完全正相關資產標準差的加權平均。在其他情況下，相關係數小於1，使得組合標準差小於兩個資產標準差的加權平均。

一個對衝資產和組合中的其他資產相關性為負。由式（7-7）可知這類資產在減少組合總風險上特別有效，而且，式（7-2）顯示期望收益並不受相關性影響。因此，其他條件不變，我們總是願意在組合中增加與組合相關性小甚至負相關的資產。

因為組合期望收益率是各個資產期望收益的加權值，而標準差小於各個資產標準差的加權平均，所以非完全正相關的資產組合在一起總是比單個資產提供更好的風險-收益機會。資產相關性越小，有效收益越大。

組合的標準差最低是多少呢？最低的相關係數是-1，代表完全負相關。在這種情況下，式（7-7）簡化為

組合標準差為

當ρ=-1時，通過解下式可以得到完全對衝的頭寸

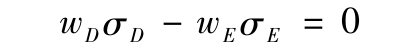
解為

這一權重使得組合標準差變為零。

【例7-1】組合的風險和收益

讓我們把這一分析方法應用於表7-1中的債券和股票基金中。用這些數據，組合期望收益、方差和標準差的方程為：

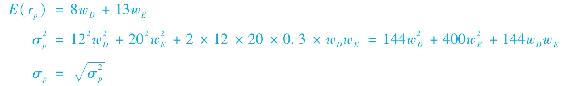
我們可以變化組合的成分比例來看整個組合期望收益和方差的變化。假設改變債券的比例，組合期望收益如表7-3和圖7-3所示，當債券比例從0變到1時，組合期望收益從13%降到8%。

表7-3　不同相關係數下的期望收益和標準差

當w_D>0，w_E>1時情況如何呢？這種情況的組合策略是賣空股票基金並將資金投於債券基金。這將會繼續降低組合的期望收益率。例如，當w_D=2，w_E=-1時，預期組合收益降到2×8+（-1）×13=3%，此時的債券基金規模是組合淨值的兩倍。

相反的情況是w_D<0，w_E>1時，這種策略需要賣空債券基金來籌資購買股權基金。

當然，不同的投資比例對組合的標準差也有影響。表7-3展示了假設不同的相關係數根據式（7-7）計算的不同組合權重時的組合標準差。圖7-4顯示了組合標準差和兩個基金權重的關係。先看ρ_DE=0.3，圖像顯示當股票投資比例從0到1，組合的標準差先降後升。只要在相關性不是很高的情況下都是如此。當兩個基金的正相關性非常高時，組合的標準差隨著組合由低風險向高風險資產轉移而上升。

（注：只要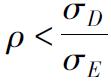，當我們從全部投資與債券開始逐漸增加股權投資時，波動率將先下降。）

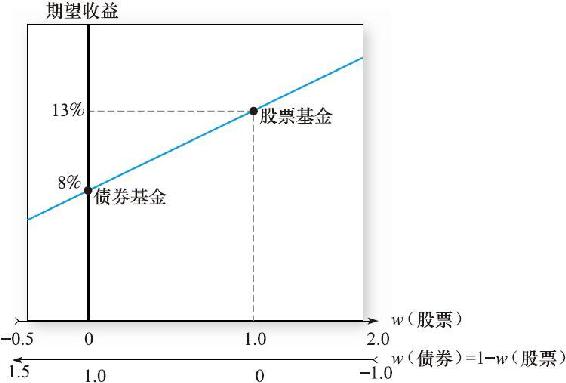
圖7-3　組合期望收益關於投資比例的函數

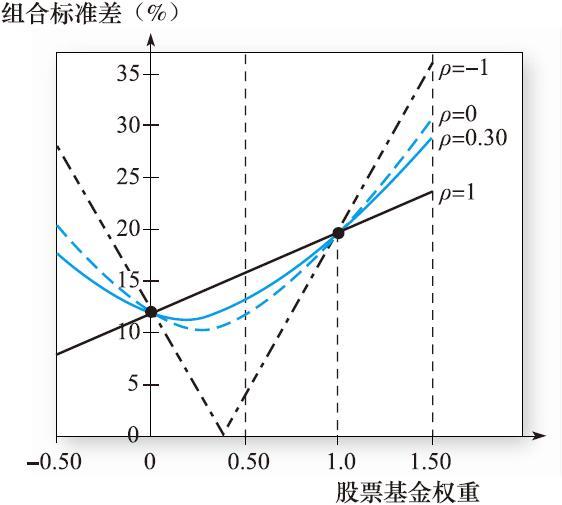
圖7-4　組合標準差關於投資比例的函數

那麼組合標準差最低是多少呢？對於表7-1中的數據來說，這一最小化問題的解是

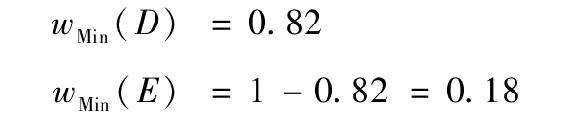
（注：這一解法利用了微積分中求極小值的方法。運用式（7-3）寫出資產組合方差的表達式，用1-w_D代替w_E，並對w_D求微分，利用導數為零來求解w_D可以得到

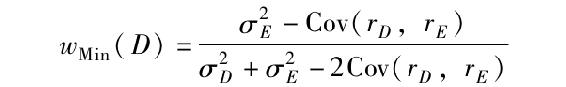
同樣，利用Excel軟件中的表單程序Solver來求解方差極小化問題，你可以獲得一個精確的解。附錄7A給出了資產組合和優化的一個實例。）

組合標準差是

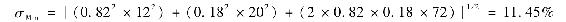
即表7-3中ρ=0.30一列的最後一行σ_p值。

圖7-4中ρ=0.3的線經過兩個未經分散化的點，w_D=1和w_E=1。注意到最小方差組合（minimum-variance portfolio）的標準差小於這兩個點的標準差。這顯示了分散化的效果。

圖7-4中另外3條曲線表示：保持每個資產方差不變時，組合的風險因兩個資產收益相關係數變化而變化，這3條曲線對應著表7-3中的3列內容。

連接了W_D=1全債券組合和W_E=1全股票組合的黑色實線給出了ρ=1完全正相關資產構成組合的標準差，這種情況下分散化是沒有意義的，組合標準差不過是兩個標準差的加權平均。

淺色虛線給出了彼此不相關的資產（ρ=0）構成的組合風險情況。資產相關性越小，分散化則更加有效，組合風險也越低（至少當兩資產都是多頭頭寸時）。ρ=0的最小組合標準差是10.29%，低於任意一個資產的標準差。

最後，折線說明了當兩資產完全負相關（ρ=-1）時可以完全對衝的情況。這時最小方差組合的解由式（7-12）給出

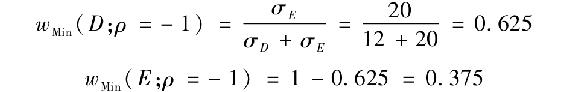
組合方差為0。

我們可以組合圖7-3和圖7-4來展示組合風險與期望收益的關係。對於任意一對投資比例w_D，w_E，我們從圖7-3中得到期望收益，從圖7-4中得到標準差。表7-3中每對期望收益率和標準差的結果如圖7-5所示。

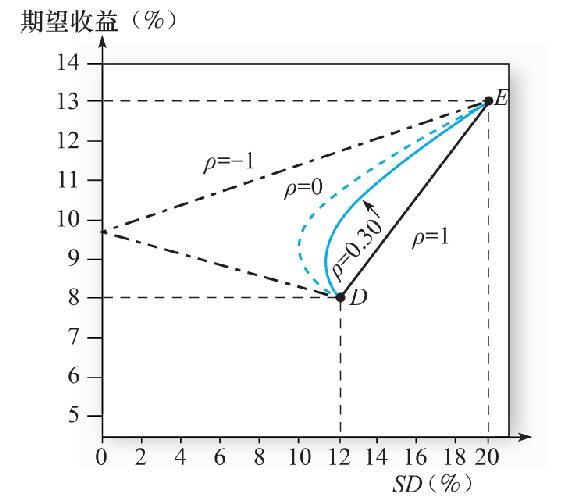
圖7-5　組合期望收益關於標準差的函數

圖7-5中的淺色實線說明ρ=0.3的投資組合可行集（portfolio opportunity set）。我們之所以稱其為投資組合可行集，是因為它表示了兩個資產構造的所有期望收益和標準差的組合。其他的曲線表示了不同相關係數下的情況。黑色實線說明完全正相關的資產分散化並沒有意義。曲線說明分散化是有意義的。當ρ=-1時，投資組合可行集是線性的，但是它提供了完全對衝的機會最大化了分散化的好處。

總之，儘管任何組合的期望收益是幾個資產期望收益的加權平均，但標準差並不是這樣。當資產相關係數小於1時分散化可以帶來好處，且相關性越低，好處越大。在完全負相關的情況下，存在完美的對衝機會來構造零方差組合。

概念檢查7-2

計算並畫出當債券和股票基金相關性為0.25時的投資組合可行集。

假設一個投資者想要從可行集中選擇最優組合，他需要考慮風險厭惡。圖7-5右上方的組合期望收益較高但是風險敞口也高。最優點取決於個人偏好。風險厭惡程度更高的投資者偏好於左下角期望收益低但是風險也相對較低的組合。

（注：給定風險厭惡水平，個人可以決定提供最高效用值的組合。在第6章我們可以用關於期望收益和標準差的效用公式來描述效用值。組合的期望收益和標準差由兩個資產在組合中的權重決定。根據式（7-2）和式（7-3），得

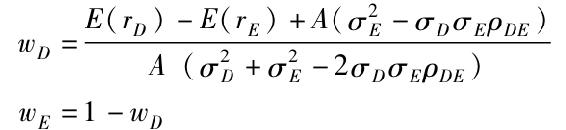
同樣，可以利用Excel的Solver程序，以式（7-2）、式（7-3）以及W_D+W_E=1（即所有權重之和為1）為約束條件來最大化效用函數。）

[1] 見附錄7B。