e1 Zvi Bodie 投資學 v10
7.1 分散化與組合風險
假設你的組合只有一隻股票——戴爾電腦公司的股票,那麼你的風險來自哪裡呢?你可能會想到兩種不確定性。第一種來自經濟狀況,比如商業週期、通貨膨脹、利率、匯率等,這些因素都無法準確地預測,並且都影響著戴爾股票的收益率。除了這些宏觀的因素,第二種不確定性來自公司的影響,比如研發有重大突破或者重大人員變動,這些因素會影響戴爾,但基本不會影響經濟體中的其他企業。
現在考慮一個簡單的分散化策略,你在組合中加入了更多的證券。例如,將你資金的一半投入埃克森-美孚,一半投入戴爾。這時組合的風險會怎樣呢?因為戴爾公司層面的因素對兩個公司的影響不同,分散化便會降低組合風險。比如,當石油價格下降時,衝擊了埃克森-美孚的價格,但是電腦價格可能在上漲,有利於戴爾公司。這兩股力量相互彌補並穩定了組合的收益。
分散化何必止於兩家公司呢?如果加入更多證券,我們便會進一步分散掉公司因素,組合的波動也會繼續下降。直到最終增加證券數量也無法再降低風險,因為實際上所有股票都受商業週期的影響,不管我們持有多少種證券都無法避免商業週期的風險敞口。
當所有風險都是公司層面上的(如同圖7-1a),分散化可以將風險降至低水平。這是因為風險來源是相互獨立的,那麼組合對任何一種風險的敞口降至可以忽視的水平。這有時被稱為保險原則(insurance principle),因為保險公司對很多獨立的風險源做保險業務從而分散降低風險。(其中的每個保單實際上構成了公司的整個組合。)
然而,當普遍性的風險影響所有公司時,即使分散化也無法消除風險。在圖7-1b中,組合的標準差隨著證券數量的增多而下降,但無法下降到零。這個無法消除的風險叫作市場風險(market risk)、系統性風險(systematic risk)或不可分散風險(nondiversifiable risk)。相反,可以消除的風險叫作獨特風險(unique risk)、公司特有風險(firm-specific risk)或可分散風險(diversifiable risk)。
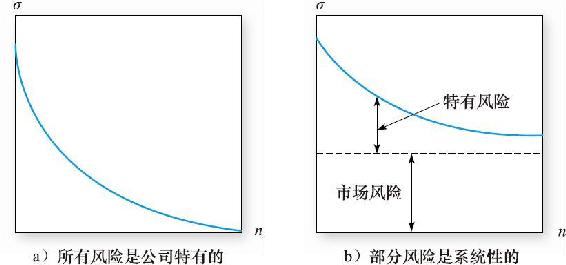
圖7-1 組合風險關於股票數量的函數
這一分析來自實證研究。應用紐約證券交易所股票數據[1],圖7-2顯示了組合分散化的影響。該圖顯示隨機抽取股票等權重構成組合的平均標準差關於股票數量的函數。總體來說,組合風險確實隨著分散化而下降,但是分散化降低風險的能力受到系統性風險的限制。
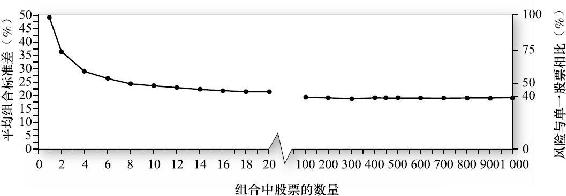
圖7-2 組合分散化
注:組合收益平均標準差隨著證券數量增多由49.2%最終降到19.2%。
資料來源:From Meir Statman“How Many Stocks Make a Diversified Portfolio?”Journal of Financial and Quantitative Analysis 22(September 1987).Reprinted by permission.
[1] Meir Statman,“How Many Stocks Make a Diversified Portfolio?”Journal of Financial and Quantitative Analysis 22(September 1987).