e1 Zvi Bodie 投資學 v10
附錄6C Kelly準則
將聖彼得堡悖論的博弈往前再推一步,考慮一個系列的單期投資計劃,每一期只有兩種可能的回報(收益率以小數表示):正的超額收益b,概率為p;負的超額回報-a(a>0),概率為q=1-p。J.L.Kelly[1]考察這個基本的資本配置問題並確定一個擁有對數效用函數的投資者每一期最優投資策略。
投資者在該計劃上投資y,剩餘資金投資於無風險資產,其總收益是1+r+by,概率為p,或1+r-ay,概率為q。鑑於Kelly用的是對數效用函數,因此期初每一美元的期望效用為
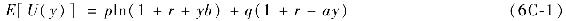
上述效用函數最大化問題便是著名的Kelly準則(或Kelly公式)。該準則即是投資於該投資風險計劃的總財富與財富水平無關,即

這是投資者的每一期的資產配置。
根據該準則,當p和b值較大時投資者應該更多地投資於該計劃,當q和a值較大時,投資者應該投資更少。因為當回報和損失相等時,即a=b,y=(1+r)(p-q)/a,回報或損失數額較大時(即較大的a和b),投資的比例越低。這就出現風險迴避問題了。無風險利率越高,投資比例越高(即收入效應)。
Kelly準則是基於對數效用函數的。人們也可以證明,擁有該效用函數的投資者每一個時期都最大化組合收益的幾何平均值。因此,Kelly公式也是一個幾何平均值最大化準則,並具有以下特性:①在式(6C-2)中風險資產中的投資比例永遠不會高於1/a,因此不會出現毀滅性風險;②當投資期數無限大時,該投資比例戰勝其他任何策略的概率接近於1;③它是短視的,即不管投資期數多少每一時段的最優策略都相同;④如果你有一個具體的財富目標(例如100萬美元),該策略實現目標的時間最短。討論Kelly準則的文獻相當多。[2]
附錄A 概念檢查答案
a.
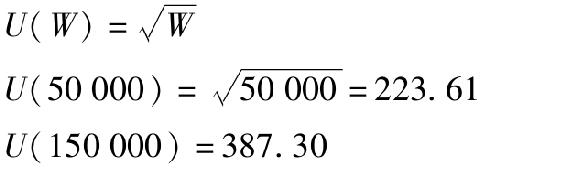
b.E(U)=(0.5×223.61)+(0.5×387.30)=305.45
c.WCE的效用水平是305.45,因此
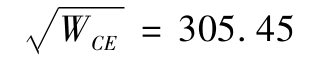
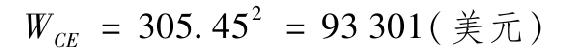
d.是,這筆風險投資的確定等價收益小於100000美元的期望收益。
e.對這一投資者而言,該筆風險投資的確定等價收益高於文中討論的對數效用函數投資者。因此,這一效用函數表達了更低的風險厭惡。
[1] J.L.Kelly Jr.,“A New Interpretation of Information Rule.”Bell System Technical Journal 35(1956),917-56.
[2] 例如,L.C.MacLean,E.O.Thorp,W.T.Ziemba,Eds.The Kelly Capital Growth Criterion:Theory and Practice(World Scientific Handbook in Financial Economic Series),Singapore:World Scientific Publishing Co.,2010.