BUSINESS BOOKS

附錄6A　風險厭惡、期望效用與聖彼得堡悖論

我們在這裡暫時偏離討論的主題，考察投資者是風險厭惡這一觀點背後的基本原理。風險厭惡作為投資決策中心觀點的看法至少可以追溯到1738年。丹尼爾·伯努利作為出身於瑞士名門的著名數學家之一，他於1725~1733年在聖彼得堡研究了下面的投幣遊戲。首先，參加這個遊戲要先付門票。其後，拋硬幣直到第一個正面出現時為止。在此之前，反面出現的次數用n表示，用來計算參加者的報酬R，對於參與者有：

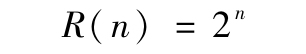
在第一個正面出現之前反面一次也沒出現的概率是1/2，相應的報酬為2⁰=1美元。出現一次反面然後正面的概率是1/4，報酬為2¹=2美元。出現兩次反面再出現正面的概率為1/2×1/2×1/2，依此類推。

表6A-1列出了各種結果的報酬與概率：

表　6A-1

所以，預期報酬為

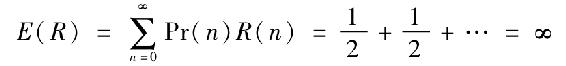
對該遊戲的平均被稱為“聖彼得堡悖論”：儘管期望報酬是無限的，但顯然參加者是願意用有限價格或適當的價格購買入門票來參與這個遊戲的。

伯努利解決了悖論問題，他發現投資者對所有報酬的每份美元賦予的價值是不同的。特別是，他們的財富越多，對每額外增加的美元賦予的“評價價值”就越少。可以用數學方法精確地給擁有各種財富水平的投資者一個福利值或效用值，隨著財富的增多效用函數數值也相應增大，但是財富每增加1美元所增加的效用逐漸減少（現代經濟學家會說投資者每增加1美元的報酬“邊際效用遞減”）。一個特殊的效用函數ln（R）分配給報酬為R美元的投資者主觀價值，報酬越多，每個美元的價值就越小。如果以這個函數衡量財富的效用，那麼這個遊戲的主觀效用值確實是有限的，等於0.693.獲得該效用值所必需的財富為2美元，因為ln（2）=0.693。因此風險報酬的確定等價物是2美元，也是投資者願意為遊戲付出的最高價錢。

1964年馮·諾依曼與摩根斯坦以完全公理體系的方式將這種方法應用於投資理論領域。避開不必要的技術細節，在這裡只討論對風險厭惡基本原理的直覺。

設想有一對雙胞胎，只是其中一個不如另一個幸運。彼得名下只有1000美元，而鮑爾卻擁有200000美元。他們各自願意工作多少小時去再掙1美元？似乎彼得（窮兄弟）比鮑爾更需要這1美元。所以彼得願意付出更多的時間。也就是說，與鮑爾得到第200001美元相比，彼得得到了更多的個人福利或賦予了第1001美元更大的效用值。圖6A-1用圖形描述了財富與財富效用值的關係，它與邊際效用遞減的概念是一致的。

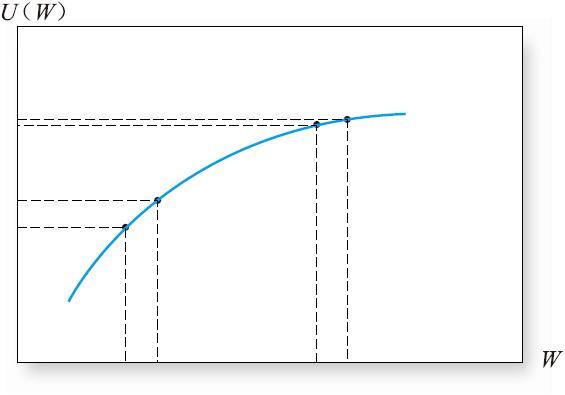
圖6A-1　對數效用函數下的財富效用

每個人都擁有不同的財富邊際效用遞減率，每增加1美元，財富的效用增加值隨之減少卻是一個固定不變的規律。表示隨著財產數量的增加每個單位的價值遞減的函數稱之為凹函數。一個簡單的例子就是中學數學中的對數函數。當然，對數函數並不適於所有的投資者，但與風險厭惡是一致的，前提假定所有的投資者都是風險厭惡型的。

現在考慮下面的簡單情景：

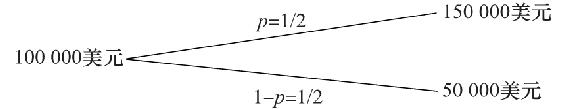
這是一個期望收益為零的公平博弈。假定圖6A-1代表了投資者的財富效用值，且為對數效用函數。圖6A-2顯示了用數值標出的曲線。

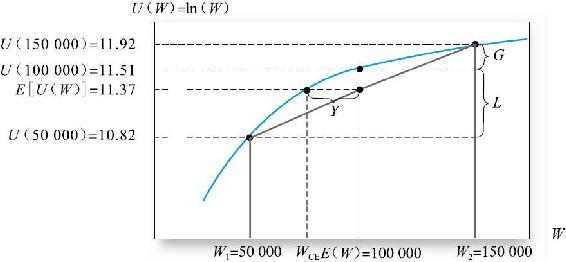
圖6A-2　公平博弈與期望效用

圖6A-2表明因損失5萬美元造成的效用減少超過了盈利5萬美元形成的效用增加。先考慮效用增加的情況，概率p=0.5時，財富從100000美元增加到150000美元。利用對數效用函數，效用從ln（100000）=11.51增加到ln（150000）=11.92，即圖上的距離G。增加的部分G=11.92-11.51=0.41。按期望效用計算，增加值=pG=0.5×0.41=0.21。

現在考慮另一端效用減少的情況，在這種情況下，財富從100000美元降到50000美元。圖中的距離L是效用的損失，ln（100000）-ln（50000）=11.51-10.82=0.69。因而，期望效用的損失為（1-p）L=0.5×0.69=0.35。它大於期望效用的增加。

我們計算風險投資的期望效用為

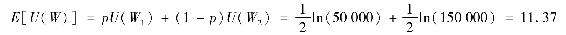
而不投資的效用為11.51，所以風險厭惡的投資者將拒絕參加公平博弈。

使用具體的投資者效用函數（如對數效用函數）使人們能夠計算給定的風險投資對投資者的確定等額價值。如果該數值能肯定得到，他會認為與風險投資具有相同的吸引力。

如果對數效用描述了投資者對財富的偏好，那麼圖6A-2還告訴我們：對他來說該投資的美元價值是多少。人們要問：效用值為11.37（等於投資的期望效用）所對應的財富水平是多少？在11.37的水平上畫出的水平線與效用曲線在W_CE點相交。這意味著：

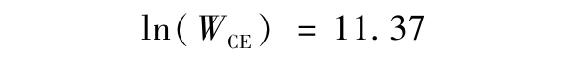
即

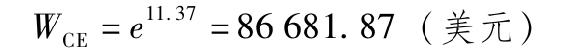
W_CE就是投資的確定等價值，圖6A-2中的距離Y是由於風險對期望收益的懲罰或向下的調整。

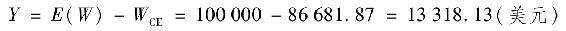
投資者認為穩拿的86681.87美元與有風險的100000美元的效用值相等。因此，對他來說二者沒有什麼區別。

概念檢查6A-1

假定效用函數為U（W）=。

a.財富為5萬美元與15萬美元時的效用水平各是多少？

b.如果p=0.5，期望效用是多少？

c.風險投資的確定等價值是多少？

d.該效用函數也表示出了風險厭惡嗎？

e.與對數效用函數比較，該效用函數表示出的風險厭惡是多還是少？

附錄6A習題

1.假設你擁有250000美元，購買了200000美元的房子並將剩餘的錢投資於年回報率為6%的無風險資產。在0.001的概率下，你的房子有可能會發生火災並被燒光，從而價值變為零。在以年末財富為變量的對數效用函數下，在年初你願意投資多少來買保險呢？（假設房子沒有發生火災，其年末價值仍然為200000美元。）

2.如果保險的價格為1美元保費保險1000美元的價值，則投保後年末財富的確定性等值為

a.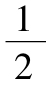的房屋的價值。

b.全部價值。

c.房屋價值的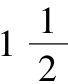倍。