e1 Zvi Bodie 投資學 v10

6.5　風險容忍度與資產配置

前面已經說明如何建立資本配置線，即資產配置決策下所有可行的風險報酬組合構成的圖形。投資者必須從可行集中選擇最優的組合。這個決策包含了風險和收益的權衡選擇。個人投資者風險厭惡程度不同，意味著給定相同的可行集（無風險利率和報酬-波動性比率相同），不同的投資者將選擇不同的頭寸。特別地，越是風險厭惡的投資者會選擇更少的風險資產，更多地選擇無風險資產。

一個面臨無風險利率rf和期望收益為E（rP）、標準差為σP的風險資產投資者會發現，對於任意y，組合的期望收益由式（6-3）給出

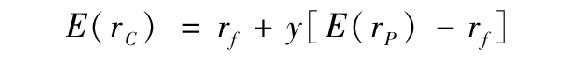
由式（6-4），整個組合的方差為

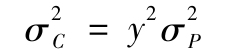
投資者試圖通過選擇風險資產的最優配置y使效用最大化。效用函數由式（6-1）給出，即U=E（r）-1/2Aσ2。當風險資產配置增加（y增加），期望收益增加，但是收益波動性也增加，因此效用可能增加也可能減少。表6-4展示了效用水平隨y值變化的數據。一開始，效用隨y增加而增加，最終隨y增加而降低。

表6-4　風險厭惡係數A=4的投資者不同風險資產比例y帶來的效用值

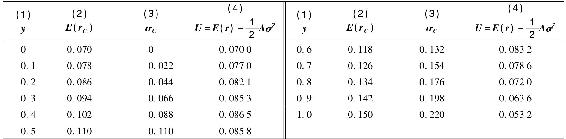
圖6-6給出了表6-4中效用函數的散點圖。效用在y=0.41時是最高的；當y＜0.41時，投資者願意為更高的期望收益而增加投資風險；而當y>0.41時，風險增加效用則會降低。

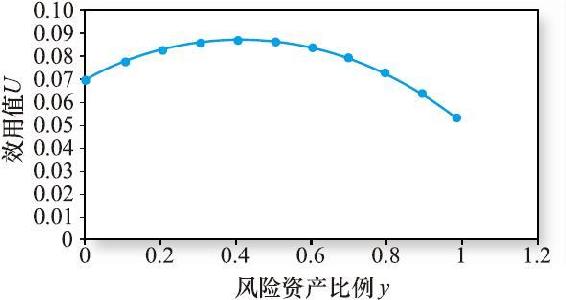
圖6-6　效用值U關於風險資產比例y的函數

為了解決這一效用最大化的問題，我們把問題寫作：

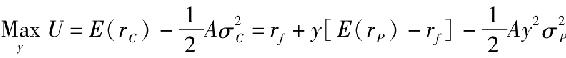
學過微積分的學生知道最大化問題是使一階導數為零。這樣求解出風險厭惡者風險資產的最優頭寸y*如下

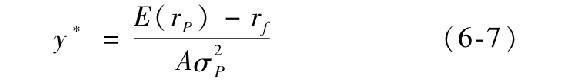
這個解顯示風險資產的最優頭寸正如你所預料的那樣，與風險厭惡程度和風險水平（由方差表示）有關。

【例6-4】資產配置

使用前述數字例子的數據（rf=7%，E（rP）=15%，σP=22%），所有收益用小數表示，一個風險厭惡係數為A=4的投資者的最優解為

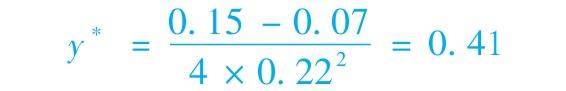
（注：對y的一階導數等於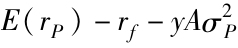，使該式為0，得到式（6-7）。）

換句話說，該投資者將會把投資預算的41%投資於風險資產，59%投資於無風險資產，如圖6-6所示，此時效用達到最高水平。

當41%投資於風險資產，整個組合的期望收益和標準差為

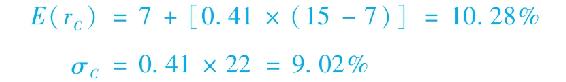
整個組合的風險溢價是E（rC）-rf=3.28%，標準差為9.2%，注意到3.28/9.02=0.36，這正是例子中所假設的報酬-波動性比率。

這個決策的圖解法是利用無差異曲線進行分析。為了理解如何構造無差異曲線，考慮風險厭惡係數A=4的一個投資者，他目前全部投資於無風險組合，收益率rf=5%。因為這個組合的方差為零，式（6-1）告訴我們它的效用為U=0.05。當投資者投資於σ=1%的風險組合時，為了獲得相同的效用，其期望收益必須上升，以彌補更高的σ值：

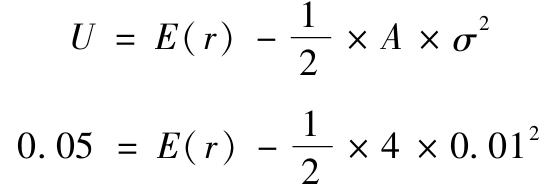
這說明必要的期望收益為

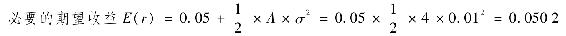
對不同的σ重複這樣的計算，可以得到保證效用值為0.05所需的E（r）。這個過程將得到效用水平為0.05時所有期望收益和風險的組合。把這些組合描點在圖上便得到無差異曲線。

可以使用Excel表格來生成投資者的無差異曲線。表6-5包含了效用值分別為0.05和0.09對於風險厭惡分別為A=2和A=4的兩個投資者的風險和收益組合。圖6-7描繪了A=2對應的期望收益和標準差組合，截距分別為0.05和0.09，對應曲線的效用水平。

表6-5　無差異曲線的數字計算

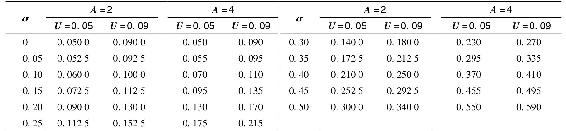
注：表中為需要達到相應效用值的期望收益。

假定任何投資者都願意投資於更高無差異曲線上的組合，獲得更高的效用。更高無差異曲線上的資本組合在給定風險水平上能夠提供更高的期望收益。例如，A=2的兩條無差異曲線形狀相同，但是對於任意水平的風險，效用為0.09%那條曲線比0.05的那條曲線的期望收益高4%。

表6-5中的第4列和第5列對風險厭惡係數更高（A=4）的投資者重複了上述分析。圖6-7反映出更高風險厭惡程度投資者的無差異曲線比低厭惡程度投資者的曲線更陡峭。更陡峭的曲線意味著投資者需要更多的期望收益來補償同樣的組合風險。

更高的無差異曲線意味著對應更高的效用水平，因此投資者更願意在更高的無差異曲線上尋找投資組合。如圖6-8所示，在表示可行集的資本配置線上加入無差異曲線，我們就可以得到與資本配置線相切的最高的無差異曲線，切點對應最優投資組合的標準差和期望收益。

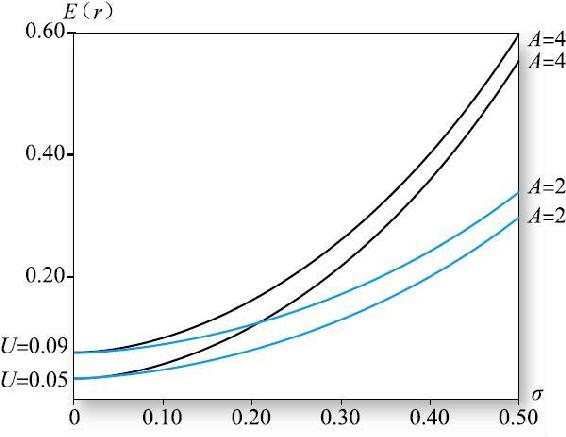
圖6-7　U=0.05和U=0.09，分別對A=2和A=4的無差異曲線

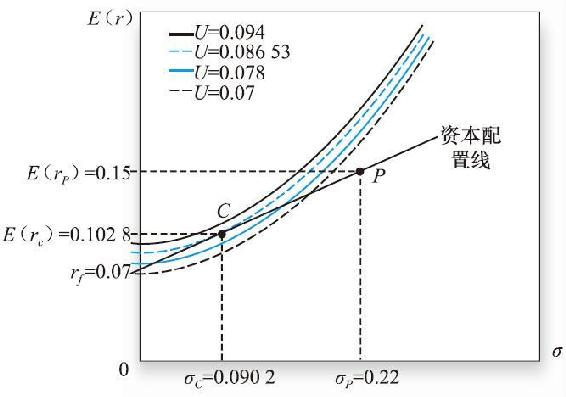
圖6-8　用無差異曲線尋找最優組合

為了證明這一點，表6-6給出了投資者A=4的4條無差異曲線（效用水平分別為0.07、0.078、0.08653、0.094）的計算。第2~5列利用式（6-8）計算出了各曲線為了得到相應的效用值對不同標準差所必需的期望收益值。列6由式（6-5）計算出E（rC）的資本配置線上各σ值對應的期望收益。

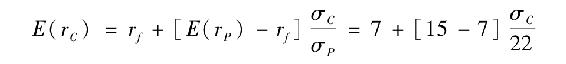
表6-6　四條無差異曲線和資本配置線對不同σ的期望收益，A=4

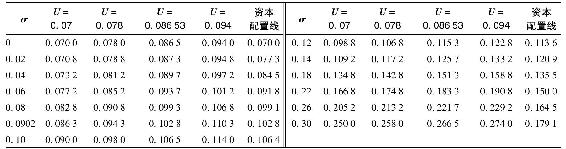
圖6-8畫出了4條無差異曲線和資本配置線，圖形反映出效用U=0.08653的無差異曲線與資本配置線相切；切點對應了最大效用值的資產組合。切點處E（rC）=10.28%，σC=9.02%。最優投資組合的風險-收益比例是y*=0.41，這個數值和用式（6-7）的算數解相同。

綜上所述，y*的決策主要取決於投資者的風險厭惡程度。

概念檢查6-7

a.如果投資者的風險厭惡係數為A=3，最優投資組合將會如何變化？整個組合新的期望收益和標準差是多少？

b.假定借入利率為9%，高於貸出利率7%，請用圖形說明投資者的最優投資組合是如何受到更高借入利率的影響的？

非正態收益

在前面的分析中我們假設收益呈正態分佈，並以標準差作為風險度量。如第5章所述，正態性的偏離會導致極端損失的可能性遠大於正態分佈的情況。這些風險敞口，一般由在險價值或預期損失來衡量。

因此，對我們之前分析的一種拓展是給投資者展示在險價值和預期損失的預測值。我們把基於正態假設下的資本配置作為分析的基礎，面對肥尾分佈的投資者也許會減少風險組合的資金配置，並增加無風險資產的配置。

有跡象表明在處理極端方面有進展（除第5章介紹的有關高頻數據的技術外）。早在20世紀初期，當時最偉大的經濟學家之一奈特將風險與不確定性區分開來。其區別是，風險中的概率為已知，但不確定性甚至忽略概率的重要性（如黑天鵝問題）。因此奈特認為對於風險和不確定要用不同的方法。

金融中大部分結果的概率可以通過經驗進行評估，這得益於有相對高頻的觀測值。但極端負值極少發生，因而精確做概率也不可能。後期在決策科學處中心地位的貝葉斯方法排斥奈特的關於客觀概率難以估計的觀點，無論如何投資者都有主觀判斷並以這些信念在貝葉斯框架下進行經濟決策，即使在處理沒有發生過的事件，人們必須要用先念概率。這樣，在該框架中，風險和不確定性的區別並不重要。今天的經濟學家回到了奈特的理論。但是高級效用函數可以區分風險和不確定性，並且對不確定性給予更大權重。