e1 Zvi Bodie 投資學 v10: 5.9 長期投資

e1 Zvi Bodie 投資學 v10

5.9　長期投資

考慮一名投資者為其25年後的退休於今天儲蓄了1美元，把這1美元投資於一個風險股票投資組合（獲得的股利也進行再投資），這個股票組合的月收益率為1%，那麼退休後他的這筆退休“基金”會增長近20倍，其終值為（1+0.01）³⁰⁰=19.79（美元）（增長了1879%）。同時比較投資於一個25年無風險月平均收益率為0.5%的國債時，投資的終值只有1.005³⁰⁰=4.46（美元）。可以看出0.5%的月風險溢價會使投資的總收益比無風險國債多3倍多，這就是複利的作用。你可能會問既然如此為什麼還會有人投資於國債，很明顯這是一個風險的超額收益問題。那麼風險與收益這種權衡關係的本質是什麼呢？一個長期收益率波動的投資風險較難理解，因此對它的刻畫十分重要。

仿照之前的例子，我們繼續用二叉樹來構造一個股票基金終值的概率分佈。與之前不同的是，這次不採用月利潤簡單相加，而是根據分佈確定一個收益率並以之按複利計算終值。例如，假設某個股票組合的月收益率可以近似看成如下分佈：月收益率50%的可能性是5.54%，50%的可能性是-3.54%。這種構造的月期望收益是1%，其風險用月收益標準差來衡量是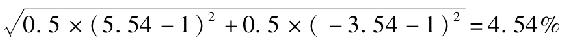。2個月後的事件樹如下所示：

300個月後二叉樹會產生301種不同的可能結果，而每種結果的概率可以通過Excel中的BINOMDIST函數來獲得。由此我們計算得到期末終值的均值為19.79，標準差為18.09。我們可以用這個標準差來度量19.79-4.29=15.5（1550%）的風險溢價嗎？回想之前小節裡講的收益分佈的非對稱性會使標準差衡量的風險水平出現偏差的情況，所以我們必須先看看這個事件樹最終的分佈情況。

圖5-9畫出了期末可能價值的發生概率，可以看出分佈的非對稱性是很明顯的。很高的正偏度表明標準差對風險的度量並不適用。實際上，以複利計算多期二項分佈的終值時，其收斂於對數正態分佈（lognormal distribution）。對數正態分佈描述的變量在取對數後服從正態分佈。

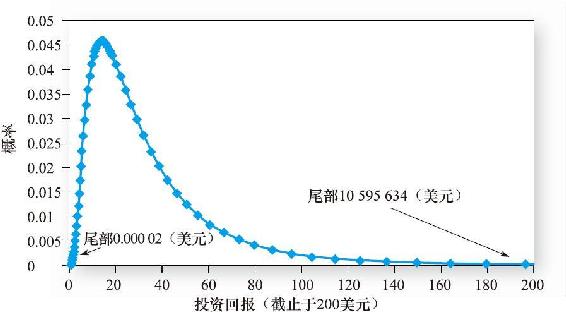
圖5-9　25年後的概率分佈服從對數正態分佈

5.9.1　正態分佈與對數正態分佈

我們前文指出過，正態分佈的一個重要特性是它的穩定性，即服從正態分佈的收益加和後的結果依然服從正態分佈。但是這一特性不適用於正態分佈收益的乘積，這樣我們依然尋找較長時段收益的分佈。例如，兩個時段的實際收益率r₁和r₂均為正態分佈，這兩個時段總收益率（1+r₁）（1+r₂）-1不是正態分佈。正態分佈不能用來做我們想象的簡化分佈，但是對數正態分佈可以。什麼是對數正態分佈？

一個隨機變量X，如果其對數形式ln（X）服從正態分佈，則X服從對數正態分佈。這樣如果瞬間股票價格服從正態分佈（即在一個極短時段收益呈正態分佈），那麼一個較長時段的複利收益以及未來的股票價格服從對數正態分佈。^[1]反過來，如果股票價格服從對數正態分佈，其連續複利收益（CC）服從正態分佈。既然不管時段多長，連續複利收益服從正態分佈，如果採用連續複利收益率而非實際收益率，我們依然可以利用正態分佈帶來的種種簡化。

回顧一下連續複利收益公式r_CC=ln（1+r），如果有實際收益率，我們即可計算連續複利收益率。如果r_CC服從正態分佈，則可以用它進行各種分析和計算。如果有需要，也可以從r_CC反推實際收益率，即r=e^r_CC-1。

我們看看當股票價格服從對數正態分佈時能得出些什麼樣的規律。假設對數股票價格服從預期年化增長率為g、標準差為σ的正態分佈。收益受到隨機衝擊時，這些波動對價格的影響並非對稱。一個正向的向上衝擊提高了股價，則下一個衝擊較上一個大。反過來也一樣，一個負向衝擊降低了股價，下一個衝擊則較小。這樣，一連串的正向衝擊將有一個較大的上行影響，一連串的負向衝擊將產生較大的下行影響。因此，即便g為0波動性推動股價上行。這種額外移動有多大？這取決於最小价格變動的大小，事實上，它恰好等於其方差的一半。這樣連續複利收益率m將大於g。預期的年化連續複利收益率（CC）等於

有了正態分佈的CC，我們預期期初財富W₀複利到年末為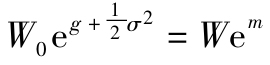。因此預期實際利率等於

如果將年化CC用到期限為T的一項投資，不管T是大於或小於1年，該投資將按照r（T）=e^r_CCT-1速度增長。預期累計收益率r_CCT與T成比例，即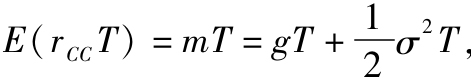預期的期末財富為

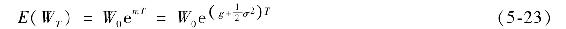
累計收益率的方差也與時段長度成比例，即Var（r_CCT）=TVar（r_CC）（注：當實際年收益率，r，呈對數正態分佈時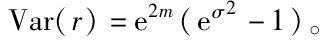，），但是其標準差與時段長度呈平方根的關係，即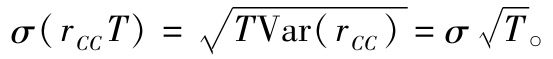

上式提供了降低長期投資風險的途徑。因為預期收益與時段長度成比例增長，而標準差增長的速度較慢，這樣一項長期風險投資的預期收益相對於其標準差增長更快。也許預期損失也隨著投資期限增加而下降。我們將在例5-11分析這種可能性。

【例5-11】短期和長期收益損失風險

預期月度收益率為1%的連續複利收益率等於ln（1.01）=0.00995（即每月0.995%）。假設無風險為0.5%/月，相當於連續複利收益率ln（1.005）=0.4988%。實際收益標準差4.54%意味著（見腳註）連續複利下月度標準差4.4928%。因此CC風險溢價是0.995-0.4988=0.4963%，標準差等於4.4928%，夏普比率等於0.4963/4.4928=0.11。換句話說，股票組合的績效劣於無風險資產的前提是股票收益較均值低0.11倍標準差。採用正態分佈，我們發現收益率低於無風險收益率的概率為45.6%（你可以在EXCEL的NORMSDIST公式輸入-0.11可得）。^[2]這是投資者後悔的概率，有了這個，投資者寧願投資於短期國庫券而非股票。

如果投資期為300個月，累計超額收益高達0.4963%×300=148.9%，標準差為4.492×=77.82，意味著夏普比率高達1.91。在NORMSDIST公式中輸入-1.91，你會發現300個月期間損失的概率僅為0.029。

注意，損失的概率並不是一種完善的投資風險度量方法。這個概率不考慮潛在損失的大小，而一些可能損失雖然發生概率小，卻意味著完全的破產。25年投資的最壞情況遠比1個月的最壞情況要差得多。圖5-10和圖5-11用圖像展示了長期風險的累積。

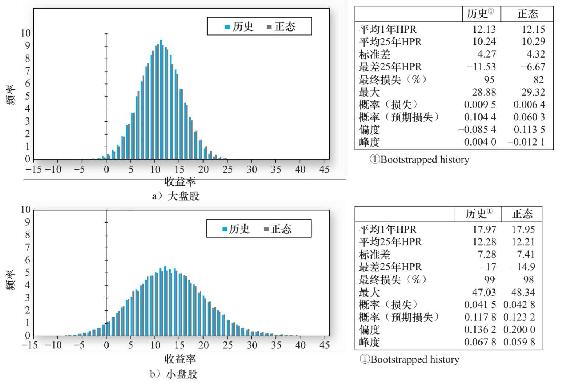
圖5-10　拔靴法和正態分佈下25年持有期收益率（50000個樣本），右側為統計值

一個更好地度量長期投資風險的方法是用可以抵禦損失的保險的市場價格。這種保險溢價必須考慮到損失的可能性和損失的大小，在之後的章節中我們會用期權定價模型來估計這種保險的合理價格。

儘管一個投資組合的保險兌現賠償的概率很低，但是可能損失的金額和時機^[3]可能會使這樣的保險擁有較高的保費。比如，用標準的期權定價模型計算得到一個10年期的投資損失的保險價格幾乎達到期初投資金額的20%左右，而與期限越長損失風險越小的結論相反，在市場上期限越長的保險保費竟然更高，甚至達到30%。

5.9.2　長期未來收益的模擬

圖5-6中的頻率分佈僅僅提供了收益分佈性質的大體描述，很難用來反映長期投資。一個從過去了解未來長期收益分佈的方法是從有效樣本中模擬出未來的收益。實現這一任務的一個流行的方法叫作拔靴法。

拔靴法是一個可以避免各類收益分佈假設的實驗過程，直接簡單假設歷史樣本中的收益結果發生的可能性相等。例如，可以從歷史年收益的樣本中隨機抽取25年的數據來模擬一個25年期投資的可能未來收益。將25個收益率按複利計算可以得到1種期末收益，這一過程重複千次便可以得到長期收益率的概率分佈。

現在讓我們再回顧一下納西姆·塔勒布（Nassim Taleb）的黑天鵝事件^[4]。塔勒布用歐洲人聞所未聞的黑天鵝比喻歷史上從未發生過的事件。黑天鵝象徵的是尾部風險：它發生概率極低，但影響巨大而且無法根據以往經驗預測。拔靴意味著將未來收益侷限在過去收益的區間或者過去極端收益發生的頻率，這將大大低估了尾部風險。注意在正態分佈條件進行模擬，我們允許不限制壞的結果，但是不允許肥尾，因此低估其發生概率。然而，因一種特定的概率分佈總是預先設定了未來事件的形態。

描述不確定的難點主要是知道投資者如何就低概率災難發生進行反映。有人認為長期投資風險較低低估了極端事件的風險。昂貴的組合保險表明絕大多數投資者不會輕視這種極端風險。就現在的實驗而言，我們證明即使以過去最糟的美國曆史數據進行模擬也會產生投資慘敗的情況。

做這一模擬實驗中的主要決策就是選取過去多長時間來獲得未來收益率觀測序列值。答案就是我們應該儘可能多地用全部可靠歷史樣本來包括低概率極值點。

這一實驗一個重要的目標就是評估美國長期股票投資收益分佈的非正態性帶來的潛在影響。基於這個目的，分別用拔靴法對大盤股和小盤股25年年收益率分佈進行模擬，並和用正態分佈得到的類似樣本進行比較。結果如圖5-10所示。其中圖5-10a顯示了美國大盤股的歷史收益和用正態收益分佈構造的頻率分佈，圖5-10b顯示的是小盤股，並附有分佈的相關統計量。

我們先看大盤股。可以看到歷史數據模擬和正態收益分佈分別構造的頻率分佈差異很小，但卻是顯著的，儘管1年期和25年期的年均收益、標準差只有很小的差別，但是偏度與峰度上微小的差別結合在一起就構成了顯著的收益損失可能性的差異。對於小盤股，因為偏度的峰度的差異太小所以形成的分佈圖非常近似。

我們如何考慮長期投資的風險呢？正如下表所示，損失的概率很小，大盤股發生損失的概率為1%，小盤股的為5%。這與我們在例5-11中的計算相符；投資期限延長，損失概率下降。

那麼對於投資者其他期限長度的長期投資風險又是怎樣的呢？圖5-11又將25年和10年做了比較。為了有可比性，我們必須考慮給10年期投資期末再加上一個15年的國債作為補充。（為了完成這一比較，從80年國債歷史中抽取15年的樣本，並給每個樣本加上從風險資產收益歷史中抽取的10個風險收益率。）結果如圖5-11所示，其概率分佈揭示了終值組合的風險差異，從統計量中也可以明顯地看出這些差異。

圖5-12顯示了25年期大盤股的財富指數和投資於國債的財富指數走勢的比較。不同股票組合的收入範圍從收入最低組合，到前1%低組合、前5%低組合、均值組合、中值組合。前5%低組合與國債投資相比還是有顯著的收益損失。綜上所述，這個分析清晰地說明投資股票的風險在長期中更小這一結論並不成立。

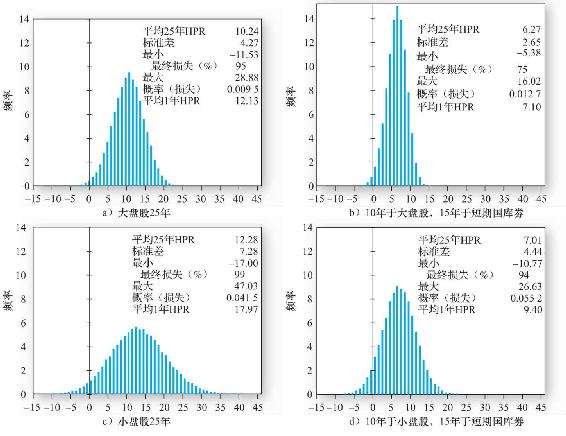
圖5-11　按年複利累計，拔靴法獲得的25年持有期收益率（50000個樣本）

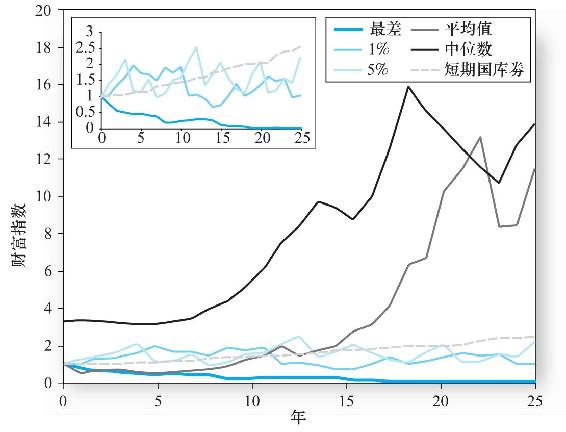
圖5-12　部分大盤股組合的財富指數和短期國庫券組合

注：注意最差組合、1%、5%和國庫券的對比。

很多業界人士認為對於長期投資者來說，投資風險不很重要。專欄5-2表明年化收益標準差對於較長時期而言下降了，但是在投資總收益方面則並無明顯變化。

華爾街實戰5-2　時間和風險

許多投資新手對股票市場持懷疑態度。他們認為權益投資就像俄羅斯輪盤遊戲一樣，玩得越久賠得越多。實際上，歷史數據告訴我們結果恰好相反。降低風險最容易的方法就是投資權益，而增加收入最容易的方法則是延長你持有投資組合的時間。

下圖中的歷史數據比較了1950~2005年不同持有期的小股票、大股票、長期和中期國債的收益率。

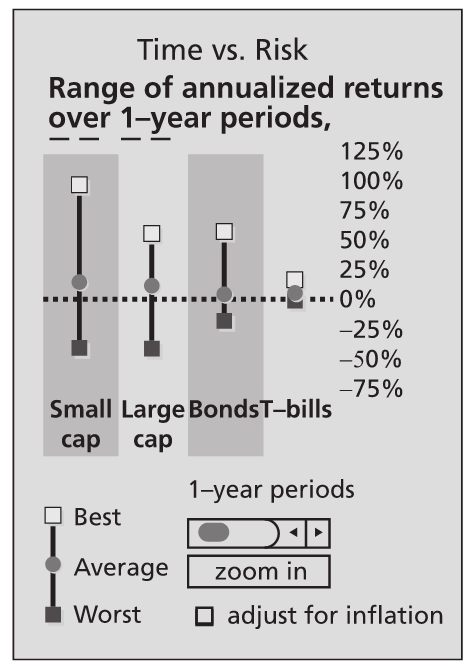
資料來源：CRSP，Federal Reserve.

圖中顯示，如果持有1年的話，那麼在這樣短的持有期內，小公司股票無疑是最好的選擇。

如果投資年限大於1年呢？你可以順著橫軸向右看，即使投資期限只增加1年變為2年，權益的波動率也會迅速下降，這時你需要點擊放大按鈕（Zoom In）才能看清楚。當投資期限變為10年時，政府債券的下行風險要比小公司股票低很多。但點擊調整通貨膨脹（adjust for inflation）按鈕後，你會看見債券的低風險完全是一種假象。通貨膨脹將使投資回報率低的投資組合的實際回報率為負值。

現在讓我們來看投資20年的收益率。調整通貨膨脹後，20年長期國債的最優收益率將明顯低於小公司和大公司股票的收益率。與公眾的預期相反，在最壞的20年裡，債券投資在調整通貨膨脹影響後實際上是賠錢的。同時，投資小公司股票在20年裡能獲取不錯的回報，即使在市場最惡劣的情況下。

5.9.3　再論無風險收益率

本章開頭在沒有談及投資期限時，簡單提出了實際和名義無風險收益率的概念。總體原則是，無風險收益率的期限應該與投資期限相匹配。長期投資者需要以長期無風險債券收益作為基準的無風險收益率。利率總體上與期限相關，越長的期限通貨膨脹越難預測。因此通脹風險與期限長短相關。

認識到風險資產的風險溢價是一個真實的數字很重要。風險資產的預期收益率等於無風險利率加風險溢價。這個風險溢價是無風險收益率的增加量，無論無風險收益率是真實的還是名義的。

投資者以每個對應期限的真實收益率作為投資的衡量基準，因此真實風險資產收益率應該是真實無風險收益率加風險溢價。即便是長期限國債的無風險名義利率由於未來通脹和利率的不確定性也包含有風險溢價。

通脹保值債券（TIP）承諾向投資者支付一定期限的保護通脹的真實利率。這樣我們可以把一定期限風險投資的預期實際收益率看作相同期限TIP國債的利率加風險溢價。

同時存在名義國債和TIP也提供有用的信息。這兩種債券預期收益率之差稱為遠期通脹率，既包含預期值也包括相應的風險溢價。

那我們為什麼在表達超額收益時通常用1月期的短期國庫券收益率呢？主要是因為我們都在討論短期投資。嚴格意義上，在討論長期投資時，必須要用相應的真實無風險利率。

5.9.4　收益率研究的方向在哪裡

要想更多地瞭解收益的分佈特別是罕見的極端事件，我們需要大量數據。通過加速收集日數據不是辦法，等我們有了大量數據時，分佈就發生變化了。但這樣做還是有些幫助。

高頻的收益率數據來自每一筆交易。最近天體物理學家開發的統計方法可以從這些數據中提取關於收益分佈的有價值成分。這一收益形成過程可以描述為由瞬間正態分佈加和形成對數正態再加上偏離正態分佈的跳躍，其中的跳躍可以分解為大量的小跳加上尾部的大跳。^[5]

希望用不了多久業界人士就可以購買這樣的研究成果，獲得各種期限風險投資的精確風險參數。

5.9.5　長期預測

我們之所以用算術平均收益來預測未來收益，是因為算術平均收益對相同持有期的期望收益的估計是無偏的。但是用短期的算術平均收益來預測長期累積收益將會出現偏差。這是因為對期望收益進行估計的樣本誤差會在長期複利計算中產生非對稱性影響，且正的誤差比負的誤差影響更大。

Jacquier、Kane和Marcus證明長期總收益的無偏預測要求計算所用的複利採用算術和幾何平均收益率的加權值。幾何平均的權重係數等於預測期的長度和樣本長度的比值。例如，用80年的歷史樣本預測25年期的投資累積收益，其無偏估計應採用的複利利率是

這個改進剪掉了大盤股0.6%的歷史幾何平均風險溢價，小盤股2%的算術平均風險溢價。預測的投資持有期越長得到的比率就越小，而當前中年投資者的預測期限就要取決於他們的壽命預期了。

[1] 如圖5-9所刻畫的二叉樹也有類似情況。儘管情況很糟糕，股票價格也不可能為負，這樣其分佈受限於零。但是在情況很好時，股票價格上漲不受限，這樣一個很長時段的複合收益表現出很長的右尾，但左尾受限於最糟糕的-100%。這就出現對數正態分佈的非對稱傾斜的特徵。

[2] 在有些版本的EXCEL，該式是NORM.S.DIST（z，TRUE）。

[3] 這裡的時機是說股票價格下降和慘淡的經濟有關聯性，而在這種情況下投資者非常需要額外的收入來彌補投資損失，所以能補償這種損失的保險其市場價值是非常顯而易見的。

[4] The Black Swan；The Impact of the Highly Improbable，New York，Random House，2010.

[5] 更詳盡瞭解這一方法，參見Yacine Ait-Sahalia and Jean Jacod，“Analyzing the Spectrum of Asset Returns：Jump and Volatility Components in High Frequency Data.”Journal of Economic Literature 50（2012），pp.1007~1050.