BUSINESS BOOKS

5.8　風險組合的歷史收益

我們現在將前一小節中的分析工具應用於6種風險投資組合，以便後續分析。我們的基礎組合是儘可能廣泛的美國股票組合，包括在NYSE、AMEX和NASDAQ上市的股票，並將此標註為“全美股票”。邏輯上說，無人管理（被動）的證券組合應該更多投資於大型公司股票，因此這個基礎組合是價值加權的組合。公司市值（market cap）一般向右高度傾斜，存在眾多小規模公司，少了巨無霸公司。因為採用價值加權，因此“全美股票”組合以大公司為主導。

這裡的數據包括1926年7月至2012年9月間的全部美國上市公司的月度超額收益，樣本覆蓋86年。我們將樣本按照樣本長度和經濟狀況一分為三，以分析這些組合在不同子樣本中如何表現。

最早的子樣本期大約是20世紀的第2個25年，即1926年7月至1949年12月，總共包括282個月，覆蓋大蕭條和“二戰”時期。

第二個子樣本期是20世紀的下半期（1950年1月至1999年12月），總共600個月，儘管其間有3次戰爭（朝鮮戰爭、越南戰爭和波斯灣戰爭），8次相對小幅度經濟蕭條和復甦期，但總體上屬於比較平穩的時期。該子樣本期結束於20世紀90年代後期的網絡泡沫。

第三個子樣本期涵蓋21世紀的前153個月，屬於困難時期，包括兩次不同類型的深度衰退，一次是網絡泡沫的破滅，另一次是2007年開始的房地產泡沫的破滅，每次泡沫破滅導致股票價格大約下跌40%。其間馬拉松式的伊拉克戰爭和阿富汗衝突使美國經濟雪上加霜。

我們以構造的4個組合與“全美股票”組合進行比較。這些供比較分析的組合主要依據具有實證證據支持與股票收益相關的兩個變量來構造的，即公司規模（股票市值）和市淨率。

在其他條件相同時，小規模公司股票收益總體上高於大規模公司股票收益。這裡的其他條件指所有能夠度量的風險。4個組合中包含兩個市值規模較高的股票組合，兩個市值規模較小的股票組合。

資產負債表中的會計數據反映公司過去資產投資的歷史成本，屬於回溯型價值度量。公司淨資產（賬面價值）等於公司市值減去負債餘額。然而，公司市值反映現有公司業務的所有現金流現值，也包含公司業務的預期成長以及尚未投產項目的現金流，可以稱之為成長機會。賬面價值與公司市值的比例優劣取決於現有資產和成長機會的相對比例。低市淨率公司一般是那些公司市值依賴於成長機會的公司，而高市淨率公司一般稱之為價值型公司，其公司市值主要源於現有公司資產。其他條件相同時，價值型公司的平均收益一般高於成長型公司的收益。

法瑪和弗倫奇廣泛證明了公司規模和市淨率效應，這些效應同樣存在於全世界的上市公司。^[1]法瑪和弗倫奇的數據按照規模大小和市淨率高中低劃分的美國股票組合的收益，並且每年年中進行組合調整。

我們放棄中等市淨率公司，並將高市淨率公司稱為“價值型”公司。低市淨率公司稱為“成長型”公司，這樣我們得到4個比照組組合，即大型/價值、大型/成長、小型/價值、小型/成長組合。一般採用價值加權方法構造組合，為了更強調小型公司並與含有更多大型公司的“全美股票”組合形成鮮明對照，這裡採用等權重法。

表5-6給出了期初期末各組合的公司數量、平均規模、平均B/M值。除21世紀因不景氣導致大量小規模公司消失外，組合的公司數量呈增加態勢。小規模公司從樣本中消失導致餘下公司的平均市值增加。所有公司的平均市值從0.57億美元增加到44.7億美元，在86年期間平均年增長5.2%，較GDP平均增速（6.7%）略慢，但較平均CPI（3.2%）高出2%。

表5-6　各組合公司數量、平均市值和平均B/M值

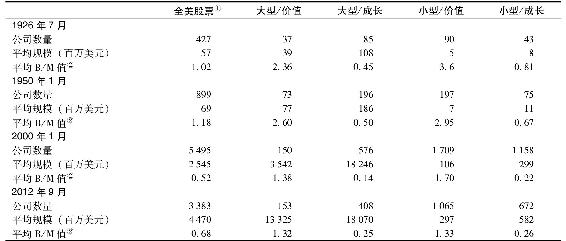
①價值加權，因此大型公司佔主導。

②B/M值以年中數計。

資料來源：弗蘭琦教授網址：http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html.

圖5-6展示了總計1035個月的短期國庫券和5個風險資產組合收益的直方圖。記住，儘管月平均收益差別不大，但對很長一段樣本期的期末財富會產生很大影響。圖5-6a顯示短期國庫券收益在-0.05%至1.5%之間^[2]，圖5-6b給出全美股票組合的月均超額收益在-20%至20%之間，相當於年化收益-93%至891%！縱軸表示各組別的收益（柱狀圖中黑色柱表示樣本收益，淡色柱表示正態分佈中的收益）。國庫券收益的組別寬度為2.5個基點（0.025%），股票組合的組別寬為50個基點。左側和右側的極端組合的組別包括了報告範圍以外（小於-20%或高於20%）的所有收益頻率。圖5-6c和圖5-6d給出兩個大公司或大市值股票組合超額收益的直方圖，圖5-6e和圖5-6f給出兩個小公司組合超額收益的直方圖。

從股票的超額收益上第一眼可以看出相對於正態分佈而言表現出肥尾特徵，意味著極端收益發生的頻率高。由於極端收益可能產生的巨大影響，一般採用剔除極端收益外的超額收益來擬合正態分佈，而將極端收益單獨進行估計。所以，圖5-6b~圖5-6f中的淺色柱子表示的是與±10%實際收益的均值和標準差相當的正態分佈下的預期頻率，各圖中左上方方格標註的是實際分佈的均值和標準差，右上方的方格中是以下分組別收益統計量：中間區域（收益在±10%之間），負向跳躍（極端收益小於-10%）和正向跳躍（極端收益高於10%）。

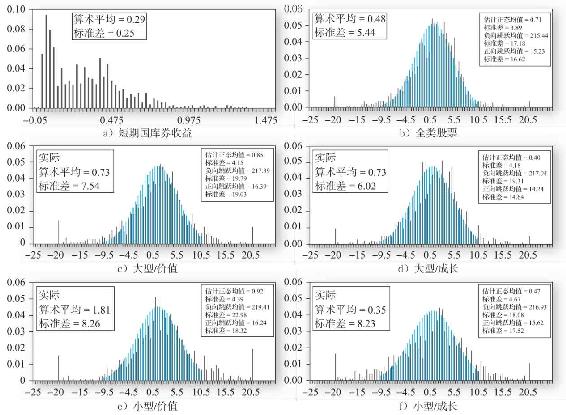
圖5-6　1926~2012年化收益分佈

資料來源：同表5-3。

直方圖使我們有了關於持有股票風險的直觀描述。這裡的風險主要是負向跳躍的頻率和幅度引起的。我們需要些規範分析來認識這些與狀態分佈的偏離是否具有經濟含義。

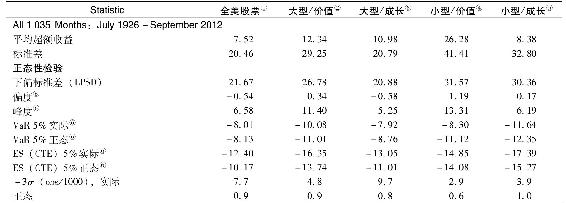
表5-7列示了全部86年期間以及3個子樣本期的5個股票組合的各類統計量。1035個月度樣本的平均超額收益顯著大於0，表明存在正的溢價。觀察價值加權的全美國股票組合，並比較各子樣本平均值可以看出，迄今為止的21世紀對於大公司而言相當困難。也不奇怪，20世紀下半期的政治和經濟相對穩定，股票組合的平均收益最高，對於等權重組合尤為如此。表5-7A對錶5-7進行了補充報告，顯示了這些平均收益情況。

表5-7　1926年7月至2012年9月股票月超額收益（年度統計）

①NYSE，AMEX，and NASDAQ，上市股票為價值加權。

②大型股票和最高1/3B/M股票，等權重。

③大型股票與最低1/3B/M股票，等權重。

④小型股票與最高1/3B/M股票，等權重。

⑤小型股票與最低1/3B/M股票，等權重。

⑥根據月度連續複利計算。

資料來源：Author’s calculations，using data from Professor Kenneth French’s Web site，http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html.

與預期相符，20世紀的第2個25年由於經歷大蕭條和股票價格翻江倒海的變化，這25年表現出最高的標準差（見表5-7B）。

所有股票組合的夏普比率在20世紀的後半期達到最好值（見表5-7C）。21世紀大型公司佔主導的全美公司組合表現最差，等權重組合表現則相對適中。令人奇怪的是，儘管經歷大蕭條時期，20世紀第2個25年的平均收益並不特別低。然而，由於這些估計值很不準確（標準差在0.2或20%之間），我們不能肯定夏普比率在各子樣本期和各組合之間有如此的差異。

表5-7A　平均超額收益

表5-7B　標準差

表5-7C　夏普比率

5.8.1　組合收益

本節主要目的是比較5個組合的收益。從價值加權的“全美股票”組合是被動投資者的自然選擇這個前提出發，我們選擇其他4個組合是因為有證據證明規模（大公司vs.小公司）和B/M（價值vs成長）是組合表現的主要推動力。表5-7A表明小公司/價值型組合事實上在所有時期的平均收益都比較高，與其他組合的平均收益差距都在統計意義上顯著。^[3]另外，等權重對比組合的平均收益（表5-7A的最右側一欄）較“全美股票”組合的高。但是在判斷這種組合更好或更壞之前，必須要證明組合收益之間的差別不能被風險所解釋。這裡，我們必須質疑標準差作為特定資產或組合風險度量的正確性。標準差度量整體波動性，因此作為一個投資者整個在險財富的證券組合風險測度是合理的，即作為廣義資產配置。作為添加與投資者財富組合上的單個資產或組合的風險應該考慮其增加的風險。這一差別需要標準差之外的其他風險測度，我們將留在後續章節討論。

表5-7B顯示的是這些股票組合的高標準差。年化標準差在15%~63%。就以最小的標準差計算，組合價值在1年期間也算很正常。很明顯規模與波動性相關，兩個小規模股票組合的波動性較高，而兩個大公司組合的波動性較低。而且價值型股票組合的波動性比成長型股票的高，但兩者之間的差異並不很顯著。

無論怎樣考慮這些組合的收益問題，我們必須首先決定標準差是不是風險的一個合適的測度。表5-7表明部分組合在部分時期表現出負偏，但是所有組合在所有時期都表現出正的峰度。這表明必須謹慎地評估這些偏離對於在險價值（VaR）、預期損失（ES）以及-3σ頻率的影響。最後，因為圖5-6分離出±10%範圍內和±10%收益之外的月度超額收益分佈，我們可以量化這些極端收益產生的影響。

我們從實際收益分佈的VaR與相應正態分佈（相同均值和標準差）的差異分析開始。記住5%VaR是指對應於第5個百分位的收益分佈的損失。它是一個極端結果的風險測度，因為它關注極左側尾部分佈，因此一般稱為尾部風險。我們對比實際VaR與對應的正態分佈VaR來比較歷史尾部風險和正態分佈尾部風險的差異。超額VaR指歷史實際分佈VaR與正態分佈VaR的差異，負數代表更大的損失。

表5-7D顯示整個樣本期VaR值並不比相應正態分佈的尾部風險大。最差的超額VaR（21世紀的大型/價值組合的VaR為-1.71%）比該組合月度收益標準差（6.01%）的1/3還小。

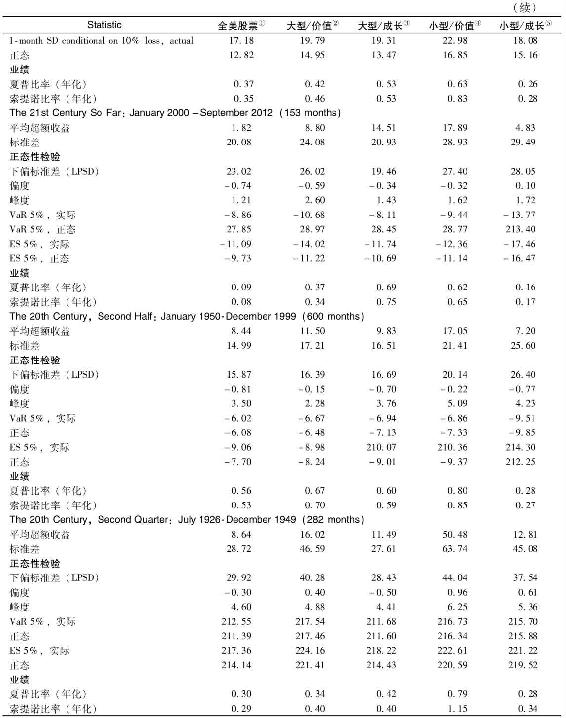
然而另外的風險測度則表明尾部風險較相應正態分佈的大。表5-7中的實際超額收益的預期損失（ES）比相應正態分佈的負值更小（與正峰度為標誌的肥尾一致）。為評價偏離正態分佈的經濟影響，我們在表5-7E中給出各種組合的預期損失與月度收益標準差的分數。負號表明多數-5%的實際觀察值較對應的正態分佈更糟，但是這種差異並不顯著。其量差與月度收益標準差之比從未超過0.77。從整個樣本期看，預期損失沒有超過月度收益標準差的0.44倍。這說明，我們沒有證據表明正態分佈的假設不合適。

表5-7F列示了大於3個標準差的負月度收益或跳躍的實際數量以及正態分佈假設下的數量。在每1000個月實際數為2.9~9.7，而正態分佈下的只有0.6~1.0。這是什麼含義呢？-3σ收益確實是巨大的負面衝擊。為便於理解，我們計算超額跳躍之間的預期時長（以年表示），這裡的超額跳躍是指超出正態分佈的跳躍時長。我們還計算了該段時期的預期收益（以標準差的倍數表示，見表5-7F）。數據表明每9~36年觀察到一次超額跳躍，其間組合的超額收益約為16~104倍標準差。因此跳躍風險似乎對長期股票收益的均值和風險影響不大。

最後，我們剖析±10%收益以外的跳躍幅度，在圖5-6中有預示。為量化風險，我們提出如下問題：當我們觀察1035個月中低於-10%月度收益時，它們的標準差是多少？與這些樣本均值標準差相同的正態分佈下的尾部標準差是多少？表5-7G給出了上述問題的答案。很明顯，正如圖5-6所示，實際的標準差比正態分佈下的標準差要大。在最差的時期實際標準差比正態分佈下的標準差高出近43%。在所有分析過的統計指標中，這也是直接以正態分佈近似實際分佈得出的最可怕的結果。

表5-7D　VaRC除以度標準差

表5-7E　預期損失（除以月度標準差）

表5-7F　-3σ收益

表5-7G　低於-10%月度收益標準差

總結一下，以正態分佈近似組合收益總體上不壞，但是在特殊時期這可能低估投資風險。不過我們可以通過細緻估計極端收益標準差來彌補其缺陷。無論如何，我們在應用正態分佈條件下的理論和推理時應該更加謹慎。總體上，應該確保資產或證券組合的標準差反映尾部風險。

下一章我們將回頭討論這些組合並分析其中的“全美股票”組合是否是風險-收益權衡下的最有效組合。我們也將考慮規模-B/M組合表現的相應調整。不過，對於資產收益近似正態分佈的假設令人欣慰，這使我們的分析更順暢同時也更準確。

5.8.2　全球視野下的歷史數據

隨著全球金融市場的發展，金融市場變得越來越透明化，美國投資者正在謀求通過國際化投資使投資組合更加多元化。一些國外投資者為了降低風險，還投資於可以看作避風港的美國市場作為其本國市場投資的額外補充。這就相應提出了美國股市和全球股市相比表現到底怎樣的問題。

圖5-7列出了16個發達國家股票市場1900~2000年這100年間的平均名義收益率和實際收益率。我們發現從平均實際收益率來看美國排在第4位，處於瑞典、澳大利亞和南非之後。圖5-8列出了這16個國家股票和債券實際收益的標準差，發現股票標準差按照從低到高排列，美國與其他3個國家並列排在第3位。可見，美國的表現還不錯，但是與這些國家相比並不突出。

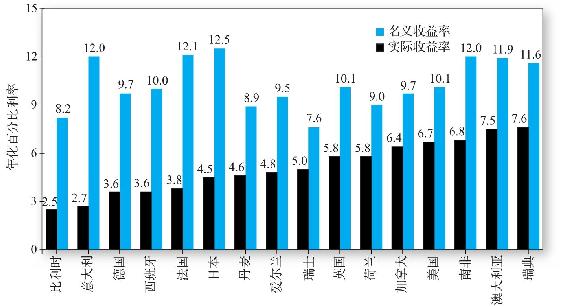
圖5-7　1900~2000年各國股票的名義和實際收益率

資料來源：Elroy Dimson，Paul Marsh，and Mike Staunton，Triumph of the Optimists：101 Years of Global Investment Returns（Princeton：Princeton University Press，2002），p.50.Reprinted by permission of the Princeton University Press.

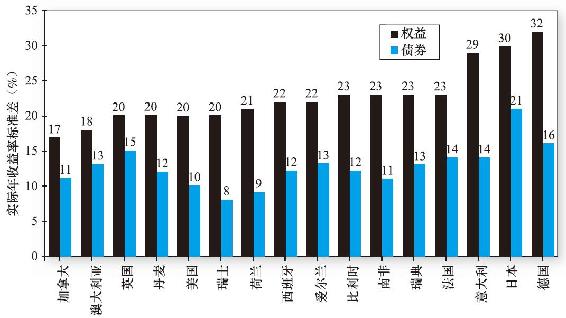
圖5-8　1900~2000年各國股票和債券實際收益率的標準差

資料來源：Elroy Dimson，Paul Marsh，and Mike Staunton，Triumph of the Optimists：101 Years of Global Investment Returns（Princeton：Princeton University Press，2002），p.61.Reprinted by permission of the Princeton University Press.

這些數據一個有趣的特點在於按照平均實際收益率與標準差的比值來計算，表現最差的是意大利、比利時、德國和日本——第二次世界大戰中受創最嚴重的國家；表現最好的國家有澳大利亞、加拿大和美國，而這些國家恰恰是20世紀受戰爭影響最小的國家。此外16個國家的實際收益率差距非常小。平均實際收益率最高的國家（瑞典7.6%）和16個國家的平均值（5.1%）差距只有2.5%。同樣，最低的國家（比利時2.5%）和均值的差距只有2.6%。取平均標準差23%，觀測樣本100個，差距2.6%的t統計量為：

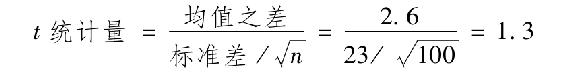
這個數值遠小於常見的t統計量顯著性水平，所以結論是美國的表現不應該作為特例而被排除，美國股票市場作為收益特徵的評判標準是合理的。

最近，業內人士和學者正在爭論：美國大盤股超過短期國庫券7.92%的歷史平均風險溢價是否可以作為長期合理的預測值。這個爭議的焦點落在兩個問題上：第一，歷史上主導的經濟因素是否充分代表了預測假設中主導的經濟因素？第二，歷史所得的算術平均值是否可以作為長期預測的有效基準？

[1] 這類文獻最早開始於他們的1992年文章，“股票的預期截面收益”，Journal of Finance，第47期，427-465.

[2] 這是連續複利計算的超額收益，最接近於正態分佈。下節中再討論這個問題。

[3] 平均收益差的t值為平均收益除以收益差的標準差。