e1 Zvi Bodie 投資學 v10: 5.7 偏離正態分佈和風險度量

e1 Zvi Bodie 投資學 v10

5.7　偏離正態分佈和風險度量

前面可以看出超額收益的正態分佈大大簡化了組合選擇的過程。正態分佈保證標準差是衡量風險的完美度量，因此夏普比率是證券表現的完美度量。然而，很多投資者通過觀察相信資產收益對正態分佈的偏離已經很顯著，不可忽視。

正態偏離可以通過計算收益分佈的高階矩來看到。超額收益R的n階中心矩為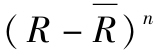，一階矩為0，二階矩為方差的估計值。

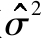（注：對於一個關於均值對稱的分佈，比如正態分佈而言，所有的奇數矩量（n=1，3，5，…）的期望都為零，而所有的偶數矩量都僅僅是標準差的一個函數。比如，四階矩為3σ⁴，六階矩為15σ⁶。因此，對於服從正態分佈的收益率而言，標準差σ提供了風險的全部信息，而資產組合的投資績效可以通過夏普比率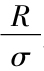來計算。然而對於其他非對稱分佈而言，奇數階矩可能非零。一個比正態分佈更大的偶數階矩，加上一個負的奇數階矩，意味著發生極端惡劣狀況概率的增加。）

一個關於不對稱性的度量，稱為偏度（skew），計算公式如下：

偏差的立方有正有負。因此，如果分佈是右偏，則如圖5-5a中黑色的曲線，偏度為正。左偏如淺色曲線所示，偏度為負。當偏度為正時，標準差高估風險；當偏度為負時，標準差低估風險。

另一個正態偏離的度量考慮分佈兩端極端值出現的可能性，即從圖像上來看有肥尾特徵的情況，分佈的尾部發生的概率較正態分佈預測的要高，分佈中部發生的概率則較正態分佈的低，如圖5-5b所示。這種度量稱為峰度（kurtosis），計算公式如下：

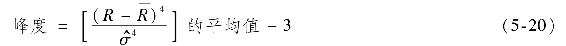
之所以減去3是因為正態分佈的上述比率為3，所以正態分佈的峰度為零，峰度為正則說明存在肥尾現象。圖5-5b中的肥尾曲線峰度為0.35。

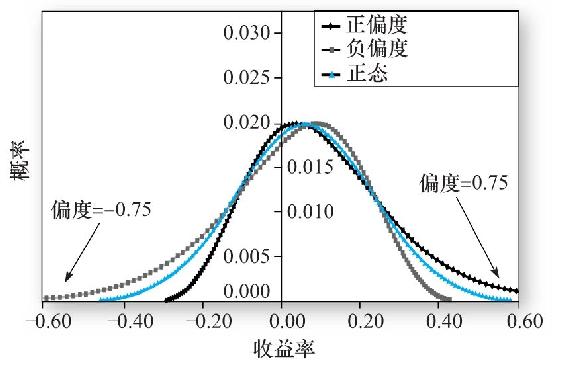
圖5-5a　正態和偏度分佈（均值6%，SD=17%）

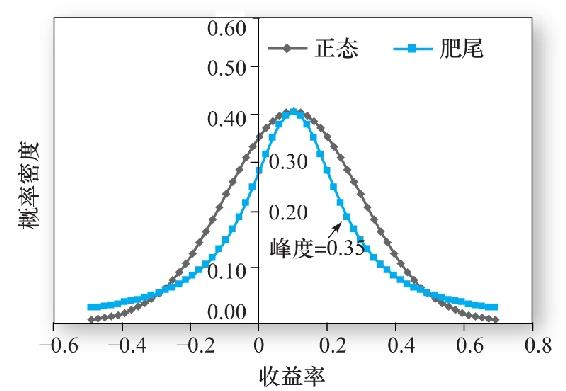
圖5-5b　正態和肥尾分佈（均值0.1，SD=0.2）

極端負值可能由負偏度以及負峰度產生。因此，我們需要一個風險度量來衡量極端負收益率的發生情況。注意偏度和峰度都為純數值。它們不會隨著高頻觀測值的年化而變化。極端負收益的頻繁發生會導致出現負偏和肥尾。因此，我們需要揭示極端負收益發生的風險測度。我們將討論業界最普遍使用的該種測度：在險價值、預期損失、下偏標準差和極端收益頻率（3-sigma）。

概念檢查5-7

估計表5-5中5個概率的偏度和峰度。

5.7.1　在險價值

在險價值（value at risk，VaR）是度量一定概率下發生極端負收益所造成的損失。在險價值一般會寫入銀行的管理條例並由風險管理人員監控。在險價值的另一個名稱是分位數。一個概率分佈的q分位數是指小於這一分位數的樣本點佔總體的比例為q%。因此，當q=50時的分位數就是中位數。從業者通常估計5%的VaR，它表示有95%的收益率都將大於該值。因此，這一VaR實際上是5%的最壞的情況下最好的收益率。

當投資組合的收益率為正態分佈時，VaR可以從分佈的均值和標準差中直接推導出來。標準正態分佈（均值為0，標準差為1）的5%分位數為-1.65，因此相應的VaR為

VaR（0.05，正態分佈）=均值+（-1.65）×標準差

我們可以將觀測值從高到低排列以獲取VaR的估計值，VaR就是樣本分佈的5%分位數。通常，受樣本數量的影響，我們必須對分位數做插值處理。假設樣本由84個年收益率組成（1926~2009年），則5%的觀測的序號為4.2。我們必須在從下往上數的第4個觀測和第5個觀測之間進行插值運算。假設最低的5個收益率為

-25.03%，-25.69%，-33.49%，-41.03%，-45.64%

則相應的VaR在-25.03%和-25.69%之間，並被計算如下

VaR=-25.69+0.2×（25.69-25.03）=-25.56%

5.7.2　預期尾部損失

當我們通過觀測最壞的5%的情況來評估尾部風險時，VaR是所有這些情況中收益率最高（損失最小）的。一個對損失敞口頭寸更加現實的觀點是：關注最壞情況發生條件下的預期損失。這樣的一個值有兩個名稱：預期損失（expected shortfall，ES）或條件尾部期望（conditional tail expectation，CTE），後者強調了其與左尾分佈之間的密切關係。在本書中，我們使用預期損失這一名稱。

我們對前一節VaR的例子進行拓展，我們假設每一個樣本點發生的概率相同。因此，我們需要求最底部的5%的觀測的平均值。和前面的插值過程一樣，我們給最底部的4個值的權重為4/4.2，而給第5個值的權重為0.2/4.2，這樣可以求得ES=-35.94%，顯著小於VaR的值-25.56%。

（注：Jonathan Treussard給出了正態分佈下ES的一個公式（見“The Nonmonotonicity of Value-at-Risk and the Validity of Risk Measures over Different Horizons”，IFCAI Journal of Financial Risk Management，March 2007）。其公式為

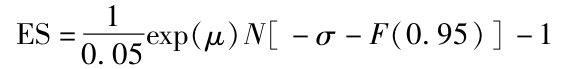
其中μ為連續複利計算的收益率的均值，σ是其標準差，N（·）為標準正態分佈的累計分佈函數，F是其逆函數。在上面的例子中，μ和σ的估計值分別為5.47%和19.54%。正態分佈假設下，我們有ES=-30.57%，這表明這一分佈相比於正態分佈有更大的左尾值。需要注意的是，雖然VaR和ES都是利用歷史樣本估計的無偏估計值，但是仍然可能包含很大的估計誤差。）

5.7.3　下偏標準差與索提諾比率

正態分佈情況下用標準差作為風險的度量存在以下幾個問題：①分佈的非對稱性要求我們獨立地考察收益率為負的結果；②因為無風險投資工具是風險投資組合的替代投資，因此我們應該考察收益對無風險投資收益的偏離而不是對平均投資收益的偏離。

下偏標準差（lower partial standard deviation，LPSD）可以解決這兩個問題。其計算方法和普通標準差的計算相似，但只使用造成損失的那些樣本，即它只使用相對於無風險收益率負偏（而非相對於樣本均值負偏）的那些收益率，類似求方差一樣求這些偏離的平方和的平均值，然後再求其平方根就得到了“左尾標準差”。因此下偏標準差實際代表的是給定損失發生情況下的均方偏離。注意到這樣一個值忽略了負超額收益的頻率，不同的負的超額收益的分佈可能產生相同的下偏標準差值。

從業人員用下偏標準差來替代標準差，同樣也用超額收益率對下偏標準差的比率來替代夏普比率（平均超額收益率對標準差的比率）。夏普比率的這一變形被稱為索提諾比率（Sortino ratio）。

5.7.4　-3σ收益的相對頻率

這裡我們關注大幅度負收益與相同均值和標準差正態分佈相比的相對發生頻率。當股票價格發生大幅度變動時，我們稱這種極端收益為跳躍（jumps）。我們比較低於均值的3倍標準差或以上的收益發生的樣本數與正態分佈下-3σ收益發生的相對頻率。

這一程度對於股票價格下行風險有信息價值，實踐中它在高頻大樣本中更有用。觀察圖5-4，-3σ跳躍的相對頻率為0.13%，即每1000個觀察值中有1.3次。因此，在小樣本中很難得到具有代表性的結果，或者很難反映真實的關於極端變化的統計預期。

在下節分析一些常見投資工具收益的歷史數據時，我們再說明為什麼從業人員需要這麼多統計和績效測度來給風險投資做分析。專欄5-1介紹了這些測度日益受歡迎的程度，特別是對肥尾和極端值的關注。

華爾街實戰5-1　基金不再靠正態曲線度量風險

2008年，一個包含60%的股票和40%的債券的典型投資組合約損失1/5的價值。標準的投資組合理論認為這種情況111年才會發生一次。經典的投資組合理論認為收益率服從一個鐘形分佈，但數學家和投資者都知道市場運行並不像理論假設的一樣完美。如果收益率真的是鐘形分佈，那麼2008年那種下跌發生的概率只可能在概率極小的左尾附近發生，這意味著這種事件幾乎是不可能發生的。

近期的歷史數據表明，發生這種情況的可能性並非如預測的那麼低。在過去20多年裡，投資者們經受了1987年股市崩盤、長期資本管理公司的破產、高科技股泡沫的破裂等事件。

華爾街許多新的金融工具都假設市場收益服從肥尾分佈，在這一假定下，2008年將近40%的股票下跌這種事情發生的概率就比之前要大多了。這些假設給出了對風險的另一種認識。考慮之前提到的60%的股票和40%的債券這樣一種投資組合。在肥尾分佈的假設下，投資組合下跌20%的事件每40年就可能發生一次，而不是之前鐘形分佈假設下的111年。（最近一次像2008年一樣嚴重的危機發生於1931年。）

一個潛在的缺陷是：我們關於稀有事件的歷史樣本太少，以至於很難構建相應的模型。MSCI Barra的首席分析師Lisa Goldberg說：“數據稀缺是個內在的問題。”

新金融工具的發展同樣限制了傳統風險測度的作用。正如諾貝爾經濟學獎得主哈里·馬科維茨於20世紀50年代所指出的，標準差作為一種風險度量可以測量一個投資組合收益率在一段時間內的變化幅度。但是它受收益率向上變化和向下變化的影響相同，而許多投資者相比於獲取利潤而言更害怕遭受損失。同時，標準差也沒有考慮分佈肥尾性的影響。

最近幾十年，一個考慮了下行風險的新風險指標受到越來越多的關注。這一指標就是在險價值VaR，它可以告訴你在一個特定交易日你有5%的概率損失3%以上的投資之類的事情，但它並沒有考慮極端惡劣情況的影響。

為了考慮極端風險，許多公司開始使用預期損失或條件在險價值（conditional VaR）指標，它們代表了當損失超過在險價值時，投資組合的預期損失。條件在險價值估計了不利情況下的預期損失，如J.P.摩根和MSCI Barra等公司都在使用這一指標。