BUSINESS BOOKS

5.6　正態分佈

正態分佈在日常生活中頻繁出現。例如，一個國家或地區全部人口的身高、體重情況都很好地符合正態分佈。實際上，很多由一連串隨機事件構成的變量都會呈現出正態分佈的形態，例如在連續生產中用於向標準容器中灌1加侖（1加侖=3.78立方米）液體的機器每次的灌裝誤差。同樣的邏輯，如果投資者對收益的期望是理性預期，那麼實際收益率應該是服從以此期望為均值的正態分佈。

正態分佈為什麼是“正態”的呢？假設一個報社在生意好的一天賺100美元，生意不好則不賺不賠，且兩種情況發生的概率各為50%。因此，它平均每天的收益是50美元。我們可以據此畫一個二叉樹來描述所有可能發生的狀況，下面的事件樹（event tree）展示了兩天生意可能發生的情況。注意到，兩天會產生3種不同的結果，而總的來說，n天會產生n+1種情況。在上圖情況下，最有可能發生的是生意一天好、一天壞，概率為0.5，兩種極端情況發生的概率各為0.25。

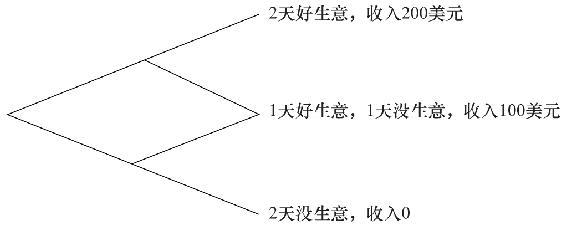
那麼在很多天生意之後利潤情況會是怎樣呢？比如200天之後，可能性達到201種，但是最可能發生的還是位於正中間的結果，而且抵達這種結果的路徑多了很多。比如，只有一條路徑能形成連續200天慘淡生意的結果，然而100天生意興隆、100天生意慘淡的結果卻有很多種排列的可能性。隨著天數的增多，這樣的概率分佈最終會形成大家熟悉的鐘形形狀。^[1]

圖5-4展示的是一個均值為10%、標準差為20%的正態分佈。這個圖形展示了在給定這些參數下各種收益水平發生的理論概率。較小的標準差意味著可能的收益表現更多地聚集在均值附近，較大的標準差則意味著可能實現的收益水平更加分散。任何一個特定收益率實現的概率都由均值和標準差來決定，換句話說，一個正態分佈的形態完全由其均值和標準差這兩個參數來決定。

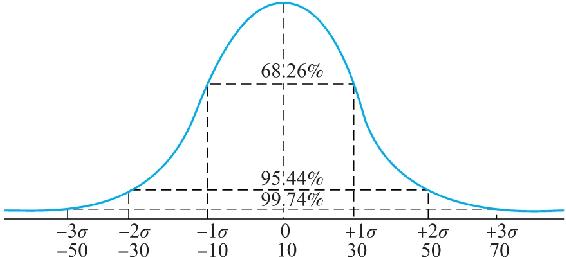
圖5-4　正態分佈（均值10%，標準差20%）

如果收益率的分佈可以用正態分佈來近似擬合的話，投資管理將變得更加有理有據。第一，正態分佈是左右對稱的，也就是說，均值左右程度一樣的偏離其發生的概率也一樣。沒有對稱性的話，用收益的標準差來衡量風險顯然是不合適的。第二，正態分佈具有穩定性，意味著對於具有正態性的不同資產，其構成組合的收益同樣服從正態分佈。第三，當資產或資產組合收益分佈只有兩個變量時，對其未來的情境分析因為需要考慮的變量很少而會變得簡單許多。第四，當構造證券組合時，我們必須考慮證券收益的相關性。總體來說，這種相關性是多層面的。但是如果收益是正態分佈，收益之間統計相關性可以以相關係數來表達。這樣我們在描述任何兩個證券的相關性時只需估計一個參數。

實際的收益分佈需要與正態分佈相似到什麼程度時我們才可以使用正態分佈代替收益的實際分佈呢？顯而易見，收益的分佈是無法用正態分佈完美代替的。比如，與正態分佈不同的是，實際收益率並不會低於-100%，但這並不是說正態分佈就一無是處。在其他環境中類似的問題同樣存在。比如，一個新生兒的體重會去跟所有新生兒體重的分佈做對比，而顯然新生兒的體重並不存在零或負值。但是在這種情況下，仍然使用正態分佈來表示新生兒群體的體重分佈情況，因為體重的標準差和體重的均值相比起來較小，問題中出現負值的概率基本可以忽略不計（注：實際上，均值為3958克，標準差為511克。一個負的體重的概率要在離均值7.74個標準差以外，在正態分佈的假設下，這一情況發生的概率為4.97×10^-15，於是負的出生體重在實際研究中可以不用考慮。）。所以，類似地，我們必須給出一定的標準來決定收益率的正態假設的合理性。

【例5-10】Excel中的正態分佈函數

假定標準普爾500的月收益率近似符合均值為1%、標準差為6%的正態分佈。那麼在任何一個月指數收益為負的概率是多少？使用Excel建立一個函數能很快解決這個問題。在正態分佈函數中觀察的結果小於臨界值的概率用NORMDIST（臨界值，均值，標準差，TRUE）得到。在這個例子中想得到小於零的概率，即計算NORMDIST（0，1，6，TRUE）=0.4338，也可以在Excel中建立標準的正態函數來求均值低於1/6個標準差的概率：NORMDIST(-1/6)=0.4338。

概念檢查5-6

在例5-10中指數收益低於-15%的概率是多少？

[1] 歷史上，早期18世紀對正態分佈的描述基於很多期“二叉樹”的結果，如同我們之前分析的一樣。這一表達在實際中多用於期權定價，第21章會具體介紹。