BUSINESS BOOKS

5.5　歷史收益率的時間序列分析

5.5.1　時間序列與情境分析

在著眼未來的情境分析中，我們設定一組相關的情境和相應的投資回報，並對每個情境設定其發生的概率，最後計算該投資的風險溢價和標準差。相反，資產和組合的歷史收益率只是以時間序列形式存在，並沒有明確給出這些收益率發生的概率，因為我們只觀察到日期和持有期收益率。所以必須從有限的數據中推斷收益率的概率分佈，或者至少是分佈的一些特徵值，比如期望收益和標準差。

5.5.2　期望收益和算術平均值

使用歷史數據時，我們認為每一個觀測值等概率發生。所以如果有n個觀測值，便將式（5-11）中的p（s）替換為1/n，這時期望收益可表示為：

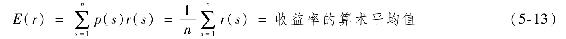
【例5-6】算術平均值與預期收益

表5-5顯示了標準普爾500指數在2001~2005年間持有期收益率的時間序列。在樣本期間中，將n=5的觀察期間每一個持有期收益率看作樣本期間的年度收益，並等可能發生，概率為1/5，表中的B列使用0.2作為概率值，C列顯示每年持有期收益。運用式（5-13），可以得到持有期收益的算術平均值。

表5-5　標準普爾500持有期收益的時間序列

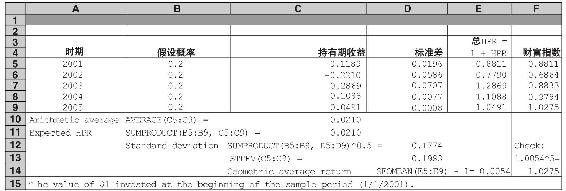
例5-6舉例說明了算術平均值在投資學中廣泛應用的邏輯。如果每個歷史收益的時間序列都真實代表了可能的概率分佈，那麼從歷史數據中計算得到的算術平均值就是預期持有期收益的恰當估計。

5.5.3　幾何（時間加權）平均收益

我們看到算術平均值是期望收益率的無偏估計，那麼關於整個樣本期間的投資組合的實際表現，這些時間序列是如何體現的呢？我們繼續運用例5-6來進行說明。對於比較長時期的結果，我們在後續章節中討論。

表5-5中F列顯示了2001年年初投資1美元在標準普爾500指數上的財富指數。2005年年末財富指數的數值為1.0275美元。這是1美元的最終價值，意味著5年投資持有期收益率為2.75%。

樣本期間的收益表現可以用某一年化持有期收益率來衡量，由時間序列中複利終值反推而得。定義該收益率為g，則有

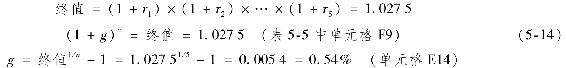
式中，1+g是時間序列的總收益1+r的幾何平均數（可以使用Excel中GEOMEAN命令），g是年化持有期收益率。

投資者稱g為時間加權（區別於貨幣加權）的平均收益，它強調了在平均過程中每個歷史收益為等權重的。兩種平均方法的差別十分重要，因為投資經理作為投資者常常要經歷基金數目顯著變化的情況，可能需要購買或者贖回其投資份額，而規模大時比規模小時能獲得更多的投資回報（或損失），不能單純看收益率。在業績評估一章將更深入討論這種差異。

收益率波動越大，兩種平均方法的差異越大。如果收益服從正態分佈，預期差異為分佈方差的1/2，即

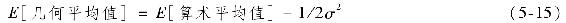
（注意：使用式（5-15）時，需要將收益率換成小數形式，而不是百分數形式。）當收益率服從正態分佈時，式（5-15）的擬合效果較好^[1]。

【例5-7】幾何平均值與算術平均值

例5-6中的幾何平均值0.54%顯著小於算術平均值2.1%。這種差異有時使人們困惑，主要是來自投資收益率的正負對組合終值的影響不同。

觀察到2002年和2003年的收益分別為-0.221和0.2869，這兩年的算術平均值是0.03295。然而，如果你在2002年年初投資100美元，2002年年末你也許只能得到77.90美元。要彌補這個虧損，2003年你需要賺21.1美元，這將得到一個相對巨大的收益率27.09%，為什麼只是彌補虧損，這個數值會比2002年你損失的22.1%大這麼多呢？這是由於你以2003年的數值為基準，這個基準明顯小於100美元。較小的基準就意味著它將產生較大的收益率。即使投資組合在2003年的收益率達到28.69%，即收益為77.90×1.2849=100.25美元，這也只是高於100美元的數值。這揭示了兩年的年化收益率（幾何平均）只有0.12%，明顯小於算術平均值3.295%。

概念檢查5-4

2018年年初投資100萬美元於標準普爾500指數基金。給定2018年收益率為-40%，2019年需要收益率為多少才可以彌補2018年的損失？

5.5.4　方差和標準差

當人們考慮風險時，關注的是偏離期望收益的可能性。實際中，無法直接預期，所以通過偏離期望收益估計值的平方和來計算方差。改動式（5-12），按每個觀測值等概率出現，樣本平均值作為E（r）：

方差=離差平方的期望值

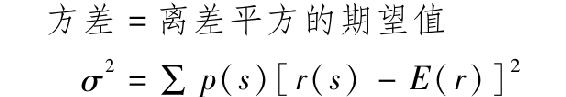
使用歷史數據，估計方差為：

由式（5-16）估計得到的方差是有偏的，這是由於採用的是對樣本算術平均值r的偏差，而不是未知的真實期望E（r），故導致了一些估計誤差。這又稱為自由度偏差，可以通過方差算術平均值與因子n/（n-1）的乘積來消除誤差。方差和標準差變為：

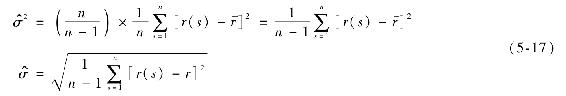
【例5-8】方差和標準差

數據表5-5D列顯示了偏離算術平均值的平方，D12單元格給出標準差為0.1774，為偏離平方與概率乘積和的平方根。

D13單元格顯示了標準差的無偏估計值為0.1983，這略微大於D12中0.1774。如果樣本很大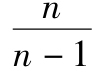，接近於1，這時自由度的調整可以忽略不計。

5.5.5　高頻數據中的均值與方差估計

觀測值的頻率越高是否導致估計值越準確呢？這個問題的答案令人驚訝：觀測值的頻率不會影響均值估計的準確性。樣本時段的長度而非樣本觀測值的數量能改進估計的準確性。

10年總收益率除以10與12乘以120個月平均收益率能提供同樣精度的預期年化收益率估計。平均月度收益率與10年的平均收益率具有一致性，額外的月度收益率觀測值對平均收益估計提供不了額外的信息。但是，更長的樣本期，相比10年的收益率，100年的收益率能提供更準確的收益率估計，這裡有個前提條件，即100年間收益分佈不發生改變。

這裡暗示一個規則：即使使用很長時段的樣本，你依然相信收益分佈不變。不幸的是，老數據往往包括較少的信息。19世紀的數據是否可以用來做21世紀的收益率？可能不行，這說明我們在估計平均收益時受到侷限。

相反，增加樣本值可提高標準差或更高階矩的估計準確性。所以我們可以用變頻觀測值來提高標準差和更高階矩的估計準確性。

標準差估計先從方差估計開始。當日度收益不相關時，月度方差可以簡單相加。當月度方差相同時，年化方差等於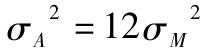。^[2]總的來說，T個月的方差等T乘以單個月的方差。所以，標準差的增長率為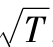，即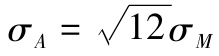。均值和方差隨時間段成比例增長，而標準差隨時間段長度的平方根的增長而增長。

5.5.6　收益波動性（夏普）比率

【例5-9】夏普比率

參見表5-4，投資股指基金的情境分析得到5.76%的風險溢價，超額收益的標準差為19.49%。這表明夏普比率等於0.3，與歷史股指基金的業績一致。在下面的一些章節中將繼續討論這種重要的度量方法，證明它在度量分散化投資組合風險-收益的權衡時是一種合適的方法，但是將其運用在單個資產比如投資組合中的單個股票時是不合適的。

概念檢查5-5

用表5-5中2003~2005年的年度收益。

a.計算算術平均收益。

b.計算幾何平均收益。

c.計算收益的標準差。

d.計算夏普比率，假設無風險利率為6%。

最後，必須注意到，應該假定投資者關注的是他們購買投資組合相對於國庫券獲得的預期超額收益和相應的風險。儘管國庫券的利率不固定，我們仍然知道購買債券並持有到期的收益。其他投資比安全的國庫券收益率更高，也難免帶來更多的風險。投資者為風險資產定價使得其風險溢價能夠彌補預期超額收益帶來的風險。這樣利用溢價的標準差代替總收益標準差來衡量風險更好。

收益（風險溢價）和風險（通過標準差來衡量）之間的權衡意味著人們需要利用投資的風險溢價與標準差的比率來度量投資組合的吸引力。

注意，夏普比率將風險溢價（與時段長度等比例變化）除以標準差（與時段長度為平方根關係）。因此，用高頻收益計算年化收益時夏普比率增大。例如，用月度收益計算年化夏普比率，分子乘以12，分母乘以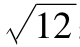；這樣年化的夏普比率為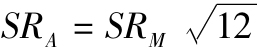。總體來說，一項長期投資為T年的夏普比率以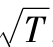比率增加。

這一比率被廣泛用於評估投資經理的業績。

[1] 我們被告知，度量某時段的歷史收益時採用幾何平均值，而估計未來收益表現時用算術平均。問題是，如果同樣的樣本出現在未來，收益採用幾何平均，那麼這是否是預期收益的最佳估計呢？令人驚訝的是，答案是否定的。未來的結果總是包括正的或負的意外（與預期相比）。一連串的正的意外相對一連串負的意外對期末財富影響較大。正因為這種非對稱性，幾何平均是對未來平均收益的低估。這個低估等於方差的一半，所以採用算術平均來糾正這個誤差。

[2] 當月度收益不相關時，我們可以不關心它們之間的協方差。12個月度收益之和的方差等於12個月方差之和。如果月度收益相關，年化方差時需要調整收益之間的序列相關性。