BUSINESS BOOKS

5.4　風險與風險溢價

5.4.1　持有期收益率

假設你正在考慮投資於股票指數基金。每一份額的現價為100美元，持有期為1年。實現的投資收益率由每份額年末價格和這一年的現金股利決定。

假定每份額的期末價格為110美元，這一年的現金股利為4美元。實現的收益率，也叫作持有期收益率（HPR，holding-period return，在這種情況下，持有期為1年）可以表示如下：

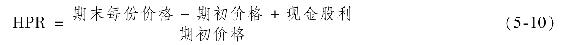
本例中

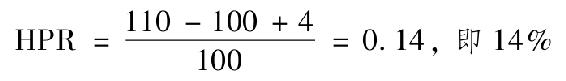
持有期收益率的定義假設股利在持有期期末支付。如果股利支付提前，那麼持有期收益率便忽略了股利支付點到期末這段時間的再投資收益。來自股利的收益百分比被稱為股息收益率（dividend yield），所以股息收益率加上資本利得收益率等於持有期收益率。

5.4.2　期望收益率和標準差

1年以後的每份基金價格和股利收入具有很大的不確定性，所以無法確定最終的持有期收益率。我們將市場狀況和股票指數市場進行情境分析，將其分為四種情況，如表5-4A~E欄所示。

表5-4　股票指數基金持有期收益率的情境分析

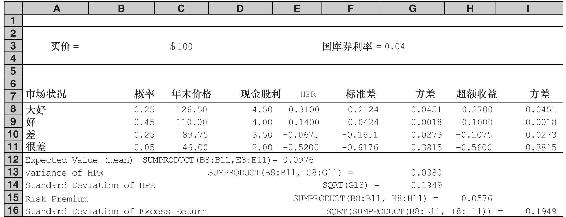
我們怎樣來評價這種概率分佈？通過本書，我們將會用期望收益率E（r）和標準差σ來表示收益率的概率分佈。期望收益值是在不同情境下收益率以發生概率為權重的加權平均值。假設P（s）是各種情境的概率，r（s）是各種情境的持有期收益率，情境由s來標記，我們可以將期望收益寫作

將表5-4中的數據運用到式（5-11）中，我們會得到該股票指數基金的期望收益率為

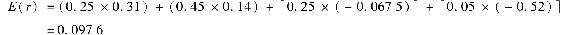
表5-4表明這個和可以很簡單地由Excel得出，運用SUMPRODUCT公式先計算出一系列數字對的乘積，然後將這些乘積相加。在此，數字對是每種情境出現的概率和收益率。

收益率的標準差（σ）是度量風險的一種方法。它是方差的平方根，方差是與期望收益偏差的平方的期望值。結果的波動性越強，這些方差的均值就越大。因此，方差和標準差提供了測量結果不確定性的一種方法，也就是

因此，在本例中

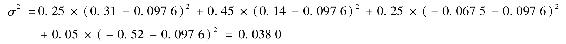
這個值已經運用SUMPRODUCT公式在表5-4的G13格計算出來。在G14格的標準差可以這樣計算：

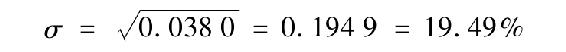
顯然，困擾該指數基金潛在投資者的是一個市場崩盤或市場變壞的下跌風險，而不是市場變好帶來的上漲潛力。收益率的標準差並沒有區分好的市場或是壞的市場。它在兩種情況下都僅僅表達的是對平均值的偏離程度。只要概率分佈大致是關於平均值對稱的，標準差就是一個風險的適當測度。在特殊情況中我們可以假設概率分佈為正態分佈（即眾所周知的鐘形曲線），E（r）和σ就可以完美地刻畫出分佈。

5.4.3　超額收益和風險溢價

你應該投資多少到指數基金中？首先，你必須知道承擔股票投資風險可以期望的收益有多高。

我們把收益表示成股票指數基金的預期持有期收益率和無風險收益率（risk-free rate）的差值，無風險收益率是當你將錢投入無風險資產比如說短期國庫券、貨幣市場基金或者銀行時所獲得的利率。我們將這種差值稱為普通股的風險溢價（risk premium）。在我們的例子中無風險年利率為4%，預期指數基金收益率為9.76%，所以風險溢價為每年5.76%。在任何一個特定的階段，風險資產的實際收益率與實際無風險收益率的差值稱為超額收益（excess return）。因此，風險溢價是超額收益的期望值，超額收益的標準差是其風險的測度。

概念檢查5-3

你投資27000美元於一個公司債券，每1000美元面值債券售價為900美元。在第2年，1000美元債券能夠提供的利息是75美元。年末債券的價格取決於當時的利率水平。你依據以下情境分析：

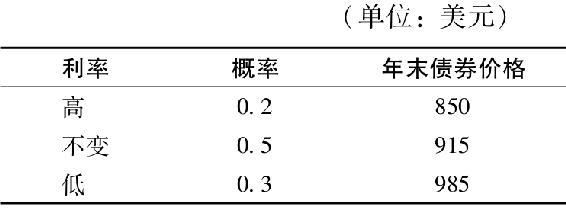
你的另一種投資則是國庫券，它能夠提供的收益率為5%。計算每種情況的持有期收益率、E（r）和風險溢價。你投資的年末期望價值是多少？

投資者投資股票的意願取決於其風險厭惡（risk aversion）水平。投資者是風險厭惡的，當風險溢價為零時，人們不願意對股票市場做任何投資。理論上說，必須有正的風險溢價來促使風險厭惡的投資者繼續持有現有的股票而不是將他們的錢轉移到其他無風險的資產中去。

雖然情境分析解釋了量化的風險和收益背後的概念，你可能仍然想知道對於普通股票和其他證券來說怎樣更加準確地估計E（r）和σ。歷史給我們提供了敏銳的視角。歷史上關於有價證券收益的記載運用了各種各樣的概念和統計工具，所以首先讓我們來做一個初步討論。