e1 Zvi Bodie 投資學 v10: 5.2 比較不同持有期的收益率

e1 Zvi Bodie 投資學 v10

5.2　比較不同持有期的收益率

考慮一個尋求安全投資的投資者，比如投資美國國庫券^[1]。假設我們觀察很多不同期限的零息票國庫券。零息票債券會在第14章進行更深入的討論，簡單地說是以票面價值折價出售，收益來自購買價和最終票面價值^[2]的差價。假設國庫券價格為P（T），面值為100美元，持有期為T年。我們把期限為T年的無風險收益率表示成投資價值增長的百分比。

當T=1時，式（5-6）提供了1年期的無風險收益率。

【例5-2】年化收益率

假定面值為100美元的零息國庫券的價格和不同的年限如下所示。我們運用式（5-6）可以計算出每一種證券的總收益率。

不出意料的是，在例5-2中持有期越長，總收益率越高。我們應該怎樣比較不同持有期的投資收益呢？這就需要我們將每一個總收益換算成某一常用期限的收益率。我們通常把所有的投資收益表達為有效年利率（effective annual rate，EAR），即一年期投資價值增長百分比。

對於1年期的投資來說，有效年利率等於總收益率r_f（1）。總收入（1+EAR）是每一美元投資的最終價值。對於期限少於1年的投資，我們把每一階段的收益按複利計算到1年。比如，對例5-2中6個月的投資，我們按2.71%的收益率複利計算得到1年後的投資終值1+EAR=1.0271²=1.0549，意味著EAR=5.49%。

對於投資期長於一年的投資來說，通常把有效年利率作為年收益率。比如，例5-2中，持有期為25年的投資在25年裡增長了4.2918（也就是1+3.2918）。所以有效年利率可以表達為：

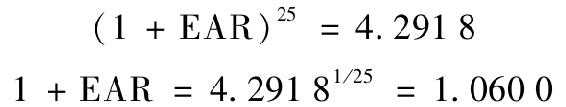
總的來說，我們可以把有效年利率與總收益率r_f（T）聯繫在一起，運用下面的公式計算持有期為T時的回報。

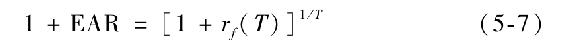
我們可以用一個例子來說明。

【例5-3】有效年收益率與總收益率

對於例5-2中的6個月的國債來說，T=1/2，1/T=2，因此

1+EAR=（1.0271）²=1.0549，EAR=5.49%

對於例5-2中25年的國債來說，T=25，因此

1+EAR=4.2918^1/25=1.060，EAR=6.0%

5.2.1　年化百分比利率

短期投資（通常情況下，T＜1）的年化收益率是以簡單利率而不是複利來報告的。這被稱為年化百分比利率（annual percentage rate，APR）。比如，當涉及月收益率（例如信用卡的利率）時，年化百分比利率即為12乘以月率。通常說來，如果把一年分成n個相等的期間，並且每一期間的利率是r_f（T），那麼，APR=n×r_f（T）。反之，你可以通過年化百分比利率得到每個期間的實際利率r_f（T）=T×APR。

通過這個過程，例5-2中6個月債券（6個月的利率為2.71%）的年化百分比利率為2×2.71=5.42%。概括一下對一個期限為T的短期投資來說，每年有n=1/T個複利計算期。因此，複利計算期、有效年利率和年化百分比利率的關係可以用下面的公式來表示

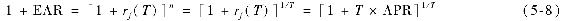
即

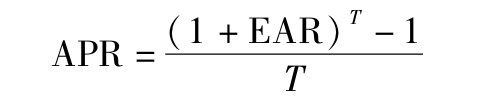
【例5-4】有效年利率與年化百分比利率

在表5-1中我們運用式（5-8）可以得出有效年利率為5.8%的與不同複利計算期限時相對應的年化百分比利率。相反，我們同樣可以得到年化百分比利率為5.8%時有效年利率的值。

表5-1　年化百分比利率和有效年利率

5.2.2　連續複利

從表5-1（和式（5-8））中可以明顯地看到年化百分比利率和有效年利率隨複利計算頻率變化而產生的差異。隨之而來的問題是，隨著計算利息的頻率不斷提高，年化百分比利率和有效年利率的差異可以達到多大？換句話說，當T不斷變小的時候，（1+T×APR）^1/T的極限是多少？當T趨近於零，我們得到連續複利（continuous compounding），並且可以用下面的指數函數得到有效年利率與年化百分比利率（在連續複利時，用r_cc表示）的關係：

e大約為2.71828。

為了從有效年利率得出r_cc的值，我們將式（5-9）化簡，如下所示：

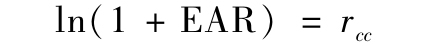
這裡ln（·）是一個自然對數函數，是exp（·）的反函數。指數函數和對數函數都可以在Excel中進行計算，分別叫作EXP（·）和LN（·）。

【例5-5】連續複利利率

當給定有效年利率為5.8%時，連續複利計算的年化百分比利率r_cc為5.638%（見表5-1），與按日複利計算的年化百分比利率差不多。但對複利頻率較低的利率（比如半年）來說，為了得到相同的有效年利率，年化百分比利率的值竟然高達5.718%。也就是說當計算複利頻率較低時，達到相同有效回報所需的年化百分比利率會更高。

概念檢查5-2

一家銀行提供給你兩種3年定期存款100000美元的利率選擇：①月利率1%；②年連續複利利率12%，你選擇哪一個？

儘管連續複利看起來是煩瑣的數學，但在很多情況下運用這種利率能夠簡化預期回報和風險的計算。舉例來說，在連續複利情況下，對於任何期限T，總收益r_cc（T）就可以簡單表示為exp（T×r_cc）^注1。換言之，總收益與時間階段T之間成正向關係。這比用指數按不同階段的複利計算要簡單得多。另一個例子是，回顧式（5-1），實際利率rr、名義利率rn和通貨膨脹率i之間的關係rr≈rn-i，只是一個近似值，式（5-3）已給予證明。但是當我們將所有的利率都看作連續複利，式（5-1）就是完全準確的^注2，也就是r_cc（實際利率）=r_cc（名義利率）-i_cc。

注1：推導自式（5-9）若。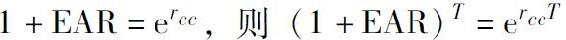

注2：

[1] 國庫券收益和不同期限債券的收益率可以在網絡上找到，比如雅虎財經、MSN財經或者直接從美聯儲獲取。

[2] 美國財政部發行的短期國庫券為零息債券，期限最長為1年。而金融機構通過購買一般國庫券進行本息分離來構造最長達30年的零息票國庫券。此內容第14章有詳細介紹。