BUSINESS BOOKS

12.7　總項目時間估算

為了計算項目按時完成的概率，必須知道每一活動標準差，標準差可從如下表達式獲得：

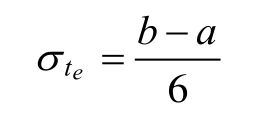
其中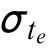 為期望時間te 的標準差。另一個有用的表達式是方差ν ，它是標準差的平方。方差主要用於期望值的比較，然而，除了確定是否一個、兩個還是三個σ區間方差外，使用標準差確實簡單。圖12-15表示了圖12-6的關鍵路徑、計算期望時間的相關值及標準差。整個路徑標準差通過各活動標準差平方和的平方根計算而得，如下表達式：

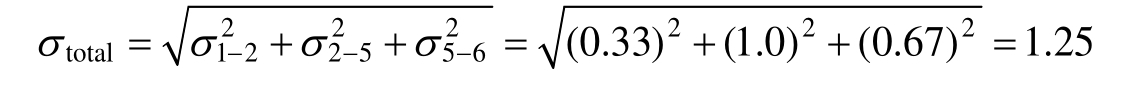
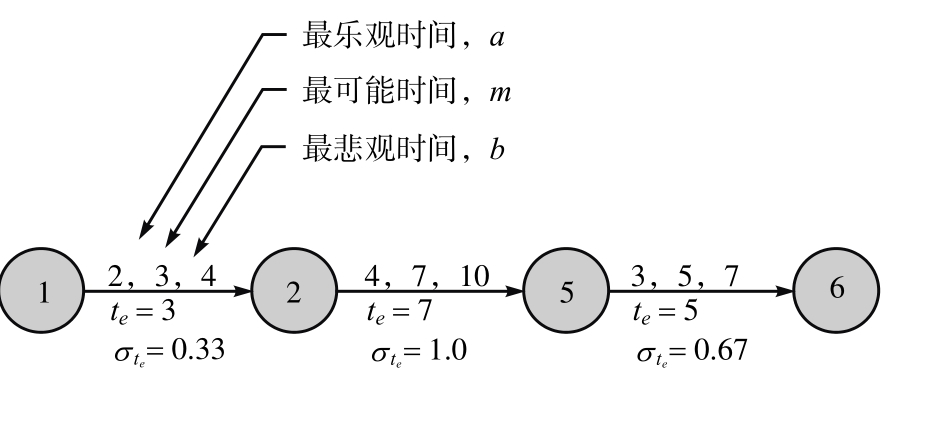
圖12-15　關鍵路徑事件的期望時間分析

計算σ的目的在於它可以為每項活動和關鍵路徑設立一個置信區間。從統計學的角度講，使用正態分佈的方法，我們知道一個標準差內完成項目的概率是68%；兩個標準差內完成項目的概率是95%；三個標準差內完成項目的概率是99.73%。

這種分析方法可以用在計算評估時存在的風險、完成每項活動的風險以及完成整個項目的風險。換句話說，標準偏差、σ 是風險測量的一種手段。這種分析方法以正態分佈的運用為前提，然而現實中往往不是這樣的。

舉個衡量風險的例子，一個網絡在關鍵路徑上只有3個活動，如下：

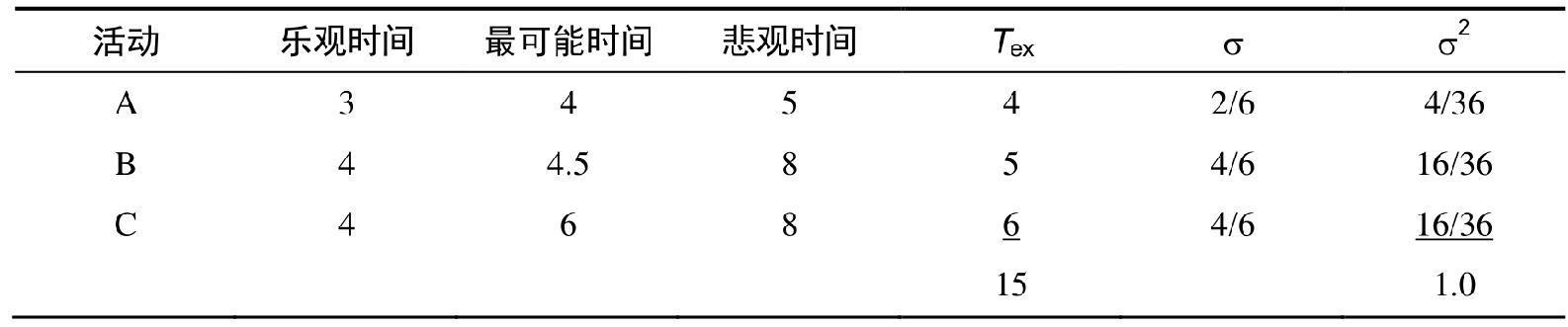
從上面的表格看出，關鍵路徑的長度是 15周。方差（也就是 σ2 ）是 1.0，那麼 σpath （方差的平方根）一定是1周。

現在我們可以計算在一定時間限制內完成項目的可能性有多大：

• 在16周內完成工作的可能性是50%+(1/2)×(68%)，即84%。

• 在17周內，可能性是50%+(1/2)×(95%)，即97.5%。

• 在14周內，可能性是50%−(1/2)×(68%)，即16%。

• 在13周內，可能性是50%−(1/2)×(95%)，即2.5%。