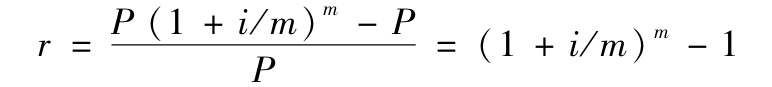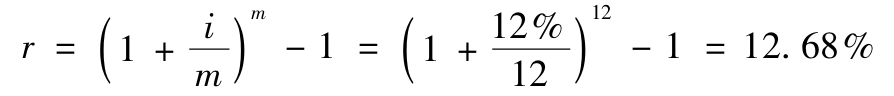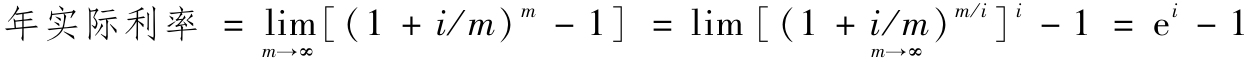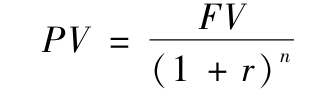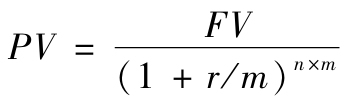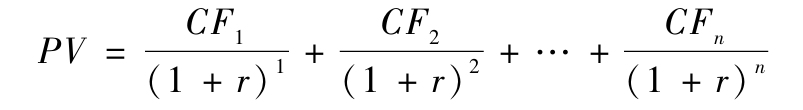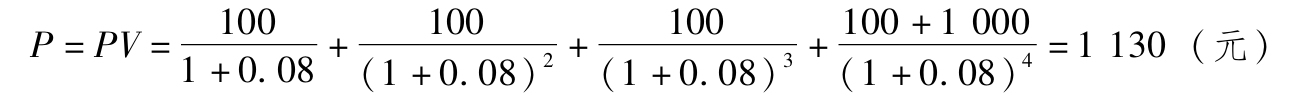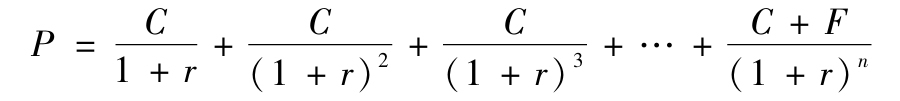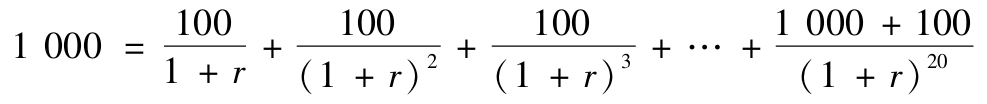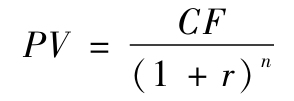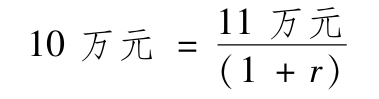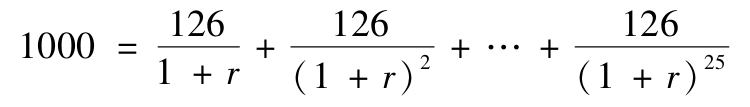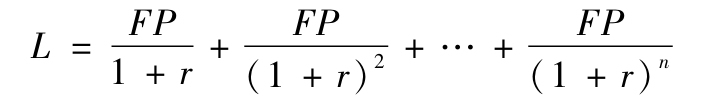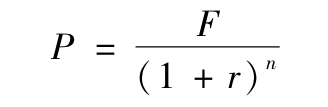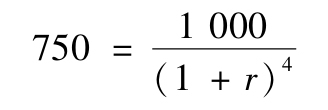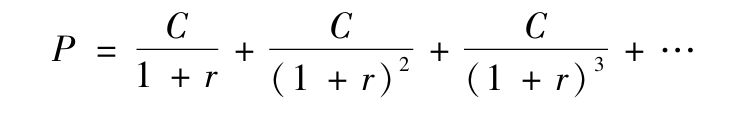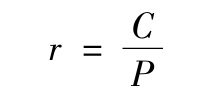e5 貨幣金融學 v2 蔣先玲
第二節 利息的計算與運用
一、單利與複利
利率的出現使各種金融工具的利息可以計算、量化,但不同的計算方法會得出不同的結果。利息有兩種基本的計算方式,即單利和複利。
(一)單利
單利 (simple interest) ,是指以本金為基數計算利息,而借貸期內所生利息不再加入本金計算下期利息的一種利息計算方法,即在當期產生的利息不作為下一期的本金,只是把每一期產生的利息累加到投資期末。其計算公式為:
利息為I=P×r×n
本利和為S=P+I=P(1+r×n)
式中,I為利息額;P為本金;r為年利率;n為借貸期限;S為本金與利息之和,簡稱本利和。
例如,一筆5年期限、年利率為6%的10萬元貸款,在單利計息的情況下,貸款到期時利息總額為30000(=100000×6%×5)元,本利和為130000(=100000+30000)元。
(二)複利
複利 (compound interest) ,俗稱“利滾利”,是指本期產生的利息自動計入下一計息期的本金,連同原來的本金一併計息的一種利息計算方法。其計算公式為:
本利和為S=P(1+r)n
利息為I=S-P
承上例,在複利計息的情況下,本利和大約為133823(=100000×(1+6%)5 )元,利息則為33823(=133823-100000)元。可見,按複利計息的利息比單利計息多3823(=33823-30000)元。顯然,複利反映了利息的本質,因為利息在未清償時也相當於債權人借給債務人使用的資本,應算為債權人的本金範疇。這樣處理對債權人、債務人雙方較為公平、合理。
如果一年內計息次數(或複利次數)為m次,此時,複利下的本利和為:
S=P(1+r/m)mn
承上例,如果改為每月計息一次,則一年內計息次數為12次,5年後的本利和為:
S=100000×(1+6%÷12)12×5 =134885(元)
可得,利息為34885元,比每年計息一次的利息多1062(=34885-33823)元。可見,複利計息次數越多,利息額就越大,因而對債權人越有利。
最極端的例子是計算瞬間複利或連續複利,即每一秒鐘都在生息。計算連續複利的公式為:
S=ern P
式中,e=2.71828…,即自然對數的基。那麼,在同樣的條件下,連續複利會不會是一個天文數字呢?仍以上面的條件為例,連續複利為S=ern P=e0.06 ×5 ×100000=134986(元),利息為I=134986-100000=34986(元)。
可見,在上面的例子中,即使每秒鐘都計算利息,與一年計算一次相比,利息也不過多了1163(=34986-33823)元。
(三)複利計算下的名義利率與實際利率
當計息週期小於一年的時候,一個問題就會出現:如何將名義利率轉化為實際利率呢?推導過程如下。
設年名義利率為i,一年內計息次數為m次,則計息期利率為i/m,則有:
一年後本利和為S=P(1+i/m)m
利息為I=P(1+i/m)m -P
換算成年實際利率r,則為:
這就是在複利計息的情況下年名義利率i與年實際利率r的換算公式,二者的關係是:當m=1時,即一年計算一次利息時,年名義利率等於年實際利率;當m>1時,即一年計息多次時,年實際利率大於年名義利率。計算次數越多,年實際利率越大。
例如,在每月計息一次的情況下,對於年名義利率為12%的貸款,其年實際利率為12.68%:
再如,如果有一筆貸款,按月計息,月利率為0.8%,該貸款的年利率是多少呢?根據上面的公式,該貸款的年利率應為(1+0.8%)12 -1=10.03%,而不是9.6%(=12×0.8%)。
同樣,當m→+∞,即按連續複利計息時,年實際利率的計算公式為:
例如,對於一筆年利率為12%的貸款,在連續複利的情況下,其年實際利率為12.75%(=ei -1=e0.12 -1)。
因此,一年內計息次數越多,其摺合成的年實際利率就越高(12.75%>12.68%)。
二、現值
(一)現值的概念
複利公式在經濟生活中應用很廣,現值就是一例。
準確來講,現值 (present value,PV) ,是指將未來某一時點或某一時期的貨幣金額(現金流量)折算至基準年的數值,也稱折現值。它是對未來現金流量以恰當的折現率進行折現後的價值。將前述複利公式進行一般化處理,即用FV代表未來某一時點的資金,稱為終值 (future value) ;用PV代表現在的一筆資金,即現值,則得到以年為時間單位計算的現值公式為:
以小於年的時間單位計算的現值公式為:
未來系列現金流量的現值公式為:
通俗地說,通過利率可以計算出現在的一筆資金在未來值多少,也可以計算出未來的一筆資金等於今天的多少,這就是終值與現值的概念。
專欄3-1
彩票中獎的價值是多少
現值的概念非常有用。一種有趣的用途是確定彩票中獎金額究竟價值多少。例如,加利福尼亞州政府通過廣告宣稱,它有一項彩票的獎金為100萬美元,但那並不是獎金的真正價值。事實上,加利福尼亞州政府承諾在20年內每年付款5萬美元。你當然十分興奮,可是你真的贏得100萬美元了嗎?
從現值的意義來講不是這樣的,你所得到的100萬美元折算成今天的價值要少得多。如果我們假定利率是10%,第一次支付的5萬美元顯然等於今天的5萬美元。但第2年支付的5萬美元用今天的價值來衡量,只有50000美元/(1+0.10)=45454.5美元,遠遠小於5萬美元。接下來一年支付的5萬美元的現值為50000美元/(1+0.10)2 =41322.3美元,依此類推。將所有這些現值相加,結果為468246美元。你仍然會十分興奮,但由於懂得現值的概念,你清楚地意識到你受到了廣告的愚弄。因為你事實上並沒有贏得100萬美元,你所得到的還不到100萬美元的一半。
(二)現值的運用
現值公式是一個非常重要的公式,在整個金融學的學習中會反覆使用。需要注意的是,在計算現值時使用的利率通常被稱為貼現率 [1] (discount rate) ,即使未來值與現在值相等的利率。
從上述公式可以看出,現值的基本特徵是:①終值越大,現值越大。②時間越短,現值越大,這一點很好地體現了貨幣的時間價值。③貼現率越小,現值越大。
應用一:評價未來資金與現在資金的價值關係
例如,如果從現在起2年後要買15000元的東西,假定利率為10%,那麼現在需要存多少錢呢?
這就是一個求現值(本金)的問題,代入上面現值的公式,可得到:
PV=FV/(1+i)n =15000/(1+10%)2 =12396.7(元)
即大約要存入12396.7元,你在2年後才能取出15000元。換句話說,在利率為10%的情況下,現在的12396.7元與2年後的15000元價值是相等的。
應用二:評價有價證券的理論價格
例如,某國債的面值是1000元,息票利率為10%,期限4年,假定某投資者要求的收益率為8%,向該投資者能以面值購買嗎?其市場價格應為多少?
將該國債的投資收益(包括本金)根據8%的收益率折現為現值,此現值之和就是該國債的理論價格。即
該國債的理論價格為1130元,即只有以1130元購買,投資者才會實現8%的投資收益率。因此,投資者不會以面值來購買。
三、到期收益率
(一)到期收益率的概念
在上面計算現值時,我們都假定收益率是多少,再將未來一筆資金折現為現值。即在現值公式中,給定利率和現金流量,計算出來的值就是現值。現在將問題倒過來,給定未來現金流量和現值,要計算利率(收益率),這個利率就是到期收益率。
到期收益率是一個非常重要的利率概念,甚至被經濟學家視為衡量利率的最為精確的指標。例如,在利率期限結構理論(見本章第四節利率期限結構相關內容)中,收益曲線就是描述到期收益率與時間的關係,儘管人們會簡化為利率與時間的關係。另外,在上面計算現值時是給定利率的,實際上,這一利率就是到期收益率或必要回報率。因此,到期收益率是一個非常關鍵的利率指標。
到期收益率 (yield to maturity,YTM) ,是指使某金融工具未來所有收益的現值等於其當前市場價格的利率。簡單地說,到期收益率是這樣一種利率,它剛好使得某種金融工具的現值與其現行市場價格相等。
以債券為例,按單利計算的債券到期收益率,是指買入債券後持有至期滿得到的收益(包括利息收入和資本損益)與買入債券的市場價格之比,也就是前述持有到期時的實際收益率。計算公式為:
到期收益率=(票面利息±本金損益)/市場價格
例如,某種債券的票面金額為100元,10年還本,每年利息為7元,張三以95元買入該債券並持有到期,那麼他每年除了得到7元利息收益外,還獲得0.5(=(100-95)/10)元的本金盈利。這樣,他每年的實際收益就是7.5元,其到期收益率為7.90%(=7.5/95)。
在實踐中,到期收益率多數按複利計算,且由於債券等固定收益證券的利息收入容易獲得,在計算其價格時只需確定貼現率(利率)即可。因此,作為利率精確指標的到期收益率在債務工具中使用普遍,它是指能使未來收益現值等於債務工具當前市場價格的貼現率。其計算公式根據不同的債券工具有所不同,下面分別介紹。
(二)到期收益率的估算與運用
為了更好地理解到期收益率,下面考慮四種典型的債務工具到期收益率的計算:息票債券、銀行貸款、貼現債券和永久債券。
1.息票債券的到期收益率
息票債券 (coupon bond) 又稱附息債券,是指按期支付定額利息,到期償還本金的債券。息票債券概念的來源是,早期這種債券的券面上都印有“息票”或“息票附券”,作為按期(一般為6個月或1年)支付利息的憑據。債券持有人在持有期內付息時,便從債券上剪下息票附券憑以領取本期的利息。當然,現在息票債券已沒有這種利息附券了,只是規定票面利率而已。息票債券往往適用於期限較長或在持有期限內不能兌現的債券。息票債券一般是固定利率,也是最常見的債券付息方式。
息票債券的到期收益率公式為:
或簡單地表示為:
式中,r為到期收益率;P為債券的當前價格;C為每期利息;F為面值。
例如,對於面值為1000元,票面利率為10%的20年期息票債券,某投資者平價購買並持有至到期,該債券的到期收益率是多少?
根據到期收益率公式,有:
計算得r=10%,即該息票債券的到期收益率為10%。這一結果與債券的票面利率相等,表明到期收益率等於票面利率有著嚴格的前提條件,即息票債券的價格等於其面值。一旦債券的現行價格不等於其面值,那麼到期收益率也就不再等於票面利率了,其可能低於或高於票面利率,這取決於債券價格是高於還是低於面值。
根據上面的計算公式,可知息票債券的到期收益率與其票面利率之間存在著以下關係:第一,債券價格高於面值(溢價出售)時,到期收益率低於票面利率;第二,債券價格低於面值(折價出售)時,到期收益率高於票面利率。第三,債券價格等於面值時,到期收益率等於票面利率。
從以上到期收益率與票面利率的關係不難看出,息票債券的到期收益率與價格是負相關的。也就是說,隨著債券價格上升,到期收益率會下降;反之,隨著債券價格下降,到期收益率會上升。
2.銀行貸款的到期收益率
首先,以簡單貸款為例,即貸款人向借款人提供一定數額的資金,借款人在到期日前一次性歸還本金及利息。許多貨幣市場工具都屬於這種類型,如對企業發放的短期商業貸款和對個人發放的小額裝修貸款等。根據到期收益率的概念,簡單貸款的到期收益率十分易於計算。例如,傑克向銀行借款10萬元,期限1年,1年後償還銀行11萬元本利和,問銀行發放這筆貸款的到期收益率是多少呢?
根據現值的定義有:
式中,PV為貸款金額10萬元;CF為1年後的現金流11萬元;n為年數1。
因此,有:
計算得r=0.10×100%=10%,可以看出,到期收益率與貸款的利率相等。於是得出結論,對於簡單貸款來說,利率等於到期收益率。
再來看固定支付貸款,所謂固定支付貸款,也稱分期償還貸款,是指貸款人向借款人提供一定數量的資金,在約定的若干年內借款人每個償還期(如每年或每月)償還固定的金額給貸款人,其中既包括本金,也包括利息。例如,如果你向銀行借款1000美元,銀行要求你在25年內每年償還126美元,那麼這筆貸款的到期收益率是多少呢?
根據到期收益率的定義,我們有:
式中,r就是這筆貸款的到期收益率。
更一般地,對於任何固定支付貸款,有:
式中,L為貸款額;FP為固定支付額;n為貸款期限。
式中的貸款額、每年固定支付額和貸款期限都是已知的,只有到期收益率是未知的。因此,我們可以從這個等式中求解到期收益率r。由於這一計算比較煩瑣,許多財務計算器都提供了根據貸款金額L、每年固定支付額FP、貸款期限n等信息求解到期收益率的程序。
3.貼現債券的到期收益率
貼現債券 (discount bond) ,又稱貼水債券,是指在票面上不規定利率,發行時按某一折扣率(貼現率),以低於票面金額的價格發行,到期按面額償還本金的債券。發行價與票面金額之差即為利息。例如,投資者以70元的發行價格認購了面值為100元的5年期債券,那麼在5年到期後,投資者可兌付到100元的現金,其中30元的差價即為債券的利息,年息平均為8.57%(=(100-70)÷70÷5×100%)。美國的短期國庫券和日本的貼現國債,都是較為典型的貼現債券。我國1996年開始發行貼現國債,期限分別為3個月、6個月和1年。
貼現債券的到期收益率r的計算公式為:
假設某公司發行的貼現債券面值是1000元,期限為4年,如果這種債券的銷售價格為750元,則其到期收益率為7.5%。
解得r=7.5%。
4.永久債券的到期收益率
永久債券是指定期支付固定息票利息,沒有到期日,不必償還本金的一種債券。假設永久債券每年年末支付利息額C,債券市場價格為P,則其到期收益率r的計算公式為:
根據無窮遞減等比數列的求和公式可知,上式的右邊等於C/r,因此永久債券的到期收益率計算公式可以簡化為:
例如,每年可得到利息收入100元、價格1000元的永久債券,到期收益率為10%(=100/1000×100%)。
以上介紹了四種典型的債務工具的到期收益率計算方法。瞭解到期收益率的含義之後,我們就不難正確回答可能容易迷惑的問題,如永久債券不償還本金,零息債券不支付利息,還有人買嗎?答案是肯定的,因為它們如果能夠給持有者帶來合適的到期收益率,就會有投資者購買。
[1] 貼現一詞在經濟學或金融學的教科書中經常被提到,但是在不同的地方有不同的含義。在這裡,它是指已知終值求現值的計算中使用的利率,即貼現過程中的利率。而在其他地方,如貨幣政策的貼現率,它是指中央銀行對商業銀行貼現票據時使用的利率。