練習題答案

第1章

1.1　預期回報為12.5%，回報率的標準差為17.07%。

1.2　由式（1-1）及式（1-2）得出，預期回報為12.5%，回報率的標準差為

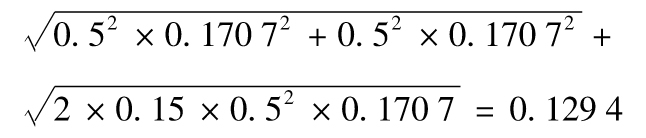
即12.94%。

1.3

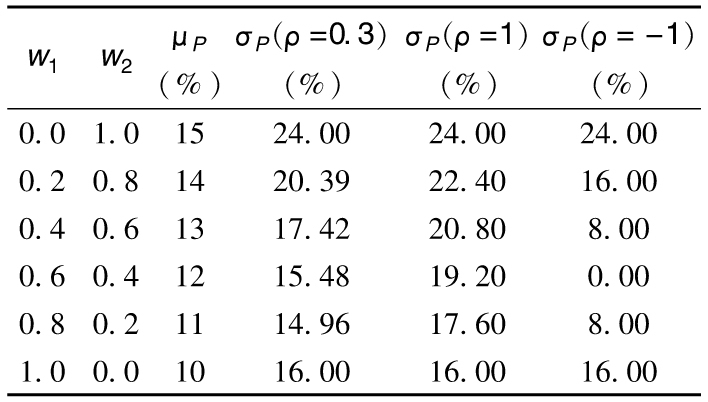
1.4　非系統性風險可以被分散，系統性風險不能被分散。系統性風險對於股票投資者更重要，兩類風險均可以導致企業的破產。

1.5　我們假定投資者在預期回報與風險之間找到平衡，對於一個指定的預期回報，投資者想儘可能使回報率的標準差達到極小，所有人對於特定投資所求得的預期回報、回報率的標準差及回報之間的相關係數的估計均相等。再有，投資者均能夠以無風險利率借入及借出資金，結果是投資者都想在圖1-4所示的“新有效邊界”之上，他們選擇同樣的有風險投資與以無風險利率為利息的借入或借出資金的組合。

1.6　（a）7.2%；（b）9%；（c）14.4%。

1.7　資本資產定價模型假定只有一個單一因子決定回報，套利定價理論假定有多個因子。

1.8　在許多國家和地區，企業債券利息可用於減稅，而股票股息則不行，公司利用債券融資可以節省稅務費用，但是隨著債券發行量的增大，破產概率也會增大。

1.9　風險分解是指將風險逐一處理的過程，而風險聚集是指將風險進行彙總並進行處理的過程。採用風險分解方法，我們需要對每一個風險都有深入瞭解，而採用風險聚集方法，我們需要了解風險間的相關性。

1.10　當潛在損失很大時，我們不能將損失進行聚集並假定損失會被分散，而是有必要將損失單獨進行處理，在處理過程中我們可以利用保險合約以及內控等措施。

1.11　這對應於盈利不小於資產的-4%的概率，該盈利水平為4.6/1.5=3.067倍的標準差，因此銀行股票為正的概率為N（3.067），其中N為標準正態分佈，其解為99.89%。

1.12　銀行有從存款人那裡取得資金的特權，而零售及製造業公司不能做到這一點。

1.13　專業服務費用（每月為1 000萬美元），銷售量下跌（人們不願意同正在重組的公司再打交道），重要高管的辭職（缺乏業務的連續性）。

1.14　alpha為0的對衝基金的回報為0.05+0.6×（0.10-0.05）=0.08，即8%。因為alpha等於4%，對衝基金回報為8%+4%=12%。

第2章

2.1　銀行系統變得更加集中化，大銀行佔有巨大市場份額，銀行數量由14 483家減至5 060家。

2.2　20世紀初，許多州紛紛設定法律禁止銀行開啟多於1家以上的分行，1927年的《麥克法登法案》禁止銀行在不同的州開設分行。

2.3　風險是當利率升高時，如果存款被延期，銀行必須支付更高利率，而收入的貸款利率不變，從而會造成銀行利差收入的降低，同時還有流動性風險。

2.4　DLC的損失超出了其股權資本金，公司可能會解體，次優先級長期債券的500萬美元投資會有損失，存款人會拿回全部資金。

2.5　銀行的淨利息收入等於利息收入減去利息支出。

2.6　信用風險主要影響貸款損失。非利息收入包括交易的盈虧，因此市場風險影響非利息收入，如果資產和負債不匹配，市場風險也會影響淨利息收入；操作風險主要會影響非利息費用。

2.7　私募是指面向少數大型金融機構新發行證券的行為。公募是指面向公眾新發行證券的行為。在非包銷交易中，投資銀行向投資者出售證券，但對證券是否可以售出並不保證；在包銷交易中，投資銀行以某個價格從發行證券的公司買入證券，並隨後在市場上以更高價格出售。

2.8　從高到低，競價排序為H、C、F、A、B、D、E和G。競標人H、C及F的競標數量均為140 000股，A的競標數量為20 000股，競標的清盤價格由A給出，即100美元，H、C和F以這一價格買入100%的競標數量的股票，A以這一價格買入一半的競拍數量的股票。

2.9　荷蘭式拍賣潛在地吸引大批競標者，如果市場上所有感興趣的人均參與競標，成交價格應與剛剛IPO之後的市場價格非常接近。因此在正常的IPO情況中，應避免出現價格遠遠低於市場價格的情形。另外，在荷蘭式拍賣中，投資銀行不能只銷售給自己最好的當前和潛在客戶。谷歌的IPO過程不同於標準荷蘭式拍賣，在其IPO過程中，谷歌對發行股票數量有發言權，並且在看到競標後，可以改變分配給競標人的股票數量。

2.10　毒丸計劃可以給管理人員提供談判的工具，即使是當公司董事會有權推翻毒丸計劃或使之失效時，這一點仍然正確。當管理人員與一個潛在的買方產生對抗時，管理人員可以採用毒丸計劃來爭取時間以得到一個更好的賣出價格，或尋找其他買方。但毒丸計劃的存在，也可能導致其他投資者望而卻步。

2.11　銀行的經紀子公司可能會推薦銀行的投行部賣出的證券，商業銀行子公司可能將一些機密信息傳給投資銀行子公司。當一家銀行與另外一家公司進行業務往來（或者想進行業務往來），銀行可能會說服經紀子公司將這家公司的股票評級為“買入”。商業銀行子公司可能會說服自己的貸款客戶來發行債券，而銀行這麼做的實際動機是因為對客戶貸款的信用產生擔心（同時，銀行可以讓自己的投行部門來說服其客戶買入這些債券，從而承擔信用風險）。以上利益衝突是通過所謂的防火牆來處理的，防火牆可以防止銀行不同部門之間的信息滲透。

2.12　交易賬戶包含那些出於交易目的而持有的項目，這些項目要進行每日的盯市計價。銀行賬戶包括那些預期持有到期滿的項目，例如對公司和個人的貸款。

2.13　根據《國際財務報告準則第9號》（IFR9）和類似美國財務會計準則委員會（FASB）的會計準則，銀行必須在其財務報表中將預計貸款損失從貸款中扣除。

2.14　在發起-分銷模式中，銀行首先發放貸款，然後將貸款打包出售給投資者。在2007年7月以前的7年間，以上經驗模式在市場上盛行。2007年7月，投資者對證券化產品失去了信心，銀行不得不放棄這種經驗模式（至少是暫時）。

第3章

3.1　定期壽險持續一定的期限（例如5年或10年），投保人支付保費，如果投保人在壽險期限內死亡，保險收益人所得賠償就等於保單的面值；終身壽險為投保人終生提供保險，投保人通常每年定期向保險公司支付保費（每年數量為恆定），在投保人死後，保險公司向受益人提供賠償。在終身壽險中，有一定的投資成分，這是因為在保險初期，保費高於預期賠償（在保險後期，保費低於預期賠償），投資所得的稅務可以被延遲到投保人的死亡時刻。

3.2　變額壽險是終身壽險的一種特殊形式，投保人可以指明在保險最初的年份裡的盈餘保費（即保費超出保險精算費用）的投資方式。在投保人死亡時的賠償有一個最低數量保證，但如果投資表現好，賠償數量會遠遠高於最低數量。萬能壽險也是終身壽險的一種形式，在這種保險中，投保人可以將保費減至不造成保險失效的某個最低水平。盈餘保費被保險公司投資（一般是固定收益產品），保險公司將擔保最低回報率，如果投資表現良好，在投保人死亡時投保受益人回報可能高於最低的回報率。

3.3　年金產品對於長壽風險有風險敞口；人壽保險對死亡風險有風險敞口。

3.4　由累計價值所產生的終身年金由以下利率的最大一個來計算：（a）市場利率；（b）實現預定的最低利率。

3.5　女性在第1年死亡的概率為0.003 182，在第2年死亡的概率為0.003 473×（1-0.003 182）=0.003 462，假定持平保費為X，我們有

1 000 000×（0.003 182+0.003 462）=X+（1-0.003 182）X

由此得出X=3 327，持平保費為3 327美元。

3.6　一個男性活到30歲的概率為0.975 19，活到90歲的概率為0.177 35。一個男性在活到30歲的條件下，活到90歲的概率為0.177 35/0.975 19=0.181 86。一個女性在活到30歲的條件下，活到90歲的概率為0.291 04/0.986 35=0.295 07。

3.7　最大的風險來源於類似於地震和颶風的災難，以及一些責任義務（例如，美國關於石棉的索賠），這是因為大數定理不再給保險公司提供任何幫助，這些事件要麼不發生，因此也沒有任何索賠，但事件一旦發生，索賠數量會巨大。

3.8　CAT債券（巨災債券）給承擔災難性風險（例如颶風及地震）的保險公司提供了一種再保險產品，通過這種產品，保險公司可將災難性風險轉嫁，CAT債券由保險公司發行，債券的券息比政府債券券息要高，當保險公司面臨災害索賠時，在實現確定的損失範圍內，CAT債券持有者必須同意放棄將來券息甚至本金。

3.9　CAT債券沒有太多的系統性風險，自然災害的發生與市場回報無關，CAT債券的風險可以由投資組合的其他風險而分解。B級債券具有系統性風險，其系統性風險不可以被分散，因此CAT債券是投資組合的一個更好的附加投資。

3.10　在加拿大和英國，醫療服務由政府來提供；在美國，公共醫療非常有限，大多數人需要從某種類型的私立保險公司買入醫療保險。在英國，私立醫療系統與公共醫療系統並存。

3.11　道德風險和逆向選擇均會產生潛在問題，保險的存在會造成投保人不再努力去保護自己的工作，確實出現過一些投保人故意地失去工作來獲得保險賠償的事件。還有，主動買入保險的投保人往往來自那些有高風險會失去工作的群體。

3.12　對財產險的賠償比對人壽保險的賠償的變動性更大，這是由於類似於地震和颶風的災難，以及一些責任義務（例如，美國關於石棉的索賠）所觸發賠償的變動性而造成。

3.13　賠付率等於1年內賠償數量與保金數量的比；費用比率等於1年內費用數量（如銷售提成和為確認損失而付出的費用）與保金數量的比。以上說法不正確，因為投資收入一般都很大，保費是在年初收入，賠償是在年中的任意時刻，甚至是在年末。

3.14　在一個養老金固定供款計劃中，僱員的供款（包括僱主為僱員的供款）均以僱員的名義存入單獨的賬戶並進行投資。當僱員退休時，累積供款和投資收益一般會轉換為年金產品。在固定收益計劃中，所有僱員的供款被統一在一起來進行投資，僱員收到的養老金數量取決於僱員為公司服務的時間以及僱員的最終工資。在任意一個時刻，固定收益計劃資金均可能會處於資金不足或資金盈餘狀態。

3.15　僱員工資按實值計算為常數，假定工資為每年X（X的單位與我們的計算無關），養老金為0.75X，實際回報為0，因為僱員工作年限為40年，所以僱員的供款的貼現值為40XR，其中R為供款佔工資的比率，僱員所得養老金福利的貼現值為20×0.75X=15X，比率R應保證養老金資金量充足，即

40XR=15X

即R=0.375。因此，僱員和僱主供款總和佔工資的比率至少應為37.5%。

第4章

4.1　開放式基金總數量在有更多的投資者買入基金時會增長，而當有更多的投資者賣出基金時會下降；封閉式基金類似於一家發行固定數量股票的公司。

4.2　共同基金的淨資產價值是在每天下午4點定出，等於基金持有資產價值除以當前共同基金的數量。

4.3　投資者在2018年和2019年分別有300美元和100美元資本收益，在2020年，投資者有200美元的資本虧損。

4.4　指數基金的設計是為了跟蹤特定的股票指數，例如標準普爾500指數。一種構造指數基金的做法是買入指數中的所有（或具有代表性的部分）股票，有時還會採用關於指數的期貨。

4.5　前端收費是投資者首次買入基金份額時支付費用，這個費用按投資數量的比例計算；後端收費是投資者在贖回基金份額時支付的費用，這個費用也是以投資數量的比例為計量。

4.6　跟蹤標準普爾500指數的交易所交易基金（ETF）的過程如下：機構投資者首先將一個用於跟蹤標準普爾500指數的股票交易組合存入基金，作為回報，該機構投資者收到ETF份額。機構投資者可以在任何時候，在ETF份額和構成ETF的股票的份額間進行轉換。與開放式基金相比，ETF的優點在於投資者可以隨時進行基金份額交易，也可以賣空基金，ETF基金管理人並不需要賣出基金資產來應對贖回的基金份額，因此不必刻意保持基金的高流動性；與封閉式基金相比，ETF的優點在於ETF份額價格與每個份額的淨資產價值十分接近。

4.7　n個數字的算術平均值等於這n個數字的和除以n，幾何平均值等於這n個數字的乘積再開n次方，算術平均值永遠大於或等於幾何平均值，將某項投資持有若干年，我們需要使用幾何平均（而不是算術平均值）來計算年回報（過程為首先計算“1加上每年回報”的幾何平均值，然後再減去1）。

4.8　延遲交易是一種違法交易行為，做法是在下午4點以後下單，並以下午4點的價格買入或賣出開放式基金份額；擇時交易是指基金經理允許一些特殊的客戶頻繁地買入或賣出基金的份額來盈利，他們之所以可以這麼做是因為在下午4點計算基金淨資產價值時，有些股票價格沒有被更新；搶先交易是某些人在大型金融機構進行可以影響市場變動的交易之前，搶先交易的行為；定向經紀涉及共同基金與經紀商之間的不當行為，其中經紀商向共同基金推薦客戶，作為回報，共同基金將業務交給該經紀商。

4.9　共同基金必須披露他們的交易策略；共同基金使用槓桿時，會有限制；共同基金不能賣空；他們也不能使用衍生產品。

4.10　如果一個對衝基金通過交易可轉換證券來盈利，則其利益所得一定是建立在其他交易對手損失的基礎上。如果大多數交易員都是對衝基金的話，不可能所有的人都盈利。

4.11　門檻回報率是指只有在業績超出這個最小回報率時，績效費才適用；高潮位標記條款是指前期損失必須在全部補齊的情況下，績效費才適用；分紅追回條款指投資者有權收回以前發出的績效費來彌補將來的損失。

4.12　如果回報率為X（>2%），投資者支付的費用為0.02+0.2（X-0.02），因此

X-0.02-0.2（X-0.02）=0.2

X=0.27，因此回報率在達到27%以上時，才能滿足條件。

4.13　如果對衝基金槓桿很高，短期的收益就變得非常重要，短期損失會引發保證金催付，這可能會摧毀對衝基金。

4.14　機構經紀人對於對衝基金所能夠持有的槓桿有決定權，這從而會影響對衝基金所能持有的風險頭寸。

第5章

5.1　當交易員進入遠期合約的多頭時，他同意在將來一定的時刻以某指定價格買入標的資產；當交易員進入遠期合約的空頭時，他同意在將來一定的時刻以某指定價格賣出標的資產。

5.2　某交易員對某資產有風險敞口，如果他採用衍生產品來減少自己的風險敞口，這時他的行為被稱為是對衝；在投機行為中，交易員最初沒有需要減小的風險敞口，他是在對今後的資產價格變化進行賭博；在套利行為中，交易員進行兩個或更多的市場交易以鎖定盈利。

5.3　在第一種情形中，交易員有義務以50美元的價格買入資產（這時他沒有其他選擇）；在第二種情形中，交易員有權利以50美元的價格買入資產（他可以選擇不行使期權）。

5.4　賣給某人看漲期權等於你給了期權持有者在將來以指定價格從你這裡買入某種資產的權利，買入看跌期權給了你在將來以指定價賣給期權出售者某種資產的權利。

5.5　（a）投資者在每英鎊價值為1.290 0美元時，有義務以每英鎊1.300 0美元的價格賣出英鎊，因此收益為（1.300 0-1.290 0）×100 000=100 0美元。（b）投資者在每英鎊價值為1.320 0美元時，有義務以每英鎊1.300 0美元的價格賣出英鎊，損失為（1.320 0-1.300 0）×100 000=2 000美元。

5.6　（a）交易員賣出價格為每磅50美分，資產的實際價格每磅48.20美分，收益=（0.5-0.482）×50 000=900美元。（b）交易員賣出價格為每磅50美分，資產的實際價格為每磅51.30美分，損失為（0.513 0-0.5）×50 000=650美元。

5.7　你賣出了一個看跌期權。當期權持有者決定行使期權時，你必須以每股40美元的價格買入100股，期權持有者只有在股票價格低於40美元的時候才會行使期權，假如在期權到期時股票價格為30美元，你必須以40美元的價格買入實際價格只有30美元的股票，這時你每股損失10美元，整體損失為1 000美元；如果價格為20美元時，期權得以行使，你每股損失20美元，整體損失為2 000美元；損失的最壞情形為在3個月內股票價格幾乎為0，這種不太可能會發生的事件會使你損失4 000美元。作為對將來損失的補償，你會從期權買入方收到期權的買入費。

5.8　場外交易是由電話及計算機將金融機構、基金經理及企業資金管理人結合在一起的網絡系統。在這種網絡系統中，有需求的交易雙方能夠達成令雙方均滿意的協議。場內市場是由交易所組織的市場，在場內市場交易員可以見面或進行電話交流，市場交易的產品由交易所定義。（a）場外交易（OTC）；（b）交易所交易；（c）兩者均可；（d）場外交易；（e）場外交易。

5.9　一種策略是買入200股股票，另外一種策略是買入2 000份期權，當股價上漲時，第二種策略會有更大的收益。例如，假如股票價格上漲為40美元，第二種策略的收益為2 000×（40-30）-5 800=14 200美元，而第一種收益僅為200×（40-29）=2 200美元，但是如果股票價格下跌，第二種策略所對應的損失更大，例如，如果股價跌為25美元，第一種策略的損失為200×（29-25）=800美元，第二種策略會失去所有的投資，即5 800美元。這一實例顯示了期權的槓桿效應。

5.10　你可以買入5 000份看跌期權（或者50份合約），期權執行價格為25美元，到期期限為4個月，這種合約提供某種保險，如果在4個月時，股票價格低於25美元，那麼你可以行使期權，這時你以每股25美元的價格賣出股票，這種策略的代價是需要支付買入期權的費用。

5.11　股票期權並不能給發行股票的公司帶來任何資產，這種產品是交易員之間的交易，發行股票的公司並不介入。與此相比，股票在最初發行時要賣給投資者，因此這時會給公司帶來資金。

5.12　忽略貨幣的時間價值，如果在3月時股票價格大於52.50美元，期權持有者會盈利，因為這時的期權回報超過了買入期權所付出的費用，即2.5美元，在期權到期時如果股價大於50美元，期權持有者會行使期權，注意如果股票價格介於50美元與52.50美元之間，期權會被行使，但期權持有者仍會蒙受損失。

5.13　忽略貨幣的時間價值，如果在6月股票價格大於56美元，期權的賣出方會盈利，因為這時向期權持有者支付的費用小於賣出期權所帶來的收入，在到期時如果股價小於60美元，期權會被行使，注意當股票價格介於56美元與60美元之間時，期權的賣出方即使在期權被行使時也會盈利。

5.14　一個4個月期限的看跌期權的多頭給期權持有者提供了保險，這一保險保證外匯的賣出價格不低於執行價格。

5.15　這家公司可以進入在6個月時買入100萬加元的遠期多頭，這樣做可以鎖定將來的外匯利率，並使得其等於現在觀察到的遠期外匯利率。另一種做法是公司可以買入看漲期權，這一看漲期權給公司一個在6個月後以某指定匯率買入100萬加元的權利，如果在6個月時加元強勁，這一權利就給公司提供了保險。如果在6個月時加元疲軟，則公司仍然可以從中謀利。

5.16　ICON的回報是：（a）定期債券；（b）進入一看漲期權空頭，期權面值為169 000日元，執行價格為1/169；（c）進入一看漲期權的多頭，期權面值為169 000日元，執行價格為1/84.5的三種交易組合而成。本頁下面的表格說明了這一點。

5.17　（a）交易員買入180天期限的看漲期權，並且同時進入180天期限的遠期合約的空頭。（b）交易員買入90天期限的看跌期權，並且同時進入90天期限的遠期合約的多頭。

5.18　進入5年期互換合約，在合約中支付3.30%固定利率，並且收入LIBOR利率，投資整體效應為LIBOR-0.30%。

5.19　進入5年期互換合約，在合約中收入3.26%固定利率，並且支付LIBOR利率，借入資金的淨費用為LIBOR+1.74%。

5.20　進入3年期互換合約，在合約中收入LIBOR浮動利率，並且支付3%固定利率，3年借入資金費用為每年4%。

5.21　假定天氣不好，農場主的收成比期望的要差，其他農場主也會受到類似的天氣影響，這時玉米產量整體來講比較低，因此玉米價格會相對較高。同實際產量相比，農場主的對衝可能過了頭。產量低的問題可能會因為期貨空頭而雪上加霜。這一問題強調在進行對衝時，我們一定要有一個宏觀的概念。農場主應該仔細斟酌，只考慮對衝價格的風險而同時忽略其他風險肯定不會是一個好主意。

5.22　公司蒙受損失或取得盈利的概率相等，這意味著用遠期合約來進行投機就像賭硬幣正反面一樣。但是即使這樣，航空公司利用遠期合約來對風險進行對衝，而不對價格進行投機仍然是很有意義的事情，遠期合約有減少風險的效果，在持有對衝合約的情況下，航空公司不會讓股東承擔將來油價所帶來的風險。

5.23　微軟公司選擇交易組合的期權而不是期權的交易組合，交易組合的期權一定會比期權的交易組合價格更加便宜，這是因為某種資產的價格的增長可能會被另外一種資產的價格的下降而中和，現在讓我們比較：（a）一個交易組合的期權，執行價格為20美元，交易組合由兩種資產組成，每個資產的價格均為10美元；（b）兩個期權組成的交易組合，每個期權的執行價格均為10美元，如果兩個資產的價格同時增長或同時下降，（a）和（b）的回報相同，但是如果一個資產價格下降而另一個資產價格上漲，則（a）的回報要比（b）低。亞式及一攬子期權特性均可以幫助微軟減小期權費用，這是因為盈利及虧損有相互抵消的可能。

5.24　這意味著能源價格可升可降，但長期來講，會趨向於長期平均水平，電力迴歸均值的速度最快，石油迴歸速度最慢。

5.25　當我們增大觀察資產價格的頻率時，觀察到的價格達到障礙的概率會增大，敲出期權的價格會減小。

5.26　每一天的平均溫度為華氏75°，每一天CDD為10，月累積CDD為10×31=310，看漲期權的回報為（310-250）×5 000=300 000（美元）。

5.27　一個對於2019年5月的5×8合約是為了保證在一週的5天內非高峰期（晚上11點至早上7點）提供電力，如果合約註明是天行使方式，則期權持有者可以在一週的每一個工作日以某特定價格買入電力；如果合約是月行使方式，則期權持有者只有在月初有一次機會來闡明自己是否會在整個月以某指定價格買入電力，日行使方式顯然價格更高。

5.28　需要進行兩次計算來確定初始保證金。第一次計算：500×（3.5+0.2×57-3）=5 950，第二次計算：500×（3.5+0.1×57）=4 600。初始保證金是其中的較大者，即5 950美元。這其中的一部分可以來自賣出期權提供的500×3.5=1 750美元。

5.29　股票的費用為500×50，即25 000美元。賣空這些股票時，所得資金被用作保證金的一部分。在這個例子中，全部的保證金要求是1.6×25 000，即40 000美元。因此，額外的保證金要求為15000美元。這部分保證金可以現金或滿足保證金要求的證券的形式提供。當股票價格上升到S時，標的股票的價值為500S。如果滿足以下不等式，則會產生保證金催付

40 000 < 1.3 × 500S

即S > 61.54。

5.30　經紀商會設置初始保證金和維持保證金要求。當保證金賬戶的餘額低於維持保證金水平時，經紀商的客戶就需要將保證金餘額恢復到初始保證金的水平。場內清算所在與其會員進行業務時，會將初始保證金和維持保證金要求設置在相同的水平上。客戶每日的保證金餘額必須維持在這個水平上。

第6章

6.1　按揭貸款常常被證券化，在證券化過程中，唯一保存的信息是按揭申請人的FICO分數及按揭的貸款與價值比率。發起人知道這種情況，因此他們只關心這些信息。

6.2　許多人被說服接受了他們並不能夠承擔的按揭，因此供需關係出現了一個短期的失調。

6.3　當按揭損失率為5%時，ABS的中間檔沒有損失，因此ABS CDO的任何分檔都沒有損失；當按揭損失率為12%時，ABS的中間檔損失為7/20，即35%，因此ABS CDO的權益檔和中間檔（夾層檔）的損失為100%，ABS CDO的優先檔的損失為10/75，即13.333%。

6.4　通常ABS分檔比較單薄，其損失的概率分佈和債券有很大不同。如果損失發生，ABS分檔往往會100%損失，而債券全部損失的可能性很低。

6.5　ABS是由貸款、債券、信用卡應收款項所構成投資組合所生成的分檔債券；CDO是由債券等固定收益資產所生成的一種ABS；ABS CDO是以不同ABS的特定分檔（例如，由BBB級分檔）作為資產所生成的ABS。

6.6　投資者低估了在市場受壓情況下，抵押貸款違約相關性會變得非常高，他們也沒有認識到ABS CDO的分檔其實很單薄，因此其損失狀態是要麼不損失，要麼全部損失。另外一個不幸的誤判是，投資者將某一評級的分檔等同於相同評級的債券。根據上面提到的原因，這一假設是不成立的。

6.7　代理成本是指兩方利益不完全一致的情形。交易員、貸款發放者、估價者、結構化產品的創立者和評級機構的不同動機是造成代理成本的原因。

6.8　瀑布式現金流定義了來自標的資產的利息和本金現金流如何在不同的分檔之間進行分配。在典型的合約中，利息收入被優先用於支付承諾給最高級分檔的收益。剩餘的部分（如果有剩餘的話）被用於支付次優先級分檔的收益，依此類推。本金的償還類似，也是以分檔的優先級排序。權益份額只有在其他更高級別的份額收到回報後才會產生利息和本金回報。

6.9　一般ABS CDO是由BBB級的ABS分檔來生成的，這是因為在市場上很難找到願意對ABS的BBB分檔進行投資的投資者。

6.10　Mian和Sufi說明在美國1996年按揭申請遭到拒絕的比率最高的地區也是在2000～2007年，按揭增長速度尤其快的地區。

6.11　ABS或ABS CDO的中間檔是處於分檔優先級排序中中間部分的分檔，它排在優先檔之下、權益檔之上，因此其承擔損失的順序先於優先檔而晚於權益檔。

6.12　當違約相關性增大時，ABS的優先檔風險增大，這是因為優先檔出現損失的機會增大；當違約相關性增大時，權益檔風險變小。為了理解這一點，注意在極限情形下，即完全相關時（同時假定回收率為0），所有的按揭具有相同的損失，因為所有的公司要麼同時違約，要麼沒有任何一家違約。因此，當完全相關時，按揭變得更相似，優先檔的風險更高，權益檔的風險更低。

6.13　年終獎一般僅僅反映一年的表現，交易員和銀行其他僱員常常只關心自己的年終獎（而不是自己所做決策的長期後果），因此他們的決策往往是基於短期目標。目前已有將獎金變為延遲發放並可以收回的趨勢，這有望改變這種局面。

第7章

7.1　由式（7-3），概率等於N（d₂），其中

因此，概率等於N（-0.482 5）=0.315。

7.2　由式（7-4）

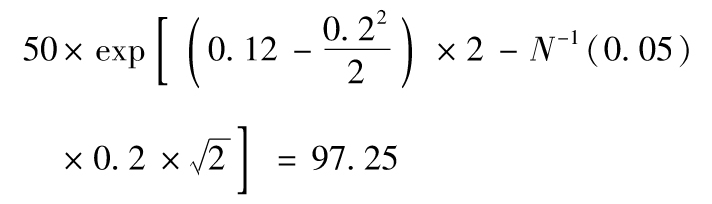
即97.25美元。

7.3　風險中性定價理論認為，當我們對衍生產品定價時，假設投資者是風險中性的（即投資者並不為承擔的風險而索要更高的預期回報），那麼得出的結果對所有的世界都適用（包括真實世界）。

7.4　在真實世界中的價值會更高。更高的價值反映了投資者對承受風險所要求的補償。

7.5　通過購買這兩種衍生產品，一方在98美元的初始投資時能獲得2美元收益。因此，無風險利率為2/98=2.04%（年複利）。違約的風險中性概率為100π/（1+0.020 4）=3，即π=3.061 2%。

7.6　回報的風險中性概率由式（7-3）給出，其中V=30，S₀=25，σ=0.3，μ=0.03，以及T=0.25。因此

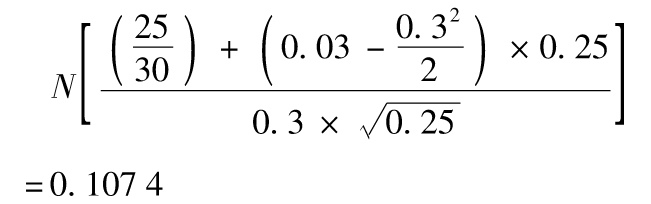
所以，期權的價值為100×0.107 4×e^-0.03×0.25=10.66美元。對真實世界中回報的概率，我們設公式中的μ=0.1而不是0.03，得出的值為0.130 5。

7.7　真實世界被用來模擬標的變量一年內可能出現的值。然後使用風險中性世界來計算每一次模擬試驗中，組合在一年後的價值。

7.8　均值迴歸這一術語用來描述一個變量的值，例如利率和商品價格，有趨於一箇中心值的趨勢這樣一種現象。當然，在迴歸均值的過程中會有隨機不確定性。

7.9　哥薩諾夫定理告訴我們，當我們從真實世界變換到風險中性世界時（反之亦然），市場變量的預期變化率會改變，但是波動率保持不變。

第8章

8.1　交易組合價值減少10 500美元。

8.2　交易組合價值增長400美元。

8.3　兩種情形下的增長量均為0.5×30×2²=60（美元）。

8.4　delta等於0.7意味著在股票價格上漲一個小的數量的同時，期權價格的上漲大約是股價上漲的70%，同時當股票價格下跌一個小的數量的同時，期權價格的下跌大約是股價下跌量的70%，1 000份期權的空頭的delta等於-700，我們可以通過買入700份股票的形式使交易組合達到delta中性。

8.5　一天的theta等於-100意味著在股價及波動率均沒有變化的情況下，期權價格每天減少100美元，如果一個交易員感覺股價及隱含波動率都不會變化，他就可以賣出期權，這時期權的theta越高越好（在絕對值意義下），相對來講，短期限的平值期權具有最高的theta值。

8.6　期權的gamma是期權的delta同資產價格變化的比率，例如gamma等於0.1意味著當資產價格上漲一定數量時，delta增長的數量是資產價格上漲數量的10%，如果一個期權承約人的gamma絕對值較大，gamma本身為負，並且delta等於0，這時期權承約人會在市場變動較大（或者上漲或者下跌）的情況下有很大的損失。

8.7　為了對衝期權風險，我們有必要構造相反方向的合成期權交易。例如，為了對衝看跌期權多頭，我們應該構造合成看跌期權的空頭，構造人工期權交易的過程也就是對衝期權風險的反過程。

8.8　看漲及看跌期權的多頭都具備正的gamma，由圖8-9我們可以得出，當gamma為正時，對衝者在股票價格變化較大時會有收益，而在股票價格變化較小時會有損失，因此對衝者在（b）情形下收益更好，當交易組合包含期權的空頭時，對衝者在（a）情形下收益會更好。

8.9　delta的數值說明，當歐元匯率增長0.01時，銀行頭寸價格會增長0.01×30 000=300美元；gamma的數值說明，當歐元價格增長0.01美元時，交易組合的delta會下降0.01×80 000=800，為了做到delta中性，我們應賣出30 000歐元。當匯率增長到0.93時，我們期望交易組合的delta下降（0.93-0.90）×80 000=2 400，變為27 600，為了維持delta中性，銀行應該對歐元空頭進行2 400歐元的平倉，這樣可以保證歐元淨空頭量為27 600。如果一個交易組合的delta為中性，同時gamma為負，當資產價格有一個較大變動時會引發損失。因此我們的結論是銀行可能會蒙受損失。

8.10　當採用書中所描述的方式時，我們需要假設波動率為常數。從理論上講，我們可以實施一個靜態期權複製機制，在這一機制下有三個維度：時間、股票價格以及波動率。我們要在這個三維空間中的曲面上進行價格匹配。

8.11　大約需要10個普通期權。對應於邊界上任意一點我們都會有一個方程，總共有10個方程。

8.12　隨著時間的推移，亞式期權的回報會越來越確定，因此在接近到期日時，我們需要對衝的不確定性會越來越小。

8.13　考慮與某單一資產有關的期權組合，無論交易組合的大小我們只需要進行一個交易就可以使得組合變得delta中性。

8.14　期權的價格、delta、gamma、vega、theta及rho分別是0.021 7、-0.396、5.415、0.002 03、-0.000 062 5及-0.001 19，當匯率變化0.001時，delta預測價格下降的數量為0.000 39，這正是我們求得的數值；當匯率增長到0.751時，期權價格下降0.021 3。

第9章

9.1　這時利率不匹配為100億美元，在今後3年，銀行的淨利息收入會每年下降1億美元。

9.2　如果長期利率僅僅反映了將來預期短期利率，我們會看到長期利率小於短期利率的情形與長期利率大於短期利率的情形一樣頻繁（這是基於投資者在一半情況下認為利率會上漲，而在另一半情況下認為利率會下跌的假設）。流動性偏好理論認為長期利率高於將來預期短期利率，這意味著長期利率在多數時間會高於短期利率，當長期利率低於短期利率時，市場會產生利率將急速下滑的預期。

9.3　有兩個原因：①銀行所需的為支持自己所持有的國債的資本金數量要比其他類似的低風險投資產品所需要的資本金數量低；②美國對於國債的稅務處理比其他固定收益產品有利，這是因為持有國債產品無須繳納州稅。

9.4　在隔夜指數互換中，交易的一方支付美聯儲基準利率在某個時間段內（如3個月）的幾何平均值，而收入某一事先確定的固定利率。

9.5　LIBOR-OIS利差可以衡量銀行間相互拆借意願的大小。

9.6　久期信息描述了收益率曲線小的平行移動對於債券價格的影響。交易組合價格減小的百分比等於組合久期乘以利率的小的平行移動的數量。其侷限性是這一方法只適用於利率的小的平行移動。

9.7　（a）債券價格為86.80美元；（b）債券久期為4.256年；（c）久期公式估計當收益率減小0.2%時，債券價格上漲0.74美元；（d）對應10.8%收益率的債券價格為87.54美元，這與（a）及（c）大體一致。

9.8　（a）債券價格為88.91美元；（b）債券修正久期為3.843年；（c）久期公式估計當收益率下降0.2%時，債券價格上漲0.68美元；（d）債券價格對應10.8%收益率（以年複利）的價格為89.60美元，這與（a）及（c）大體一致。

9.9　債券價格為104.80美元，債券久期為5.35年，凸性為30.60，收益率增長1%對於價格的影響可由式（9-4）估算，其對應數值

104.80×（-0.01×5.35+0.5×30.60×0.000 1）=-5.44

變化後的債券價格為99.36美元，這與我們的估算一致。

9.10　我們可以：（a）擾動收益曲線上的每一點（見圖9-5）；（b）擾動曲線上的一段（見圖9-7）；（c）擾動構造收益曲線產品的報價。

9.11　delta（當因子載荷以基點數衡量時，因子單位造成的投資組合價值變化）分別為-5.64及225.63。

9.12　對於組合的影響（佔組合價值的比例）為

-（2.0×0.001+1.6×0.000 8+0.9×0.000 7+1.6×0.000 6+2.0×0.000 5-2.1×0.000 3-3.0×0.000 1）=-0.002 34

即投資組合減少0.234％。

9.13　絕對額久期等於組合的久期乘以其價格。絕對額凸性等於組合的凸性乘以其價格。

9.14　局部久期的和等於整體久期。DV01等於整體久期乘以組合價值，再乘以0.000 1。

第10章

10.1　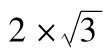，即3.46%。

10.2　每天百分比變化的標準差為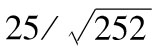，即1.57%，在95%置信度下所對應的置信區間為-3.09%～3.09%。

10.3　開市時的波動率比閉市時要大很多，交易員在計算波動率時往往採用交易天數而不是日曆天數。

10.4　隱含波動率是使得由布萊克-斯科爾斯-默頓模型所計算出的期權價格等於市價時所對應的波動率，隱含波動率的求解方法通常是採用試錯法的方式。因為不同期權對應於不同的隱含波動率，所以交易員實際上使用了與布萊克-斯科爾斯-默頓模型不同的假設（見第25章有關討論）。

10.5　計算標準差的一般公式所給出的結果為每天0.547%，由式（10-4）的簡單方法得出的結果為每天0.530%。

10.6　由冪律得出0.01=K×500^-2，因此K=2 500，（a）2 500×1 000^-2=0.002 5或0.25%，（b）2 500×2 000^-2=0.062 5%。

10.7　在第n-1天結束時所估計的第n天的方差等於λ乘以在第n-2天所估計的第n-1天的方差加上1-λ乘以第n-1天的回報的平方。

10.8　GARCH（1，1）對EWMA模型進行了改進，對於長期平均方差設定了一定權重。EWMA不具備迴歸均值的特性，而GARCH（1，1）具備方差迴歸均值的特性。

10.9　在這種情形下σ_n-1=0.015，u_n-1=0.5/30=0.016 67，由式（10-8）我們可得出

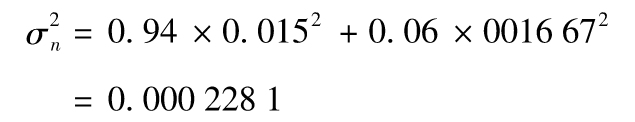
因此在第n天，波動率的估計值為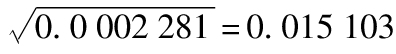，即1.510 3%。

10.10　將λ由0.95減至0.85意味著對於近期的觀察值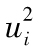設定更大的權重，而對於更早的數據設定較小的權重。採用λ=0.85所計算出的波動率對最新信息的反映較快，也會比採用λ=0.95時所計算的波動率變動更大。

10.11　採用通常的符號，u_n-1=20/104 0=0.019 23，因此

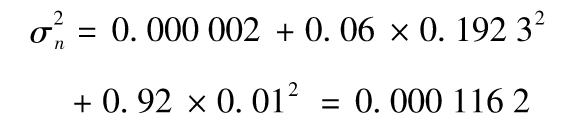
σ_n=0.010 78，對於最新波動率的估計為每天1.078%。

10.12　價格變化的比率為-0.005/1.500 0=-0.003 333，當前每天的方差估計為0.006²=0.000 036，對於每天方差的新估計為

0.9×0.000 036+0.1×0.003 333²=0.000 033 511

波動率的新的估計值為以上數值的平方根，即0.579%。

10.13　長期平均方差所對應的權重為1-α-β，長期平均方差率為ω/（1-α-β），增大ω會促使長期平均方差的增長。增大α會增大為近期數據所設定的權重，同時減小對長期平均方差所設定的權重，以及增大長期平均方差率。增大β會增大對於前一個方差所設定的權重，減小對於長期平均方差所設定的權重，並且增大長期平均方差的水平。

10.14　長期平均方差率為ω/（1-α-β），即0.000 004/0.03=0.000 133 3，長期平均波動率為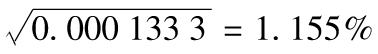，描述方差迴歸長期平均的方程式為

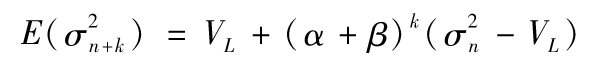
這時

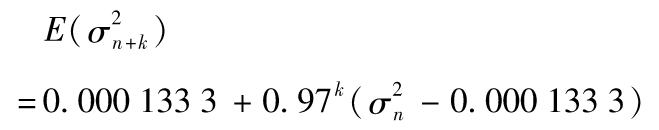
如果當前波動率為每年20%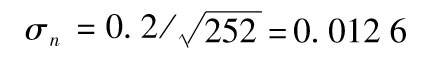，，在20天后預期方差為

0.000 133 3+0.97²⁰（0.012 6²-0.000 133 3）=0.000 147 1

因此20天后預期波動率為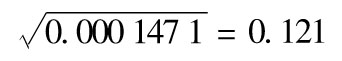，即每天1.21%。

10.15　FTSE用美元表達為XY，X為以英鎊表達的價值，Y為匯率（1英鎊所對應的美元的數量），定義x_i為X在第i天的價格百分比變化，y_i為Y在第i天的百分比變化，XY的比例變化大約為x_i+y_i，x_i標準差為0.018，y_i的標準差為0.009，X及Y變化的相關係數為0.4，因此，x_i+y_i的方差為

0.018²+0.009²+2×0.018×0.009×0.4=0.000 534 6

因此x_i+y_i的波動率為0.023 1，即2.31%，這就是以美元為計量的FTSE的波動率。注意，這一波動率比以英鎊為計量的FTSE的波動率更大。這是由於正相關性的影響，當FTSE增長時，英鎊與美元匯率也往往會增長，以美元為計量的FTSE會進一步增加。類似地，我們也可以討論FTSE下降的情形。

10.16　這時V_L=0.000 000 3/0.02=0.000 15，式（10-14）給出了30天后的方差期望值為

0.000 15+0.98³⁰×（0.01²-0.000 15）=0.000 123

波動率為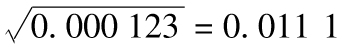，即每天1.11%。

10.17　這時V_L=0.000 002/0.02=0.000 1，在式（10-15）中，V_L=0.000 1，a=0.020 2，T=20及V（0）=0.000 169，因此波動率為19.88%。

第11章

11.1　你需要兩個變量的標準差。

11.2　不嚴格地講，相關係數是衡量兩個變量的線性關聯性的指標。它並不能反映關聯性。當y=x²時，x及y有一個完美的關聯性（即完全相關），但是E（xy）=E（x³）。當x服從正態分佈（或服從以0點為中心的對稱分佈）時，E（x³）和E（x）均為0，因此x和y的相關係數也為0。

11.3　在因子模型中，兩個變量的相關性完全取決於它們與其他變量的相關性，這些變量被稱為因子，因子模型減少了對大量變量進行相關性分析時所需的計算量。

11.4　一個半正定矩陣對所有的向量w均滿足式（11-4）。如果一個相關矩陣不是半正定的，那麼內部相關性一定不一致。

11.5　（a）由波動率及相關性所計算出的協方差為0.25×0.016×0.025=0.000 1；（b）假如在交易結束時，資產收盤價為20.5美元及40.5美元，資產價格百分比變化分別為0.5/20=0.025及0.5/40=0.012 5，新的協方差估計為

0.95×0.000 1+0.05×0.025×0.012 5=0.000 110 6

資產A的新的方差估計為

0.95×0.016²+0.05×0.025²=0.000 274 45

因此新的波動率為0.016 6。資產B的新的方差估計為

0.95×0.025+0.05×0.012 5²=0.00 060 156 2

因此新的波動率為0.024 5，新的相關性估計為

11.6　X和Y的最新回報分別為1/30=0.033 33及1/50=0.02。協方差先前的值為0.01×0.012×0.50=0.000 06，新的估計為

0.000 001+0.04×0.033 33×0.02+0.94×0.000 06=0.000 008 41

X的新的方差估計為

0.000 003+0.04×0.033 333²+0.94×0.01²=0.000 141 4

X的新的波動率估計為，即1.189%；Y的新的方差估計為

0.000 003+0.04×0.02²+0.94×0.012²=0.000 154 4

Y的新的波動率估計為，即1.242%；對於資產相關性的估計為

0.000 084 1/（0.011 89×0.012 42）=0.569

11.7　沿用練習題10.15中的符號，定義z_i為標準普爾500指數在第i天的百分比變化，x_i與z_i之間的協方差為0.7×0.018×0.016=0.000 201 6，y_i與z_i之間的協方差為0.3×0.009×0.016=0.000 043 2，x_i+y_i與z_i之間的協方差等於x_i與z_i之間的協方差加上y_i與z_i之間的協方差，即

0.000 201 6+0.000 043 2=0.000 244 8

由練習題10.15，x_i+y_i的波動率為2.31%。x_i+y_i與z_i之間的相關係數為

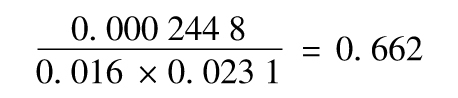
注意，標準普爾500指數的波動率在計算中沒有出現。

11.8　

11.9　公式為

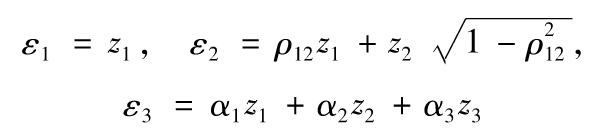
其中

這意味著

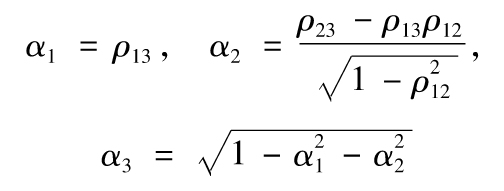
11.10　尾部相關是描述兩個或更多變量同時產生極值的趨勢，Copula的不同選擇會影響尾部相關性，例如學生t-Copula函數給出的尾部相關性比高斯Copula函數要大。

11.11　由二元學生t-分佈得出的抽樣被顯示在圖11-5中，將抽樣以分位數對分位數的形式映射到正態分佈。

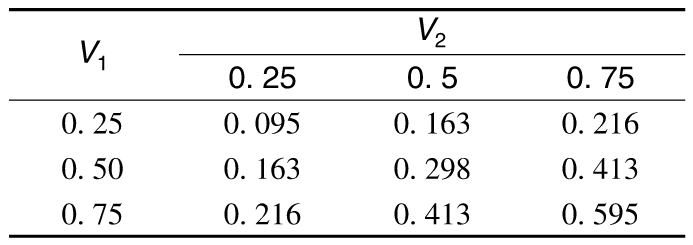
11.12　V₁<0.1的概率為0.05，在V₁<0.1的條件下，V₂<0.1的條件概率為0.006/0.05=0.12；在V₁<0.1的條件下，V₂<0.2的條件概率為0.017/0.05=0.34，等等。

11.13　當V₁=0.2時，我們有U₁=-0.84，由二元正態分佈的性質得出U₂的中值為-0.5×0.841 6=-0.420 8。因此，條件中位數的百分位數為N（-0.420 8）=0.336 9，轉換為x的V₂的中值，其中2x²=0.336 9，則對應的V₂的中值為0.410 5。

11.14　這時

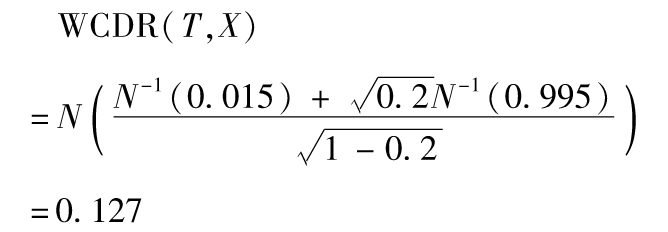
“99.5%最壞情形”的損失絕不會超過12.7％。

11.15　最大似然估計法估算的違約概率和Copula相關係數分別為3.92%和11.18%。

第12章

12.1　VaR是指在一定的置信水平下損失不能超過的數量；ES是在損失超過VaR的條件下損失的期望值。ES永遠滿足次可加性（風險分散總會帶來收益）條件。

12.2　譜函數型風險測度在測算風險時對損失分佈的分位數設定一定的權重，滿足次可加性條件的測度對於第q個分位數設定的權重一定是q的非遞減函數。

12.3　有5%的機會你會在今後一個月損失6000美元或更多。

12.4　在一個“糟糕的月份”，你的預期損失為6000美元。糟糕的月份的定義是，該月的回報小於月回報分佈的5%分位數。

12.5　（a）100萬美元；（b）ES為0.9×10+0.1×1=9.10（百萬美元）；（c）有0.009²=0.000 081的概率會損失2 000萬美元，2×0.009×0.991=0.017 838的概率會損失1 100萬美元，有0.991²=0.982 081的概率會損失200萬美元。置信度為99%時的VaR為1 100萬美元；（d）ES為（0.000 081×20+0.009 919×11）/0.01=1 107（萬美元）；（e）因為1+1<11，所以VaR不滿足次可加性條件。但是9.2+9.2>11.07，所以ES滿足該條件。

12.6　（a）2×1.96=3.92（百萬美元）；（b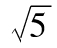）×2×1.96=8.77（百萬美元）；（c）×2.33=10.40（百萬美元）。

12.7　（b）變為996萬美元；（c）變為1 182萬美元。

12.8　邊際VaR是VaR隨第i個資產增加而增長的比率；增量VaR是指第i個資產對於VaR的影響（含有第i個資產VaR與不含有第i個資產VaR的差）；成分VaR是指整體VaR對於第i個資產的分配（成分VaR的總和等於整體VaR）。

12.9　總數為17或更多例外發生所對應的概率為

1-BINOMDIST（16，1000，0.01，TRUE）

即2.64%。在5%置信水平下我們應該拒絕這一模型。

12.10　聚束效應是指例外情形會以聚集的形式發生，而不是隨機地分佈在整體時間區間內。

12.11　我們希望計算ΔP₁+ΔP₂+…+ΔP_T的標準差。其數量為

其中σ_i為ΔP_i的標準差，ρ_ij為ΔP_i與ΔP_j的相關係數。這時對於所有的i，σ_i=σ，以及當i>j時ρ_ij=ρ^i-j。進一步進行運算，我們可以得出式（12-5）。

12.12　3個月標準差為。N^-1（0.98）=2.054。3個月展望期、置信度為98%的VaR為3.464×2.054=7.11（百萬美元），相同展望期和置信度下的ES為3.464×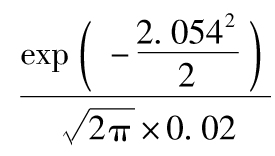=8.39（百萬美元）。

第13章

13.1　這裡的假設為：決定明天市場變化的統計過程與決定過去500天市場變化的統計過程相同。

13.2　

因此當λ趨近於1時，權重趨向於1/n。

13.3　估算的VaR的標準誤差為

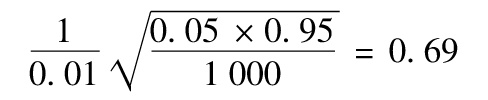
即69萬美元。

13.4　（a）1天展望期、95%置信度的VaR對應於第25大損失的情景，即156511美元；（b）1天展望期、95%置信度的ES為最大的24個損失的平均值，為209310美元；（c）1天展望期、97%置信度的VaR對應於損失中第15大損失的情景，即172 224美元；（d）1天展望期、97%置信度的ES為最大的14個損失的平均值，即240 874美元。

13.5　在表單（名為“Scenarios”）中，交易組合頭寸改變是將單元格L2∶O2中的數據改為2 500，將損失由大到小排序，1天展望期、99%置信度的VaR對應於第5個最大損失，即238 526美元。最大的4個損失的平均值為372 872美元。這是一天99%的ES。

13.6　在表單4（“Scenario with Weights”）中，將單元格F2中的變量λ由0.995變為0.99，將損失由大到小進行排序，最大損失477 841美元（情景494）所對應的累計權重為0.009 48。第二大損失345 435美元（情景339）所對應的累計權重為0.011 47。1天展望期、99%置信度的VaR對應於第二大損失，即345 435美元。一天的ES等於0.948×477 841+0.052×345 435=470 917美元。

13.7　將表單9（“Loss Adjusted for Loss SD”）中單元格K1中的變量λ由0.94變為0.96，將損失由大到小進行排序，第5大損失為541337美元，該量即為1天展望期、99%置信度的VaR。前4大損失的均值為707 146美元。此為1天展望期、99%置信度的ES。

13.8　即為

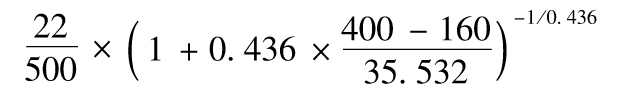
即0.001 623。

13.9　VaR（以千計）等於

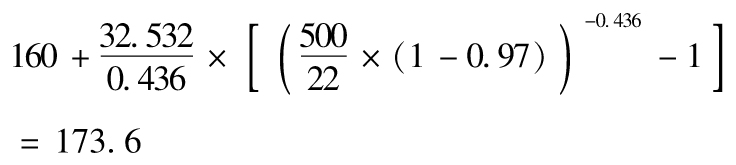
即173 600美元。

13.10　由最大似然估計得出的ξ及β分別為0.353及34.05，1天展望期、99%置信度的VaR為230 725美元，1天展望期、99.9%置信度的VaR為452 831美元。1天展望期、99%置信度的ES為327 336美元，1天展望期、99.9%置信度的ES為670 499美元。

13.11　從波動率更新過程中所得出的損失排序後必須傳到表單11（“Extreme Val Theory”）中。當u=400時，n_u=17時，由最大似然估計得出的ξ及β分別為0.438及82.838，1天展望期、99%置信度的VaR為534 100美元。1天展望期、99.9%置信度的VaR為1 096 661美元。1天展望期、99%置信度的ES為785 819美元。1天展望期、99.9%置信度的ES為1 786 335美元。損失大於600 000美元的概率為

第14章

14.1　每一項資產投資的標準差為1 000美元，交易組合每天價格變化的方差為

1 000²+1 000²+2×0.3×1 000×1 000=2 600 000

交易組合的標準差為以上數量的平方根，即1 612.45美元，因此5天展望期、97%置信度的VaR等於

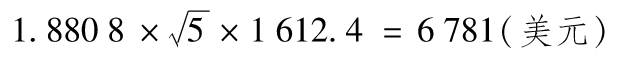
5天展望期、97%置信度的ES為

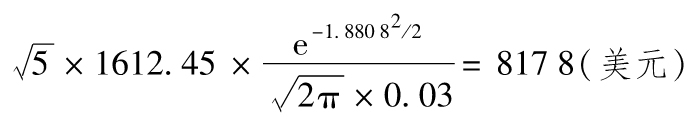
14.2　如本章介紹的，以模型構建法計算VaR時，對利率的三種不同處理方法為：（a）應用久期模型；（b）利用資金流映射的方法；（c）利用主成分分析法。

14.3　10年期頂點的敏感度為30 000美元，因為該比率每增加一個點，12年期頂點的敏感度就會增加0.6個基點。類似地，15年期頂點的敏感度為20 000美元。其他點則沒有敏感度。

14.4　ΔP=3.9Δx，ΔP的標準差為3.9×0.007=0.027。因此交易組合10天展望期、99%置信度的VaR等於0.027×2.326×=0.20。

14.5　關係式為ΔP=3.9Δx+0.5×4.3×Δx²，即ΔP=3.9Δx+2.15Δx²。

14.6　一天內投資組合價值變動的方差為（以千美元計）為

（10×7）²+（8×8）²+2×10×7×8×8×0.8=16 164

由於N^-1（0.98）=2.054，ES為

即688 200美元。

14.7　投資組合的風險度量（VaR或ES）等於投資組合的標準差乘以β，風險因子的風險權重是風險因子的標準差乘以β。投資組合的風險敏感度是投資組合因風險因子的1%或1個基點變化而變化的金額。

14.8　交易組合的每天的方差為

6²×20²+4²×8²=15 424

每天標準差為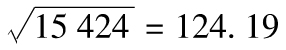美元，因為N^-1（0.9）=1.282，5天展望期、90%置信度的VaR為

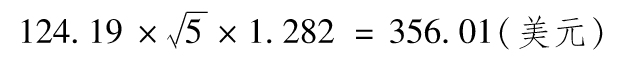
14.9　（a）2.0；（b）43.9。

14.10　期權delta為期權價值變化同標的資產的變化比率。當標的資產上漲一個小數量時，期權價值的下降為標的資產變化的30倍。期權的gamma為期權delta變化同標的資產價格變化的比率，當資產價格增長一個小的數量時，期權的delta的下降為標的資產價格下降數量的5倍。delta和gamma同比例的變化分別為：-30×20=-600和-5×20×20=-2 000。

這時E（ΔP）=-0.10，E（ΔP²）=36.03，E（ΔP³）=-32.415。這意味著交易組合在一天內的變化為-0.1，標準差在一天內的變化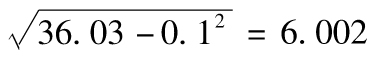為，偏態為

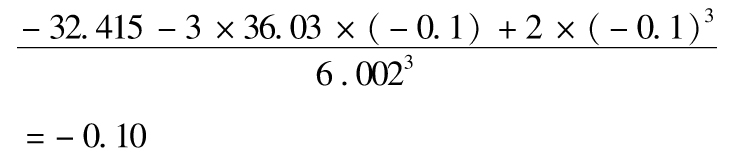
採用前兩階矩，我們得出1天展望期、99%置信度的VaR為14.08美元，當採用三階矩並利用柯尼斯-費希爾展開時，我們求得的VaR為14.53美元。

14.11　定義σ為每年的波動率（百分比），ΔS代表σ的一天變化量，Δσ為σ的一天內波動率的變化量，我們將σ計為1%的倍數，因此當前σ的價值為。delta-gamma-vega模型為

ΔP=-30ΔS-0.5×5（ΔS）²-2Δσ

或

ΔP=-30×20Δx-0.5×5×20²（Δx）²-2Δσ

其中Δx=ΔS/S。以上公式可簡化為

ΔP=-600Δx-1 000（Δx）²-2Δσ

交易組合的變化與兩個市場變量有關。

14.12　期權的價值變化與標的資產的價值變化的關係並不是線性的。當標的變量為正態分佈時，期權價格分佈並不是正態的。線性模型假定期權價格服從正態分佈，因此這一模型僅僅是一種近似模型。

14.13　這一合約由一個英鎊債券的多頭與一個美元債券的空頭結合而成。英鎊債券的價格為1.53e^-0.05×0.5，即1.492（百萬美元），美元債券價格為1.5e^-0.05×0.5，即1.463（百萬美元），合約價值每天變化的方差為

1.492²×0.000 6²+1.463²×0.000 5²-2×0.8×1.492×0.000 6×1.463×0.000 5=0.000 000 288

相應的標準差為0.000 537（百萬美元），10天展望期、99%置信度的VaR等於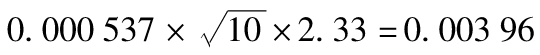（百萬美元），即3 960美元。

14.14　alpha應變為2 500。當波動率和相關性是由等權重模型估計時，1天展望期、99%置信度的VaR為226 836美元，ES為259 878美元；當採用λ=0.94的EWMA模型時，1天展望期、99%置信度的VaR為487 737美元，ES為558 783美元。

14.15　1天展望期、99%置信度的VaR由471 025美元變為389 290美元，ES由539 637美元變為445 996美元。

14.16　一種方法是假設第一項結構的頂點和第二項結構的頂點之間的相關性相對於所有頂點都是相同的。另一種方法是分別計算各期限結構變化對投資組合的影響，並利用相關性將兩種影響疊加。

第15章

15.1　競爭者的出局可能會對公司（非銀行）有一定好處，但是銀行之間有許多交易。當一家銀行破產時，其他銀行會因與這家破產銀行進行的交易而蒙受損失。另外銀行破產會使公眾對銀行系統失去信心，這也會給銀行系統帶來不利影響。

15.2　不論金融機構承擔什麼樣的風險，存款保險會使存款人的利益得到保護。這會促使金融機構承擔更大的風險，因為這時它們並不會為失去存款客戶而擔心。因此，這樣的措施可能會造成更多的銀行破產，從而使存款保險系統的賠款量加大。監管部門要求銀行必須持有與自己風險相匹配的資本金以避免破產的發生。

15.3　互換中的信用風險是指互換價格對銀行為正價值時，對手違約的風險。

15.4　貨幣互換價值偏離0的趨勢要大於利率互換價值偏離0的趨勢，這一現象是由於貨幣互換中最終本金的交換，因此貨幣互換中因對手違約所造成的潛在損失會更高。

15.5　的確存在某種風險敞口。儘管對手現在違約，不會引發任何損失，但是利率可能會有所變化，因此在將來某時刻，這一互換對於金融機構可能具有正的價值，那時交易對手違約會給金融機構帶來損失。在《巴塞爾協議Ⅰ》的要求下，由表15-2得出的資本金數量為互換面值的0.5%。

15.6　三個交易的風險加權資產分別為：（a）187.5萬美元；（b）200萬美元；（c）300萬美元，整體為687.5萬美元，資本金為0.08×6.875=55萬美元。

15.7　NRR為2.5/4.5=0.556，等價信用量為2.5+（0.4+0.6×0.556）×9.25=928萬美元。風險加權資產為464萬美元，資本金需求為37.1萬美元。

15.8　這時淨額結算不會提供任何價值。

15.9　這可將估算的資本金轉換為風險加權資產，資本金數額為風險加權資產的8%。

15.10　交易賬戶中的資產主要包括市場上交易活躍的並且每天盯市計價的產品。銀行賬戶上的產品主要包括貸款，這些產品並不是每天都要盯市計價。變化的效應是將客戶的貸款由銀行賬戶轉移到交易賬戶，這會減少資本金要求（但是第16章將要討論的《巴塞爾協議Ⅱ.5）中的增量風險資本計提會將資本金要求提升回原有的水平）。

15.11　在《巴塞爾協議Ⅰ》中，企業貸款的資本金要求與企業的信用評級無關，這造成了銀行在給高信用客戶貸款業務的資本金回報相對較低的現象。在《巴塞爾協議Ⅱ》中，資本金的要求與借貸人的信用狀況有緊密關係，因此給高信用客戶貸款又可能成為一個吸引人的業務。

15.12　監管資本金套利會涉及進行一些完全是為了以減少監管資本金為目的的交易，這些交易通常不會對承擔的實際風險產生影響。

15.13　EAD為違約時對風險敞口的估計；LGD為違約損失率的估計，其定義為違約損失與整體風險敞口的比率；WCDR為每千年出現一次的不良年度的違約概率；PD為一般年度的違約概率；MA為期限調節量，其設定是為了考慮產品期限長於一年時，產品在一年內違約或降級可能會引發的損失。

15.14　在簡單法中，對有擔保品掩護的風險敞口部分，交易對手的權重會被擔保品的權重所替代。在綜合法中，敞口大小會被調整，調整時要考慮敞口增大的可能性和擔保品價值減小的可能性。交易對手的風險權重被應用於經調整後的風險敞口與經調整的擔保品的差額。

15.15　標準法採用外部信用評級來確定資本金的數額（但比《巴塞爾協議Ⅰ》更為複雜）。在IRB法中，我們需要採用《巴塞爾協議Ⅱ》的相關性模型來計算資本金，PD參數由銀行提供。在高級IRB法中，我們採用《巴塞爾協議Ⅱ》的相關性模型來計算資本金，其中PD、LGD、EAD及MA均由銀行自己提供。

15.16　在基本指標法中，整體資本金為平均年毛收入的15%。在標準法中，對於不同的業務類別要分別計算毛收入，不同業務類別採用不同的比例從毛收入數量中計算相應的資本金。在高級計量法中，銀行採用內部模型來計算1年展望期、99.9%置信度的VaR。

15.17　ρ=0.121 6，WCDR=0.091 4，資本金（以百萬美元計）為200×0.7×（0.091 4-0.01），即1 139萬美元，這其中至少有一半必須是第一類資本。

15.18　發生5次或更多例外的概率為

1-BINOMDIST（4，250，0.01，TRUE）

即10.8%。我們可以認為監管機構是利用10%置信水平（而不是通常的5%）來選擇是否拒絕模型。

第16章

16.1　《巴塞爾協議Ⅱ.5》的3個主要組成部分是：壓力VaR的計算、增量風險資本計提和對依賴信用相關性的產品的全面風險計量。

16.2　《巴塞爾協議Ⅲ》的6個主要組成部分是：資本金定義及要求、資本金留存緩衝、逆週期緩衝、槓桿率、流動性比率和交易對手信用風險。

16.3　一般定義下的VaR由最近一天一直到過去4年內的日數據計算得出。壓力VaR的計算要選取歷史上使銀行當前投資組合的表現非常差的250天。

16.4　增量風險資本計提由交易賬戶上的信用產品在1年展望期內、99.9%置信度下的VaR求得。計算過程中要考慮信用評級的變化和流動性區間，引入這個概念是因為過去交易賬戶上的產品所需的資本金少於銀行賬戶上相應的產品。

16.5　一個AAA級的ABS的資本金要求是面值的1.6%，而一個AAA級的ABS CDO的資本金要求是面值的3.2%。

16.6　第一類股權資本金的要求由2%增加到7%，而且股權資本的定義更加嚴格。

16.7　（a）40%；（b）20%。

16.8　在槓桿比率中，分母不是風險加權資產，而是資產負債表上無加權的全部資產加上一些表外項目，例如貸款承諾。

16.9　流動性覆蓋比率是在30天承壓期內，高質量流動性資產與淨流出資金的比率。淨穩定資金比率是資產負債表上“負債和淨值”一側項目的加權總和除以“資產”一側的項目的加權總和。

16.10　穩定資金量變為81.6，NSFR變為81.6/74.25=110%。

16.11　CVA是衍生產品交易中，由於交易對手可能違約帶來的預期損失而對收入進行的計提。新的監管規則要求，對信用價差的CVA敞口要被包含在市場風險資本金中。

16.12　CoCo債券在銀行資本金低於預先定義的觸發條件時自動轉換為股權。這類債券對銀行具有吸引力，因為在轉換前，它們對股本回報率不產生影響；這類債券對監管機構也具有吸引力，因為在市場受壓的情況下，它們會成為吸收損失的資本金的來源。

第17章

17.1　當使用ISDA主協議時，場外衍生產品交易的雙方都會承擔對方違約的風險。當使用CCP時，CCP充當雙方的中介，因此雙方都與CCP進行交易。

17.2　金融機構之間的標準交易必須通過CCP清算。對金融機構間雙邊清算的衍生產品，初始保證金和變動保證金都會需要。初始保證金的數額必須能有99%的把握抵禦市場受壓情況下10天內的損失。

17.3　金融機構需要為它們的衍生產品賬戶提供的擔保品的數量（一般來說是現金或國債）會增加。

17.4　用於某金融產品的折減率是該產品用作擔保品時所計的價值與其市場價格相比所減少的百分比。例如，如果某產品的價格為100美元，折減率為10%，那麼該產品用來滿足90美元的擔保品要求。

17.5　如果在衍生產品交易中，簽署了ISDA主協議的雙方中有一方不能繳納擔保品或按照要求付款，那麼我們就認為發生了違約。違約發生後，會接著發生提前終止事件。未違約的一方會終止與違約的一方進行的所有未到期交易。

17.6　A方的風險敞口（包括對CCP的風險敞口）減至70，不包括對CCP的風險敞口保持為0。B方的風險敞口（包括對CCP的風險敞口）減至100，不包括對CCP的風險敞口減小到70。C方的風險敞口不受影響。三方平均的風險敞口，包括對CCP的敞口，由110下降到86.7，不包括CCP的風險敞口由70下降到53.3。

17.7　如果發生以下情況，公司將遭受損失：①CCP違約；②有某一方違約，並且沒有向CCP繳納足夠的保證金和違約基金來抵禦其交易被平倉所造成的損失。

17.8　所需擔保品的數額一般是所有為完結交易的市場價值的淨額。為確定結算額，價值為正的交易會與價值為負的交易淨額結算。

17.9　再抵押的含義是，A方給B方提供的擔保品，被B方用來滿足C方對B方的擔保品要求。

17.10　CCP的業務行為比銀行簡單得多。

17.11　計算方式如下：提前終止時交易對未違約方的市場中間價加上買賣價差的一半。

第18章

18.1　在《巴塞爾協議I》中，市場風險資本金由10天展望期、99%置信度的VaR求出，而該值又通過1天展望期、99%置信度的VaR乘以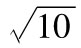得出。在《巴塞爾協議Ⅱ.5》中，市場風險資本金由兩部分組成，一部分是基於當前99%置信度的VaR（即《巴塞爾協議Ⅰ》），另一部分來自10天展望期、99%置信度的壓力VaR。這兩部分都假設等於相對應的一天VaR的倍。在FRTB中，資本金由置信度為97.5%的壓力預期虧空得出，其展望期為一個依賴於投資組合流動性的可變量。

18.2　97.5%的ES為。

18.3　考慮歷史模擬法是如何實現的。由第0日到第10日的變化有9天與從第1日到第11日的變化重合。因此，它們不是相互獨立的。實際上，我們預期這兩個變量在大部分模擬中會很相近。

18.4　ES與VaR相比，理論上的優點是它能滿足第12.5節中討論的次可加性（分散性）；從實用性上講，它能更好地量化尾部風險。

18.5　交易賬戶包含那些出於交易目的而持有的項目，這些項目要進行每日的盯市計價。銀行賬戶包括那些預期持有到期滿的項目。除非遭遇嚴重不良，這些項目會以歷史成本法計價。交易賬戶和銀行賬戶的資本金計算方式有很大不同，而監管機構不希望銀行能夠通過自主決定項目所放賬戶的方式達到減少資本金要求的目的。

18.6　信用價差風險的處理方式和其他市場風險是一致的。突發違約風險的處理與銀行賬戶中項目的信用風險的處理類似。

第19章

19.1　穆迪的10個投資級別為：Aaa，Aa1，Aa2，Aa3，A1，A2，A3，Baa1，Baa2，Baa3。

19.2　標準普爾的10個投資級別為：AAA，AA+，AA，AA-，A+，A，A-，BBB+，BBB，BBB-。

19.3　由式（19-2）得出，平均風險率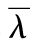滿足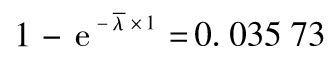，這一方程的解為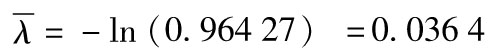，平均違約密度為每年3.64%。

19.4　在前兩年沒有違約情況下，公司在第三年違約的概率為

（0.044 92-0.025 83）/（1-0.025 83）=0.019 60

將第三年平均違約密度記為，我們有關係式，因此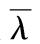等於每年1.98%。

19.5　信用保護賣出方在0.5年、1.0年、1.5年、2.0年、2.5年、3.0年、3.5年及4.0年收入300 000 000×0.006 0×0.5=900 000美元，賣出方在違約發生時（4年零2個月）會收到最終付款300 000美元（=300 000 000×0.060×2/12），信用保護賣出方在違約發生時的支付金額為30 000 000×0.6=180 000 000美元。

19.6　有時交易雙方會達成實物交割協議，有時會達成現金交割協議。如果在違約時為實物交割，則信用保護的買入方會以債券票面的價值將違約債券賣給信用保護的賣出方，可賣出債券的總面額等於信用互換的面額。如果在違約時為現金交割，這時會有一個第三方來計算在違約後一定天數之後最便宜可交割債券的價格，信用互換的現金回報等於違約債券的面值減去估算出的債券價格。

19.7　風險中性違約概率由信用互換及債券價格計算得出，真實世界違約概率是從歷史數據中計算得出的。風險中性違約概率被應用於產品定價，真實世界違約概率被應用於情景分析及信用VaR的計算。

19.8　CDS的賠償支付為L（1-R），L為CDS面值，R為回收率。

19.9　由式（19-3），我們得出今後3年的平均違約密度為0.005 0/（1-0.3）=0.007 1，即每年0.71%。

19.10　由式（19-3），我們得出今後5年的平均違約密度為0.008 0/（1-0.4），即每年1.333%。類似地，今後3年的平均違約密度為每年1.166 7%，這意味著4～5年的平均密度為

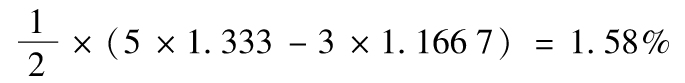
19.11　真實世界違約概率應該用於計算信用風險VaR，風險中性違約概率應該用於對衍生產品價格進行信用風險調節。

19.12　債券的回收率等於在債券發行方違約不久後債券的價格與面值的比率。

19.13　表19-5第2列第1個數字的計算方法為

即每年0.03%。表19-5第2列第2個數字通過類似的方法得出

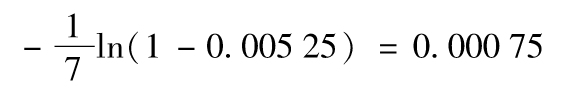
依此類推。最後的數字為

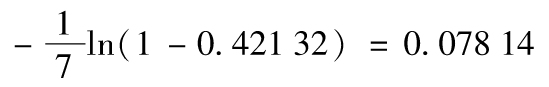
表19-6中第4列等於將表19-5中第2列的風險率（以基點表示）乘以0.6。對Caa級別，結果為781.4×0.6=460。

19.14　債券的無違約價值為

2e^-0.03×0.5+2e^-0.03×1.0+…+102e^-0.03×4.0=103.66

市場價格為96.16。一個類似於表19-3的分析說明，如果Q為每年違約概率，違約損失為272.69Q，隱含違約概率滿足103.66-96.16=272.69Q，因此隱含違約率為每年2.47%。

19.15　如果Q₁為在時間0.5年、1.5年及2.5年的違約概率，類似於表19-3的分析顯示第一個債券違約損失的貼現值為每100美元面值178.31Q₁。債券的無違約價值為

4×e^-0.035×1+4×e^-0.035×2+104×e^-0.035×3=101.23

市場價格為98.35。因此178.31Q₁=101.23-98.35，從而Q₁=0.015 7，即1.57%。令Q₂為時間3.5年及4.5年違約的概率，類似於表19-3的分析顯示第二個債券違約損失的貼現值為180.56Q₁+108.53Q₂。這一債券的無違約價值為

4×e^-0.035×1+4×e^-0.035×2+…+104×e^-0.035×5=101.97

債券的市場價格為96.24。因此180.56Q₁+108.53Q₂=101.97-96.24，代入Q₁求得Q₂=0.026，即2.60%。

19.16　我們假定在互換到期時有本金交換，這種假設並不會影響互換的價格。如果利差為0，浮動利率支付方對應於1美元本金現金流的貼現值為1美元。因此以LIBOR加利差計息的現金流的貼現值為1+V。1美元單位面值債券產生的現金流的當前價值為B^*。對應1美元單位面值，債券現金流支付方的最初付出費用為1-B（如果這一數值為負，那麼浮動利率的支付方必須首先付費B-1），因為資產互換的最初價格為0，我們得出

1+V=B^*+（1-B）

因而

V=B^*-B

19.17　由默頓模型得出債券價格為V₀-E₀，即

V₀-V₀N（d₁）+De^-rTN（d₂）=De^-rTN（d₂）+V₀N（-d₁）

令s為信用價差，以上數量等於De^-（r+s）T，因此

De^-（r+s）T=De^-rTN（d₂）+V₀N（-d₁）

代入De^-rT=LV₀，我們得出

Le^-sT=LN（d₂）+N（-d₁）

因此

s=-ln［N（d₂）+N（-d₁）/L］/T

19.18　這時，E₀=2，σ_E=0.50，D=5，r=0.04，T=1。對兩個方程求解得出V₀=6.80及σ_V=14.82。違約概率為N（-d₂），即1.15%。

19.19　在前四年的每個季度結束時，賣出方收到100萬美元付款。賣出方在4年零2個月之後支付7 000萬美元。賣出方收到最終付款666 667美元。

19.20　信用違約互換提供對參照實體發行的企業債券的信用保護，其大致的作用是將企業債券轉換為無風險債券。因此，信用違約互換的買入方實際上是將一個企業債券與無風險債券做交換。這意味著，買入方持有無風險債券的多頭和企業債券的空頭。

19.21　CDS的回報取決於某公司是否違約，有人認為有些市場參與者對於公司的信用狀態有更多信息（見業界事例19-2）。

19.22　假定面值為100美元。如果債券是無風險的，其貼現值為

2.5e^-0.06×0.5+2.5e^-0.06×1+…+2.5e^-0.06×5+100e^-0.06×5=95.357 9

因此，預期違約損失的貼現值為95.357 9-90=5.357 9。構造資產互換時首先保證最初付費為10美元，然後每6個月支付2.5美元。作為交換，收入為LIBOR加上利差，互換的面值為100美元，固定利息付款的貼現值為

10+2.5e^-0.06×0.5+2.5e^-0.06×1+…+2.5e^-0.06×5+100e^-0.06×5=105.357 9

因此，高於LIBOR的利差的貼現值為5.357 9。每6個月支付1美元，連續支付5年的當前貼現值為8.510 5。因此，每6個月收入的利差為5.357 9/8.510 5=0.629 6美元，資產互換的利差等於2×0.629 6，即每年1.259 2%，本題為練習題19.16的結果提供了一個說明。

第20章

20.1　一個新的交易在以下兩種情形下會增大銀行對於交易對手的風險敞口：第一種情形為現存的交易對於銀行來講價值為正，新交易價值也為正；第二種情形為現存的交易價值為負，新交易價值也為負。但是當新交易價格同現在交易價值有抵消作用時，新交易附加效應是減小信用風險。

20.2　一家公司本身的股票對這家公司的交易對手來說，不會是好的擔保品。當與該公司的交易違約時，公司股票也可能不會太值錢。

20.3　（a）和（b）均正確，（c）不正確。假定v_X及v_Y分別是對X及Y的風險敞口，v_X+v_Y的期望值等於v_X的期望值加上v_Y的期望值，但對應於95%置信區間的限制，以上結論並不正確。

20.4　假設違約只發生在遠期合約的到期日。在無違約風險的世界，遠期合約是一個歐式看漲期權的多頭與一個歐式看跌期權的空頭的組合，這裡的兩個期權的執行價格均等於遠期合約交割價格，期權的到期日等於遠期合約的到期日。如果無違約遠期合約在到期時價格為正，看漲期權價格為正，看跌期權價值為0，違約對於遠期合約的影響與違約對於看漲期權的影響相同；如果無違約遠期合約在到期時價值為負，看漲期權價值為0，看跌期權價值為正，這時違約不會有任何影響，在這種情況下，違約對於遠期合約的影響也與遠期合約對於看漲期權的影響等同。綜上所述，我們得出遠期合約的價值等價於一個與違約有關的看漲期權的多頭以及與違約無關的看跌期權的空頭。

20.5　布萊克-斯科爾斯-默頓模型得出的價格必須乘以e^-0.012×3=0.964，該模型高估價格大概為3.6%。

20.6　當公司X與許多公司簽有的合約中使用了同樣的降級觸發條件時，其效果可能會增加風險。如果公司被降級，降級觸發條款被激活，那麼持有對於X而言價值為負的合約的對手方會向X索取擔保品。其結果是，公司X會面臨流動性困難，甚至會造成公司破產。

20.7　當交易商和交易對手進入一個交易對手賣出信用保護的CDS合約或交易對手進行投機時，交易商容易產生錯向風險。當交易商與交易對手進行的CDS合約中，交易對手從交易商買入了信用保護，或者新交易是為了部分地對衝交易對手的風險敞口時，交易商具有正向風險。

20.8　補救期是指在CVA計算中從違約事件發生到交易被終止的時間。

20.9　如果B方違約，那麼A方與B方之間的所有未清償交易都被當作一個交易來處理。因此，A方在計算損失時，會考慮所有與B方之間未清償交易的價值。

20.10　當銀行遭遇財務危機時，其違約可能性增大。這使得交易對手對銀行違約的預期損失增大。對銀行來說，這就是DVA，DVA會在賬面上增加交易對銀行的價值。

20.11　在《巴塞爾協議Ⅲ》中，與交易對手信用價差變化有關的CVA被包含在市場風險的計算中。

20.12　如果在提前終止事件前15天內，交易商與交易對手之間交易的價值朝向對交易商有利的方向變化500萬美元，交易商的CVA模型會產生損失。假設交易商無法從對手方處獲得額外抵押品，或交易對手無法歸還從交易商處獲得的抵押品。

第21章

21.1　在Vasicek模型及Credit Risk Plus模型中，信用損失在違約發生時發生。在CreditMetrics模型中，信用的降級及違約都會引發損失。Vasicek模型採用了違約時間的高斯Copula模型；Credit Risk Plus模型對每年的違約率的概率分佈採用了某種假設；CreditMetrics模型採用了高斯Copula模型來定義信用評級的變化。

21.2　風險水平恆定假設中假定一段時間t之後，某產品X被另一產品Y替換，其中Y與X的初始評級相同。再經過另一段時間t之後，Y被Z替換，Z也具有和X的初始評級相同的評級，依此類推。

21.3　一家Aaa級的公司在兩年後仍保持Aaa評級的概率為82.77%。其評級變為Aa的概率為15.12%。

21.4　一家Aaa級的公司在6個月後仍保持Aaa評級的概率為95.35%。其評級變為Aa的概率為4.40%。

21.5　所有公司的信用價差在下一天的變化可以被認為是過去500天的日變化中的一個隨機抽樣。該方法的缺點是公司違約的可能性為0，並且並不是所有的公司都有準確的每日信用價差數據。

21.6　使用二項分佈，產生6個或更多損失的概率是0.0005。

21.7　在這種情況下，我們必須求出對應於0.5%損失概率的二項累積分佈和1.5%損失概率的二項累積分佈的均值。有6個或以上違約事件發生的概率為0.0021。這說明，引入相關性會造成尾部風險上升。

21.8　自相關性為0.546。這說明信用VaR的估計應考慮最近的違約記錄。如果去年的違約率較高，則今年的違約率很可能也會較高。

第22章

22.1　我們可以由以下做法來產生情景：（a）對類似利率、股票價格等核心變量進行較大擾動；（b）令所有市場變量的擾動等於歷史上某一天市場變量的劇烈變化；（c）建立一個委員會來產生情形。

22.2　逆向壓力測試是指利用算法來尋求會造成巨大損失的情形。通過這一做法，我們可以確定實施壓力測試的恰當情形。

22.3　金融機構可能會認為如果所考慮的情景會引發巨大損失，則監管機構將提高資本金要求。

22.4　交通燈期權只有在保險業監管機構所規定的情景發生的情況下才產生回報。買入這一產品的危險是，當金融機構買入這種產品時，它們所得到的保護範圍很窄。對某些與保險公司監管機構所考慮的情形相似，但並不完全相同的情形，金融機構並沒有得到保護。

22.5　高管所處的位置對產生壓力測試情景最有利。高管介入壓力測試的產生過程，會使他們更認真地對待壓力測試結果，並將這些結果實施於決策過程。

22.6　優點是不同銀行都會考慮同樣的情形，並且系統性風險也可以被評估。這些情形可能比銀行自己考慮的情景更加惡劣（見練習題22.3）。缺點是在這種做法下，銀行可能不再積極地開發自己的壓力情景。

22.7　客觀概率由數據來產生，主觀概率具有一定的主觀性，它反映了個人的判斷。

22.8　壓力情形的整體概率為1.5%，因此，歷史情形所對應的概率為98.5%，每個歷史情形所對應的概率為0.197。將這些情形及所對應的概率進行排序，在99%置信度下的VaR值為284 204美元（對於340 000美元的損失量，累計概率為0.009 43；對於284 204美元的損失量，累計概率為0.011 41）。

22.9　這時，頭寸價值分別為941.34、-164.39、-1 349.94及-78.36，最糟糕的情形是資產價格為60、波動率為30%的情形，損失量為341.39美元。

第23章

23.1　這一定義包括所有的內部風險及外部風險，但不包括名譽風險及戰略決策風險。

23.2　根據Shih所報告的結果，損失量為100×3^0.23，即1.287億美元。

23.3　Prob（v>x）=Kx^-0.8，當x=20時，概率為0.1，這意味著K=1.098 6。對於特定損失被超出的概率為：（a）5.74%；（b）3.30%；（c）1.58%。

23.4　對於道德風險的處理方式包括設立免賠額度或者將保險費與過去索賠記錄掛鉤。對於逆向選擇的處理是首先在同意承保前儘可能取得關於司機的信息，然後隨著獲得的信息越來越多，再適當對保險費進行調整。

23.5　公司的CEO一定要簽署公司的財務報告來保證財務報表的準確性，如果財務報告出現重大問題並需要改動，CEO必須歸還自己的獎金。

23.6　如果交易員在遵守自己額度的條件下蒙受了交易損失，這種風險屬於市場風險；如果交易員超出額度交易並造成損失，這種風險屬於操作風險。

23.7　（a）即使存在人壽保險，一個人也不太可能不關心自己的健康。不過確曾發生過人壽保險受益人為獲得保金而謀殺投保人的事件。（b）壽命比較短的人往往會比壽命長的人更容易買人壽保險。

23.8　外部數據是與其他銀行損失有關的數據，其取得方式是與其他銀行達成協議來共享數據，或者銀行可以從數據銷售商處獲取數據。外部數據用來決定相對損失程度。這些數據可以用來計算業務部門A的損失平均值同業務部門B的損失平均值的比率，或者計算業務部門A的損失標準差與業務部門B的損失標準差的比率。

23.9　泊松分佈常常被用來描述損失頻率，對數正態分佈常常被用來描述損失程度。

23.10　幾個重要的風險指標的例子包括：僱員的離職率、不成功交易的數量、臨時僱員的數量、管理人員與僱員的比例、空置的職位和過去12個月中未連續休假10天的僱員比例。

23.11　當損失頻率等於3時，整體損失的平均值為3.3，標準差為2.0，當損失頻率增長到4時，整體損失的平均值大約為4.4，標準差為2.4。

23.12　關鍵的投入是業務指標和（對於業務指標超過10億元的銀行）過去10年的損失。業務指標是衡量銀行規模的指標，與操作風險相關。

23.13　A銀行的損失（以百萬歐元計）是7×20+7×20=280，B銀行的損失是7×20+7×20+5×20=380。A銀行的內部損失乘數是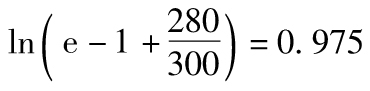，B銀行的內部損失乘數是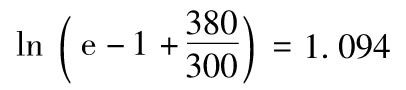。A銀行的SMA資本要求是110+（300-110）×0.975=295，B銀行的SMA資本要求是110+（300-110）×1.094=318。

第24章

24.1　投資者對產生分檔的基礎按揭資產並不瞭解，而且瀑布現金流非常複雜。

24.2　提供報價的公司及個人準備以50美元買入資產，並以55美元賣出資產，市場中間價為52.5美元，買賣價差比率為5/52.5，即0.095 2。

24.3　公司A的股票的買賣價差為0.01×5000=50美元，公司B的股票的買賣價差為0.02×3 000=60美元，對組合進行平倉的費用為（50+60）/2，即55美元。

24.4　對於第一家公司，在95%的置信區間下，買賣價差不會超出5 000×（0.01+1.645×0.01）=132.24美元。對於第二家公司，在95%的置信區間下，買賣價差不會超出3 000×（0.02+1.645×0.03）=204.04美元，在95%的置信區間下，平倉費用不會超出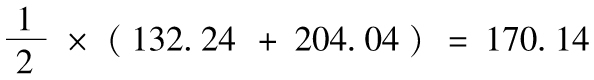美元。

24.5　在接下來的幾天中交易數量分別為15.9、12.9、10.0、7.4、5.2、3.4、2.2、1.4、0.9及0.7。買賣價差為13.4美元（單位為百萬），總方差為36.6，因此，在95%的置信區間下的VaR為美元（目標函數的取值使得以上數量的和達到極小，即23.3美元）。

24.6　LCR測試一家銀行是否有足夠的流動性來承受30天的極端壓力（信用降級、存款損失、信貸額度減少等）。NSFR測試資產和負債的到期匹配程度，防止過度依賴短期資金來滿足長期需求。

24.7　在市場受壓的條件下，批發存款更加容易消失。

24.8　它們的對衝交易產生損失，而被對衝的部分會產生盈利。問題在於，對衝交易的損失會引發保證金催付，而被對衝的頭寸雖然價值增加，但這些產品的流動性並不好。

24.9　正反饋是指交易員的交易會加重市場價格的變動，即交易員在價格上漲時買入，在價格下跌時賣出；負反饋是指交易員的交易會減緩市場價格的變動，即交易員在價格下跌時買入，在價格上漲時賣出。正反饋會導致流動性問題。

24.10　這個VaR測度包括在對交易進行平倉時，因買賣價差造成的費用。

24.11　流動性黑洞產生於市場參與者均在市場同一側的情況。監管規則對於流動性黑洞的產生有一定責任。因為金融機構所受的金融監管約束完全類似，所以它們對外部經濟事件的反應也相似。

24.12　流動性黑洞的產生往往是由於眾多的交易員採用同樣的交易策略，當交易員採用不同的交易策略時，流動性黑洞出現的可能性不大。

第25章

25.1　盯市計價涉及利用交易市場上的同類或相似產品的價格來對頭寸定價，按模型定價是指模型在決定價格時起決定性作用。

25.2　模型可能存在基本誤差，或者使用不當。

25.3　模型開發人員可能會離開。此外，金融機構的其他工作人員及其監管者也可以瞭解已完成的工作。

25.4　對簡單看漲期權及看跌期權進行定價時，交易員以布萊克-斯科爾斯-默頓模型作為插值工具。他們利用市場上交易活躍的期權來計算隱含波動率。通過對不同執行價格及期限進行插值，由此他們可以計算出其他期權的隱含波動率，這些波動率又被重新代入布萊克-斯科爾斯-默頓模型來計算這些期權的價格。但是在用於對衝時，布萊克-斯科爾斯-默頓模型就不再只是插值工具。

25.5　13.45%。我們可以採用以下兩種方法得出同樣的答案：（a）先在執行價格介於1.00與1.05之間進行插值，然後在期限介於6個月及1年之間進行插值；（b）先在6個月及1年之間進行插值，然後在執行價格1.00與1.05之間進行插值。

25.6　物理模型用於描述物理現象，而金融模型最終是為了描述人類的行為。

25.7　該機構可能會注意到，其某項業務的業務量很大，因為自己的報價與同業競爭者的報價有差別。另一種找出價格差別的方法是，將交易平倉並因而向同業競爭者詢價。另外我們可以通過訂購報價數據的形式來取得交易商提供的對於某些類別交易的月平均價格。

25.8　模型內對衝是指對模型所包含的隨機變量進行對衝，模型外對衝是指對模型所假設的“常量”進行對衝。

25.9　布萊克-斯科爾斯-默頓模型假定股票在1個月內的價格的概率分佈為對數正態分佈，這裡考慮的股票價格顯然不是對數正態分佈。一個合理的假設是分佈可能是兩個對數分佈的迭加，這時的分佈有兩個峰值，顯然布萊克-斯科爾斯-默頓模型不適用。

25.10　第1類交易是指活躍市場中相同交易中有報價的交易，第2類交易是指活躍市場中類似交易或不活躍市場中相同交易中有報價的交易，第3類交易是指需要模型假設。

25.11　過度擬合是指為了完美地擬合而匹配的東西過多。過度參數化是指通過引入額外的參數使模型變得過於複雜和難以使用。

25.12　執行價格為0.90、期限為1.5年的期權的隱含波動率為14.85%。執行價格為0.95、期限為1.5年的期權的隱含波動率為0.6×14.85％+0.4×14.20％=14.59％。

25.13　盯市計價是指在產品再定價（通常是每天）時，我們要保證產品的價格與市場價格一致，對於市場交易活躍產品計算出的價格通常反映了市場價格信息。這時模型僅僅是一個插值工具，因此盯市計價所得出的價格通常十分準確。而結構性產品價格通常與模型有關，因此這些產品是以模型定價的。

第26章

26.1　經濟資本金是銀行對自身所需要的資本金的一個估計，監管資本金是監管機構要求銀行必須持有的資本金數額。

26.2　AA級公司一年內違約的概率。

26.3　業務風險包括與業務戰略及名譽有關的風險。

26.4　對於市場風險及操作風險，計算經濟資本金的模型與計算監管資本金的模型會比較類似。在計算信用資本金時，銀行可能採用自認為更為合理，但與計算監管資本金不同的相關性模型以及相關性參數。

26.5　99.97%的置信水平所對應的最壞損失的對數為0.5+4×3.43=14.23，因此99.97%置信水平所對應的最壞損失為151萬美元。由於對數正態分佈的性質，我們得出預期損失為exp（0.5+4²/2），即4915美元，因此資本金需求大約為150.5萬美元。

26.6　部門1的經濟資本金為96.85，部門2的經濟資本金為63.87，整體資本金為124.66。

26.7　部門1對於整體經濟資本金的遞增效應為60.78，部門2對於整體經濟資本金的遞增效應為27.81，這意味著60.78/（60.78+27.81）=68.61%的經濟資本金應該分攤到部門1及27.81/（60.78+27.81）=31.39%的經濟資本金應該被分攤到部門2。將部門1的規模增大0.5%對於整體資本金的邊際效應為0.4182，將部門2的規模增大0.5%對於整體資本金的邊際效應為0.2056。歐拉定理得以滿足，因為整體資本金大約等於0.4182/0.005與0.205 6/0.005的和。

26.8　資本金為3 800萬美元，稅前收入為700萬美元，稅前RAROC為18.4%（=7/38）。在實踐中，多元化可能會降低資本金數量，並使RAROC有所增加。

26.9　RAROC可以用來比較不同業務部門的表現（績效評估）及用於預測業務部門將來的預期表現（決定資本金分配）。

第27章

27.1　在自上而下法中，整個機構的風險限額由高管或董事會決定。在自下而上法中，風險限額針對各個業務部門來設定。在企業風險管理中，兩種方法都需要，因為我們需要確保各業務部門的風險限額彙總後與整個企業的風險限額保持一致。

27.2　鮑曼悖論來源於對實證數據的觀察，在企業制定重大戰略規劃時，承擔高風險往往會造成更低的回報。

27.3　危險在於決策僅考慮短期效益，但是會導致長期的問題（例如，負面的公眾曝光、聲譽損失和法律訴訟）。業界事例5-4、業界事例27-1、業界事例27-2和業界事例27-3給出了相關實例。

27.4　年度獎金的一部分可以推遲發放，甚至可以被收回。

27.5　企業風險管理採用整體的方法（大圖景）來進行風險管理，而不是單獨考慮不同風險類別的管理（信用風險、市場風險、操作風險等）。

27.6　在式（27-1）中，我們設R=-0.2，R_F=0.03，R_M=0.117 4，σ_M=0.188 6及p=0.9。相對應的beta為1.49。

27.7　從第二年後開始的每個季度，利率將增加4%。16個季度後，利息將高達1.76+16×4%=65.76%。

27.8　認知偏差的例子包括：（a）錨定效應（對最初的估計僅進行小的調整）；（b）可得性啟發（最近的信息會獲得過高的權重）；（c）代表性啟發（過於依賴過去的有限的或對目前形勢沒有代表性的經驗）；（d）條件倒置。

第28章

28.1　當先前通過中介相互作用的雙方開始直接相互作用時，就會發生脫媒。當一種新的技術中介（提供與以前中介不同的服務）在非中介化之後進入市場時，就會發生復媒。

28.2　機器學習是人工智能的一個分支，計算機學習時不需要顯示編程。分佈式賬本技術是一種諸如區塊鏈的技術。在該技術中，數據庫可以跨多臺計算機共享和同步。

28.3　生物特徵識別授權使用個人獨特的生物學特徵來驗證他們是誰。指紋、視網膜掃描、面部識別、語音認證和心跳監控就是例子。

28.4　數字貨幣可能更容易控制貨幣供應量和管理通貨膨脹。

28.5　在P2P貸款中，借貸雙方使用技術公司提供的在線平臺直接進行交易。股權眾籌是一種允許廣大投資者通過在線平臺為初創企業提供資金的機制。

28.6　監管是金融科技進入的障礙。為了符合監管，金融科技公司有時不得不通過一家成熟的金融機構提供服務。

28.7　的確，如果每個人僅投資於指數基金，就不會有價格發現。我們需要一些投資者和基金經理關注新聞報道，並積極尋找應該買進或賣出的股票。

28.8　監管科技（RegTech）是指應對法規遵從性挑戰的技術開發。例如，用於在線實時報道的系統，用於篩選客戶和交易以避免合規性問題的系統，以及使金融機構可以輕鬆檢索有關不同國家、不同主題法規信息的在線圖書館。

28.9　IBM意識到不能依靠大型機銷售，因此改變了文化與商業模式以反映市場變化。柯達沒有像攝像市場變化那樣改變其文化和商業模式。為了生存，銀行將需要改變其文化和商業模式。