e1 John Hull 風險管理與金融機構 v5
| Site: | CLASE CHINO |
| Course: | BUSINESS BOOKS |
| Book: | e1 John Hull 風險管理與金融機構 v5 |
| Printed by: | Guest user |
| Date: | Saturday, 5 July 2025, 7:32 AM |
Table of contents
- 版權信息
- 風險管理與金融機構(原書第5版)
- 譯者序
- 作者簡介
- 譯者簡介
- 前言
- 第1章 引言
- 1.1 投資者的風險-回報關係
- 1.2 有效邊界
- 1.3 資本資產定價模型
- 1.4 套利定價理論
- 1.5 公司的風險以及回報
- 1.6 金融機構的風險管理
- 1.7 信用評級
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第一部分 金融機構及其業務
- 第2章 銀行
- 2.1 商業銀行
- 2.2 小型商業銀行的資本金要求
- 2.3 存款保險
- 2.4 投資銀行業
- 2.5 證券交易
- 2.6 銀行內部潛在的利益衝突
- 2.7 今天的大型銀行
- 2.8 銀行面臨的風險
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第3章 保險公司和養老基金
- 3.1 人壽保險
- 3.2 年金
- 3.3 死亡率表
- 3.4 長壽風險和死亡風險
- 3.5 財產及意外傷害險
- 3.6 健康保險
- 3.7 道德風險以及逆向選擇
- 3.8 再保險
- 3.9 資本金要求
- 3.10 保險公司面臨的風險
- 3.11 監管條款
- 3.12 養老金計劃
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第4章 共同基金和對衝基金
- 4.1 共同基金
- 4.2 交易所交易基金
- 4.3 主動管理型基金與被動型指數基金
- 4.4 監管
- 4.5 對衝基金
- 4.6 對衝基金的策略
- 4.7 對衝基金的收益
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第5章 金融市場上的交易
- 5.1 市場
- 5.2 清算所
- 5.3 資產的多頭和空頭
- 5.4 衍生產品市場
- 5.5 普通衍生產品
- 5.6 非傳統衍生產品
- 5.7 奇異期權和結構性產品
- 5.8 風險管理的挑戰
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第6章 2007年信用危機
- 6.1 美國住房市場
- 6.2 證券化
- 6.3 危機爆發
- 6.4 什麼地方出了問題
- 6.5 危機的教訓
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第7章 定價和情景分析:風險中性世界和真實世界
- 7.1 波動和資產價格
- 7.2 風險中性定價
- 7.3 情景分析
- 7.4 兩個世界必須同時使用的情況
- 7.5 實踐中的計算
- 7.6 對真實世界中的過程進行估計
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第二部分 市場風險
- 第8章 交易員如何管理風險敞口
- 8.1 delta
- 8.2 gamma
- 8.3 vega
- 8.4 theta
- 8.5 rho
- 8.6 計算希臘值
- 8.7 泰勒級數展開
- 8.8 對衝的現實狀況
- 8.9 奇異期權對衝
- 8.10 情景分析
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第9章 利率風險
- 9.1 淨利息收入管理
- 9.2 利率的種類
- 9.3 利率久期
- 9.4 凸性
- 9.5 推廣
- 9.6 收益曲線的非平行移動
- 9.7 主成分分析法
- 9.8 gamma和vega
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第10章 波動率
- 10.1 波動率的定義
- 10.2 隱含波動率
- 10.3 金融變量的每日變化量是否服從正態分佈
- 10.4 冪律
- 10.5 監測日波動率
- 10.6 指數加權移動平均模型
- 10.7 GARCH(1,1)模型
- 10.8 模型選擇
- 10.9 最大似然估計法
- 10.10 採用GARCH(1,1)模型來預測波動率
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第11章 相關性與Copula函數
- 11.1 相關係數的定義
- 11.2 測量相關係數
- 11.3 相關係數和方差-協方差矩陣
- 11.4 多元正態分佈
- 11.5 Copula函數
- 11.6 將Copula應用於貸款組合:Vasicek模型
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第12章 在險價值和預期虧空
- 12.1 VaR的定義
- 12.2 計算VaR的例子
- 12.3 VaR的缺陷
- 12.4 ES
- 12.5 一致性風險測度
- 12.6 VaR和ES中的參數選擇
- 12.7 邊際、遞增及成分VaR測度
- 12.8 歐拉定理
- 12.9 VaR和ES的聚合
- 12.10 回溯測試
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第13章 歷史模擬法和極值理論
- 13.1 方法論
- 13.2 VaR的精確度
- 13.3 歷史模擬法的擴展
- 13.4 計算問題
- 13.5 極值理論
- 13.6 極值理論的應用
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第14章 市場風險:模型構建法
- 14.1 基本方法論
- 14.2 推廣
- 14.3 涉及4個投資的例子
- 14.4 對於期限結構的處理
- 14.5 基本步驟的擴展
- 14.6 風險權重和加權敏感性
- 14.7 處理非線性情況
- 14.8 模型構建法與歷史模擬法的比較
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第三部分 監管規則
- 第15章 《巴塞爾協議Ⅰ》《巴塞爾協議Ⅱ》及《償付能力法案Ⅱ》
- 15.1 對銀行業進行監管的原因
- 15.2 1988年之前的銀行監管
- 15.3 《1988年巴塞爾協議》
- 15.4 G30政策建議
- 15.5 淨額結算
- 15.6 《1996年修正案》
- 15.7 《巴塞爾協議Ⅱ》
- 15.8 《巴塞爾協議Ⅱ》中的信用風險資本金
- 15.9 《巴塞爾協議Ⅱ》對於操作風險的處理
- 15.10 第二支柱:監督審查過程
- 15.11 第三支柱:市場紀律
- 15.12 《償付能力法案Ⅱ》
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第16章 《巴塞爾協議Ⅱ.5》《巴塞爾協議Ⅲ》及其他後危機修訂
- 16.1 《巴塞爾協議Ⅱ.5》
- 16.2 《巴塞爾協議Ⅲ》
- 16.3 未定可轉換債券
- 16.4 標準化方法和SA-CCR的使用
- 16.5 《多德-弗蘭克法案》
- 16.6 其他國家的法案
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第17章 OTC衍生產品市場的監管
- 17.1 OTC市場清算
- 17.2 危機後的監管改革
- 17.3 OTC交易新規定帶來的影響
- 17.4 CCP倒閉的風險
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第18章 交易賬戶基本審查
- 18.1 背景
- 18.2 標準法
- 18.3 內部模型法
- 18.4 交易賬戶和銀行賬戶的對比
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第四部分 信用風險
- 第19章 估測違約概率
- 19.1 信用評級
- 19.2 歷史違約概率
- 19.3 回收率
- 19.4 信用違約互換
- 19.5 信用價差
- 19.6 由信用價差來估算違約概率
- 19.7 違約概率的比較
- 19.8 利用股價來估計違約概率
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第20章 CVA和DVA
- 20.1 衍生產品的信用敞口
- 20.2 CVA
- 20.3 新交易的影響
- 20.4 CVA風險
- 20.5 錯向風險
- 20.6 DVA
- 20.7 一些簡單例子
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第21章 信用在險價值
- 21.1 信用評級遷移矩陣
- 21.2 Vasicek模型
- 21.3 Credit Risk Plus
- 21.4 CreditMetrics
- 21.5 信用價差風險
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第五部分 其他內容
- 第22章 情景分析和壓力測試
- 22.1 產生分析情景
- 22.2 監管條例
- 22.3 如何應用結果
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第23章 操作風險
- 23.1 操作風險的定義
- 23.2 操作風險的分類
- 23.3 《巴塞爾協議Ⅱ》下的監管資本
- 23.4 標準計量法
- 23.5 操作風險損失的預防
- 23.6 操作風險資本金的分配
- 23.7 冪律的應用
- 23.8 保險
- 23.9 《薩班斯-奧克斯利法案》
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第24章 流動性風險
- 24.1 交易流動性風險
- 24.2 融資流動性風險
- 24.3 流動性黑洞
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第25章 模型風險
- 25.1 監管要求
- 25.2 物理和金融模型
- 25.3 簡單的模型:代價高昂的錯誤
- 25.4 標準產品的模型
- 25.5 非標準產品的模型
- 25.6 盯市計價
- 25.7 如何建立成功的定價模型
- 25.8 構建模型過程中的誤區
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第26章 經濟資本金與RAROC
- 26.1 經濟資本金的定義
- 26.2 經濟資本金的構成成分
- 26.3 損失分佈的形狀
- 26.4 風險的相對重要性
- 26.5 經濟資本金的彙總
- 26.6 經濟資本金的分配
- 26.7 德意志銀行的經濟資本金
- 26.8 RAROC
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第27章 企業風險管理
- 27.1 風險偏好
- 27.2 風險文化
- 27.3 識別重大風險
- 27.4 戰略風險管理
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第28章 金融創新
- 28.1 技術的進步
- 28.2 支付系統
- 28.3 貸款
- 28.4 財富管理
- 28.5 保險
- 28.6 監管和合規
- 28.7 金融機構應如何應對
- 小結
- 延伸閱讀
- 練習題
- 作業題
- 第29章 避免風險管理失誤
- 29.1 風險限額
- 29.2 對於交易平臺的管理
- 29.3 流動性風險
- 29.4 對於非金融機構的教訓
- 29.5 結束語
- 延伸閱讀
- 第六部分 附錄
- 附錄A 利率複利頻率
- 附錄B 零息利率、遠期利率及零息收益率曲線
- 附錄C 遠期合約及期貨合約的定價
- 附錄D 互換合約定價
- 附錄E 歐式期權定價
- 附錄F 美式期權定價
- 附錄G 泰勒級數展開
- 附錄H 特徵向量和特徵值
- 附錄I 主成分分析法
- 附錄J 對信用遷移矩陣的處理
- 附錄K 信用違約互換的定價
- 附錄L 合成CDO及其定價
- 練習題答案
- 術語表
- RMFI軟件說明
- x≥0時N(x)的數表
- x≤0時N(x)的數表
華章教材經典譯叢
風險管理與金融機構(原書第5版)
Risk Management and Financial Institutions (Fifth Edition)
(加)約翰·赫爾(John C. Hull) 著
王勇 董方鵬 張翔 譯
ISBN:978-7-111-67127-5
本書紙版由機械工業出版社於2021年出版,電子版由華章分社(北京華章圖文信息有限公司,北京奧維博世圖書發行有限公司)在 中華人民共和國境內(不包括香港、澳門特別行政區及臺灣地區)製作與發行。
版權所有,侵權必究
客服熱線:+ 86-10-68995265
客服信箱:service@bbbvip.com
官方網址:www.hzmedia.com.cn
新浪微博 @華章數媒
微信公眾號 華章電子書(微信號:hzebook)
本書側重講述銀行和其他金融機構所面臨的風險,首先從風險與回報的替代關係入手,逐步深入地討論了市場風險、信用風險和操作風險等。在討論基礎風險類型的同時,本書還用大量篇幅討論了《巴塞爾協議Ⅲ》,並列舉了近年來發生在金融界的重大損失案例。此外,本書章後習題能幫助學生進一步理解概念、掌握操作程序及流程。
本書適合金融專業以及相關經濟專業的師生作為教材使用,也適合作為專業人士的參考用書。
譯者序 The Translators' Words
一本好書可以改變你的人生方向,助你成就事業。約翰·赫爾教授的著作對於金融從業者,尤其是對於金融衍生產品以及風險管理領域的從業者,有著持續、廣泛而深入的影響。對這種影響,我們三位譯者有著切身的體會。儘管前後相差數年,但我們都是循著赫爾教授的著作,先後跨進了金融業的大門。時至今日,在我們的日常工作中,他的著作仍在很多方面時時影響、幫助著我們。在當前信息爆炸的時代,找書讀似乎變得異常容易,但事實上,尋覓一本好書卻更加困難了。赫爾教授的這本《風險管理與金融機構(原書第5版)》無疑是金融風險管理類著作中的精品。
本書內容深入淺出,作者巧妙地避免了枯燥地講述金融學中常見的數學理論、定理和公式,而是將它們與業務直觀的、具體的例子結合在一起。本書可以作為高校金融專業的教材,在傳授知識之餘,更能幫助學生開拓思維並學以致用。特別是作者對書中所列舉的業界事例(Business Snapshot)及其借鑑意義的透徹分析,會成為金融專業畢業生進入風險管理領域的敲門磚。書中的練習題以及作業題會幫助學生進一步理解概念並掌握操作流程。我們相信本書會成為高校學生的良師益友。
我們對於很多術語的翻譯,力求做到與國內業界普遍採用的術語保持一致;對一些較新出現的概念,我們在給出自己的翻譯的同時,還保留了英文原文,以避免不必要的誤解。同時,對本書之前版本中的錯誤和筆誤,我們也竭力進行了排查和糾正。
在本書的翻譯過程中,我們的家人給予了巨大的支持、體諒和關懷,對此,我們銘記在心。我們還得到了許多人的熱情幫助,他們分別是歐伊露、黃昕和沈佳磊,在此我們向他們表示感謝。
我們還要特別感謝機械工業出版社華章分社的編輯,他們對於本書的翻譯提供了幫助,並對譯稿提供了寶貴的意見及建議。本書的中文翻譯肯定會有不盡如人意之處,衷心希望讀者批評和指正。
王勇 董方鵬 張翔
作者簡介 About the Author

約翰·赫爾 衍生產品及風險管理教授。他是一位享有國際盛譽的金融學教授,現任職於多倫多大學約瑟夫·羅特曼管理學院,關注的領域側重於應用。他曾在衍生產品以及風險管理領域出版過多本著作,發表過多篇文章。1999年,他被國際金融工程師協會(International Association of Financial Engineers)評為“年度金融工程大師”(Financial Engineer of the Year)。他曾為北美、日本和歐洲的多家金融機構提供金融諮詢。赫爾教授曾榮獲多項大獎,其中包括多倫多大學著名的Northrop Frye教師大獎。
譯者簡介 About the Translators

王勇 博士,國家千人計劃專家,上海市千人計劃專家,現任天風證券首席風險官和首席信息官,曾任光大證券首席風險官、加拿大皇家銀行風險管理部董事總經理。王勇博士持有加拿大達爾豪斯大學數學博士以及特許金融分析師(CFA)和金融風險管理師(FRM)證書。
王勇博士著有《金融風險管理》(升級版),並且翻譯了《期權、期貨及其他衍生產品》《區塊鏈:技術驅動金融》《數字化金融》《商用機器學習》《金融數智化未來》等多部頗具影響力的著作。

董方鵬 博士,現任加拿大皇家銀行資本市場量化分析總監。他曾任職於加拿大皇家銀行市場風險部、蒙特利爾銀行、德勤等機構,從事金融工程、衍生產品定價、風險管理、數據分析等工作。董方鵬博士是註冊金融風險管理師(FRM),他曾與王勇博士合作翻譯了《風險管理與金融機構(原書第4版)》和《價值投資:原理與實踐》。

張翔 博士,副教授,現任西南財經大學大數據研究院副院長、博士生導師,中國系統工程學會金融系統工程專業委員會委員、中國通信學會金融科技委員會委員、中國金融四十人論壇(CF40)青年會員、四川省天府萬人計劃專家。他曾任美國加州大學伯克利分校哈斯商學院訪問教授。他的主要研究方向為資產定價、金融風險管理以及金融大數據在衍生產品市場、量化投資與監管創新中的應用。
前言 Preface
在過去3年中,金融機構的風險管理實踐及其面臨的監管要求都在不斷變化,為了反映這些變化,我在《風險管理與金融機構》一書的新版中,對於相應的內容進行了擴充和更新。該書和我的另外一本暢銷書《期權、期貨及其他衍生產品》[1](Options, Futures,and Other Derivatives)一樣,其目的是為風險管理從業人員和相關專業學生提供幫助,準備FMA和PRM考試的專業人士會發現這本書尤其有用。
本書可用作風險管理或金融機構課程的教材,學生在選修以本書為教材的課程之前,無須先修有關期權和期貨市場的課程,但如果學生確實已經學過這類課程的話,那麼本書前9章的某些內容在課程中就可以跳過。
在對書中的內容進行擴充時,為了使盡量多的讀者讀懂本書,我儘量做到深入淺出,盡力降低書中數學知識內容的複雜度。例如,在第11章中講述Copula函數內容時,我首先將Copula這個概念直觀化,然後舉出一個較為詳細的數值例子;在第10章中講述極大似然方法以及在第13章中講述極值理論時,我儘可能給讀者提供詳盡的數值例子,以使讀者可以根據這些例子開發出自己的Excel表單。我也提供了很多相關應用的Excel計算表單,讀者可以從我的網站www-2.rotman.utoronto.ca/~hull上下載。
本書的主題是風險管理,因此涉及衍生產品定價的內容比較少(這是我的另外兩本書《期權、期貨及其他衍生產品》和《期權與期貨市場基本原理》[2](Fundamentals of Futures and Options Markets)的主要內容)。但在本書後面的附錄中,我會簡要描述一些在風險管理實踐中有重要意義並與定價相關的重點內容,這其中提到的RMFI(1.00版本)軟件可以從我的網站上下載。
本版新增的內容
我對第5版的內容做了全面的更新,更新內容中包含了許多嶄新的內容,特別是:
(1)新增了一章講述金融創新(第28章)。
(2)新增了一章講述對場外衍生產品市場的監管(第17章),包括已清算和未清算的交易,同時還解釋了什麼是標準初始保證金模型(SIMM)。
(3)重寫了第18章關於交易賬戶基本審查(FRTB)的部分,以便提供更完整的描述並反映最新的變化。
(4)重寫了第14章關於運用模型構建方法估計在險價值和預期虧空的部分,以更好地反映市場變量對利率的反應,以及在SIMM和FRTB下使用模型構建的方法。
(5)重寫了第23章關於操作風險的部分,以反映這方面的監管發展。
(6)重寫了第25章關於模型風險管理的部分,不僅僅涵蓋了估值模型,還包括諸如SR11-7之類的監管要求。
(7)在本書的不同章節中,還介紹了諸如IFRS 9和SA-CCR等監管的最新發展。
幻燈片
在我的個人網站或Wiley高教(Wiley Higher Education)網站上,讀者還可以下載數百張幻燈片。歡迎採用本書的教師對這些幻燈片進行適當修改,以用於教學。
問題解答
每章最後的問題被分為練習題(Practice Questions and Problems)和作業題(Further Questions)兩組,並在本書的最後為練習題提供瞭解答。對於作業題及相關軟件,採用本書的教師可以從Wiley高教網站上獲取解答手冊。
教師手冊
Wiley高教網站還為採用本書作為教材的教師提供了教學手冊,其中包括作業題的答案以及相關的Excel工作表、對每章教學內容的註解和對課程組織的一些建議。
鳴謝
在本書的寫作過程中,許多人提供了幫助,我在此表示感謝。在與許多學術界及金融風險管理從業者的交流中,我受益匪淺。我要感謝選修我在多倫多大學MBA和金融碩士項目中開設的金融風險管理課程的學生,這些學生提出了很多有益的建議,這些建議使得本書內容更加完善。
我要特別感謝我在多倫多大學的同事艾倫·懷特(Alan White)教授,艾倫和我在一起共事了大約30年。在此期間,我們在衍生產品以及風險管理方面有許多合作研究,同時我們也一起給其他機構提供過許多諮詢服務。在這個過程中,我們花了大量的時間共同探討一些關鍵性問題。本書中的很多新想法以及用來解釋已有概念的新方法是艾倫和我共同擁有的,艾倫還是RMFI軟件的主要開發者。
我還要特別感謝Wiley出版社的許多工作人員,尤其是本書編輯Bill Falloon、Mike Henton、Kimberly Monroe-Hill、Judy Howarth和Steven Kyritz。我衷心感謝他們給予的熱情幫助,非常感謝他們提供建議和鼓勵。
歡迎讀者對本書提出建議,我的e-mail地址是:hull@rotman.utoronto.ca。
約翰·赫爾
多倫多大學約瑟夫·羅特曼(Joseph L.Rotman)管理學院
[1] 中文版已由機械工業出版社出版。——譯者注
[2] 中文版已由機械工業出版社出版。——譯者注
第1章
引言
假如你是一家大公司的首席風險官(Chief Risk Officer,CRO),公司首席執行官(CEO)想了解你對一個項目的看法。呈現在你面前的大量風險報告顯示這個項目的當前價值為正,同時該項目也會提升股價,那麼公 司CEO想從你這裡得到什麼樣的分析和建議呢?
作為CRO,你需要考慮的是如何將該項目融入公司現有投資組合之中,找出該項目與公司其他業務的關係。你要回答當公司的其他業 務表現欠佳時,該項目的回報[1]是會同樣變得很差,還是會在其他業務上下波動時,起到抑制震盪的 作用。
公司為了生存發展必須承擔風險,風險管理部門的主要責任就是要了解公司現有業務組合的風險以及將來發展計劃可能帶來的風險,風 險管理部門必須判別當前持有業務的風險是否可以接受。如果風險不能接受,則應提出相應的解決措施。
本書主要是討論銀行以及其他金融機構的風險管理方法,當然,我們在此將要討論的很多想法和方法也同樣適用於其他行業。在過去幾 十年中,風險管理在所有企業的管理行為中變得越來越重要。尤其金融機構發現自己必須加強對風險管理的投入。如果銀行能夠建立較為完善的交易數據管理流程,那麼 諸如1995年巴林銀行(Barings Bank)、2002年愛爾蘭聯合銀行(Allied Irish Bank)、2007年法國興業銀行(Société Générale)及2011年瑞銀(UBS)等因為無賴交易員(rogue trader)所造成的重大金融損失則完全可以避免。如果風險管理人員確實能做到說服公司高管拒絕承擔那些不可接受的風險,類似花旗集團(Citigroup)、瑞銀、美 林(Merrill Lynch)在次債危機中的損失也許可以大大降低。
本章的主要目的是為我們今後將要闡述的問題介紹背景知識。在本章的開頭,我們將對投資者的股票以及債券組合中風險-回報的替換 關係這些經典理論進行回顧,然後討論這些經典理論是否也適用於一些新項目的判別,以及這些經典理論是否可用於管理風險頭寸。在本章的最後,我們將給出幾個原因 來說明公司(特別是銀行)應注重管理自身面臨的整體風險,而不只是關心那些已經做到風險分散的投資者所看到的風險。
[1] return,也稱收益。——譯者注
1.1 投資者的風險-回報關係
所有的基金經理都知道,投資時風險和回報之間有一個替換關係:風險越大,可能實現的回報越高。事實上這種替換關係介於風險和預 期回報之間,而並非風險與實際回報之間,“預期回報”一詞有時會使人產生誤解,在日常生活中“預期”一詞通常被理解為非常可能發生的事情,但統計學家卻將某一 變量的預期值定義為其平均值。因此預期回報是指對投資回報的加權平均,這裡的權重對應於這一投資回報所出現的各種可能的概率。可能的回報及相應的概率可以從歷 史數據中估計,或者通過主觀估計。
表1-1 將10萬美元資金投資於股票在1年後所得的回報
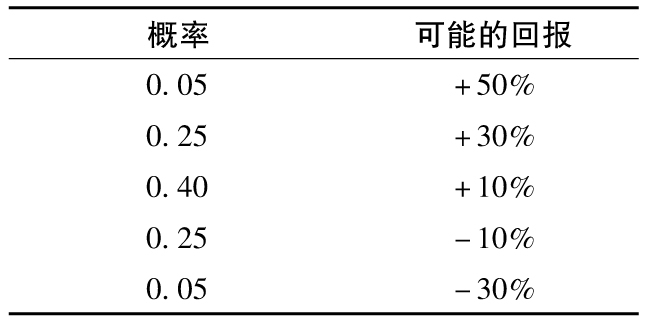
例如,假定你用10萬美元資金進行投資,投資期限為1年。一種可能是將所有資金投資於國債,其相應的年回報率為5%[1], 此項投資無風險,但預期回報率只有5%。另外一種可能是將所有資金投入某隻股票。為簡單起見,我們用表1-1來顯示該股票各種可能的回報以及相對應的概率。表 中回報率+50%所對應的概率為0.05,回報率+30%出現的概率為0.25,其他不同的回報率以及概率在表中均有顯示。將回報率記為小數點形式,股票的預 期回報率為
0.05×0.50+0.25×0.30+0.40×0.10+0.25×(-0.10)+0.05×(-0.30)=0.10
計算結果顯示,當你願意承擔一定的風險時,投資的預期回報率可以由投資國債的5%提高到10%。如果投資一切順利,你的回報也 可能達到+50%,但如果投資不順利,也可能是-30%,其相應損失為3萬美元。
馬科維茨(Markowitz,1952)是研究投資風險-回報替換關係的先驅之一,後來夏普(Sharpe,1964)及其 他人以馬科維茨理論為基礎,進一步發展了資本資產定價模型(capital asset pricing theory)。資本資產定價模型顯示了預期回報和系統性風險的關係。1976年,羅斯(Ross)發表了風險套利定價理論(arbitrage pricing theory),這一理論將資本資產定價理論中單一系統性風險假設延伸到多系統性風險。這些頗具洞察力的理論研究成果對投資組合管理人理解和分析風險-回報關係產生了巨大 影響,在下一節中我們將回顧這些重要理論。
1.1.1 風險量化
當你選定某一投資後,如何將所面臨的風險進行量化呢?一種便捷的方式是將風險量定義為年回報率的標準差,也就是
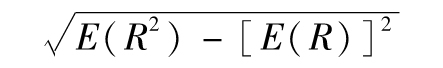
其中R指年回報率,E為 預期符號,E(R)代表年回報率的期望值。由表1-1可 知,我們可以算出E(R)為0.1。為了計算E(R2),我們必須以概率為權重對回報率的平方進行 加權平均:
E(R2)=0.05×0.502+0.25×0.302+0.40×0.102+0.25
×(-0.10)2+0.05×(-0.30)2=0.046
故年回報率的標準差為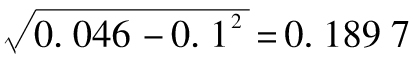 ,
即18.97%。
,
即18.97%。
1.1.2 投資機會
假定用期望值及標準差來描述完全不同的投資機會,我們可以用圖1-1來表示具有不同風險的投資可能,其中橫軸表示回報率的標準 差,縱軸表示預期回報。
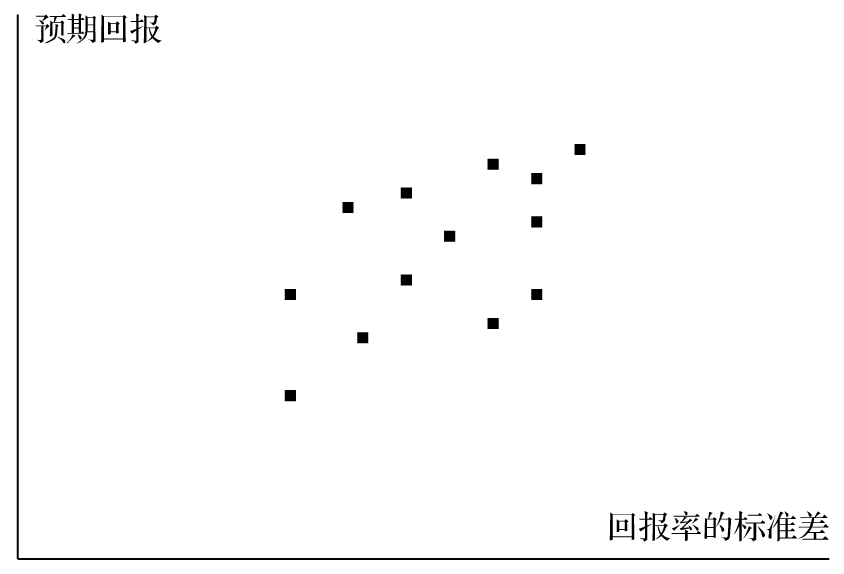
圖1-1 具有不同風險的投資資產
當得出某些投資回報率的標準差以及預期回報後,我們自然會想如果將這些投資進行不同的組合又會產生什麼效果呢?假設兩種投資資 產的回報率為R1和R2,如果我們按w1的 比例投入第一種資產,按w2=1-w1的比例投入第二種資產,這樣所產生的投資組合的回報率為
w1R1+w2R2
投資組合的預期回報為
μP=w1μ1+w2μ2
(1-1)
其中μ1為第一 種資產的預期回報,μ2為第二種資產的預期回 報。投資組合回報率的標準差為
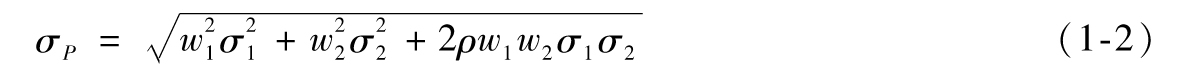
其中σ1與σ2分別為R1和R2的 標準差,ρ是R1和R2的相關係數。
假定μ1為 10%,σ1為16%,μ2為15%,σ2為 24%;R1和R2的相關係數為0.2。表1-2顯示出在不同比例投資下投資組合的預期回報以及回報率的標準差。以不同比 例投資於兩種資產會給投資者帶來範圍廣泛的回報組合,圖1-2是其圖形顯示。
表1-2 由兩種投資資產構成的投資組合的預期回報以及回報率的標準差
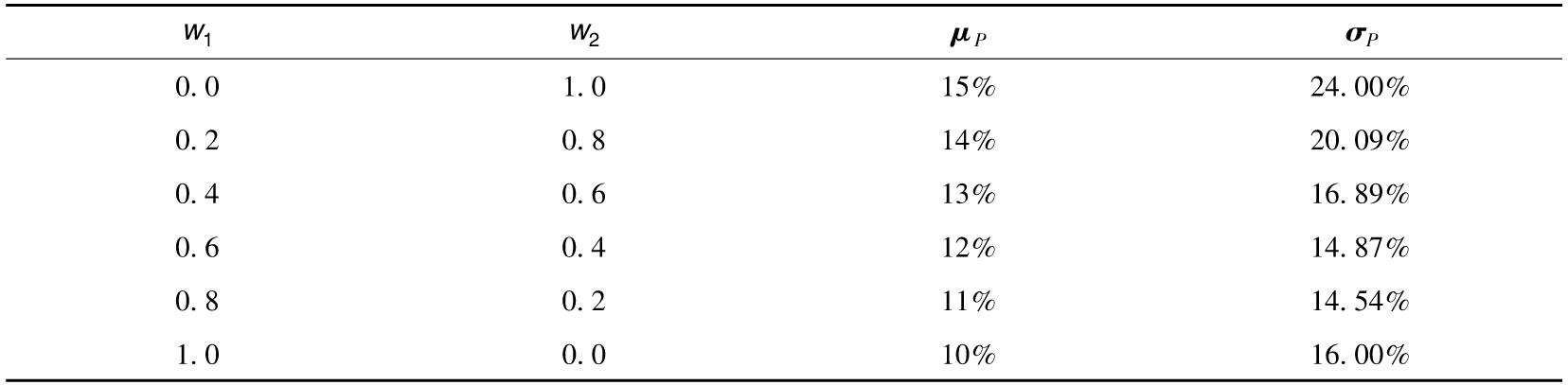
注:兩種資產的預期回報分別為10%及15%,回報率的標準差分別為16%及24%,兩種資產回報的相關係數為0.2。
大多數投資者都厭惡風險(risk-averse),他們希望在增加預期回報的同時也減少回報率的標準差,體現在圖1-1及圖 1-2中,他們希望自己的投資回報曲線朝“西北”(左上角)方向移動。從圖1-2中我們可以看到,對兩種投資進行不同的組合可以幫我們達到目的。例如,在第一 種資產中投入60%的資金,而在第二種資產中投入40%的資金,這樣做投資的預期回報率可以達到12%,其所對應的回報率的標準差為14.87%。這種組合比 只投資於第一種資產的效果要好(預期回報提高了2%,而回報率的標準差降低了1.13%)。
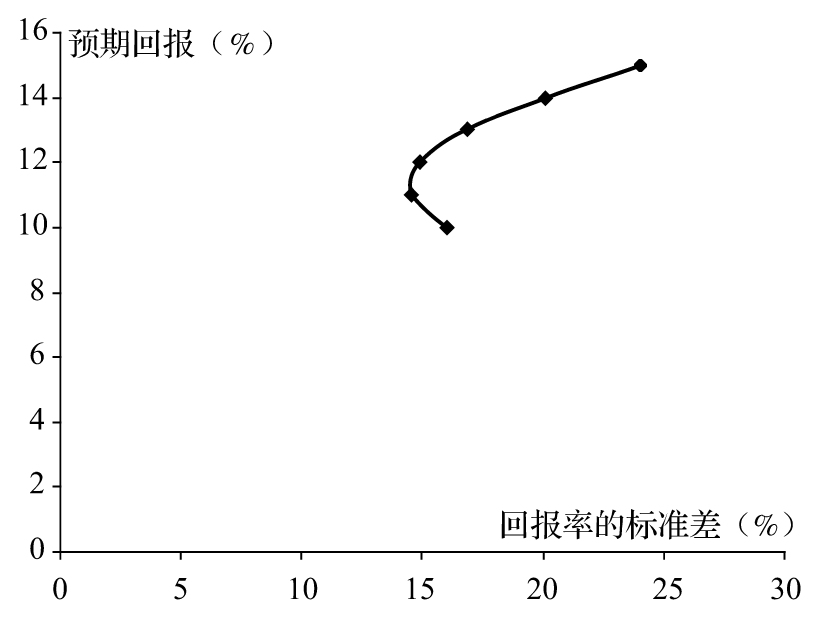
圖1-2 表1-2計算出的兩種資產構成的投資組合的不同的風險-回報
[1] 這一數值比較接近歷史平均值,但顯著高於2008年以來美國國債及其他一些國債的收益率。
1.2 有效邊界
在這裡我們引入第三種投資資產。這種資產可同前面的兩種資產進行任意組合,這樣做可以進一步產生不同的風險-回報組合,使我們 的投資回報率進一步往“西北”方向移動。在這之後我們又可以引入第四種資產,而這第四種資產又可以同前面3種資產進行不同的組合而產生新的投資機會,我們繼續 這一過程,當我們考慮了所有由圖1-1所顯示的風險投資資產以後,我們就可以構造出所謂的有效邊界(efficient frontier)。在圖1-3中,有效邊界是我們的回報曲線朝西北方向移動的極限。對應有效邊界的任意一點,我們不可能找到某種投資會比其更優化。這句話是 指我們不可能會找到某一資產投資回報比有效邊界的點所對應的投資回報更高,而同時所對應的標準差更低。圖1-3中有效邊界的東南方向代表所有不同的投資可能, 對應於有效邊界的“東南”(右下角)方向的任何一點A,我們都可以在有效邊界中找到一點並使其風險-回報替 換關係比所對應的點A的風險-回報替換關係更好。
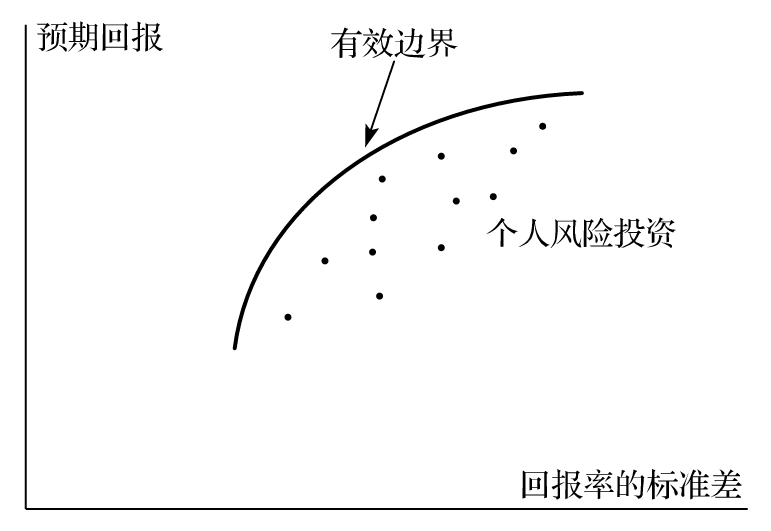
圖1-3 由具有不同風險的投資資產所產生的有效邊界
在圖1-3中我們只考慮了具有風險的投資。如果引入所有可能投資的話,那麼有效邊界又會變成什麼樣子呢?特別地,當我們引入無 風險投資時,會發生什麼情況呢?假定無風險投資所對應的回報率為RF, 在圖1-4中,我們用F點來代表無風險投資,從F點開始 我們引入同原有效邊界相切的一條直線,M代表切點。以下我們將要說明,直線FJ將 會是新的有效邊界。
如果將佔整體資金百分比βI(0<βI<1)的資金投入風險投資組合M, 然後將其他所有資金投放於無風險資產之中,這樣做會帶來什麼效果呢?如式(1-1)所示,我們進行這樣的組合之後,投資組合的預期回報E(RI)由下式給出
E(RI)= (1-βI)RF+βIE(RM)
由式(1-2)可知,我們得出投資組合回報率的標準差為βIσM[1],這裡σM代 表投資組合M的標準差。在圖1-4中,我們用I點來代表 以上表達式所闡明的風險-回報關係,從預期回報以及標準差兩方面來看,點I與F的 距離與點M與F的距離的比例為βI。
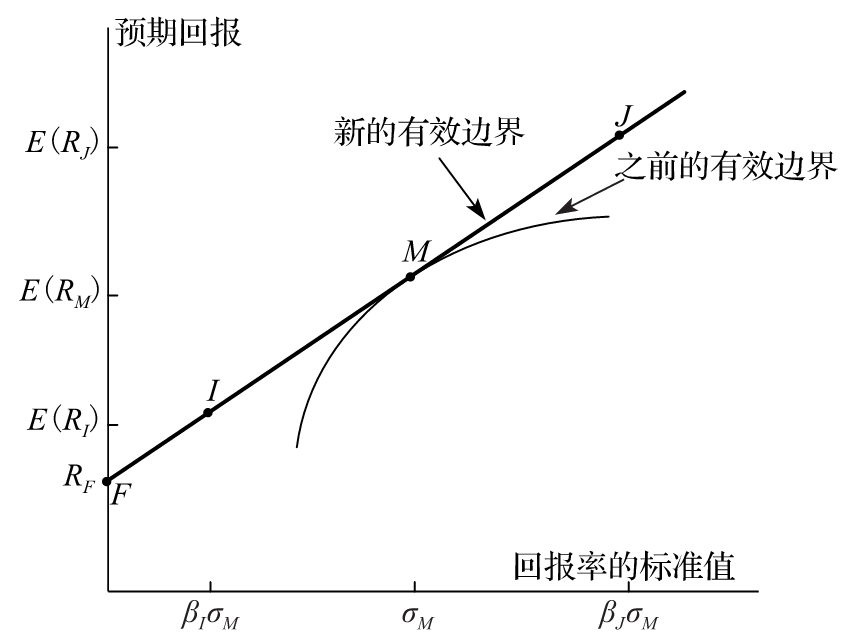
圖1-4 包含所有投資資產的有效邊界
注:I點所對應的投資由投入百分比為βI數量的資金在投資組合M中和1-βI數量的無風險資產所組成,J點 所對應的投資是以無風險利率借入的βJ-1數量 資金,然後將所有的資金(擁有的和借入的)全部投入投資組合M中所組成的。
直線FM上的所有點均可以由投放一定數量資金在M投 資組合以及一定數量資金在無風險資產F來取得,此直線上任意一點所對應的風險-回報關係要優於我們之前所討 論的有效邊界上的風險-回報關係,直線FM也因此成為新的有效邊界。
假定我們可以按利率RF借 入及借出資金,我們因此可以構造出從F點至M點以至於超 出M點的射線。假定我們的目的是構造出由圖中J點所表示 的組合投資,J點至F點距離是M點 至F點距離的βJ(βJ>1)倍。我們首先借入βJ-1數量的資產,然後將所有資產投入M點 投資組合之中。去掉應付利息之後,新的投資組合J所對應的預期回報為
E(RJ)=βJE(RM)-(βJ-1)RF=(1-βJ)RF+βJE(RM)
J點的標準差為βJσM。這樣我們清楚地展示了J點所對應的風 險-回報關係。
這裡的討論說明:當引入無風險投資後,有效邊界變成一條直線。換句話說,在由圖1-4所示的有效邊界上,預期回報與標準差之間 一定有一種線性的替換關係。所有的投資者都應選擇同樣的風險性資產,即M點所對應的投資組合,然後將風險性 資產與借入或借出的無風險資金進行不同比例的組合來體現他們的風險偏好。
現在要簡要說明一下投資組合M必須包含所有可能的風險投資資產。假設某個特 殊的投資資產沒有含於投資組合M之中,這樣就會造成沒有投資者持有這一資產,其價格會下跌,預期回報會增 加,最終成為組合的一部分。我們還可以進一步說明,為了保證每種投資資產的供需關係,每個風險投資資產的價格會得到調整,因此組合M中 的各個風險資產數量必須同整個經濟中所有可能投資資產成一定比例,這樣的投資組合M通常被稱為市場投資組合(market portfolio)。
[1] RF是無風險利率,為常數,E[RF]=RF,σF=0。 ——譯者注
1.3 資本資產定價模型
當投資者投資於某些資產時,他們如何判定自己需要的預期回報呢?我們的以上分析說明,市場投資組合會起一個決定性的作用,投資者對於某資產回報所需要的預期回報在一定程度上要反映此資產對市場投資組合風險的奉獻量。
一個較常用的方式是以投資資產的回報及市場投資組合回報的歷史數據來得出某種最佳線性迴歸關係。這種線性迴歸關係式可表達為
R=α+βRM+ε
(1-3)
其中R代表投資資產的回報,RM代表市場投資組合的回報,α和β都是常數,ε是指回歸誤差,為隨機變量。
式(1-3)顯示了除了常數項α以外,資產回報有兩個組成部分。
(1)一部分對應於βRM,此項為市場投資組合回報的某種倍數。
(2)另一部分對應於ε,此項與市場投資組合的回報無關。
這裡對應的風險,第一部分被稱為系統性風險(systematic risk),而第二部分被稱為非系統性風險(nonsystematic risk)。
首先讓我們考慮非系統性風險。如果我們假定對應於不同投資資產的ε項相互獨立,在大型投資組合中,非系統性風險幾乎被分散殆盡,因此投資者不應該關心非系統性風險,也就是說投資者不應該因承擔非系統性風險而索取高於無風險利率之上的回報。
系統性風險是投資者應該關心的內容,當持有一個大型而風險分散均衡的投資組合時,由βRM表示的系統性風險並沒有消失,因此承擔這一系統性風險,投資者應索取補償。
由圖1-4可知,我們可以看到預期回報與系統性風險之間的關係,β=0對應於非系統性風險,其所對應投資回報為RF。當β=1時,投資資產的回報與M點對應,此時的預期回報為E(RM)。一般來講,我們有關係式
E(R)=RF+β[E(RM)-RF]
(1-4)
式(1-4)就是所謂的資本資產定價模型,這一公式說明某投資的預期回報超出無風險投資回報的數量等於市場投資組合的預期回報超出無風險投資回報的數量與β的乘積。圖1-5中顯示了這一關係式。參數β被稱為是投資的β係數。
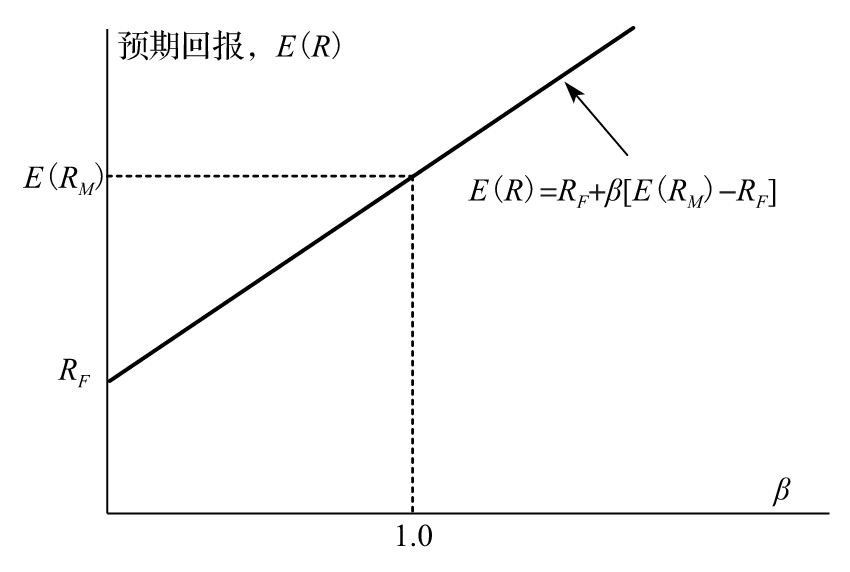
圖1-5 資本資產定價模型
【例1-1】 假定無風險投資利率為5%,市場投資的預期回報率為10%。如果一項投資的β為0,那麼該投資的預期回報為5%,這是因為投資中的風險可以被完全分散;如果一項投資的β為0.5,那麼該投資的預期回報為
0.05+0.5×(0.1-0.05)=0.075
即7.5%;如果一項投資的β為1.2,那麼該投資的預期回報為
0.05+1.2×(0.1-0.05)=0.11
即11%。
係數β被稱為投資組合的beta係數,等於ρσ/σM,其中ρ是投資資產與市場投資組合的相關係數,σ是指投資資產回報率的標準差,σM是市場投資組合回報率的標準差,beta係數體現了投資組合對於市場投資組合的敏感性,我們可以用式(1-3)來定義任何一種投資組合的beta係數,而資本資產定價模型式(1-4)中對應於這一投資組合的回報率R。在圖1-4中,由M點所代表的市場投資的beta係數為1.0,由F點所代表的無風險投資的beta係數為0,而由I和J所代表的投資資產的beta係數分別為βI及βJ。
1.3.1 假設
以上分析帶給了我們一個驚人的結論,那就是所有的投資者均想持有一個同樣的投資組合(即圖1-4中M點所表示的投資組合),這一結論顯然不成立。如果以上結論成立,那麼投資者相互之間不會再進行交易,市場也會停止運作。在實際中,不同的投資者對於股票及其他風險投資產品有著不同的看法,正因為如此,投資者之間才相互進行交易,從而促成了市場價格的產生。
在以上分析中,我們採用了多個隱含假設,這些假設造成了其得出的結論與現實市場有所出入。假設包括:
(1)我們假設投資者只關心他們投資組合的預期回報及回報率的標準差,換句話講,投資者只關心回報分佈中的前兩階矩(first two moments)。如果回報服從正態分佈,那麼投資者這麼做確實合理,但是,我們知道許多投資組合的回報並非服從正態分佈。事實上,許多投資組合的分佈具有偏態(skewness)以及超額峰度(excess kurtosis)特性。偏態與分佈的第三階矩有關,峰度與分佈的第四階矩有關。與正態分佈相比,具有正偏態的分佈會產生更多的高回報和更少的低迴報,具有負偏態的分佈會產生更多的低迴報和更少的高回報。超額峰度分佈產生高回報和低迴報的機會均多於正態分佈。許多投資者對出現極端負回報的可能性非常擔心,他們可能願意在具有負偏態或具有超額峰度的投資組合裡得到更高的預期回報。
(2)我們假設在式(1-3)中對應於不同投資的ε項為相互獨立,這等於是說投資回報的相關性完全取決於投資本身與市場組合的相關性,這一假設顯然不成立。福特和通用汽車同屬於汽車行業,兩家公司的股票會有一定的相關性,這一相關性並非來自它們與市場的相關性。以上討論說明對應於不同投資的ε項並非相互獨立。
(3)我們假設投資者只關心某一特定時段的投資回報,而且我們假設不同投資者所選定的時段均相同,這一假設顯然不成立。有些投資者(如養老基金)的投資期限很長,而有些投資者(如當日交易員(day trader))的投資期限很短。
(4)我們假設投資者可同時以相同的無風險利率借入或借出資金。在正常的市場條件下,對於信譽好的大型金融機構而言,以上假設近似成立;對於小投資者而言,這一假設不成立。
(5)我們在分析中不考慮稅收。我們知道,某些地區對資本收益(capital gain)的稅收處理不同於對股息和其他收入,而某些投資產品會有特殊的稅收優惠;還有,並非所有的投資者均會受同一稅率的制約。在實際中,投資者進行投資會將稅收考慮在內。對免稅的養老基金適用的投資可能並不適用於需要支付很高稅率的某紐約居民,這一說法反過來也成立。
(6)最後,我們假設所有投資者對任意給定的投資資產的預期回報、回報率的標準差的估算,以及對投資產品之間的相關係數的估算相同。換句話講,我們假設投資者具有一致性預期性(homogeneous expectations),這顯然不成立。事實上,正如以上討論所示,在一致性世界裡不會出現交易行為。
即使如此,資本資產定價模型已經被證明是管理人員進行投資組合管理的強有力的工具。關於股票的beta估計已經非常容易取得,同時由資本資產定價模型所計算出的投資期望值通常被管理人員用來當作檢驗投資好壞的標準,我們接下來將進一步解釋這一點。
1.3.2 alpha
當我們觀察市場回報為RM時,我們對一項beta值等於β的投資組合的預期為多少?資本資產定價模型將投資組合的預期回報與市場的預期回報聯繫在一起,同時模型也將投資組合的預期回報與市場的真實回報聯繫到一起
E(RP)=RF+β(RM-RF)
其中RF為無風險利率,RP為投資組合的回報。
【例1-2】 考慮一個beta為0.6的投資組合,無風險利率為4%。
當市場回報為20%時,投資組合的預期回報為
0.04+0.6×(0.2-0.04)=0.136
即13.6%;當市場回報為10%時,投資組合的預期回報為
0.04+0.6×(0.1-0.04)=0.076
即7.6%。當市場回報為-10%時,投資組合的預期回報為
0.04+0.6×(-0.1-0.04)=-0.044
即-4.4%。投資組合的預期回報與市場回報的關係如圖1-6所示。
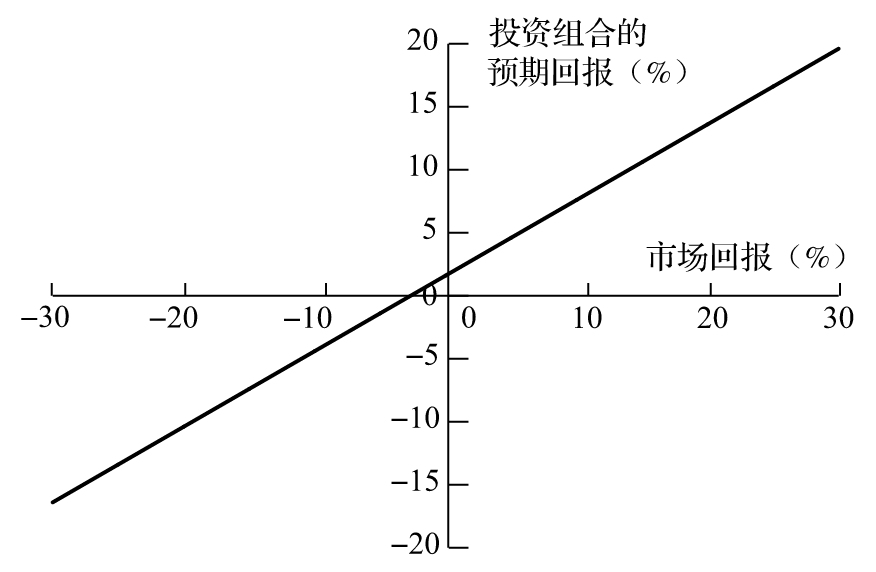
圖1-6 投資組合的預期回報與市場真實回報的關係(組合的beta為0.6,無風險利率為4%)
假定投資組合的真實回報大於預期回報,即
RP>RF+β(RM-RF)
我們可以說,對於一定數量的系統性風險而言,投資組合經理產生了更為突出的回報,而額外回報量為
α=RP-RF-β(RM-RF)
該額外回報通常被稱為是由投資組合經理產生的alpha。[1]
【例1-3】 某投資組合的beta為0.8,1年期無風險利率為5%,市場在1年內的回報為7%,投資組合經理的回報為9%,該經理產生的alpha為
α=0.09-0.05-0.8×(0.07-0.05)=0.024
即2.4%。
投資組合經理會不斷地努力來產生正的alpha,其中一種做法是尋找比市場表現更好的股票,另一種方法是市場擇時(market timing)。這一做法涉及對市場變化做出預測,當預計市場會上漲時,投資經理會將資金從保守的國債投資轉移到股票市場;當預計市場會下跌時,投資經理會將資金從股票市場轉移到保守的國債投資。在第4章中,我們解釋了對衝基金生成正的alpha的投資策略。
雖然資本資產定價模型採用了一些簡化的假設,但是由模型產生的alpha和beta參數被廣泛應用於描述投資的特性。beta描述了由於承擔系統性風險取得的回報,beta值越高,投資組合所承擔的系統性風險也越高,回報中有更多的成分取決於市場回報;alpha代表了投資組合管理得當(或者是因為運氣好)所帶來的額外回報。一個投資者取得正的alpha一定是建立在另一個投資者取得負的alpha的代價之上,所有投資者的alpha的加權平均為0。
[1] alpha也被稱作詹森阿爾法,因為它是由邁克爾·詹森(Michael Jensen)在衡量對衝基金表現時首先引入的,見第4.3節。
1.4 套利定價理論
套利定價理論(arbitrage pricing theory)可以被看作對資本資產定價模型的擴展。在套利定價理論中,投資者的回報被假設取決於多種因素(這些因素可能是國民生產總值(GNP)、國內利率以及通貨膨脹率)。通過構造與這些風險因素呈中性的投資組合,套利定價理論展示投資資產的預期回報同這些因素呈某種線性關係。
式(1-3)中投資資產的ε項相互獨立這一假設保證了資本資產定價模型中投資的預期回報取決於單一因素(因此也就只有一個系統性風險因素),這一因素就是市場投資組合的回報。在套利定價理論中有多種因素決定投資的回報。這些因素中的每一項都是一個系統性風險源。套利定價理論中的非系統性風險(即可分散的風險)是與以上多種因素無關的風險。
1.5 公司的風險以及回報
我們現在進一步考慮某一公司的風險與回報的替換關係,一家公司如何來判別某項投資所帶來的回報可以足夠補償其帶來的風險呢?
一家公司的最終擁有者是其股東,公司管理的最終目標是股東利益最大化。因此,一個新的項目可以自然地被理解為在股東投資組合之上的疊加。公司應該計算一個投資項目的beta係數及其預期回報。如果此項投資的預期回報高於由資本資產定價模型所決定的預期回報,那麼該投資會給股東帶來好處,因此該投資可以被接受,否則該投資應該被否決。
這個觀點說明在決定是否接受某種投資時,非系統性風險因素不應該在考慮之列。在實際中,公司既應考慮系統性風險又應考慮非系統性風險。例如,大多數公司會為其公司的建築物購買火災保險。即便這種風險完全是非系統性的,而且可以通過股東分散投資得以緩解。企業為了迴避高風險,會對它們所面臨的匯率、利率、商品價格及其他市場因素所帶來的風險進行對衝。
收益的穩定性、公司的生存能力都是公司管理的目標,公司在運作過程中會嘗試新的業務,並試圖保證新業務的預期回報與股東既定的風險-回報關係相一致,但無論如何承受的風險量不能過大。
大多數投資者對他們所投資公司的整體風險的大小也會關心。投資者不喜歡被驚嚇,他們喜歡將資金投放於有強勁增長並能達到預期目標的公司。投資者喜歡將資金投放於那些能夠小心管理及控制自己面臨的包括系統性及非系統性風險等整體風險的公司。
第1.1~1.4節中的理論結果指出的投資者的行為應同以上的討論截然不同,當預期回報同系統性風險替換關係對於公司可以接受時,投資者應該鼓勵公司儘可能投資於高風險項目。在投資者的投資組合中,某些公司會破產,某些公司會生存得很好,對投資者來講,投資的最終目的是保證整體回報的優良。
投資者的行為有時會不追求最佳結果嗎?由於投資者有分散風險的需要,公司承擔了更多非系統性風險是否會給投資者帶來更多的好處呢?一種著名的理論指出事實並非如此,該理論被稱為“破產成本”理論。這一理論不但可以用於解釋一家公司為什麼會約束自己所發行的債券量,而且也可以被延伸到整個風險領域。
1.5.1 破產成本
在一個完美的世界裡,破產應該是一個非常簡捷的事件,公司的有形及無形資產都以一個公平的市場價格被出售,所得的資金會在一個完善規則之下在債券持有者、股權持有者及其他公司權益持有者之間進行分配。如果我們生活在這樣的完美世界中,破產應該不會破壞股東的價值。不幸的是我們生活的世界並不完美,破產過程會觸發破產成本(bankruptcy cost)。
破產成本的實質是什麼呢?當一家公司宣佈破產時,公司的顧客及供應商不再願意同公司進行業務接觸;此時公司資產會不得不以低於破產前的價格被出售;此時公司的無形資產,例如公司的商標價值及市場名聲均受到了損害;公司已經不能在保護股東利益前提下進行運作,此時公司往往會支付大量的手續費給會計師及律師;此時公司的厄運接連不斷。雖然業界事例1-1中所講的故事是虛構的,但其代表性同實際生活相差並不太遠,這一事例顯示,某一高風險決策的失敗給公司帶來的後果可能是毀滅性的。
業界事例1-1
隱含的破產成本
幾年前某一公司擁有市價為20億美元的資本金,同時其發行債券總數為5億美元。公司總裁決定以10億美元現金收購一公司,這裡的現金由銀行貸款及發行債券的融資所組成。收購該公司的價格與市場價格相近,同時買入價格體現了在成交時買入公司的預期回報及市場的系統性風險,但是,那些關鍵的會給公司盈利帶來威脅的因素被忽略了。
在此之後,此項交易的許多促成因素都沒有得以實現,買入的業務沒有盈利。3年之後公司CEO被迫辭職。公司新任CEO以1億美元(原價格的10%)賣出了此項投資,同時公司也宣佈其業務將集中於某核心業務。此時公司的債務槓桿比率大大提高,經濟週期中的一個暫時下滑就促成了公司不能償還債務,公司宣佈破產。
此時公司裡充斥了大量形形色色的會計師及律師,這些人代表不同人(像貸款銀行、不同證券持有者、股東、公司及公司董事會)的利益。這些會計師及律師給公司每月帶來了大約1000萬美元的費用,此時因無人願意同一家破產公司進行業務往來,所以公司喪失了銷售能力,公司的其他主要高管也辭職了,公司的股票價格暴跌。
兩年又過去了,經過3次改組,公司終於在諸多參與者之間達成一個協議,併成立了一家市價為70萬美元的新公司,新公司將繼續經營其盈利業務,此時新公司的擁有者為貸款銀行及債券持有者,原公司的股東利益損失殆盡。
發生在2008年9月15日的雷曼兄弟破產是迄今美國歷史上最大的破產案例。在雷曼兄弟破產兩年後,即2010年9月14日,《金融時報》(Financial Times)報道稱,在美國和歐洲,與雷曼控股公司所有分支機構破產程序有關的法律和會計費用已經達到20億美元,儘管其中一些服務的收費已經打了折扣。
我們前面指出,公司的生存是公司管理的一個主要目標,權益持有者不希望公司本身承擔過多的風險,現在我們明白了這樣做的原因。國與國之間的破產法可以相差甚遠,但這些法律的共同效果是:公司的價值在債權持有者為獲得補償而進行的爭鬥中受到了損害。如果公司選擇風險很高的項目(但預期回報高於圖1-4中的有效邊界),那麼公司破產的可能性很大。當考慮預期破產成本時,總風險(系統性和非系統性)較高的項目可能會被拒絕。這就解釋了為什麼股東喜歡公司限制其承擔的總風險,並投資那些能控制風險以滿足盈利預期的公司。
當一個新的項目在醞釀之中時,決策人要考慮的一個關鍵問題是新項目是否同公司的其他風險相匹配。由於分散化帶來的好處,一個相對較小的投資往往會有減少整體風險的效果,但一個大的投資可能會大大地增加整體風險。許多投機型公司的失敗(見業界事例1-1)往往可以歸咎於公司CEO在較大的收購(常常使用較高槓杆)決策上的失誤。
1.5.2 金融機構
與非金融企業相比,在金融機構的決策中破產成本的重要性尤為突出,比如一家銀行必須保證其破產概率非常小。大的銀行依賴批發存款和諸如商業票據等工具來融資。信心是銀行得以生存的根本。如果市場認為某家銀行違約的風險不夠低,就會對其喪失信心,而銀行的資金來源也就因此而枯竭。銀行會陷入被迫清算的境地,即便此時它仍可能具有正的所有者權益從而具備償付能力。雷曼兄弟的破產是美國歷史上最大的破產案例;在英國,北巖銀行(Northern Rock)的破產也是一個轟動的案例。在這兩個案例中,導致其破產的元凶都是信心崩潰及傳統資金來源枯竭。
1.5.3 監管機構
即便銀行的管理層不顧以上所討論的風險,並且希望能夠承擔更多的風險,他們也不被允許這樣做。與其他企業不同的是,金融機構要接受嚴格的監管。世界上任何一國政府都希望本國有一個穩健的金融體系。個人和企業對與其進行業務往來的銀行和保險公司應具有足夠的信心,這一點非常重要。監管措施的設計要確保銀行和保險公司遭遇嚴峻財務困難的概率很小。在2008年次債危機中,各國政府對金融機構的救助說明了政府非常不情願讓大的金融機構破產,而受監管的金融機構必須考慮整體風險(系統性的及非系統性的)。
顯而易見,破產往往是由於銀行正在遭受虧損。監管機構的目標是保證銀行持有的用於緩衝損失的資本金達到一定水平,在很高的概率下,足以應付損失。例如,假定金融機構在1年內出現損失超出20億美元的概率為0.1%,監管機構也許會要求銀行持有20億美元的股權資本金,這樣會保證股權資本可以承擔損失的概率為99.9%。在以後的章節中我們將討論監管機構所採用的模型。
這裡的重點是,監管機構最為關心的是整體風險,而不僅僅是系統性風險。監管人員的最終目標是使發生破產事件的可能性非常小。
1.6 金融機構的風險管理
對金融機構(及其他機構)來講有兩大類風險管理策略:一是對每一種風險進行識別,然後對各類風險單獨管理,這種管理方式有時被稱為風險分解(risk decomposition);二是用多元化的管理方式來緩解風險,這種方式有時被稱為風險聚集(risk aggregation)。在實踐中,銀行採用這兩種方式來管理以下將要討論的市場風險與信用風險。
作為實例,我們考慮一家美國銀行交易業務所面臨的市場風險。市場風險起源於多個市場變量(利率、匯率、股價)在將來的變化的不確定性。為了實施風險分解模式,交易平臺會指定交易員來管理某一特殊市場變量(或一定小數量的市場變量)。例如,交易平臺可能指定一個交易員(或一組交易員)來管理所有美元/日元匯率交易,在每個交易日結束時,交易員要保證相關的交易額度要在事先由銀行設定的額度之內。在一天的交易即將結束時,交易員如果發現某個或多個交易額度將超出銀行規定,交易員或要取得批准來持有當前頭寸,或進行新的對衝交易來減持頭寸以保證額度要求(在第8章中,我們將討論交易員計算風險額度的方法)。
風險管理人員在銀行的中臺(middle office)對市場風險實施風險聚集管理,管理過程涉及在每天結束時將銀行市場風險進行彙總,來計算銀行所面臨的由於市場變動所觸發的整體風險。對風險進行彙總後,銀行希望自身所面臨的風險已被有效地分解,並希望自身面臨的市場風險足夠小。當風險達到不可接受的程度時,銀行必須找出根源並採取相應措施。我們將在第12~14章中討論對風險進行彙總計算的模型。
風險聚集管理模式是保險公司採用的重要管理工具。考慮某汽車保險公司,單一保單所對應的賠償數量具有不確定性,但是,保險公司可以做到在一定的精度下對100 000個保單的整體賠償進行預測。
信用風險的傳統管理方式是對信用組合進行多元化管理(也就是風險聚集),如果銀行將其40%的資金借給某個單一借貸人,這樣做會使得風險沒有得以分散,其後果將是銀行面臨巨大風險。當借貸人的自身財務狀況出現問題以至於不能支付貸款利息及本金時,銀行可能會解體。
當銀行選擇另外一個多元化的政策,例如,將0.01%的資金分別借給10 000個不同的借貸人時,銀行會處於一個相對更為安全的位置。假設在某一年,借貸人的違約概率為1%,這樣在這一年我們將看到大約有100個信貸人違約,而由此所造成的損失會被其他99%的貸款的盈利所彌補。為增大風險分散的效果,銀行應在不同的地區及不同的行業選擇借貸人,一個在全球範圍有不同借貸人的國際性銀行的風險要比一個只在得克薩斯州對石油公司進行放貸的區域性銀行的風險分散性好。
當然無論如何分散風險,銀行仍然不能完全消除系統性風險。該風險會造成所有借貸人的違約概率隨時間而變化。我們的例子中採用的1%的違約率是正常年份所見的。當經濟形勢很好時,違約概率會小於這個數字,而當經濟轉入下滑時,則會顯著高於這個數字。我們會在以後的章節中討論用於捕捉系統性風險的模型。
從20世紀90年代後期開始,我們看到信用衍生產品市場的勃然興起,信用衍生產品可以使得銀行對信用風險一一進行化解(也就是風險分解),而不是僅僅依靠風險分散的手段。衍生產品市場也給銀行提供了對於宏觀經濟中整體違約的保護產品。但是,對應於每個信用買入方,總會有一個賣出方。許多信用保護的賣出方(無論是單個公司還是公司的投資組合)在2007年的信用緊縮中蒙受巨大損失,我們將在第6章中對信用緊縮做進一步的討論。
1.7 信用評級
信用評級被金融市場的參與者廣泛地用於信用風險管理。信用評級是對債務類金融工具如債券的信用質量的度量。然而,企業或者主權債券的評級通常被當作一個關於債券發行者而不是債券本身的屬性。因此,如果一家公司發行的債券擁有一個AAA評級,該公司通常也被稱作一家AAA評級的公司。
穆迪、標準普爾和惠譽是三家最主要的評級機構。穆迪評級中最好的級別是Aaa。擁有該評級的債券被認為是幾乎不可能違約的。次優級的評級為Aa,接下來依次是A、Baa、Ba、B、Caa、Ca和C。與穆迪評級依次對應的標準普爾評級分別是AAA、AA、A、BBB、BB、B、CCC、CC和C。為更加細緻地區分評級,穆迪還將Aa級細分為Aa1、Aa2和Aa3;將A級細分為A1、A2和A3,依此類推。類似地,標準普爾將其AA級細分為AA+、AA和AA-;將A級細分為A+、A和A-,依此類推。穆迪的Aaa級和標準普爾的AAA級沒有再細分,通常最低的兩個級別也不會再細分。惠譽的評級跟標準普爾類似。
通常,不同評級機構給出的信用等級存在相互對應的關係。比如,標準普爾的BBB+級被認為對應於穆迪的Baa1級。評級為BBB-(Baa3)以上的證券被認為具有投資級別(investment grade)。評級為BBB-(Baa3)以下的被稱作是非投資級(noninvestment grade)或投機級(speculative grade)或垃圾債(junk bonds)。2012年8月,標準普爾將美國國債的評級從AAA級降到了AA+級,這在市場上引起了不小的震動。
在後面的章節中,我們還將對信用評級進行更深入的探討。例如,第6章討論了在2007年開始的信用危機中信用評級扮演的角色。第15章和第16章介紹了信用評級是如何在監管規則中使用的。第19章給出了擁有不同信用評級的公司違約率的統計數據。第21章描述了公司的信用評級是如何隨時間而變化的。
小結
金融理論中一個非常重要的原則是風險和回報有一種替換關係,要取得高回報通常要以承擔高風險作為代價。投資者在理論上講不應擔心那些可以被分散的風險。投資者所期望的回報應反映在他們所承擔的不可以被分散的系統性風險中。
公司在進行風險管理時,不僅要考慮其股東對系統性風險的承受能力,也要考慮整體風險。股東個人可以通過投資多元化來分散非系統性風險,但對公司來說仍不可以忽略這一風險,其中的一個原因是破產成本的存在——股東必須為破產過程埋單。
對銀行和保險公司等金融機構而言,另一個需要考慮的因素是監管法規。最大限度地降低受監管的金融機構破產的可能性是監管機構最關注的議題。破產可能性依賴於承受的整體風險,而不僅僅是股東不能分散的風險。在後面的章節中,我們將會看到,監管機構的目標是保證金融機構對自己整體的風險敞口持有足夠的資本金。
管理風險的兩個重要方式是風險分解及風險聚集(集中),風險分解管理將風險一一分解,並針對單一風險進行管理;風險聚集藉助於風險分散的效果達到減少風險的目的。銀行採用以上兩種方式來管理市場風險。管理信用風險傳統上是採用風險聚集的方式,但隨著信用衍生產品的發展,風險分解的方式也逐漸被用於信用風險管理過程之中。
延伸閱讀

練習題[1]
1.1 某項投資的不同的回報率為40%,30%,15%,-5%;-15%;其對應的概率分別為0.1,0.2,0.35,0.25及0.1,這一投資所對應的期望值及標準差為多少?
1.2 假定某兩項投資的回報及所對應的概率如練習題1.1所示,兩項投資的相關係數為0.15,將資金以均等方式分別投入兩項投資後所產生的組合投資資產的預期回報及標準差為多少?
1.3 兩項投資如圖1-2及表1-2所示,對於以下列舉的相關係數,計算風險-回報的不同組合關係:(a)0.3;(b)1.0;(c)-1.0。
1.4 系統性風險與非系統性風險有何區別?對投資者來講哪一項更為重要,這兩項風險中哪一項會引發企業破產成本?
1.5 投資者選擇相同市場投資組合的主要理論依據及假設前提是什麼?
1.6 某一投資組合的預期回報為12%,無風險投資回報率為6%,beta係數分別等於(a)0.2;(b)0.5;(c)1.4的投資的預期回報各為多少?
1.7 “套利定價理論是資本資產定價理論的延伸。”請解釋這一觀點。
1.8 “一家公司所採用的資本結構取決於破產成本及債券所帶來稅率優勢的替換關係。”請解釋這一觀點。
1.9 風險分解和風險聚集管理方法的含義是什麼?哪一種方法需要對單一風險深入瞭解?哪一種方法需要風險相關性的詳細信息?
1.10 一個銀行的操作風險的起因包括僱員詐騙、自然災害、訴訟費用等。管理操作風險最好應採取風險分解還是風險聚集方式(操作風險在第13章中會有所討論)?
1.11 一個銀行在下一年盈利的回報服從正態分佈。回報期望值為整體資產的0.6%,而標準差為整體資產的1.5%。銀行的股權資本佔整體資產的4%。在忽略稅收情況下,銀行在下一年仍有正的股權資本的概率為多大?
1.12 為什麼銀行監管要保證銀行不能承擔過多風險,而對其他行業公司(例如製造業和零售業)沒有此項要求?
1.13 請列舉業界事例1-1中的破產成本。
1.14 去年的市場回報為10%,無風險利率為5%,某對衝基金的投資組合的beta為0.6,alpha為4%。對衝基金經理的回報為多少?
[1] 各章練習題答案見本書最後。
作業題
1.15 假定某一項投資的預期回報為8%,標準差為14%;另一項投資的預期回報為12%,標準差為20%。兩項投資相關係數為0.3。請構造一個類似圖1-2的風險-回報組合情形。
1.16 市場的預期回報為12%,無風險利率為7%,市場回報率的標準差為15%。一個投資者在有效邊界上構造了一個投資組合,預期回報為10%;另一個投資者在有效邊界上構造了另一個投資組合,預期回報為20%。兩個投資組合的標準差各為多少?
1.17 一家銀行在下一年度的盈利服從正態分佈,其期望值及標準差分別為資產的0.8%及2%。在99%及99.9%置信度下,為使年終時股權資本為正,銀行的資本金持有率(以資產作為分母)分別應為多少?(在分析中忽略稅收。)
1.18 一個投資組合經理主動地管理某投資組合,投資組合的beta係數為0.2。在去年,無風險利率為5%,主要股指的表現都很差,回報大約為-30%。投資組合經理的回報為-10%,投資組合經理自稱在這樣的市場條件下,自身表現很好。請對投資組合經理的觀點進行討論。

第2章
銀行
“銀行”這一詞彙源於意大利語中的“banco”,指在幾百年前意大利佛羅倫薩銀行家所用的蓋了一個綠色桌布的桌子或長凳。銀行的傳統角色是吸收存款併發放貸款,貸款的利息大於存款的利息,這兩個利息之間的差額用於支付管理費用以及貸款損失(即借款方未按約定償還利息和本金所觸發的費用),同時提供令人滿意的股權收益率。
今天的多數大型銀行既參與商業銀行業務,也參與投資銀行業務。商業銀行業務包括我們以上提及的吸收存款、發放貸款以及一些其他基本業務;投資銀行業務包括幫助企業客戶發行證券和股票、為企業併購和重大公司重組提供諮詢以及其他融資業務。大型銀行一般還參與證券交易業務(例如,提供經紀服務)。
商業銀行業務可劃分為零售銀行業務及批發銀行業務。顧名思義,零售銀行業務(retail banking)涉及從個人或小企業客戶中吸收小額存款,並同時向這些客戶發放小額貸款;批發銀行業務(wholesale banking)涉及向大中型客戶提供銀行服務。批發銀行業中的存、貸款量遠大於零售銀行業中的存、貸款量。有時某些銀行完全通過在金融市場的拆借來支撐自身的批發及零售銀行業務。
批發銀行貸款利率與資產費用利率的利差通常比零售銀行的利差要低,但這一不利條件常常被低費用而彌補(比較相同數量的批發銀行貸款和零售業務貸款,我們通常會發現批發銀行貸款的預期損失及管理費用要低很多)。那些主要依賴批發銀行業務並同時通過金融市場拆借來支撐其運作的銀行被稱為貨幣中心銀行(money center bank)。
在這一章中我們將討論在過去的100年中美國商業銀行及投資銀行的進化過程,我們將會討論銀行的監管方式、銀行面臨的各種風險以及為損失提供緩衝的資本金的關鍵作用。
2.1 商業銀行
幾乎世界上所有的國家都設定了嚴格的銀行監管法規,這是因為大多數國家的政府都認為無論個人或者企業都應該對銀行系統持有信心。監管法規涉及的事項包括:銀行必須持有的資本金數量、銀行所能經營的業務範圍、存款保險、允許併購的範圍及外資持股比例等。在20世紀,各國銀行監管法規的特點影響了不同國家的商業銀行結構,為了說明這一點,我們將以美國為例。
美國的特點是其銀行數量巨大(2017年共有5 060家)。因此,與那些銀行數目較少的國家相比,美國的銀行支付系統相對複雜。美國有一些規模較大的貨幣中心銀行,比如花旗銀行以及摩根大通;美國也擁有數百家地區性銀行,其業務涵蓋了零售和批發兩種形式;另外,美國還有數千家社區銀行,其業務形式主要是零售。
表2-1綜述了1984年及2017年美國銀行規模的分佈情況。這期間,美國銀行的數目下降了超過65%。與1984年相比,在2017年,小型社區銀行數量減少,而大型銀行數量增加。雖然在2017年資產超過100億美元的銀行只有102家(佔整體數量的2%),但這些銀行持有的資產佔整個銀行系統的84%。
表2-1 1984年及2017年美國銀行規模的分佈情況
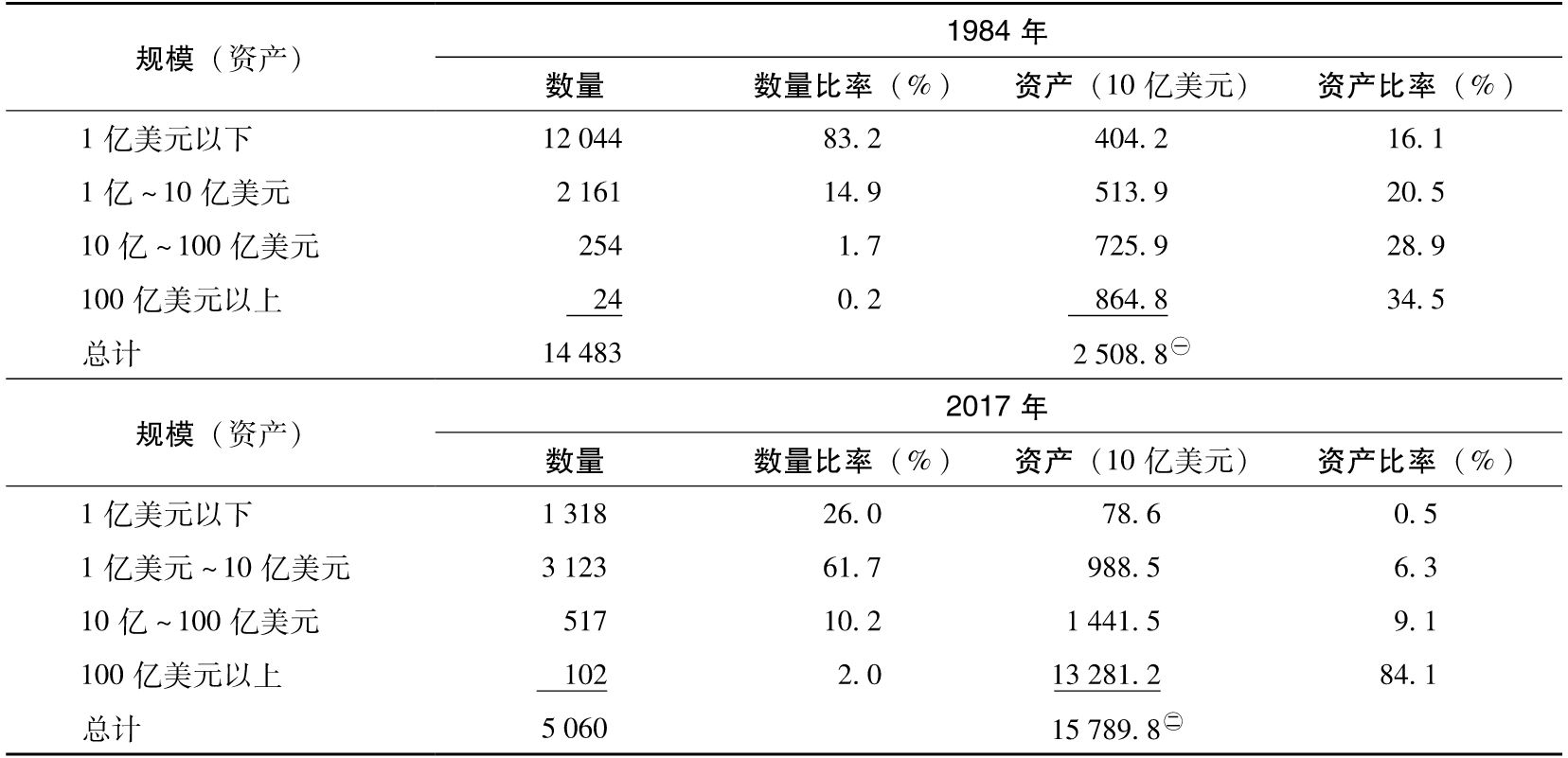
資料來源:FDIC Quarterly Banking Profile,www.fdic.gov.
⊖ 原書為2 508.9,疑有誤,更正為此。——譯者注
 原書為15 789.5,疑有誤,更正為此。——譯者注
原書為15 789.5,疑有誤,更正為此。——譯者注
美國銀行系統結構的特點主要是源於監管法規中關於跨州經營的限制。20世紀初期,大多數美國銀行只開設一個營業部給客戶提供服務。20世紀早期,許多銀行紛紛開始增設分行以保證更好地為客戶提供服務。這樣做受到兩種不同的阻力。首先,那些只有單個營業部的小銀行擔心它們會失去市場份額;其次,那些大的貨幣中心銀行擔心多分支銀行將會提供支票清算(check-clearing)及其他支付業務,從而侵蝕它們在這些業務中的利潤。以上阻力對社區銀行的擴展產生了壓力。隨之有若干個州通過了法律,對銀行在一州之內開設多家分行的能力做出了限制。
《麥克法登法案》(McFadden Act)在1927年通過,其修正案在1933年通過。該法案對銀行在多個州開設分行做出了限制。法案適用於全部全美註冊及州內註冊的銀行。一種繞過《麥克法登法案》的做法是成立多銀行控股公司(multibank holding company),即成立一家母公司並收購多家銀行作為其子公司。截至1956年,美國共有47家多銀行控股公司,這導致了在後來通過了針對《銀行控股公司法》(Bank Holding Company)的《道格拉斯修正案》(Douglas Amendment)。該修正案不允許銀行控股公司在禁止州外併購(out-of-state acquisition)的州收購銀行,但是在1956年前的收購仍然有效(也就是說,多銀行控股公司並不一定要將1956年前收購的子銀行進行剝離)。
銀行在試圖擺脫監管限制方面很有創造力,當有利可圖時,這一創造力表現得尤其明顯。1956年後,一種做法是成立一家銀行控股公司,這家公司只將一家銀行作為子公司,而在其他州成立非銀行子公司,這些非銀子公司提供的金融服務包括客戶融資、數據處理、租賃等業務,這麼做的實際效果是在其他州也實現了銀行的存在。
1970年的《銀行控股公司法》進一步對單銀行控股公司的行為實行了限制。在這一法案下,控股公司只允許從事那些與銀行業務密切相關的經營活動,控股公司收購其他公司要經過美聯儲的批准,控股公司必須對那些不符合該修正案的子公司進行剝離。
20世紀70年代以後,對於跨州銀行的限制逐漸消失。各州紛紛通過法律允許其他州的銀行進入並收購本地銀行(1978年緬因州首先通過了這樣的法令)。其中有些州允許外州的銀行自由進入,而其他一些州雖允許外州的銀行進入,但條件是其所在州須制定互惠協定(reciprocal agreement,即如果州B的銀行可以進入州A,那麼州A的銀行也可以進入州B)。還有些州共同建立了區域性銀行群,從而將跨州銀行業務合法化。
1994年美國國會通過了《裡格爾-尼爾州際銀行及分行效率法》(Riegel-Neal Interstate Banking and Branching Efficiency Act,簡稱《裡格爾-尼爾法案》),將全面跨州銀行變成了現實。該法案允許銀行控股公司在其他州收購分行,並廢除了以前各州訂立的基於州際互惠協議或區域性協議的跨州銀行法案。從1997年開始,銀行控股公司可以將本州外的銀行子公司轉為在同一銀行下的分行。許多人認為這種整合方式對於擴大美國銀行規模,從而能夠在全球範圍內進行競爭十分有必要。《裡格爾-尼爾法案》為美國銀行的合併潮提供了基礎(例如,摩根大通收購了化學銀行、大通銀行、貝爾斯登以及華盛頓互惠銀行)。
2007年開始的信用危機導致了一大批銀行的破產。危機爆發後,2010年7月21日,奧巴馬總統簽署了《多德-弗蘭克華爾街改革與個人消費者保護法案》(Dodd-Frank wall street Reform and Consumer Protection Act,簡稱《多德-弗蘭克法案》)。第16.5節將對此進行了詳細討論。
2.2 小型商業銀行的資本金要求
為了說明資本金在銀行業務中的作用,在這裡我們假想出一個名叫DLC的銀行(Deposits and Loan Corporation),DLC銀行只經營傳統的存貸款業務,表2-2是該銀行在2018年年末的資產負債表,表2-3是其在2018年的利潤表。
表2-2 DLC銀行在2018年年末的資產負債表 (百萬美元)

表2-3 DLC銀行在2018年的利潤表 (百萬美元)

表2-2顯示這家銀行有1億美元的資產,其中大部分(佔80%)是銀行發放給私人及小型企業的貸款。現金及有價證券佔總資產的15%,另外5%的資產由一些固定資產(建築、設備等)組成。可見,DLC 90%的支撐資產的資金來源於客戶各種形式的存款,另外5%的資金來源於次優先級長期債券(subordinated long-term debt,這種債券由銀行發行,破產清算時其優先級低於銀行吸收的存款)。最後5%的資金來源於股東擁有的股權資本。股權資本由股東最初的現金投資及銀行的留存收益(retained earning)所組成。
現在讓我們考慮表2-3所示的2018年的利潤表。表中第一項收入為淨利息收入,此項收入為利息收入與利息費用的差,這項收入佔總資產的3%。管理利息收入並在不同利息環境下達到利息收入平穩對銀行至為重要,在第9章中我們將進一步討論這一點。
表中第二項為貸款損失。這裡的損失量佔當年總資產的0.8%。顯然,信用風險的管理及其量化對銀行至關重要。但在貸款前,無論銀行如何謹慎地評估客戶的財務狀態,部分客戶仍然會違約,從而造成貸款損失。在不同的經濟條件下,貸款的違約率會有所浮動。在某些年,貸款違約率會較低,而在其他年,違約率會較高。
下一項內容為非利息收入。這項內容是銀行非信貸業務所帶來的收入,其中包括為客戶提供服務收取的各種費用。在DLC銀行的利潤表中,非利息收入佔總資產的0.9%。
表中最後一項為非利息費用,在這個例子中,該項佔整體資產的2.5%。非利息費用包括利息以外的其他所有費用,其中包括薪水以及同技術有關的其他開銷等。在一些大型企業中,如果不小心控制,此項費用將會有逐年增長的趨勢。銀行應儘量避免訴訟、業務停頓、僱員欺詐等事件造成的損失。與這些損失相關的風險被稱作操作風險(operational risk)。在第23章中,我們將對此項風險進行討論。
資本充足率
衡量銀行表現的一個指標是淨資產收益率,即股權收益率(return on equity,ROE)。如表2-2和表2-3所示,DLC銀行的稅前ROE為0.6/5或12%。如果這個表現不能令人滿意,DLC銀行可採用以下手段改善ROE:回購部分股票,並以吸納的存款替換它們。這樣股權資本降低從而導致ROE提高。例如,如果採用表2-4所示的平衡表,將股權佔總資產的比率降低為1%,並將存款提高為總資產的94%,則DLC銀行的稅前ROE會猛增到60%。
表2-4 DLC銀行對應於資本充足率為1%情形下的資產負債表 (百萬美元)
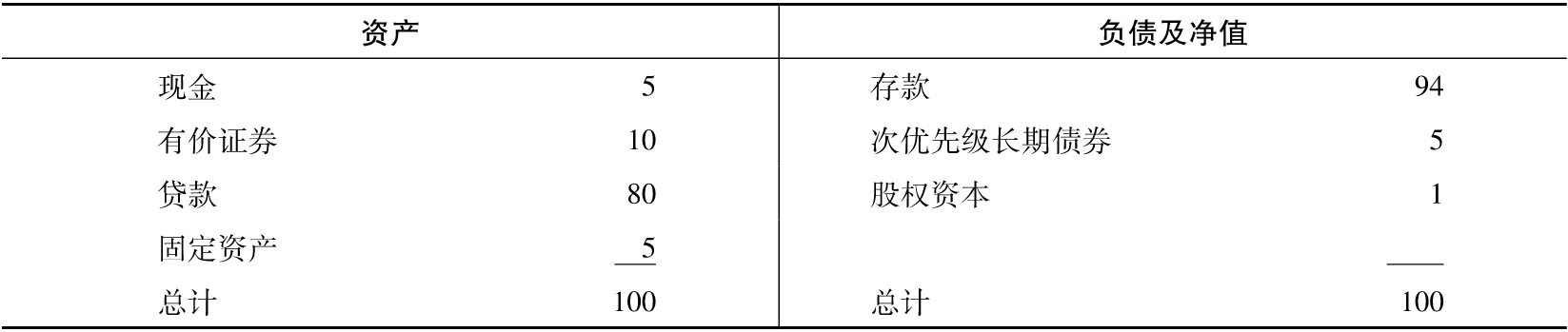
DLC銀行到底需要多少股權資本呢?一種回答這一問題的方法是考慮在極端條件下,銀行是否可以生存。假定在第二年經濟極為蕭條,銀行的貸款損失佔資產的比率上升了3.2%,達到4%。我們假定銀行的其他收入沒有受到影響。在此情形下銀行的稅前運營損失佔資產的2.6%(0.6%-3.2%=-2.6%)。假定稅率為30%,在此稅率下,稅後損失佔資產的1.8%。[1]
表2-2顯示出股權資本佔資產的5%,佔資產1.8%的損失雖然令人失望,但對銀行來講,仍然可以承擔得起,資本充足率這時會減至3.2%,即使第二年有一個類似的損失,資本金也不會被徹底耗盡。
如果DLC銀行採用瞭如表2-4所示的更加激進的資本結構,則其生存的可能性會大大降低。在這種情形下,損失為資產4%會徹底耗盡股權資本,這樣的損失會使銀行陷入巨大的財務困境之中。毫無疑問,在困境之中銀行希望提高資本金持有率,但在一個虛弱的財務狀況下,銀行幾乎不可能找到自己所尋求的資本。在銀行危機到來時,會造成存款人的“擠兌現象”(run on deposit,這時所有的存款人可能會同時提取存款)。這樣的事件可能會造成銀行破產,如果所有資產可以以賬面價格賣出(這是一個很樂觀的假設),長期債權人可以收到420萬美元而不是500萬美元的本金(長期債權人吸收了超出股權資本部分的損失),而存款人能得到全額的存款。
顯然,銀行的股權資本只佔資產的1%是不充足的。如表2-2所示,股權資本佔資產的5%更為合理一些。我們注意到股權資本及次優先級長期債券都是資本的來源,股權資本給銀行在不利情形下提供了最好的保護(在我們的例子中,當持有500萬美元而不是100萬美元的資本時,銀行是不太可能會破產的),次優先級長期債券在破產時排名低於存款,但是次優先級長期債券抵禦風險的效果不如股權資本,我們的例子顯示次優先級長期債券並不能抵禦銀行破產。
在第15~18章中,我們將會看到銀行監管機構一直在積極地參與銀行資本金充足率的管理,以保證銀行有足夠強的能力抵禦風險。風險類型包括市場風險、信用風險及操作風險。股權資本為第一類資本(tier 1 capital),而次優先級長期債券為第二類資本(tier 2 capital)。
[1] 假設稅收損失可以結轉以抵消以前的利潤。
2.3 存款保險
為了保證儲戶和投資者對銀行系統的信心,許多國家的政府監管機構引入了擔保制度。在擔保制度下,儲戶的存款在一定數額內受到保護。
擁有大量小型銀行的美國尤其會出現銀行破產現象。在1929年股票市場暴跌之後,美國經歷了一場十分嚴重的大蕭條,1930~1933年有近萬家銀行破產,銀行擠兌及市場恐慌現象十分普遍。1933年,美國政府成立了聯邦存款保險公司(Federal Deposit Insurance Corporation,FDIC),其目的是保護存款人。最初,存款所受保護的最高數額為2500美元。其後,這一受保水平幾次得以提高。到2008年10月,每個儲戶在每家銀行的受保儲蓄額最高可達250000美元。為了得到保護,銀行須支付保險費,保費為其吸收的國內存款的一定比例。自2007年後,保費的數額同資本金及與監管機構認定的銀行風險承受能力掛鉤。對資本金充足的銀行,保費可低至受保金額的0.1%;對資本金不足的銀行,保費可高至受保金額的0.35%。
截至1980年,這套系統運作良好。市場上沒有出現銀行擠兌現象,銀行破產也十分罕見。但是在1980~1990年,銀行破產數量顯著增長。這10年間銀行破產數量超過了1000家(超出了1933~1979年的總和)。造成銀行破產有幾個原因,其中一個原因是銀行管理利率風險不當。對這一話題,我們將在第9章中進行討論。另一個原因是石油及商品價格的下滑觸發了許多石油、天然氣及從事農業生產的公司的貸款違約。
造成銀行破產的進一步原因是存款保險制度的存在造成了銀行過分追求高風險策略,這些策略在沒有存款保險的前提下是不可行的。例如,銀行為了吸引存款客戶,可以提高存款利率,並將存款用於發放高風險貸款。在沒有保險的前提下,銀行不能實施這樣的策略,因為儲戶可以看到銀行的所作所為,他們可以認定銀行風險太高,從而撤回資金,而在有了保險的前提下,銀行可以實施這樣的高風險策略。因為儲戶認為在最糟的情況下,他們的存款仍受到FDIC的保護。這一現象就是所謂的道德風險(moral hazard)。我們將在第3章中對道德風險進行深入的討論。道德風險可以被定義為因為保險的存在,受保方改變其行為的可能性。以前介紹的以風險為基礎的存款保險定價方式在某種程度上可以降低道德風險。
20世紀80年代,FDIC的資金受到嚴重消耗,它不得不從美國財政部借入300億美元資金。1991年12月,美國國會通過《FDIC改善法案》(FDIC Improvement Act),消除了FDIC在將來的任何破產可能。1991~2006年,美國銀行破產事件相對罕見,到2006年為止,FDIC的儲備金已經達到500億美元。可是2007年信用危機爆發後,因為銀行破產的增加,FDIC再次陷入資金不足的窘境。
2.4 投資銀行業
投資銀行從事的主要業務是為政府及企業發行證券和股票進行融資,其業務包括證券的發行、承銷以及向投資者配售。在一個典型的企業與投行的合約中,企業會註明其融資形式,即債券、股票或混合金融工具,例如可轉換債券(convertible bond)。發行證券要附有法律文件,法律文件中要闡述證券持有者的權利。通常還需要製作說明公司過去以及將來表現的招股說明書(prospectus)。發行證券的公司所面臨的風險包括重大法律訴訟等要被闡述清楚。證券發行過程中要有“路演”(road show)。在路演中,投行以及公司高管將會竭力爭取得到大型基金經理的青睞。投行與公司之間會對所發行的證券的價格達成協議,然後投行將證券在市場上進行銷售。投行與企業之間的協議可以有多種形式。有時發行證券是以私募(private placement)的形式。在私募形式中,證券將被賣給少數人壽保險公司或養老基金等大型機構投資客戶,投行從中收取手續費。另一種發行方式為公開發行(public offering)。在公開發行中,發行對象是一般的投資者。公開發行可以是代銷(best effort)模式或包銷(firm commitment)模式。在代銷模式中,投行盡其所能將證券在投資者中進行銷售,投行所得的收入與證券銷售量掛鉤;在包銷模式中,投行同意從證券發行人手中以固定價格買入證券,然後再以稍高的價格在市場上銷售。投行的盈利取決於證券售出價格和買入價格的差。如果因某種原因投行沒有將證券全部賣出,投行就只能持有這些證券。例2-1對以上兩種銷售模式的差別做了進一步說明。
【例2-1】 一家投行同意對ABC公司發行的5000萬份股票進行承銷,投行與ABC公司通過談判商定股票的目標價格為每股30美元,這意味著公司將取得30×5000萬=15億美元的資金。投行可以給客戶提供代銷模式。在這一模式中,投行每銷售1股將收取0.30美元的手續費,因此假定所有的股票均能在市場上售出,投行的收入為0.3×5000萬=1500萬美元;投行也可以提供另外一種銷售模式,即包銷模式。在這種模式中,投行以每股30美元的價格從ABC公司買入股票。
投行有信心可以賣出全部股票,但對賣出股票的價格沒有把握。為了保證對銷售風險有所認識,投行可以考慮兩種不同情形。在第一種情形下,投行可以以每股32美元的價格賣出股票;在第二種情形下,投行可以以每股29美元的價格賣出股票。
在代銷模式中,無論在哪種情形下,投行所取得的收入均為1 500萬美元,在包銷模式中,投行的收入與其賣出股票的價格有關,如果投行能夠以每股32美元價格賣出所有的股票,因為投行可以從ABC以每股30元的價格買入股票,所以其盈利為(32-30)×5 000萬=1億美元;如果投行只能以每股29美元賣出股票,投行仍需以每股30美元的價格從ABC公司買入股票,其損失為(30-29)×5 000萬=5 000萬美元。以上不同情形所對應的結果在下表中給出。投行的銷售決策取決於投行對於不同情形所認定的概率以及投行自身的“風險偏好”(risk appetite)。

如果一家公司已經是上市公司,在進行股票融資時,投行可以用新股發行前幾天的股價作為基準來確定新股出售的價格。一般增發股票的價格比當前股票價格要稍低一些,這時最大的風險來自增發之前股價大幅下跌。
2.4.1 首次公開募股
當一家非上市公司希望上市時,其發行的股票被稱為首次公開募股(initial public offering,IPO)。IPO股票的承銷一般是代銷模式。最初的合理發行價格難以確定,一般取決於投行對發行股票公司價值的估計。投行對公司市場價格的估計等於公司價值除以發行股票的數量。但一般來講,投行設定的價格會低於其市場價格。這是因為投行不想承擔股票不能賣出的風險(一般來講,投行每賣出一股,就會得到手續費,而與賣出的股票價格無關)。
市場上常常看到的一種情況是當股票在最初發行後,股票價格馬上會顯著上漲(有時會高達40%),這說明公司原本可以將股票價位定得更高來取得更多的資金。正因為如此,IPO對於許多投資者而言具有吸引力。投行常常將IPO分配給基金經理以及其他大公司的高管。投行這麼做的目的是在將來贏得更多的業務(投行的這一做法被稱為“違規派送行為”(spinning),通常監管人員對這一行為嗤之以鼻)。
2.4.2 荷蘭式拍賣
一些公司用荷蘭式拍賣(Dutch auction)的方式來進行IPO發行。在一個常規的IPO發行過程中,發行公司要提供一個招股說明書並進行路演,購買股票的個人或機構客戶要表明希望買入股票的價格和數量。股票首先分配給出價最高的客戶,然後分配給出價次高的客戶,依此類推,直到股票全部售完為止。全部成功中標者所需支付的最後價格為所有股票分配完時,最後一個投標者所出的價格。例2-2說明了荷蘭式拍賣過程。
【例2-2】 一家公司想在IPO中賣出100萬份股票,該公司決定採用荷蘭式拍賣形式進行發行。下表顯示了投標人所給出的價格。在這一例子中,股票會首先分配給C,然後是F,然後是E,然後是H,然後是A。到此為止800000份股票已全部被分配,接下來最高的競標價由D給出,投資者D想買入300000份股票,因為這時只有200000份股票沒有被分配,投資者D只能買入其競標數量的2/3。最終,所有投資者需要付出的價格與D的競標價相同,即29美元。
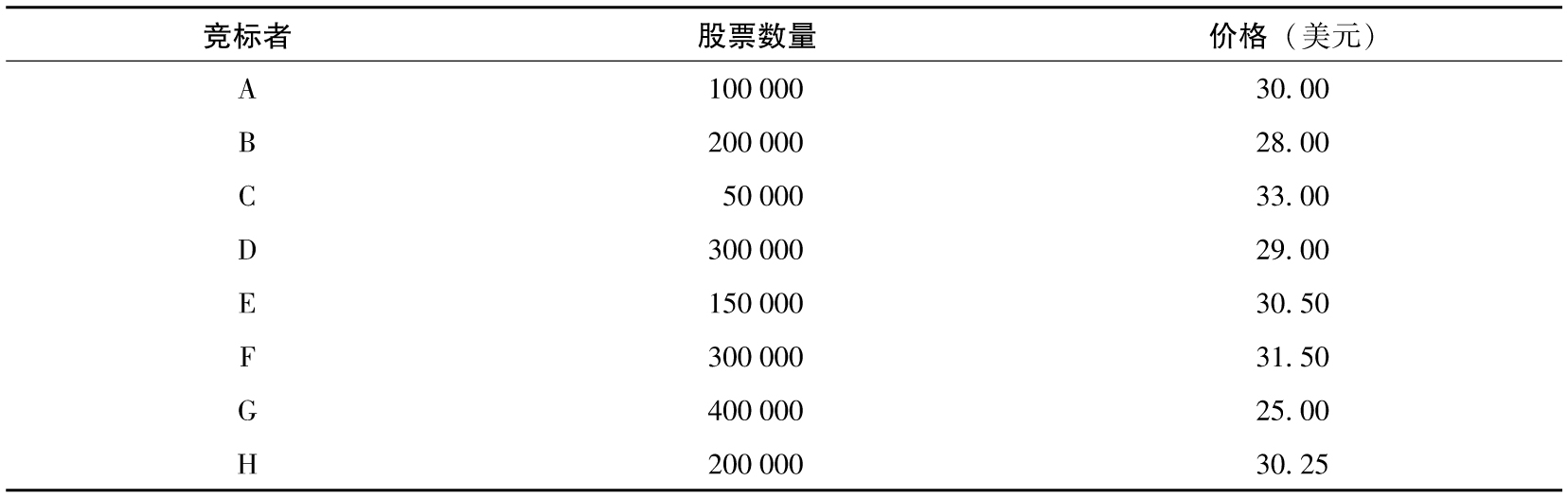
荷蘭式拍賣解決了傳統IPO過程中的兩個潛在問題。首先,市場的出清價(例2-2中的29美元)相當於所有的潛在投資者進行競標後的市場價;其次,避免了投行進行IPO發行時給予某些客戶不當優惠的現象。但是,在這一過程中,IPO公司不能充分利用投行與其大型客戶之間的業務關係,而這些關係通常可以幫助投行快速地完成IPO股票銷售。一個非常著名的使用荷蘭式拍賣的IPO案例是2004年穀歌的上市,其過程在業界事例2-1中進行了討論。
業界事例2-1
谷歌的首次公開募股
著名的網絡搜索公司谷歌決定在2004年公開上市發行股票。該公司選擇了荷蘭式拍賣形式。其IPO過程由兩家投行,即摩根士丹利(Morgan Stanley)及瑞士信貸第一波士頓(Credit Suisse First Boston)來協助。美國證券交易委員會(SEC)批准谷歌的融資限額為2 718 281 828美元(為什麼是這麼怪的數字?因為數學常數e=2.718 281 8…)。谷歌採用的IPO方法並不是純粹的荷蘭式拍賣,因為谷歌保留了權利,在看到投標結果後,可以改變發行股票的數量以及給每一個投標者分配的股票比例。
有些投資者認定股票的預期價格會高達120美元。但是當谷歌看到投標後,決定發行股票的數量將為19 605 052股,每股價格為85美元(這意味著谷歌所取得的資金總額為19 605 052×85,即16.7億美元)。競標價為85美元或更高的投資者取得的股票數量為其投標數量的74.2%。谷歌IPO的日期為2004年8月19日。許多公司很可能會給出價85美元及以上的競標者分配其初始競標數量100%的股票,並因此取得22.5億美元而不是16.7億美元的資金。谷歌之所以給競標人分配的股票份額這麼低,也許是因為它(股票代號為GOOG)準確地估計到自己可以在市場上以更高的價格出售剩下的股票。
谷歌最初的市值為231億美元,其中的90%由僱員持有,僱員包括公司的創立者謝爾蓋·布林、拉里·佩奇和公司首席執行官埃裡克·施密特。在股票發行後第一個交易日,谷歌的收盤價達100.34美元,比最初發行價高出了18%。在第二個交易日,股票又上漲了7%。谷歌的最初發行價確實是低估了,但其低估的程度比利用傳統IPO方法發行股票的其他高科技公司要小。
谷歌IPO的費用(即向投行支付的費用)為其所得融資量的2.8%,其他採用常規IPO的公司所支付費用平均為4%。
谷歌IPO過程中出現了一些錯誤,但幸運的是這些錯誤沒有對谷歌的上市計劃造成影響。謝爾蓋·布林和拉里·佩奇在2004年4月接受了《花花公子》(Playboy)雜誌的採訪,採訪內容發表在《花花公子》9月期雜誌上。這違反了SEC的規定。SEC要求在IPO之前,要有一個“靜默期”(quiet period)。在靜默期內,公司不能進行任何股票促銷活動。為了避免SEC的處罰,谷歌在向SEC遞交的申請中附上了《花花公子》雜誌的採訪內容(並附上了一些關於實際情況的說明)。谷歌還曾“忘記”對2 320萬份股票和560萬份股票期權進行登記。
谷歌股票價格在IPO後一路攀升。在1年後(2005年9月),谷歌又增發14 159 265股,每股價格為295美元,共融資41.8億美元(為什麼數字又是這麼怪?因為數學常數π=3.141 592 65…)。
2.4.3 顧問服務
除了幫助公司發行證券,投資銀行也為企業併購、退出、重大重組等活動提供諮詢服務。投行可以幫助企業尋求併購合夥人、收購對象,也可以幫助希望出售某些分支機構或子公司,從而從投資中退出的企業中尋找潛在買家。投行還可以為已成為併購目標的公司提供顧問服務。在某些情況下可以為公司提供避免被併購的應對措施。這些措施被稱為毒丸(poison pill)。毒丸的例子如下:
(1)一家潛在的目標公司可以在其公司章程中加入如下條款:當另一家公司持有的股份數量超過全部股份的1/3時,其他持股人有權以最近市場平均成交價兩倍的價格向該公司出售自己持有的股票。
(2)一家潛在的目標公司可向其核心僱員發放僱員股票期權。當公司被收購時,期權持有者可以馬上行使期權。這種做法可以使核心僱員在公司被收購時立刻出走,從而給公司新主人只留下一個空殼。
(3)一家潛在的目標公司可以在其公司章程加入新的條款,規定新擁有者不能在買入公司後的1年或2年內更換現任董事會成員。
(4)一家潛在的目標公司可以發行優先股(preferred share),這些優先股在公司的控制權變更時自動轉換為普通股。
(5)一家潛在的目標公司可以在其公司章程中加入新條款,規定現有持股人有權在公司被收購時或收購後,以低價買入公司股票。
(6)一家潛在的目標公司可以改變其投票制度,使得管理層持有的股票所對應的投票權大於其他持股人所擁有的股票。
毒丸方案在美國之外的許多國家是違法的,該方案的執行一定要獲得股東批准。一般來講,股東會反對毒丸方案,因為這類方案以公司管理人員的利益為出發點。在業界事例2-2中我們討論了仁科公司所提出的異乎尋常的毒丸計劃。
業界事例2-2
仁科公司的毒丸計劃
2003年,經營人力資源系統的仁科公司(People Soft)對甲骨文公司(Oracle)的收購意向十分擔憂。甲骨文公司的業務專長是數據庫管理系統。為了避免被收購,仁科公司向其客戶提供了非同尋常的擔保。擔保聲明如果在2年內仁科公司被收購,並且在4年內公司提供的客戶支持服務有所減少,客戶可以提出退款,退款數量為客戶付出的軟件使用授權費的2~5倍。這一擔保可能會給甲骨文公司帶來高達15億美元的費用。仁科公司提出的擔保遭到了股東的反對(因為這一擔保明顯與股東利益不一致)。仁科公司在2004年4月終止其擔保承諾。甲骨文公司最終在2004年12月買入了仁科公司。雖然仁科公司的某些職位被撤銷,但甲骨文公司還是保留了仁科公司產品開發部以及產品支持部門90%的職位。
估值、戰略和戰術是投資銀行提供諮詢服務的幾個關鍵層面。例如,某投行為公司A提供關於買入公司B的諮詢服務,投行首先要對公司B有一個合理估值,併為公司A估測在兩家公司合併後的增效作用(synergies),同時投行也要替公司A考慮應向公司B的股東提供現金還是換股交易(share for share exchange,即以一定數量公司A的股票換取公司B的股票),最初的出價應為多少?為了保證交易成功,最終的底價應為多少?投行要考慮以什麼方式接觸公司B的高管,以及高管會被什麼樣的條件打動。投行要判斷出這項收購協議是否會被認為是惡意的(即公司B的管理層會反對)或者是善意的(即公司B的管理層會支持)。在某些情況下的併購會涉及反壟斷法律問題,這時的收購定要有政府有關部門的批准。
2.5 證券交易
證券交易、經紀服務以及為某些證券進行做市是銀行常見的業務。在這些領域,銀行與那些不從事其他非銀業務的較小規模的證券公司進行競爭。[1]前面已經提過,美國的《多德-弗蘭克法案》不允許銀行進行自營交易。在其他一些國家,自營交易雖然是被允許的,但通常需要在架構上保證自營交易的損失不能對儲戶產生影響。
大部分大型投資和商業銀行都有大量的交易活動。除了自營交易外(合規與否暫且不論),很多交易是為了給客戶提供服務。例如,一家銀行可能會跟自己的一個企業客戶進行一筆衍生產品交易,幫助客戶降低匯率風險。同時,銀行也會為了對衝自身的風險進行交易(這類交易通常在同業之間)。
在證券交易中,經紀商扮演的角色是從其客戶處收取交易指令,並提交到交易所執行完成交易。有些經紀商可在全國範圍內經營業務,而其他一些經紀商只在某個特定的區域內從業。有些經紀商可以為客戶提供投資研究和顧問服務,這類經紀商被稱作全套服務經紀商。還有一類折扣經紀商(discount broker),他們收取的手續費較低,但不提供顧問服務。有些經紀商提供在線服務(online service),還有些經紀人提供電子交易(如E*trade)平臺,客戶可以在沒有經紀商協助的情況下通過交易平臺進行交易。
在證券交易中,做市商的作用是隨時向市場提供證券的買入價以及賣出價。做市商接受詢價時,通常不必知道對方是要賣出還是要買入。做市商的利潤來自買賣證券的價差,但其面臨的風險有時會高至不可接受。
許多股票、期權、期貨交易所採用做市商制度。交易所通常會規定做市商可收取的最大買賣價差。除了交易所內交易的產品,長期以來,銀行還為其他許多場外交易(OTC)市場產品(例如遠期合約、互換合約以及期權)做市(見第5章關於這些產品及場外交易市場的討論)。目前,這些產品的交易和做市活動越來越多地在電子平臺上進行,例如美國的互換執行設施(Swap Execution Facility,SEF)及歐洲的有組織交易設施(Organized Trading Facility,OTF)(見第16.5節和第17.2節)。
[1] 這種說法對歐美混業經營的銀行來說沒有什麼問題,但並不適合用來描述當前中國的銀行。——譯者注
2.6 銀行內部潛在的利益衝突
在同一家企業旗下,銀行的商業銀行業務、證券服務業務及投資銀行業務之間存在許多潛在的利益衝突,例如:
(1)當某投資者向銀行諮詢理財業務時,銀行往往可能向客戶推薦其投行部門正在銷售的證券。當銀行持有某個託管賬戶(fiduciary account,即銀行代理客戶進行交易的賬戶)時,銀行可能將那些難以賣出的證券硬塞到這些賬戶下。
(2)銀行向某客戶提供貸款時,往往會取得一些關於該客戶的保密信息。之後銀行可能會將這些信息傳遞給自己投行的併購部門。併購部門就可以利用這些信息,幫助其正在提供併購諮詢服務的客戶尋找潛在併購目標。
(3)證券研究部門可能會刻意將某公司的股票推薦為“買入”級,以取悅該公司的管理層,從而獲取投資銀行業務。
(4)假定某商業銀行在取得了關於某公司的保密信息後,認定這家公司破產的可能性在增大,銀行因此不準備繼續持有併為該公司提供貸款。這家商業銀行可能要求其投行部安排該企業發行債券,然後利用發行債券融來的資金償還貸款。這麼做的效果是利用那些信息不靈通的投資者的投資替換了自己發放的貸款。
正是由於這些潛在的利益衝突,過去有些國家試圖將商業銀行和投行分業經營。美國在1933年通過的《格拉斯-斯蒂格爾法案》(Glass-Steagall Act)限制商業銀行及投行業務的交叉運作。商業銀行可以繼續承銷某些國債或地方政府債券,它們也允許進行私募交易,但不得從事諸如公開發行股票等業務;類似地,投行也不能吸收存款以及發放商業貸款。
1987年,美聯儲在一定程度上放鬆了監管規則,即允許銀行控股公司有兩個分支來從事投行及商業銀行業務,但投行業務的收入佔集團整體收入的比率要在一定水平之下。
1997年,銀行監管法規進一步放鬆,商業銀行可以收購已存的投資銀行。最終在1999年,美國通過了《金融服務現代化法案》(Financial Services Modernization Act)。該法案事實上消除了銀行、保險公司以及證券公司運作上的限制。2007年,美國有5家(幾乎)不從事商業銀行業務的大型投行,它們分別是高盛集團、摩根士丹利、美林、貝爾斯登以及雷曼兄弟。2008年的信用危機導致了雷曼兄弟的破產,貝爾斯登被摩根大通收購,美林被美國銀行(Bank of America)收購,高盛集團及摩根士丹利變身為既從事商業銀行業務也從事投行業務的銀行控股公司(因此,這兩家銀行必須降低槓桿比率,並且要受到更多的監管審查)。2008年宣告了美國投行時代的結束。
我們還沒有重回商業銀行和投行必須分業經營的《格拉斯-斯蒂格爾法案》時代,但是越來越多的銀行被要求對存款業務進行絕緣防護,保證其不被投行業務的損失波及。
2.7 今天的大型銀行
今天的大型銀行在全球範圍內運作,其業務往往涉及不同地區。這些銀行仍然從事傳統商業銀行業務,例如吸收存款、發放貸款並進行支票結算(國內及國際)。這些銀行也向客戶發放信用卡、提供電話銀行服務、網絡銀行服務、自動取款機(ATM)服務,同時這些銀行還為企業提供工資支付服務,它們還進行規模巨大的交易活動。
銀行為企業及私人客戶提供信用額度(line of credit),也為從事出口的企業提供各類不同的服務。企業可以同銀行之間進行交易以對衝自身面臨的由於外匯、商品價格、利率以及其他市場變量引起的風險,我們將在後面幾章中對這些合約進行討論。在此,我們想指出,一些甚至與氣候有關的風險也可以被對衝。
從事證券研究的銀行可以對各只股票給出“買入”“賣出”以及“持有”的不同評級,這些銀行同時從事經紀服務(折扣經紀及全面服務經紀)。它們也從事信託服務,即替客戶管理投資組合。銀行內部設有經濟部,其職責是研究宏觀經濟走向以及中央銀行相關的政策。經濟部對利率、匯率、大宗商品價格及其他市場變量的走向提供預測。銀行還提供不同類型的共同基金。有些銀行本身也擁有對衝基金,現在有越來越多的銀行還提供保險產品。
銀行的投行部可以暢通無阻地承銷政府及企業發行的證券,還可以向客戶提供關於併購以及其他與企業融資有關的諮詢服務。
第2.6節所描述的利益衝突又是怎麼被合理管理的呢?解決辦法就是被稱為“防火牆”的職能分管制度。職能分管制度是指為了防止不利於銀行客戶的信息從銀行的一個部門傳播到另一個部門而設定的內部障礙。在一些大銀行中曾發生過一些著名的違規事例,這些違規事件導致了鉅額罰款以及法律訴訟。銀行最高管理層有加強職能分管制度實施力度的動機,這不只是由於罰款及法律訴訟,而且也是因為銀行的名譽是其最寶貴的資產。有關利益衝突的反面報道會讓投資者對銀行的信心產生損害,從而使銀行在很多領域喪失業務機會。
2.7.1 會計規則
現在是一個很好的時機來簡要討論一下銀行如何計算各種業務的盈利與虧損。對那些收取手續費的大多數投行業務活動,計算盈虧十分簡單。計算方式為應計制會計規則(accrual accounting),這與其他行業相應的會計規則十分相似。
對於銀行的其他業務,我們應該認識到“銀行賬戶”(banking book)與“交易賬戶”(trading book)的區別。顧名思義,交易賬戶包括所有銀行的交易行為產生的資產和負債。這些資產及負債的價值均以每天盯市計價的方式進行計量。這意味著該賬戶中每天的價值變化均反映市場價格的變化。如果一個銀行交易員在某天以100美元的價格買入某資產,假定在第二天價格下跌至60美元,銀行馬上會計入40美元的損失,即使在短期內無意賣出該資產,損失仍然會出現在賬面上。有時因為市場沒有相似交易,所以某些資產的價值並不是十分容易估計。例如,市場上可能沒有足夠的流動性,或者某種複雜的非標準衍生產品交易頻率很低,不足以生成市場參考價。即使在此類情況下,因為財會準則的要求,銀行還是必須得出一個市場價格。常見的做法是引入模型。這種通過模型得出市場價格的過程也被稱為以模型定價(marking to model)(在第25章中我們將進一步討論模型風險及會計準則存在的問題)。
銀行賬戶包括銀行向企業及個人客戶發放的貸款。對這些產品,銀行不需要盯市計價。然而,由於國際會計準則理事會頒佈了新的會計準則IFRS 9,以及美國財務會計準則理事會的類似會計準則更新,這種情況正在發生改變。新的會計準則要求貸款機構估計其貸款組合中預期的信貸損失金額,並相應地調整貸款組合的價值。新規定部分是由於2007年開始的金融危機所致,銀行的次級抵押貸款投資組合表現不佳,但在實際發生之前不必報告損失。
如業界事例2-3所示,有時銀行會採用一些人為的方式來避免認定已發生的貸款損失。
業界事例2-3
如何維持良好的貸款質量
當貸款人面臨財務困難並且不能支付到期貸款的利息及本金時,銀行有可能會給借款人發放更多的貸款以保證借款人能夠按時償付既存貸款。這是一種財會遊戲,也被稱為債務重新安排(debt rescheduling)。通過這種做法,應收貸款利息能夠繼續累計,並且可以避免(至少可以延遲)對貸款損失的認定。
20世紀70年代,美國以及其他國家向東歐、拉丁美洲和其他欠發達國家發放了大量貸款,這些貸款的一部分是用於這些國家的基礎設施建設,但有些貸款的目的並不十分正當(例如,有一項貸款是為了幫助非洲的某個統治者執政),有時這些款項進入了一些獨裁者的腰包,例如,菲律賓的馬科斯家族被控將數十億美元轉入了自家的銀行賬戶。
20世紀80年代初期,許多欠發達國家難以繼續償付貸款,這些國家的一種選擇是債務拒付(debt repudiation),但另一個更誘人的做法是債務重新安排。事實上,債務重新安排的實質是將利息計入資本金,因此銀行為支撐貸款所需的資金會進一步增加。
1987年,花旗銀行(現在的花旗集團)首先站出來拒絕給這些欠發達國家提供貸款重新安排。花旗銀行在對預期貸款損失進行了重新認定以後,將其貸款損失儲備上調了30億美元,隨後其他對欠發達國家有較大敞口的銀行也紛紛效仿這種做法。
2.7.2 發起-分銷模式
我們在表2-2~表2-4中所討論的虛擬小銀行DLC的業務模式是吸收存款並使用存款資金來發放貸款。另外一種模式被稱作發起-分銷模式(originate-to-distribute model)。在這種模式下,銀行僅發放貸款,但並不一直持有該貸款。銀行將貸款打包、分級,然後再將各分級銷售給投資者。
美國住房按揭市場採用發起-分銷模式由來已久。為了增加按揭市場的流動性,並保證住房擁有率的增長,美國政府成立了3個由政府支持的機構:政府國民抵押貸款協會(Government National Mortgage Association,GNMA,簡稱“吉利美”(Ginnie Mae))、聯邦國民抵押貸款協會(Federal National Mortgage Association,FNMA,簡稱“房利美”(Fannie Mae))以及聯邦住房抵押貸款公司(Federal Home Loan Mortgage Corporation,FHLMC,簡稱“房地美”(Freddie Mac))。這些機構從銀行或其他發放住房按揭貸款的機構買入按揭池,並對按揭的利息及本金償還提供擔保,然後將現金流打包,再賣給投資者。投資者一般承擔提前償付風險(prepayment risk)。這類風險是由利息下降時,按揭會被提前償還而造成的風險。但投資者並不承擔信用風險,因為這些按揭貸款是由GNMA或FNMA或FHLMC擔保的。從1999年起,FNMA及FHLMC開始為次級貸款提供擔保,結果造成這兩家機構陷入了嚴重的財務危機。[1]
長期以來,發起-分銷模式一直被銀行用來處理各種形式的貸款,其中包括學生貸款、商業貸款、商業按揭、個人住房按揭以及信用卡應收款項等。在很多情況下,這些貸款是沒有擔保的,因此貸款被打包銷售後,投資者將承擔信用風險。
發起-分銷模式也被稱為證券化(securitization),因為從銀行發放的貸款產生的現金流中生成了證券。這種模式對銀行具有吸引力。通過證券化,銀行可以將貸款從資產負債表上分離,因此可以騰出更多的資金來發放更多的貸款。這麼做也可以將資本金釋放出來,用於覆蓋銀行其他部門的風險(當銀行認為監管部門對貸款所要求的資本金過高時,這麼做尤其有吸引力)。銀行在發放貸款時會掙得手續費,在貸款被賣出後,如果仍對貸款進行日常管理,那麼銀行還可以繼續收取手續費。
如我們在第6章中將要討論的,發起-分銷模式在2000~2006年失去了控制。銀行放鬆了按揭貸款發放標準,因此證券化後的證券信用質量大幅下滑。由此導致了一次嚴重的信用危機。在這期間發起-分銷模式沒有任何市場,因為投資者對證券化產品完全喪失了信心。
[1] GNMA一直由美國政府擁有,而FNMA及FHLMC是由權益人所擁有的私有化公司。在2008年的危機中,美國政府不得不採取緊急措施來接管FNMA及FHLMC。
2.8 銀行面臨的風險
銀行的業務運作會觸發許多不同類型的風險,在本書後面的內容中我們將會詳細討論。
中央銀行的監管人員要求銀行必須持有足夠的資本金以應對自身的風險。1988年,一種決定資本金的國際規則終於誕生。在第15~17章中,我們將討論這些規則以及其進化過程。目前,銀行持有的資本金應能應對3種風險,即信用風險、市場風險及操作風險。
信用風險是指貸款業務及衍生產品交易中對手違約所觸發的風險。傳統上該類風險是銀行所面臨的最大風險類型,因此相應的監管資本金數量也最高。市場風險主要來自銀行的交易業務,該類風險與銀行交易賬戶上資產價值下跌的可能性有關。操作風險是指由銀行內部系統失效或外部事件造成損失的風險。在考慮信用風險及操作風險時,我們設定的展望期為1年,而市場風險所對應的展望期通常要短得多。監管機構設定資本金的目的是保證銀行的資本金數量足夠大,從而使銀行破產的可能性變得很小。例如,在考慮信用風險及操作風險時,資本金設定的要求是使非預期損失超過資本金數額的概率僅為0.1%。
除了計算監管資本金,大多數銀行還設定系統來計算經濟資本金(見第26章)。經濟資本金是銀行使用自有模型,而不是監管部門所設定的模型計算出的銀行自認為所需的資本金。經濟資本金一般會小於監管資本金,但是銀行必須保證所持有的資本金要高於監管資本金。資本金的構成類型(股權資本、次優先級債券等)要由監管機構來定義。為了避免陷入不得不在短期內籌措大量資本金的境地,銀行一般會將持有的資本金數額設定在遠高於最小監管資本金要求的水平。
在2007年及2008年,銀行紛紛公佈其次債組合的鉅額損失,其中很多不得不緊急籌集新的股權資本。由多個國家政府掌握的主權財富基金(sovereign wealth fund)為銀行注入了一定的資本金。例如,在花旗集團公佈其遭受了400億美元的損失後,2007年11月阿布扎比投資局(Abu Dhabi Investment Authority)對其投入了75億美元的股權資本金。接下來在2008年1月新加坡及科威特政府又投入了145億美元的資本金。之後,花旗集團及其他銀行為了生存又不得不從自己的政府請求注入資金。
小結
大銀行是從事各種不同業務的全球性機構。今天世界上最大型的銀行從事的業務包括存款、貸款、證券承銷、交易、提供經紀和託管服務、為各類企業融資行為提供諮詢、設立共同基金、為對衝基金提供服務等。銀行內存在潛在的利益衝突,為此銀行設定了內部管理規定。公司管理層要強化管理力度以確保僱員服從這些管理規定。由於不當行為造成的名譽、法律訴訟方面的損失以及罰款可能使銀行付出高昂的代價。所謂不當行為一般是指為個別客戶(或銀行自身)謀利而使其他客戶(或銀行)的利益受到損害的行為。
現在針對銀行的監管,已有國際協議。這意味著銀行在不同國家經營業務時,對銀行所持有的資本金要求不會因業務所在國家的不同而有顯著差別。許多國家為小額存款提供了存款保險制度,這對確保公眾對銀行系統的信心,避免出現因為銀行負面消息(或許只是謠言)的公佈而導致的擠兌現象非常關鍵。
延伸閱讀
練習題
2.1 美國銀行系統的分佈情況在1984~2017年產生了什麼樣的改變?
2.2 美國政府通過什麼樣的政策造成了大量小型社區銀行的出現?
2.3 銀行以短期存款支撐長期貸款會有什麼樣的風險?
2.4 假定一個名為DLC銀行(見表2-2和表2-3)的失控交易員在進行外匯交易時損失了700萬美元,你認為由此會觸發什麼事情?
2.5 利息收入的含義是什麼?
2.6 第2.2節的DLC銀行收入中哪一項會主要受到以下風險的影響?(a)信用風險;(b)市場風險;(c)操作風險。
2.7 解釋名詞“私募”及“公募”的含義。在公募中“代銷”及“包銷”的含義是什麼?
2.8 一個荷蘭式拍賣的競標價如下。
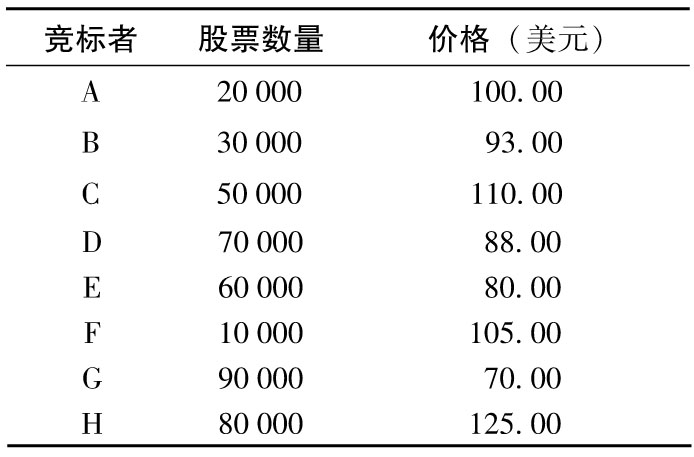
如果拍賣股票數量為150 000股,投資者所付的價格為多少?每個投資者會被分配多少份股票?
2.9 荷蘭式拍賣與正常IPO比較的好處是什麼?谷歌的IPO過程與標準荷蘭式拍賣過程有哪些不同?
2.10 企業高管有時認為毒丸計劃符合股東的最大利益,因為這可以使高管從可能的併購中套取更高的股價,討論這一觀點。
2.11 給出一個大銀行內3個潛在的利益衝突,對這些衝突應該如何處理?
2.12 銀行賬戶與交易賬戶的區別是什麼?
2.13 在2007~2008年金融危機後,貸款賬戶發生了什麼變化?
2.14 什麼是發行-分銷模式?
作業題
2.15 監管人員在計算DLC銀行(見第2.2節)時,假定收入回報服從正態分佈,均值為60萬美元,標準差為200萬美元。除了表2-2給出的資本金,銀行還需要多少股權資本以保證在99.9%的把握之下,銀行的資本金不會被完全消除?
2.16 解釋在存款保險機制下的道德風險,如何克服這一類風險?
2.17 某荷蘭式拍賣的競標價如下。
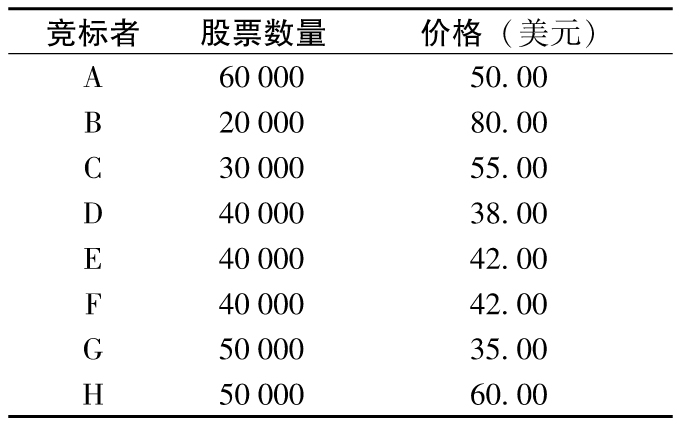
拍賣股票數量為210 000,投資者最終所付價格為多少?每個投資者所分配的股票數量為多少?
2.18 某家投行要為某公司發行1 000萬份股票,投行試圖確認是以包銷或是非包銷的形式來實施股票發行,包銷形式中每份股票價格為10美元,非包銷形式中每銷售1份股票,收費為20美分,比較兩種不同承銷方式的優缺點。
第3章
保險公司和養老基金
保險公司的作用是為不利事件提供保護。尋求保護的公司或個人被稱為投保人(policyholder)。投保人向保險公司定期支付保費(premium),並在某一約定的受保事件發生後從保險公司取得賠償。保險一般可分為人壽保險及非人壽保險,而健康保險常常被認為是保險中的獨立分支。非人壽保險有時也被稱為財產及意外傷害險,我們在今後將沿用這個詞。
人壽保險一般持續時間較長,保險公司在投保人死亡後會向受益人支付賠償。財產及意外傷害險的合約期限通常為1年(雖然合約一般可以延續),這類保險在出現事故、火災、被盜或其他類似事件時會向受保人支付賠償。
保險合約已存在多年。遠在公元前200年,古希臘就存有一種形式的保險合約,在這種合約中,個人可以一次性支付一筆款項(數量與年齡有關)。在付款之後,這個人在其餘生內每個月均可收到一定的收入。古羅馬有一種不同形式的合約,在合約中投保人可以買入某合同,而當投保人死後,他的親戚可以收到一定的賠償。在中國古代也存在一種財產災害保險合約,合約是在商人群體之間達成的,合約註明如果某個商人的商船不幸沉沒,那麼其他商人需要提供賠償。
養老基金計劃是由公司僱主為其僱員安排的一種保險合約,其設計是為了保證在僱員退休後,保險計劃將在僱員的餘生內為其提供收入。一般僱員及僱主每個月都要定時向養老基金計劃進行供款,計劃中的基金將這些資金進行投資,為退休人員提供收入。
在本章中,我們將討論保險公司合約的運作方式,還將討論保險公司所面臨的風險以及對其的監管方式。此外我們還將討論與養老金有關的一些其他關鍵問題。
3.1 人壽保險
在人壽保險合同中,保險公司向投保人支付的賠償在一定程度上與投保人的死亡時間有關。在美國以外的地區,人壽定險(life assurance)是用來描述在將來某一時刻,受保事件必定發生後,為受保人所提供保護的合約(例如,在投保人死亡後,保險公司將賠償100 000美元的合約),而人壽保險(life insurance)是指為將來有可能發生,也有可能不發生的事件所提供的保險合約(例如,在受保人意外死亡時提供回報的合約)。[1]在美國,這兩類保險都被稱為人壽保險(即life insurance)。本書中提到的人壽保險也將採用這個定義。
根據國家的不同,市場上有許多不同的人壽保險產品,我們在下面將介紹常見的幾種。
3.1.1 定期壽險
定期壽險(term life insurance)有時也被稱為暫時壽險(temporary life insurance),這種合約只持續一定的年限。如果投保人在保險期限內死亡,那麼保險公司會向合約中指定的受益人支付賠償,賠償數量等於保單面值所示的賠償額;如果投保人在合約期限內沒有死亡,那麼保險公司不會支付任何賠償。保險投保人要每月或每年定期向保險公司支付保費,保費一直要支付到合約的到期日或投保人的死亡日(以兩個日期中較早的一個為準)。保單的保額一般為恆定或隨時間而遞減,保費一般為恆定或隨時間而遞增。有一種合約被稱為每年可續簽(annual renewable term)合約。在這種合約中,保險公司保證保險可以按年續簽,但收取的保費會隨投保人的年齡增長而增長,而與投保人的健康狀況無關。
定期壽險存在的原因往往是按揭貸款。例如,某個年齡為35歲的人可能持有一個25年的按揭,他可能會買入一個25年期限的保險合約(保額逐漸降低),合約闡明當投保人死亡時,保險公司會為其子女提供賠償來還清按揭貸款。
3.1.2 終身壽險
終身壽險(whole life insurance)有時也被稱為永久壽險(permanent life insurance),這種保險合約為投保人終生提供保險,投保人在其餘生內每月或每年定期向保險公司支付保費,在投保人死後,保險公司向投保人指定的受益人提供賠償。在定期壽險中,最終保險公司會不會支付賠償具有不確定性,但在終身壽險中,只要投保人一直支付保金,最終的賠償沒有不確定性,唯一不確定的是賠償時間。終身壽險的費用要遠高於定期壽險,這一點不出所料,通常在終身壽險中,保額以及保金數量不隨時間變化而變化。
投保人常常會提前退保(redeem或surrender),或者以保單作為貸款的抵押物。當投保人想提前退保時,有時其他投資者能夠以高於保險公司支付的退保額的價格從投保人手中買入保單。然後,投資者繼續支付保費,並且在投保人死亡時會從保險公司收到賠償。
我們可以將終身壽險的年度保費與當年的定期壽險成本進行比較。假定一個40歲的男性買入面值為100萬美元的終身壽險,每年所付的保費為20000美元。我們在今後將看到,一個40歲男性在一年內死亡的概率為0.00209,這說明一年的保險的公允價值為2090美元,這意味著在第一年的保費中有17910美元的盈餘數量(surplus premium)可被用於投資。一個41歲男性在一年內死亡的概率為0.00224,這說明第二年保險的公允價值為2240美元,這意味著在第二年的保費中有17760美元的盈餘數量可被用於投資。每年保險成本隨著投保人年齡的增大而逐漸增長。在某一個時間段,保險成本會超過保費。在我們的例子中,在投保30年後,每年的保險成本將超過保費。男性在70歲時,一年內死亡的概率為0.02353(在第30年時,保險的公允價格為23530美元,這比保險公司每年收入的20000美元保費要大)。圖3-1比較了保費數量與每年的保險成本。在受保前期,保險公司將盈餘保費進行投資,投資回報可以用於彌補保費與後期成本的差距。圖3-1顯示了保費中有一個儲蓄的成分(saving element)。在受保前期,保險公司代表投保人將保費中超出覆蓋保險支出風險的那一部分資金進行投資。
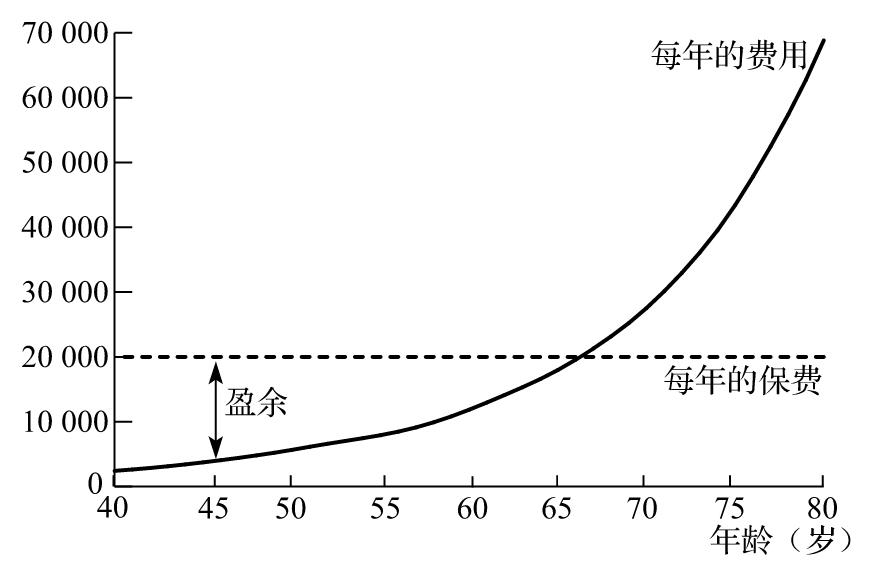
圖3-1 人壽保險每年的成本與終身壽險年度保費的比較
在許多國家,保險合約可以享受稅務優惠。如果投保人將盈餘保費另外進行投資,那麼投資回報通常要被徵稅。但是當盈餘保費作為保單的一部分進行投資時,稅收政策往往對受益人更為有利。只有在投保人死亡後,投資回報才被徵稅。在有些情況下,保險受益人得到的賠償金是不用繳納所得稅的。
3.1.3 變額壽險
終身壽險合約要涉及將投保人的資金進行投資,對該類保險的一個自然擴展是允許投保人指定資金的投資方式。變額壽險(variable life (VL) insurance)是終身壽險的一種特殊形式,在該險種中,以上討論過的盈餘保費投資於投保人指定的基金。基金可以是股票型基金、債券型基金以及貨幣市場基金。在投保人死亡時,賠償數額有一個最小保證,但如果基金表現良好,賠償數額可能會很高,投資所得可用於作為保費,投保人也可以隨時將資金在基金間進行轉換。
3.1.4 萬能壽險
萬能壽險(universal life (UL) insurance)也是終身壽險的一種形式。在這種保險中,投保人可以將保費減至不造成保險失效的某個最低水平。以上討論的盈餘保費被保險公司投資於債券、按揭和貨幣市場產品之中。保險公司將擔保最低回報率,例如4%。投保人有兩種選擇:一是在死亡時,保險受益人得到固定收益;二是受益人可以在投資回報高於擔保最低收益時,得到更多的賠償額。顯然,對應於第一種選擇,投保人須繳納的保費會更低。
3.1.5 變額-萬能壽險
變額-萬能壽險(variable-universal life (VUL) insurance)綜合了變額壽險及萬能壽險的不同特性。投保人可以將盈餘保費投資於不同形式的投資產品之中。保險公司對於投保人死亡的賠償額底線提供擔保,投資的回報可用於支付保費,保費也可減至為保證保單仍然有效的一個最低數量。
3.1.6 儲蓄壽險
儲蓄壽險(endowment life insurance)有一定期限,賠償金在投保人於合同期內死亡或於合同到期時一次性支付。市場上存有不同形式的儲蓄壽險。儲蓄壽險的最終支付額可以被提前說明,而與投保人在保險到期時是否健在無關。有時保險的支付與投保人有重大疾病有關。在帶利儲蓄壽險(with-profit endowment life)合約中,保險公司可以定期根據投資的表現來定出合約的分紅數量,分紅會逐漸累積。假定投保人的壽命超出了保險期限,累積分紅可以增大最終向投保人所支付的賠償金額。在投資聯結儲蓄壽險(unit-linked endowment insurance)中,保險最終支付的金額與投保人選擇的基金的表現有關。在一個生存儲蓄壽險(pure endowment insurance)合約中,保險最終的支付是建立在合約到期時投保人仍然健在的條件上。
3.1.7 團體壽險
團體壽險(group life insurance)在一個合約下為許多人提供保險,這種保險常常是公司僱主為其僱員購買,合約的形式可能是參與型(contributory)或非參與型(noncontributory)。在參與型團體壽險中,僱主和僱員共同支付保費;在非參與型團體壽險中,僱主支付全部保費。團體壽險有一定的規模經濟(economy of scale)效應,出售和管理保單的成本會較低。在單人壽險中,投保人要做身體檢查,而對團體壽險一般沒有這個要求。保險公司清楚,在某些受保人身上承擔的風險會低於平均水平,而在另外一些受保人身上承擔的風險會高於平均水平。
[1] 從理論上講,英文中的人壽定險合約是指那些投保事件一定會發生,但合約是否會提供賠償具有不確定性的保險合約。因此,為一個投保人在今後10年內死亡提供保險的合約屬於這種類型。在實際中,合約的區分(即life assurance與life insurance的區分)並不是十分嚴格。——譯者注
3.2 年金
許多保險公司提供年金合約,人壽保險合約的效應是將許多定期繳納的保金轉化為一次性償付,而年金的效應正好相反,即將一次性繳納的保金轉化為定期的償付。在一個典型的年金合約中,投保人向保險公司進行一次性付款,然後保險公司向投保人支付年金,支付從某一個特定的時間開始,一直到投保人生命的結束。在有些情況下,年金支付在投保人一次性繳納保金後馬上開始。更為常見的形式是投保人在年金付款開始的幾年以前進行一次性繳納,保險公司在收到年金後馬上進行投資來保證年金付款(這樣的年金被稱為延遲年金(deferred annuity))。有時投保人不採用一次性繳納的形式,而是按月、季度或年繳費,相當於將儲蓄轉化成了年金。
與人壽保險類似,年金常常可以給投保人帶來稅務延遲方面的好處。這是因為在通常情況下,投保人收到年金後才需要繳稅。由保險公司代表投保人進行投資的資金所取得的收益被稱為累積結餘(accumulated value)。一般來講,投保人可以提前提取資金,但通常會伴有罰款。換句話講,年金合約的提前退保價值(surrender value)往往小於累積結餘,這是因為保險公司必須收回賣出及管理資產的成本。有些合約允許投保人在一年內提取累積結餘或初始投資的一定比例,而無須繳納罰款。如果在開始支付年金前,投保人死亡(或者在某些情形下,投保人住進了有全職護士服務的養老院(nursing home)),則累積結餘也可被提取,而無須繳納罰金。
美國的一些延遲年金產品中內含期權。累積結餘有時會與股指掛鉤,例如標準普爾500指數。收益增長的上下限會被指明,如果指數在某年的增長率低於某個下限,累積結餘的增長率就以下限增長率為準;如果指數在某年的增長高於某個上限,累積結餘的增長率就以上限增長率為準;否則累積結餘的增長率就以標準普爾500指數的增長率為基準。假定累積結餘的增長率下限為2%、上限為8%,這說明投保人的累積結餘在任何一年增長率的下限為2%,但同時也放棄了增長率超過8%以上的超額收益。在該類合約中,投保人不會如股票市場投資者一般得到股指中的股息分紅,同時保險公司也有權改變某些年累積結餘的增長率的上下限。這類產品對那些想取得股票市場收益,但又不想承擔累積結餘下跌風險的投資者十分有吸引力。有時累積結餘的年度增長率會是股指回報的一個複雜函數。
過去,英國保險公司提供的年金合約通常會提供一個用於計算累積結餘支付額的最小保底利率。許多保險公司將這些保證(實際上是投保人持有的利率期權)當作市場營銷的必要費用,因而沒有計算這些期權的費用,也沒有對其風險進行對衝。當利率降低並且投保人的壽命延長時,許多保險公司就會陷入財務困境,如業界事例3-1所示,一家保險公司因此而倒閉。
業界事例3-1
公平人壽保險公司
英國公平人壽(Equitable Life)保險公司成立於1762年,在其最鼎盛時期,該保險公司共有150萬投保客戶。從20世紀50年代開始,公平人壽保險公司開始出售年金產品。在年金產品中,公平人壽保險公司為計算年金的利率下限提供擔保(這種產品被稱為保本年金期權(guaranteed annuity option))。由於競爭以及利率的提高,年金產品的保底利率逐漸升高。1993年年底,利率開始下降,同時人類的壽命預期也開始升高,保險公司不得不增大撥備以應對將來高年金的支出。公平人壽保險公司沒有采取任何措施,反而為了增長賣出保底利率更高的新產品。2000年,公平人壽保險公司不得不停止出售新的保單。Ann Abraham[1]在2008年7月發表的報告對監管局提出了強烈批評,該報告還要求對投保人提供賠償。
這個故事的有趣一面是監管人員曾要求提供保本年金期權的保險公司對利率下跌這一風險進行對衝。因此,許多保險公司紛紛開始與銀行進行交易,確保在利率下跌時自身會得到保護,而銀行為了對衝風險紛紛買入債券。這些債券在利率下跌時,價值會有上漲。市場上有太多的銀行和保險公司都這麼做,以至於市場對債券的需求大幅增長。長期利率急速下跌(這從而加大了保險公司的風險敞口中未對衝部分的損失)。這個故事說明,當大量不同的公司持有相似風險時,如果這些公司同時想對衝風險,就會出現問題。在市場價格不變的情況下,往往不會有足夠多的投資者願意進行相反的交易。
[1] 時任英國議會醫療服務監察員。——譯者注
3.3 死亡率表
死亡率表是人壽保險合約定價的關鍵,表3-1是美國社會保障部(Department of Social Security)給出的2013年的人類死亡率表。為了理解這一表格,我們考慮對應於年齡為31歲的一行,表中第2列顯示一個31歲男性在1年內死亡的概率為0.001505(即0.1505%)。第3列顯示了一個男性能夠活到31歲的概率為0.97376(即97.376%)。第4列顯示一個31歲男性的剩餘預期壽命(remaining life expectancy)[1]為46.89年。這意味著平均來講,一個男性的預期壽命為77.89歲。表中的其他3列是關於女性的數據,一個31歲女性在一年內死亡的概率為0.000705(即0.0705%),一個女性能活到31歲的概率為0.98569(即98.569%),31歲女性的剩餘預期壽命為51.04年。
表3-1 死亡率表
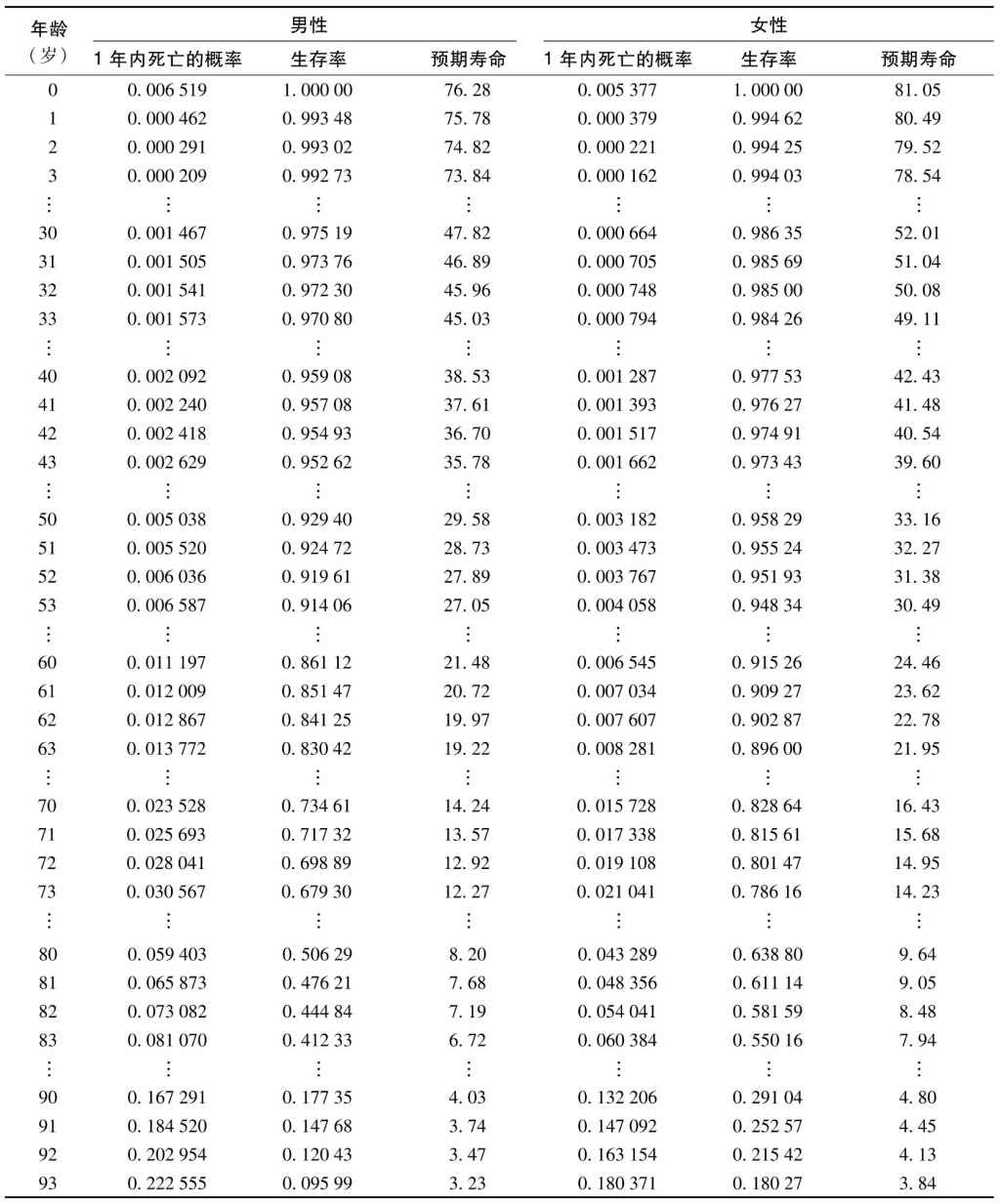
資料來源:美國社會保障部,www.ssa.gov/OACT/STATS/table4c6.html.
表格數據顯示,在生命的前10年,一個人在下一年死亡的概率是年齡的遞減函數;在10年之後,死亡的概率是年齡的遞增函數。女性的死亡率數據比男性好看一些,如果一位男性能活到90歲,他在下一年的死亡概率為16.7%;數據還顯示當男性活到100歲時,他在下一年死亡的概率為35.4%;活到110歲時,下一年死亡的概率為57.6%。對於女性而言,相應的概率為13.2%、30.5%及54.6%。
表3-1中的所有數據都可以從“一年內死亡的概率”這一列中的數據計算出來。一個人活到n+1歲的概率是這個人活到n歲的概率與1減去一個n歲的人在下一年內死亡的概率的乘積。例如,男性活到61歲的概率可以計算為0.861 12×(1-0.011 197)。
接下來考慮某個年齡段的人的預期壽命。這可以根據第1年、第2年、第3年以及往後年份的死亡概率來確定。從表3-1中來看,一個現年90歲的男性在1年內死亡的概率是0.167 291。他在第2年(介於91歲和92歲之間)死亡的概率等於他在第1年仍然活著的概率乘以他在91歲後1年內死亡的概率。根據表格第2列的數字,可以表示為
(1-0.167 291)×0.184 520=0.153 651
類似地,一個現年90歲的男性在將來的第3個年間(即介於92歲和93歲)死亡的概率為
(1-0.167 291)×(1-0.184 520)×0.202 954=0.137 817
假設死亡平均發生在每年的年中,一個90歲男性的預期剩餘壽命為
0.5×0.167 291+1.5×0.153 651+2.5×0.137 817+…
【例3-1】 假定對應於所有期限的利率均為4%(每半年付息一次),保險的保費在年初時支付,為一個具有平均健康狀態的90歲男性投保一個保額為100 000美元的人壽保險的盈虧平衡保費(break-even premium)為多少?假定保險期限為1年,預期賠償值為0.167 291×100 000,即16 729美元。假定賠償支付時間在年正中(在平均意義上,這是一種準確的估計);保費等於預期賠償以6個月的利率進行貼現得到的當前值,我們已知貼現利率為4%,利率一年複利兩次,賠償值的貼現值等於16 729/1.02,即16 401美元。
接下來假定保險的期限為2年,在第1年的預期賠償貼現值如上所述,即為16 401美元。受保人在第2年死亡的概率為(1-0.167 291)×0.184 520=0.153 651,因此在第2年的預期賠償為0.153 651×100 000=15 365美元。假定賠償支付時間在第18個月,預期賠償的貼現值為15 365/1.023=14 479美元。因此整體預期賠償的貼現值為16 401+14 479=30 880美元。
接下來我們計算保費的支付。首先我們知道第1次保費一定會在第1年年初被支付;第2次保費在第2年發生的概率為男性在第1年內仍然生存的概率,即1-0.167 291=0.832 709。如果保費數量每年為X,所有保費支付的貼現值等於
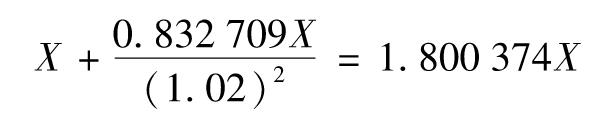
盈虧平衡保費X會保證預期保費支付的貼現值等於預期賠償的貼現值,即
1.800 374X=30 880
即X=17 152,因此盈虧平衡保費為17 152美元。
[1] 即在給定年齡下,一個人繼續生存的年限。——譯者注
3.4 長壽風險和死亡風險
長壽風險(longevity risk)是指醫學進步以及生活方式的改變使人類壽命延長,從而給保險公司業務帶來的風險。壽命的延長會給大多數年金合約的盈利帶來不利影響(因為年金支付時間會加長),但大多數人壽保險合約的盈利會增加(因為保險的最終賠償被延遲了,而對於定期壽險,最終支付賠償的可能性減小了)。不同國家人口的預期壽命各不相同,世界大多數地區的人類預期壽命都在逐漸增長。在美國,生於2013年的人比生於1929年的人的平均預期壽命增加了差不多20歲。表3-1中的統計數據基於2013年不同年齡人群的死亡率得出。如果人類預期壽命繼續增加,表3-1的數據就會變成低估值。
死亡風險(mortality risk)是指戰爭、艾滋病(AIDS)等傳染病、“西班牙型流行性感冒”(Spanish Flu)等流行病事件使人類壽命低於預期而引發的風險。這些事件會給大多數保險合約帶來不利影響(因為保險賠償金會被提前支付),但這些事件會增大年金合約的盈利(因為年金支付的時間縮短了)。在計算某種事件對死亡風險的影響時,我們一定要考慮事件對人口中哪些年齡層次的人群影響最大。
從某種程度上講,長壽和死亡風險對於保險公司的年金業務影響會中和這些風險對於常規人壽保險業務的影響,保險精算師必須仔細評估保險公司的業務在不同情形下的淨敞口。我們可以採用再保險(reinsurance)合約或長壽衍生產品(longevity derivatives)來對衝長壽風險,我們接下來將要討論長壽衍生產品,在本書後面的一些章節中我們將會討論再保險合約。
長壽衍生產品
長壽衍生產品為保險公司和養老基金公司提供對衝年金及養老基金產品所面臨的長壽風險的工具。一個典型的合約是長壽債券(longevity bond),也稱為生存者債券(survivor bond)。這類債券在20世紀90年代末首先被引入市場。在這種債券中,首先要定義一個年齡段的群體,債券在某個給定時刻的券息與定義群體中生存的人數成正比。
誰會賣出這樣的債券給保險公司或養老基金公司呢?答案是某些投機者認為這類債券很吸引人,因為它們幾乎不具有任何系統性風險(見第1.3節)。支付的債券券息只與某些人的壽命有關,而與市場回報基本沒有任何相關性。
3.5 財產及意外傷害險
財產及意外傷害險(property-casualty insurance)可細分為財產險和意外傷害險,財產險為投保人的財產損失(由於火災、水災、盜竊等)提供保險;意外傷害險為投保人的法律責任(例如,對第三者身體的意外傷害而導致的)提供保險。有時財產及意外傷害險被包含在同一個保險合約之中,例如,某個住房擁有者可能買入為不同損失提供保險的合約,損失種類包括住房被損壞及被偷竊,以及其他人在其房產中受傷所帶來的法律責任等。類似地,汽車保險所投保的損失包括自身汽車被盜、受損以及其他人受傷帶來的法律糾紛等。
一般來講,財產及意外傷害險每年要進行更新。如果保險公司評估預期賠償將升高,就會在保險更新時提高保費(這與人壽保險中的保費有所不同,人壽保險中的保費在許多年內為恆定的)。財產保險公司的業務面較寬,其業務經營有一種自然的風險分散效應。對於某些風險,大數定理(law of large numbers)會起作用,例如某保險公司為250000個家庭提供了失竊和火災險,我們可以較為準確地預報預期賠償數量,這是因為保險公司是在為一個大數量的獨立(或幾乎獨立)事件提供保險(當然,損失事件及平均賠償數量可能會有某種趨勢,保險公司應該跟蹤這些趨勢,並對保費數量做出相應調整)。
由類似於颶風這樣的自然災害所帶來的財產損失對保險公司而言十分難以預測,例如,2005年夏天發生在美國的“卡特里娜颶風”(Hurricane Katrina)以及2007年1月發生在歐洲西北部的12蒲福氏風級[1]暴風雪所帶來的損失十分巨大。這類風險被稱為災難風險(catastrophic risk)。災難風險的難以處理之處在於不同的投保人並不相互獨立。保險公司要面對兩種情形:一種情形是颶風在某年發生,保險公司因而必須應對大量與颶風有關的索賠;另一種情形是颶風根本就沒有發生,因此也沒有任何索賠。許多大的保險公司擁有與地理、地震和氣象數據有關的模型來估算災難發生的概率以及相關損失,這些模型為確定保費數量提供了基礎,但模型本身沒有改變保險公司所面臨的“全有或全無”(all-or-nothing)的風險特性。
與災難保險類似,責任保險每年所付出的賠償有所不同,賠償量十分難以估計。例如,由於石棉對工人的危害而觸發的索賠為美國的保險公司帶來了十分昂貴的費用。責任保險的一個特性被稱為長尾風險(long-tail risk)。長尾風險是指在投保期過後的若干年出現索賠的可能性。對於石棉一例,健康危害是在接觸石棉多年以後才表現出來的。因此,保險索賠往往是與幾年以前的保險合約有關。這一特性為精算師和會計師帶來了麻煩,保險公司不能在每年年末馬上結賬並計算盈虧,而必須考慮那些現在並沒有出現,但在今後的某一段時間可能會出現的索賠。
3.5.1 巨災債券
衍生產品市場已經出現了若干種不同的產品可以用來對衝災難風險,最為流行的產品是巨災債券(CAT bond)。這些債券通常由保險公司的子公司發行,其券息比一般債券要高。為了收入高券息,債券的持有者必須在某種類型的災難事件發生時承擔損失。根據CAT債券條款的不同,債券的券息以及本金(或者兩者)都可能被用來支付保險索賠。
假定某保險公司在加州對地震有7 000萬美元的風險敞口。這家公司想對損失中超出4 000萬美元的部分進行保護。保險公司可以發行巨災債券,面值為3 000萬美元,當地震發生時,如果保險公司在加州的損失超過了4 000萬美元,債券持有者將失去其部分或全部本金。另一個做法是,保險公司可以發行一個更大數額的債券,使得只有券息會受到地震損失的影響。還有一種做法是發行3只不同的債券,其承擔損失範圍分別為4 000萬~5 000萬美元、5 000萬~6 000萬美元、6 000萬~7 000萬美元。
巨災債券的特性是其投資者有很高的概率獲取高券息,而蒙受高損失的概率比較低。為什麼有投資者對以上產品感興趣呢?原因在於類似長壽債券,巨災債券風險與市場風險之間沒有統計上的強相關性,[2]正因為如此,對投資者來說,巨災債券往往是一個可以添加到投資組合中的具有吸引力的選擇。這些債券沒有系統性風險,它們的整體風險完全可以在一個大的交易組合中得以分散。如果一個巨災債券預期回報大於無風險利率(通常是這樣),那麼這種債券可以用於改善風險與回報的替換關係。
3.5.2 財產保險公司盈虧比率的計算
保險公司對於不同類型的保險要計算賠付率(loss ratio),等於1年內賠償數量與全部保費的比。一般來講,這一賠付率大約在60%~80%,A.M.Best所發表的統計數據顯示,這一比率在美國正在逐漸升高。保險公司的費用比率(expense ratio)是指每年費用與全部保費的比,保險公司的兩個最大費用是理賠費用及銷售費用。理賠費用(loss adjustment expense)是指為了確認索賠是否合法以及確認索賠數量所觸發的費用,銷售費用(selling expense)包括對保險經紀的支付以及購買其他業務所帶來的費用。在美國,銷售費用比率在25%~30%,這一費用每年都有減小的趨勢。
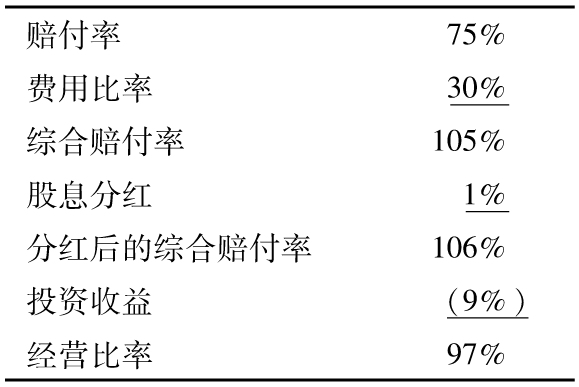
綜合賠付率(combined ratio)是賠付率與費用比率的和。假定對於某個保險合約,在某年的賠付率為75%,費用比率為30%,綜合賠付率便為105%。有時保險公司會支付一定小數量的分紅給投保人。假定分紅為保費的1%,將分紅考慮在內,我們可以求得分紅後的綜合賠付率(combined ratio after dividends)。在我們的例子中,這一比率為106%,該比率說明保險公司對於這一保險合約的稅前損失為6%。但事實並非如此,因為保費是在每年的年初由投保人向保險公司支付,而索賠賠償是在一年中,或在之後的一年由保險公司向投保人支付,保險公司因此可以掙得在收入保費及支付賠償損失之間的利息。假定在我們的例子中投資收益為保費的9%。將投資收益考慮在內,我們求得的比率為106%-9%=97%,該比率被稱為經營比率(operating ratio),表3-2是對這一例子的總結。
表3-2 一家財產保險公司計算其經營比率的過程
[1] 蒲福氏風級由愛爾蘭人法蘭西·蒲福海軍上將在1805年左右制定,是劃分風力等級的方法,按強弱將風力劃分為0~12級,共13個等級。——譯者注
[2] See R. H. Litzenberger, D.R. Beaglehole, and C.E. Reynolds, “Assessing Catastrophe Reinsurance-Linked Securities as a New Asset Class,” Journal of Portfolio Management (Winter 1996):76-86.
3.6 健康保險
健康保險(health insurance)具有某些財產及意外傷害險的特性,也具有人壽保險的特性。有時這類保險被列為一個單獨的保險類型。不同國家政府所提供的健康服務有所不同。在美國,傳統上政府提供的公眾健康服務十分有限,因此選擇保險公司是大多數人考慮的一項重要事項。加拿大是另一個極端,幾乎所有的健康服務均是由政府資金來支持的,醫生基本不能私下行醫。加拿大健康保險的主要作用是為了擔負政府不承擔的處方藥費及牙醫費用。在其他大多數國家,公共醫療體系及私立醫療體系共存。例如,英國有一個公共醫療體系,但人們在買入保險後也可以得到私立醫療服務。英國的私立醫療設施與公共醫療設施共同為患者提供服務(擁有私立醫療體系的優點是患者可以縮短非緊急外科手術的等待時間)。
2010年奧巴馬總統簽署了《患者保護與平價醫療法案》(Patient Protection and Affordable Care Act),致力於改革美國的醫療體系並增加醫保覆蓋的人口。醫療救助項目(Medicaid,一個針對低收入者的項目)的申請條件被放寬了,政府同時對中低收入家庭提供補助以幫助他們購買醫療保險。法案禁止醫療保險公司考慮投保人投保前的健康狀況,並強制僱主為僱員購買醫療保險,否則需要繳納額外的稅項。美國和其他很多國家的不同之處在於美國醫療服務的提供者多數為私立機構而不是公共部門,這一點在醫改後不會有大的變化。
與其他保險類似,健康保險的投保人需要按期支付保費,在一定投保事件發生後,保險公司要進行賠償。在健康保險中,投保事件包括投保人的醫療檢查、購買藥品以及住院等。通常當整體醫療體系費用增加時,投保人的保費會增大,但如果只是投保人的健康狀態變得惡化,那麼保險公司不能增加保費。關於這一點,我們可以比較健康保險、汽車保險以及人壽保險運作的不同。如果投保人的駕駛記錄顯示將來賠償的可能性增大,或者是汽車修理費用增大,保險公司可以提高投保人的保費(保險公司確實是這麼做的);在人壽保險合約中,即使投保人被診斷患有嚴重甚至影響壽命的疾病,人壽保險的保費也不會增長;健康保險的保費與人壽保險類似,即保險公司對賠償風險的預測的改變不會影響保費,但是,類似於汽車保險,整體索賠數量的增長會觸發保費的增長。
當然,在最先開出保單時,保險公司會盡力去確認自身承擔風險的大小。在人壽保險方面,保險公司會質詢投保人的健康狀態,並且要求投保人的身體健康要滿足一定的條件,保險公司會要求投保人進行體檢;在汽車保險方面,投保人的駕駛記錄要被調查;對於人壽保險及汽車保險,保險公司可以拒絕投保人的投保申請;在健康保險方面,保險公司要依據法律規定來確定是否拒絕投保人的申請。如前面所述,《患者保護與平價醫療法案》使得美國的醫療保險公司很難再以投保人的健康狀況不佳為由拒絕受理保險申請。
健康保險常常是以僱主所提供的團體健康保險計劃(group health insurance plans)而給出的。這些計劃覆蓋的對象通常包括僱員及僱員的家屬,通常僱員並不會因為其健康條件差而遭到拒絕。保險費用通常是由僱主及僱員共同承擔,不同計劃的費用有所不同。在美國,大多數健康保險計劃會覆蓋投保人基本的體檢費用和對一些常見病的治療所帶來的費用、外科手術以及住院費用。懷孕的費用可能在也可能不在保險覆蓋範圍之內,而美容手術的費用一般不在健康保險覆蓋範圍之內。
3.7 道德風險以及逆向選擇
我們接下來討論保險公司所面臨的兩類風險:道德風險和逆向選擇。
3.7.1 道德風險
道德風險(moral hazard)是指因為保險合約的存在造成投保人的行為與不持有保險時的行為有所不同,從而觸發的風險,這種行為的不同往往會增大保險公司的風險,預期賠償也會增加。道德風險的實例包括:
(1)一個車主買入了汽車失竊保險,因此,這位車主不鎖車門的可能性會更大;
(2)某人買入一種健康保險,正是因為保險的存在,投保人可能會更多地利用醫療服務設施;
(3)因為政府資助的存款保險的存在,銀行可能會承擔更多的風險,因為銀行認為這麼做並不會失去存款人(我們在第2.3節中曾討論過這一點)。
道德風險並不是人壽保險公司面臨的一個大問題,傳統上,保險公司採用幾種辦法來應對財產及意外傷害險以及健康險中的道德風險問題。一般來講,保險公司在進行理賠時要求投保人首先支付免賠額(deductible),這意味著投保人首先要承擔損失的第一部分,有時保險合約中會闡明共保條款(co-insurance provision),保險公司只是支付損失超出免賠額之上損失的一定比例(而不是100%)。另外,保險合約中一般會設定一個上限(policy limit,即賠償的上限),這些條款的目的是保證投保人與保險公司利益的一致性。
3.7.2 逆向選擇
逆向選擇(adverse selection)是用來描述保險公司在提供保險之前不能區分好的風險和壞的風險而帶來的問題。對於不同客戶,如果保險公司為所有投保人提供的產品價格相等,就會給保險公司帶來更多壞的風險。如果一家保險公司不能區分好的駕駛員和壞的駕駛員,從而給兩類駕駛員提供的保險價格相同,就會吸引更多壞的駕駛員來投保;如果一家保險公司不能區分健康和不健康的投保人,從而給他們同樣價格的健康保險,這家保險公司肯定會吸引更多不健康的投保人。
為了減小逆向選擇的不利影響,保險公司在提供保險之前儘量會找出投保人的信息。在提供人壽保險之前,保險公司常常要求投保人在指定的醫生那裡進行體檢;在提供汽車保險之前,保險公司會盡量取得投保申請人的駕駛記錄。而在汽車保險投保後,保險公司也會繼續收集投保駕駛員風險的信息(如車禍的次數和超速駕駛的次數等)。根據這些信息,保險公司會對每年保費的數量做出相應的調整。
逆向選擇問題不可能完全被克服。有趣的是,即使要求強制體檢,買入人壽保險的投保人死亡的時間往往還是會早於死亡率表給出的預計時間。相反地,買入年金產品的投保人長壽的概率平均比死亡率表中所反映的概率要大。
3.8 再保險
再保險(reinsurance)是保險公司從其他保險公司買入保險,來使得自己免受巨大損失的一種手段。賣出保險的第二家保險公司會得到一定的手續費,但要為第一家保險公司的投保事件出現損失時提供賠償。與沒有再保險的情況相比,再保險合約可以使得保險公司承銷更多的保險合約。再保險合約的對手往往是其他保險公司或一些私人企業,還有一些對手是專門經營再保險業務的公司,例如瑞士再保險(Swiss Re)以及巴菲特的伯克希爾-哈撒韋(Berkshire Hathaway)公司等。
再保險合約有若干種形式,假定一家保險公司對於佛羅里達州有1億美元關於颶風的風險敞口,這家公司想將其風險敞口降至5 000萬美元,該公司的一種選擇是進入一個再保險合約,對手將按比例承擔50%的損失(對手因此也會收到保費的50%)。如果在某一年暴風所帶來的損失為7 000萬美元,那麼保險公司支付的賠償只是0.5×7 000=3 500萬美元,再保險公司支付的賠償也是3 500萬美元。
另外一種更為流行的做法所涉及的再保險保費會更低一些,保險公司可以買入再保險來應對額外損失層(excess cost layers)。例如,第一層的賠償是為了覆蓋5 000萬~6 000萬美元的損失;第二層的賠償是為了覆蓋6 000萬~7 000萬美元的損失;依此類推。每一個再保險合約均被稱為超額損失(excess-of-loss)再保險合同。
3.9 資本金要求
人壽保險公司(life insurance companies)以及財產保險公司(property-casualty insurance companies)的資產負債表有所不同,這是因為這兩類保險公司所面臨的風險各不相同,因此為將來的賠償所設定的儲備金也會有所不同。
3.9.1 人壽保險公司
表3-3展示了一家人壽保險公司簡要的資產負債表。人壽保險公司的大多數投資為企業債券,保險公司會盡量將其資產與負債的期限進行匹配,但是該類保險公司會承擔信用風險,因為債券的違約率可能會比預期的更高。
表3-3 一家人壽保險公司簡要的資產負債表

與銀行有所不同的是,保險公司的資產和負債都會給公司帶來風險,損失儲備金(資產量的80%)是由精算師基於賠償數量而得出的,當人壽保險投保人的死亡時間提前或年金持有者的壽命延長較長時,這一估計值可能會太低。資產負債表中10%的股權資本包括最初股權人投資以及留存收益(retained earnings),股權為損失提供了緩衝,例如,如果賠償數量超出儲備金的數量達到資產總量的5%,股價會下跌,但保險公司不會破產。
3.9.2 財產保險公司
表3-4展示了一家財產保險公司簡要的資產負債表,表3-3與表3-4最重要的不同之處在於經營財產保險公司的股權佔資產的比率要遠高於人壽保險公司的股權佔資產的比率。這個不同是由於這兩類保險公司所持有的風險不同。財產保險公司所面臨的賠償要遠比人壽保險公司難以預測,誰會知道颶風襲擊邁阿密的具體時間?誰能預測下一個因石棉事件所觸發的索賠額有多大?資產負債表中負債部分中的未期滿保費(unearned premium)是指今天已經收到的保費,但這些保費適用於將來時間段。如果一個投保人在6月30日付清了一年的保費,為2 500美元,那麼截至12月31日,保險公司只掙得了1 250美元。表3-4中的投資主要是由流動性好的債券構成的,表中債券的期限比表3-3中債券的期限要短。
表3-4 一家財產保險公司簡要的資產負債表

3.10 保險公司面臨的風險
保險公司所面臨的最顯著的風險是其儲備金總量不能滿足投保人的索賠數量。雖然保險精算師的估計通常十分保守,但賠償總量超出估計數量的可能性仍然存在。除了以上風險,保險公司還會面臨自身投資資產表現不佳的風險。保險公司的大多數投資資產為企業債券,如果企業債券的違約高於平均值,那麼保險公司的盈利一定會受到不利影響。保險公司的債券組合要做到在不同的業務行業及區域進行多元化,保險公司也要監測自身投資資產流動性的表現。與上市或交易活躍債券相比,流動性差的債券(illiquid bond,例如保險公司買入的私募基金)通常會提供較高的收益率,但是,這些債券並不易於轉換為現金並用於支付沒有預計到的高數量的索賠。保險公司要與銀行及再保險公司進行業務往來,這會給保險公司帶來信用風險。同銀行類似,保險公司從事業務也會面臨操作風險及業務風險(business risk)。
監管部門一般會闡明保險公司的最低資本金要求,這些資本金為保險公司所面臨的風險提供緩衝。與銀行類似,保險公司也紛紛研發了內部模型來計算經濟資本金(即保險公司自身所估計的應持有的資本金數量(見第26章))。
3.11 監管條款
美國和歐洲對於保險公司有非常不同的監管方式。
3.11.1 美國
美國在1945年通過的《麥克倫-福克森法案》(McCarran-Ferguson Act)確定了保險公司的監管職責歸各個州,而不是在聯邦範圍(與這一點不同的是,銀行監管是在聯邦範圍)。各州的監管者關注保險公司的償付能力以及它們應付保險合約持有者索賠要求的能力。他們同時也關注各保險公司的業務操守(如保費如何確定、廣告、保險合約條款、保險經紀和代理人資質的發放等)。
美國保險監理官協會(National Association of Insurance Commissioners,NAIC)是一個由50個州的保險業監管當局主管官員組成的組織。該組織為保險監管者討論共同面臨的問題提供一個全國性的機制。有時該組織也會為各州的監管當局提供服務。例如,該委員會提供所有的經營財產及意外傷害保險業務的公司的賠付率統計數據。這樣做可以幫助各州的監管當局識別那些賠付率超出正常範圍的保險公司。
保險公司要向各州監管機構提供詳細的財務報告,各州的監管人員還要定期現場檢查。監管當局採用由NAIC確定的、經風險調節的標準來確定資本金的數量。資本金設定的數量的大小是為了應對以下風險:保險儲備金的設定不足、交易對手違約以及投資資產收入低於預期。
投保人的利益在保險公司破產時(因而不能支付索賠時)受到保險擔保協會的保護。一家保險公司想在某一州取得業務執照,首先得成為該州保險擔保協會的成員。當該州內的一家保險公司破產時,這個州內的其他保險公司必須向該州保險擔保基金(state guaranty fund)支付一定的資金,支付資金數量與保險公司在這一州內收入的保費有關。保險擔保基金首先用於支付破產保險公司的小額投保人(小額投保人的定義在不同州的含義也各不相同)。保險公司每年度向擔保基金所支付的資產可能會有一個上限,這一規定可能會造成投保人要等上若干年才能拿回擔保基金支付的全部賠償。對於人壽保險的情形,保單會持續很多年,破產保險公司的投保人往往會由其他保險公司接管,但是接管保險公司可能會對保單進行修改,修改後的保單對投保人可能會變得更加不利。
由上所述,美國保險公司的擔保系統與銀行擔保系統存在不同。在銀行系統中,銀行通過向FDIC支付保金,以保護存款,從而建立了一個永久性的基金。保險系統中沒有這樣的永久基金,在某家保險公司解體後,其他保險公司才必須貢獻一定的資金。只有紐約州的財產意外險保險公司是一個特例,它設定了一個永久保險擔保基金。
州一級對保險行業進行監管在一些方面並不能令人滿意。各個州之間的監管規定並不一致。這意味著一個在全美國範圍內經營業務的大型保險公司必須要應對很多個不同的監管當局。還有一些保險公司像銀行一樣進行衍生產品交易,卻不受類似銀行業所受到的監管。這就可能帶來麻煩。2008年,一家大型保險公司AIG(American International Group)在信用衍生產品的交易中遭受了鉅額損失,因而不得不接受聯邦政府的救助。
2010年通過的《多德-弗蘭克法案》成立了一個歸財政部領導的聯邦保險辦公室(Federal Insurance Office,FIO),負責監督保險行業和識別各州監管制度中的差別。它可以向金融穩定監督委員會(Financial Stability Oversight Council)提出建議,使類似AIG的大型保險公司作為非銀金融公司受到美聯儲的監管。同時它也與全球其他國家的監管機構(特別是歐盟國家的監管機構)建立聯繫,以便於建立趨同的監管規則。《多德-弗蘭克法案》要求FIO“進行研究並向國會提交一份如何現代化及改進美國保險業監管體系的報告”。FIO於2013年12月向國會遞交了該報告。[1]報告中提出了為改進美國保險業監管體系而需要做出的改變。從中看來,美國要麼將保險監管規則的制定放在聯邦層面而把日常管理仍放在州一級,要麼把二者都收歸聯邦層面。
3.11.2 歐洲
歐洲的保險公司由歐盟集中監管,這意味著從理論上講,一個統一的保險監管框架適用於歐盟成員國的所有保險公司。這一框架最先創立於20世紀70年代,被稱為《償付能力法案Ⅰ》(Solvency Ⅰ)。該法案的內容受荷蘭Campagne教授的研究結果影響很大,Campagne教授的研究結果顯示,如果資本金等於保額的4%,那麼人壽保險公司將有95%生存的機會。投資風險沒有被明確包括在《償付能力法案Ⅰ》中。
歐洲的若干國家(像英國、荷蘭及瑞士等)均提出了本國的計劃以應對《償付能力法案Ⅰ》中的不足。歐盟現在正在致力於《償付能力法案Ⅱ》(Solvency Ⅱ)的研究。該法案設定的資本金覆蓋的風險類型比原法案更廣泛,並在2016年開始實施。我們將在第15章中進一步討論《償付能力法案Ⅰ》和《償付能力法案Ⅱ》。
[1] See “How to Modernize and Improve the System Insurance Regulation in the United States,” Federal Insurance Office, December 2013.
3.12 養老金計劃
養老金計劃是公司為其僱員設立的。一般來講,在僱員為公司工作的時間內,僱主和僱員都要為養老金計劃供款。當僱員退休以後,他在其餘生內將得到養老金收入。因此,養老基金的實質是通過定期供款計劃來創立一個僱員餘生內的年金產品。這與人壽保險公司提供的產品十分相似。市場上有兩種養老金計劃,即固定收益計劃和固定供款計劃。
在固定收益計劃(defined benefit plan)中,僱員在退休後所得到的養老金數量由該計劃事先定義。通常的計算方式是一個與僱員為公司服務的時間以及僱員的工資有關的公式。例如,每年的養老金數量等於僱員最後為公司服務的3年的平均工資乘以僱員為公司服務的時間的長度,然後再乘以2%。如果僱員先於其配偶辭世,那麼其配偶仍有可能拿到養老金(數量有所減少);如果僱員在受僱期間辭世,那麼養老金計劃通常會向經濟上依賴該僱員的親屬一次性支付一筆款項,而僱員的配偶和未獨立子女每月可能還會得到一筆收入。有時養老金要隨通貨膨脹每年進行調整,這種調整被稱為指數化(indexation)。例如,一個固定收益養老金計劃每年的指數化可以是按消費者價格指數(consumer price index)增量的75%進行遞增。由政府支持的養老金計劃(如美國的社會保險)與固定收益計劃類似,它們都要求參與人定期供款到一定年齡,然後才可以在餘生中享受養老金。
在一個固定供款計劃(defined contribution plan)中,僱主及僱員的供款均以僱員的名義進行投資。當僱員退休時,僱員有幾種選擇將供款的最後數量(包括投資增量)轉換為年金產品。有時僱員可以選擇收到一次性付款而不是年金。
固定供款計劃與固定收益計劃的區別在於固定供款計劃的資金與僱員個人掛鉤。在固定供款計劃中,每個僱員均有一個投資賬戶,僱員所收到的養老金的數量均以僱員個人賬戶中的資產數量為基準。與此相反,在固定收益計劃中,所有的供款均被集中於一個投資組合中,給退休僱員支付的養老金均來自這個投資組合。美國的401(K)計劃是一種形式的固定供款計劃,僱員可以選擇將其一定數量的收入直接投放這一計劃中(可能還會有來自僱主的相同數量的供款),僱員可以在不同類型的投資產品(如股票、債券、貨幣市場產品等)中進行投資。
固定收益及固定供款計劃的一個關鍵特性是僱員的收入稅被延遲了。僱員向養老金支付的款項是免稅的,並且僱主向養老金的支付可以在收入表中減除,僱員只有在收到養老金收入時才需要繳稅(而此時僱員收入的邊際稅率往往已經變低了)。
固定供款計劃對於僱主而言幾乎沒有風險。如果養老金計劃的投資比預期的差,那麼僱員將承擔所有的損失;與之相反,固定收益計劃為僱主帶來了非常大的風險,因為僱主最終要負責支付承諾的養老金數量。我們假定一個固定收益計劃中的資產數量為1億美元,但精算師估算出的養老金義務的貼現值為1.2億美元,該養老金資金不足數量達2 000萬美元,僱主必須補齊這個資金缺口(通常需要若干年),固定收益給公司帶來的這種風險造成了有些公司逐漸將固定收益計劃轉化為固定供款計劃。
對固定收益計劃的債務的貼現值進行估算不是一件容易的事情。估算中最重要的一點是如何選取貼現利率。貼現利率越高,養老金債務的貼現值越低。以往,一種經常使用的計算貼現率的方法是以養老金資產中的平均回報率作為貼現率。這種做法會鼓勵養老金將資產投資於股票,因為股票市場的平均回報高於債券市場,這麼做會將養老金債務壓得很低,從賬面上,這很好看。現在的會計準則已經意識到企業對養老金計劃中負債的義務類似於債券。因此,準則要求非上市公司的養老金義務應以AA級債券的收益率進行貼現,固定收益計劃的資產價值與其債務的差別必須以資產或負債的形式納入公司的資產負債表。因此,如果一家公司的養老金有資金不足的現象,那麼公司的股權值會被相應地減少。如果養老金資產價值大幅下跌,同時用以計算義務的貼現率也大幅下跌,那麼公司的債務狀況就會產生一個“完美風暴”(perfect storm)(見業界事例3-2)。
業界事例3-2
一個完美風暴
1999年12月31日~2002年12月31日,標準普爾500指數由1469.25點跌至879.82點,跌幅達40%;同時20年期的美國國債收益率由6.83%跌至4.83%,跌幅達200個基點。這些事件的第一個影響是養老金資產的市價大幅下跌,另一個影響是養老金負債的貼現率下降,因此由精算師估算出的負債的公允價值(fair value)上漲。對於一個固定收益計劃而言,以上兩個效應促成了一個完美風暴。許多資金盈餘的養老金一下子變得資金不足,一些原本資金稍稍不足的養老金一下子變得資金嚴重不足。這3年間的股票價格與利率的下跌為管理固定收益養老基金的經理帶來了噩夢。
一家公司如果持有一個固定收益養老金計劃,新的會計規則會要求養老金計劃的盈餘或虧損情況應在該公司的股權價值上反映出來。因此,對於很多公司試圖將固定收益計劃轉化為固定供款計劃,以防止股權價值被侵蝕的做法,我們也就不必感到吃驚了。
固定收益計劃能行得通嗎
一個典型的養老金計劃會為其僱員提供最終工資的70%,並且公司要對養老金計劃進行通貨膨脹指數化調整。我們要將僱員工作期收入的多大比率作為儲備,才能保證養老金支出呢?對於這個問題的回答取決於我們對於利率的假設,以及僱員收入的增長幅度等。如果我們諮詢一家保險公司對所提供的養老金的報價,保險公司給出的報價會是:供款佔工資收入的比率大約為25%(練習題3.15及作業題3.19給出了計算過程提示)。保險公司會將保費投資於企業債券(這與保險公司對人壽保險保費以及年金合約的投資形式一致),因為投資於企業債券可以最好地將投資收入與賠償進行匹配。
事實上,固定收益計劃的供款(僱主加上僱員)遠低於收入的25%,在一個典型的固定收益計劃中,僱主和僱員的供款分別只佔收入的5%,因此整體供款只是保險精算師所求得保費的40%,許多養老金資金不足的現象也就不足為奇了。
與保險公司不同,養老基金會將資產的一大部分投放於股票市場(一個典型養老基金的投資組合由60%股票及40%債券組成)。通過投資股票,養老基金為補齊資金缺口並達到資金盈餘創造了機會,但同時也留下了資金嚴重不足的隱患。如果股票市場表現好,例如,在1960~2000年,世界上許多地區的股票市場表現甚佳,養老金完全可以應付自身的負債;但是如果股票市場表現不佳,養老金可能就會出現問題。
以上的討論引出了一個有趣的問題:誰要為資產不足的養老金買單呢?答案是:第一個買單的會是公司的股權持有者;進一步,如果公司宣佈破產,政府則可能以養老金計劃擔保的形式承擔損失。[1]以上兩種情形,均存在將財富由下一代轉移到退休人員中的現象。
許多人認為將財富由下一代轉移給上一代的做法不可取,將養老金的供款比率提至25%也是不可接受的做法。如果固定收益的養老金計劃仍然持續的話,那麼這種計劃的條款一定要得到改革,來由退休人員和下一代共同承擔風險。如果在受僱期內,市場表現不佳,則僱員必須接受退休後養老金收入較低這一現實;如果市場表現好,退休人員可以收到全額養老金收入,並且可以將養老基金的額外收入轉移給下一代。
長壽風險是養老金面臨的主要風險,我們曾在前面指出,1929~2013年,人類平均壽命延長了20年。如果這種趨勢繼續延續,到2029年,人類壽命將還要延長5年,固定收益計劃中的資產不足問題(包括公司管理的以及政府管理的養老金)會變得更加嚴重。許多國家的僱員在超出正常退休年齡後仍然可以工作。這一點不奇怪,這樣可以緩解養老基金面臨的資金短缺問題。一個僱員決定在70歲而不是在65歲退休可以為養老金繼續供款5年,另外,其接受養老金收入的退休期也縮短了5年。
[1] 例如,美國的養老福利擔保公司(Pension Benefit Guaranty Corporation,PBGC)為私立固定收益養老金提供擔保,但如果該公司從不同養老金計劃所收到的保費不能滿足索賠數量,則政府必須介入。
小結
保險公司經營業務有兩類:人壽保險和財產及意外傷害險。人壽保險公司提供一系列產品,這些產品在投保人死亡後會提供賠償。定期壽險只有在投保人在一定時間段內死亡才提供賠償;終身壽險不管投保人在什麼時刻死亡,均會提供賠償。終身壽險中有一個儲蓄因素。通常來講,早期的保費中超出預期賠償的那一部分被用於投資,投資所得是為後期的預期賠償提供支持。終身壽險會給投保人帶來稅務優惠,因為投資回報的應繳稅款一直被推遲到賠償的支付日。
人壽保險公司也提供年金合約,年金合約的持有者首先支付一筆款項,之後保險公司在一定時間以後為投保人提供終身支付。死亡率數據為保險公司的人壽保險及年金產品定價提供了重要依據,但是保險精算師還必須考慮以下風險:①長壽風險(即投保人比預期壽命活得更久);②死亡風險(由於艾滋病及西班牙流感等傳染病和流行病造成某個人口群體壽命縮短的可能)。
財產及意外傷害險是為了財產損失提供保險,同時也為個人及公司的法律責任提供保險,最難以估計賠償數量的事件是那些與同一事件有關,但會觸發眾多投保人同時索賠的事件,這類事件包括地震和颶風。由法律責任所觸發的賠償數量通常也難以估計。
健康保險具有人壽保險及某些財產及意外傷害險的特性,健康保險的保費與人壽保險的保費類似,即保險公司對賠償風險估計的改變不會觸發保費的改變,但是如果整體健康系統的費用增大時,保費也像在財產及意外傷害險中那樣會有所增長。
保險公司面臨兩類重要風險,即道德風險及逆向選擇。道德風險是指持有保險的個人及公司在投保後,行為有所改變而觸發的風險;逆向選擇是指買入保險的個人或公司所對應的預期賠償相對較高而觸發的風險。保險公司會採取措施儘量減少以上兩類風險,但無論如何,保險公司不可能將兩類風險同時消除。
與銀行不同的是,保險公司的資產及負債均面臨風險。一家財產保險公司的股權資本對總資產比例要比人壽保險公司更高。在美國,對保險公司監管由各州負責,而不是由聯邦負責,這一點也和銀行業的情況不一樣;在歐洲,保險公司受歐盟及各國政府的監管。歐盟現在正在致力於制定一套新的資本金管理規則,即《償付能力法案Ⅱ》。
市場上有兩類養老基金計劃:固定收益計劃及固定供款計劃。固定供款計劃十分簡單,由公司及僱員所支付的供款以僱員名義被存於某個單獨賬戶,資金以僱員名義投資,在僱員退休後,投資回報以及本金將被轉換為年金;在固定收益計劃中,僱員和僱主的供款被存入同一個資金池中,然後進行投資。退休人員所得到的養老金數量取決於其受僱時的工資。固定收益計劃的可行性現在已經受到一定質疑,許多固定收益計劃資產不足,只有在股票市場表現異常出色的情況下,養老金才能滿足當前退休人員及將來退休人員的養老金支付。
延伸閱讀

練習題
3.1 定期壽險和終身壽險的區別是什麼?解釋終身壽險在稅務處理方面的優勢。
3.2 解釋變額壽險和萬能壽險的含義。
3.3 一家保險公司同時提供終身壽險和年金產品,這兩種合約哪一種對以下風險會有風險敞口:(a)長壽風險;(b)死亡風險。
3.4 “公平人壽保險公司給持保者發放了免費的期權。”討論這一期權的特性。
3.5 利用表3-1計算保險公司給出的一個關於50歲女性、面值為100萬美元、2年期的人壽保險最低保費,假定保費是在年初支付,利率為0。
3.6 由表3-1來計算一個30歲男性能活到90歲概率為多大?同樣,一個30歲女性能活到90歲的概率為多大?
3.7 財產保險公司保單上的哪一個條款會觸發最大的風險?
3.8 解釋巨災債券的運作。
3.9 考慮兩個債券,它們具有同樣的券息、期限以及價格,一個債券為B級企業債券,另一個為CAT債券,歷史數據顯示這兩個債券的預期風險相同,假定你為組合資產經理提供諮詢,你將推薦哪一個債券,為什麼?
3.10 美國的保險公司與加拿大及歐洲保險公司的不同之處在於哪裡?
3.11 一家保險公司決定是否為某人失去工作提供保險,保險公司面臨的問題是什麼?
3.12 為什麼財產保險公司持有的資本金要高於人壽保險公司?
3.13 財產保險公司所計算的“賠付率”和“費用比率”的含義是什麼?如果一家保險公司盈利,那麼其賠付率加上費用比率一定會小於100%,討論這個觀點。
3.14 固定收益及固定供款養老基金計劃的區別是什麼?
3.15 假定在一個固定收益養老計劃中:
(a)僱員為公司工作40年,工資隨通貨膨脹而增長;
(b)僱員退休時所得養老金為工資的75%,養老金隨通貨膨脹而增長;
(c)退休人員將收入20年養老金;
(d)養老金的收入將投資於債券,債券收益等於通貨膨脹率。
如果公司沒有破產(即仍支持養老金),僱員的供款作為工資的比率至少為多大?(提示:在計算中採用實際貨幣量(real dollar)而不是名義貨幣量(nominal dollar)。)
作業題
3.16 採用表3-1來計算保險公司為一個60歲男性提供的面值為500萬美元、期限為3年的保險的最低保費。假定保費是在每年年初支付,死亡發生在年中,無風險利率為每年6%(每年複利2次)。
3.17 某保險公司假定某類損失的分佈可以被合理地估計為正態分佈,均值為1.5億美元,標準差為5000萬美元(假定風險中性的損失與真實世界的損失沒有差別),1年的無風險利率為5%,估計以下合約的費用:
(a)一個按比例承擔保險公司1年內60%損失的合約;
(b)在1年內,當損失超過2億美元時,合約將承擔1億美元的損失。
3.18 假定在某年,利率降低了200個基點(2%),股票價格沒有變,討論這個市場變化對一個將60%資產投資於股票市場,同時將40%資產投資於債券市場的固定收益養老金計劃的影響。
3.19 假定在一個固定收益養老金計劃中:
(a)僱員為公司工作45年,工資以實際利率2%遞增。
(b)退休人員收入的養老金為最終工資的70%,養老基金遞增比率為通貨膨脹率減去1%。
(c)在18年後收到養老金付款。
(d)養老基金的收入將被投資於債券市場,回報率等於通貨膨脹率加上1.5%。
假定公司仍不破產,計算僱員供款應占工資的比率(提示:在計算中採用實際貨幣量,而不是名義貨幣量)。
第4章
共同基金和對衝基金
共同基金(mutual fund)、交易所交易基金(ETF)和對衝基金(hedge fund)代表個人與企業進行投資,在這3種投資方式中,不同投資者的資金被彙集到一起來進行投資,投資資產的選擇由基金經理來確定,投資的原則是為了達到某個事先闡明的目的。某些國家將共同基金稱為“單位信托”(unit trusts),共同基金和交易所交易基金的目的是滿足一些相對較小規模的投資者的需求,對衝基金是為了吸引一些富有的個人以及類似於養老基金的機構投資者。對衝基金所受的監管規定要遠遠弱於共同基金和交易所交易基金,同共同基金相比,對衝基金可以實施較大範圍的投資策略,對衝基金的運作透明度相對較差。共同基金和交易所交易基金需要在投資者可獲得的招股說明書中解釋其投資策略。
在本章中,我們將討論不同形式的共同基金和交易所交易基金及對衝基金,我們將討論對於這些基金的監管方式以及基金的收費形式,我們還將討論這些基金如何做到為投資者提供豐厚的回報。
4.1 共同基金
對於小客戶而言,共同基金所提供的一個投資亮點是基金提供的分散投資機會。如我們在第1章中看到的那樣,分散投資會改善投資者風險與回報的平衡關係,但一個小投資者很難持有足夠大數量的股票來保證投資組合實現充分的風險分散,另外,持有一個良好的多元化投資組合可能會觸發較高的交易費用。共同基金為投資者提供了一個好的投資途徑,許多小投資者將資金彙集到一起進行投資,因此在付出較少費用的前提下達到了分散風險的效應。
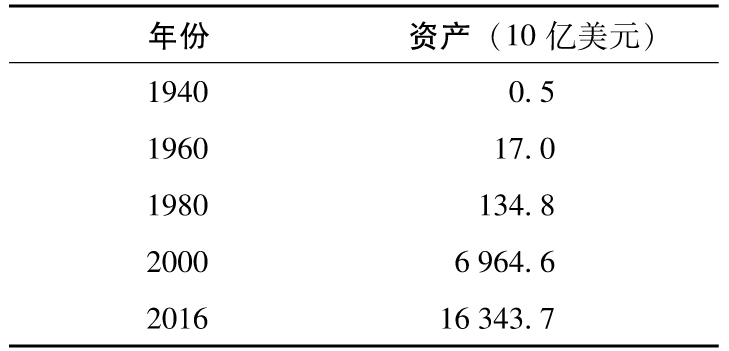
共同基金的投資者擁有該基金一定數量的股份。最常見的共同基金是開放式基金(open-end fund)。這意味著,當投資者購買更多股票時,流通在外的股票總數上升,而當股票被贖回時,流通在外的股票總數下降。自第二次世界大戰以來,開放式共同基金發展非常迅速。表4-1是對自1940年以來美國開放式共同基金持有資產規模的估計。截至2016年,共同基金資產規模已經超過了16萬億美元,大約有44%的美國家庭擁有共同基金。有些共同基金由專長於資產管理的公司提供,例如富達基金(Fidelity Company)。其他基金由銀行提供,例如摩根大通。有些保險公司也提供共同基金,例如,在2001年,美國大型保險公司州立農業保險公司(State Farm Insurance Company)在美國開始提供10種不同的共同基金,客戶可以通過網絡、電話或從州立農業保險公司的代理人那裡購買基金。
表4-1 美國開放式共同基金資產的增長幅度
資料來源:Investment Company Institute.
貨幣市場共同基金投資於1年以內到期的附有利息的金融產品,例如國債、商業票據和銀行承兌匯票。這些產品是付息銀行存款賬戶的另外一種選擇,而且這些產品的利息通常會更高一些,因為政府的存款保險機構並不對此類產品承保。有些貨幣市場基金還提供支票賬戶的功能,這與銀行賬戶很類似。貨幣市場投資者一般厭惡風險,不希望投資的本金遭受損失。也就是說,投資者希望在扣除了管理費後,得到正收益。[1]在正常市場條件下,做到這一點不太難。但有時負收益的情況會發生,並導致投資者損失部分本金。這種情況也被稱作“跌破淨值”(breaking the buck),因為1美元投資的淨值低於了1。2008年9月雷曼兄弟破產後,美國曆史最悠久的貨幣市場基金首要儲備基金(Reserve Primary Fund)就面臨這種局面,因為該基金不得不註銷雷曼兄弟發行的短期債務。為了防止出現對貨幣市場基金的擠兌情況(這意味著即使是財務狀況健康的公司的債券也會面臨無人問津的局面),政府推出了一個由政府支持的擔保項目。該項目執行了大概1年左右。
投資期限較長的基金主要有三類:
(1)投資於期限大於1年的固定收益債券的債券型基金;
(2)投資於普通股及優先股的股票型基金;
(3)投資於股票、債券及其他產品的混合型基金。
其中股票型基金是目前市場上最為流行的一種。
共同基金的價值是在每天下午的4點定出。為了定出價值,共同基金經理要計算出共同基金投資組合中各項資產的價值,並以此定出基金的整體價值。每份基金的價格等於基金整體價值除以共同基金的數量。該價格被稱為淨資產價值(net asset value,NAV)。投資者可以隨時從基金中買入基金的份額,也可以向基金賣出份額。當投資者發出買入或賣出共同基金份額指令後,下一個計算出的淨資產價值會被應用到該筆交易中。例如,如果一個投資者在某個業務日的下午2點決定買入一個份額,下午4點計算出的淨資產價值將會被用於決定投資者應付金額的數量。
投資者通常需要為基金收益而付稅,就像其個人持有基金投資組合中的資產一樣。因此當基金收到股息分紅時,基金的擁有者必須為所得股息付稅,即使投資者將股息再投資於基金,也仍然如此;當基金賣出證券時,投資者會馬上得到資本的收益或虧損,即使投資者並沒有賣出自己的基金份額。假定某投資者最初以100美元買入一定數量的基金,因為基金資產交易,投資者在第一年有每股20美元的股本收益,而在第二年有每股25美元的股本虧損,投資者必須在第一年申報20美元的股本收益,而在第二年申報25美元的股本損失。當投資者賣出基金份額時,也會有資本收益或虧損。為了避免被重複計量(double counting),每份基金的價格要被調節以反映已被計入的投資者的盈虧。在我們的例子中,如果投資者在第一年年末賣出基金份額,則基金價格會被定為120美元,以反映資本的盈虧;如果投資者在第二年年末賣出基金份額,則投資者用於計算資本盈虧的價格會被定為95美元。
4.1.1 指數基金
某些基金的設計是為了跟蹤特定的股票指數,例如標準普爾500指數及富時100指數(FTSE 100)。為了確保跟蹤效果,最簡單的做法是買入指數中的所有股票,買入股票的數量要反映股票在指數中的權重,例如,如果IBM在某個股指中的權重為1%,那麼1%跟蹤股指的交易組合要被投資於IBM股票。另外一種跟蹤股指的做法是選擇一個小型股票組合,股票數量的選取要經過研究,來保證這個小型股票組合確實可以有效地跟蹤選定的股票指數。還有一種跟蹤股指的做法是利用股指期貨。
在美國市場,最早的股指基金之一是由約翰·博格在1975年12月31日推出的跟蹤標準普爾500指數的股指基金。在最初發行時,基金共持有價值達1100萬美元的資產,這一基金最初被調侃為“非美國式”(un-American)和“博格傻帽”(Bogle’s folly)。然而後來,這隻基金被命名為先鋒500指數基金(Vanguard 500 Index Fund)。2017年,該基金賬戶下管理的資產達5000億美元。
指數基金能夠做到有多麼準確地跟蹤指數呢?兩個相關的度量指標是跟蹤誤差(tracking error)和費用比率(expense ratio)。一隻基金的跟蹤誤差的定義有兩種比較常見的形式:一種是基金的年回報率與指數的年回報率的均方根誤差(即二者回報率的差,平方後取均值,再開平方根),另一種是二者回報率之差的標準差。[2]費用比率是每年為管理基金付出的費用佔總資產的比例。
4.1.2 費用
共同基金有幾種不同形式的費用,其中包括運作費用、營銷佣金支出、會計費用以及其他管理費用、交易費用等。為了補償這些費用,並同時取得盈利,基金管理人會向投資者收費。前端收費(front-end load)是管理人在投資者首次買入基金份額時向投資者收取的費用,並不是所有的基金均收取這個費用。收取這個費用的基金被稱為前端收費基金,在美國,前端收費的數量不能超過投資數量的8.5%。有些基金在投資賣出基金份額時收費,這類基金被稱為後端收費(back-end load)基金。所有的基金均收取年費。有些基金會專門收費來支付管理費、產品分配費用等。總費用比率(total expense ratio)是每份基金所收取的費用與每份基金價格的商。
Khorana等(2009)研究人員比較了17個國家的共同基金的收費。[3]Khorana等在他們的分析中假定投資者會持有基金5年,因此每年的總持有費用(total shareholder cost)等於

表4-2是對其研究結果的總結。股票型基金的平均費用從澳大利亞的1.41%到加拿大的3%不等。股票型基金的收費平均高於債券型基金收費大約50%,指數基金的收費低於常規基金的收費。這是因為基金不需要僱用那些高薪酬的股票選擇員及分析員,某些美國的指數基金的費用低至每年0.15%。
表4-2 共同基金每年的平均費用(作為資產的比例,%)
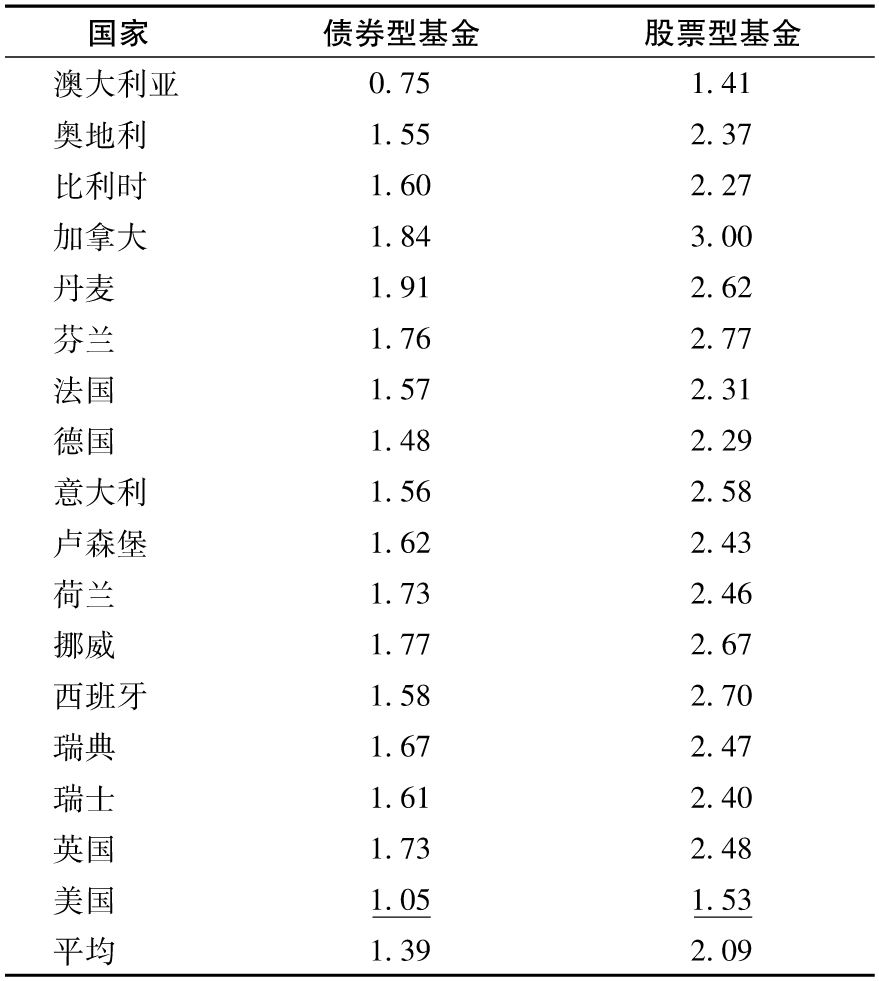
注:假定基金被持有5年。
資料來源:Khorana, Servaes, and Tufano, “Mutual Fund Fees Around the World,” Review of Financial Studies 22(March 2009): 1279-1310。
4.1.3 封閉式基金
截至目前,我們討論的基金均為開放式基金。開放式基金是最為普遍的共同基金形式。基金中的份額數量每天都有所變化,這是因為每天都有投資者買入或賣出基金份額。封閉式基金就如同一般企業,其基金份額數量是固定的。基金份額每天都在股票交易所進行交易。對於封閉式基金我們可以計算兩類淨資產價值:一種是基金份額在交易中的成交價格,另一種等於基金投資組合的市場價值除以全部份額數量。第二個淨資產價值被稱為基金份額的公允市場價值(fair market value)。一般來講,封閉式基金份額價值小於其公允市場價值。有一些研究人員試圖解釋這一現象的原因。羅斯(2002)的研究結果顯示,對基金經理支付的費用可以解釋這一點。[4]封閉式基金遠沒有開放式基金受歡迎,2016年,它們在美國的資產總額為2 620億美元。
[1] 穩定價值基金(stable value fund)是一種很受歡迎的、不同於貨幣市場基金的選擇。這類基金通常投資於期限為5年左右的債券和類似產品。銀行或其他公司為這些基金提供保障,保證收益不為負值(當然要為此收取一定的費用)。
[2] 均方根誤差被認為是一種更好的方法。標準差法的問題是,如果二者回報率的差很大但很穩定,標準差會很小。
[3] See A. Khorana, H. Servaes, and P. Tufano, “Mutual Fund Fees Around the World,” Review of Financial Studies 22(March 2009):1279-1310.
[4] See S. Ross, “Neoclassical Finance, Alternative Finance, and the Closed End Fund Puzzle,” European Financial Management 8(2002):129-137.
4.2 交易所交易基金
交易所交易基金(exchange-traded fund,ETF)在1993年首次出現於美國市場,並在1999年出現於歐洲市場。該類基金通常是跟蹤某個指數,因此ETF產品是那些期望取得近似股指回報率的投資者的另一個選項。最著名的一隻ETF基金被稱為蜘蛛(Spider),其跟蹤標準普爾500指數,交易代碼是SPY。2008年3月,一項對於專業投資者的調查顯示,67%的被調查對象認為ETF是過去20年來最有創造性的投資工具,並且有60%的被調查對象認為ETF從根本上改變了他們構造投資組合的方式。2008年,美國SEC批准了主動管理型ETF基金的成立。
ETF是由機構投資者創立的產品,一般來講,某個機構投資者首先將一系列的資產存放於ETF基金中,並因此取得ETF份額(也被稱為創立基數(creation units))。某些或全部的ETF份額會在股票交易所上市交易。這賦予了ETF某種封閉式基金而不是開放式基金的特性。但是,ETF的一個重要特性是,機構投資者在交易時可以將大量的份額與對應的標的資產互換。投資者可以放棄他們持有的ETF份額而接收資產,或者存入資產而收到新的份額。這麼做的目的是保證ETF在交易所交易的價格與其公允價格沒有太大出入,這一特性正是ETF與封閉式基金的重要區別,這一點使得ETF對投資者來講比封閉式基金更有吸引力。
同開放式基金相比,ETF有若干好處,它可以在一天的任意時刻被買入或賣出,投資者可以像賣空股票那樣來賣空ETF(見第5章關於賣空策略討論)。ETF持有資產每天要被公佈兩次,這保證了投資者會對基金標的資產有充分的瞭解。與之相比,共同基金公佈其資產的次數沒有這麼頻繁,當共同基金的份額被賣出時,基金管理人常常要賣出基金中所持股票以確保擁有足夠的資金來支付給投資者。而當ETF的份額被賣出時,並不一定非要賣出資產,這是因為其他投資者可以提供現金。這意味著管理人可以節省交易費用,減少了轉嫁給基金持有者的無計劃資本收益和虧損。最後,ETF的費用比率一般要低於共同基金的費用比率。ETF越來越受歡迎,到2016年,它們的資產達到2.5萬億美元。
4.3 主動管理型基金與被動型指數基金
當購買共同基金或交易所交易基金時,投資者可以在一隻被動型指數基金(跟蹤某一特殊指數,如標準普爾500指數)和一隻主動管理型基金(依賴於基金經理的選股與擇時技能)之間選擇。主動管理型基金的費用比率往往高得多。因此,一個關鍵問題是,主動管理型共同基金的表現是否優於標準普爾500指數等股票指數。有些基金在某些年份表現很好,但這可能是運氣好,而非良好投資管理的結果。研究人員面臨的兩個關鍵問題是:
(1)平均來講,一隻主動管理型基金會比股指表現更好嗎?
(2)在第一年表現好的基金,在第二年會持續嗎?
對於以上兩個問題的回答看來都是否定的。在一項經典的研究中,Jensen(1969)採用115只共同基金的10年數據來檢驗它們的表現。[1]在研究過程中,他計算了每年每隻基金的alpha項(如第1.3節所示,alpha是超過資本資產定價模型預測的回報)。考慮到各項費用,所有基金的平均alpha為零,扣除費用後,平均alpha為負值。Jensen同時也檢驗了一個具有正的alpha的基金是否會持續產生正的alpha。表4-3是對Jensen結果的總結,表中第一行顯示在1 150個觀察數據中,有574只基金具有正的alpha(近50%),在這些具有正的alpha基金中,有50.4%的基金在隨後一年仍有正的alpha。表中第二行顯示,當在2年內基金的alpha均為正時,在接下來一年基金的alpha為正的機會有52%,表中的數據依此類推。結果顯示,當一個基金經理在1年中(或幾年內)取得了正的alpha以後,在接下來一年只有50%的機會取得高於平均水平的回報率。這些研究結果說明基金經理取得正的alpha回報往往是因為運氣,而不是投資技巧。某些經理人的回報率會一直高於市場平均回報率,但這些經理人只佔整體數量的一小部分。一些更新的研究結果也證實了Jensen的結論。平均來講,共同基金經理的表現不會比市場表現更好,並且過去的表現不能代表將來。股指基金的成功說明了Jensen的研究結果確實影響了許多投資者的觀點。
表4-3 共同基金良好回報的一致性

共同基金常常會取得令人吃驚的回報率。但是,這個回報率也許只是屬於某一隻特殊的基金,這一基金可能是同一機構發行的眾多基金中的一隻,只不過恰好取得了高於平均水平的回報而已。將好運氣與好表現進行區分並非易事。假定某資產管理公司有32只基金,每隻基金均採用不同的交易策略,假設基金經理沒有什麼特殊技巧,每隻基金的年回報高出市場回報的機會為50%,某隻基金在連續5年內的回報均高於市場的機會為(1/2)5,即1/32,這意味著在32只基金中,一定會有一隻基金在5年的時間內表現會高於市場表現!
另外一點需要說明的是關於幾年內回報率的表達方式。一個共同基金的廣告可能會說“在過去5年內,我們平均年回報為15%”,另外一個廣告可能會說“將你的財富投資於我們的共同基金,你的財富將以每年15%的比率增長”。以上兩種說法聽起來類似,但事實上它們有不同的含義(見業界事例4-1)。在許多國家,監管當局設定管理規則來確保共同基金回報率的報告方式不能誤導投資者。
業界事例4-1
共同基金的回報率可能會令人誤解
假定某共同基金經理報告的在過去5年內的年回報率(以年複利)為15%、20%、30%、-20%及25%。
這些回報率的算術平均值等於以上5個數值的和除以5,即14%。但是如果一個投資者將資金投入該共同基金,並投資5年,那麼其平均每年的回報率會小於14%。100美元的投資在5年後的價值為
100×1.15×1.20×1.30×0.80×1.25=179.40(美元)
而以年複利14%的回報率計算,相應的值將為
100×1.145=192.54(美元)
在5年後,終端值為179.40美元所對應的年回報率為12.4%,這是因為
100×1.1245=179.40(美元)
那麼,基金經理應該報告哪一個回報率呢?基金經理常常會做出以下聲明:“在過去5年,我們平均每年的回報率為14%。”雖然這一聲明沒有錯,但它會令人產生誤解。而以下聲明就不太會使人誤解:“投資者在過去5年將資金投入我們的共同基金,所得的回報率為每年12.4%。”在有些地區,監管當局的準則要求基金經理以第二種形式報告回報率。
以上現象是數學家所熟悉的一個著名結論:一組數據(不全部相等)的幾何平均值總是小於算術平均值。在我們的例子中,回報每年的乘數項為1.15、1.20、1.30、0.8和1.25。這些數字的算術平均為1.14,而它們的幾何平均值為1.124。一個將資金投資若干年的投資者所得回報率為幾何平均,而非算術平均。
[1] See M.C. Jensen, “Risk, the Pricing of Capital Assets and the Evaluation of Investment Portfolios,” Journal of Business 42(April 1969):167-247.
4.4 監管
因為共同基金是為了吸引小客戶,而許多小客戶的投資經驗並不豐富,所以監管當局對共同基金設定了非常嚴格的管理規定。在美國,SEC是共同基金的主要監管機構。共同基金必須向SEC提交註冊文件。基金在招股書中必須向潛在投資者提供詳盡和準確的財務報告,SEC也設定了監管規則以避免利益衝突、欺詐和收費偏高事件的發生。
即使有監管條款的存在,共同基金市場仍然會出現一定數量的醜聞。其中一種醜聞為延遲交易(late trading),如本章前面所述,如果一個投資者在下午4點之前向其經紀人發出了買入或賣出共同基金的指令,則決定投資者支付或收到的價格是基金下午4點的淨資產價值。在實際中,因某種原因,買入或賣出指令有時在4點以前可能並沒有由經紀人傳給共同基金,這就可能會造成經紀人與投資者合謀,並在4點之後提出一個新的交易指令,或者將原有交易指令進行修改。即使投資者使用4點後的市場動向(尤其是海外市場動向),但4點設定的淨資產價值仍然對投資者有效。SEC監管條款禁止延遲交易,並在21世紀初對一些違規人員進行了起訴,且因此觸發了數以百萬計的罰款,許多人也因此丟掉了自己的飯碗。
另外一種醜聞被稱為擇時交易(market timing)。擇時交易是指一些特殊的客戶可以頻繁地買入或賣出基金的份額(例如,每幾天進行一次交易)而無須為此付出任何代價,他們之所以願意這麼做可能是他們沉溺於延遲交易能帶來非法盈利,另一個原因是他們試圖找出那些近期價格沒有更新的股票對基金淨資產價值的影響。假定某隻股票在幾個小時內價格沒有更新(這可能是因為股票交易不頻繁,或者是股票是在不同時區的交易所進行交易),如果美國市場在過去的幾小時內上漲(下跌),計算出的淨資產價值可能會低估(高估)基金的標的投資組合的價值,這是一個短期交易機會。利用這樣的機會並從中盈利並不一定違法。但是,如果共同基金給某些特殊客戶一定的交易特權,那麼共同基金的做法就是違法的,因為交易費用(例如,那些為滿足客戶經常性地賣出份額而提供的流動性所觸發的費用)是由所有客戶共同分擔的。
其他類型的醜聞包括搶先交易和定向經紀。搶先交易(front running)是指共同基金在計劃一個大交易時,預計市場會受到影響,在交易前共同基金通知一些特殊客戶和一些合夥人,允許他們事先用自己的賬戶進行交易。定向經紀(directed brokerage)涉及共同基金與經紀商之間的不當行為,其中經紀商向客戶推薦共同基金,作為回報,共同基金向經紀商發出買賣股票及債券的指令。
4.5 對衝基金
對衝基金與共同基金的區別在於對衝基金所受的監管約束要比共同基金少得多,這是因為對衝基金的資金侷限於那些對財務有經驗知識的投資者和機構。共同基金的監管條例包括:
(1)共同基金的客戶可以隨時贖回其持有的份額;
(2)淨資產價值每天要進行計算;
(3)必須披露投資策略;
(4)對槓桿的使用有限制。
對衝基金往往不受以上條款的限制,因此可以有很大的自由度來開發複雜、非傳統及自營投資策略。對衝基金有時也被稱為另類投資(alternative investments)。
第一家對衝基金公司A.W.Jones & Co是由阿爾弗雷德·溫斯洛·瓊斯(Alfred Winslow Jones)於1949年在美國創立的,它採用普通合夥制(general partnership),目的是避免SEC的監管。瓊斯在其交易組合中持有他認為價格被低估的股票的多頭和價格被高估的股票的空頭,並利用槓桿來放大回報率。該對衝基金將盈利的20%作為管理費,基金的表現十分出色。對衝基金(hedge fund)這一名詞是1966年卡羅爾·盧米斯(Carol Loomis)在報紙上發表的一篇關於A.W.Jones & Co的文章中首先引入的,這篇文章指出,在扣除手續費後,對衝基金的表現比大多數共同基金要好。不出所料,這篇文章引發了投資界對對衝基金及對衝基金投資策略的極大興趣。其他對衝基金的先驅還有喬治·索羅斯、沃爾特·施洛斯以及朱利安·羅伯遜。[1]
對衝基金一詞意味著基金的風險是被對衝的,瓊斯的交易策略確實涉及對衝,他的頭寸對市場的整體方向沒有太大的風險敞口,因為他的多頭(他認為被低估的股票)在任意給定時刻基本上與他的空頭(他認為被高估的股票)持平。但是對於其他一些對衝基金而言,採用“對衝”一詞來描述並不合適,因為這些對衝基金在沒有任何對衝策略的情況下對於市場的變動採用激進的投資策略。
歷年來,投資基金的規模一直在增長。2017年,對衝基金吸納的投資額超過3萬億美元的規模。但我們在後面將會看到,2009~2016年,很多對衝基金的表現不如標準普爾500指數。許多對衝基金註冊地在稅率較為優惠的地區,例如開曼群島。基金的基金(funds of funds)的設立是為將資金投資於不同的對衝基金。對衝基金是一個不能忽略的投資群體。紐約和倫敦股票市場每天成交量的很大一部分得益於對衝基金的貢獻。它們還是可轉換債券、信用違約互換、美國不良債權、非投資級債券交易的主要參與者。它們在ETF上的交易也非常活躍,而且常常持有空頭頭寸。
4.5.1 收費
對衝基金與共同基金的一個重要區別在於對衝基金的收費遠高於共同基金,並且對衝基金的收費與基金的表現有關。對衝基金通常每年收取的管理費為其管理資產數量的1%~3%,這一費用是為了支付操作費用,但也可能是用於審計、會計管理以及交易員分紅等費用。另外,對衝基金還會收取績效費(incentive fee),該費用通常是盈利(如果有)的15%~30%。績效費的設定是為了吸引最有天賦的以及經驗豐富的投資經理,因此,一種常見的對衝基金的費用被稱為“2%+20%”,這是指對衝基金每年收取2%的資產管理費,並收取20%的盈利。除了收取較高的管理費,對衝基金通常會有一個資金鎖定期(lock up period),即投資資金至少在1年內不能被抽回。有些業績表現好的對衝基金收取的管理費要高於平均收費,例如,文藝復興科技公司(Renaissance Technologies Corp.)的吉姆·西蒙斯(Jim Simons)的手續費為“5%+44%”(西蒙斯曾經是數學教授,他在2017年的身家為180億美元)。
對衝基金所提供的協議可能包括一些使得績效費變得更易於被投資者接受的條款,例如:
(1)通常條款中會註明一個門檻回報率(hurdle rate),也就是說只有在業績超出這個最小回報率時,績效費才適用。
(2)通常條款中會註明一個高潮位標記條款(high-water mark clause),該條款闡明前期損失必須在全部補齊的情況下,績效費才適用。因為不同的投資者入股對衝基金的時間可能會不同,所以對於所有投資者,高潮位標記條款也各不相同。有時在合約中闡明一個按比例調整條款(proportional adjustment clause),該條款闡明如果投資者抽回資金,對衝基金對於前期損失只是按比例進行彌補。假定一個對衝基金初始價值為2億美元,對衝基金損失了4000萬美元,假定投資者想收回資金8 000萬美元,高潮位標記條款會註明,只有在剩下的8 000萬美元資金的回報必須完全彌補4 000萬美元的損失之後,對衝基金才能收取績效費。而按比例調整條款會將彌補數量減至2 000萬美元,因為在提取資金後,基金規模只是資產提取前規模的一半。
(3)有時條款中會有一個分紅追回條款(clawback clause),該條款可以保證投資者通過收回以前發出的績效費來彌補自身的損失。投資者每年給出的績效費的一部分被存入回收賬戶(recovery account),賬戶中的資金將用於彌補投資者將來的部分損失。
由於對衝基金收取豐厚的手續費,所以許多基金經理也逐漸變得富有起來。2016年,《福布斯》統計出排名前25位的對衝基金經理的收入總值為109億美元,其中兩位的收入超過了10億美元,分別是文藝復興科技公司的吉姆·西蒙斯(16億美元)和橋水投資公司的雷·達利奧(Ray Dalio,14億美元)。
如果一個投資者在一家對衝基金擁有一個投資組合,那麼需要繳納的費用可能非常高昂。舉一個簡單的例子,假設一個投資被均分給兩家基金A和B。兩家基金都收取2%+20%的費用。在第一年,基金A的回報率是20%,而B的回報率是-10%。投資者的平均回報率是0.5×20%+0.5×(-10%)=5%。給基金A繳納的費用是2%+0.2×(20%-2%)或5.6%。給基金B繳納的費用是2%。給基金的平均費用佔整個投資的3.8%。投資者實際只得到1.2%的回報率。如果2%+20%的收費只作用於整體5%的回報,那麼投資者得到的實際回報會加倍。
如果涉及對衝基金的基金,還會有一層額外的收費,那麼投資者實際的回報會更少。對衝基金的基金的一個典型收費標準為管理資產數量的1%以及所投資的對衝基金的淨盈利(除去獎勵和管理費用)的10%。假定一個對衝基金的基金將其資金在10只對衝基金之間進行分配,所有的對衝基金收費標準為“2%+20%”,而基金的基金收費為“1%+10%”,聽起來投資者付費為“3%+30%”,但實際上費用遠比這還要高。假定10只對衝基金中有5只的回報為-40%,另外5只為40%。對每隻盈利的基金,要支付38%的20%即7.6%的獎勵費用。因此,總的獎勵費用為總投資的3.8%。另外,還有交給對衝基金2%的年費和交給基金的基金1%的年費。投資者的回報是-6.8%(在付費後,標的資產數量比付費前減少6.8%)。
4.5.2 對衝基金經理的激勵
對衝基金經理的收費形式為這些經理提供了取得盈利的動機,但同時也鼓勵了基金經理承擔更大的風險。基金經理實際上持有關於基金內資產的看漲期權。眾所周知,當標的資產價格的波動率增大時,看漲期權價值也會增大。這意味著對衝基金經理可以通過承擔增加基金資產波動性的風險來增加期權的價值。當臨近績效考評週期的末尾但當期回報率是負數或很低時,他們尤其有動機這麼做。
假定一個對衝基金面臨一個投資機會,其中有0.4的概率投資回報率達60%,而有0.6的概率回報損失達60%,對衝基金的收費為“2%+20%”,投資的預期回報率為0.4×60%+0.6×(-60%),即-12%。
雖然這一預期回報很糟糕,但基金經理仍然可能會接受這種投資。如果投資回報為60%盈利,對衝基金收費為2%+0.2×58%,即13.6%;如果投資回報為60%損失,對衝基金收費為2%,因此,基金經理的預期收費為0.4×13.6%+0.6×2%=6.64%。
即收費為管理資產的6.64%,預期管理費為2%,預期績效費為4.64%。
對於投資者而言,預期回報率為0.4×(0.8×58%)+0.6×(-60%-2%),即-18.64%。
表4-4是對以上例子的總結,該例顯示,即使在預期回報率為負的情況下,對衝基金的收費結構仍然會促成基金經理承擔高風險。我們可以採用門檻回報率、高潮位標記條款以及分紅追回條款來減少基金經理承擔高風險的傾向。但是對投資者而言,這些條款並不像聽起來那麼有效,其中一個原因是投資者必須持續地將資金投放到對衝基金上才能享受其好處。另外一點是當對衝基金的損失累積太大後,對衝基金經理很可能就此從對衝基金隱身而退,然後再開始一家新的基金。
表4-4 高風險投資回報
注:回報率為60%及-60%所對應的概率分別為0.4和0.6,對衝基金的收費為“2%+20%”。
我們這裡所說的動機是有據可查的。你可以想象一下,如果你是對衝基金Amaranth(希臘語為“不凋花”的意思)的投資者,你會有何感想。Amaranth的一個交易員Brian Hunter喜歡對天然氣價格下大賭注,2006年以前,他的賭注往往是對的,因此他也被認為是明星交易員。據說包括分紅在內,他的工資在2005年高達1億美元。2006年,他的賭注終於出現了錯誤,因此賬下資產數量達90億美元的Amaranth損失了65億美元(這一數量比另一個對衝基金,即長期資本管理公司(Long Term Capital Management)在1998年的損失還要大)。Brian Hunter並沒有交回他以前的分紅所得,他只是離開了Amaranth,並隨之試圖再建立一個自己的對衝基金。
有趣的是,從理論上講,兩個人串通起來可以採用以下形式創立一個生錢機器(money machine),第一個人可以創立一個對衝基金,並且進行一些高風險(並且是祕密)投資,另外一個人也創立一個對衝基金,但其投資策略完全與第一個人相反。例如,第一個對衝基金買入了100萬美元的白銀,第二個對衝基金應該賣空相同數量的白銀。在創立基金時,這兩個人可以簽訂合約來共享績效費,兩個對衝基金中的一個(但我們並不知道是哪一個)的收益一定會很好,並且掙得了一個較好的績效費,另外一個的表現會很差,因此不能掙得績效費。只要這兩個對衝基金可以找到投資者,它們就有了一個生錢機器。
4.5.3 機構經紀人
機構經紀人是為對衝基金提供服務的銀行。通常來講,對衝基金在剛剛創立時,會選擇一家特定的銀行作為其機構經紀人。這家銀行將會處理對衝基金的交易(可以是與機構經紀人本身之間進行的交易,也可是與其他經紀交易商進行的交易),進行淨值結算決定對衝基金是否還要補充抵押品;當對衝基金想進入賣空交易時,幫助對衝基金借入證券;為對衝基金提供現金管理和投資組合報告服務;為對衝基金提供貸款服務等。有時機構經紀人會提供風險管理及諮詢服務,並向對衝基金介紹潛在投資者。機構經紀人對對衝基金的投資組合十分了解,並一般會對投資組合進行壓力測試以決定它準備給基金提供多少槓桿。
雖然對衝基金不受監管的嚴格制約,但它們受制於機構經紀人的質詢。對對衝基金來說,機構經紀人往往是最主要的借貸資金來源。機構經紀人會監督對衝基金承擔的風險,並決定對衝基金可採用多大的槓桿。通常來說,對衝基金借貸時,要向機構經紀人繳納抵押品。當對衝基金交易產生損失時,需要繳納的抵押品價值會更大;如果對衝基金拿不出足夠多的抵押品,那麼它就別無選擇,只能將交易平倉。如果一個交易在長遠來講會盈利,而在短期會虧損,那麼對衝基金應該做出謹慎決策。比如,某家對衝基金可能認為目前市場上的信用價差已經太高,因此在此交易中使用了高槓杆,決定買入BBB級債券,並且賣空政府債券。但是,信用價差在降低之前有可能會進一步升高,這時對衝基金可能沒有足夠的抵押品,它只能被迫將交易平倉並承擔巨大的損失。
當對衝基金的規模變大後,對衝基金往往會採用多個機構經紀人,這意味著沒有一家銀行可以看到對衝基金的全部交易,也不會完全知曉對衝基金投資組合的構成。與多家機構經紀進行交易給對衝基金在談判中帶來更多的發言權,這可以幫助對衝基金降低其交易費用。高盛集團和摩根士丹利以及其他大銀行,均為對衝基金提供機構經紀服務,這些銀行發現經紀服務確實可以給自身帶來豐厚的盈利。[2]
[1] 來自奧馬哈(Omaha)的著名的巴菲特也可以被認為是對衝基金的先驅。1956年,他創立了巴菲特有限合夥人公司,當時公司共有7位合夥人,每人投股100100美元。巴菲特向每個合夥人收取的手續費是超出25%門檻回報率以上的盈利的25%。巴菲特專長於特殊情形投資、併購套利、公司分割獨立(spin-off),以及不良債權投資,巴菲特的平均回報率是每年29.5%。巴菲特的合夥人公司在1969年解散,之後巴菲特成立了伯克希爾-哈撒韋公司(持股公司,並非對衝基金)。
[2] 銀行向對衝基金提供貸款時會承擔一定的風險,反之對衝基金選定某家銀行作為機構經紀人時也會承擔一定的風險。許多對衝基金選定雷曼兄弟為機構經紀人,當雷曼兄弟在2008年破產時,對衝基金發現不能收回自身的資產。
4.6 對衝基金的策略
在本節中我們將討論對衝基金所採用的某些策略,我們這裡採用的分類與道瓊斯瑞信(Dow Jones Credit Suisse)所給出的分類相似。道瓊斯瑞信提供跟蹤對衝基金表現的指數。並不是所有的對衝基金均可以按這種形式分類,有些對衝基金採用我們討論策略的若干種,有些對衝基金的策略在這裡根本就沒有列舉(例如,一些對衝基金專長於氣候衍生產品)。
4.6.1 股票多空型
如在前面所述,多空股票(long/short equity)策略曾被對衝基金的先驅瓊斯採用。這種策略仍然是對衝基金策略中最為流行的一種。在該策略中,對衝基金經理首先識別一組價格被市場低估的股票和一組價格被市場高估的股票,然後基金經理會持有第一組股票的多頭並持有第二組股票的空頭。通常來講,對衝基金必須向其機構經紀人每年支出1%的費用,這一費用是租用在空頭頭寸中借入的股票的租金(見第5章關於空頭的討論)。
多空股票策略的關鍵在於股票的選取。如果在交易策略中,價格被高估以及低估的股票選取得很好,那麼該交易策略無論是在牛市還是在熊市中均能產生好的收益。對衝基金經理常常會非常重視還沒有受到股票分析員關注的小股票,並進行大量的基本面分析(fundamental analysis)。這種分析法的先驅是本傑明·格雷厄姆。對衝基金經理可能會偏向於一個淨多頭頭寸,即做空的數量比做多的數量稍少;或者偏向於一個淨空頭頭寸,即做多的數量比做空的數量稍少。瓊斯在其成功運用該策略中,持有一個淨多頭頭寸。
一個股票市場中性(equity-market-neutral)對衝基金採用多空股票策略,但沒有任何淨多頭或淨空頭。一個絕對額中性(dollar-neutral)對衝基金是一個股票市場中性基金,其中以貨幣量為計的多頭頭寸數量等於以貨幣量為計的空頭頭寸數量。一個beta中性(beta-neutral)對衝基金是一個更為複雜的股票市場中性基金,其做多的股票的加權平均beta等於其做空的股票的加權平均beta。所以整個投資組合的整體beta為0。如果資本資產定價模型成立,那麼beta中性對衝基金對市場變動不具有敏感性。有時beta中性交易可以利用股指期貨的多頭或空頭來實現。
有時股票市場中性基金會走得更進一步,某些對衝基金會保持一個行業中性(sector neutrality),其中交易組合中的多/空頭頭寸以行業為基準。還有一些基金保持因子中性(factor neutrality),其中交易組合對於某個因子,例如石油價格或利率水平或通貨膨脹率為中性。
4.6.2 專營賣空型
專營賣空(dedicated short)的基金經理會花其全部精力專門尋找那些價格被高估的公司,並賣空這些公司的股票。他們的交易策略是利用經紀人和股票分析員輕易不願發出變賣建議(sell recommendation)這一特點,雖然我們可以很合理地認為在任意時刻市場上價格被高估的公司數量與被低估的公司數量是大致相當的。一般來說,專營賣空的基金經理所選擇的公司往往是那些財務狀態較弱、經常更換審計公司、延遲向SEC提供財務報告、行業產能過剩、被起訴或試圖會讓賣空其股票的投資者保持沉默的那些公司。
4.6.3 不良證券型
信用級別為BB級或更低的債券被稱為“非投資級”(non-investment grade)或“垃圾債券”(junk bond)。信用級別為CCC級的債券被稱為不良(distressed)債券,信用級別為D級的債券是處於違約狀態的債券。一般來講,不良債券的價格遠低於其票面價值(par value),不良債券的回報率可能會比政府債券回報率高1000個基點(10%)以上,當然投資者只有在這些債券仍能支付利率和本金的前提下才能掙得高回報率。
專長於不良債券的基金經理會謹慎地計算對於不同情形以及在不同的概率情況下,債券的公允價格。不良債券通常不能被賣空,因此基金經理會努力在市場上尋找價格被低估的不良債券。破產過程通常會導致公司的重組或清算,基金經理要了解司法系統的運作,要通曉公司解體時資產支付的優先權,要懂得如何估計回收率,並預測公司管理層的應對措施等。
有些基金經理是被動投資者,他們的策略是在不良債券價格很低時買入債券,然後等待;有些對衝基金採用主動投資方式,他們可能會買入大量市場上既存的不良債券,然後再設法去影響公司今後的重組建議。在美國破產法第11章關於重組的規定中,對於一個重組計劃,只有在超過每個層級債權人(class of claim)的2/3多數贊成的情況下,重組計劃才能被批准。在公司重組時,股權的價格常常會變得一文不值,而沒有償付的債券會轉換成新的股權。有時,一個主動型基金經理的目標是買入超過1/3的債券,取得對目標公司的控制權,並設法從中盈利。
4.6.4 併購套利型
併購套利(merger arbitrage)涉及在兼併和收購消息公佈後進行交易,同時寄希望於併購交易的達成。市場上有兩種併購形式:現金交易和換股交易。
首先考慮現金交易。假定公司A準備以每股30美元的價格買入公司B的所有股份,公司B的股價在消息公佈時為每股20美元。消息一經公佈,其股價可能會漲到28美元。股價不會一下子漲至30美元,原因如下:①併購交易不一定達成;②市場需要一定的時間才能完全理解併購交易的影響。併購套利型對衝基金可能以每股28美元的價格買入公司B的股票,然後等待。如果收購協議確實達成了,那麼公司B股票變為30美元,對衝基金盈利為每股2美元;如果併購協議達成的價格超過30美元,那麼對衝基金的盈利會更高。但是,如果併購協議沒有達成,對衝基金將蒙受損失。
接下來考慮換股交易的情形。假定公司A宣佈將以自身的1股股票換取4股公司B的股票。假定在消息公佈前公司B的股票價格為公司A的股票價格的15%。在消息公佈後,公司B的股票價格可能會漲至公司A的22%。一個併購套利型對衝基金可能會買入一定數量公司B的股票,同時賣空等於這一數量25%的公司A的股票。如果換股比例確實按宣佈的消息順利執行,或者換股比率對公司B更有利,那麼這種交易策略會給對衝基金掙得盈利。
併購套利型基金可以產生穩健但並不令人吃驚的回報。我們應該區分併購套利與伊凡·博斯基(Ivan Boesky)的行為以及其他在併購消息公佈之前進行的內部交易行為。[1]內部交易是違法行為,因內部交易,伊凡·博斯基被判3年徒刑,並且被罰款1億美元。
4.6.5 可轉換債券套利型
可轉換債券是指那些在將來某個時刻可以轉化為債券發行人股票的債券,並且指明瞭根據可能兌換的時間,每份債券可換取等額股票數量。債券發行人一般有權在將來,在一定條件下買回債券(比如,以指定價格贖回債券)。通常,債券發行人會以贖回債券的形式來強迫債券持有者將債券轉換為股票(如果債券不被贖回,債券持有者會盡量延遲將債券轉換為股票的時間)。
可轉換債券套利型對衝基金一般都研發了複雜模型對可轉換債券進行定價。可轉換債券的價格以某種複雜的方式取決於以下變量:股票價格、股票波動率、利率水平以及發行人的違約率等。許多可轉換證券的交易價格低於其公允價格。對衝基金經理往往會買入這樣的證券,並以賣空股票的形式來對衝風險(這是第7章討論的delta對衝的一種應用)。基金經理可以通過賣空債券發行公司的其他非轉換債券的形式來對衝利率和違約風險。另外一種做法是利用利率期貨、資產互換或信用違約互換等產品來對衝風險。
4.6.6 固定收益套利型
進行固定收益產品交易的最基本工具是零息收益率曲線。該曲線可以依據本書附錄B中所描述的方法進行構造。對衝基金可以採用的一種固定收益產品策略是相對價值(relative value)策略。在該策略中,對衝基金經理買入那些由收益曲線表明被市場低估的債券,同時賣出那些由收益曲線表明被市場高估的債券。市場中性(market neutral)策略與相對價值策略十分相似,唯一不同之處是市場中性策略會保證基金對利率的變動沒有風險敞口。
有些固定收益型對衝基金採用一些方向性的投資策略,即它們的持倉量建立在某些利率的利差或者利率水平本身會朝某個特定的方向變動這一假設上。這些基金一般具有很強的槓桿特性,因此要支付抵押品。因此它們所面臨的風險是:長期來講,它們的決策是正確的,但短期市場變動觸發了損失,導致它們不能支付足夠的抵押品,並因此不得不將交易平倉而蒙受損失。這種風險恰恰發生在對衝基金長期資本管理公司身上(見業界事例19-1)。
4.6.7 新興市場型
新興市場型對衝基金專長於對發展中國家的投資。有些基金注重於股票投資,它們從市場中篩選那些價格被高估和低估的股票。基金經理會通過到發展中國家進行商務旅行、出席會議、與分析員會晤、與公司管理人員討論並採用僱用諮詢人員的方式取得信息。一般他們會選擇在當地交易所上市的股票進行投資,但有時他們也會利用美國存託憑證(American Depository Receipts,ADR)的形式來進行投資。ADR是在美國發行並在美國交易所交易的憑證,這些憑證由外國公司的股票作為支持。ADR可能比外國公司的股票的流動性更好,交易費用更低。有時ADR與標的資產價格會有差別,這因此也會產生套利機會。
另外一種新興市場的投資產品是發展中國家發行的債券。歐洲債券(Eurobond)是由一個國家發行,以美元或歐元硬通貨計價的債券;布雷迪債券(Brady bond)是由美國財政部支持的以美元計價的債券;當地貨幣債券(local currency bond)是由當地貨幣計價的債券。對衝基金會投資於以上3種債券。無論當地貨幣債券或歐洲債券均具有風險。俄羅斯、阿根廷、巴西及委內瑞拉曾多次對其發行的債券違約。
4.6.8 全球宏觀型
全球宏觀型(global macro)對衝基金採用超級明星管理人喬治·索羅斯和朱利安·羅伯遜等採用的交易策略,其基金經理進行的交易反映了全球經濟的走向。他們試圖尋求那些市場因某種原因脫離其平衡點的情形,並且對經濟狀態會返回平衡點而下賭注。他們經常會對利率及匯率市場下賭。喬治·索羅斯的量子基金(Quantum Fund)在1992年的一個策略是對英國英鎊價值走低進行下賭,這為基金帶來了10億美元的盈利。最近,對衝基金對於美國的國際收支赤字會造成美元貶值下了賭注(賭注結果有好有壞)。全球宏觀型對衝基金的重要問題是他們並不知道經濟平衡會在何時恢復。因某種原因,世界市場不平衡狀態可能持續很長時間。
4.6.9 管理期貨型
對衝基金經理利用管理期貨(managed futures)策略來預測將來大宗商品價格的變動。有些基金依賴於基金經理的判斷;有些基金利用計算機程序來進行交易;有些基金的交易是基於技術分析(technical analysis),技術分析是指用過去的價格變動規律來預測將來的價格;另外一些基金採用基本面分析(fundamental analysis)來決定交易決策,基本面分析是從經濟、政治或其他相關因素來確定大宗商品價格。
當利用技術分析時,交易策略要首先應用於歷史數據,這種檢測被稱為回溯測試(back-testing)。如果(往往是這樣)某個交易規則是基於歷史數據歸納得出,那麼分析員必須進行樣本外檢驗(即將策略應用於那些沒有用於產生規則的數據)。分析員應該認識到數據挖掘的潛在危險性。分析員可能開發出了成千上萬個不同的交易規則,並用歷史數據來檢驗這些規則。可能是由於運氣,一些規則的表現會很好,但不意味著這些規則在將來表現就一定會好。
[1] 邁克爾·道格拉斯(Michael Douglas)在得獎影片《華爾街》(Wall Street)所扮演的角色戈登·蓋柯(Gordon Gekko)的原型就是伊凡·博斯基。
4.7 對衝基金的收益
與評估共同基金的收益相比,對對衝基金的收益進行評估不是件容易的事情。市場上並沒有包含所有對衝基金信息的數據庫。研究人員可以取得TASS對衝基金數據庫,但參與這一數據庫與否取決於對衝基金自身的意願。小的對衝基金或表現差的對衝基金不願意公佈其業績,因此數據庫中也就不包括這部分數據。當對衝基金公佈業績時,這些數據也會用來彌補這個對衝基金以前的空白數據,而這會造成數據偏差。如上所述,對衝基金一般會在收益好的情況下才開始報告收益。在剔除數據偏差後,有些研究人員發現對衝基金的實際回報並不比共同基金更好,特別是考慮到管理費以後。
有人認為,對衝基金可以改善養老基金的風險-回報替代關係。這是因為養老基金不能(或者是因為自身的選擇不願)進行賣空交易、槓桿化、衍生產品投資或從事其他複雜的交易,而這些交易往往被對衝基金採用。投資對衝基金(在付費條件下)是養老基金直接擴大其投資範圍的一種形式,這麼做也許會改善有效邊界的結構(見第1.2節關於有效邊界的討論)。
我們常看到有些對衝基金在某些年會給出令人瞠目的回報,然後突然香消玉殞。長期資本管理公司在1994年、1995年、1996年、1997年給出的回報率分別是28%、59%、57%、17%,而在1998年,該對衝基金基本損失了其全部資本金。有人指出對衝基金的回報就如同承約一個虛值期權(賣出一個虛值期權)。在大多數情況下,這些期權不會帶來損失,但有時這一期權也會觸發巨大損失。
這看起來似乎對對衝基金不太公平。對衝基金的支持者認為對衝基金確實可以找到盈利的機會,而許多其他投資者沒有資源及能力做到這一點。他們可以舉出一些頂級基金經理的例子,說明這些人確實可以找到好的投資機會。
在2008年以前,對衝基金的表現確實很好。2008年,雖然對衝基金總體上是虧損的,但表現還是超過了標準普爾500指數。但在2009~2016年,標準普爾500指數的表現遠遠超過一般的對衝基金。[1]巴克萊對衝基金指數是一個剔除了費用(可能有些前面提到的偏差)後的資產加權回報率指數。表4-5比較了該指數的回報與標準普爾500指數的總回報。
表4-5 對衝基金表現
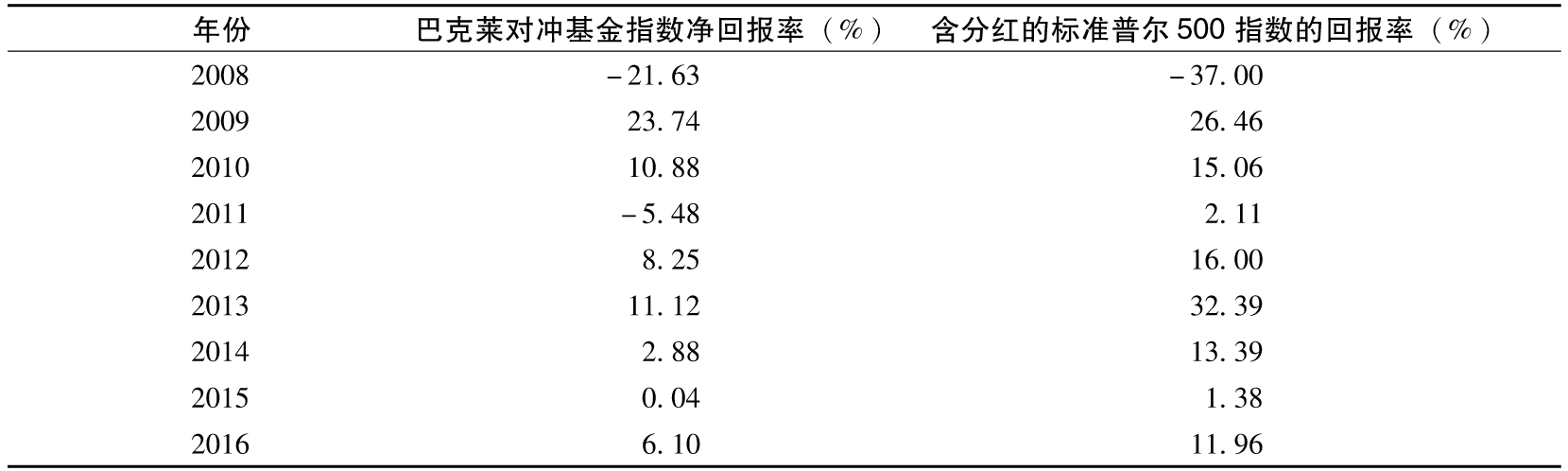
[1] 需要說明的是,對衝基金的beta通常小於1(例如,多空股票型基金通常被設計成beta接近0),所以在市場表現非常好的時段,回報率低於標準普爾500指數並不一定意味著投資組合的alpha是負的。
小結
共同基金和交易所交易基金給小投資者提供了分散風險的途徑。有證明顯示,整體來講,主動型共同基金的表現沒有好過市場,這造成了許多投資者將資金投放於那些跟蹤市場指數,例如標準普爾500指數的基金。
許多共同基金為開放型,即隨著投資者買入(賣出)份額,基金的份額數量會增大(減小)。開放式基金在每個工作日下午4點計算其份額的淨資產價值,該價值被用於在4點前24小時內買入和賣出訂單的價格。封閉式基金的份額固定,其交易方式類似於其他企業的股票交易。
交易所交易基金(ETF)是對開放式基金和封閉式基金的一種替代,這種基金十分流行。在任意一個時刻,基金的份額為已知,大型機構投資者可以在任意時刻將持有基金的份額轉換為基金中的資產,這可以保證ETF的份額(不同於封閉式資金)的交易價格十分接近於資金的淨資產價值。ETF的份額可以被隨時交易(而不僅僅是在下午4點),ETF的份額可以被賣空(這不同於開放式基金的份額)。
對衝基金是為了迎合大型投資者的需求。相比共同基金,對衝基金所受的監管制約很少。對衝基金的收費遠高於共同基金。典型的收費是“2%+20%”,這意味著對衝基金每年會將管理資產規模的2%,以及基金盈利的20%(如果有的話)作為管理費。對衝基金經理持有自己管理的基金中資產的看漲期權,因此,對衝基金經理可能會有增大管理資產的風險的動機。
對衝基金所採用的交易策略包括多空股票、專營賣空、不良證券、併購套利、可轉換債券套利、固定收益套利、新興市場、全球宏觀和管理期貨。在扣除管理費以後,對衝基金是否比指數基金提供更好的風險和回報的平衡仍是一個有爭議的問題。對衝基金可能會在連續幾年提供良好的回報後,突然給投資者帶來毀滅性的損失。
延伸閱讀

練習題
4.1 開放式基金與封閉式基金的區別是什麼?
4.2 一個開放式基金的淨資產價值是如何計算的?在一天什麼時候計算?
4.3 一個投資者在2018年1月1日,以每份30美元的價格買入了100份共同基金,基金在2018年及2019年的資本收益分別為每股3美元和每股1美元,假定沒有任何股息收入。投資者在2020年以每股32美元的價格賣出了基金。投資者在2018年、2019年和2020年的資本收益及虧損分別為多少?
4.4 什麼是指數基金?如何生成指數基金?
4.5 什麼是對衝基金的(a)前端收費和(b)後端收費?
4.6 解釋一個跟蹤標準普爾500指數的ETF的運作方式。與以下基金比較,ETF的優勢是什麼?(a)開放式對衝基金;(b)封閉式對衝基金。
4.7 一列數字的幾何平均與算術平均的區別是什麼?在計算共同基金回報時,我們應該用哪一種平均方式?
4.8 解釋以下詞彙的含義:(a)延遲交易;(b)擇時交易;(c)搶先交易;(d)定向經紀。
4.9 給出那些限制共同基金,但不能限制對衝基金的規則。
4.10 “如果70%的可轉換證券交易與對衝基金有關,我預計這種交易的盈利會降低。”討論這個觀點。
4.11 解釋與對衝基金績效費有關的條約的含義:門檻回報率、高潮位標記條款、分紅追回條款。
4.12 一個對衝基金收費為“2%+20%”,投資者期望在付費後回報率仍能達到20%,對衝基金在收到投資者的付費之前的投資回報率最小為多少才能滿足投資者的要求?假定獎勵費用按扣除資產管理費後的淨回報計算。
4.13 “對對衝基金而言,長期盈利十分重要,而短期的盈虧並不重要。”討論這一觀點。
4.14 “對衝基金的風險由其機構經紀人來掌控。”討論這一觀點。
作業題
4.15 一個投資者在2018年1月1日,以每份50美元的價格買入了100份共同基金,基金在2018年及2019年得到的股息分別為每股2美元和每股3美元,股息被再次投資於基金。基金在2018年及2019年的資本收益分別為每股5美元和每股3美元,投資者在2020年以每股59美元的價格賣出了基金。解釋投資者如何交稅。
4.16 一個共同基金的高回報之年馬上緊跟一個低迴報之年,其每年回報率為+8%、-8%、+12%、-12%,投資者4年的整體回報為多少?
4.17 一個基金的基金將其資金投資於5個對衝基金,5個對衝基金在某年的回報率分別為-5%、1%、10%、15%和20%。基金的基金管理費為“1%+10%”,每個對衝基金的管理費為“2%+20%”。對衝基金的獎勵費按扣除管理費後的淨回報計算;基金的基金的獎勵費按所投資的對衝基金的淨平均回報(扣除對衝基金的管理費和獎勵費)扣除自身的管理費後計算。投資的整體回報是多少?這些回報將如何在基金的基金、對衝基金以及投資者中分配?
4.18 一個對衝基金收費為“2%+20%”,一個養老基金將資產投資於此對衝基金。畫出養老基金回報作為對衝基金回報的函數的圖形。
第5章
金融市場上的交易
金融機構交易大量不同類型的金融產品,交易的目的多種多樣,有些交易是為了滿足其客戶的需求,有些是為了管理自身的風險,有些是為了尋求套利機會,還有一些是為了反映自身對市場走向的預測(第16章中將要介紹的《多德-弗蘭克法案》中的沃爾克法則禁止美國金融機構出於最後兩個目的進行交易)。
我們將在今後的章節中討論金融機構如何管理自身的交易風險。這一章的目的是介紹用於交易的產品、描述交易的過程以及產品的使用方式,以便為以後的討論奠定基礎。在介紹不同的交易所交易產品時,我們將討論交易所保證金的使用。保證金是交易所要求交易者擔保的抵押品(通常以現金形式),以保證他們履行義務。在後續章節中你將看到,保證金已經成為場外交易市場的一個重要特徵。
5.1 市場
金融產品交易市場可分成兩類:第一類市場為交易所交易市場(exchange traded market),第二類為場外交易市場(over-the-counter market,OTC market)。
5.1.1 交易所交易市場
在交易所交易金融產品已經有非常悠久的歷史。有些交易所,例如紐約證券交易所(NYSE,www.nyse.com),主要進行股票交易,而在其他的交易所,例如芝加哥證券交易所(CBOT,www.cbot.com)及芝加哥期權交易所(CBOE,www.cboe.com),主要進行期貨以及期權等衍生產品交易。
交易所的主要職責是定義交易合約、組織交易並使得交易雙方的利益同時得到保護。傳統上交易雙方在交易所相見並通過複雜的手勢系統達成交易。這種交易方式被稱為公開叫價(open outcry)交易。而現在大部分交易所已經全部或部分採用電子交易系統(electronic trading)代替了公開叫價。交易員通過鍵盤將所期望的交易輸入系統,由計算機來撮合買方和賣方。並不是所有的人都認為電子交易系統更為可取。同傳統形式相比,電子交易在體力上更為輕鬆,但從某種意義上講,交易變得不像以前那麼有趣了,交易員也沒有機會通過觀察其他交易員的行為和肢體語言來預測市場的短期走向。
有時做市商(market maker)會協助交易的達成。做市商可以是個人或機構交易者,他們通常隨時既提供買入報價(bid price),又提供賣出報價(offer price)。例如,當市場上的一個交易者向做市商索要關於某股票的報價時,做市商給出“以30.30美元買入,以30.35美元賣出”的報價,這是指做市商願意以每股30.30美元的價格買入該股票,同時願意以每股30.35美元的價格賣出該股票。在提供報價時,做市商並不知道詢價者是想買入還是賣出股票。交易所一般會指定做市商可以提供的買入-賣出的最大差價。做市商可以從差價中取得利潤,但他們必須謹慎地管理所持有的頭寸,以控制自身對市場價格變化的風險敞口。
5.1.2 場外交易市場
場外交易市場是由為金融機構和大企業工作的交易員以及基金經理構成的一個龐大的網絡。在場外交易市場上交易的產品很多,例如債券、外匯和衍生產品。銀行是場外交易市場的重要參與者,並常常扮演一些常規金融產品做市商的角色。例如,為了幫助大型企業進行大宗交易,許多銀行願意提供外匯的買入價和賣出價。
場外交易的最大優點是合約的內容不受交易所的限制,市場上的交易雙方可以根據自己的需要來構築合約。場外交易市場交易的電話通常是被錄音的。當交易雙方產生分歧時,電話錄音可以被用來解決爭端。場外交易市場交易的數額往往會遠遠大於交易所內的交易。
5.2 清算所
交易所交易的衍生產品合約由清算所進行管理。清算所由一定數量的會員構成,來自非會員的交易需要經由會員做通道。會員需要向由清算所管理的保證基金繳納費用。
假設在某交易所市場上,交易者X同意向交易者Y出售一個期貨合約。實際上,清算所會介於二者之間,交易者X將合約賣給清算所,而交易者Y從清算所購入該合約。這樣做的優點是交易者X不必擔心交易者Y的信用狀況,反之亦然。兩位交易者都只同清算所打交道。如果其中一個交易者已經是清算所成員,那他可以直接與清算所進行交易;如果不是清算所成員,那麼交易需要通過其他成員進行。
如果一位交易者的交易未來可能會產生損失(如該交易者進行了期貨或期權交易),那麼清算所會要求交易者提供現金或有價證券作為抵押品。這些抵押品被稱作保證金(margin)。如果沒有保證金,清算所就會承擔市場對交易者的不利變動以及由此引發的交易者違約的風險。清算所設定的保證金要求通常要有99%的把握確保此類情況不會發生。如果此類情況確實發生了,保證金會被用來償付。因此,清算所違約的概率極低。
長期以來,部分場外交易也通過清算所進行,這些清算所被稱作共同對手方(或中央對手方,central counterparty,CCP)。CCP的角色和交易所場內的清算所類似。它介於交易的雙方之間,從而隔離交易雙方對對手的信用風險敞口。CCP也由會員構成,會員同樣需要繳納保證基金份額,並提供交易保證金。現在,監管部門要求金融機構之間的標準化衍生工具必須通過CCP清算。我們將在第17章中對此做進一步的討論。
5.3 資產的多頭和空頭
最簡單的交易是以現金買入資產,或賣出資產來取得現金,例如:
(1)買入100股IBM股票;
(2)用100萬英鎊兌換美元;
(3)買入1 000盎司[1]黃金;
(4)賣出價值100萬美元的通用汽車公司發行的債券。
以上的第一個交易往往會發生在交易所內,而另外其他3個交易可能是場外交易。這些交易被稱為現貨交易(spot trades),因為這些交易往往會觸發資產的即時(on the spot)交付。
當投資者想通過其經紀人買入某項資產時,投資者通常可以通過交納保證金向經紀人借入資產成本的一半買入資產,並以該資產作為抵押物放在經紀人手中,即保證金買入(buying on margin)。經紀人面臨著該資產價格劇烈下跌的風險。因此,經紀人需要監控保證金賬戶的餘額。這是投資者支付的購買價格的一部分,根據資產的收益或損失進行調整。如果保證金賬戶的餘額低於資產價值的25%,那麼投資者必須補充保證金,將保證金餘額恢復到之前的水平。假設一名投資者以保證金購買的方式買入1 000股每股120美元的股票,該投資者必須支付一半的成本,即60 000美元。如果股價跌至78美元,就會損失42 000美元,保證金賬戶的餘額就變成18 000美元。保證金比例變成18 000/78 000,即23.1%,投資者必須補充1 500美元到保證金賬戶,使保證金賬戶的餘額達到78 000美元的25%。如果投資者不能及時補充保證金,經紀人就會對該資產進行平倉。
資產賣空交易
在某些市場,你可以賣出現在你並不擁有,而在今後有意買回的產品。此類交易被稱為資產賣空(借賣),我們下面以賣空股票為例來說明如何進行賣空交易。
假定某投資者想通過其經紀人來賣空500股IBM股票。經紀人往往會通過借入某位客戶的股票,並將股票在交易所進行變賣來執行投資者的指令(借入股票可能要支付一定的費用)。投資者可以按其意願,將賣空交易持有到任意時刻,其前提是經紀人可以隨時借到股票。在今後的某一時刻,投資者可以買入500股IBM股票對自己的賣空交易進行平倉。這些買入的股票用於償還在此之前借入的股票。當股票價格下跌時,投資者會有所盈利;當股票價格上漲時,投資者會有所損失。在賣空交易平倉之前,如果經紀人不能再借入股票,投資者就會受到賣空擠壓(short-squeezed)。此時,無論投資者是否願意,都必須對其交易進行平倉,也就是說,此時投資者必須馬上償還其借入的股票。
在賣空交易中,賣空投資者必須向經紀人支付所有賣空資產的收入,例如股票的股息及債券的券息等。這些收入是在一般情況下賣空資產的應得收入,經紀人會將這些收入轉入股票借出方的賬戶。假設某投資者在4月股價為120美元時,進入500股賣空交易。在7月當股價為100美元時,對交易進行平倉。假定股票在5月支付了每股1美元股息。在4月交易最初,投資者收到500×120=60 000美元。在5月,因為股息,投資者要支付500×1=500美元,在7月交易平倉時,投資者要支付500×100=50 000美元。投資者的淨收益為
60 000-500-50 000=9 500(美元)
在表5-1中,我們詳細展示了賣空交易的現金流,由表5-1我們可以看到,在賣空交易中投資者的現金流就如同在4月買入並在7月賣出的一筆正常股票交易的現金流的鏡像反射(假設借入資產無須支付任何費用)。
表5-1 買入以及賣空股票所對應的現金流

在賣空交易中,賣空方一定要在經紀人那裡開一個保證金賬戶,這是為了保證在股票價格上漲時投資者不會違約。我們將在本章後面的內容中討論保證金賬戶。
關於賣空的規則經常改變,美國SEC在2007年7月取消了賣空交易中的上漲拋空規則(uptick rule),但在2009年4月重新引入了這一規則(在這一規則下,只有證券價格在最近一段時間呈上升狀態時,才允許賣空)。2008年9月19日,為了阻止銀行股票價格大幅下跌,SEC對799家金融公司的股票暫時實施了禁止賣空的規定,這一規定與在前一天英國金融服務局(Financial Services Authority,FSA)所發佈的關於禁止賣空的規定十分相似。
[1] 1盎司=28.35克。——譯者注
5.4 衍生產品市場
衍生產品是指價格取決於(或來源於)其他更基礎的市場變量的產品,例如,股票期權是價格取決於股票價格的一種衍生產品。
衍生產品在交易所和場外交易市場均進行交易,兩個市場的規模都很大。雖然這兩個市場的統計結果不具有完全可比性,但很顯然,場外交易市場規模遠大於交易所市場。國際清算銀行(Bank of International Settlement,www.bis.org)從1998年起開始統計這一數據。圖5-1比較了:①1998年6月~2016年12月場外交易市場交易的標的資產面值總和;②同一時間段的交易所合約中標的資產的總價值。從這些數據中我們看到,截至2016年12月,場外交易市場的交易量為482.9萬億美元,而交易所市場的交易量為67.2萬億美元。[1]圖5-1顯示,場外市場在2007年之前一直保持快速增長,但此後幾乎沒有淨增長。2014年和2015年市場下滑在很大程度上是因為受壓。這是兩個或兩個以上的交易對手相互重組交易而導致本金減少的結果。

圖5-1 1998~2016年場外交易和交易所交易衍生產品市場的規模
在解釋這些數據時,我們應該認識到場外交易市場交易產品的面值與其價值並不是一回事。例如,某一場外交易市場交易合約為1年期,以某一指定匯率以英鎊買入1億美元,這一交易的總面值為1億美元。但是這一交易的價值可能只有100萬美元。國際清算銀行估計截至2017年6月,所有場外交易市場合約的市場總價值大概為12.7萬億美元。[2]
[1] 當衍生產品通過中央對手方清算時,如第17章所描述的,會產生兩個相互抵消的交易合約,因此會誇大場外交易市場的實際規模。
[2] 一個對於某一方價值為100萬美元,而對另一方價值為-100萬美元的交易的總價值被計為100萬美元。
5.5 普通衍生產品
在這一節中,我們將討論衍生產品市場的標準或交易最普遍的合約,這些合約被稱為普通(plain vanilla)衍生產品。
5.5.1 遠期合約
遠期合約約定合約的買方在將來某一時刻以一個固定價格買入某種資產。遠期合約交易是一種場外交易,在遠期合約中,同意在將來某一時刻以某一約定價格買入資產的一方稱為多頭寸方(long position),同意在將來某一時刻以同一約定價格賣出資產的一方稱為空頭寸方(short position)。
外匯遠期合約在市場上非常流行,表5-2顯示2017年6月9日某跨國銀行給出的英鎊(GBP)及美元(USD)匯率的買入價及賣出價,這裡的匯率價格是指每英鎊所對應的美元價值。表中的第1行數字顯示該銀行準備以每英鎊1.273 2美元的價格在現貨市場買入英鎊,同時這家銀行也準備以每英鎊1.273 6美元的價格在現貨市場賣出英鎊;表中第2行顯示該銀行準備在一個月後以每英鎊1.274 6美元的價格買入英鎊,同時銀行也準備在一個月後以每英鎊1.275 1美元的價格賣出英鎊。表5-2中其他行的含義也依此類推。
表5-2 2017年6月9日USD/GBP即期及遠期的買入價及賣出價

注:GBP代表英鎊,USD代表美元,表中所示價格為每英鎊所對應的美元價格。
遠期合約可以被用來對衝外匯風險。假定在2017年6月9日,美國某企業的財務部主管已經預知在1年後(2018年6月9日)公司業務要支付100萬英鎊,這位主管準備對衝外匯風險。他可以同銀行達成一個如表5-2所示的遠期合約。此合約約定在1年後,這家企業必須以每英鎊1.288 9美元的價格買入100萬英鎊。在此遠期合約中該企業為英鎊多頭寸方,也就是說此企業在2018年6月9日將以128.89萬美元的價格買入100萬英鎊。銀行在合約中處在英鎊空頭寸方的位置,也就是說銀行必須在2018年6月9日以128.89萬美元的價格賣出100萬英鎊。該企業及銀行對合約的履行均做出了有約束力的承諾。
遠期合約在簽署以後會產生什麼樣的結果呢?在該遠期交易中,企業有義務在1年後以每英鎊1.288 9美元的匯率,買入100萬英鎊。如果匯率上漲,假如說在1年後1英鎊值1.500 0美元,這時企業能夠以遠期合約規定的每英鎊1.288 9美元的價格(而不是以每英鎊1.500 0美元的價格)買入100萬英鎊,這對企業來講,遠期合約價值為211 100美元(=(1.500 0-1.288 9)×1 000 000)。當然,對於企業而言,最終的合約價值也可能為負。如果1年後,匯率跌至每英鎊1.100 0美元,按照遠期合約,企業仍必須以每英鎊1.288 9美元的價格(而不是以每英鎊1.100 0美元的價格)買入100萬英鎊,這會給企業帶來188 900美元的損失(=(1.288 9-1.100 0)×1 000 000)。以上例子說明,持有遠期合約的多頭所帶來的收益可正可負,遠期合約多頭的收益等於資產即期價格減去合約的執行價格,如圖5-2a所示。

圖5-2 遠期合約的收益
在以上例子中,銀行持有遠期合約的空頭,其持有頭寸是企業頭寸的鏡像反射。銀行同意在6個月後以匯率每英鎊1.288 9美元的價格賣出100萬英鎊。如果在1年後1英鎊值1.500 0美元,按照遠期合約,這時銀行必須以每英鎊1.288 9美元的價格(而不是以每英鎊1.500 0美元的價格)賣出100萬英鎊。這會給銀行帶來211 100美元的損失。如果在1年後,匯率跌至每英鎊1.100 0美元,按遠期合約,這時銀行能夠以每英鎊1.288 9美元的價格(而不是以每英鎊1.100 0美元的價格)賣出100萬英鎊。這會給銀行帶來188 900美元的收益,遠期合約空頭的收益等於執行價格減去資產的即期價格,如圖5-2b所示。遠期合約的定價及遠期價格的確定會在附錄C中給出。
5.5.2 期貨合約
期貨合約同遠期合約類似,它也約定合約雙方在將來某一時間以某一約定價格進行資產的買賣。期貨合約同遠期合約的不同之處在於期貨交易是在交易中心進行的。在交易中心交易也就意味著交易合約必須標準化,即交易中心定義單位合約的資產數量、交割時間、交割資產的品種等。每一個期貨合約是以其交割月份來識別的。例如,2019年9月黃金期貨對應於交割日為2019年9月的期貨合約。遠期合約的到期日通常是對應於某一天,期貨合約交割往往對應於到期月內的若干天。交易中心還會定義關於交割地點和時間的備選方案,期貨合約的空頭寸方可以提出交割。基本上總是持有空頭的一方有權啟動交割過程,並在關於交割地點和時間的備選方案中做出選擇。
大部分期貨合約在市場上交易活躍,其價格由市場供求關係決定。當2019年9月到期的黃金期貨價格為每盎司1 280美元時,如果市場上買方多於賣方,期貨價格會上升;類似地,如果市場上賣方多於買方,期貨價格會下跌。
進行期貨交易的一個最大優點是平倉手續的簡單化,如果你在2019年3月5日買入了(即持有多頭)2019年9月的黃金期貨合約,那麼你可以在2019年6月5日通過賣出(即持有空頭)同一個合約來從期貨合約中退出。對遠期合約平倉就不會像對期貨合約平倉那麼容易,因此,遠期合約到期往往會促成標的資產(underlying asset)的交割。而在期貨交易中,一般來講,合約會在到期月前被平倉。業界事例5-1中令人捧腹的故事指出,在平倉時出現的錯誤也會造成期貨合約中資產的交割。
業界事例5-1
出乎意料的期貨資產交割
這個(聽起來有點像編造的)故事是多年前某家金融機構的主管親口講述給本書作者的。故事的主人公是一個剛剛進入這家金融機構而在金融界沒有任何經驗的新手。該金融機構的一個客戶為了對衝風險而常常需要進入活牛期貨交易的多頭。通常這個客戶在期貨到期前的最後一個交易日向銀行發出指令,將交易進行平倉(在芝加哥商業交易所中所採用的活牛交易合約中的標的資產為40 000磅[1]活牛)。這位新僱員的職責是管理這個客戶的賬戶。
當期貨合約接近到期日時,這位僱員注意到客戶仍然有一個多頭頭寸沒有被平倉,他隨後就指示交易市場的交易員又進入一個多頭(而不是空頭)。這一錯誤的後果是導致該金融機構持有兩份期貨合約的多頭。當交易錯誤被發現時,期貨合約交易已經結束。
金融機構(而不是客戶)要對其錯誤負責,這一錯誤的直接後果就是金融機構本身必須要去處理一群活牛的交割工作。而對這種交割,該金融機構毫無經驗。期貨合約規定空頭寸方可以在交割到期月的某個時間在美國境內幾個不同的地點交付牲畜。因為在此期貨交易中作為多頭寸方的金融機構只有等待空頭寸方交易所提供交割資產意向的通知(notice of intention to deliver),交易所再向金融機構發出交割通知。
最後金融機構終於收到了由交易所發出的交割通知,交割通知中註明活牛將在通知後的第一個星期二於2 000英里[2]以外的一個地點交割。這位新僱員被安排到交割地點處理交割事務。在交割地點,每個星期二都有牲畜拍賣,期貨合約的空頭寸方在拍賣市場買下牲畜隨後就進行了交付。不幸的是某星期買下的牲畜必須在下一個星期才能進行拍賣,這位不幸的新僱員就不得不留下來安排牲畜的存養。這位新僱員選取了這麼一個“有趣”的方式開始自己在金融界的創業生涯。
通常期貨合約的價格與遠期合約的價格十分類似,本書的附錄C給出了期貨合約和遠期合約的價格與即期價格的關係。期貨合約和遠期合約的一個不同之處是期貨合約每天結算,而遠期合約只在合約到期時才做最終結算。例如,如果在某一交易日中期貨價格上漲,那麼在交易日結束時,持有期貨空頭一方的資金會流入持有期貨多頭的一方;如果期貨價格下跌,那麼資金會按相反的方向流動。因為期貨合約是每天結算的,而遠期合約在合約到期時結算,所以兩類合約所實現的損益的時間也不同。如業界事例5-2所示,這一區別有時會令人困惑。表5-3比較了遠期合約和期貨合約的不同。
表5-3 遠期合約和期貨合約的比較
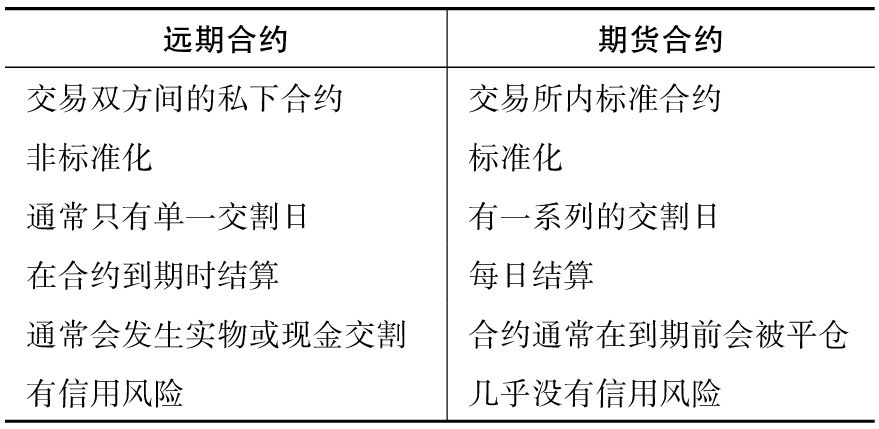
業界事例5-2
是系統錯誤嗎
一個銀行的外匯交易員進入了一個在3個月後買入100萬英鎊的遠期合約。遠期合約中的匯率為1.300 0。同時,另一個交易臺的交易員進入了16個3個月期限的英鎊期貨的多頭頭寸。期貨價格為1.300 0,並且每份期貨的規模為62 500英鎊。因此遠期和期貨交易的頭寸一樣。在進入交易後,遠期和期貨價格都漲至1.304 0。銀行系統顯示期貨交易員獲利4 000美元,但遠期合約交易員的獲利只有3 900美元。遠期合約交易員馬上打電話給銀行系統部門進行抱怨。遠期合約交易員的抱怨合理嗎?
答案是否定的。期貨合約每天進行交割保證了交易員馬上兌現盈利,盈利數量等於期貨價格的漲幅。如果遠期合約交易員馬上對其頭寸進行平倉,即進入執行價格為1.304 0的遠期合約空頭,遠期合約交易員在3個月時能夠以1.300 0的匯率買入100萬英鎊,並同時能夠以1.304 0的價格賣出100萬英鎊,這因此會產生4 000美元盈利,但這一盈利是在3個月以後。遠期合約交易員的盈利為4 000美元的貼現值。
遠期合約交易員可以從盈利與虧損的對稱性中得到些許安慰。如果遠期/期貨價格下跌至1.296 0,而不是上升到1.304 0,那麼期貨交易員馬上會損失4 000美元,而遠期合約交易員卻只損失3 900美元。還有,在合約3個月期限之間,期貨合約的整體損益會等同於遠期合約的整體損益。
期貨交易在期貨清算所進行結算。期貨清算所面向交易雙方,確保交易雙方支付所要求的款項。期貨清算所有許多會員,如果交易員或經紀人不是期貨清算所會員,則必須安排會員對交易進行清算。
期貨清算所要求會員繳納初始保證金和變動保證金。一天的變動保證金可以為正也可以為負,並且可以涵蓋當日的收益和損失。初始保證金是交易所持有的一筆額外金額,以應對結算會員的違約風險。此外,交易所要求其結算會員繳納違約基金(也稱為擔保基金)。這為交易所提供了額外的保護。如果一個會員違約,而其初始保證金和違約基金出資不足以彌補損失,則可以使用其他會員的違約基金供款。
期貨清算所會員在同意結算交易時要求經紀人和其他交易者提供保證金,而經紀人要求客戶提供保證金。經紀人和客戶之間的關係通常涉及初始保證金的繳納(大於會員要求的初始保證金)。當客戶保證金賬戶中的餘額(按每日損益調整)低於維持保證金水平時,客戶須補足餘額至初始保證金水平。
5.5.3 互換
第一筆互換交易產生於20世紀80年代,在80年代後隨著互換市場的蓬勃發展,到目前為止互換交易已經佔據了場外衍生產品市場的主導地位。
在互換合約中,交易雙方同意在將來交換現金流,合約闡明現金流的交換時間以及現金流的計算方式,通常在計算現金流時會涉及利率、匯率以及其他市場變量的將來值。
一個遠期合約可以被看作一個最簡單的互換合約。假定現在時間為2019年3月1日,某公司簽署了一個1年期的遠期合約。在合約中,這家公司同意在1年後以每盎司1 300美元的價格購買100盎司的黃金。在一年後,公司收到黃金後可以馬上在現市市場上將黃金變賣。這個遠期合約可以被認為是一個互換合約,在互換合約中,公司同意在1年後,也就是在2020年3月1日,以130 000美元現金交換數量為100倍黃金現市價格的美元。
遠期合約可以等同為在今後的某個單一時間點現金流的互換,而互換合約通常闡明在今後的若干時間點進行現金流互換。最流行的互換合約是簡單利率互換(plain vanilla interest rate swap),其中固定利率現金流與浮動利率LIBOR[3]現金流進行交換。在利率互換合約中,計算浮動及固定利率所用的名義本金相同。圖5-3顯示一家公司同意以3%的固定利率來換取以LIBOR為基準的浮動利率(注意,本例中的所有利率都是半年複利)。假定,互換合約的浮動利率每6個月設定一次,互換合約的面值為1億美元,互換合約的期限為3年。表5-4顯示公司A的現金流,表中第2列顯示出6個月期的LIBOR利率,這裡利率互換在2019年3月3日開始。在利率互換初始日,6個月期的LIBOR利率為每年2.2%,這相當於每6個月利率為1.1%,由此我們可以得出在2019年9月3日浮動利率現金流為0.011×10 000萬美元=110萬美元。而在2019年9月3日,6個月期浮動利率為每年2.8%(每6個月為1.4%),從而我們可以算出在6個月之後的浮動現金流為140萬美元。依此類推,我們可以計算出所有浮動現金流。由固定利率所決定的現金流一直為150萬美元(此值是1億美元以3%計息,6個月應得利息)。請注意在利率互換中,現金流的計算時間與LIBOR利率的通行時間相對應。這就是說,通常在某一時間段開始時確定利率,該利率用以計算在該利率時間段結束時應支付的現金流。
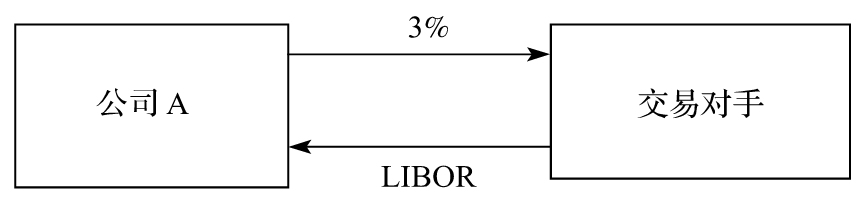
圖5-3 簡單利率互換
表5-4 圖5-3中顯示的利率互換中公司A的現金流,互換期限為3年,面值為1億美元 (金額單位:百萬美元)
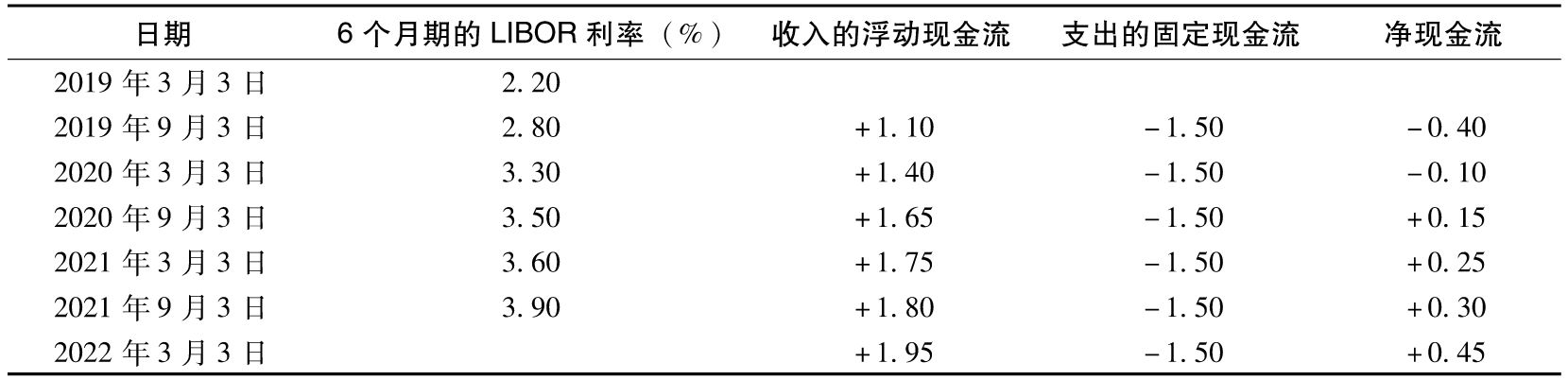
注:在計算表5-4中的現金流時,我們沒有將計息天數約定、假期等因素考慮在內。利率為每半年複利一次。
簡單利率互換在市場上非常流行,其原因是這一產品的用途較為廣泛。圖5-3顯示利率互換可以把公司A的以LIBOR+1%為浮動利率的借貸轉為4%固定利率的借貸。對公司A而言,進行利率互換後的合成效果是:
(1)在貸款中,支付LIBOR+1%;
(2)在互換合約中,收入LIBOR;
(3)在互換合約中,支付3%的固定利率。
淨支出為4%。利率互換也可以將公司A的2.5%的固定收益轉化為LIBOR-0.5%的浮動收益,進入利率互換的合成效果是:
(1)在投資中,收入2.5%;
(2)在互換合約中,收入LIBOR;
(3)在互換合約中,支付3%的固定利率。
整體收益為LIBOR-0.5%。
【例5-1】 假定一家銀行有一個浮動利率存款及5年期固定利率的貸款。我們在第9章中將討論,該資金結構會給銀行帶來很大的風險。當利率增加時,銀行存款人會選擇續存而使得銀行淨利息收入降低。此時銀行可以像公司A那樣進入類似圖5-3所示的利率互換來對衝風險,利率互換使得銀行的浮動利率存款轉為固定利率存款,從另一個角度,可以看作是將固定利率貸款轉為浮動利率貸款。
許多銀行已經成為利率互換市場的做市商,表5-5是某家銀行給出的利率互換的價目表。[4]表5-5第1行顯示,這家銀行在2年期利率互換中,願意支付2.55%固定利率並同時收取LIBOR利率;同時在2年期利率互換中,這家銀行也願意收取2.58%固定利率並同時付出LIBOR利率。表5-5所示的收入與付出利率的差值為3~4個基點,收入與付出利率的平均值被稱為互換利率(swap rate),表中最後一列顯示了對應於不同期限的互換利率。
表5-5 某利率互換做市商提供的互換利率(年利率,%)
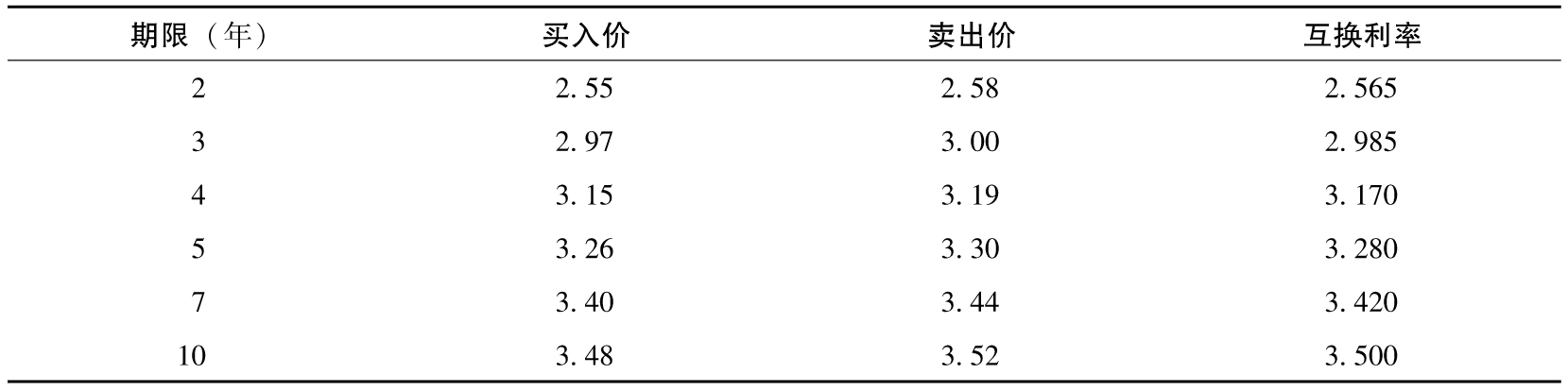
本書的附錄D討論了簡單利率互換的定價。
5.5.4 期權
期權產品在交易所交易市場及場外交易市場均進行交易。產品可以分成兩個基本類型:看漲期權(call option),其持有者有權在將來某一確定時間以某一確定價格買入某種資產,看跌期權(put option),其持有者有權在將來某一確定時間以某一確定價格賣出某種資產。期權合約闡明的約定價格被稱為執行價格(exercise price)或敲定價格(strike price);期權合約闡明的特定時間被稱為到期日(expiration date)或期限(maturity)。美式期權的持有者在到期前的任何時間內,均可以行使期權;歐式期權的持有者只能在到期日這一特定時間行使期權。[5]在交易所買賣的期權大多為美式期權,標的資產數量通常為100股股票。歐式期權比美式期權分析起來要容易一些,美式期權的大多數特性是從歐式期權的特性中演繹而來的。
平值期權(at-the-money option)是指期權執行價格同標的資產的價格相等。[6]虛值期權(out-of-the-money option)是指在看漲期權中執行價格高於標的資產價格,也可能是在看跌期權中執行價格低於標的資產價格。實值期權(in-the-money option)是指在看漲期權中執行價格低於標的資產價格,也可能是在看跌期權中執行價格高於標的資產價格。
這裡應該強調期權賦予持有者某種權利去做某一項事情,當然持有者可以選擇不去行使這一權利。與此對比,遠期及期貨合約中的雙方必須去買入或賣出標的資產,這裡我們應該注意到進入遠期或期貨交易不需要任何費用,而擁有期權必須付費,這個費用就是期權費(option premium)。
芝加哥期權交易中心(CBOE,www.cboe.com)是世界上最大的股票期權交易中心。表5-6顯示出英特爾(Intel,股票記號INTC)美式股票期權在2017年6月12日的收盤價。這裡期權的執行價格分別為34美元、35美元、36美元及37美元。表中所示期權到期日期分別為2017年8月、2017年10月及2017年12月。這其中8月期權的到期日為2017年8月18日;10月期權的到期日為2017年10月20日;12月期權的到期日為2017年12月15日。[7]英特爾公司的股票價格為35.91美元。
表5-6 2017年6月12日英特爾公司股票期權價格(股票價格為35.91美元)

假定某投資者向其經紀人發出購買英特爾股票10月看漲期權的指令,期權執行價格為36美元,經紀人在收到指令後會向CBOE的某交易員發出購買指令。而這一交易員隨即會在CBOE交易所內尋找願意賣出10月到期的、執行價格為36美元的看漲期權的交易員。期權的成交價會在交易員之間達成。假如,期權價格如表5-6所示,10月期權的價格為1.66美元。這一價格是指單位(也就是能買入1股股票)期權的價格。在美國,期權合約通常對應標的資產的數量為100股,因而投資者必須通過經紀人向交易中心注入166美元資金,然後交易中心會將此項資金轉給期權的賣出方。
在我們的例子中,投資者以166美元的價格買入了在將來某時刻以每股36美元價格買入100股英特爾股票的權利。期權的賣出方會收入166美元資金,其所付的代價就是當期權持有者行使權利時,賣出方必須以每股36美元的價格賣出100股英特爾股票。如果在2017年10月20日之前,英特爾的股票沒有高於36美元,從而期權持有者不會行使權利,投資者(期權持有者)因此也就損失了166美元。但是,如果英特爾公司的股票表現好,在期權被行使時,英特爾股票價值50美元,這時期權持有者能夠以每股36美元的價格買入每股實際價值為50美元的股票。這會給投資者帶來1400美元的盈利,將最初的買入期權費用考慮在內,期權持有者實際盈利為1234美元。
如果投資者不看好英特爾公司股票,一個可供選擇的期權是執行價格為36美元、12月到期的看跌期權。由表5-6我們可以計算出購買此項期權合約的費用為100×2.25=225美元,投資者因而以225美元的價格買入了一個在2017年12月15日前以每股36美元的價格賣出100股英特爾股票的權利。如果英特爾股票價格一直高於36美元,期權也就不可能被行使,從而會給投資者造成225美元的損失。但是如果期權到期時股票價格為25美元,投資者可以通過以每股36美元的價格賣出實際價值只有25美元的100股英特爾股票,投資者因此可獲得1100美元的收益,將最初的期權價格考慮在內,投資者實際收益為875美元。
在CBOE交易所內交易的期權為美式期權,但為了便於討論,我們假設這些期權為歐式期權,也就是假設這些期權只能在到期日才能被行使。圖5-4給出了期權收益與到期時英特爾股票價格的函數。
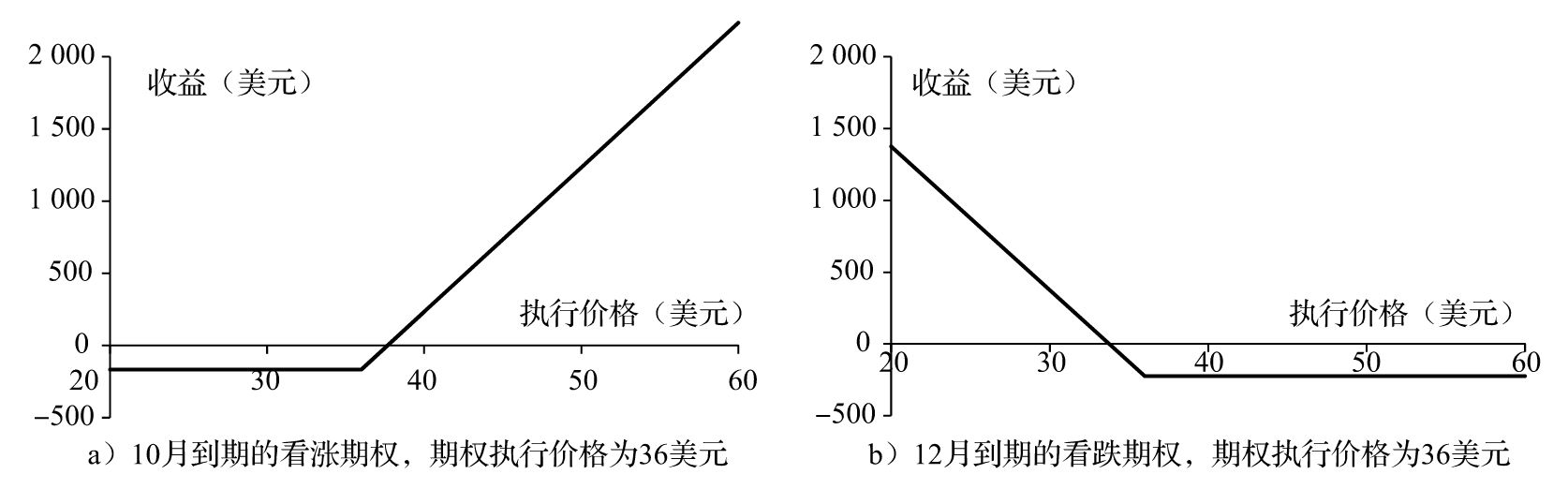
圖5-4 假設無提前行權,持有英特爾公司股票期權多頭的淨收益
在期權交易時,有4種交易形式:
(1)買入看漲期權;
(2)賣出看漲期權;
(3)買入看跌期權;
(4)賣出看跌期權。
期權的買入方稱為多頭寸方(long positions),期權的賣出方稱為空頭寸方(short positions),賣出期權也稱為期權承約(writing the option)。
當交易者以現金購買期權時,沒有保證金要求,因為交易在未來不會成為交易者的負債。在美國,可以通過保證金購買持續時間超過9個月的股票期權和股票指數。初始保證金和維持保證金是期權價值的75%。
當賣出期權時,空頭寸方存在潛在的未來負債,因此必須繳納保證金。當賣出的是股票的看漲期權時,初始保證金和維持保證金是以下兩者中的較大者:
(1)期權價值的100%加上標的股票價格的20%減去期權的價外價格(若有)。
(2)期權價值的100%加上股價的10%。
當賣出的是看跌期權時,取以下兩者的較大者:
(1)期權價值的100%加上標的股票價格的20%減去期權的價外價格(若有)。
(2)期權價值的100%加上執行價格的10%。
如果交易員持有該股票的其他頭寸,則這些保證金要求可能會降低。例如,如果交易員有一個完全回補的頭寸(交易員賣出了一定數量的股票的看漲期權,並擁有相同數量的股票),則空頭期權頭寸就沒有保證金要求。
期權交易無論是在場外交易市場或交易所交易市場都十分活躍。期權的標的資產包括股票、外匯以及股票指數等。事實上,場外交易市場的期權交易量已經超過了交易所交易市場內期權的交易量,交易所交易的期權類型一般是美式期權,而場外交易的期權常常為歐式期權。場外交易期權的優勢是到期日、執行價格以及合約大小等均可以按客戶的特殊需要定製,而不必和交易所的標準期權保持一致。場外期權交易一般比交易所交易要更大。
在本書的附錄E和附錄F中,我們將給出用來計算期權價格的數學公式及數值計算方法,這些公式及計算方法適用於不同類型的標的資產。
5.5.5 利率期權
在場外交易市場交易的重要利率衍生產品包括利率上限(cap)、利率下限(floor)以及互換期權(swap option,即swaption)。如表5-4所示,利率互換是關於一系列浮動利率與固定利率的交換。顧名思義,利率上限對浮動利率進行了限制,其實質是關於浮動利率(通常是LIBOR)的一系列看漲期權。當浮動利率高於一定的執行利率(也被稱為上限利率)時,期權持有者會得到收益。收益數量等於浮動利率超出執行利率的那一部分;如果浮動利率低於上限利率,那麼持有者不會得到任何收益。收益支付時間與互換現金流支付時間一致,即在利率所覆蓋區間的最後。
因為在進入上限合約時,第一時間段利率為已知,所以通常這一時間沒有收益。考慮某交易員在2019年3月3日進入為期3年的關於6個月LIBOR利率上限的合約,上限利率為3.2%,面值為1億美元,假定市場實現的利率如表5-4第2列所示。2020年3月3日,期權沒有任何收益。2020年9月3日所對應的收益為0.5×(0.033 0-0.032 0)×100(以百萬計),即50 000美元;類似地,期權在2021年3月3日、2021年9月3日及2022年3月3日的收益分別為150 000美元、200 000美元及350 000美元。
利率下限是關於浮動利率的一系列看跌期權,如果以上例子是一個利率下限,而不是上限,在2020年3月3日,期權的收益為0.5×(0.032 0-0.028 0)×100,即200 000美元,在其他時間,期權沒有任何收益。
互換期權的持有者在將來某個時刻有權進入某個利率互換,互換的固定利率就是期權的執行利率。互換期權分為兩類:一類是期權持有者有權在將來支付固定利率,收入浮動利率LIBOR;另一類是期權持有者有權在將來支付浮動利率,收入固定利率。
[1] 1磅=0.453 6千克。——譯者注
[2] 1英里=1 609米。——譯者注
[3] LIBOR代表倫敦銀行間資金拆借利率。這一利率是指銀行在批量資金存儲時的利率,在第9章中我們會討論。
[4] 在美國的標準利率互換合約中,固定利率一般是每6個月支付一次,而浮動利率為每3個月支付一次。表5-4的分析假定固定利率及浮動利率均為6個月支付一次。
[5] 這裡的術語歐式期權及美式期權同這些產品的交易地點及交易中心無關,有些在北美交易中心交易的期權是歐式期權。
[6] 在某些情況下,平值(at the money)可能有不同的含義。比如,有時平值期權是指期權的行權價格的當前價值(即將行權價格以期權的期限貼現)等於資產的價格。平值期權還可以指那些delta為0.5的看漲期權或delta為-0.5的看跌期權(我們將在第8章第8.1節中介紹delta的定義)。
[7] 交易所選擇的到期日為交割月份的第3個星期五之後隨即的一個星期六。
5.6 非傳統衍生產品
對於經濟現象中的各種風險,金融工程師總會開發出一些衍生產品來幫助市場參與者應對風險敞口。金融機構通常扮演中間人的角色,並設法將風險轉移到:①持有相反風險敞口的其他市場參與者;②願意承擔風險的投機者。在本節中,我們將討論為滿足市場參與者的特殊要求而開發出的衍生產品。
5.6.1 氣候衍生產品
許多公司的業務表現會被惡劣氣候所影響,[1]可以很形象地講,這些公司對於氣候風險對衝的需求類似於某些公司對於外匯或利率風險的對衝需求。
第一個氣候衍生產品是在1997年引入的。為了解釋氣候衍生產品的機制,我們接下來需要定義兩個變量:
·HDD:熱度日(heating degree days);
·CDD:冷度日(cooling degree days)。
一天的HDD定義如下
HDD=max(0, 65-A)
一天的CDD定義如下
CDD=max(0, A-65)
其中A是指某個指定氣象臺報告的每天最高溫度以及最低溫度的平均值,這裡的溫度以華氏[2]為計量單位,例如某一天(子夜與子夜之間)的最高溫度為華氏68°,最低溫度為華氏44°,這裡的A=56,因此HDD=9,CDD=0。
典型的場外氣候衍生產品包括遠期合約及期貨合約,合約的回報通常與一個月累積的HDD、CDD有關(累積HDD及CDD分別等於一個月內HDD之和及CDD之和)。例如,某交易商在2018年1月賣給客戶標的變量為2019年2月累積HDD的看漲期權,溫度觀測地點為芝加哥O’Hare機場氣象臺,合約執行價格為700美元,而對於天氣的每一度(高於700),期權回報為10 000美元,如果實際的累積HDD為820,那麼期權回報為120萬美元(=10 000×(820-700))。一般在合約中包括一個上限,如果我們例子中的合約上限為150萬美元,這時客戶的頭寸等於是一個標的變量為累積HDD、執行價格為700美元的看漲期權的多頭以及一個標的變量同樣為累積HDD、執行價格為850美元的看漲期權的空頭。
一天的HDD是為了檢測一天取暖所需要的能源消耗,一天的CDD是為了檢測一天製冷所需要的能源消耗。大多數氣候衍生產品的客戶是能源供應商以及能源消耗者,但是零售商、超級市場、食品及飲料製造商、健康服務公司、農產品生產商以及娛樂服務業都可能是氣候衍生產品的用戶。氣候風險管理協會(The Weather Risk Management Association,www.wrma.org)的建立就是為了給氣候衍生產品的客戶提供服務。
1999年9月,芝加哥商業交易所(Chicago Mercantile Exchange)開始交易氣候期貨以及歐式氣候期貨期權,合約的標的變量為某氣象臺所觀測到某月的累積HDD以及CDD,合約的交割方式為現金,交割時間為每月末當HDD及CDD均為已知的時刻,報為20美元乘以累積HDD或CDD。芝加哥商業交易所(CME)現在為全球許多城市提供天氣期貨和期權。它還提供有關颶風、霜凍和降雪的期貨和期權。
5.6.2 石油衍生產品
原油是世界上最重要的大宗商品。美國能源信息管理局(United States Energy Information Administration,www.eia.gov)預計全球每天對原油的需求量是9000萬桶。10年期的固定價格合約已經在場外交易市場流行了許多年,還有些互換協議將固定價格的原油與浮動價格的原油進行交換。
根據比重度和含硫量的不同,原油可以分為很多不同的等級。兩個重要的原油定價基準是布倫特(Brent,開採自英國北海)原油和西得克薩斯中質(WTI)原油。從原油中可提煉出汽油、取暖用油、燃料油和煤油等。
在場外交易市場,可以用普通股票、股票指數作標的變量的幾乎所有衍生產品都能夠以油價作為標的變量。關於油價的互換協議、遠期合約以及期權已經非常普遍。合約的交割形式有時是現金,有時是現貨(即交付石油)。
交易所交易的產品也非常流行。芝加哥商業交易所(CME)以及洲際交易所(International Exchange,ICE)交易多種石油期貨及期貨期權。有些期貨的交割方式為現金,而其他合約的交割方式為實物。例如,在ICE交易的布倫特原油期貨的交割方式為現金交付,在CME交易的WTI原油期貨的交割方式為現貨。兩種情形中單一合約均對應1000桶原油。CME同時也交易兩種精煉油的合約,即取暖油及汽油。這兩種合約每份所對應的油量均為42000加侖[3]。
5.6.3 天然氣衍生產品
20世紀八九十年代,世界範圍內的天然氣市場經歷了一輪去監管化的過程,同時政府的壟斷被打破。天然氣的供應商並不一定是天然氣的生產商,供應商每天都要面臨保證天然氣需求的問題。
一個典型的場外合約的目的是闡明在某一個月以大體一致的速度交付一定數量的天然氣。在場外交易市場有遠期合約、期權以及商品互換交易,天然氣的賣出方要負責通過利用天然氣管道將天然氣送達某指定地點。
CME交易合約的計量單位為100億(即10 000百萬)英國熱量單位(British thermal units)的天然氣,如果合約沒有被提前平倉的話,那麼賣出方需要在某個月以大體一致的速度將天然氣運達路易斯安娜(Louisiana)的指定天然氣樞紐,ICE在倫敦也交易類似的合約。
天然氣是建築供暖常用的能源。它還可以被用來發電,電又可以被用於空調。因此,對天然氣的需求是季節性的,並取決於天氣。
5.6.4 電力衍生產品
電力是一種非同尋常的商品,這是因為電力很難儲存。[4]在某一地區,某時刻的最大電力供應與在這一地區的最大發電能力有關。美國的電力系統分成140個控制區域(control areas)。在某一控制區域內,電力的需求以及供應首先要達到匹配,然後額外電力才能賣給其他的控制區域。這些額外能源是電力交易市場的主要構成產品。一個控制區域賣給另外一個控制區域的電力數量取決於兩個地區之間的輸電能力。不同地區的電力傳輸會涉及傳輸費用,這一費用由輸電設備的擁有者掌握,在輸電過程中往往會有電力能源的損耗。
電力的主要用途之一是為空調系統提供能源,因此對於電力的需求以及價格在夏天要高於冬天。電力的不可儲存性有時會造成現貨市場價格的大幅度波動。熱浪有時會在短時間內將即時電價推高1 000%。
像天然氣市場那樣,電力市場近期也經歷了去監管化,政府的壟斷已被取消,同時產生了電力衍生產品市場。CME現在能夠交易標的變量為電力價格的期貨合約,遠期、期權以及互換產品的交易在場外交易市場上也很普遍。一個典型的合約(交易市場型或場外型)允許某交易方在某一指定月份以一定的價格收到一定千瓦時(megawatt hours)的電力。在一個5×8合約中,電力接收時間為在某指定月份每週5個工作日(週一至週五)的非高峰時間(晚上11點至早上7點);在一個5×16合約中,電力接收時間為某指定月份每週5個工作日的高峰時間(早上7點至晚上11點);在一個7×24合約中,電力接收時間為指定月份的每天的任意時刻。期權合約的行使權利有按天行使(daily exercise)以及按月行使(monthly exercise)兩種形式,在按天行使形式中,期權持有者可以選擇在某月的哪些天(必須有一天的準備期)以某指定價格接收一定數量的電力;在按月行使形式中,期權持有者必須在某個指定月的開始決定是否以某指定價格接收一定數量的電力。
電力及天然氣市場上一種有趣的合約為擺動期權(swing option)或即用即付期權(take and pay option),這些合約通常指明瞭期權持有者在指定的月份中以某指定價格每天和整個月份總共可獲取能源的最低數量與最高數量。期權持有者可以更改(或者說擺動)在當月中買入能源的快慢,但一般來講,改變的次數會有一定限制。
[1] 美國能源部估計有1/7的美國經濟會受氣候風險影響。
[2] 華氏度是溫度單位,符號為℉,它與攝氏度(符號為℃)的換算關係為:F=32+1.8C。——譯者注
[3] 1美製加侖=3.785升,1英制加侖=4.546升。——譯者注
[4] 具有剩餘電力能源的生產商可以採用水泵將水輸入發電廠高處,並在今後需要能源時以水力發電,這大概是生產商所能做到的最好的電力儲存方式。
5.7 奇異期權和結構性產品
許多奇異期權(exotic option)和結構性產品(structured product)在場外交易市場進行交易,雖然這些產品的交易數量小於在第5.5節中討論的標準衍生產品的交易數量,但這些產品對銀行而言仍非常重要,這些奇異期權和結構性產品的盈利要比簡單產品更為豐厚。
以下是一些奇異期權的例子。
·亞式期權(Asian options):亞式期權同一般簡單期權相近,只是在期滿時回報有所不同,亞式期權的回報與標的資產在某一固定時間段價格的平均值有關。例如,一個1年期的亞式期權在期滿時的回報等於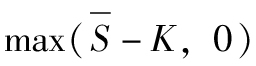 ,其中
,其中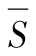 為過去一年資產價格的平均值,K為執行價格。
為過去一年資產價格的平均值,K為執行價格。
·障礙期權(barrier options):這些期權往往在標的資產的價格達到一定水平後,才得以存在或者消失。例如,一個敲出(knock-out)看漲期權的執行價格為30美元,障礙價格為20美元,敲出看漲期權與普通看漲期權的唯一區別就是當標的資產價格低於20美元時,這一期權自動消失。
·一攬子期權(basket options):這種期權的標的資產為一個投資組合而不是單一資產。
·二元期權(binary options):這種期權在某種條件滿足時會給出一個固定數量的回報,例如,一個1年期二元期權的回報可以是在1年期內股票價格高於20美元時,回報等於1 000美元。
·複合期權(compound options):這種期權的內含標的資產也是期權,複合期權有4種形式——看漲看漲期權(a call on a call)、看漲看跌期權(a call on a put)、看跌看漲期權(a put on a call)以及看跌看跌期權(a put on a put)。例如,一個看漲看漲期權給期權持有者一個權利買入期權,此期權中最原始標的資產當前價格為15美元,複合期權中第一層期權的到期期限為1年所對應的執行價格為1美元,複合期權的期限為3年,對應的執行價格為20美元。
·回望期權(lookback options):此類期權在到期時所對應的回報與標的資產在過去一段時間內的極大值或極小值有關,例如,一個1年期的期權在到期時回報等於ST-Smin,其中ST為到期時的標的資產價格,而Smin為從現在到1年到期時的資產價格的最低值。
有時奇異期權比標準期權能更為有效地對衝風險。如業界事例5-3所述,微軟公司(Microsoft)採用亞式一攬子期權來管理其外匯風險。
業界事例5-3
微軟公司的對衝策略
微軟公司一直十分積極地管理其所面臨的匯率風險。在某些國家及地區(例如,歐洲、日本及澳大利亞),微軟公司的收入為本地貨幣,每月需將收入轉化為美元。在這些以當地貨幣計量收入的國家,自然微軟公司也就會有對當地貨幣的風險敞口,而在其他國家和地區(例如拉美、東歐以及南亞),微軟公司的收入直接以美元來計量,乍一看微軟公司在這些國家沒有匯率風險,其實不然。
假如美元相對於業務直接以美元計量的國家的貨幣升值了,這些國家的人會發現買入微軟公司的產品會更加困難,本地人需要用更多的本地貨幣換取美元,然後再買入微軟公司的產品。美元升值會迫使微軟公司降價,否則公司的銷量就會降低。從而我們可以得出結論:無論是以當地貨幣計價或直接以美元計價,微軟公司都會有匯率風險,這一點再一次闡明構造對衝決策時一定要從大局考慮。
微軟公司希望用期權來對衝其匯率風險。假設微軟公司選擇了1年的期限。微軟發現自身的外匯風險(例如日元/美元)同匯率在一年中的月平均值有關,這是因為微軟公司在每月有相同數量的日元被轉化成美元,因此公司決定採用亞式期權而不是歐式期權來對衝其風險敞口。進一步,微軟公司認識到其總風險敞口是其經營業務所在國的匯率加權平均,進而採用一攬子期權(也就是期權的標的資產為某些變量的加權平均)。綜上所述,微軟公司希望在金融機構購買的期權為亞式一攬子看跌期權,這種期權的費用遠遠小於以每個月作為期限,並由各種匯率作為標的變量的看跌期權的組合費用(見練習題5.23),亞式一攬子看跌期權可以準確地為微軟公司提供匯率保護。
微軟公司也面臨其他類型的財務風險。例如,公司持有投資組合會對利率有風險敞口(當利率增加時,投資組合會有損失),公司也會對兩種不同形式的股票有風險敞口,一種敞口是針對其投資的公司的股票,另一種敞口是針對自身股票的風險敞口,這是因為公司要定期買自身股票以作為對僱員的獎勵。針對這些風險因素,微軟公司往往會採用較複雜的期權來對衝。
結構性產品是銀行為滿足投資者和企業的特殊需求而創造出來的,一種產品是保底證券(principal protected note),其中銀行向投資者提供機會,讓其賺取標準普爾500指數收益的一定比例,並同時保證收益不會為負。另外一類(高度)結構性產品如業界事例5-4所示[1](在這個例子中,信孚銀行(Bankers Trust)究竟是在滿足客戶需求,還是試圖推銷客戶並不需要的來獲取利潤,仍十分有爭議)。
業界事例5-4
寶潔公司的怪異交易
寶潔公司(P&G)在1993年11月2日同信孚銀行(BT)做了一筆被稱作“5/30”的離奇的互換交易,這一交易期限為5年,每半年有資金交付,交易的面值為2億美元,信孚銀行在交易中付年息為5.3%的固定利率,而寶潔公司支付給信孚銀行的利率為30天的CP(商業票據)的平均利率減去75個基點再加上某個利差,這裡的商業票據的平均利率是在利率觀測區間的30天的商業票據利率的平均值。
在第一個付款日(1994年5月2日),利差為0。在接下來的幾個付款日,利差為

公式中CMT為固定期限國債利率(該利率是由美國聯邦儲備銀行報告的5年國債利率),30年期的TSY價格是在2023年8月期滿的,券息為6.25%的美國國債的買入價與賣出價的中間值。注意,以上計算公式的計量為百分比,而不是以基點為計量。例如以上公式所求得的利差為0.1而CP平均利率為6%,由此可以算出信孚銀行利息為6%-0.75%+10%=15.25%。
寶潔公司做此交易時,希望利差大約為負,因此公司可將5.3%的固定利率轉化為此商業票據減去75基點的浮動利率。而事實上,1994年的利率飛漲,債券價格下跌。這筆交易令寶潔公司付出了慘重的代價(見作業題5.38)。
[1] 這一交易在後來成為一個訴訟的焦點,其細節在許多公開區域可以獲得,見D.J. Smith, “Aggressive Corporate Finance: A Close Look at the Procter & Gamble-Bankers Trust Leveraged Swap,” Journal of Derivatives 4, no.4(Summer 1997):67-79.
5.8 風險管理的挑戰
期貨、遠期、互換、期權和結構性等衍生產品變化多端,它們可以用來對衝風險也可以被用來投機及套利(對衝可以減少風險;投機通常要承擔風險;套利通常是通過進入兩種交易或更多交易來鎖定盈利)。產品的多變性會帶來危害,有時一些被指定只能做對衝或套利的交易員會在自覺或不自覺之中成為市場投機者,而投機的後果有時是災難性的。法國興業銀行的傑洛米·科維爾(Jerome Kerviel)給我們提供了典型的反面教材(見業界事例5-5)。
業界事例5-5
2008年法國興業銀行的鉅額損失
衍生產品是用途廣泛的金融工具。它們可以被用來對衝風險,也可以被用來投機和套利,有時某些被指定只能做對衝或套利的交易員會在自覺或不自覺之中成為市場投機者,這正是機構在交易衍生產品時所面臨的挑戰之一。
傑洛米·科維爾於2000年加入法國興業銀行,從事合規監管工作。2005年,他被提升為銀行Delta One產品(即那些delta值約為1的產品)團隊的初級交易員,負責交易股票指數產品,如德國DAX指數、法國CAC40指數和歐元區Stoxx 50指數。他的工作目標是尋找套利機會。當同一個股指的期貨價格在不同的交易市場上不同時,套利的機會就會出現。當股指期貨的價格與構成指數的股票價格不吻合時,也會有套利的機會。
科維爾利用他對銀行監控過程的瞭解,把投機行為假扮成了套利行為。他在股票指數上持有巨大的頭寸,並構造了虛假交易,使得他的頭寸看上去是被對衝的。實際上,他對股票指數會朝某個方向移動下了巨大的賭注。隨著時間的推移,他持有的裸露頭寸達到了數十億歐元的規模。
2008年1月,銀行發現了他未經授權的交易。在3天內,銀行以49億歐元的損失為代價,將他持有的頭寸平倉。在當時,這是金融史上由欺詐行為造成損失最大的一起案例(當年晚些時候,這一記錄就被伯納德·麥道夫(Bernard Madoff)的龐氏騙局打破)。
無賴交易員給銀行造成鉅額損失的例子在2008年以前也屢見不鮮。例如,20世紀90年代,巴林銀行的尼克·利森(Nick Lesson)擔負與科維爾類似的職責,負責在大阪交易所與新加坡交易所之間識別日經225(Nikkei 225)指數期貨的套利機會。而在交易過程中,利森由一個套利者變成了一個投機者。通過期貨和期權,他對日經225指數的走向下了巨大的賭注,並導致了10億美元的損失,最終造成一家存在了近200年的銀行破產。2002年,愛爾蘭聯合銀行的約翰·拉斯納克(John Rusnak)在未經授權的外匯交易中損失7億美元。2011年,瑞銀Delta One團隊的基庫·阿杜伯利(Jérôme Kerviel)以類似傑洛米·科維爾的手段給銀行造成23億美元的損失。
這些損失帶給我們的教訓是:在交易中,金融或非金融機構一定要給交易員設置一個清楚的限額,對限額要進行仔細的監督,以保證交易員遵守限額。
要想避免類似法國興業銀行的錯誤,金融或非金融機構一定要控制其衍生產品的交易。衍生產品一定要被用於正確的目的,在交易中必須設置風險額度,銀行必須監控交易員的交易以保證交易額度制度的貫徹執行。我們將在本書以後的章節中討論這一觀點。
小結
金融產品在兩類市場進行交易:交易所交易市場以及場外交易市場。2008年金融危機後,場外交易市場正在經歷一系列重大的變化。在本章中我們簡要介紹了這些變化,我們將在第17章中做進一步的詳細討論。
在這一章中我們討論了現貨交易、遠期合約、期貨、互換以及期權產品。遠期合約或期貨合約賦予合約持有者一種義務,持有者必須在將來某一指定時刻以某一約定價格買入或賣出某標的資產。互換合約約定互換的雙方在將來交換現金流,而交換的現金流的數量可能與某種或多種市場變量有關。期權合約分成兩種:看漲期權及看跌期權。看漲期權給期權持有者一種權利,在某一時刻以某一指定價格買入某資產;看跌期權給期權持有者一種權利,在將來某一時刻以某一指定價格賣出某一資產。
遠期、期貨及互換合約可以用來鎖定將來要發生的交易的價格。與此相比,期權提供價格保險,這一保險使得在將來某時刻的交易價格不會比某一選定價格更差。奇異期權或結構性產品可以用來滿足企業財務部的特殊要求。例如,在業界事例5-3中我們看到亞式一攬子期權可以被微軟公司用來對衝公司在某一特定時間區間內對於幾種不同風險源的風險敞口。
市場上有大量針對不同標的變量的衍生產品交易。在本章中我們回顧了與氣候、石油、天然氣和電力有關的衍生產品,我們還討論了奇異期權和結構性產品。
延伸閱讀

練習題
5.1 遠期合約空頭和多頭的區別是什麼?
5.2 請解釋對衝、投機以及套利的不同之處。
5.3 在某遠期交易中,投資者在遠期價格為50美元時進入多頭寸方,而另一個交易是投資者買入執行價格為50美元的看漲期權。這兩個交易的不同之處是什麼?
5.4 請詳細解釋賣出看漲期權及買入看跌期權的不同之處。
5.5 某投資者作為一遠期合約的空頭寸方同意在某一時刻以每英鎊1.3000美元的價格賣出10萬英鎊。在合約結束時匯率分別為:(a)1.2900;(b)1.3200,對應以上匯率投資者的盈虧分別為多少?
5.6 某交易員作為棉花遠期合約的空頭寸方同意在將來某時刻以每磅50美分價格賣出棉花,合約面值為50000磅棉花。當合約結束時棉花的價格分別為:(a)每磅48.20美分;(b)每磅51.30美分,對應以上價格交易員的盈虧為多少?
5.7 假定你賣出了一個執行價格為40美元、3個月期限的看跌期權,當前股票的價格為每股41美元,每份期權合約是關於100股股票。賣出這一期權後,你有什麼樣的義務呢?在此合約中你的盈利及虧損會為多少?
5.8 場外交易市場和交易所交易市場的區別是什麼?在這兩個市場中哪一個會進行如下產品的交易?(a)遠期合約;(b)期貨;(c)期權;(d)互換;(e)奇異期權。
5.9 你投機於某股票,希望價格會上漲。當前市場上股價為29美元,而3個月期限的執行價格為30美元的看漲期權的價格為2.9美元,假設你有5800美元可以用於投資,請陳列出兩種可以達到你的投資目的的投資方式,第一種投資方式只涉及股票投資而第二種方式應涉及期權,在兩種投資中可能的盈虧各為多少?
5.10 假如你擁有5000股每股價格為25美元的股票,你如何採用一個看跌期權而使得在將來4個月時價值得到保護?
5.11 股票在最初發行時會給公司提供資金,而對期權來講這種說法是否正確?請討論。
5.12 假如一個在3月到期的看漲期權的價格為2.5美元,期權執行價格為50美元。假設期權一直被持有至到期日,在什麼情形下期權持有者會盈利?在什麼情形下持有者會行使期權?
5.13 假如一個在6月到期的執行價格為60美元的看跌期權價格為4美元。假設期權被一直持有至到期日。在什麼情形下期權的賣出方(即空頭寸方)會盈利?在什麼情形下期權會被行使?
5.14 假如一家公司得知今後4個月時會收到一筆外匯,什麼樣的期權可以用來作為這筆外匯的對衝產品?
5.15 一家美國公司得知在將來的6個月要支付100萬加元。請解釋如何採用(a)遠期合約及(b)期權產品來對衝匯率風險。
5.16 20世紀80年代,信孚銀行開發了一種指數貨幣期權債券(index currency option notes,ICON)。債券持有者在到期時收到的回報與匯率有關,信孚銀行某交易對手是日本長期信用銀行(Long Term Credit Bank of Japan),在ICON中約定,如果在到期日(1995年)匯率高於169(YEN/USD),那麼債券持有者會收到1000美元。而當到期日的匯率低於169(YEN/USD)時,債券持有者的回報為
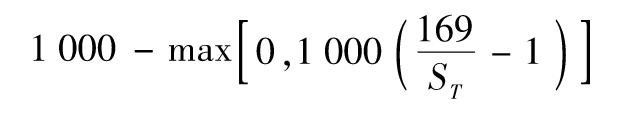
當到期日的匯率低於84.5時,債券持有者回報為0。請證明ICON是由一個簡單債券與兩個期權的組合。
5.17 假如USD/GBP現市及遠期匯率如以下表所示。

當以下(a)和(b)兩種情形同時出現時,會給套利者創造什麼樣的機會?
(a)180天期,執行價格為1.27(USD/GBP)的歐式期權價格為2美分;
(b)90天期,執行價格為1.34(USD/GBP)的歐式期權價格為2美分。
5.18 一家公司已經持有在今後5年提供3%的固定收益率的投資,此公司希望以表5-5所示的互換價格將固定回報投資轉化為浮動回報投資。請解釋公司如何達到這一轉換。
5.19 假定一家公司在今後以固定利率5%借入資金,請解釋公司如何用表5-5所示的互換價目表來將固定利息的負債轉化為浮動利息負債。
5.20 一家公司有一個利息為LIBOR+1%的浮動利息負債,請解釋這家公司如何用表5-5所示的價目表將這一浮動利息負債轉化為3年固定利息負債。
5.21 一個玉米農場的農場主有以下論點:“我不採用期貨來對衝我面臨的風險,我的真正風險並不是玉米價格的變化,我所面臨的真正風險是糟糕的氣候可能使我顆粒無收。”請討論這一觀點,這個農民是否應該對玉米預期產量有所估計然後採用對衝策略來鎖定預期價格?
5.22 一個航空公司主管有以下論點:“對衝航空燃料價格毫無意義,這樣做會得不償失。”請解釋此主管的觀點。
5.23 為什麼說微軟公司採用的一個亞式一攬子看跌期權的價格要遠遠低於一個相應的包含所有其中貨幣及期限的看跌期權的組合的價格(見業界事例5-3)?
5.24 “油價、天然氣以及電力價格都具有迴歸均值的性質。”這句話的含義是什麼?哪個產品具有最快的迴歸均值速度?哪個產品具有最慢的迴歸均值速度?
5.25 當我們增加觀測標的資產是否達到障礙水平的頻率時,一個敲出看漲期權的價格是有所增加還是有所減小?
5.26 假定在7月每一天的最低溫度為華氏68°,最高溫度為華氏82°,一個關於7月份累積CDD、執行價為250的期權收益為多少?假定每一度的收益為5000美元。
5.27 解釋一個5×8並且在2019年5月按天行使的電力期權運作方式。解釋一個5×8並且在2019年5月按月行使期權的運作方式。哪一個期權價值更高?
5.28 一位美國投資者簽署了5份看漲期權合約(即購買了500股股票的期權)。期權價格是3.5美元,執行價格是60美元,股票價格是57美元。初始保證金要求是多少?
5.29 一個交易者在股價為50美元時做空500股股票。初始保證金是160%,維持保證金是130%。投資者最初需要多少保證金?股票價格要漲到多高才會有追加保證金通知?
5.30 交易所要求其會員就期貨合約支付的保證金,與經紀人要求其客戶支付的保證金有何不同?
作業題
5.31 一家公司簽訂了一個空頭期貨合約,以每蒲式耳250美分的價格出售5000蒲式耳的小麥。初始保證金為3000美元,維持保證金為2000美元。什麼樣的價格變動會導致追加保證金?在什麼情況下可以從保證金賬戶中提取1500美元?
5.32 交易員以保證金購買200股股票。股票價格為每股20美元。初始保證金為60%,維持保證金為30%。交易者最初需要繳納多少保證金?需要追加保證金的股價是多少?
5.33 股票的當前市價為94美元,同時一個3個月期執行價格為95美元的歐式期權價格為4.70美元,一個投資者認為股票價格會漲,但他並不知是否應買入100股股票或者買入2000份(相當於20份合約)期權,這兩種投資所需資金均為9400美元。在此你會給出什麼樣的建議?股票價位漲到什麼樣的水平會使得期權投資盈利更好?
5.34 一個由標準石油公司(Standard Oil)發行的債券的形式如下:債券持有者不會收到通常的券息,但在債券到期時公司會給債券持有者償還1000美元本金並附加石油價格在債券持有期內的增值,這一增值等於170乘以在到期時石油價格高於25美元的差額,增值的最大限額為2550美元(該價格對應每桶40美元)。請說明這一債券是由一個簡單債券、一個執行價格為25美元的看漲期權多頭和一個執行價格為40美元的看跌期權空頭組合而成。
5.35 當前黃金市價為每盎司1500美元,一個1年期的遠期合約的執行價格為1 700美元,一個套利者可以以年利率5%借入資金,套利者應如何操作以達到套利目的?這裡我們假設黃金存儲費為0,同時黃金不會帶來任何利息收入。
5.36 某公司某項投資回報率為LIBOR-0.5%。請解釋此公司如何用如表5-5所示的價目表來將公司浮動利率投資轉化為期限分別為:(a)3年;(b)5年;(c)10年的固定利率投資。
5.37 一個投資者在遠期合約進入買入方,執行價格為K,到期時間為將來某一時刻。同時此投資者又買入一個對應同一期限,執行價格也為K的看跌期權,將這兩個交易組合會造成什麼樣的效果?
5.38 請計算由業界事例5-4所示的“5/30”互換合約中寶潔公司在以下情形下要付的利率:(a)商業票據(CP)利率為6.5%,國債利率為水平6%;(b)CP利率為7.5%,國債利率為水平7%。這裡的國債利率一年複利兩次。
第6章
2007年信用危機
本章有兩個學習目標:第一是調查2007~2008年金融危機的起因、發展以及它帶給我們的經驗與教訓,第二是解釋資產證券化是如何運作的。
從2007年開始,美國經歷了自20世紀30年代以來最嚴重的金融危機。這場危機非常迅速地由美國向世界其他地區,以及由金融市場向實體經濟蔓延。這場危機不但造成了許多金融機構破產,而且還迫使許多其他金融機構紛紛尋求本國政府的救助。21世紀的第一個10年對金融機構而言是災難性的,金融機構的風險管理實踐正在遭到多方面的批評。在以後的章節中我們將會看到,金融危機導致對金融機構的監管發生了巨大的變化。
第5章涵蓋了期貨、遠期、互換和期權,它們可以使風險從一個經濟實體轉移到另一個經濟實體。另一種重要的風險轉移方式是資產證券化。本章將介紹資產支持證券(ABS)和債務抵押債券(CDO),並討論它們在危機中所起的作用。
6.1 美國住房市場
要討論2007~2008年的信用危機,我們應當從美國住房市場談起。圖6-1展示了1987年1月~2017年3月的標準普爾10城市房價Case-Shiller指數(S&P/Case-Shiller Composite-10 index)。該指數跟蹤美國10個主要大都市區的房價。大約從2000年開始,房屋價格的上漲速度遠遠超過了前一個10年同期的上漲速度。2002~2005年的低利率是造成價格上漲的另一個重要原因,但住房市場價格泡沫形成的原因主要是房屋貸款政策的鬆懈。
2000~2006年,美國按揭市場的一個顯著特點是次級按揭貸款的激增。次級按揭貸款的風險明顯要高於按揭貸款的平均風險。在2000年以前,大部分被分類為次級的按揭貸款是借款人的第二個按揭(second mortgage),但在2000年以後,金融機構逐漸接受了第一次級按揭貸款(subprime first mortgage)這一名詞,自此,第一次級按揭貸款開始變得普遍。
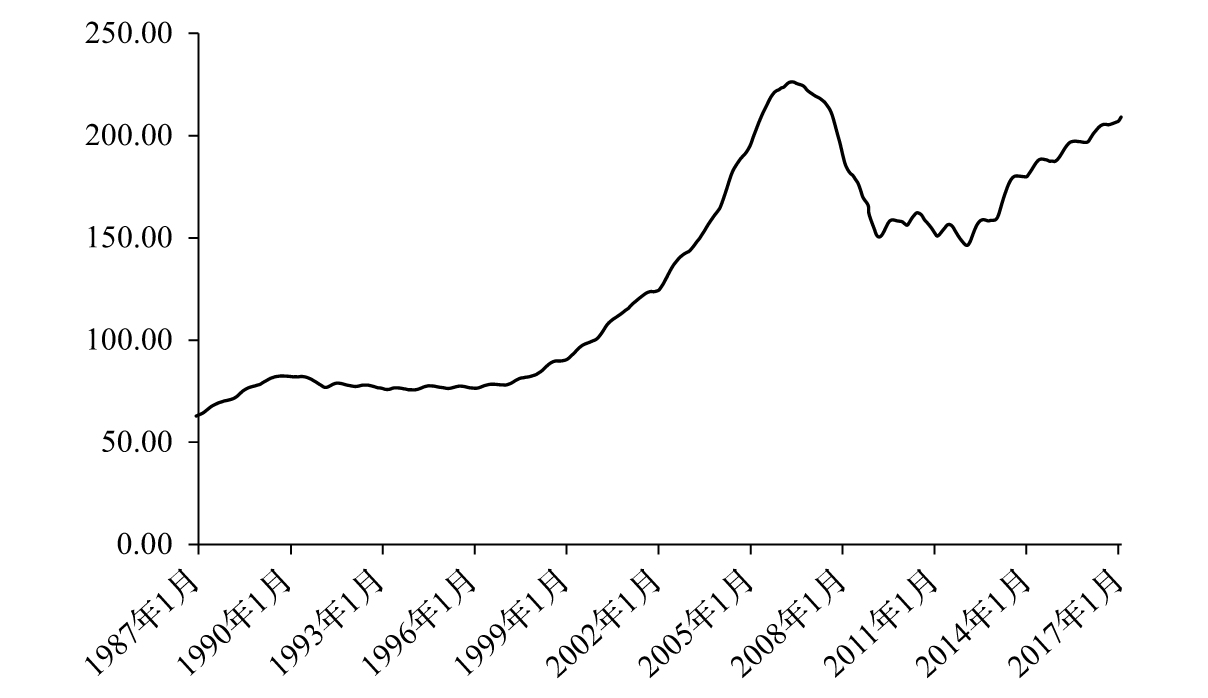
圖6-1 標準普爾/Case-Shiller美國10城市房價指數(1987~2017年)
6.1.1 借貸標準的降低
從2000年開始,房屋貸款商紛紛開始降低貸款標準。對那些信用不夠好、以前沒有資格取得貸款的家庭而言,這時候購買住房也成了現實。而這些家庭的存在,增加了市場對房屋的需求,因此房價開始上漲。對貸款經紀人和貸款商而言,房屋價格上漲以及大數量的借貸需求無疑是個好消息,更多的借貸意味著更大的盈利,並且房屋價格的上漲意味著貸款會有很好的抵押品,即使借貸人違約,由違約所引起的止贖事件(foreclosure,即銀行強行收回房屋並拍賣以償還欠款)也不會造成損失。
貸款經紀與貸款商如何保持盈利的增長呢?他們所面臨的問題是隨著房屋價格的上漲,首次買房的購房者會越來越難以承擔高房價。怎麼樣才能持續性地吸引新客戶呢?貸款經紀及貸款商必須設法進一步降低貸款標準。果不其然,他們就是這樣做的。貸款標準降低的結果是貸款面額與房屋價值的比例提高了。這時市場開發出了可調整利率按揭(adjustable rate mortgages,ARM),在這一產品中,最初的前期優惠利率(“teaser” rate)很低,這一低利率會延續2~3年,而隨後的利率可能會很高。[1]在這期間,貸款商在審查貸款申請時也變得越來越漫不經心,以至於他們常常對申請貸款人的收入及其他有關信息都沒有仔細審查。
為什麼政府沒有對貸款商的行為進行謹慎管理呢?答案是自20世紀90年代開始,美國政府一直致力於擴大住房擁有率,並常常對貸款商施壓來使其加大對中低收入群體的貸款力度。有些州的立法人(例如,俄亥俄州和佐治亞州)曾表示對貸款現狀的憂慮,並且試圖通過立法來抑制掠奪性貸款現象。[2]但是法院認定,全國的貸款標準應具有優先權。
在信用緊縮之前,市場上有一系列的術語用於描述按揭發放過程,其中一個為“騙子貨款”(liar loan),用來描述按揭貸款申請人知道貸款申請過程中不會進行背景調查,因此在申請表上進行撒謊的行為。而另外一種貸款人被稱作“忍者”(NINJA,指沒有收入、沒有工作、沒有資產)。有些分析師認識到按揭貸款風險已經很高,但市場上由按揭貸款支持的證券的價格顯示,直到2007年,市場的參與者才真正認識到風險的嚴重程度和潛在影響。
Mian和Sufi的研究結果證實了按揭借貸的標準確實有所降低。[3]在他們文章中,Mian和Sufi定義了“高拒郵編號”(high denial zip codes)為那些在1996年按揭申請被拒比率較高的地區所對應的郵編號碼。Mian和Sufi發現,2000~2007年,高拒郵編號地區的按揭貸款增長速度尤其快,另外,Mian和Sufi的研究結果顯示按揭貸款制度隨時間有一個逐步,而非一次性的放鬆過程,這是因為高拒郵編號地區的按揭發行量在2000~2007年是一個時間的遞增函數。Zimmerman(2007)的研究結果對這一點做了一定的證實,[4]其研究結果表明,2006年發行的按揭質量比2005年要差,而2005年發行的按揭質量比2004年要差。標準普爾的估測表明,2006年一年內的次債發行總量為4210億美元。AMP資本投資者公司(AMP Capital Investors)的數據顯示在2007年7月全部次級按揭貸款總量為1.4萬億美元。
6.1.2 泡沫破裂
貸款制度的放鬆造成了房屋價格的泡沫,2000~2006年,住房價格飛速上漲。我們知道所有的泡沫最終總會破裂,住房價格泡沫也不例外。在2006年下半年,房價開始下跌。造成房價開始下跌的原因之一是房價上漲了,需求開始下降;另一個原因是當初期優惠利率結束後,許多貸款持有者發現自己並沒有能力支付貸款,這造成了斷供的上升,使許多房屋重新回到市場上,增大了房屋供應量。這造成了惡性循環:那些借貸數量為房屋價格100%或接近100%的貸款人這時發現他們的資產變成了負數(因為按揭貸款的數額超出了房屋的價值)。很多人選擇違約,這導致更多的斷供,市場供應量進一步加大,從而進一步壓低了房價。
美國房屋市場的一個特點是在許多州按揭具有無追索(nonrecourse)條款,這意味著當貸款人違約時,貸款借出方可以收回住房,但對貸款人的其他財產是不能追索的。[5]因此,貸款人持有一個免費的美式看跌期權,他可以在任何時候以按揭的當前本金餘額的價格將房屋賣給貸款借出方(在最初優惠利率期間,按揭本金往往會增加,這使得期權的價值變得更高)。市場參與者在後來認識到這一期權非常昂貴,但為時已晚。如果貸款人的淨值為負,這時最好的策略是以本金餘額的價格賣出住房,房屋隨之在市場上拍賣,從而造成了市場價格的進一步下跌。
假設所有按揭違約人的處境都相同會是一個很大的錯誤。有些人不能承受按揭付款,當他們放棄房屋時會麻煩重重。但市場上有許多違約者是出於投機,他們買入房屋是為了出租,這些人會適時選擇行使看跌期權,這會給房屋的租客帶來麻煩。還有報告顯示,有的房屋擁有者(並非投機者)十分有創意地抽取看跌期權的價值,當他們將鑰匙還給住房貸款借出方後,隨即就以更好的價格買入那些已經斷供並被拍賣的住房。假設兩個相鄰並且結構相似的房屋均已喪失了贖回權,兩個房屋的按揭均為250 000美元,而且兩個房屋的價值均為200 000美元,斷供房屋的拍賣價均為170 000美元。這時房屋擁有者的最佳策略是什麼?答案是每個房屋擁有者均行使看跌期權,並隨即買入鄰居的屋子。
當斷供增加時,按揭貸款的損失也增加。損失會增加是因為斷供的房屋周圍通常還有其他斷供的房屋在市場上銷售。房屋的狀況通常也很糟。另外,銀行還要承擔法律和其他的費用。在正常的市場條件下,貸款借出方一般可以回收貸款餘額的75%。2008~2009年,某些地區的回收率只有25%。
美國並不是唯一的房價下跌的國家,世界上許多其他國家的房價也難逃厄運。當時英國的房價下跌幅度也非常大。如圖6-1所示,2012年年中~2017年3月,美國的平均房地產價格開始回升。
[1] 例如,一個“2/28”可調整利率按揭(“2/28”ARM)是指該產品在最初2年為固定利率,而在今後的28年為浮動利率。當房地產價格上漲時,貸款商預料貸款人會在優惠利率結束前提前付清按揭,併購買一個新的按揭。但是,次級貸款中對提前償付的懲罰可能會很高,而類似的懲罰在優質按揭貸款中一般是不存在的。
[2] 掠奪性貸款是指貸款借出方以欺騙的手段與客戶簽訂的不公平的貸款合約。
[3] See A. Mian and A. Sufi, “The Consequences of Mortgage Credit Expansion: Evidence from the US Mortgage Default Crisis,” Quarterly Journal of Economics 124, no.4(November 2009):1449-1496.
[4] See T. Zimmerman, “The Great Subprime Meltdown,” Journal of Structured Finance (Fall 2007):7-20.
[5] 在某些州,雖然按揭沒有無追索條款,但存在某些法規使得債主很難追索房產以外的資產。
6.2 證券化
按揭貸款的發行方在許多情形下並不保留按揭資產,而是將按揭賣給對其進行打包併產生證券的公司,這一過程被稱為證券化(securitization)。許多年來,證券化是市場上一個十分重要的有效的融資工具,證券化是發起-分銷模式的基礎。這種工具在2007年前被銀行普遍採用,在第2章中我們曾經對此有過討論。
證券化對房價泡沫的產生起了一定的作用,按揭的最初發行方知道貸款最終會被證券化,這一點會影響發行方的行為。[1]這時,在考慮是否接受按揭申請時,按揭發行者不再關心“是否願意承擔信用風險”,而會更加關心“是否可以將按揭賣給其他人來盈利”。
當按揭被證券化後,按揭支持證券的買入方所得到的唯一信息是貸款與價值的比率(loan-to-value ratio,即貸款數額與房屋估價的比率),以及貸款人的FICO信用分數[2]。貸款發行者並不關心貸款申請人的收入狀況、申請人在其住址上居住的年份等信息,因為這些信息被認為是無關緊要的。對於貸款發行方而言,最重要的是按揭貸款是否可以被賣給其他人,而這主要取決於貸款與價值比率,以及貸款申請人的FICO分數。
有時即使通過了貸款與價值比率和FICO分數檢驗的按揭也可能具有較差的信用質量,這一點耐人尋味。在貸款發放時,有時需要物業價格評估師(property assessor)確定物業的價值,有時評估師會給出虛高的價格,因為他們知道貸款發放人希望較低的貸款與價值比。有時一些潛在的貸款人可能會得到一定的諮詢,以設法改善自身的FICO分數。[3]
我們接下來將要討論由按揭所派生出的產品以及其在市場上的出售過程。
6.2.1 資產支持債券
資產支持債券(asset-backed security,ABS)是由貸款、證券、信用卡應收付款、按揭、飛機租用費等類似的資產現金流而產生的證券,有時甚至音樂唱片的將來收入所產生的現金流也可以用來產生證券。證券的產生過程如圖6-2所示,資產發行人首先將投資組合(例如次級貸款組合)賣給一個特殊目的機構(special purpose vehicle,SPV),然後將資產現金流分配到不同的分檔(tranche),並對分檔進行出售。圖6-2中債券共有3個分檔:優先檔、中間檔以及權益檔。投資組合的面值為1億美元,組合資產被分為:優先檔面值為7 500萬美元,中間檔面值為2 000萬美元,權益檔面值為500萬美元,優先檔承諾的回報率為6%、中間檔為10%、權益檔為30%。
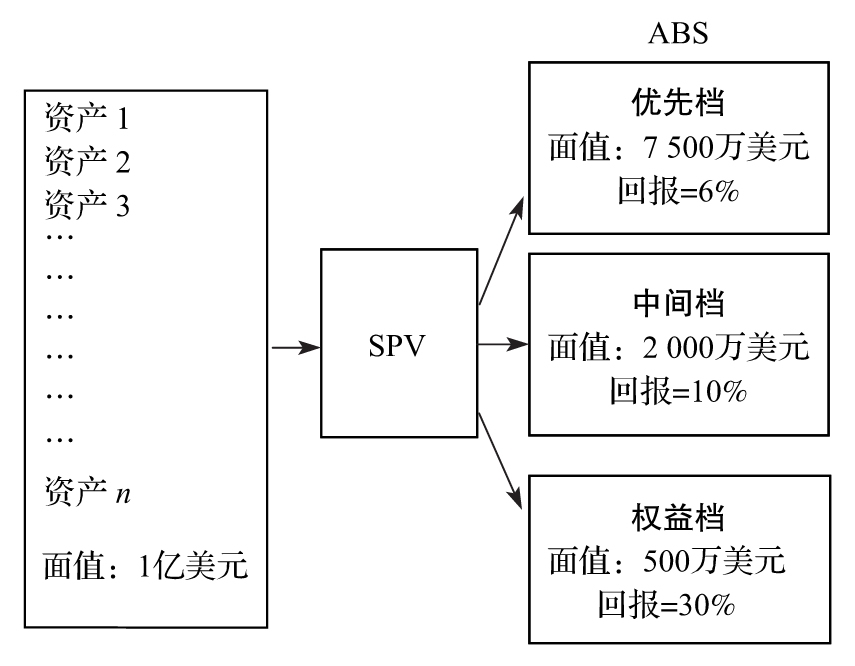
圖6-2 一個資產支持證券(簡化版)
乍看起來權益檔最為合算,但實際並非如此。權益檔拿到回報的可能性要小於其他兩個等級的分檔,證券化的現金流是以所謂的瀑布(waterfall)式進行分配的,瀑布式現金流分佈如圖6-3所示。利息和本金的現金流是兩個分開的瀑布。利息現金流首先要分配給優先檔,直到這個分檔收到所有的承諾回報後,現金流才會向較低檔進行分配。假定優先檔所承諾的回報可以被滿足,現金流可以進一步向中間檔來分配,如果中間檔所承諾的回報也被滿足,而且利息現金流仍有剩餘,這時剩餘的部分才會向權益檔進行分配。本金現金流也是先用來償還優先檔的本金,然後是中間檔,最後是權益檔。[4]
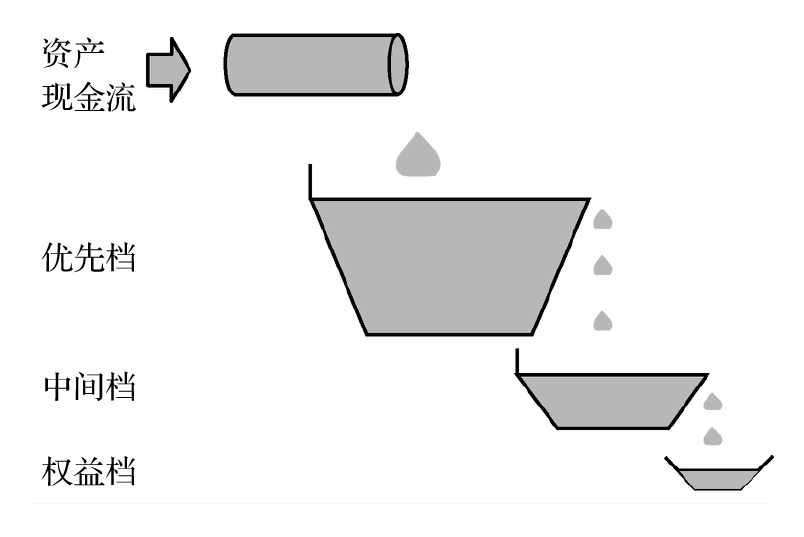
圖6-3 資產支持證券中的瀑布式現金流
圖6-2中的結構一般要持續幾年。各檔所收到的本金取決於資產的損失程度。最初資產5%的損失由權益檔承擔;如果損失超過5%,權益檔將會損失全部本金。中間檔也會損失一定本金;如果損失超過25%,中間檔將損失全部本金,優先檔也會損失一定本金。
因此,我們可以用兩種方式來看資產支持證券的結構:一種是以圖6-3所示的瀑布式現金流形式。現金流首先會分配給優先檔,然後是中間檔,最後才是權益檔;另一種是以承擔損失的方式,權益檔首先承擔損失,然後是中間檔,最後才是優先檔。
資產支持證券的設計方式是保證優先檔的信用評級為AAA,中間檔的信用評級為BBB,權益檔通常沒有信用評級。與一般債券評級不同,資產支持證券各檔的評級常常被稱為“協商評級”(negotiated rating)。ABS發行者的目標是產生最大數量的優先檔資產,並保證其信用評級達到AAA級(這樣做可以將資產結構的盈利最大化)。在發行證券之前,ABS的發行者首先要查看信用評級公司如何來對各檔進行評級,然後向評級公司提供幾種債券發行的初選方案,最終選定一種結構來發行證券。資產支持證券的生成人一般會盈利,因為標的資產組合的加權平均回報高於賣出的各檔證券的加權平均回報。
一種特殊的資產支持證券就是所謂的擔保債務憑證(collateralized debt obligation,CDO),這種債券的標的資產為固定收益債券。附錄L介紹了市場上用以定價一個CDO的步驟。
6.2.2 基於ABS的CDO
尋找願意向由次級貸款所派生出的高級AAA檔的投資者並不困難。權益檔常常由按揭發行人持有,而且對衝基金也有興趣購買權益檔,但尋找中間檔的投資者會比較困難。這時金融工程師發揮了其想象力(有人說太具有想象力了),他們由ABS的中間檔進一步創造出新的ABS。以這種形式產生的債券被稱為ABS CDO或中層ABS CDO(mezz ABS CDO),其產生過程如圖6-4所示。ABS CDO的優先檔的評級為AAA,這意味著我們例子中的所有AAA級產品的面值佔基礎按揭組合面值的90%(75%加上20%的75%),這一比率看起來已經很高,但如果考慮將中層ABS CDO進一步證券化,那麼AAA級證券面值佔基礎按揭組合面值的比率會更高。
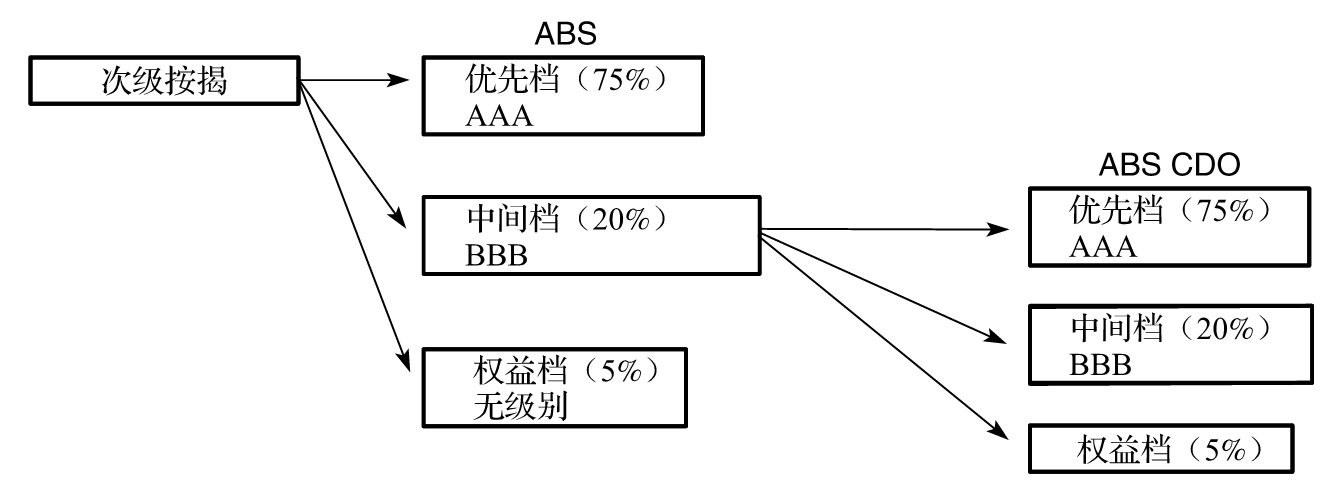
圖6-4 一個簡化的ABS CDO
在圖6-4所示的例子中,ABS的AAA檔在2007年下半年可能已經被降級,但是,如果基礎按揭資產的損失小於25%,因為有更低檔的證券來承擔本金損失,該檔仍可能會收到其承諾回報。圖6-4所示ABS CDO的AAA檔會更加危險。當基礎按揭組合的損失小於10%時,該檔會收到其承諾回報。這時ABS中間檔所承擔的損失小於或等於ABS本金面值的5%,[5]因為ABS CDO中間檔的面值為ABS面值的20%,其所對應的最大損失(以ABS資產為基準)為5/20,即25%,因此,在最差的情況下(25%的ABS CDO損失,即標的資產損失為10%),ABS CDO的權益檔及中間檔會全部耗盡,但最優先檔沒有任何損失。
當標的投資組合的損失高於10%時,ABS CDO的優先檔會有損失。例如,當標的投資組合的損失為20%時,這時ABS中間檔的損失率達15/20,即其面值的75%,最初25%的損失由ABS CDO權益檔及中間檔承擔,ABS CDO的優先檔損失率達50/75,即67%。表6-1是對這一結果及其他情形所對應損失的總結。
表6-1 圖6-4中各檔的損失 (%)

許多銀行因持有ABS CDO的優先檔而蒙受損失。這些投資承諾的回報通常遠高於銀行的融資成本。因為投資資產的信用級別為AAA,投資所對應資本金要求會比較低。美林證券就是因投資ABS CDO而蒙受了巨大損失。2008年7月,美林以每一美元面值按22美分的價格向Lone Star Funds出售了總面值為306億美元、信用級別曾被評為AAA級的ABS CDO優先檔。[6]
6.2.3 實際中的ABS及ABS CDO
圖6-2和圖6-4說明了證券化過程的實質。在實際中,證券化產品具有更多分檔,許多厚度比圖6-2和圖6-4中的分檔更薄(即承擔損失範圍會更窄)的分檔被創建出來。圖6-5展示了一個更接近於真實的結構,這一結構選自Gorton的文章,它最初來源於UBS的一篇文章。[7]
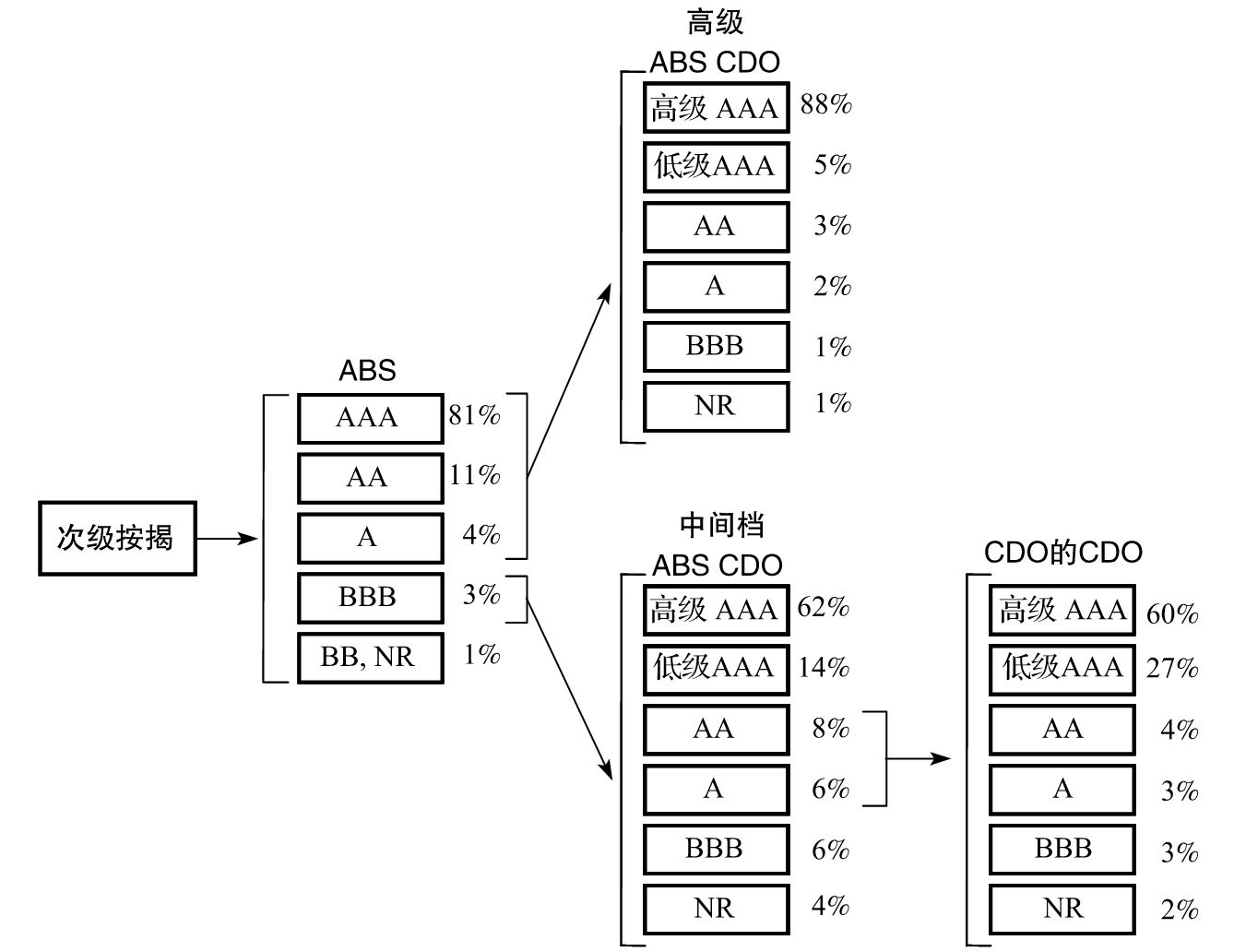
圖6-5 一個現實的次級債證券化過程,其中ABS、ABS CDO和CDO的CDO設有超額抵押和超額利差機制
圖6-5顯示,由ABS可以產生兩類ABS CDO:一類由ABS的BBB級分檔來產生(見圖6-4中的ABS CDO),另一類由ABS中的AAA級、AA級及A級分檔來產生。圖形展示由中層ABS CDO可以派生第三層證券。通常我們會設定一個少量的所謂超額抵押(over-collateralization)機制,即按揭抵押資產的面值要比ABS證券的面值更高(1%或2%)。這對投資者提供了一定的保護,但只要做一個類似於表6-1中的分析,我們就會發現,事實上當基礎的次貸抵押貸款的損失稍微高一點時,很多分檔的投資者都會損失本金。
ABS CDO中AAA級分檔的風險以及相對來講風險較小的ABS的AAA級分檔的風險,要比投資者和評級公司所意識到的更高,其中一個原因是相關性。ABS分檔的價值與基礎按揭資產中違約相關性有關,而ABS CDO分檔的價值更加依賴於違約相關性。如果按揭違約的相關程度並不很高(一般情況是這樣),整體來講,高違約率並不太可能發生,因此AAA級分檔是相當安全的。但被很多分析師忽略的一個事實是,在受壓市場下,違約相關性總是會增加。2005~2006年,投資者和評級機構所採用的模型中假設的違約率相關性太低,特別是在很多觀察者已經預見到美國房地產市場很可能發生動盪的情況下。如業界事例6-1所示,分析人員所犯的一個錯誤是對ABS中的BBB級分檔與企業BBB級債券等同處理,但這兩類債券有顯著差別,而這些差別對於ABS CDO分檔中的風險有很大影響。
業界事例6-1
並非所有BBB級債券都是一樣的
分析人員在對由中間檔所派生出的CDO進行分析時,往往假設BBB級的ABS中間檔與一般BBB級證券是等同的,這是非常糟糕的假設。評級機構的模型試圖保證ABS的BBB級分檔具有和BBB級債券同樣的損失概率或預期損失。但實際上,二者的損失概率分佈大相徑庭。例如,BBB級別的ABS分檔損失100%面值的可能性要遠遠高於一般BBB債券損失100%面值的可能性(這一風險有時被稱作“懸崖風險”(cliff risk))。這意味著ABS CDO分檔的風險特性與由債券產生的CDO債券的風險特性有很大不同。當分檔的厚度變薄時,這些差別會變得更加顯著。
由此得出的一個教訓是,將ABS分檔(或其他結構性產品)的級別等同於一般證券的信用級別的做法是很危險的。相似評級的債券和結構化產品,它們損失的概率分佈有顯著不同。
[1] Keys等的研究結果表明,證券化的發展與按揭篩選條件的寬鬆有一個關聯性,見B.J. Keys, T. Mukherjee, A. Seru, and V. Vig, “Did Securitization Lead to Lax Screening? Evidence from Subprime Loans,” Quarterly Journal of Economics 125, no.1(February 2010):307-362。
[2] FICO是由費埃哲公司(Fair Isaac Corporation)開發的一套信用評分體系,在北美被廣泛使用。信用分數的取值範圍是300~850。
[3] 一種做法是持續幾個月對信用卡進行按時付款。
[4] 這裡給出的優先權規則是被簡化了的。精確的現金流分配方式可能非常複雜,用以說明的法律文件可能長達幾百頁。
[5] 即高於權益檔5%上的額外的5%損失。——譯者注
[6] 事實上,這個交易對美林來講情況可能會更糟,因為美林要為售價的75%提供資金支持。當分檔價格低於每一美元面值16.5美分時,美林可能會發現這些資產實際上又回到了自己賬上。
[7] G. Gorton, “The Subprime Panic,” European Financial Management 15, no.1(2008):10-46.
6.3 危機爆發
在美國,住房抵押貸款的違約引發了一系列後果。購買了ABS和ABS CDO分檔產品的金融機構與其他投資者蒙受損失。一些抵押貸款發行人也遭受損失,因為他們對一些被證券化的抵押貸款提供了保護,還因為他們的借貸行為產生的法律訴訟。
就像債務市場上經常發生的,當一個行業發生損失時,會造成安全投資轉移(flight to quality)現象。投資者不再願意承受任何信用風險,而是趨向於買入國債和類似的安全投資。信用價差(為承擔信用風險而需要的超額收益)大幅度增加。很多非金融企業很難從銀行取得貸款。實際上,銀行之間也不願相互貸款,同業拆借利率也大幅攀升。
2007年下半年,ABS和ABS CDO分檔的評級被下調。市場上這些分檔的流動性變得非常差。投資者認識到,他們並沒有像以前所認為的那樣真正理解這些分檔,而且他們過於依賴評級信息了。這也折射出金融市場透明度的重要性。危機爆發前出現的產品非常複雜。[1]投資者直到問題爆發才意識到這一點,然後他們發現,這些產品的流動性如此之差,自己只能以清倉甩賣的價格來拋售了。
花旗集團、UBS和美林等銀行遭受了嚴重損失,政府不得不對很多金融機構進行救助。雷曼兄弟則被放棄,陷入破產。世界經受了自20世紀30年代以來最嚴重的金融危機。失業率增加,甚至連世界偏遠角落裡和美國金融機構沒什麼聯繫的人也被波及。
銀行業現在仍在為危機付出代價。我們將在第16章中看到,現在銀行要保留更多的資本金,要維持一定的流動性比率。諸如《多德-弗蘭克法案》等新的立法加強了對金融機構的監督並限制銀行進行某些活動,如自營交易和衍生產品交易。
[1] 有些產品的複雜性甚至超過第6.2節中的描述。例如,有時候,ABS CDO分檔被包括在投資組合中,生成新的ABS CDO。
6.4 什麼地方出了問題
非理性繁榮(irrational exuberance)這一說法是美聯儲前主席艾倫·格林斯潘首先提出的,用來描述20世紀90年代股票市場牛市時某些投資者的行為。這對信用危機爆發前的那個階段同樣適用。按揭貸款提供商、由住房按揭貸款生成的ABS和ABS CDO分檔的投資者,以及賣出對這些分檔的保護的那些公司假設“美好的時光”能永遠持續下去。他們認為美國房地產價格能永遠漲下去。個別地區的房價也許會有下降,但如圖6-1中出現的那種大範圍的下降被認為是不可能的。
造成2007年危機的因素有很多。按揭發行者降低了貸款標準,市場上產生了在保證盈利的情況下將信用風險轉移給投資者的產品。評級公司將其傳統評級業務轉移到了對結構性產品進行評級,而這些產品是比較新的,歷史數據也比較少。投資者購買的產品很複雜,並且在很多情形下,投資者甚至評級公司只具有關於標的資產質量的不準確和不完整的信息。結構性產品的投資者以為自己發現了印鈔機,這些投資者將評級公司所提供的信息用來取代自己關於標的資產的風險分析。評級為AAA級的結構性產品承諾的回報率也高於同樣評級的傳統債券。
6.4.1 監管套利
很多按揭貸款的發行人是銀行,而銀行也是從按揭貸款生成的證券分檔的主要投資者。為什麼銀行選擇將按揭貸款證券化,然後再去買入證券化產品呢?答案是因為“監管套利”(regulatory arbitrage)的存在。銀行持有由按揭貸款證券化產生的分檔所需要的監管資本金遠小於持有按揭貸款本身所需的資本金。這是因為按揭貸款需要放在銀行賬戶(banking book),而分檔產生的證券可以放在交易賬戶(trading book)。銀行賬戶和交易賬戶所需的監管資本金是不同的。對這一點,我們將在第15~18章中進一步討論。
6.4.2 獎勵機制
經濟學家所指的代理成本(agency cost)是描述在某個商業行為中,兩個不同參與者的利益不完全一致的情形。不幸的是,按揭貸款的發行、證券化以及在銷售給投資者的過程中恰恰存在代理成本。
按揭貸款發行人的動機是使貸款能夠被ABS和ABS CDO分檔的創建人所接受。按揭貸款所購買的房屋的估價人的動機是提供一個儘可能高的估價,使得貸款價值比儘可能低,以取悅貸款提供商(取悅貸款提供商的好處是以後可以拿到更多的生意)。ABS和ABS CDO的創建人主要關心的是證券結構的盈利水平(也就是加權平均後流入資金與流出資金的比值)。他們希望自己產品中AAA級分檔的比重能儘量的高,並找到了根據評級機構發佈的評級信息來達到這一目的的方法。評級機構從被評級的產品的發行商那裡獲得報酬,他們有大約一半的收入來自結構化產品。
另一類代理成本與金融機構和其僱員有關。僱員的薪酬分成三類:一般工資、年終現金分紅以及股票和股票期權。金融機構中許多不同級別的高級僱員(特別是交易員)的薪酬很大一部分是以年終現金分紅形式給出的。這種薪酬形式側重於短期表現。如果某個僱員在某年盈利很高而在今後的幾年損失很大,則該僱員在第一年會收到很高的現金分紅而在今後幾年不需要歸還已得到的分紅。僱員也許因為第二年的損失而失去工作,即便如此,對他來講,也沒什麼大不了。令人驚訝的是,金融機構好像很願意僱用那些簡歷上有損失記錄的人員。
假設你是一位在2006年投資於ABS CDO資產的一家金融機構的僱員。幾乎可以肯定,你已經意識到美國房屋市場存在泡沫並認定這一泡沫最終會破裂。但是你仍然可能會決定進行ABS CDO投資。如果這一泡沫在2006年12月31日之前不破裂,那麼你仍可能在2006年年底收到一筆可觀的分紅。
6.5 危機的教訓
從危機中,風險管理人員應學到以下的教訓:
(1)風險管理人員應注意那些存在非理性繁榮的機構,並且保證高層管理人員能意識到美好的時光不會永遠持續下去。
(2)在市場受壓的情況下,相關性總是增加的。在考慮情況能變得多糟糕時,風險管理人員不能使用正常市場條件下估算的相關性。
(3)不僅對於按揭貸款,對於大部分債券,當違約率上升時,回收率會下降(見第19.3節)。當考慮情況能變得多糟糕時,風險管理人員不應使用從正常市場條件下得來的回收率數據。
(4)風險管理人員應保證,對交易人員的獎勵和其他個人激勵措施應保證他們做出的決定與公司的利益一致。由於金融危機,很多金融機構已經更改薪酬政策。現在分紅往往被分攤到幾年內發放,而不是在一年內全部付清。如果前一年的表現很好而接下來一年的表現很差,那麼在表現好的年份的分紅中還沒有發放的部分有可能被收回(claw back)。
(5)如果一個交易看上去好得讓人難以置信,那它多半就不是真的。結構化產品中AAA評級的分檔承諾提供比同樣評級的普通債券高100個基點的回報。對這一點,一個明智的投資者應當得出結論:進一步的分析很有必要,因為分檔中很可能存在評級機構沒有考慮到的風險。
(6)投資者不能過於依賴評級。他們應該清楚評級機構使用的假設,並進行自己的分析。
(7)金融市場的透明度很重要。如果缺乏透明度(例如ABS CDO的例子),那麼當壞消息來臨時,市場的流動性很可能喪失殆盡。
(8)生成ABS CDO和CDO的CDO產品的再證券化(re-securitization)是個非常糟糕的主意。用以在第一層證券化中生成ABS的資產也應儘量分散。進一步證券化不會產生任何有益的結果。
業界事例6-1表明,很多從業者以為評級為BBB級的ABS分檔和BBB級的債券是等同的。而業界事例6-2表明,認識到事實並非如此的人可以採用一個交易策略從中獲利。
業界事例6-2
一個交易機會?
一些交易員與次貸市場對賭,並賺取了豐厚利潤。假設你正在分析2005年和2006年的市場,但是並不清楚次級貸款表現會如何。那是不是還有一個交易機會呢?
答案是,ABS CDO的中間檔真的會帶來一個機會。圖6-5簡要描述了分檔是如何產生的。在實際中,通常存在3個ABS分檔:BBB+、BBB和BBB-。每層都很薄,只有1%左右。獨立的ABS CDO的中間檔分別從這三層中產生。考慮從BBB+分檔生成的ABS CDO的中間檔。交易者可能會合理地得出以下結論:從不同的按揭貸款組合中生成的BBB+分檔要麼是安全的(因為沒有地產危機),要麼會全部損失(因為這些份額只有1%的厚度,部分損失是不太可能的)。這意味著,所有從ABS的BBB+級分檔創建的ABS CDO的中間檔要麼是安全的,要麼會全部損失。因此所有ABS CDO中間檔的評級應該是一樣的(在本例中,應為BBB+)。
認識到這一點後,交易員該怎麼做呢?他應該買入初級ABS CDO分檔(因為評級低,會更便宜),同時賣空ABS CDO的優先檔(相對更貴些)。如果標的資產的面值相同,則交易員已經輕鬆地鎖定了利潤。
這再次說明,業界事例6-1中的BBB級分檔(特別是當分檔很薄時)不能被等同於BBB級債券。
小結
2007年開始的信用危機給全球金融市場帶來了災難性的效應。這一危機最初源於美國房屋市場。美國政府曾熱衷於鼓勵住房所有權。利率一度很低。按揭經紀以及按揭發行商發現可以通過降低貸款標準來贏得更多的業務。市場上產生了證券化產品使投資者所面臨的信用風險不同於最初按揭發行人所面臨的信用風險。信用評級公司對證券化的優先檔給出了AAA的評級,市場上出現大量AAA級分檔的投資者,這是因為高分檔AAA級債券的回報要高於AAA-級債券。銀行認為這一“美好時光”將會持續,而且因為交易員的獎勵集中於其短期表現,所以房屋市場泡沫以及所交易的這些複雜產品對於市場的潛在影響被選擇性地忽略了。
當初次購房者及投機者一起進入市場時,房價就上漲了。有些按揭包括適用於最初兩三年的優惠利率,當優惠利率結束後,許多貸款的還款利息會顯著增加。因不能償還高利息貸款,貸款人只能違約,從而造成了斷供的增大,同時也增加了賣方市場的供應。2000~2006年市場上漲現象終於戛然而止,投機者及其他投資者發現他們所欠按揭的價值大於其違約的房屋價值(即他們資產的淨值為負),於是選擇違約,這進一步加重了房價的下滑幅度。
造成美國房地產泡沫和由此產生的衰退的因素很多。這些因素包括:市場參與者的非理性繁榮、糟糕的獎勵措施、對評級機構的過度依賴、投資者分析的欠缺和產品的高度複雜化。危機帶給風險管理人員很多啟示。在本書後面的章節中我們將會看到,危機導致了對銀行監管系統和立法系統的非常大的調整。
延伸閱讀

練習題
6.1 為什麼在2000~2007年,按揭發行人常常不檢查按揭申請人的背景信息?
6.2 為什麼2000~2007年的房價上漲被稱為泡沫?
6.3 表6-1所對應的標的資產損失率(a)5%及(b)12%的含義是什麼?
6.4 ABS分檔的風險和同樣評級的債券的風險有何不同?
6.5 解釋以下資產的差異:(a)ABS;(b)ABS CDO。
6.6 市場是如何錯誤地判斷了ABS CDO的風險的?
6.7 “代理成本”的含義是什麼?
6.8 什麼是證券化的瀑布式現金流?
6.9 ABS CDO是如何產生的?產生ABS CDO的動機是什麼?
6.10 研究人員Mian及Sufi如何說明按揭發行人在2000~2006年確實降低了貸款發行標準?
6.11 什麼是中間檔?
6.12 解釋違約相關率上升的影響:(a)ABS中權益檔的風險;(b)ABS中優先檔的風險。
6.13 解釋為什麼年末的現金獎金是一個短期獎勵。
作業題
6.14 假定ABS和ABS CDO的優先檔、中間檔及權益檔所對應的本金比例為70%、20%和10%,而不是圖6-4所示的75%、20%和5%,這一變化對錶6-1的影響是什麼?
6.15 試著解釋如果圖6-4中ABS中間檔的厚度減小,並且減小的分檔被平分給優先檔和權益檔,那麼會發生什麼情況?特別地,對錶6-1的影響是什麼?
第7章
定價和情景分析:風險中性世界和真實世界
定價(或估值)和情景分析是金融機構進行的兩項重要的活動。二者都涉及未來現金流的估算,但是它們的目的不一樣。在定價過程中,金融機構的意圖是估算未來現金流的當前價值。要做到這一點,需要求出未來現金流的期望值(即未來可能出現的所有情形下的現金流的平均值),然後將該期望值貼現到當前。而在情景分析中,金融機構的目的是探究在未來某一個時間點上,所有可能出現的情況。通常,那些帶來不利後果的情景會得到最多的關注,因為金融機構工作的風險管理人員往往需要回答這樣的問題:“情況到底會糟糕到什麼地步?”
假設一家金融機構賣出了以某股票為標的的1年期看漲期權100萬股。當前股票的價格是每股50美元,期權的執行價格是55美元。該機構計算出的期權的價值對買家而言是+450萬美元,對自己而言是-450萬美元。如果賣出期權的收入是500萬美元,則公司可以取得50萬美元的利潤。但是情景分析可能得出這樣的結果:在1年內,該股票的價格有5%的可能會達到80美元。這意味著,在考慮了最初賣出期權的收入後,這筆交易有5%的可能會造成2 000萬美元的損失。這個例子說明了定價和情景分析的關鍵區別。定價關注的是可能發生的情況的平均(在上面的例子中,450萬美元是期權可能的收益的平均值貼現後的結果),而情景分析關注的重點是極端情況下的結果(在上面的例子中,這筆交易可能給公司帶來2 000萬美元的損失)。
在本章中我們將討論在實踐中如何進行定價和情景分析。我們會介紹如何區分真實世界中的預測和風險中性世界中的預測,前者是情景分析的基礎,而後者是定價的基礎。風險中性定價可以用於諸如資產價格一類隨時間變化的變量,也可以用來處理那些結果依賴於某一離散事件是否會發生(如一家公司是否違約)的情況。本章將介紹如何進行蒙特卡羅模擬,並解釋在預測資產價格時一般需要做哪些假設。
7.1 波動和資產價格
在討論定價和情景分析之前,我們先來介紹幾點與資產價格的表現有關的常用知識。假設資產的當前價格為S0,一個常見的假設是價格每年會以一個常量μ(以連續複利計)增長,價格的波動率也是一個常量,每年為σ。[1]我們可以證明,在T年後,資產價格ST的概率密度函數為[2]
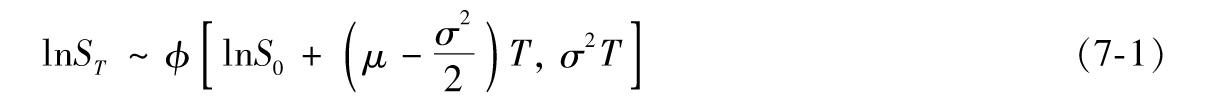
其中,ϕ(m,v)表示均值為m、方差為v的正態分佈,ln為自然對數函數。變量ST服從對數正態分佈,因為它的自然對數是一個正態分佈。lnST的均值是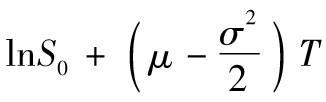 ,標準差是
,標準差是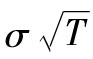 。
。
ST小於某個值V的概率,等於lnST小於lnV的概率。根據正態分佈的性質,我們可以得到
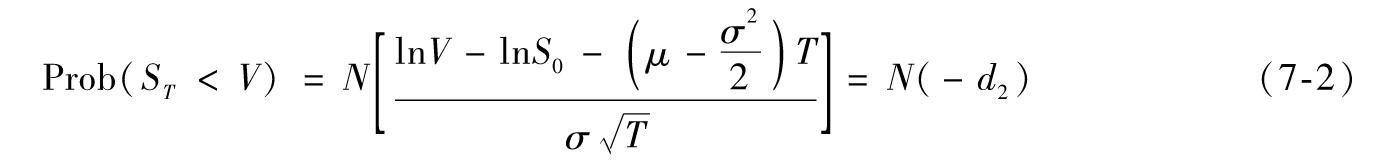
其中
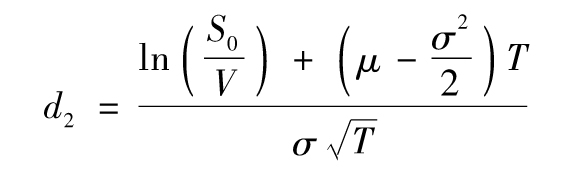
N為正態累積分佈函數,可由Excel軟件中的NORMSDIST函數計算得出。在T時刻,ST大於V的概率為
Prob(ST>V)=1-N(-d2)=N(d2)
(7-3)
最後,假設我們希望找到V,使得ST的值大於V的概率是q,也就是說Prob(ST>V)=q。由式(7-3),我們有N(d2)=q,即
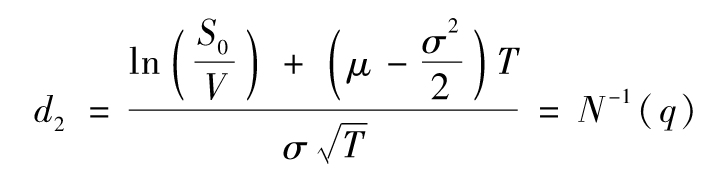
或者
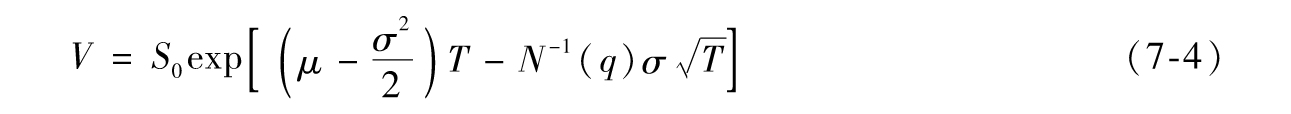
其中N-1是正態累積分佈函數的反函數,可由Excel的NORMSINV函數算出。類似地,若ST的值小於V的概率是q,即Prob(ST<V)=q,由N(-d2)=q或d2=-N-1(q),可知
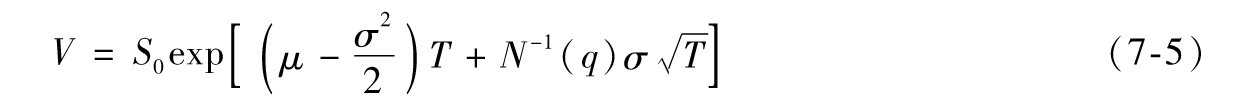
[1] 我們在附錄A中對於連續複利做了介紹。顧名思義,波動率是一個度量股票價格不確性的手段,在第10章中我們將對它進行更精確的定義。
[2] 推導過程可見J. Hull, Options, Futures, and Other Derivatives, 9th ed. (Upper SaddleRiver, NJ: Pearson, 2015)。
7.2 風險中性定價
衍生產品定價最重要的一個手段就是風險中性定價。一個風險中性世界(risk-neutral world)可以是一個想象中的世界,在這個世界中投資者不要求為所承擔的風險得到補償。也就是說,在該世界中,一項有風險的投資需要提供的預期回報與無風險的投資是一樣的,均為無風險利率。我們生活的真實世界顯然不是風險中性的。我們身邊的投資者均要求為自己承擔的風險獲得補償(第1章給出了一個便於理解風險-回報替代關係的框架)。但是,風險中性定價方法顯示我們可以通過假設世界是風險中性的來為任何衍生產品定價,而且我們不僅可以在風險中性世界中得出正確的定價結果,該結果還可以用在任何其他世界中。
乍看上去,風險中性定價的結果似乎完全不合理。投資者並不是生活在風險中性的世界中。當他們面對的風險上升時,他們通常會要求得到更高的回報,這一結論適應於衍生產品及其他投資。[1]但當我們試圖理解風險中性定價時,需要注意關鍵一點,對某一衍生產品進行定價,我們計算的價格是與標的資產價格有關(例如,股票期權價值的計算與標的股票的價格有關),而標的資產的價格反映了市場參與者對風險-回報的權衡。如果市場參與者認為由於資產的風險他們應該獲得更多(更少)的回報,資產的價格就會下降(上升)。而風險中性定價認為將標的資產價格轉換成衍生產品價格的計算公式是獨立於投資者的風險偏好的。
在風險中性世界中,所有未來的現金流都以無風險利率進行貼現。這極大地簡化了定價。假設我們要給一隻股票的看漲期權定價,無風險利率是3%。風險中性定價的步驟如下:
(1)假設股票未來的預期回報率是3%(平均值);
(2)計算看漲期權的預期收益;
(3)以3%的貼現率將預期收益貼現,得到期權的當前值。
一個很自然的問題是:“既然在真實世界中定價更為自然,為什麼我們還需要風險中性世界?”答案在於,雖然在理論上我們可以在真實世界中對一個看漲期權進行定價,但在實踐中這樣做很困難。我們需要履行以下的步驟:
(1a)估計股票在真實世界中的預期回報率(平均值);
(2a)計算真實世界中看漲期權的預期收益;
(3a)以適當的貼現率將期權的預期收益貼現,作為期權的當前價值。
在步驟(1a)中,我們有可能得到一個合理的、在真實世界中的股票未來預期回報率。為此,我們需要估計股票的beta,並使用第1章中介紹的資本資產定價模型。但完成步驟(3a)將非常困難。用來對真實世界預期收益進行貼現的正確貼現率依賴於期權的(而不是股票的)beta,而這個值在期權的生命週期中很有可能是變化的。隨著股票價格的變化,期權中隱含的槓桿會發生變化,貼現率也會跟著變化。如果在看漲期權的整個生命週期中使用單一貼現率,那麼得出的期權價值會非常高;同樣地,如果在一個看跌期權的生命週期中使用單一貼現率,那麼得出的期權價值會非常低,通常是負值。我們是怎麼知道這些情況的?我們可以使用風險中性定價,算出期權的價值,然後從這個答案倒推,看看要得到同樣的答案,在真實世界中正確的貼現率應為多少。後面我們會以一個二元期權為例,說明這一點。
風險中性定價是一個看上去很神奇的結論。它意味著我們無須關心諸如衍生產品的風險大小和市場對標的資產及衍生產品的回報要求之類的問題。我們需要問自己的唯一的問題是:如果我們生活在一個投資者對任何投資所要求的回報均等於無風險利率的世界中,我們如何對衍生產品進行定價?如果沒有風險中性定價,衍生產品的定價將會更加複雜(而且更加不準確)。
需要強調的是,風險中性定價(或者說“投資者在決定投資的預期回報時,並不關心投資的風險”這一假設)只不過是用來給衍生產品定價的一種人工設備。從中得到的定價結果不僅在風險中性世界中是正確的,在其他所有世界中也是正確的。當我們從風險中性世界變化到真實世界中時,會同時發生兩件事情:衍生產品的預期收益會發生變化,同時用於對預期收益進行貼現的貼現率也會發生變化。這兩個變化總是恰好相互抵消。
7.2.1 在遠期合約中的應用
作為風險中性定價的一個簡單例子,讓我們考慮一個遠期合約的多頭的定價,合約的標的資產是一隻不付股息的股票。假設交割價為K,期限為T。在到期日,合約的價值為
ST-K
其中ST是股票在T時刻的價格。根據風險中性定價的論點,該遠期合約在當前時刻(即零時刻)的價值即為它在風險中性世界中T時刻的價值以無風險利率貼現後的值。設遠期合約的價值為f,我們有
f=e-rTÊ(ST-K)
其中Ê表示無風險世界中的期望值,r為無風險利率(假設為常量)。因為K為常量,我們有
f=e-rTÊ(ST)-Ke-rT
(7-6)
在無風險世界中,股票價格的增長率是r。由此我們得到
Ê(ST)=S0erT
其中S0為股票的當前價格。將上式代入式(7-6)中
f=S0-Ke-rT
(7-7)
類似地,遠期合約空頭的價值為
Ke-rT-S0
(7-8)
上述結果和附錄C中的結果是一致的。
7.2.2 在二元期權合約中的應用
在本節中,我們給出了一個風險中性定價的更進一步的例子。假設一隻不付股息的股票的價格是30美元,如果1年後股價高於40美元,某衍生產品就會支付100美元。這種衍生產品被稱為二元或指狀(digital)或者是現金或無價值(cash-or-nothing)期權。假設無風險利率為每年3%(連續複利),真實世界中股票的預期增長率是每年10%(同樣是連續複利),股票的年波動率為30%。
在風險中性世界中,股票的預期增長率是每年3%。股票價格在1年後高於40美元的風險中性概率可以通過計算得出:設式(7-3)中的參數μ=0.03,T=1,σ=0.3,S0=30,V=40。我們有
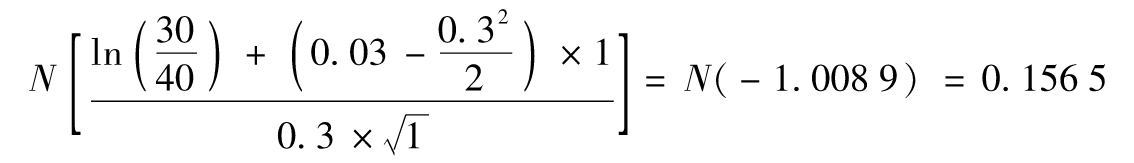
在風險中性世界中,該衍生產品的預期收益為100×0.1565=15.65美元。衍生產品的價值按3%無風險利率貼現1年後的價值為15.65e-0.03×1=15.19美元。
真實世界中股票價格在1年後高於40美元的概率是這樣來計算的:設式(7-3)中μ等於假定的股票1年後的回報10%,得出的概率為0.2190(我們將在本章後面的內容中解釋,當從風險中性世界變換到真實世界時,不需要改變波動率;反之亦然)。因此在真實世界中,期權的預期收益是21.90美元。我們前面曾經提到過,使用真實世界的預期收益進行定價的問題在於我們不知道應該使用什麼樣的貼現率。股票的價格存在風險,該風險已經被市場定價(否則股票的預期收益就不會是高於無風險利率的7%)。衍生產品可以在該風險基礎上增加槓桿,因此對衍生產品的預期收益貼現時應該使用更高的貼現率。我們知道該衍生產品正確的當前價值應為15.19美元,據此我們可以推算出真實世界中21.90美元的預期收益應使用的貼現率為36.6%(這是因為21.90×e-0.366×1=15.19)。
7.2.3 布萊克-斯科爾斯-默頓公式的應用
接下來我們考慮一隻不付股息的股票的歐式期權,執行價格為K,到期日為T,假設無風險利率為r,在T時刻的收益為
max(ST-K, 0)
其中ST為股票在T時刻的價格。因此,期權在T時刻的預期收益是
Ê[max(ST-K, 0)]
其中Ê表示風險中性世界中的期望值。使用風險中性定價的結論,該期權的價值為
e-rTÊ[max(ST-K, 0)]
(7-9)
類似地,相應的看跌期權的價值為
e-rTÊ[max(K-ST, 0)]
在進行一些代數變換後,我們可以證明這些結論可以推導出附錄E中的布萊克-斯科爾斯-默頓公式,用於歐式股票期權的定價。[2]
7.2.4 應用於離散化回報的情況
風險中性定價還可以用於回報是離散化的情況。假設在T時刻可能出現兩種互斥的結果。設π1為某衍生產品的價值,如果第一種結果出現,那麼該衍生產品在T時刻的收益為1美元,否則收益為0。同樣地,設π2為另一個衍生產品的價值,如果第二種結果出現,那麼該衍生產品在T時刻的收益為1美元,否則收益為0。如果同時買入這兩個衍生產品,那麼我們可以保證在T時刻獲得1美元的收益。在T時刻保證獲得的1美元收益的當前價值為e-RT,其中R為到T時刻的無風險利率(連續貼現)。所以我們有
π1+π2=e-RT
(7-10)
現在考慮另一個衍生產品,如果在T時刻第一種結果發生,則該產品支付V1;如果第二種結果發生,則支付V2。該衍生產品的價值為
π1V1+π2V2
進一步有
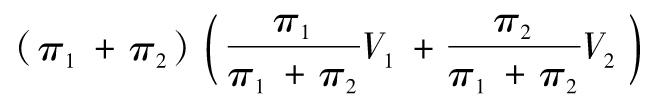
將式(7-10)的結果代入上式,該衍生產品的價值為
e-RT(p1V1+p2V2)
其中
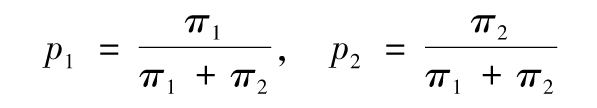
從這個結果出發,我們可以很自然地把p1和p2看作是兩種結果分別發生的風險中性概率。該衍生產品的價值也就是其在風險中性世界中預期收益以無風險利率的貼現。這個例子說明風險中性定價也適用於結果是離散的情形。
上述結果還可以擴展到結果有很多種可能的情況。假設在T時刻可能會發生n種互斥的可能的結果。設πi是一個衍生產品的價值,該衍生產品在第i(1≤i≤n)種可能結果發生時,收益為1美元,否則為0。那麼,一個在第i(1≤i≤n)種可能結果發生時,收益為Vi美元的衍生產品的價值為
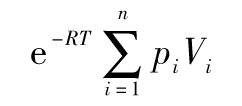
其中,pi為第i(1≤i≤n)種可能結果發生的風險中性概率,且
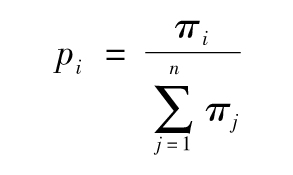
7.2.5 應用於違約概率
考慮一個金融工具,其回報取決於某家公司是否違約(這樣的工具可以定義成信用衍生產品)。根據我們在前面所做的分析,如果我們要對這樣一個衍生產品定價,那麼可以遵循以下步驟:
(1)估計違約的風險中性概率;
(2)計算衍生產品的預期收益;
(3)將預期收益按無風險利率貼現。
我們將在第19章中看到,風險中性違約概率可以由該公司發行的債券的收益率或信用違約互換利差推出。一般來說,風險中性違約概率會高於真實世界中的違約概率。
[1] 如在第1章中解釋的,對投資者來說系統性(即不能被分散的)風險是至關重要的。
[2] 按照約翰·赫爾所著的《期權、期貨及其他衍生產品》(Options, Futures, and Other Derivatives, 10th ed, Upper Saddle River, NJ: Pearson, 2018),可用三種方式推導出布萊克-斯科爾斯-默頓公式。第一種是先建立滿足所有衍生產品的微分方程,然後通過恰當的邊界條件求解;第二種是建立股票價格行為的二叉樹,然後對時間步長取極限,使其趨向於0;第三種是通過式(7-9)。這種方式的詳細步驟可在本書附錄和《期權、期貨及其他衍生產品》(原書第10版)的第15章中找到。
7.3 情景分析
現在我們討論情景分析。在情景分析中,我們希望瞭解將來可能發生的狀況。我們的目的不是定價,而未來的現金流也不會貼現到當前。在進行情景分析時,我們考慮的世界是真實世界,而不是風險中性世界。我們要強調的是,風險中性世界不過是我們為了對衍生產品進行定價而構造的一個人造的世界而已。對風險管理人員來說,他們一般不會太關心在一個人人都是風險中性的虛擬世界中,將來會發生什麼情況。
使用哥薩諾夫定理(Girsanov’s theorem),我們可以比較簡便地在真實世界和風險中性世界中切換。該定理證明,當我們從某一種風險偏好設定的世界變換到另一種風險偏好設定的世界時,市場變量,如股票價格、商品價格、匯率和利率的預期增長率會發生變化,但是它們的波動率不會變。
為說明情景分析是如何進行的,假設真實世界中的股票預期回報率為8%,目前股價為30美元,其波動率為25%。若你擁有10 000股股票,明年你的損失額會是多少?
由式(7-5)可知,在真實世界中1年內股票價格分佈的5%分位數為
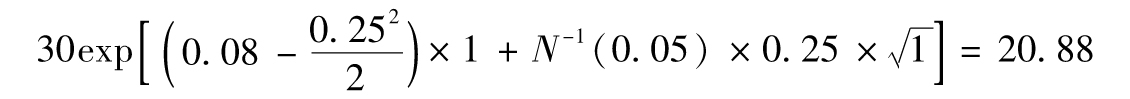
類似地,股票價格分佈的1%分位數是17.61美元。
因此,有95%的概率在接下來的1年裡損失不會超過10 000×(30-20.88)=91 200美元。同樣,可以99%地確定損失不會超過123 900美元。我們將在後面的章節中看到,這些就是所謂的風險價值評估。
這裡的關鍵是,由於我們在進行情景分析而不是評估,所以該結果是基於真實世界的預期回報率,而不是無風險回報率。
7.4 兩個世界必須同時使用的情況
在某些情況下,進行情景分析要求我們既使用真實世界,又使用風險中性世界。真實世界用來產生在需要考慮的時間範圍內可能發生的情景,風險中性世界則用來為在這個時段內仍未有效的交易進行定價。舉一個簡單的例子,假設我們剛才討論過的遠期合約是某投資組合中唯一的一筆交易。我們希望通過情景分析來研究一下6個月後,這個投資組合的價值會是什麼情況。為了達到這個目的,我們需要進行兩個步驟:
(1)計算真實世界中,6個月後股票價格的概率分佈。
(2)使用步驟(1)中得到的股票的可能價格,對6個月後的遠期合約進行定價,並得到遠期合約6個月後價值的概率分佈。此時,需要使用風險中性定價(6個月後,合約的期限為1.5年)。
假設我們想知道6個月後可能出現的“最壞”的情況。我們可以把“最壞”定義成6個月後合約價值概率分佈中對應於1%概率的低點。在這個例子中,因為該投資組合非常簡單,所以最壞的情況對應於在真實世界中6個月後股票價格可能以1%的概率達到的高點。根據式(7-4)此點對應的股票價格應為
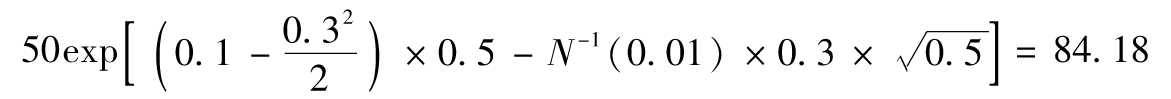
將這個股票價格代入式(7-8),得到的遠期合約的價值為
55e-1.5×0.03-84.18=-31.61
因此,6個月後,有1%的概率,合約的價值會低於-3 161萬美元。
注意,最壞情況下的股價是在真實世界中計算出來的,然後用風險中性估值法對遠期合約的最壞情況進行估計。
7.5 實踐中的計算
我們剛剛看到的例子非常簡單,因為組合中只有一個金融工具——一個2年期的股票遠期。我們知道該合約的價值隨著標的股票價格的上升而下降。當該股票的價格達到概率為1%的高點時,遠期合約的價值就會跌到概率為1%的低點。
在實踐中,一家金融機構的投資組合通常包括大量的金融工具,因此進行情景分析需要的計算可能會非常複雜。要了解自今天起始的特定時間段內真實世界中可能發生的情況,我們需要生成大量的場景,並在這些場景下對投資組合進行定價。然後,我們才能知道在某一概率下(例如1%)所對應的損失的情況。舉例而言,如果我們考慮了1 000個場景,1%概率對應的損失就是這些場景中出現的第10個的損失。
對股票價格、股指價格和匯率等市場變量,最常用的模型一般會假設預期增長率μ和波動率σ是兩個常數,或是時間的某個函數。由式(7-1)可知,如果St是市場變量在時間t的值,我們有
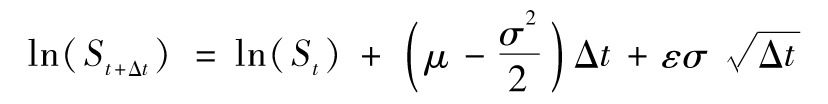
其中,ε是一個服從標準正態分佈的隨機變量(均值為0,波動率為1)。也就是說
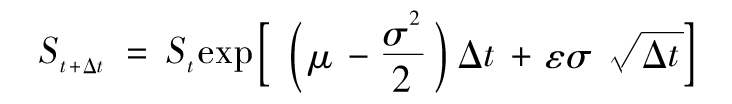
通過這個公式,我們就可以從一個標準正態分佈中取樣,以Δt為時間步長對一個市場變量進行模擬。
短期利率、波動率和商品價格等市場變量使用的模型會更加複雜。這類模型不僅考慮變量表現出的波動性,而且還假設從長期來看變量會迴歸到一個平均水平。這一現象被稱作均值迴歸(mean reversion)。在大多數情況下,我們並不假設各種市場變量的變動是相互獨立的。市場變量之間的相關性通常可以通過歷史數據估算出來。然後,這些相關性可以通過標準正態分佈隨機變量ε之間的相關性體現出來(我們在第11章中介紹特定相關係數下的多元標準正態分佈取樣的方法)。
從上面這個簡短的介紹中我們可以看出,情景分析可能非常耗費時間。在每次模擬中,除要通過取樣生成市場變量的值以外,還需要計算組合在所模擬的時間點上的價值。網格計算技術(grid computing,一種調度多個計算機資源協同工作,以完成同一個任務的分佈式計算技術)常常被用來進行這類計算。有時,為了能在合理的時間內得到結果,我們還不得不對蒙特卡羅模擬實驗的次數進行限制。
7.6 對真實世界中的過程進行估計
在情景分析中,我們面臨的一個主要問題是,我們對市場變量在風險中性世界中表現的瞭解,常常遠多過對它們在真實世界中表現的瞭解。考慮一隻股票的價格,我們知道在風險中性世界,股價的回報就是無風險利率。我們可以從歷史數據或以該股票作標的的期權價格中計算出波動率。對於消費資產(即非純粹用於投資的資產),期貨價格可用於提供有關其價格在風險中性世界中預期表現的信息。類似地,利率期限結構提供了風險中性世界中利率遵循的規律信息。
不幸的是,在真實世界中不存在這類隱含計算的方法。理論上,我們可以從歷史數據中推導。但在實際中,要得出比較準確的估計所需要的歷史數據量是很大的(遠遠超過得出合理波動率所需要的數據量)。
我們還可以使用資本資產定價模型(見第1章)。我們可以先估計這隻股票的回報與某個對整個市場有代表性的指數(如標準普爾500指數)的表現的相關係數ρ。如我們在第1.3節中解釋的,這隻股票的β可由下式計算出
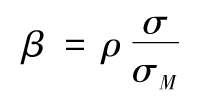
其中,σ是股票回報的波動率,σM是標準普爾500指數回報的波動率。根據資本資產定價模型,股票在真實世界中的回報率為
RF+βE
其中,RF是無風險利率,E是市場相對於無風險利率的預期超額回報(通常假設為5%或6%)。
我們可以對其他變量使用類似的方法。假設一個市場變量的波動率是σ(注意波動率在真實世界和風險中性世界中是相同的)。該變量在真實世界中的百分比變化量超出其在無風險世界中的變化量可計為λσ,其中λ被稱作該變量風險的市場價格。一般來說
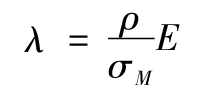
其中ρ為該變量百分比變化量與標準普爾500指數回報的相關係數。
現在考慮某一商品的價格。如果它的回報和標準普爾500指數的回報沒有相關性,我們可以假設它在真實世界中的預期回報和在風險中性世界是相等的。或者,設ρ=0.3,σM=0.2,E=0.06,我們可以推算出λ=0.09。如果商品價格的波動率是40%,則其回報率應為0.09×0.40=3.6%,即在真實世界中的預期回報高於風險中性世界中的回報。
就利率而言,市場風險價格為負(通常在-0.1至-0.2)。[1]這意味著,在風險中性的世界,利率的增長速度要快於真實世界(這使得利率不同於股票價格,而在真實世界中恰恰相反)。
[1] 參見J. Hull, A. Sokol, and A. White, “Short-Rate Joint-Measure Models,” Risk (October 2014): 59-63,以獲得估算利率風險市場價格的方法。美國聯邦儲備委員會有時會根據經驗判斷實際利率的變動幅度是每月比實際利率低一個基點。
小結
風險管理中一個比較容易讓人迷惑的問題是定價和情景分析(應該)基於對市場變量(例如股價、商品價格和匯率)表現的不同假設上。通過標的資產的價格對衍生產品進行定價,我們使用一個虛構的風險中性世界。這意味著投資組合中所有資產的預期回報都被假設為無風險利率,而預期收益也會以無風險利率貼現。風險中性定價結論的普遍適用性說明我們在風險中性世界中的定價結果在真實世界中也是正確的。
在情景分析中,我們感興趣的主要是市場變量在真實世界中(也就是我們真正生活的世界)是如何變化的。幸運的是,哥薩諾夫定理告訴我們,在真實世界和風險中性世界中,一個變量的波動率是相等的。但是,變量在這兩個世界中的預期回報很可能是非常不同的。例如,股票價格和股指價格在真實世界中的預期回報通常顯著高於它們在風險中性世界中的回報。正如我們在第1章中討論過的,這是因為投資者會為所承擔的風險要求補償。
另一個讓人迷惑之處是,有時我們需要同時考慮風險中性世界和真實世界中的情況。例如,一家金融機構持有一個衍生產品組合,且該機構希望瞭解自己未來1年可能遭受的損失,那麼它要做的就是考慮相關市場變量在未來1年內,在真實世界中會如何變化,並據此生成很多場景,然後它就可以使用風險中性定價方法來計算1年後投資組合在各場景下的價值。
延伸閱讀

練習題
7.1 一隻股票的價格的預期回報是12%,波動率是20%,當前價格為50美元。2年內股價高於70美元的概率是多少?
7.2 在習題7.1中,2年內股票能以5%的概率突破的高位是多少?
7.3 試著解釋風險中性定價的原理。
7.4 一個分析師計算一個股票指數未來的預期價格:(a)在真實世界中;(b)在風險中性世界中。你認為哪個世界中的值會更高一些?為什麼?
7.5 有一個衍生產品價值3美元,如果1年內某公司違約,該衍生產品會支付100美元。另一個衍生產品價值95美元,如果上述公司在1年內不違約,則該衍生產品會支付100美元。那麼,1年期無風險利率是多少?這家公司的風險中性違約概率是多少?
7.6 有一個二元期權,如果某股票的價格在3個月後高於30美元,則該期權會支付100美元。目前股票的價格是25美元,波動率是30%,無風險利率是3%,股票價格的預期回報是10%。該期權的價格是多少?在真實世界中,能從該期權中獲得收益的概率是多少?
7.7 我們需要進行情景分析,以確定1年後一個投資組合的價值的某一置信區間,試著說明為什麼我們既需要使用真實世界,又要使用風險中性世界。
7.8 解釋均值迴歸的含義。
7.9 解釋哥薩諾夫定理。
作業題
7.10 一隻股票的預期回報率是9%,波動率是25%,目前價格為40美元。未來18個月後,股票價格低於30美元的概率是多少?
7.11 某投資者持有某股票10 000股,股票目前的市場價格是80美元。6個月後,該組合在最壞的情況下價值是多少?這裡最壞的情況下的價值的定義是,組合的價值只有1%的概率低於該值。假設股票的預期回報率是8%,波動率是20%。
7.12 有一個二元期權,如果3個月後某股票的價格高於60美元,該期權會支付500美元。股票目前的價格是61美元,波動率是20%,無風險利率是2%,股票的預期回報率是8%。期權的價值是多少?真實世界中的預期收益是多少?

第8章
交易員如何管理風險敞口
金融機構的交易臺被稱為前臺(front office),而管理銀行所面臨的整體風險、資本充足率以及監管合規的部門被稱為中臺(middle office),管理銀行賬目的部門被稱為後臺(back office)。如同我們在第1.6節中解釋的,交易臺的風險在兩個層次被管理:第一個層次是交易前臺人員通過對衝手段來控制單一市場變量風險敞口不至於太大;第二個層次是中臺管理人員將所有交易員的風險敞口進行彙總來測算銀行面臨的整體風險,並決定整體風險是否可以被接受。在這一章中,我們將集中精力討論前臺的風險對衝行為,在以後的章節中,我們將討論中臺如何彙總及測算整體風險。
本章將討論“希臘字母”(greek letters),有時這些字母被簡稱為希臘值(greeks)。每一個希臘值都被用來度量交易中存在的不同方面的風險。在每個交易日結束時,交易員都要計算自己交易的各個希臘值,如果結果顯示風險已經超出了本金融機構確定的內部風險額度(internal risk limit),交易員應立即採取措施來減小風險敞口。如果不採取適當措施,那麼交易員可能會被解僱。
8.1 delta
假如你是美國某家銀行的交易員,你負責銀行所有與黃金有關的交易。當前黃金價格為每盎司1 300美元。表8-1顯示了你所持有的交易組合(也被稱為交易賬本或賬戶,“book”),你應該如何管理你所面臨的風險呢?
表8-1 某一黃金交易組合
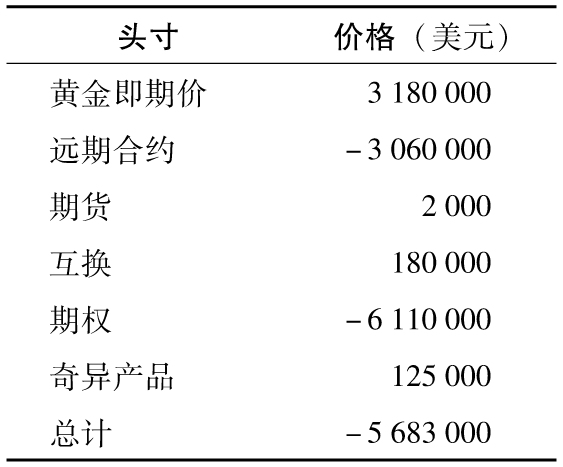
這裡你所持有的交易組合的當前價值為-5 683 000美元(這可能部分是因為你一直是期權的淨賣方,部分是因為市場走勢不利於你),一種檢測你的交易組合所面臨風險的辦法是假定黃金的價格由現在每盎司1 300美元變為每盎司1 300.10美元,然後再重新對你所持交易組合進行估價。假定當黃金價格變化後,交易組合的價格從-5 683 000變為-5 683 100美元。黃金價格增加0.1美元會觸發交易組合損失100美元,因而交易組合對黃金價格的敏感性為
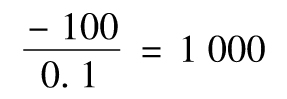
以上所討論的敏感性就是交易組合的delta。對應於每一美元黃金價格的上漲,交易組合損失1 000美元。類似地,我們可以計算出對應於每一美元黃金價格的下降,交易組合會有1 000美元的收益。
通常來講,交易組合價值對應於市場變量的delta由以下表達式來定義
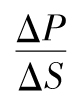
這裡的ΔS是指市場變量的微小變化,而ΔP對應於隨之而來的交易組合的價值變化。採用微積分的術語,delta(希臘字母中為Δ)是指交易組合價值對某一市場變量的偏導數,也就是說
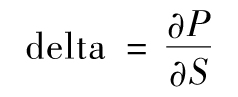
在我們的例子中,交易員可以買入1 000盎司黃金來消除delta風險。這是因為持有1 000盎司黃金的delta也是1000。當黃金價格每盎司增加1美元時,持有1 000盎司的黃金會產生1 000美元的收益,這被稱為delta對衝(delta hedging)。買入的黃金與最初交易組合迭加所產生的新的交易組合的delta為0,這樣的交易組合被稱為delta中性(delta neutral)。
8.1.1 線性產品
線性產品的價值變化與標的資產的價值變化有某種線性關係(見圖8-1)。如果標的資產的價值是一項資產(如黃金)的價格,該資產的現貨頭寸顯然是一個線性產品。頭寸的價值與資產的價格呈線性關係。遠期是一種線性產品,而期權不是。
圖8-1 某種線性產品
線性產品的風險很容易對衝。例如,一家美國銀行與某企業做了一個遠期交易,在遠期合約中這家銀行同意在1年後以130萬美元的價格賣給這家企業100萬歐元。假定歐元和美元1年期的利率(每年複利1次)分別為4%和3%。這意味著,1年後100萬歐元的現值為1 000 000/1.04=961 538歐元,1年後130萬美元的現值為1 300 000/1.03=1 262 136美元。假定在當前1歐元等於S美元,合約價值(以美元計量)為[1]
1 262 136-961 538×S
這表明合約的價值和匯率S呈線性關係。合約的delta為-961 538,這家美國銀行可以通過買入961 538歐元來對衝風險。因為這一線性關係,delta對衝對匯率的大小變動都能提供保護。
假設銀行進入相反的交易,也就是說銀行在1年後必須買入100萬歐元,遠期合約價值為
961 538×S-1 262 136
合約的delta為+961 538,銀行可以賣空961 538歐元來對衝風險,即銀行首先以4%的利率借入歐元,並隨即將歐元轉換為美元,在1年後合約到期時,收到的歐元可以用於償還歐元貸款。
通過賣空資產以對衝遠期合約並不一定總是很容易實現的,黃金就是一個有意思的實例,金融機構時常發現自己需要進入大數目的遠期合約,而在合約中需要買入黃金,這意味著金融機構必須借入大量黃金以達到對衝效果。如業界事例8-1所示,中央銀行往往是銀行借入黃金的來源,中央銀行借出黃金會收一定的費用,這一手續費利率被稱為黃金租賃利率(gold lease rate)。
業界事例8-1
金礦企業的對衝決策
金礦企業擔心黃金價格會變化而採用對衝決策,這看來非常自然。通常金礦企業要花幾年時間來開採一個礦井中的所有黃金。當一個金礦企業準備開發某一金礦時,企業自然也就會對黃金價格有很大的風險敞口。如果黃金價格暴跌,那麼一個最初看來會盈利的金礦實際上會虧損。
金礦企業在向股東解釋其採用的對衝策略時往往非常謹慎。有些金礦企業不採用對衝來規避風險,這些企業會吸引那些想在黃金價格上漲中盈利,同時能承受黃金價格下跌帶來的損失的投資者。而有些金礦企業採用對衝來規避風險,這些公司對自己在今後幾年內每月能夠開採出的黃金產量有一個大概的估計,然後根據這一估計來賣空期貨或遠期合約,以鎖定賣出黃金的價格。
假設你代表高盛集團,你同某金礦企業進入了一個遠期合約,合約約定你要以一個指定價格買入很大數量的黃金,你將如何對衝你自己的風險呢?對這一問題的答案是:你會在中央銀行借入黃金,然後將黃金在現貨市場上變賣(一些有大量黃金儲備的國家的中央銀行都願意在收取一定的黃金租賃費用的前提下借出黃金)。在遠期合約到期時,你按照合約從金礦企業那裡買入黃金以償還從中央銀行處借入的黃金。
線性產品一個很有吸引力的特性是:對衝保護對標的資產價格的大小波動同樣有效。另一個同樣非常有吸引力的特性是:一旦建立了對衝,則在交易的有效期內,都不要再調整倉位(這一特性有時被稱作“保後即忘”(hedge and forget))。為了說明這一點,再次回顧一下我們上面的例子,銀行通過遠期合約,同意在1年後以130萬美元售出100萬歐元。為了對衝風險,銀行購入了961538歐元。銀行能夠以4%的收益投資這筆歐元,1年後,投資的本息合計恰好是100萬歐元。這正好就是銀行用來完成遠期合約交割所需要的數額。因此,在1年內,銀行都沒有必要對對衝倉位進行調整。
8.1.2 非線性產品
期權以及大多數結構性產品都屬於非線性產品,這些產品的價格(變化)同標的資產的價格(變化)有某種非線性關係,而這種非線性關係使得這些產品的風險更難被對衝。首先,將一個非線性的投資組合delta中性化只能在標的資產價格變化比較小時才起保護作用。其次,我們不能採取保後即忘的策略,而必須不斷地調整對衝倉位。這被稱作動態對衝(dynamic hedging)。
例如,一個交易員賣出100 000份歐式期權,標的資產為某種無股息的股票,市場及期權變量如下:
(1)股票當前市價為49美元;
(2)期權執行價格為50美元;
(3)無風險利率為5%;
(4)股價波動率為20%;
(5)期權期限為20周。
我們假定交易員因賣出期權而得到300 000美元收入,並且假定此交易員除了這一期權交易,他不持有和這一股票有關的其他交易。
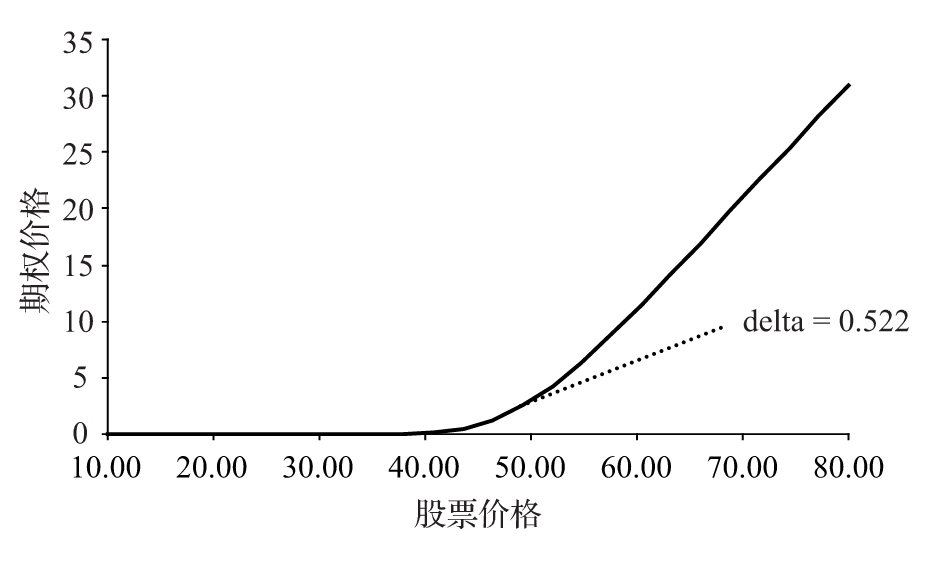
圖8-2 看漲期權價值與股票價格的變化關係
注:執行價格為50美元,無風險利率為5%,股價波動率為20%,期權期限為20周。
圖8-2顯示出期權價值與股票價格的函數關係。由於該函數是非線性的(即曲線),期權的delta取決於股票價格。當股票價格較低時,期權的價值幾乎為0,股票價格的微小變化導致的期權價值的美元增值也接近於0,這意味著期權的delta也接近於0。當股價較高時,比如70美元,看漲期權的買方會行權,因此期權的delta接近於1.0。這是因為股票價格中增加(減少)的ΔS使期權價值增加(減少)了ΔS。
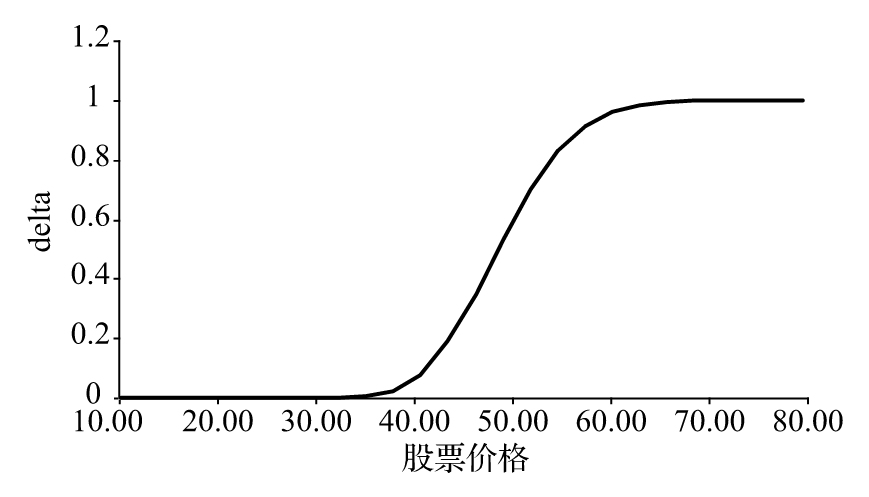
圖8-3 看漲期權的delta與股票價格的變化關係
注:執行價格為50美元,無風險利率為5%,股價波動率為20%,期權期限為20周。
在我們的例子中,股價為49美元,期權的delta是曲線在這一點上的斜率,在圖8-2中為0.522(有關歐式期權希臘值的計算見附錄E)。圖8-3顯示了一個期權的delta隨股票價格的變化關係。[2]在交易開始時,可買入1份標的股票的看漲期權的價值為2.4美元,而所對應的delta為0.522。因為該交易員賣出了對應100 000份的期權,所以交易員所持交易組合的價值為-240 000美元,交易組合所對應的delta為-52 200。交易員會因為期權的賣出價格超出了期權的理論價格60 000美元而感到興奮,但隨之而來的問題是如何對衝交易的風險以鎖定盈利。
賣出期權後,隨即買入52 200股股票可以使得交易組合達到delta中性。當股票價格有微小降低(增加)時,期權價值的收益(虧損)會被股票的損失(收益)中和。例如當股票價格由49美元漲到49.10美元時,期權價值會增加52 200×0.1=5 220美元,因此,期權的空頭會帶來5220美元的損失。這正好是股票價格上漲所帶來的收益。
對於線性產品,對衝交易在建立起來以後就無須調整。而對於非線性產品,為了保證delta中性,對衝交易要定期得到調整,這些調整過程被稱為再平衡(rebalancing)過程。
表8-2及表8-3顯示了在兩種不同情形下的再平衡模擬過程。假設對衝交易是每週進行一次。像我們在前面指出的那樣,最初的1份期權的delta為0.522,因而整個交易組合的delta為-52 200,這意味著在出售看漲期權的同時,交易員必須借入2 557 800美元並按49美元價格購買52 200股股票。借入資金的利率為5%,第1周的利息費用大約為2 500美元。
表8-2 delta對衝模擬,期權為實值期權,對衝成本為263 300美元
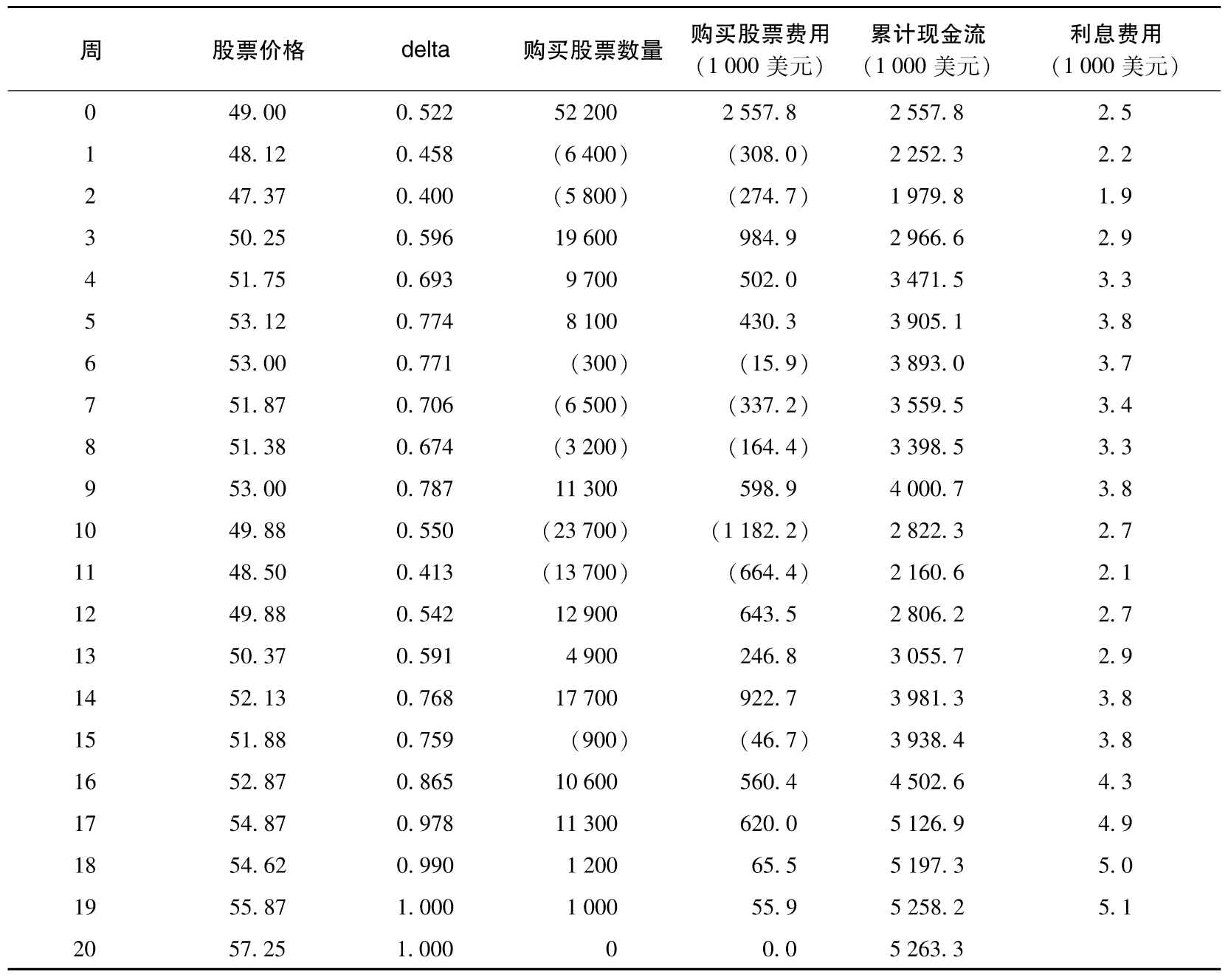
表8-3 delta對衝模擬,期權為虛值期權,對衝成本為256 600美元
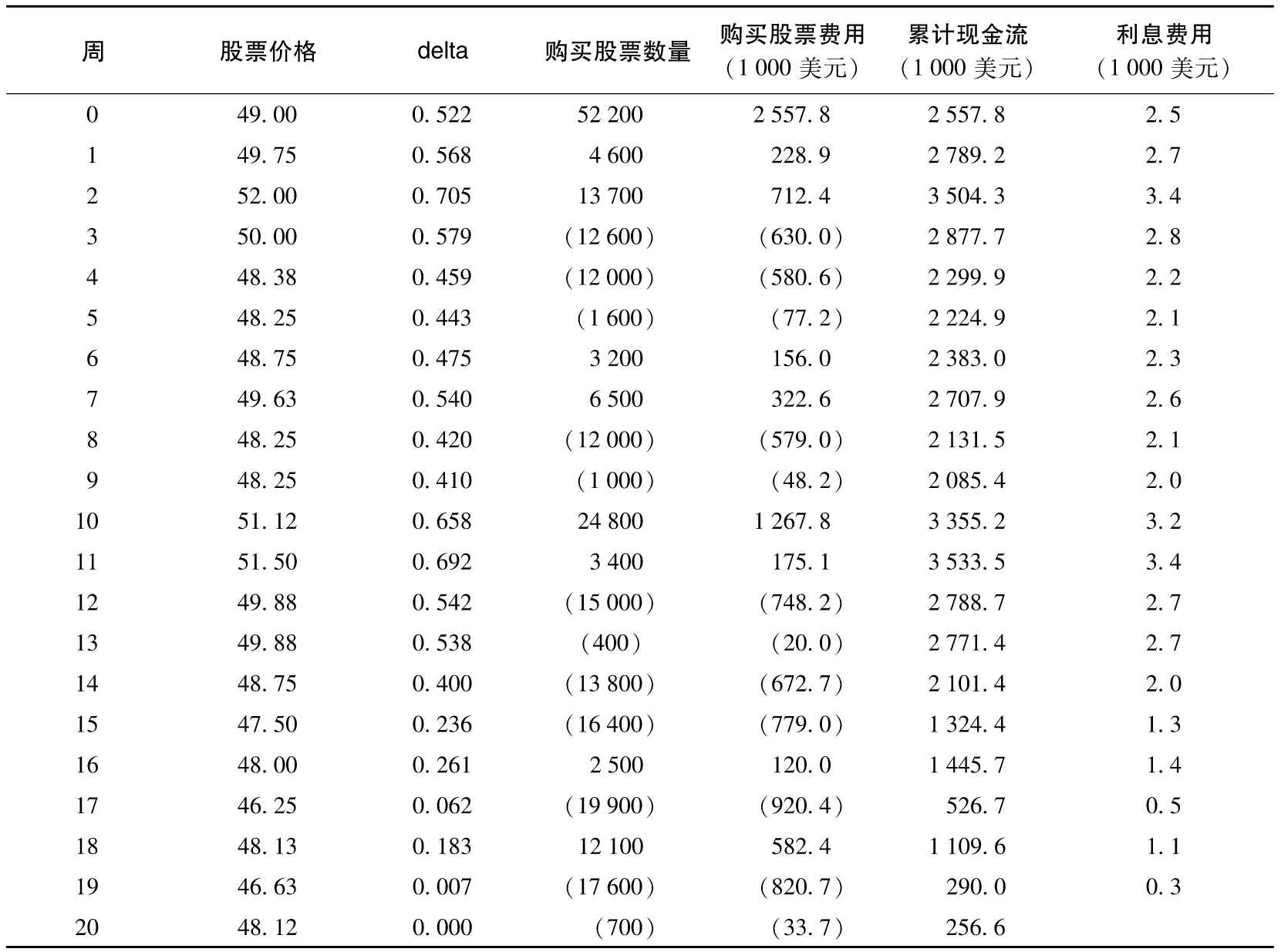
表8-2顯示,股票在1周以後價格降到了48.12美元,期權的delta也隨之降到了0.458。要保持delta中性,此時應該持有45 800股股票來對衝持有期權所帶來的風險,這意味著必須賣出6 400(=52 200-45 800)股股票,賣出股票帶來的現金收入為308 000美元,第1周的累計借款餘額減至
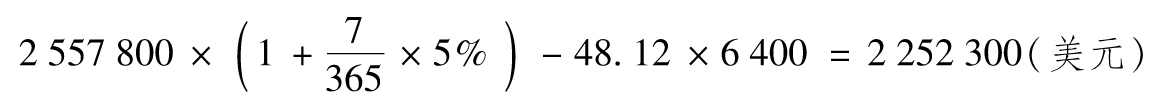
在第2周,股價繼續走低至47.37美元,期權的delta也隨之降低,保證delta中性需要再賣出5 800股股票。在第3周,股票價格上升到50美元以上,隨之delta會增加,這會造成在第3周結束時,需要買入19 600股股票。在期權接近到期時,很明顯期權將被行使,期權的delta接近於1.0。因此,在第20周結束時,對衝者會擁有100 000股股票,期權持有者會在此時行使期權,對衝者以執行價格賣出股票而收到5 000 000美元,賣出期權並對衝風險的總支出費用為263 300美元。
表8-3顯示出另一組模擬的股票價格,期權在到期時成為虛值期權,在第20周結束時,對衝者不持有任何股票,對衝總支出費用為256 600美元。
表8-2及表8-3顯示出,對衝成本的貼現接近於布萊克-斯科爾斯-默頓模型給出的理論價值240 000美元,並不完全一致。如果對衝機制是完美的,那麼在每一條股票價格的模擬路徑上,對衝成本的貼現值都應該與期權的理論價格完全相等。delta對衝成本與理論價值的差別是因為對衝交易頻率僅為一週一次,當對衝再平衡的頻率增大時,對衝成本與理論價值的差距會減小。當然,這裡的分析結果是建立在布萊克-斯科爾斯-默頓給出價格完全正確以及無交易費用等完美假設之下。
delta對衝的目的是儘量保證金融機構的交易組合價值恆定。開始時,賣出期權價值為240 000美元。如表8-2所示,第9周時的期權價值為414 500美元,因而金融機構因賣出期權損失174 500美元(=414 500-240 000)。累計現金費用在第9周時比交易開始(第0周)時要多1 442 900美元,所持有的股票的價格由最初的2 557 800美元變為4 171 100美元,增加了1 613 300美元。將所有因素彙總在一起,到第9周,金融機構的交易組合價值變化僅僅為4 100美元。
8.1.3 費用由何而來
由表8-2及表8-3所示的delta對衝機制以合成的形式構造出一個期權的多頭,而這一“合成”期權會被用來對衝交易員的期權空頭交易。正如表中所示,對衝機制會造成股價下跌後賣出股票,而在股價上升後買入,這正是所謂的“買高賣低”。240 000美元的費用來自購買股票的價格與賣出價格之間的平均差價。
8.1.4 交易費用
按以上描述方式維持一個由單一資產為標的的期權和資產本身組成的組合的delta中性而引發的交易費用會非常昂貴,以至於對交易員來說不具可操作性。但對一個由多種衍生產品組成的大的交易組合,如果這些衍生產品的標的是同一個資產,則維持delta中性的可操作性會更好,因為將整個組合的delta歸零,只需要進行一筆標的資產的交易即可。因此交易費用會更容易地被其他交易的利潤所吸收。這表明,衍生產品交易也具有規模效應,因此衍生產品市場被少數幾家大的交易商所控制也就不足為奇了。
[1] 關於遠期合約的定價,見附錄C。
[2] 圖8-2及圖8-3是由軟件RMFI產生的,這一軟件可在作者的網頁上下載,計算中採用了布萊克-斯科爾斯-默頓解析模型,讀者可選擇“Black-Scholes-European”。
8.2 gamma
如前面所述,對一個非線性的交易組合,delta中性只能在標的資產價格變化比較小的情況下才能夠提供保護。
一個期權交易組合的gamma(希臘字母中為Γ)用來衡量當標的資產的價格變化較大時,對組合價值產生的影響。gamma是指交易組合的delta的變化與標的資產價格變化的比率,也就是說,gamma是交易組合對於標的資產價格的兩階偏導數
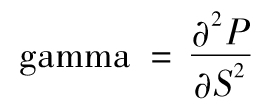
當gamma的絕對值很小時,delta變化緩慢,這時為保證delta中性所做的交易調整並不需要太頻繁。但是當gamma的絕對值很大時,交易組合的delta標的資產的價格就變得很敏感。此時在任意的一段時間內,對一個delta中性的交易組合不做調整會非常危險。圖8-4以一個股票的期權為例說明了這一點。當股票價格由S變成S′時,在delta中性假設下,期權價格由C變成C′,而事實上期權由C變成了C″。C′與C″之間的差異就造成了對衝誤差,這一誤差的大小取決於期權價格與標的資產價格曲線的曲率。gamma值正是用來度量這一曲率。[1]
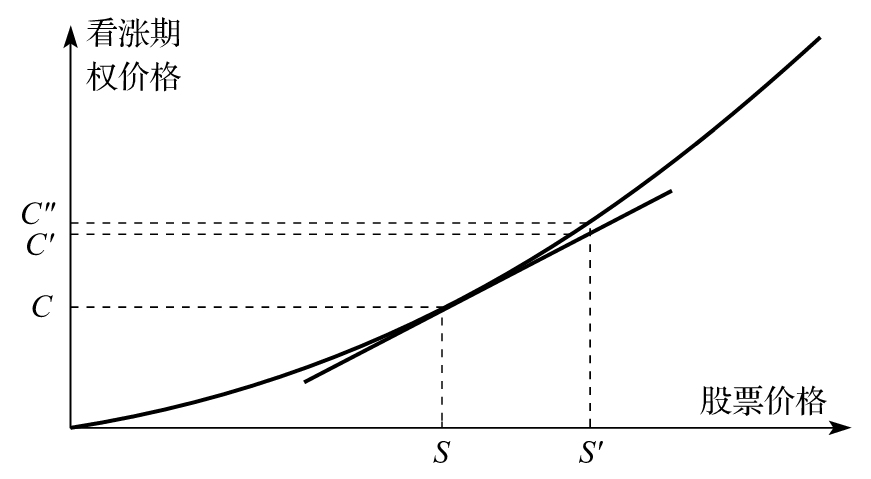
圖8-4 非線性形態所引入的對衝誤差
期權的多頭寸方gamma為正。圖8-5顯示了gamma與標的資產價格的一般關係。期權的gamma在標的股票價格接近於執行價格K時會達到最大值。
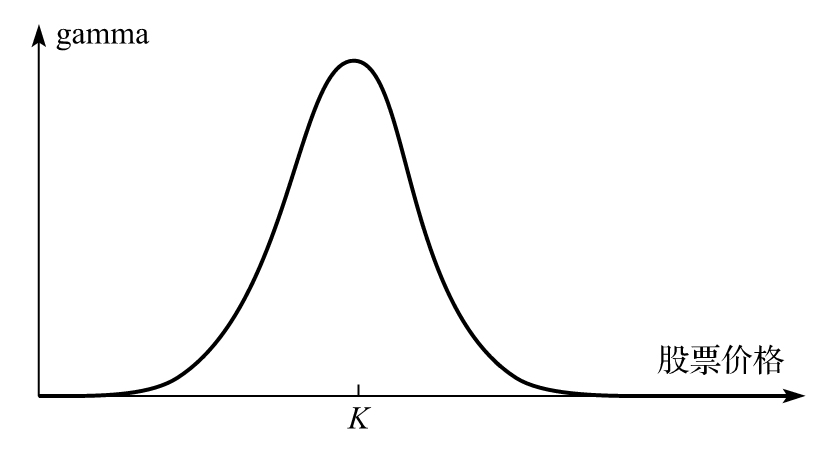
圖8-5 期權gamma與股票價格的關係,K為期權執行價格
構造交易組合gamma中性
一個線性產品的gamma為0,因此線性產品不能被用於改變交易組合的gamma,改變交易組合的gamma必須採用價格與標的資產價格呈非線性關係的產品,例如期權。
假如一個delta中性的交易組合的gamma為Γ,而某一交易所交易期權的gamma為ΓT,將wT數量的期權加入交易組合中,由此產生新的交易組合的gamma為
wTΓT+Γ
要使得交易組合gamma中性,期權的交易頭寸應為wT=-Γ/ΓT,引入交易期權會改變交易組合的delta,此時必須調整標的資產數量以保證新的交易組合delta中性,交易組合只是在較短的時間內會保持gamma中性,隨時間的變化,只有不斷調整期權數量以使得期權的頭寸滿足wT=-Γ/ΓT,才能維持交易組合的gamma中性。
對一個delta中性的交易組合進行gamma中性化,可以看作是對delta對衝中的標的資產頭寸不能連續變化這一缺陷的校正。delta中性保證了連續兩次對衝再平衡之間,交易組合價值不受股票價格微小變化的影響。而gamma中性保證在對衝再平衡之間,交易組合價值不受股票價格較大變化的影響。假定一個交易組合為delta中性,其gamma量為-3000;市場上交易的某期權的delta及gamma分別為0.62及1.50。在交易組合中加入3000/1.5=2000份期權會使得此交易組合變得gamma中性,但因此交易組合的delta也會從0變為2000×0.62=1240,為保證新的交易組合delta中性,我們必須賣出1240股股票。
[1] 事實上,期權的gamma有時被從業人員稱為曲率(curvature)。
8.3 vega
衍生產品交易的另一個風險來自標的資產價格波動率的變化。一個市場變量的波動率是用來衡量此變量將來價值的不確定性(這一概念會在第10章中被詳細討論)。在期權定價模型中,波動率經常被假設成常數,而在實踐中,波動率會隨時間而變化。現貨產品、遠期、期貨及互換產品的價值與標的資產的市場價格的波動率無關,但期權及大多數更復雜的衍生產品的價格與標的波動率有關,這些產品的價值會因為標的資產的價格、資產價格的波動率及時間的變化而變化。
一個交易組合的vega(V)是指交易組合價值變化與標的資產價格波動率變化的比率,其定義為[1]
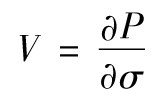
如果一個交易組合的vega絕對值很大,此交易組合的價值會對波動率變化非常敏感,當一個交易組合的vega絕對值較小時,資產波動率的變化對交易組合的價值影響也會很小。
在某個交易組合中加入某個在市場上交易的期權會改變交易組合的vega,假定某交易組合的vega為V,可交易期權的vega為VT,在交易組合中放入頭寸為-V/VT的可交易期權可使最初的交易組合vega呈中性。但不幸的是,一個gamma中性的交易組合一般不會是vega中性,投資者想使得一個交易組合同時達到gamma及vega中性,就必須引入與標的資產有關的兩種不同衍生產品。
【例8-1】 假如某一交易組合為delta中性,gamma為-5000,vega為-8000。設某個可交易期權的gamma為0.5,vega為2.0,delta為0.6。購買數量為4000的該交易期權會使得交易組合呈vega中性,這樣做同時會使得delta增至2400,因此為了保證delta中性必須賣出2400單位的標的資產,交易組合的gamma也會從-5000變成-3000。

為了保證交易組合gamma及vega中性,我們引入第二個可交易期權。此期權的gamma為0.8,vega為1.2,delta為0.5。我們用w1及w2來代表兩個可交易期權的頭寸,我們要求
-5000+0.5w1+0.8w2=0
-8000+2.0w1+1.2w2=0
以上兩個方程式的解為w1=400,w2=6000。因此加入400份上述第一種及6 000份上述第二種交易所交易期權會使得交易組合gamma及vega都呈中性。加入這兩種期權後,交易組合的delta變為400×0.6+6 000×0.5=3 240,因此必須賣出3 240份標的資產,以保持交易組合的delta中性。
期權的多頭寸方的vega為正。圖8-6顯示了vega隨標的資產價格變化的關係曲線圖。vega圖形同gamma圖形較為相似。gamma中性在兩次對衝平衡交易之間,標的資產價格發生較大幅度變化的情況下,為交易組合的價值提供保護;vega中性在兩次對衝平衡交易之間,標的資產價格波動率發生變化的情況下,對交易組合的價值提供保護。
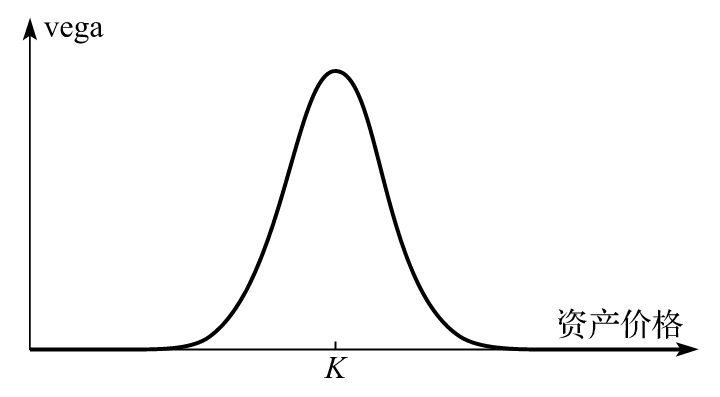
圖8-6 期權vega與標的資產價格的關係,K為期權執行價格
期限較短的期權的波動率比期限較長的期權波動率更具有多變性,因此在計算交易組合vega時,通常對期限較短的期權波動率的擾動量要比對期限較長的期權波動率的擾動量大,這一點將在第10.10節中討論。
[1] vega雖然是期權定價中“希臘值”的一個名稱,但是vega本身並不在希臘字母表中。
8.4 theta
一個投資組合的theta(希臘字母中為Θ)是指在其他條件不變的情況下,交易組合價值變化與時間變化的比率,theta常常被稱為投資組合的時間損耗(time decay)。
期權多頭寸方的theta通常為負,[1]這是因為在其他條件不變的情況下,隨著期權期限的接近,期權的價值會下降。圖8-7顯示了一個看漲期權的theta與股票價格的一般關係曲線。當股票價格很低時,theta接近於0。對應於一個平值看漲期權,theta可正可負。圖8-8顯示了在三種不同情況下,即實值期權、平值期權、虛值期權的theta隨時間變化的典型曲線。
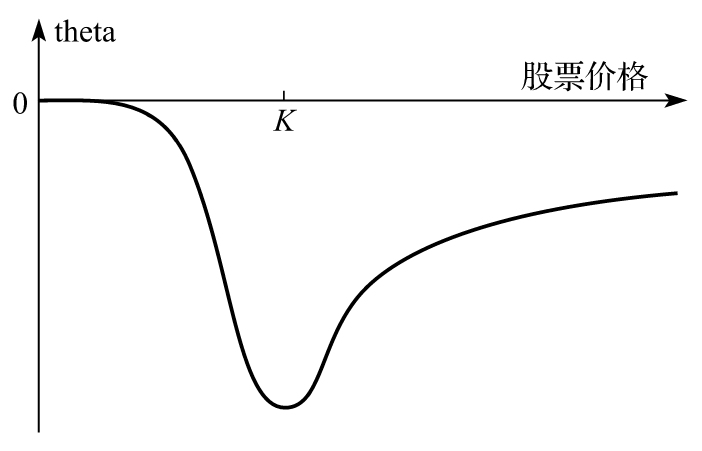
圖8-7 歐式看漲期權的theta隨股票價格變化的關係曲線
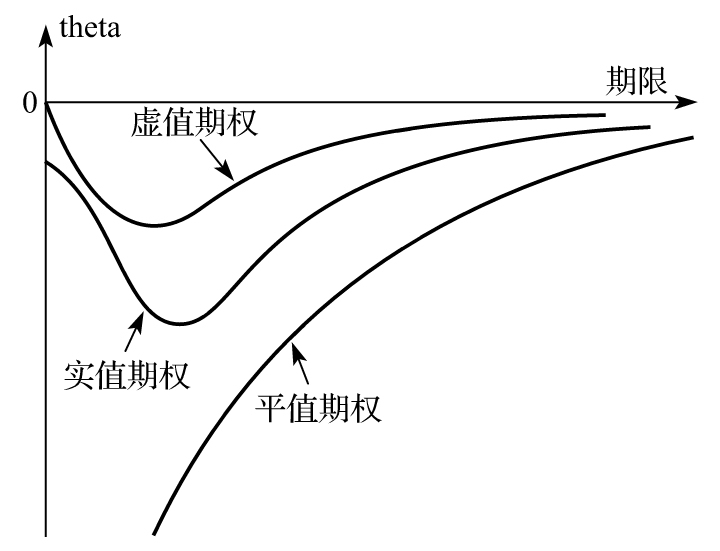
圖8-8 歐式看漲期權的theta隨時間變化的典型曲線
theta與delta等希臘值有所不同。這是因為股票將來的價格有很大的不確定性,但時間走向沒有不確定性,通過對衝來消除交易組合對於標的資產的風險十分有意義,但通過對衝來消除交易組合對於時間的不確定性就毫無意義。即使如此,許多交易員仍把theta量作為對於交易組合的描述,一個delta中性的交易如果其theta很大並且為正,那麼該交易組合的gamma常常會很大並且為負,這一關係反過來也正確。
[1] 對這一特性的反例包括:不付股息的股票的實值歐式看跌期權,或以某利率很高的外匯為標的的實值歐式看漲期權。
8.5 rho
我們最後將要考慮的希臘值為rho(希臘字母為ρ)。rho是指交易組合的價值變化與利率變化之間的比率。對於外匯期權,由於存在兩種利率,一個是本國利率而另一個是外幣利率,所以就可以得到兩個rho值。當交易組合包含債券及其他利率衍生產品時,通常交易員會謹慎考慮整個利率期限結構的變化方式。我們將在第9章中討論這一問題。
8.6 計算希臘值
在附錄E及附錄F中,我們解釋了希臘值的計算。在本書作者的網頁中,讀者可以下載一個名為RMFI的軟件,這個軟件可用於計算歐式期權和美式期權的希臘值,這裡讓我們再一次以在第8.1節中考慮的歐式看漲期權為例,這時股票價格為49美元,期權執行價格為50美元,利率為5%,股票價格波動率為20%,期權期限為20周(以年計為20/52年),表8-4顯示的delta、gamma、vega、theta和rho分別對應於一份期權的多頭與100 000份期權的空頭,這些頭寸曾在表8-2和表8-3中有所討論。
表8-4 利用RMFI軟件所得出的希臘值
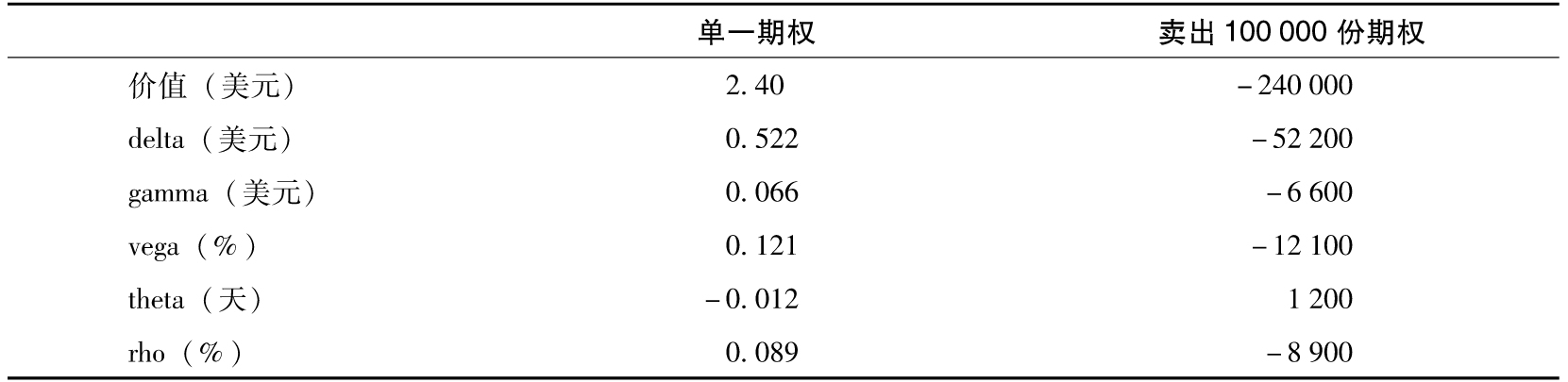
這些數字意味著:
(1)在股票價格上漲0.1美元,同時其他因素不變的情況下,期權價格會上漲0.522×0.1=0.052 2美元,100 000個空頭的價值下降5 220美元。
(2)在股票價格上漲0.1美元,同時其他因素不變的情況下,期權的delta將增加0.066×0.1=0.006 6美元,100 000個空頭的delta下降660美元。
(3)在股票價格波動率上漲0.5%,同時其他因素不變的情況下,期權價格會上漲0.121×0.5=0.060 5美元,100 000個空頭的價值下降6 050美元。
(4)一天時間過去以後,假定同時其他因素不變,期權價格下降0.012美元,100 000個空頭的價值上漲1 200美元。
(5)在利率上漲了1%(100個基點),同時其他因素不變的情況下,期權價格上漲0.089美元,100 000個空頭的價值下降8 900美元。
8.7 泰勒級數展開
在附錄G中,我們解釋了泰勒級數(Taylor series)展開過程,泰勒級數展示了在某一短時間內各個希臘值在交易組合變化中所起的不同作用。假設某交易組合價值只與某單一標的資產(變量)有關,並且利率及標的資產的價格波動率為常數。作為標的資產(變量)價格S以及時間t函數,交易組合價格P的泰勒展開式為
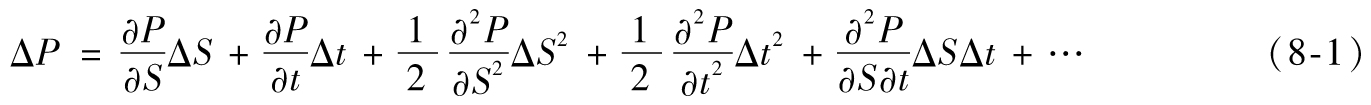
其中ΔP及ΔS分別對應於在某一短時間Δt內P以及S的變化。delta對衝可將上式右端第1項消除,第2項對應於時間損耗,是一個非隨機項,第3項可以在保證gamma中性時被消除,隨機微分方程理論顯示出ΔS的誤差級別與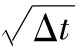 相同,這意味著右端第3項的誤差級別為Δt,右端的其他項的誤差級別高於Δt。
相同,這意味著右端第3項的誤差級別為Δt,右端的其他項的誤差級別高於Δt。
對於一個delta中性的交易組合,式(8-1)的右端第1項為0,因此

在以上表達式中,我們忽略誤差級別高於Δt的項。圖8-9顯示了交易組合價值的變化同標的資產價格的變化的曲線。當gamma為正時,如果標的資產價格的變化幅度較大,那麼交易組合會有正收益;當標的資產價格的變化幅度較小或不變時,交易組合收益會為負。當gamma為負時,以上結論相反,即標的資產價格的一個較大變動會給交易組合帶來嚴重的損失。
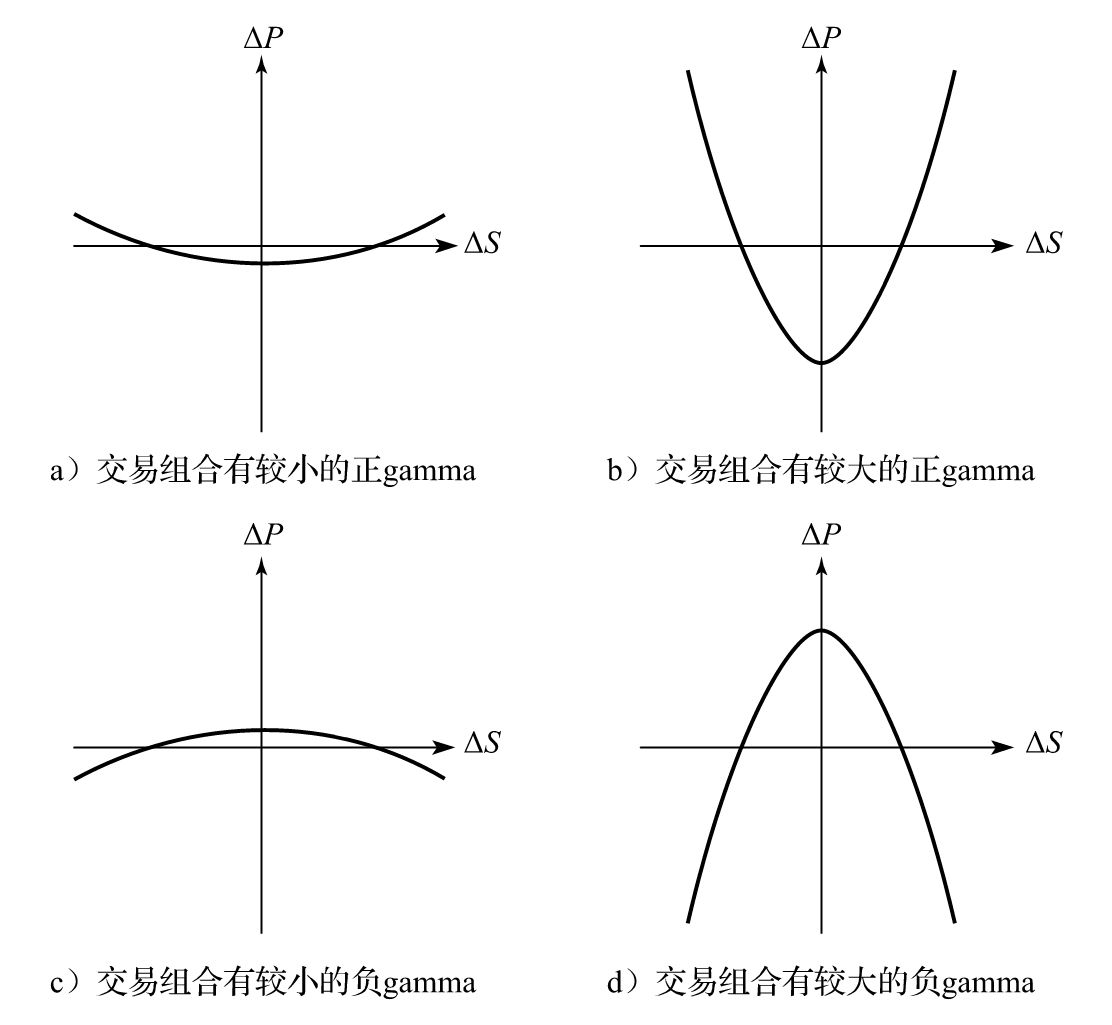
圖8-9 delta中性的交易組合的ΔP與ΔS之間的幾種關係
當標的資產價格波動率也為變量時,作為σ、S以及t的函數,交易組合價格的泰勒方程展開式為
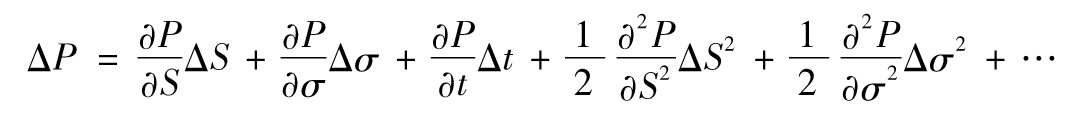
其中Δσ為波動率在Δt內的變化量。此時,delta中性可以消除右端第1項。vega中性可消除第2項,第3項為非隨機項,第4項可被gamma中性消除。
交易員經常也會對泰勒展開式的高次項進行定義,例如,∂2P/∂S∂σ被稱為vanna,∂2P/∂σ2被稱為vomma,∂2P/∂S∂t被稱為charm。
【例8-2】 假定一個delta中性的交易組合的gamma為-10 000,並且在某個短的時間段,資產價格變化為+2(Δt可以假設為0)。式(8-2)顯示,交易組合非預期減值大約為0.5×10 000×22=20 000美元,注意如果價格變化為-2,則非預期減值數量相等。
8.8 對衝的現實狀況
在一個完美的世界,金融機構的交易員可以隨時調整對衝交易以確保交易組合delta、gamma及vega均為0。在現實中,這樣做是不可能的,在管理與某標的資產有關的交易組合時,交易員通常是通過每天對標的資產進行交易以確保交易組合的delta為0或接近於0,而保證gamma及vega為0就十分困難,這是因為在市場上很難找到價格合理並且適量的期權以達到對衝目的(見業界事例8-2中有關動態對衝的討論)。
業界事例8-2
實踐中的動態對衝
金融機構一般指定某一個交易員或某一個交易組來負責管理價值與某一特定資產有關的交易組合。例如,高盛集團的某一個交易員被指定負責與澳元有關的所有衍生產品交易組合。交易組合的市價及有關的希臘值風險均通過某一計算機系統來產生。對應於每一個風險會設定不同的風險額度,如果交易員的交易量在交易日結束時超過額度,就必須得到特殊批准。
delta額度的表示形式通常是等價的標的資產最大交易量。例如,假設高盛集團的delta額度為1000萬美元。假如微軟公司的股價為50美元,這意味著對應的delta數量不能超過200 000。vega的交易額度通常表達為當價格波動率變化1%時所對應的價格變化的最大限量。
事實上,交易員在每個交易日結束時會保證交易組合delta中性或接近中性。gamma及vega會得到監控,但這些風險量並不是在每天都得到調整。金融機構常常發現自己因業務需要要向客戶賣出期權,最終它們自己會積累一個負的gamma及vega。因此金融機構往往會尋求適當的機會以合適的價格買入期權來中和自己面臨gamma及vega的風險。
在利用期權來管理gamma及vega等風險時,我們要特別注意,當期權剛剛被賣出時,期權一般為平值(或很接近平值),而此時期權的gamma及vega會接近最大值。但隨著時間的流逝,當標的資產價格變化足夠大後,期權會變成實值或虛值期權,此時期權的gamma及vega會很小,從而這些風險量對交易組合的影響很小。當一個期權接近到期而且標的資產價格與執行價格較為接近時,對交易員來說是件很棘手的事情。
期權交易具有經濟規模效應,在以前我們曾指出,保持單一期權的delta中性成本太高,不具可行性,但對一個擁有上百個期權的交易組合維持delta中性是可行的,這是因為每天的再平衡費用可以被大量交易所帶來的利潤所支持。
8.9 奇異期權對衝
我們常常可以採用以上關於簡單產品的對衝方式來對衝奇異期權(見第5.7節)。正如業界事例8-3所示,有時奇異期權的delta對衝較為容易,而另外一些時候卻很困難。當利用delta對衝方式來對衝某些奇異期權產品不可行時,我們可使用另外一種被稱為靜態期權複製(static options replication)的方式。圖8-10解釋了靜態期權複製。我們用S代表標的資產價格,t代表時間,資產在當前(t=0)的價格記為S0。在靜態期權複製對衝決策中,我們要在{S,t}空間選擇標的資產以及時間會達到的某一邊界,然後再選擇簡單期權組合並使得簡單期權組合在邊界上某些選定點上與奇異期權產品有相同的價值。奇異期權的組合可以被簡單期權組合的空頭對衝。當邊界值被達到時,用來對衝的簡單組合會被平倉,然後可以通過靜態期權複製再建立一個新的對衝倉位。
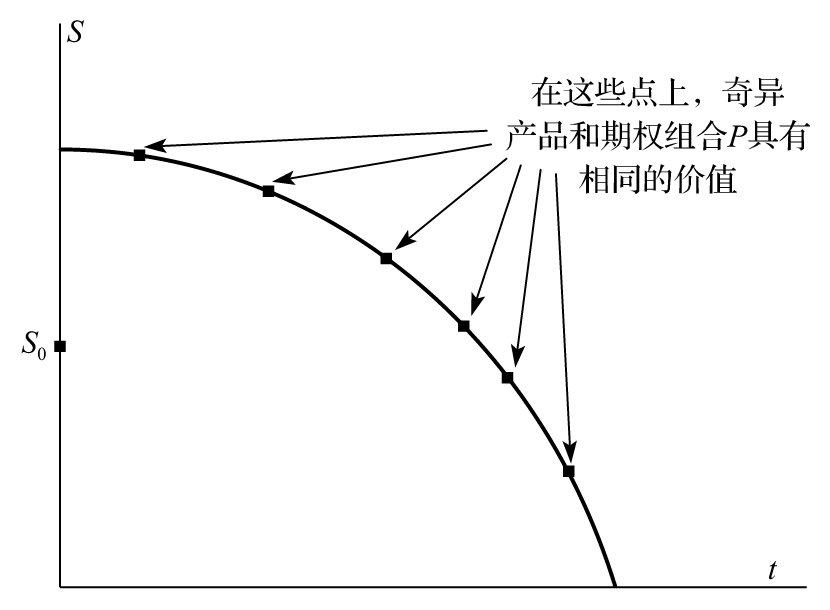
圖8-10 靜態期權複製
注:在靜態期權複製對衝策略中,我們建立一個簡單的期權組合P,使其在給定的標的資產價格以及時間的邊界點上,與奇異產品有相同的價值。
靜態期權複製的理論根據是,如果兩個交易組合在{S,t}邊界所有點上的價值相同,那麼這兩個交易組合也會在{S,t}空間內到達邊界值前所有點上的價值相同。但在實踐中,最初的奇異期權交易組合和用來對其進行復制的簡單期權交易組合的價值通常只能在邊界上的某些點而不是全部點上達到一致。所以,實際上這一做法假設,當兩個交易組合在足夠多的邊界點上價值相同時,這兩個交易組合在邊界其他點上的價值也往往會很接近。
業界事例8-3
對於奇異產品實施delta對衝是更加困難還是更加容易
我們可以通過構造delta中性交易,並不斷地對交易組合進行調整,維持delta中性這一方法來對衝奇異產品。這樣做的同時,我們會發現對有些奇異產品的對衝比簡單產品對衝要更加容易,而對某些奇異產品的對衝要比簡單產品的對衝更難。
例如,亞式看漲期權(見第5.7節亞式期權)的對衝相對來講就較為容易。隨著時間的推移,我們會觀察到越來越多的資產價格,而這些價格被用來計算最後的平均值。這意味著隨著時間的流逝,最終期權回報的不確定性會逐漸減小。因此,期權也就會逐漸變得越來越容易被對衝。在期權接近期滿的最後幾天,標的資產價格對期權價格的影響越來越小,期權的delta趨近於0。
與以上形成鮮明對照的是,障礙期權(見第5.7節)的對衝難度就相對較大。我們考慮一個歐式敲出看漲期權。期權基礎變量為匯率,當前匯率比障礙匯率高0.000 5,在當前匯率達到障礙匯率時,期權價值變為0,當障礙沒有達到時,期權的回報十分可觀,障礙期權的delta在障礙值附近不連續,這種跳躍使得對於障礙期權實施傳統式對衝會很困難。
8.10 情景分析
除了監控諸如delta、gamma、vega等風險量之外,期權交易員也常常進行情景分析。情景分析包括計算在某一指定時間內在不同的情景下交易組合的損益,分析中時間長度的選擇通常與產品的流動性有關,分析中所用的情景可由管理人員選定,也可由模型產生。
考慮某銀行持有一個匯率期權組合,此交易組合價值取決於兩個主要變量:匯率及匯率波動率。假定當前匯率為1.0,匯率波動率為每年10%。銀行可以用類似表8-5的表格來計算顯示在兩週內不同情景下交易組合的盈虧。在表中,我們考慮了7種不同的匯率及3種不同的波動率。
表8-5 在不同情景下某匯率期權交易組合在兩週內的損益 (百萬美元)

表8-5顯示,最大損失位於該表的右下角。這一損失對應的波動率為12%,匯率為1.06。在類似表8-5的情景分析中,最大損失通常位於表格的角落位置,但這一特性並不永遠正確。例如,在圖8-9中,當gamma為正時,最大的損失是對應於標的資產市場價格不變的情景。
小結
銀行的交易員通過監控自己負責的與某一市場變量相關的所有交易的敏感度,即希臘值來保證它們位於銀行指定的風險額度範圍內。
變量delta(Δ)是交易組合的價值的變化與標的資產價格變化的比率。delta對衝就是指構造delta為0的交易組合(有時被稱為delta中性)。因為標的資產的delta為1,所以持有一個-Δ頭寸的標的資產可以達到對衝交易組合風險的目的。對於期權及更復雜的產品,對衝交易要得到經常性的調整,這一調整過程也被稱為再平衡交易。
對於某一交易組合,一旦做到delta中性,下一步我們往往要關心交易組合的gamma。gamma變量是指交易組合的delta的變化與標的資產價格變化的比率。這一變量可以衡量交易組合價值與標的資產價格之間關係曲線的曲率。另外一個常用於對衝的重要變量為vega。vega用來衡量交易組合價值變化與標的資產波動率變化的比率。通過交易標的資產的期權可以改變交易組合的gamma及vega。
在實際中,為使得delta中性,交易員通常每天調整(再平衡)一次交易組合。要保證在一般情形下的交易組合gamma及vega的中性並不十分容易。交易員通常對這些變量進行測算,當這些變量變得太大時,交易員或者要做對衝交易來減小風險量,或者要將交易進行平倉。
延伸閱讀

練習題
8.1 一個交易組合價值對於標準普爾500指數的delta值為-2100。標準普爾500指數的當前市價為1000。請估計當標準普爾500指數上漲到1005時,交易組合的價格為多少。
8.2 某一衍生產品組合對於USD/GBP匯率的vega為200(每1%變化),請估算一下當波動率由12%變為14%時,衍生產品組合價格的增值為多少。
8.3 一個delta中性的交易組合的gamma為30(見前述gamma的定義),請估測以下兩種標的資產變化對交易組合價值的影響:(a)標的資產突然漲價2美元;(b)標的資產突然下跌2美元。
8.4 一個期權的delta=0.7的含義是什麼?如何將賣出的1 000份期權交易變為delta中性?這裡我們假定買入單位期權的delta為0.7。
8.5 一個期權的theta量每天為-100的含義是什麼?假如一個交易員認為股票價格及期權隱含波動率在將來不會改變,對交易員來講,什麼樣的期權交易(買入或賣出)較為合理?
8.6 一個期權的gamma含義是什麼?一個交易的gamma較大並且為負,並且delta為0,此時這個期權的風險是什麼?
8.7 請解釋以下觀點:“人工合成一個期權交易也就是期權對衝交易的反過程。”
8.8 一家公司對其持有的交易組合進行delta對衝,交易組合由看漲期權及看跌期權的多頭組合而成,期權的標的變量為某匯率。以下哪種情形會使交易組合增值更大?(a)現期匯率基本不變;(b)現期匯率劇烈變化。假如在交易組合中引入一筆期權賣空交易,以上分析會有什麼變化?
8.9 一個銀行持有USD/EURO匯率期權交易組合,交易組合的delta為30 000,gamma為-80 000,請解釋這些數字的含義。假設當前匯率(1歐元所對應的美元數量)為0.90,你應該進行什麼樣的交易以使得交易組合具備delta中性?在某短時間後,匯率變為0.93,請估計交易組合新的delta。此時還要追加什麼樣的交易以保證交易組合delta呈中性?假如最初銀行實施delta中性決策,匯率變化後銀行是否會有損益?
8.10 “在靜態期權複製理論中,波動率被假設為常量。”請解釋這句話的含義。
8.11 假定一個交易員採用一組簡單期權及靜態期權複製來計算某一奇異交易期權組合的價值。交易員希望簡單期權組合在某邊界上的10個點同奇異期權價值相同,簡單期權組合需要含有多少個期權交易?請解釋你的答案。
8.12 為什麼亞式期權比一般期權更加容易對衝?
8.13 為什麼在期權對衝過程中會有經濟規模效應?
8.14 我們考慮一個標的變量為匯率的6個月期限的美式看跌期權,匯率為0.75(對應於每一單位外幣的本國貨幣數量),期權執行價格為0.74,本國利率為5%,外國利率為3%,匯率的波動率為每年14%。請利用RMFI軟件(100步二叉樹)來計算期權的價格以及期權的delta、gamma、vega、theta以及rho,將匯率變為0.751,並計算對應期權價格,由此來檢驗delta的正確性。
作業題
8.15 一個delta中性的交易組合的gamma及vega分別為50以及25,請解釋當標的資產價格下跌3美元以及波動率增加4%時,交易組合的價值變化為多少?
8.16 讓我們考慮一個歐式看漲期權。標的資產股票價格為30美元,執行價格為30美元,無風險利率為5%,股票價格波動率為每年25%。請應用RMFI軟件來計算期權價格以及期權的delta、gamma、vega、theta以及rho。將股價變為30.1美元時計算期權價格,並由此來檢驗delta的正確性,通過計算期權在標的價格為30.1美元時的delta來計算gamma,並由此來檢驗gamma的正確性,對其他變量vega、theta以及rho,請進行相應的計算,並驗證計算結果的正確性。
8.17 一家金融機構持有以下場外期權交易組合,標的資產為英鎊。
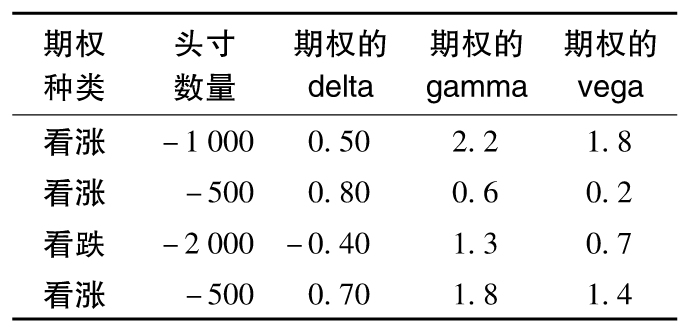
某可交易期權的delta為0.6,gamma為1.5,vega為0.8:
(a)用多少可交易期權及英鎊可使交易組合同時達到gamma及delta中性,期權和英鎊應為多頭還是空頭?
(b)用多少可交易期權及英鎊可使交易組合同時達到vega及delta中性,期權和英鎊應為多頭還是空頭?
8.18 在作業題8.17中,引入第二種可交易期權,假定期權的delta為0.1,gamma為0.5,vega為0.6。採用什麼樣的交易可使交易組合delta、gamma以及vega均為中性?
8.19 用RMFI軟件檢驗表8-2的前3行,計算對應於前3周的期權的gamma與theta,並計算交易組合的價值變化(計算時間為每週末再平衡交易之前),並以此檢驗關係式(8-2)(注意:RMFI軟件計算的theta以天為計量單位,而式(8-2)中的theta以每年為計量單位)。
第9章
利率風險
同其他市場變量相比,例如股價、匯率及商品價格等,利率風險更加難以管理。一個複雜的問題是,對於任何一種貨幣,往往都會有幾種不同的利率(國債利率、銀行之間的拆借利率、房屋貸款利率、儲蓄利率、最優貸款利率等)。雖然這些利率一般會同時變動,但它們並不是完全相關的。另一個造成利率風險複雜的原因是我們不能僅僅只用一個數字來描述利率,而需要一個與期限有關的函數。這種函數關係被稱為利率期限結構(interest rate term structure),或者稱為收益曲線(yield curve)。該曲線所考慮的利率通常是零息利率(zero-coupon interest rate),有時也被稱為零利率。如果所有利息和本金都在期末支付,則這個利率就是整個持有期的利率(例如持有期間沒有現金流,最終只支付面值的債券)。
在此讓我們考慮一個管理美國國債的交易員的交易組合,這一交易組合由不同期限的很多國債組成。因此該交易員會對1年期、2年期、3年期等各種利率有風險敞口,從而這個交易組合的delta會比表8-1中黃金交易員的更加複雜。該交易員必須考慮美國國債收益率曲線形狀可能隨時間變化而發生的各種改變。
本章開始的部分介紹了金融機構對利率風險進行管理的傳統手段,其中包括對金融機構來說非常重要的幾種利率。接下來我們還要介紹久期及凸性等概念。這些變量可類比為第8章討論的delta及gamma。隨後我們將介紹管理曲線非平行移動的不同方法,這些方法包括局部久期、計算多項delta以及主成分分析法等。
本章不討論度量利率時的複利頻率以及零息利率的期限結構計算等問題。這些計算過程包含在附錄A和附錄B中。
9.1 淨利息收入管理
銀行風險管理活動的一項核心內容是管理銀行的淨利息收入。如第2.2節中介紹的,淨利息收入是指利息收入與利息支出的差。確保淨息差的穩定是資產負債管理部門的職責。淨息差(net interest margin)是淨利息收入和全部生息資產的比值。在本節中我們將討論這一目標是如何達到的。
為了展示淨息差的變動是如何發生的,我們假定某銀行給客戶提供1年及5年的存款利率,同時又給客戶提供1年及5年的住房貸款利率。這些利率如表9-1所示。為了簡化分析,我們假設市場投資者認為將來的1年期利率同今天市場上的1年期利率相同。簡單地講,市場認為利率增加與利率減少有相同的可能性,由此我們可以說表9-1顯示的利率是“公平”的,它們正確地反映了市場的期望。在這個公平假設下,將資金投放1年然後再滾動投資4年同一個5年的投資帶來的回報是相同的。類似地,以1年期利息借入資金然後再滾動借入4年同一個5年的貸款產生的融資費用是相同的。
表9-1 銀行給客戶提供各種利率
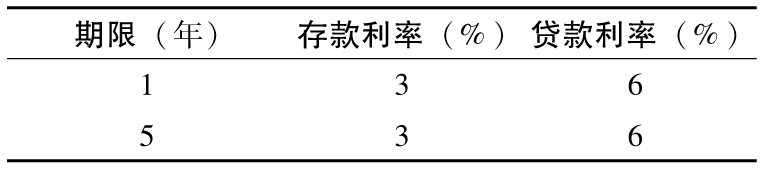
假定你將資金存入銀行,並且你認為利率上升與下降有相同的可能性,你此時會將資金以3%的利率存入1年還是會以3%的利率存入5年?你往往會將資金存入1年,因為將資金鎖定在一個較短期限裡會給你帶來較多的財務靈活性。
下一步假定你需要一個住房貸款,你仍然認為利率上升與下降的可能性均等,你此時是會選一個1年期6%的住房貸款還是會選一個5年期6%的住房貸款?這時你往往會選擇一個5年期的住房貸款,因為這樣做會給你帶來較小的再融資風險。
根據銀行提供的如表9-1所示的利率,大多數存款客戶會選擇1年期存款,同時大多數住房貸款客戶會選擇5年期貸款。這樣一來,銀行的資產及負債就會產生不匹配,從而對淨利息收入產生風險衝擊。用來支撐5年期利率為6%的貸款的存款需要每年滾動。這在利息降低時不會產生問題,銀行的貸款收入仍為6%,而支撐貸款的存款利息低於3%,因此利息收入會增加。但當利率增加時,銀行貸款收入仍為6%,存款費用高於3%,由此觸發銀行的淨利息收入降低。假如頭兩年內利率增長了3%,第3年的淨利息收入將為0。
資產負債管理部門的職責就是將這種利率風險降到最低。達到這一目的的方法之一是將帶來收入的資產的期限與產生利息費用的負債的期限進行匹配。在我們的例子中,一種達到這種匹配目的的方法是同時提高5年期的存款利率和住房貸款利率。例如將利率調整為如表9-2所示的情形,其中5年期的存款利率變為4%,5年期的貸款利率變為7%。在這種情況下,5年期存款及1年期住房貸款會變得相對更有吸引力。一些選擇表9-1中的1年期存款的儲戶會將自己的資金轉入如表9-2中所示的5年期存款,一些選擇表9-1中的5年期住房貸款的顧客會選擇1年住房貸款。這樣所帶來的效果是資產及負債得以匹配。如果客戶仍然過多地選擇1年期存款及5年期住房貸款而造成資產負債的不平衡,那麼我們可以進一步提高5年期存款及貸款利率,這樣會逐漸消除資產負債的失衡。
表9-2 提高5年期利率以達到資產負債的匹配

所有的銀行均按以上所描述的方式來進行資產負債管理,其效果是長期利率要比預期的將來短期利率高,這一現象就是所謂的流動性偏好理論(liquidity preference theory)。這一現象造成長期利率在通常情況下比短期利率要高,即使當市場預測短期利率稍有下降時,流動性偏好理論也會使得長期利率高於短期利率,只有當預測利率會有急劇下降時,長期利率才會低於短期利率。
許多銀行已經建立了較為完善的系統來監控客戶的業務決策行為,當看到客戶所選的資產與負債期限不匹配時,銀行可以對提供的利率進行細微調整。有時利率互換等衍生產品可以用來管理利率風險敞口(見第5.5.3節中的例5-1)。所有這些措施的結果是銀行的淨息差較穩定,但並不是所有的銀行都能時刻做到這一點。20世紀80年代,美國很多信貸公司和大陸伊利諾伊銀行(Continental Illinois)的倒閉在很大程度上是因為資產和負債期限的不匹配。
流動性
除了侵蝕淨息差,資產和負債不匹配還可能導致流動性問題。一家靠短期存款支持長期貸款的銀行必須不斷地以新的存款置換到期的存款,這也被稱作存款滾動(rolling over)。如果存款人對銀行喪失信心,銀行的這種做法就難以為繼。金融機構因為流動性問題而倒閉的一個廣為人知的案例是英國的北巖銀行,該銀行以批發存款支持其按揭組合,有些批發存款的期限只有3個月。從2007年9月開始,因為美國市場出現的狀況,存款人開始擔心。結果北巖銀行不能再為其資產融資,只能於2008年年初由英國政府接管(參見業界事例24-1)。在美國,雷曼兄弟和貝爾斯登也遇到類似的問題,不能滾動它們的批發存款。
2007年信用危機中的很多問題實際上是由於流動性短缺引起的。如同市場受壓時通常會發生的那樣,由於投資者尋求更安全的投資方式並且不打算承擔信用風險,從而引發安全投資轉移現象。現在,銀行監管機構已經意識到,應像設定資本金要求那樣為銀行設定流動性要求。第16章解釋了《巴塞爾協議Ⅲ》中的流動性要求。第24章對流動性問題進行了更深入的討論。
9.2 利率的種類
在這一節中,我們將介紹幾種對金融機構非常重要的利率。
9.2.1 國債利率
國債利率(treasury rate)是投資者投資短期國債和長期國債[1]得到的利率。政府通過發行國債的方式用本幣融資。日本國債利率就是日本政府以日元發債的利率,美國國債利率就是美國政府以美元發債的利率,依此類推。通常,我們假設一個國家的政府是不會對本幣負債違約的。[2]因此,投資者購買短期國債或長期國債,總會如約收回本金和利息,所以國債利率可以被看成是無風險利率。
9.2.2 LIBOR
LIBOR的全稱為倫敦銀行間同業拆借利率(London interbank offered rate)。它是銀行間無抵押短期拆借的利率。傳統上,每天發佈的LIBOR利率包含多種不同的幣種和期限,拆借期限從1天到1年。在世界範圍內,以LIBOR為參照利率的交易規模達到數萬億美元。一種非常常見並且非常重要的以LIBOR為參照利率的衍生產品是利率互換(見第5章)。LIBOR利率是由18家全球銀行在每個工作日的上午11:00(英國時間)之前發佈其可以從其他銀行借入資金的利率報價來估計的。每種幣種以及拆借期限最高的4個報價和最低的4個報價均會被捨棄,對剩餘的報價進行平均以確定當天的LIBOR報價。提交報價的銀行通常具有AA信用等級。因此,通常將LIBOR視為AA級銀行的無抵押借款利率的估計值。
一些為銀行工作的交易員被指控試圖操縱LIBOR報價。他們為什麼要這樣做?假設銀行從衍生產品中獲得的收益取決於特定日期的LIBOR變動,隨著LIBOR的增加,收益也增加。交易員有動機在那天提供更高的報價,並試圖說服其他銀行也這樣做。湯姆·海斯(Tom Hayes)是第一個因操縱LIBOR而被定罪的交易員。2015年8月,他被英國一家法院判處14年徒刑(後減刑為11年)。該機制的一個問題是,沒有足夠多的銀行間拆借交易能為所有的幣種/期限組合提供準確的拆借利率估計,因此做出一些調整是不可避免的。為了改善現狀,對LIBOR包含的不同幣種的數量從10個減少到5個,將不同的拆借期限從15個減少到了7個。此外,對拆借利率估計過程的監管得到了加強。
現在人們認識到,將LIBOR作為衍生產品交易的參考利率並不理想,因為它是根據銀行的估算而不是實際市場交易價格確定的。衍生產品市場正在考慮使用其他參考利率,例如OIS利率(將在稍後討論)。
9.2.3 LIBOR/互換零息曲線
正如前面所述,LIBOR的報價期限區間在1天到1年之間,因此,我們只可以定義期限小於1年的零息LIBOR利率曲線。LIBOR利率曲線將如何被延伸到一年以外呢?有兩種做法:
(1)構造期限大於1年的AA級公司借入資金的利率曲線;
(2)構造一個AA級公司在某個時刻短期借入資金的利率曲線。
瞭解這兩種構造方式的不同之處非常重要。如果對於所有期限的利率均為4%,假定利率曲線是通過第一種辦法構造而成的,那就意味著AA級公司今天借入資金的期限無論多長,利率均為4%;假定利率曲線是通過第二種辦法構造而成的,那就意味著市場已經認定AA級公司在將來短期內借入資金利率為4%(見附錄B中遠期利率的定義和計算)。第一種方法構造的曲線給出了今天信用級別為AA級的公司的遠期短期拆借利率,而第二種方法構造的曲線給出了遠期合約期限所覆蓋的將來某時段開始時信用級別為AA級的公司借入短期資金的利率。
在實踐中,LIBOR利率曲線是通過第二種方法構造的。互換利率(見表5-5)可以用來將利率曲線的期限延伸到1年之外(見附錄B)。[3]LIBOR利率曲線有時也被稱為互換利率曲線或LIBOR/互換利率曲線。為了理解為什麼互換利率可以在第二種方法中來延伸LIBOR曲線,我們應該注意到銀行可以利用短期LIBOR貸款利率來生成互換利率,例如,銀行可以進行以下交易:
(1)借給一家信用級別為AA級的公司一筆資金,期限為6個月,並且在以後連續9次,每次以6個月為期限將相同數量的資金借給該公司(或信用級別也為AA級的其他公司)。
(2)進入一個5年期的互換交易,收入現金流為5年期互換利率,付出LIBOR。
這意味著,互換利率代表了銀行從一系列對AA級公司發放的短期貸款中能獲得的預期收益。因此,它有時也被稱為持續更新利率(continually refreshed rate)。[4]
9.2.4 LIBOR和國債利率
無風險利率對於金融產品的定價非常重要。我們可能會認為國債利率應該很自然地被用作無風險利率。但實際上,市場通常認為國債利率是被人為壓低的,這是因為:
(1)對銀行來說,持有國債所需要的資本金要求(通常為0)要顯著低於投資其他類似的低風險產品。
(2)在美國,對於國債的稅務規定要比其他大部分固定收益產品更為有利,投資國債的收益無須繳納州稅。
在2007年信用危機之前,金融機構一般使用LIBOR和互換利率作為無風險利率的近似。在危機以後,隔夜指數互換利率已經取代LIBOR用作無風險利率。下面我們就解釋什麼是隔夜指數互換利率。
9.2.5 隔夜指數互換利率
隔夜指數互換(overnight indexed swap,OIS)是一種互換合約,指一定期限的(例如,1個月、3個月、1年或2年)固定利率與同期隔夜利率的幾何平均值交換。[5]相關的隔夜利率來自一個由政府組織的銀行間拆借市場。在該市場上,有多餘儲備金的銀行可以將資金借給準備金不足的銀行。[6]在美國,這一市場上的隔夜拆借利率也被稱作美聯儲基準利率(fed funds rate),每日的有效美聯儲基準利率由當日借入資金的銀行向借出資金的銀行支付的利率的加權平均求得,該利率用於OIS利率中的幾何平均計算。其他很多國家也存在類似的市場,例如,歐元區的歐元隔夜指數平均利率(Euro OverNight Index Average,Eonia)相當於美聯儲基準利率;類似的還有英國的英鎊隔夜指數平均利率(Sterling OverNight Index Average,SONIA)等。
如果在一段時間內,銀行以隔夜利率借入資金(每日將貸款和利息向前滾動),則銀行所付利息是基於隔夜利率在這段時間內的幾何平均。類似地,如果銀行以隔夜利率借出資金,所得利息是基於隔夜利率在這段時間內的幾何平均。因此,OIS將隔夜資金借入或借出和一個固定利率借入或借出互換。這一固定利率被稱為OIS互換利率。
OIS互換利率通常被認為是比LIBOR利率更好的對無風險利率的近似。銀行系統中一個重要的風險指標是LIBOR-OIS利差,這是3個月期限的LIBOR利率高出3個月OIS互換利率的值。正如我們討論過的,前者是一家銀行向另一家AA級銀行提供3個月期限的無抵押貸款的利率,而後者是銀行以美聯儲基準利率借入資金,然後通過利率互換將隔夜利率轉換為3個月固定利率。理論上銀行可以以3個月OIS利率借入資金,然後以3個月LIBOR利率借出給另一家AA級的銀行,因此LIBOR-OIS利差實際上是補償一家AA級銀行在3個月內可能破產的風險的信用價差。在正常的市場條件下,LIBOR-OIS利差小於10個基點(年平均)。該利差越大,說明銀行越因為擔心對手信用,而不願相互之間拆借。
圖9-1顯示了2002年1月~2017年6月LIBOR-OIS利差的狀況。在2007年8月前,LIBOR-OIS利差小於10個基點。2007年8月,因為美國房地產市場的問題開始顯現,銀行間逐漸不願意彼此拆借,所以該利差開始上升。2008年10月初,利差達到峰值364基點。1年後,又恢復到基本正常的水平。
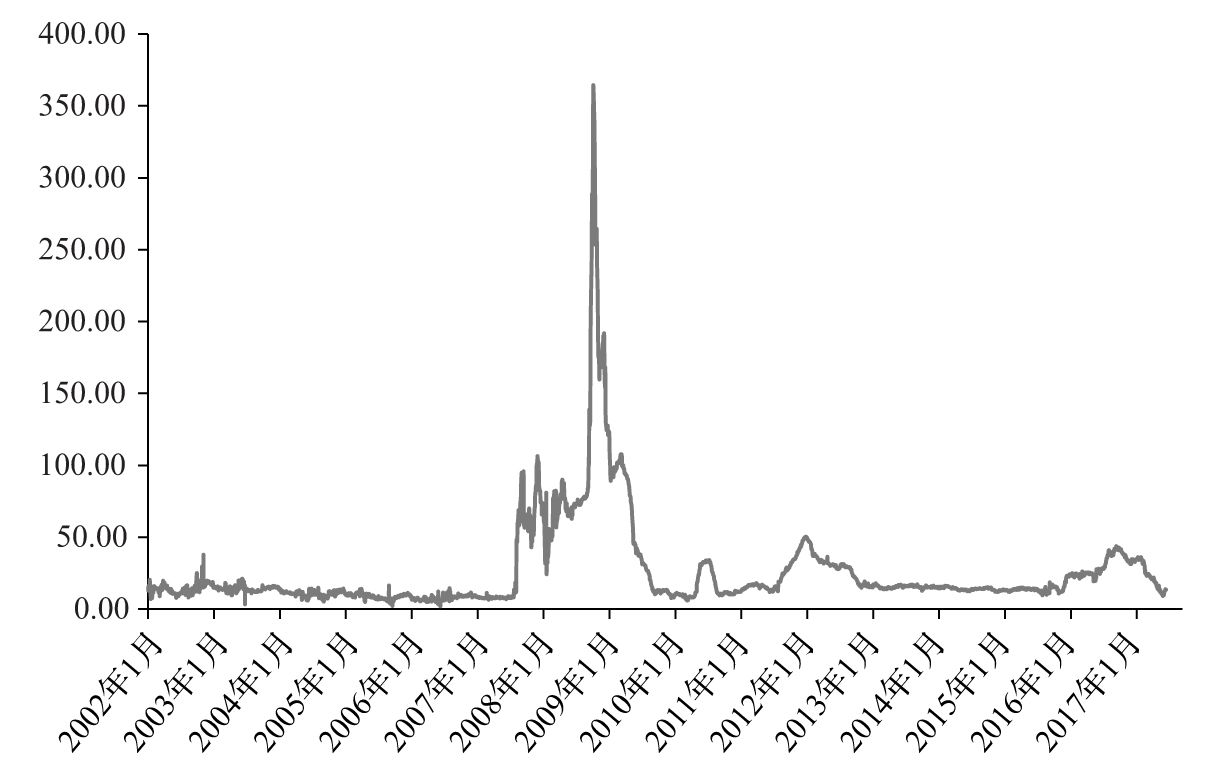
圖9-1 3個月期限LIBOR-OIS利差,2002年1月~2017年6月
9.2.6 回購利率
和LIBOR與聯邦基金利率不同,回購利率是一種有擔保的利率。在一個回購交易中,持有有價證券的金融機構同意將該證券以一定價格賣出,並保證在將來以稍高的價格將其買回。金融機構實際上是得到了一筆貸款,這筆貸款的利息就是賣出和買回該證券的差價。由此算出的利率被稱為回購利率。
如果構造嚴謹,那麼回購交易的信用風險會很小。如果借貸方不履約,那麼借出方就可以把證券據為己有。如果借出方不履約,那麼證券的最初所有方就不用歸還借出方的現金。最常見的回購是隔夜回購,這種回購經常會日復一日地向前滾動。但是,期限更長的回購,即定期回購,有時也被使用。因為是有擔保的利率,所以回購利率通常會比LIBOR或聯邦基金利率低幾個基點。
[1] 在美國,1年期以內的短期國債被稱作treasury bill。treasury bill是一種零息債券,一般以低於面值的價格出售。1年以上的中期(2~10年)和長期(10年以上)國債分別被稱作treasury note和treasury bond。——譯者注
[2] 這是因為對本幣來說,政府總是能控制貨幣供應(也就是說,政府控制著自己的印鈔機)。即便如此,一國政府也是有可能對外幣債務違約的。另外,歐元區的國家政府也有可能對歐元債務違約。
[3] 以未來LIBOR值作為標的變量的歐洲美元期貨也可用來延伸LIBOR利率曲線。
[4] See P. Collin-Dufresne and B. Solnik, “On the Term Structure of Default Premia in the Swap and Libor Market,” Journal of Finance 56, no.3(June 2001):1095-1115.
[5] 隔夜利率的幾何平均的準確含義是隔夜利率加1的幾何平均值再減1(見業界事例4-1)。
[6] 央行要求商業銀行留存一定比例的客戶存款作為準備金,準備金不能被作為貸款發放。準備金可以以現金或者央行存款的形式存在。
9.3 利率久期
久期(duration)這一概念已經被廣泛地用來度量交易組合對於利率曲線的風險敞口。假設債券收益率為y,債券價格為B,債券的久期D的定義為

或等價於
ΔB=-DBΔy
其中Δy為債券收益率的一個小的變化,ΔB為相應債券價格的變化。因此債券久期用於衡量債券價格對收益率的敏感度。利用微積分中的符號,我們有

假定一個債券在t1,t2,…,tn時刻給債券持有者提供的現金流為c1,c2,…,cn(現金流包括券息和本金),債券收益率y是使得債券理論價格等於市場價格的貼現率。如果我們用vi來表示現金流ci以y為貼現率從時間ti貼現到當前的值,則債券的價格可表示為
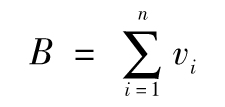
因此,債券久期D也可以定義為

式(9-3)括號中的項為ti時刻的債券支付的現金流的貼現值與債券價格的比率。債券價格等於將來所有支付的本息貼現值的總和。因此式(9-3)中久期的定義方式是付款時間ti的加權平均,而對應於ti時刻的權重等於ti時刻的現金流貼現值與債券總貼現值的比率(這裡的所有權重相加等於1),這一關係式給出了債券久期這一術語的出處。久期是指投資者收到現金流所要等待的時間。一個n年期零息債券的久期為n年,而一個n年帶息(coupon-bearing)債券的久期小於n年,這是因為國債持有者在第n年之前就已經收到部分現金付款。
如果式(9-1)中的債券收益率y以連續複利形式表示,則式(9-1)和式(9-3)是等價的(見作業題9.15)。
考慮某個面值為100美元、券息為10%的3年期債券。該債券連續複利的年收益率為12%,即y=0.12,每6個月付息一次,息值為5美元。表9-3顯示了有關債券久期計算的步驟,在計算中收益率代替貼現率,計算出的現值被呈現在表中的第3列(例如第一次付息的現值為5e-0.12×0.5=4.709),第3列的數字之和等於債券價格94.213,由第3列中的數字除以94.213,我們可以得到久期的權重,第5列的數字之和等於久期,即2.653年。
表9-3 久期的計算
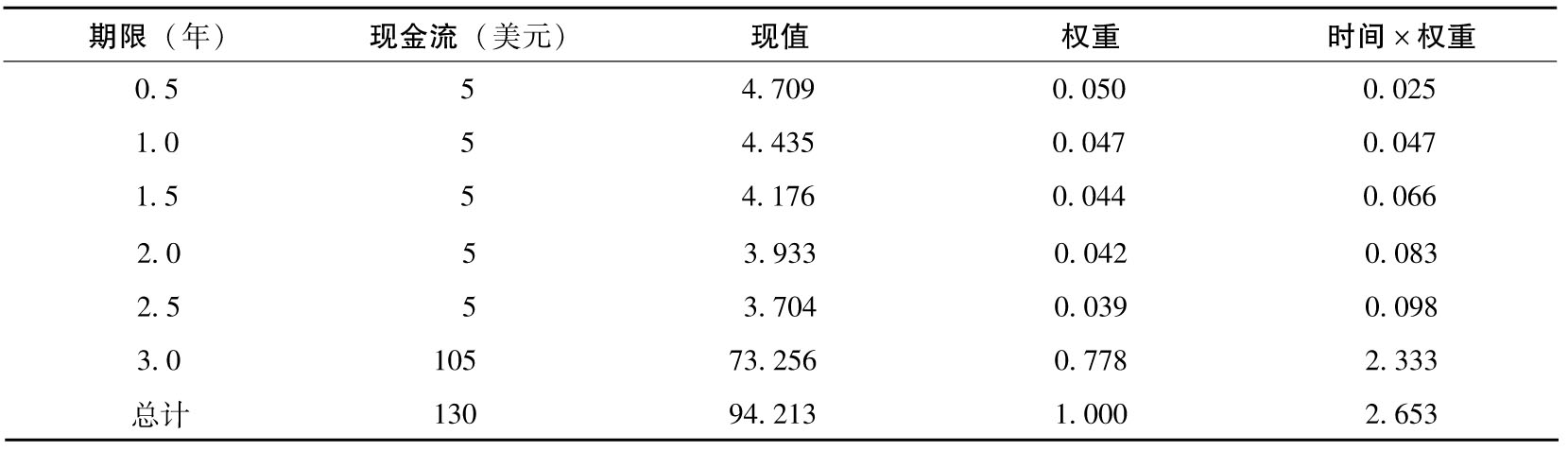
利率的微小變化通常用基點(basis point)來描述,1個基點對應於0.01%。以下例子驗證了當久期定義為式(9-3),且收益率以連續複利形式表示時,式(9-1)是正確的。
【例9-1】 由表9-3描述的債券價格為94.213,久期為2.653,根據式(9-1)
ΔB=-94.213×2.653Δy
即
ΔB=-249.95Δy
當收益率增加了10個基點(=0.1%),即Δy=+0.001時,久期公式預計ΔB為
ΔB=-249.95×0.001=-0.250
久期公式預計債券價格會下降到94.213-0.25=93.963,為了檢驗這個預測的準確性,我們計算當收益率增加10個基點到12.1%時的債券價格,其數量為
5e-0.121×0.5+5e-0.121×1.0+5e-0.121×1.5+5e-0.121×2.0+5e-0.121×2.5+105e-0.121×3.0=93.963
這一數值同我們用久期公式預計的變化相同(精確到小數點後第3位)。
9.3.1 修正久期
式(9-3)定義的久期是由麥考利(Macaulay)在1938年首先提出的,因而這一久期被稱為麥考利久期(Macaulay’s duration),在收益率y為連續複利的前提之下,式(9-3)的定義與式(9-1)等價。由式(9-1)定義的久期,在其他複利的假設前提下,為了保證等價關係,我們必須對麥考利進行一個小的調整。如果y為一年複利一次的利率,則我們需要對式(9-3)中的久期D除以1+y;在更為一般的情況下,如果y為一年複利m次的利率,則式(9-3)中的久期D需要除以1+y/m(見作業題9.15)。對式(9-3)進行這一調整以後,所定義的久期被稱為修正久期(modified duration)。
【例9-2】 由表9-3描述的債券價格為94.213,久期為2.653。每年複利2次的收益率為12.3673%(見附錄A),修正久期為
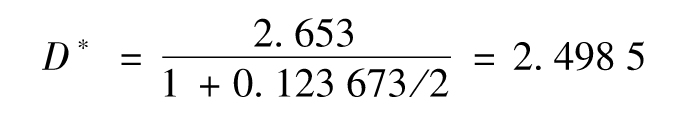
由式(9-1),我們得出
ΔB=-94.213×2.498 5Δy
或
ΔB=-235.39Δy
當收益率(一年複利2次)增加10個基點(0.1%),即Δy=+0.001時,久期關係式預計債券價格變化ΔB為-235.39×0.001=-0.235,因此債券價格下降到94.213-0.235=93.978。當收益率(一年複利2次)增加10個基點,即對應收益率y=12.4673%(或連續複利收益率增加10個基點,即對應收益率為12.0941%)時,通過一個幾乎與前面的例子相同的計算,我們得出的債券價格為93.978。這一例子說明:當債券收益率變化較小時,修正久期計算公式非常精確。
9.3.2 絕對額久期
絕對額久期(dollar duration)等於修正久期與債券價格的乘積,如果D$代表絕對額久期,由式(9-1)得出
ΔB=-D$Δy
採用微積分的記號
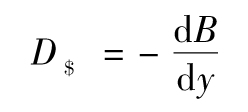
久期為債券相對價格變化(即債券價格變化與債券價格的比率)與收益率變化建立了聯繫,而絕對額久期將債券價格變化與收益率變化建立了聯繫,絕對額久期類似於我們在第8章中討論的delta測度。
9.4 凸性
對於收益曲線一個較小的平行移動,久期可以度量組合價值的相應變化。圖9-2表明具有相同久期的兩個債券,它們的相對價格變化和收益率變化之間的關係可以不同。這兩個債券在起始點的導數(切線)相同。這意味著,當收益率有較小的變化時,兩個債券價值變化同收益率變化的百分比相同,這與式(9-1)一致。當利率變化較大時,兩個債券的表現就不一樣了。債券X的曲率比債券Y要大。一個被稱為凸性(convexity)的變量是用來度量曲線的凸凹變化的程度,它可被用來改善近似式的準確性。
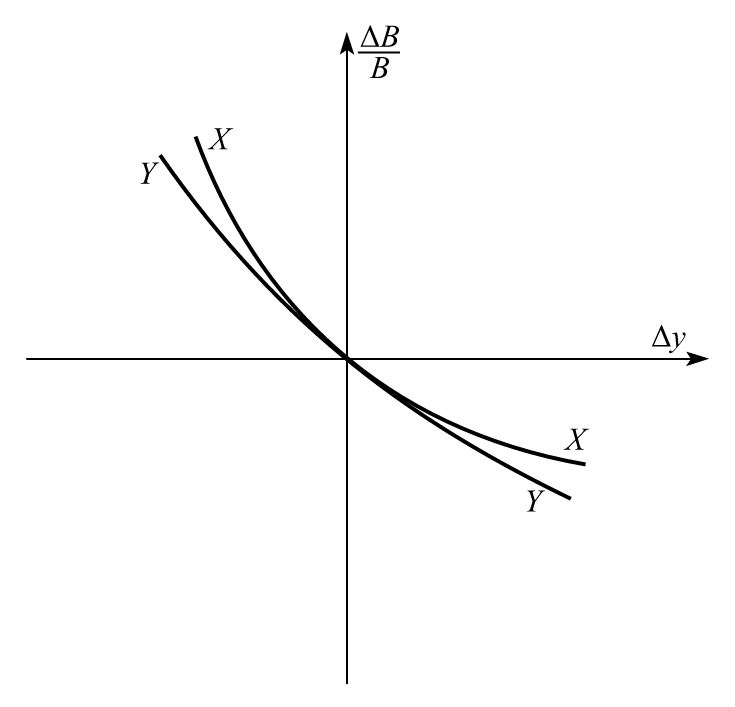
圖9-2 兩個久期相同、凸性不同的債券
債券凸性的定義為
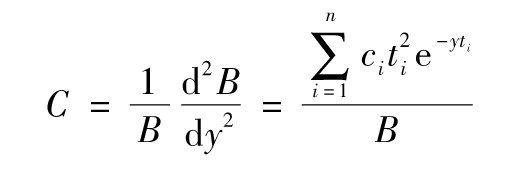
其中y對應於債券的收益率,以連續複利表示。債券凸性是將來收到現金流的時間平方的平均值,由附錄G的結論,我們可以得出關於債券價格的兩階近似式
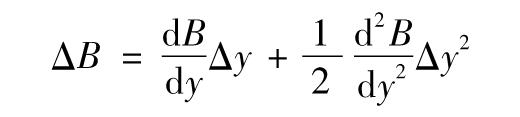
由此
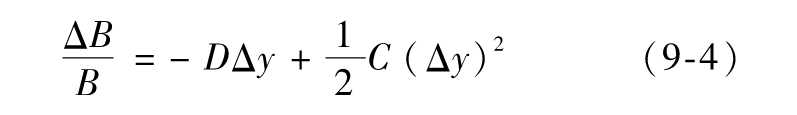
【例9-3】 由表9-3描述的債券B的價格為94.213,久期為2.653,凸性為
0.05×0.52+0.047×1.02+0.044×1.52+0.042×2.02+0.039×2.52+0.779×3.02=7.570
由式(9-4)得出
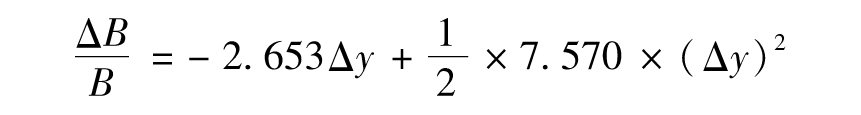
假設債券收益率由12%變為14%,即變化量為2%,久期公式預計債券價值變化將是-94.213×2.653×0.02=-4.999,凸性關係式預計變化為
-94.213×2.653×0.02+0.5×94.213×7.750×0.022=-4.856
而證券價格的實際變化為-4.859。這個例子說明:當債券收益率變化較大時,凸性公式比久期公式更為精確。
絕對額凸性
絕對額凸性(dollar convexity)C$的定義與絕對額久期類似,它等於凸性與債券價格的乘積,這意味著
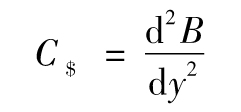
絕對額凸性類似於我們在第8章中討論的gamma測度。
9.5 推廣
到目前為止,我們採用了久期和凸性來檢測單一債券對利率的敏感度。久期和凸性可以被推廣到債券組合,或其他與利率相關的產品組合。我們將零息收益曲線的平行移動定義為將零息收益曲線上的所有點平行移動一個相同的數量(見圖9-3)。
圖9-3 零息利率的平行移動
假定P代表組合的價值,將零息收益曲線進行一平行移動,我們觀察到相應價格的變化為ΔP,久期被定義為
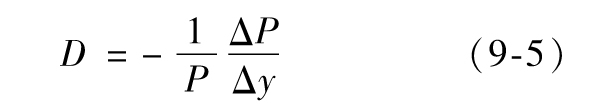
其中Δy為平行移動的變化量,[1]式(9-5)等價為

假定組合由多種跟利率相關的資產組成,第i個資產價值為Xi,其對應的久期為Di(i=1,2,…,n)。定義ΔXi為收益率變化Δy時的Xi的相應變化量,定義 ,根據式(9-5),整個組合的久期為
,根據式(9-5),整個組合的久期為
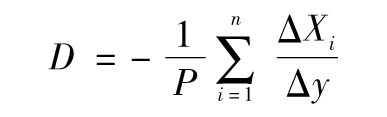
關於第i項資產的久期,由以下公式給出

因此
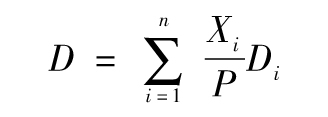
這一公式說明投資組合的久期D是其構成資產久期的加權平均,權重等於構成資產與整體組合價值的比率。
交易組合的絕對額久期D$可被定義為交易組合的久期乘以組合的價值,即
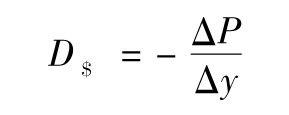
絕對額久期是交易組合對於利率的delta,與利率有關的產品所組成的交易組合的絕對額久期等於交易組合的構成資產的絕對額久期的總和。
凸性的概念同樣也可以像久期那樣推廣。假定一個與利率相關的組合其價格為P,我們定義組合的凸性C為1/P乘以組合的價值對零息收益曲線平行移動二階偏導的乘積,將B替換為P,式(9-4)仍然正確

這個公式說明了組合的凸性與構成組合的資產的凸性關係。這一關係與久期的關係式相似,也就是說,組合的凸性等於構成資產的凸性的加權平均,其權重為構成資產價格佔整體組合價格的比率。當一個交易組合的久期為一個特定值時,如果現金流在一個較長的時間內有較為均勻的分佈,則交易組合的凸性會趨向最大,而當現金流侷限在一個時間點時,債券組合的凸性趨向最小。
價值為P的交易組合的絕對額凸性可被定義為P乘以組合的凸性。絕對額凸性給出了交易組合對利率的gamma。與利率有關的產品所組成的交易組合的絕對額凸性等於組合的構成資產的絕對額凸性的總和。
交易組合免疫
通過保證久期為0,我們可以使得一個與利率有關的交易組合(由空頭和多頭組成)價值不受收益曲線小規模平行移動的影響。保證久期及凸性均為0或者接近於0,我們可以使得交易組合價值不受收益曲線較大規模的平行移動的影響。
[1] 零息收益曲線平行移動Δy數量所引起的債券收益率的變動大約為Δy。
9.6 收益曲線的非平行移動
不幸的是,利率久期的關係式(9-6)只適用於利率曲線的平行移動,由久期和凸性所組成的關係式(9-7)雖適用於較大規模的利率變動,但變動形式仍應是平行移動。
9.6.1 局部久期
一些研究人員已經擴展了久期方法以使其適用於收益曲線的非平行移動。Reitano(1992)提出了一種局部久期度量方法。在這一方法中零息收益曲線只在局部一點變動,而收益曲線的其他點保持不變。[1]例如,假定零息收益率由表9-4及圖9-4所示,將收益曲線上第5年所對應的點按圖9-5所示的形式進行移動。假定零息曲線上有n個點,交易組合對於收益曲線上第i點的局部久期Di的定義為
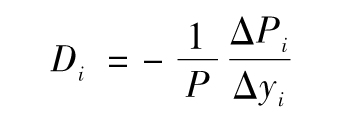
其中P為交易組合的價值,Δyi對應於收益曲線上第i個點的變動幅度,ΔPi是所對應交易組合的價值變化量。所有局部久期的和等於通常意義下的整個久期。[2]由於零息曲線第i個節點的變化Δyi所觸發的組合價值的相對變化為-DiΔyi。
表9-4 某零息收益率曲線(利率為連續複利)

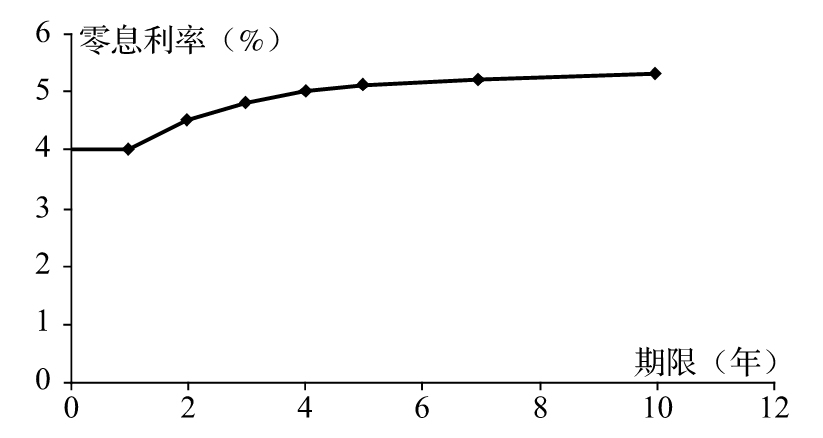
圖9-4 與表9-4對應的零息利率曲線
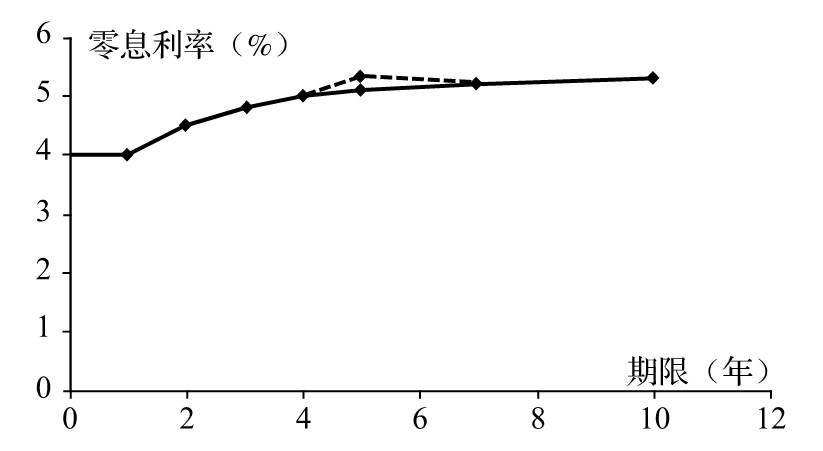
圖9-5 當某一點移動時零息收益率曲線的變化
假定表9-5顯示的是某交易組合的局部久期。整個交易組合的久期(各局部久期之和)僅僅為0.2,這說明交易組合對於收益曲線的平行移動並不是很敏感。但是從表中我們可以看到,對應於短期期限的久期為正,對應於長期期限的久期為負,這說明當短期利率上升(下降)時組合會有損失(收益),當長期利率上升(下降)時組合會有收益(損失)。
表9-5 某一投資組合的局部久期

我們現在可以進一步說明非平行移動對交易組合的影響,進一步計算投資組合價值對任何非平行移動變動的敏感性,定義一種旋轉方法,對應於1年、2年、3年、4年、5年、7年及10年的利率變動量為-3e、-2e、-e、0、e、3e及6e,這裡e為一個很小的值。圖9-6是此旋轉的圖形顯示。採用表9-5中的局部久期數據,我們得出由於收益曲線旋轉導致的交易組合價值的相對變化為
-[0.2×(-3e)+0.6×(-2e)+0.9×(-e)+1.6×0+2.0×e-2.1×3e-3.0×6e]=25.0e
對於曲線的一個小的平行移動e,交易組合價值的相對變化為-0.2e。這一結果顯示具有表9-5所示的局部久期的交易組合對於曲線旋轉的敏感性遠大於對平行移動的敏感性。
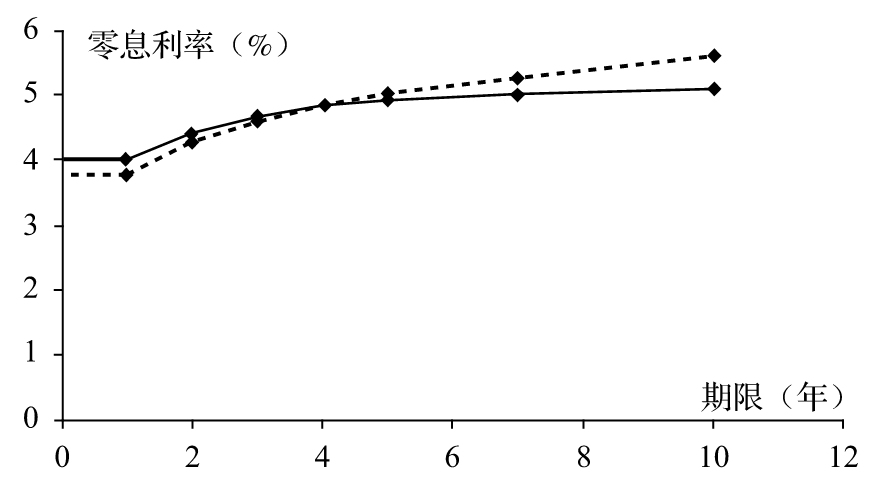
圖9-6 利率曲線的旋轉
在第9.5節中,我們解釋了通過將投資組合的價值乘以投資組合的久期,可以測度絕對額久期。類似地,局部久期是投資組合的變化率相對於期限結構一個頂點的微小變化的delta。
9.6.2 分段delta
局部久期的一種變形方法是,首先將收益曲線分成幾段或幾個區間(bucket),然後計算每一部分的變動對於交易組合的影響,在改變任意部分的利率時,要保證其他部分的利率不變。這種方法常常被應用於資產負債管理過程(見第9.1節),該管理方法也被稱為缺口管理(GAP management)。圖9-7將圖9-4所示的曲線中介於2年至3年的部分進行移動,類似於局部久期方法,所有部分的delta之和也等於DV01。
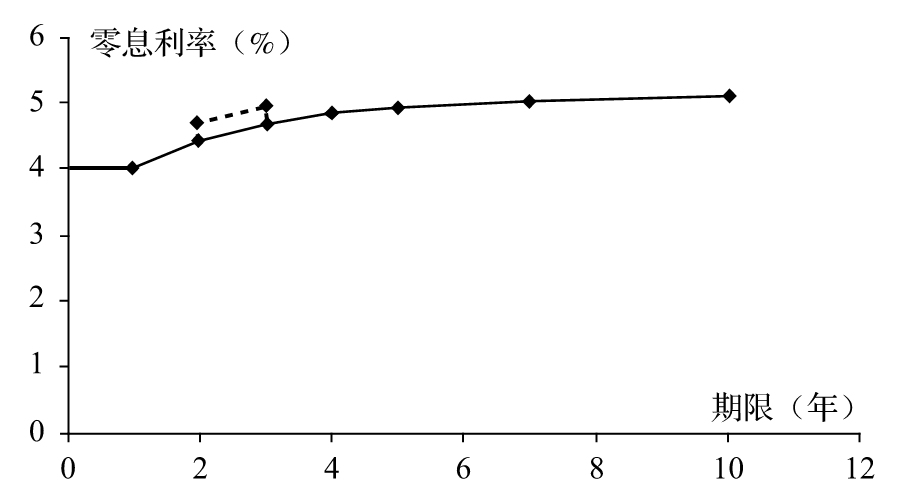
圖9-7 某區間的利率曲線變化
9.6.3 計算delta用於對衝
截至目前,我們考慮的敞口度量並不是為了方便對衝而設計的。考慮如表9-5所示的局部久期,假定我們打算用零息債券來對衝我們的交易組合,我們可以計算出1年期零息債券的頭寸來對衝2年期的利率變化。同樣我們也可以計算出2年期零息債券的頭寸來對衝2年期的利率變化,並依此類推。但是如果在對衝中採用其他工具,則對衝難度會大大增加。
在實踐中,交易員往往採用那些用於生成零息收益率曲線的產品來對衝他們的風險敞口。例如,在對衝時,一個政府債券交易員喜歡採用在市場上最活躍的,並被用來構造零息收益率曲線的政府債券。又如,當交易產品和LIBOR/互換曲線有關時,交易員更可能採用LIBOR存款、歐洲美元期貨以及互換交易等來對衝。
為了便於對衝分析,交易員常常測算那些用於構造零息收益率曲線的產品價格的微小變動對於交易組合的影響。當價格有微小變化時,零息收益率曲線會被重新產生,組合也會被重新定價。考慮某個負責交易利率上限期權(caps)以及利率互換期權(swap options)的交易員,假定對應於某一歐洲美元期貨報價的每一個基點變動,交易員的交易組合價格變化為500美元,而對應於一個基點價格變動,期貨價格變化為25美元,因此交易員可以採用20個期貨來對衝其風險;假定對應於5年期互換利率的一個基點變化,交易組合價格變化為4 000美元,而對應於這一5年期互換利率變化,一個5年期面值100萬美元的互換價格變化為400美元,因此交易員可採用一個面值1 000萬美元的互換來對衝其交易組合。
[1] See R. Reitano, “Nonparallel Yield Curve Shifts and Immunization,” Journal of Portfolio Management (Spring 1992):36-43.
[2] 當零息曲線的第i個點被移動而其他點不動時,這時的零息曲線是由被移動點和不被移動點的插值來生成的,如圖9-5所示。
9.7 主成分分析法
對於任意一個零息收益曲線,前面所述方法可能會要求分析員計算10~15個不同的delta。這看起來似乎有點小題大做,因為曲線上的變量相互之間是高度相關的。例如,曲線上5年期的收益率變化了若干基點,在大多數情況下,10年期的收益率變化也大致如此。當一個交易員在5年期有一個很大的正風險敞口,而對應於10年期有一個類似的負風險敞口時,此時該交易員不應該太擔心利率的變化。
一種可用來分析高度相關的市場變量的風險的方法是主成分分析法(principal component analysis),這種方法以市場變量的歷史變化數據為依據,並試圖從中找出解釋這些變化的主要成分或因素。
通過一個實例,我們可以更好地解釋這一方法。我們考慮的市場變量是期限為1年、2年、3年、4年、5年、7年、10年和30年的8個不同的互換利率,表9-6及表9-7顯示了基於2000~2011年2780個交易日的觀察數據產生的結果。表9-6中第1列顯示了利率期限,表中其他列顯示出描述利率變化的8個因子(主要成分)。第1個因子對應於利率曲線變化的平行移動,這一因子是表中的PC1。一個單位的PC1對應的1年期利率增加量為0.216基點,2年期利率的增加量為0.331個基點,依此類推;第2個因子位於PC2列,這一因子對應於收益率曲線的扭動(twist)或曲線坡度的變化,1~4年期利率變化為同一方向,5~30年期利率變化為另一方向;第3個因子PC3對應於利率曲線弓伸(bowing)現象,對應於這一因子,短期(1~2年)及長期利率(10~30年)朝同一方向移動,而中期利率會朝另一相反方向移動。因子所對應的利率變動被稱為因子載荷(factor loading)。在我們的例子中,對於1年期利率,第1個因子的因子載荷為0.216。[1]
表9-6 互換利率的因子載荷

表9-7 因子得分的標準差

我們的分析涉及8個利率變量以及8個因子,通過對一線性8元方程求解,可以將任意一天的利率變化表達為變化因子的線性組合,任意一天的利率變化對應某一因子的係數也被稱為這一天利率變化的因子得分(factor score)。
因子的重要性是通過因子得分的標準差來反映的,我們將例子中因子得分的標準差列在表9-7中,並按重要程度進行排列。在分析中,利率變動的計量單位為基點。因子的單位是標準差。因此第一個因子對應的1年期利率變動為0.216×17.55=3.78個基點,2年期利率變動為0.331×17.55=5.81個基點,依此類推。
用來計算表9-6和表9-7中結果的軟件可以在作者的網頁上找到。計算過程在附錄I中做了說明。主成分分析法是一個標準的統計工具。要進行主成分分析,第一步需從觀測中計算出一個方差-協方差矩陣(見第14章關於方差-協方差矩陣的討論)。在我們的例子中,該方差-協方差矩陣有8行8列,其中第1行第1列對應的是1年期利率日變動量的方差,第1行第2列對應的是1年期利率和2年期利率日變動量的協方差,依此類推。因子載荷是由該矩陣算出的特徵向量,而因子得分是由該矩陣算出的特徵值(對特徵值和特徵向量的解釋見附錄H)。
因子具有的一個性質是因子得分沒有相關性。在我們的例子中,第1個因子得分(平行移動數量)與第2個因子得分(扭動數量)在2 780個觀察日內相互獨立。因子得分的方差滿足以下性質:其和等於整個數據的方差。由表9-7得出,數據的整體方差(也就是1年期利率的觀察值的方差,2年期利率的觀察值方差等)為
17.552+4.772+2.082+…+0.532=338.8
由此可以看到第1個因子解釋了17.552/338.8=90.9%的原始數據的變化;前兩個因子解釋了(17.552+4.772)/338.8=97.7%的數據變化;第3個因子又進一步解釋了1.3%的數據變化。這說明,大部分利率變化中的風險可以由前兩個或前三個因子來解釋,這意味著我們可以將利率產品組合的風險同這些主要因子聯繫起來,因此我們並不需要考慮所有8個不同的利率。我們在圖9-8中畫出了表9-6所示的三個最重要的因子。[2]
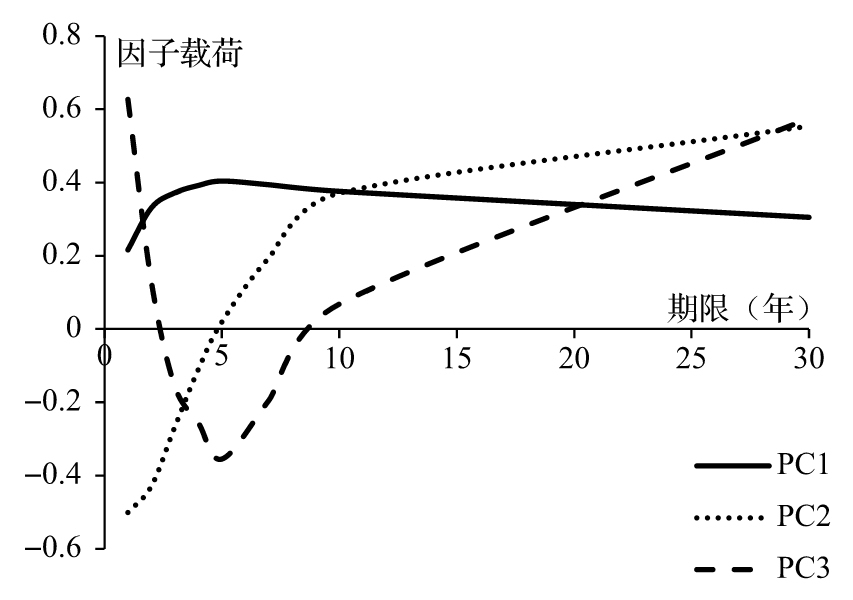
圖9-8 驅動利率變化的三個最重要因素
應用主成分分析法來計算delta
主成分分析法給計算delta提供了又一種有效的途徑。為了說明這一點,假定我們擁有一個交易組合,其對於利率變化的敞口如表9-8所示。3年期利率變化一個基點觸發組合價值增加量為1000萬美元;4年期利率變化一個基點觸發組合價值增加量為400萬美元等。如果我們採用前兩個最重要因子來模擬利率變化(如前所述,這兩個因子解釋了97%的利率變化),應用表9-6中的數據,我們算出第1個因子的delta敞口(對於每一個因子得分的一個基點變動所觸發的以百萬美元為單位的變動數量)為
10×0.372+4×0.392-8×0.404-7×0.394+2×0.376=+0.05
及第2個因子的delta敞口為
10×(-0.267)+4×(-0.110)-8×0.019-7×0.194+2×0.371=-3.88
表9-8 與一個基點利率變化相對應的交易組合價值變化 (百萬美元)

這裡的計算方法與第9.6節所描述的用局部久期來解釋非平行移動的方法相似。應用主成分分析法的優點是,這種方法會告訴你利率的哪種不同變化形式更為重要。在剛才的例子中,我們看到交易組合對於第2種利率變化的敞口是對於第一種變化敞口的80倍;但是,基於表9-7,第1種變化的標準差是第2種變化的標準差的3.7倍。某因子對於一個特定的交易組合的重要性可以通過delta敞口與因子得分的標準差的乘積來衡量。採用這個方法,對錶9-8中的交易組合,第2個因子的重要性是第1個因子的20倍。
[1] 因子載荷有一個性質:所有載荷因子的平方之和為1.0。另外,要注意,如果所有因子載荷的符號發生變化,因子不變。
[2] 將主成分分析法應用於任何一個國家的任意一收益曲線所得出的主要因子含義及解釋整體風險的數量與這裡陳述的結論基本相同。
9.8 gamma和vega
對應幾個不同利率的delta,會產生許多不同的gamma。假定在一個收益曲線的構造中涉及了10個金融產品,我們在此想測算交易組合對於每一種產品的敏感性。gamma是指交易組合價格對於基礎變量的二階偏導數∂2P/(∂xi∂xj),其中P為交易組合的價格。對於xi及xj,我們有10種不同的選擇,因此我們會有55個不同的gamma項。對所有這些值進行計算及監控,會造成“信息超負荷”(information overload)。一種變通的方法是忽略交叉項,因此我們只關心在i=j時10個gamma項。另外一種做法是將gamma定義為交易組合價值對於零息收益曲線平行移動的兩階導數,此時的gamma項是單一變量。還有一種選擇是計算交易組合價值對於主成分分析中的前兩個主要因子的gamma項。
一個利率產品交易組合的vega用來度量交易組合價值對於波動率的敞口。不同的利率衍生產品定價需要採用不同的波動率。一種測算波動率對組合價值影響的辦法是以相同數量來擾動所有的波動率,然後重新計算組合價值。另外一種辦法是採用主成分分析法,在主成分分析法中我們需要計算出能夠反映不同產品(如上限、下限、債券期權等)的波動率變化的主要因子。然後我們可以計算出對應於前兩個或三個主要因子的vega數量。
小結
銀行的淨利息收入來源於利息收入與費用之差,現在銀行已建立了較為完善的資產負債管理程序以使得淨利息收入在不同年度會保持相對穩定。
在世界範圍內,LIBOR是一種決定浮動貸款利率的重要參考利率。LIBOR利率是一個AA級公司短期的融資利率。一個完整的LIBOR曲線由LIBOR、歐洲美元期貨及互換利率計算得出。由LIBOR曲線得出的在將來某一時間段的遠期利率是在該時間段開始時,信用為AA級公司的短期貸款利率,而不是今天AA級公司的短期貸款利率。傳統上,大多數金融機構將LIBOR/互換利率結構曲線作為對無風險利率曲線的近似。但現在,隔夜指數互換利率已經取代LIBOR成為無風險貼現利率。
在利率市場中,久期是一個重要概念。久期衡量交易組合價格對零息收益率曲線平行變化的敏感度。我們有以下近似等式
ΔP=-PDΔy
其中P為交易組合價值,D為組合價值的久期,Δy為零息曲線平行移動的微小變量,ΔP是由Δy產生的組合價值變化。另外,一個更為精確的關係式為
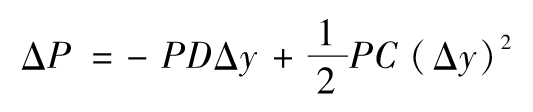
其中C為組合的凸性,這一關係式在收益曲線有一個較大的平行移動時仍然成立。但是,該關係式不適用於收益曲線的非平行移動。
為了量化利率曲線在不同時間的不同變化對投資組合的影響,我們需要引入幾種不同的久期及敏感度,其定義有多種方法。主成分分析法給計算多項敏感度提供了另一種有效的方法。它表明,實際中的收益曲線變化在很大程度上是二類或三類典型變化的線性迭加。假如一個交易組合管理人員對於這些典型變化進行了對衝,他通常也對實際中可能發生的曲線變化進行了很好的對衝。
延伸閱讀

練習題
9.1 假設銀行有一個50億美元1年期貸款及一個200億美元5年期貸款,支撐這些資產的負債分別為150億美元1年期及100億美元5年期存款。請陳述一下如果在今後3年中每年利率均增長1%,淨利息收入會受到什麼樣的影響。
9.2 為什麼通常長期利率會高於短期利率?在什麼情形下長期利率會低於短期利率?
9.3 為什麼美國國債利率遠低於無風險投資利率?
9.4 解釋隔夜指數互換是如何運作的。
9.5 為什麼說LIBOR-OIS利差是金融市場狀況的一個重要指標?
9.6 久期可以告訴你債券價格同利率變化之間有什麼樣的敏感關係?久期的侷限性是什麼?
9.7 一個年收益率為11%(連續複利)的5年期債券在每年年底支付8%的票息:
(a)債券價格為多少?
(b)債券久期為多少?
(c)運用久期公式來說明幅度為0.2%的收益率下降對債券價格的影響。
(d)重新計算年收益率為10.8%時債券的價格,並驗證計算結果同(c)的一致性。
9.8 假定收益率為一年複利一次,重複練習題9.7的計算,在計算中請採用修正久期公式。
9.9 一個6年期的債券的連續複利收益率為4%,此債券在每年的年底支付5%票息,利用久期及凸性公式來計算說明1%的收益率上升對債券價格的影響。公式計算的準確性如何?
9.10 請說明三種計算多變量delta並以此管理收益曲線非平行移動的辦法。
9.11 估算由表9-5定義的交易組合對於表9-6中前兩個因素的delta。
9.12 利用表9-5的數據來計算利率曲線的變動對一個價值為1 000萬美元的交易組合的影響,利率曲線的變動為利率曲線1年、2年、3年、4年、5年、7年和10年的利率分別增加10個、8個、7個、6個、5個、3個和1個基點。
9.13 如何定義絕對額久期和絕對額凸性?
9.14 以下關於交易組合的變量的關係是什麼?(a)久期;(b)局部久期;(c)DV01。
作業題
9.15 證明:(a)當y為連續複利時,式(9-1)和式(9-3)是等價的;(b)當y為每年複利m次時,將式(9-3)右邊除以1+y/m後,二者仍是等價的。
9.16 假定某銀行有100億美元1年期及300億美元5年期貸款,支撐這些資產的是分別為350億美元1年期及50億美元5年期的存款。假定銀行股本為20億美元,而當前股本回報率為12%。請估計要使得下一年股本回報率變為0,利率要做怎樣的變化?假定銀行稅率為30%。
9.17 組合A由一個1年期、面值為2 000美元的零息債券及一個10年期、面值為6 000美元的零息債券組成。組合B由5.95年期、面值為5 000美元的債券組成,當前所有債券年收益率為10%(連續複利)。
(a)證明兩個組合有相同的久期。
(b)證明如果收益率上升0.1%,兩個組合價值的百分比變化是相等的。
(c)如果收益率上升5%,兩個組合價值的百分比變化為多少?
9.18 作業題9.17中的交易組合的凸性為多少?久期以及凸性在多大程度上解釋了在作業題9.17(c)中組合價值的百分比變化?
9.19 假定表9-5為對局部久期的估計,解釋以下曲線移動的效果:10年利率保持不變,1年利率增加9e,1年與10年之間利率變化由0與9e之間的線性插值得出。從第9.6節中計算出的利率旋轉的結果中,如何算出本題的答案?
9.20 假設收益曲線上1年、2年、3年、4年、5年、7年、10年和30年的不同期限的利率分別增長一個基點時,交易組合價值變化分別為+5、-3、-1、+2、+5、+7、+8和+1(以百萬美元計)。估算交易組合對於表9-6所示的前三個因子的變化率,並將這三個因子對該組合的重要性進行量化。
第10章
波動率
對與組合價值相關的市場變量(如利率、匯率、股票價格、商品價格等)的波動率進行監控,對於金融機構來講至關重要。這一章將討論實現此目標所需的步驟。
在本章的開始,我們首先定義波動率。一個較為流行的假設是認為市場變量的百分比回報服從正態分佈,我們將對這一假設進行討論並展示另一種方法,即冪律分佈法。在這之後我們將介紹一些名稱看上去很“高大上”的估計波動率的方法,例如指數加權移動平均(exponentially weighted moving average,EWMA)、自迴歸條件異方差(auto-regressive conditional heteroscedasticity,ARCH)以及廣義自迴歸條件異方差(generalized auto-regressive conditional heteroscedasticity,GARCH)等方法。這些方法的一個顯著特點是它們都不把波動率設為常數。在某些時間段內波動率變化可能很小,而在其他時間段內變化可能很大,這些方法試圖跟蹤波動率隨時間的變化。
10.1 波動率的定義
某個變量的波動率σ定義為這一變量在單位時間內連續複利回報率的標準差(見附錄A關於複利的討論)。當波動率被用於期權定價時,時間單位通常定義為1年,因此波動率就是1年的連續複利回報率的標準差。但當波動率被用於風險控制時,時間單位通常是1天,此時的波動率對應於連續複利的日回報率的標準差。
定義Si為一個變量在日期i結束時的值,則該變量連續複利的日回報為
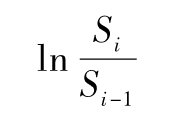
這與下式基本相等
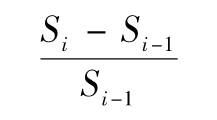
因此,日波動率的另外一種定義是變量的日相對變化的標準差。這個定義也是風險管理中常用的定義。
【例10-1】 假定一個資產的價格是60美元,日波動率為2%。這意味著一天中資產價格出現一個標準差的變化等於60×0.02,即1.20美元。如果我們假設資產價格變化服從正態分佈,則我們有95%的把握確信,在一天結束時,資產的價格將在60-1.96×1.2=57.65美元和60+1.96×1.2=62.35美元之間(這就是雙尾檢驗,即各有2.5%的概率落在分佈的上尾和下尾)。
如果我們假設,每日的回報是相互獨立的且具有同樣的方差,則T天的回報的方差為T乘以每日回報方差的積。這意味著,T天回報的標準差是日回報標準差的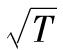 倍。這和“不確定性隨時間長度的平方根增長”這一法則是一致的。
倍。這和“不確定性隨時間長度的平方根增長”這一法則是一致的。
【例10-2】 假設例10-1中資產的價格是60美元,日波動率為2%,則5天連續複利的回報率的標準差是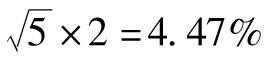 。因為5天是一個較短的時間,所以我們可以認為這和5天來價格相對變化的標準差相等。一個標準差的移動對應的價格變化為60×0.044 7=2.68美元。如果我們假設,資產價格的變化服從正態分佈,則我們有95%的把握確信,在第5天結束時,資產的價格位於60-1.96×2.62=54.74美元和60+1.96×2.68=65.26美元之間。
。因為5天是一個較短的時間,所以我們可以認為這和5天來價格相對變化的標準差相等。一個標準差的移動對應的價格變化為60×0.044 7=2.68美元。如果我們假設,資產價格的變化服從正態分佈,則我們有95%的把握確信,在第5天結束時,資產的價格位於60-1.96×2.62=54.74美元和60+1.96×2.68=65.26美元之間。
10.1.1 方差
風險管理人員常常關心方差而不是波動率。方差被定義為波動率的平方。年方差對應於變量在1年內連續複利變化的方差。在時間T內變化的標準差與時間的平方根成正比,而方差與時間成正比。嚴格來講,我們應該說方差對應於每天的變化,而波動率對應於每天的平方根的變化。
10.1.2 交易天數與日曆天數
在計算波動率時,會產生以下的問題:我們應該採用日曆天數還是交易天數?如業界事例10-1所示,研究人員已經證明在交易所營業日的波動率比在交易所非營業日的波動率要大很多,因此當由歷史數據估計波動率時,分析員常常忽略週末和節假日,在計算時通常的假定是每年有252個交易日。
業界事例10-1
什麼因素觸發了波動率
有一種關於波動率的自然假設,那就是波動率是由剛剛到達市場的新信息引起的。這些消息促使投資者改變對股票價格的觀點。股票價格變化也促成了波動率的變化,但是這種有關波動率變化根源的觀點沒有得到研究結果的支持。
應用連續幾年的每日資產價格數據,研究人員可以計算:
(1)在中間不包含非交易日時,一個交易日結束時與下一個交易日結束時資產價格回報率的方差;
(2)在週五結束時與下週一結束時資產價格回報率的方差。
第2項為3天收益率的方差。第1項對應於1天的方差。我們也許很自然地認為第2項方差為第1項方差的3倍。法瑪(Fama,1965)、弗倫奇(French,1980)以及弗倫奇和羅爾(French and Roll,1986)證明事實並非如此。三項研究結果分別證明第2項方差只分別比第1項方差高22%、19%以及10.7%。
這時,你也許會說這些結果是由於在交易開盤時有更多信息,但是羅爾(1984)的研究結果並不支持這一觀點,羅爾檢測了橙子的期貨價格。對於橙子的期貨價格而言,最重要的決定因素是氣候,而有關氣候的信息對於任何時間都有同樣的到達頻率,當羅爾做了一個類似我們剛剛描述的有關股票的分析時,他發現第2項(週五至週一)方差只是第1項的1.54倍。
唯一合理的結論就是波動率在某種程度上是由交易本身造成的(當然對這一結論,交易員接受起來沒有任何困難)。
設σyr為某一資產的年波動率,σday為相應的每天波動率。假設連續交易日的回報是獨立的,並有相同的標準差,這意味
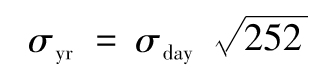
或
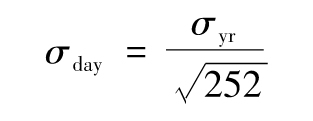
以上關係式說明,日波動率大約為年波動率的6%。
10.2 隱含波動率
儘管風險管理人員通常從歷史數據中計算波動率,但他們也會計算和跟蹤隱含波動率(implied volatility)。布萊克-斯科爾斯-默頓期權定價公式中唯一不能直接觀察到的參數就是股票價格的波動率(見附錄E)。隱含波動率是將市場上的期權價格代入公式後反推計算出的波動率。
VIX指數
芝加哥期權交易所(CBOE)會發布隱含期權指數。最流行的指數VIX由標準普爾500指數上大量30天期限的看漲和看跌期權來計算求得。[1]在VIX上的期貨交易是從2004年開始的,而在VIX上的期權交易是從2006年開始的。涉及標準普爾500指數的期貨或期權在將來的標準普爾500指數水平以及標準普爾500指數波動率兩方面下注。與此相反,VIX上的期貨或期權只在波動率上下注。一份合約是指數的1 000倍。
【例10-3】 假設一個交易員買了一份VIX上4月的期貨合約,當時的期貨價格是18.5美元(相當於30天標準普爾500指數波動率為18.5%),並在期貨價格為19.3美元(相當於30天標準普爾500指數波動率為19.3%)時平倉。交易員盈利為800美元。
圖10-1顯示了2004年1月~2017年6月的VIX指數。2004~2007年年中,指數基本保持在10~20。在2007年下半年,指數達到30;在雷曼兄弟破產後,指數在2008年10月和11月達到了破紀錄的80。在2010年早些時候,指數已經恢復到比較正常的狀態,但隨後因為市場的不確定性指數又再次升高。有時,市場參與者也把VIX指數稱作“恐慌指數”。
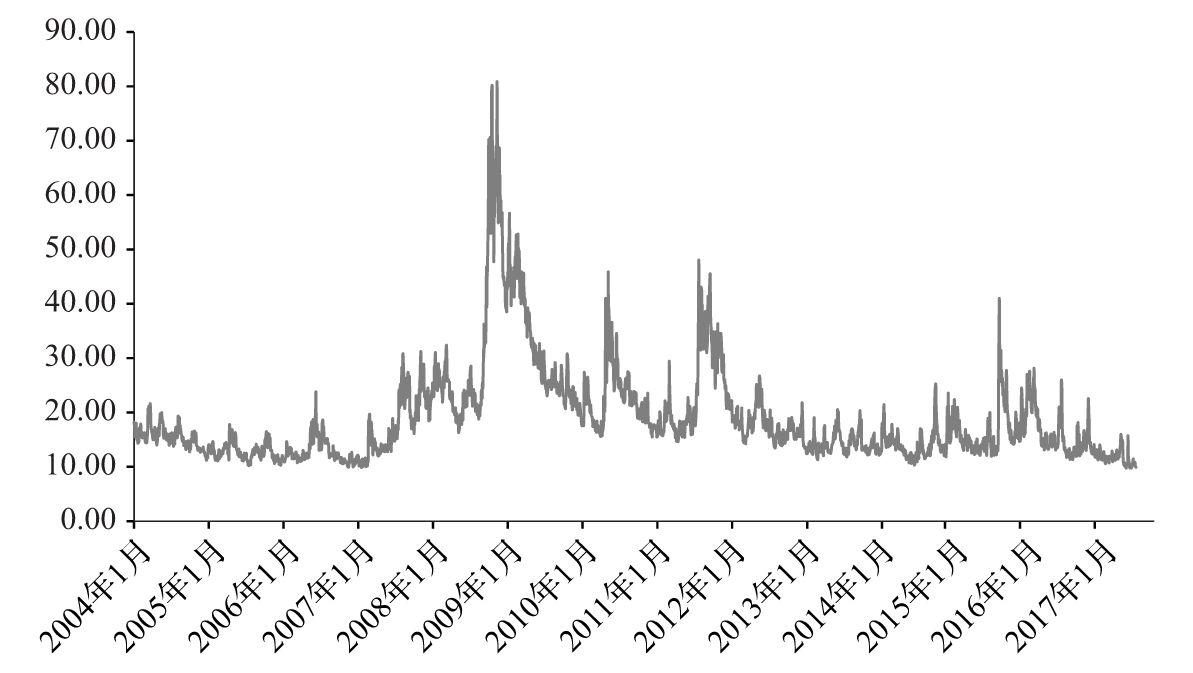
圖10-1 2004年1月~2017年6月的VIX指數
[1] 與其類似,VNX是NASDAQ 100指數的波動率指數,VXD是道瓊斯工業指數的波動率指數。
10.3 金融變量的每日變化量是否服從正態分佈
當通過波動率來計算市場變量變動的置信區間時,一個常用的假設是市場變量服從正態分佈。這也是在例10-1和例10-2中我們採納的假設。在實際中,大多數金融變量的值發生較大變化的可能性比正態分佈所給出的要大。表10-1顯示了用10種匯率在2005~2015年10年期內的日變化量來檢驗其是否符合正態分佈的結果。這10種匯率分別是美元與下列貨幣之間的匯率:澳元、英鎊、加拿大元、丹麥克朗、歐元、日元、墨西哥比索、新西蘭元、瑞典克朗和瑞士法郎。編制該表的第一步是計算每種匯率的日百分比變化的標準差,第二步是計算有多少百分比變化超過1個標準差、2個標準差,等等。將這些數字與正態分佈上對應的數字進行比較。
表10-1 價格比例變化大於1,2,…,6個標準差的天數佔全部觀察日數的比例(S.D.=價格比率變化的標準差)
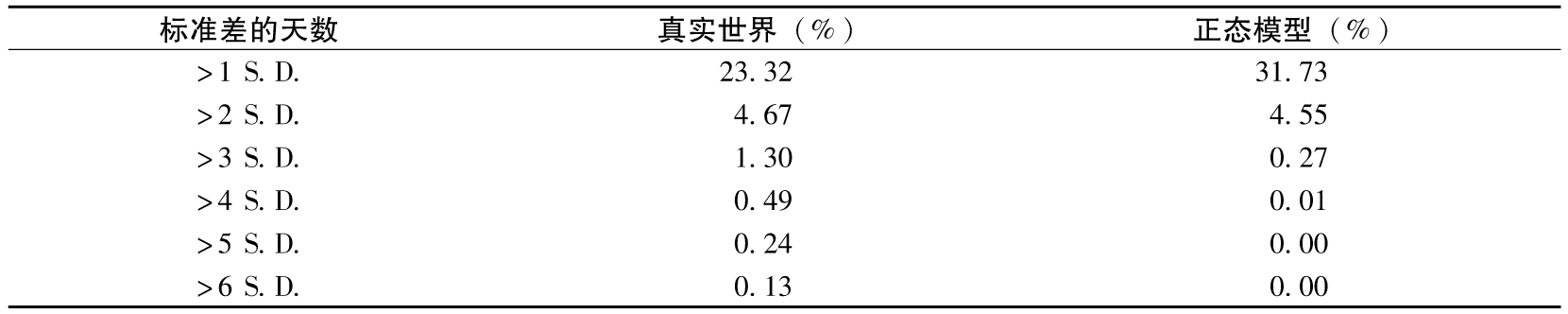
每天價格百分比變化超過3個標準差的個數佔所有觀察數據的比例為1.30%,而正態分佈所對應的比例只是0.27%。每天價格百分比變化超出4個、5個以及6個標準差的天數佔整個觀察日的比例分別為0.49%、0.24%以及0.13%,而正態分佈認為這些事件幾乎不可能發生。因此,表10-1提供了實際中的匯率變化比正態分佈的預測存在更肥大尾部的證據。
當對回報採用連續複利時,多日的回報等於其中每日回報的和。如果每日回報服從相同的非正態概率分佈,那麼統計學上的中心極限定律給出的結論是:多日的回報服從正態分佈。實際上,連續多日的回報並不服從同一個分佈(其中一個原因是,波動率並不為常數。我們會在本章的後面討論這個問題)。因此,較長觀察期內的回報以及每日回報的分佈都會呈現肥大的尾部。業界事例10-2指出,如果你早在1985年做了這一分析,你將如何賺大錢。
業界事例10-2
如何從外匯期權中盈利
布萊克、斯科爾斯和默頓在他們的期權定價模型中假設標的資產的價格在將來服從對數正態分佈。這一假設和資產的價格變化在短期(如1天內)服從正態分佈的假設是一致的。假如大多數市場參與者接受這一假設,而你剛剛做了表10-1中的分析,從而已獲知對數正態分佈並不是一個好的關於匯率的假設,那麼你應該做什麼才能從這些結論中來盈利呢?
答案是你應該買入不同幣種的深度虛值(deep-out-of-the-money)看漲及看跌期權,接下來就是等待。這些期權相對來講比較便宜並且成為實值期權的概率要比對數正態分佈模型預測的高一些,你的期權的平均收益要比期權費用高得多。
20世紀80年代中期,有一些交易員認識到匯率分佈中的“肥尾性態”,而其他交易員仍然認為布萊克-斯科爾斯-默頓模型中的對數正態分佈合理。對匯率分佈有正確認識的交易員採用了我們描述的策略並且獲得了巨大的盈利。到了80年代後期,幾乎所有人都認識到虛值期權所對應的隱含波動率應該更高,這時套利機會消失了。
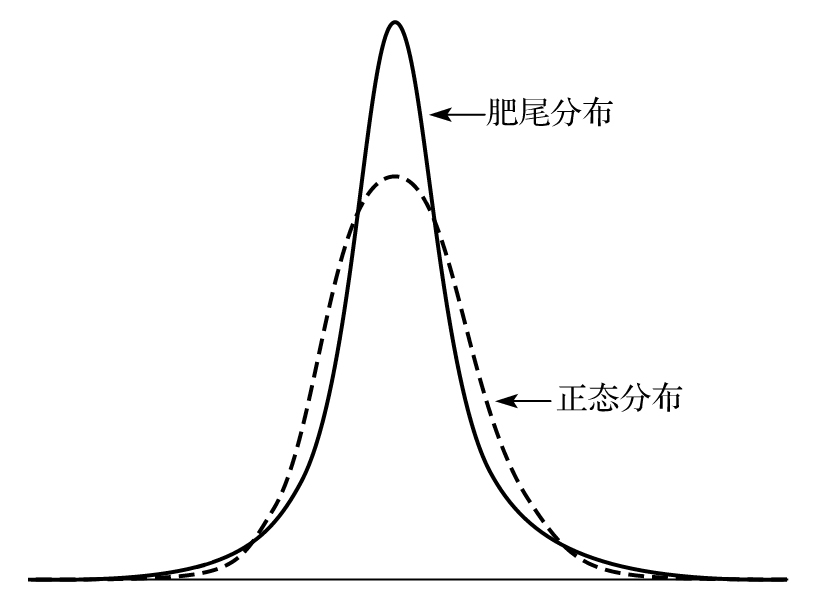
圖10-2 正態分佈與某肥尾分佈的比較
注:這裡的兩個分佈具有同樣的期望值及標準方差。
圖10-2比較了一個典型的肥尾分佈(例如匯率分佈)與一個具有同樣期望值及標準差的正態分佈。[1]肥尾分佈比正態分佈的峰值要高。在圖中我們可以看到這兩種分佈有3處不同,分別是中間部分、尾部以及介於中間及尾部的過渡部分。當從正態分佈轉移到肥尾分佈時,概率密度圖形的腰部向中央及兩尾部移動。我們在考慮市場變量的百分比變化時,肥尾分佈所對應的極大及極小變化事件的數量要比在正態分佈中相應的數量多,而相應過渡部分事件數量會少。
[1] 峰度(kurtosis)度量分佈尾部的大小。肥尾(leptokurtic)分佈比正態分佈的尾部要肥大,輕尾(platykurtic)分佈比正態分佈的尾部要瘦小,同尾(mesokurtic)分佈同正態分佈的尾部大小相等。
10.4 冪律
冪律(power law)提供了正態分佈假設外的另一種方法。冪律指出,實踐中的許多變量的值,例如v,當x很大時,以下的關係式近似成立
Prob(v>x)=Kx-α
(10-1)
其中K及α為常數。上式已經被證明在許多情形下近似成立,這裡的變量可能是指個人的收入、城市的大小或者網頁每日被點擊的次數等。
【例10-4】 假定基於經驗,我們知道某個特定的金融變量α=3,並且觀察到v>10的概率為0.05,由式(10-1)得出
0.05=K×10-3
因此K=50。我們可以估計v>20的概率為
50×20-3=0.006 25
v>30的概率為
50×30-3=0.001 9
等等。
由式(10-1),我們可以得出
ln[Prob(v>x)]=lnK-αlnx
我們因此可以畫出ln[Prob(v>x)]與lnx的關係曲線來快速檢驗等式的正確性。為了將這一過程應用於表10-1中的數據,我們將v定義為匯率在一天內變化的標準差數量。
lnx和ln[Prob(v>x)]的價值在表10-2中進行了計算,圖10-3顯示了表10-2的數據。當x≥2時,匯率變化大於x個標準差的概率的對數近似和lnx呈線性關係,這說明了冪律的正確性。當x=3,4,5,6時,利用迴歸得出最佳匹配曲線為
ln[Prob(v>x)]=-0.735-3.291ln(x)
表10-2 由表10-1所得出的數值
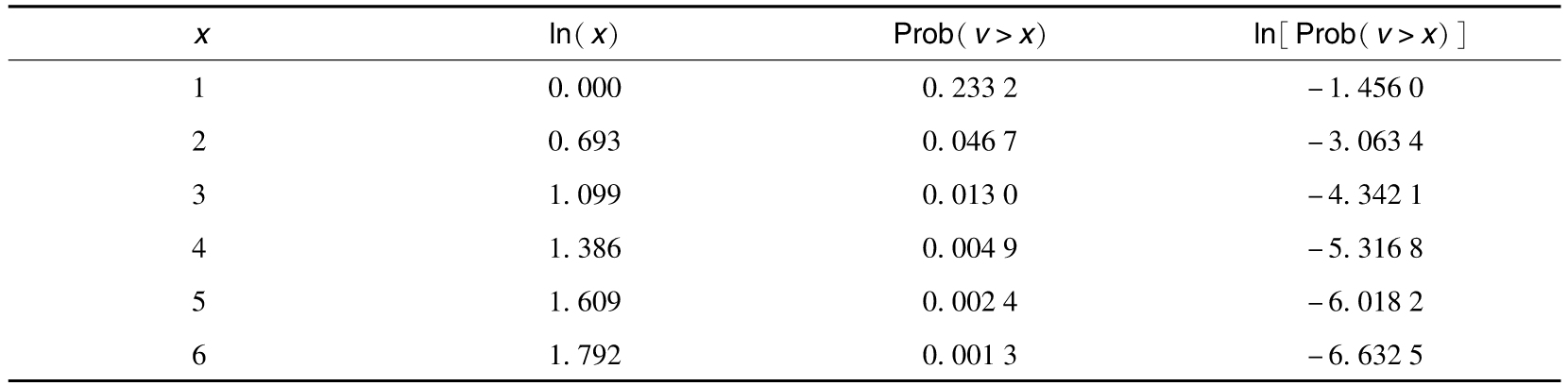
參數K和參數α的估計為:K=e-0.735=0.479,以及α=3.291。一個大於4.5倍標準差的增量的概率為
0.479×4.5-3.291=0.003 40
變化大於7倍標準差的概率為
0.479×7-3.291=0.000 794
在第13章討論極值理論時,我們將會較為正規地討論冪律以及給出更好的參數估計方式。在第23章中,我們將討論如何將冪律用於對操作風險進行檢測。
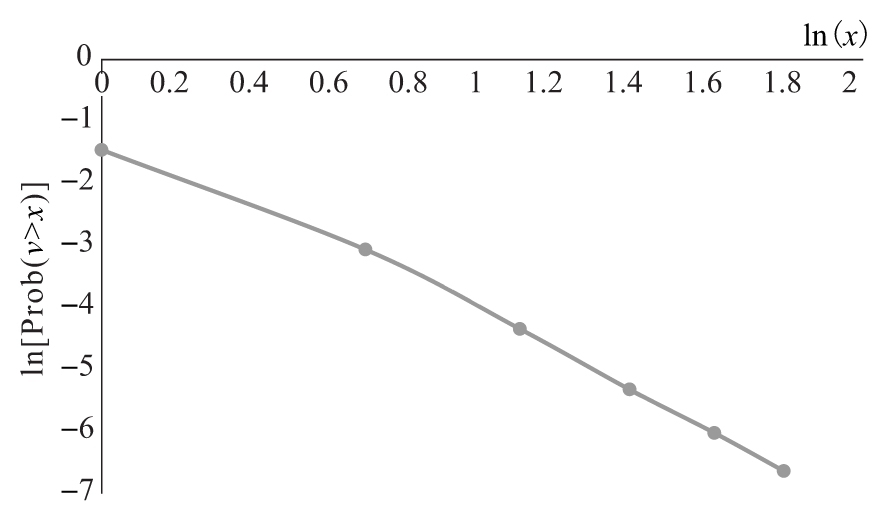
圖10-3 匯率變化超過若干標準差的概率的log-log圖
注:其中v是以標準差為度量的匯率變化量。
10.5 監測日波動率
定義σn為第n-1天結束時所估計的市場變量在第n天的波動率,相應的方差為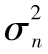 。假定市場變量在i天天末的價格為Si。定義ui為第i天連續複利收益率(第i-1天天末至第i天天末的收益),於是有
。假定市場變量在i天天末的價格為Si。定義ui為第i天連續複利收益率(第i-1天天末至第i天天末的收益),於是有
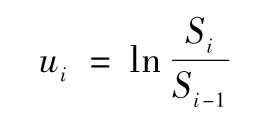
一種估計σn的方法是令其等於ui的標準差,利用ui最近m天的觀察數據和標準差的一般公式,我們得出

其中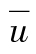 為ui的平均值
為ui的平均值
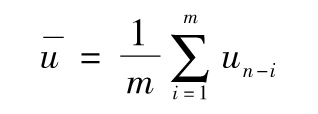
【例10-5】 表10-3顯示了股票價格的一個可能的序列。假設我們希望根據前20天對ui的觀察數據估計第21天的波動率,即n=21,m=20。在本例中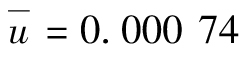 ,根據式(10-2)計算得出的日回報的標準差的估計值為1.49%。
,根據式(10-2)計算得出的日回報的標準差的估計值為1.49%。
表10-3 用來計算波動率的數據
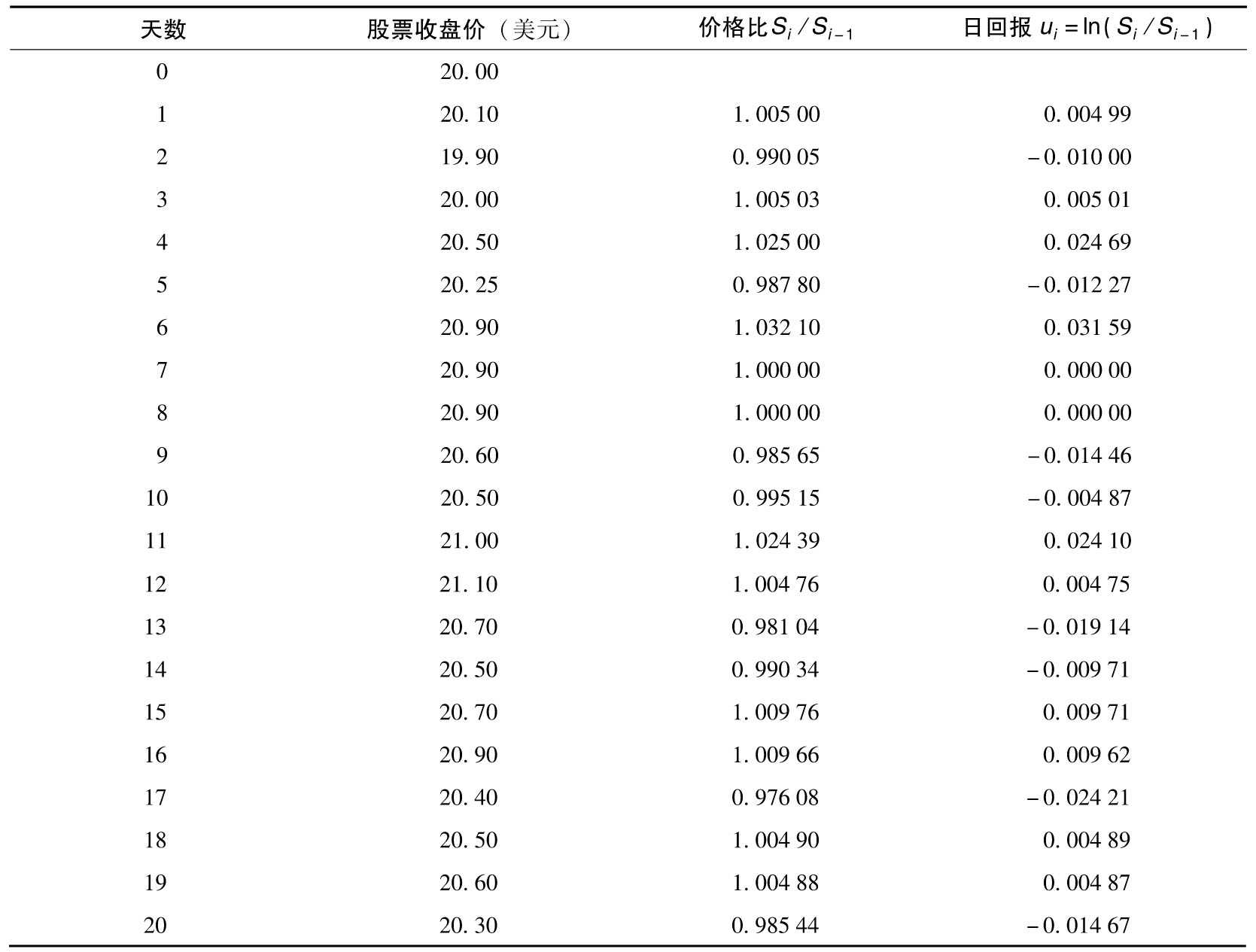
式(10-2)的以下幾種變形常常被用於風險管理過程之中。
(1)如第10.1節中介紹的,ui被定義為市場變量在第i-1天天末與第i天天末的價格百分比變化

這種計算方式與前面計算ui的方式差別不大。
(2)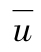 被假設為0:這種假設的前提是因為每一天市場變化期望值遠遠小於市場變化的標準差。[1]
被假設為0:這種假設的前提是因為每一天市場變化期望值遠遠小於市場變化的標準差。[1]
(3)m-1被m代替:這種做法將我們的波動率從無偏差估計轉換為最大似然估計(見第10.9節)。
以上三個變形會使得方差公式簡化為

其中ui由式(10-3)給出。
【例10-6】 再次考慮例10-5,當n=21,m=20時
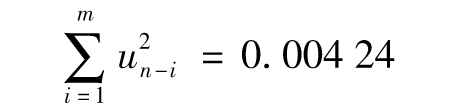
於是由式(10-4)
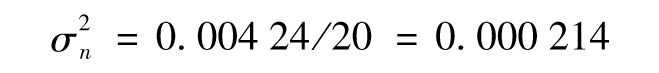
σn=0.014 618或1.46%。與例10-5相比變化很小。
加權方法
式(10-4)為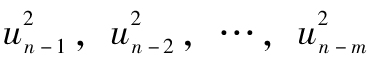 所有項賦予了相等的權重。我們的目標是估計第n天的波動率σn水平,因此賦予較新的數據更高的權重就具有合理性。一種這樣做的模型為
所有項賦予了相等的權重。我們的目標是估計第n天的波動率σn水平,因此賦予較新的數據更高的權重就具有合理性。一種這樣做的模型為

變量αi為i天前的觀察值所對應的權重,所有的α均為正。如果我們在對α賦值時保證在i>j時αi<αj,數據越久,所獲得的權重就會越低。所有權重之和必須為1,即
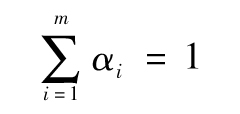
對於式(10-5)的理念,我們還可以做進一步擴展。假設存在某一長期平均方差,我們在考慮分配權重時,也應該將此均值考慮在內。這種擴展對應於以下模型

其中VL為長期方差,γ為VL所對應的權重,權重之和仍為1,我們有
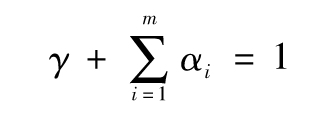
此模型被稱為ARCH(m)模型。這一模型最先由恩格爾(Engle)提出。[2]在這一模型中,方差的估計值與長期平均方差以及m個觀察值有關,觀察數據越陳舊,所對應的權重越小。令ω=γVL,我們可以將式(10-6)寫為

在接下來的兩節中,我們將討論兩種測算波動率的重要方法,這兩種方法均採用了式(10-5)及式(10-6)中的理念。
[1] 即使在我們所觀察的m天中,變量值增大或減小的速度非常快,這一假設也基本上是成立的。
[2] See R. F. Engle, “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of U. K. Inflation,” Econometrica 50(1982):987-1008.羅伯特·恩格爾因對ARCH模型的貢獻而獲得2003年諾貝爾經濟學獎。
10.6 指數加權移動平均模型
指數加權移動平均模型(EWMA)是式(10-5)的一個特殊形式,其權重αi隨著回望時間的加長而按指數速度遞減。這一模型的特殊形式為αi+1=λαi,其中λ是介於0與1之間的某一常數。在以上特殊假設下,更新波動率的公式變得非常簡潔

第n天波動率σn(在第n-1天天末估算)由第n-1天波動率σn-1(在第n-2天天末估算)及最近一天價格變化率un-1的數據來決定。
為了說明式(10-8)的權重以指數速度下降,我們將式(10-8)所算出的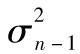 代回式(10-8)之中
代回式(10-8)之中
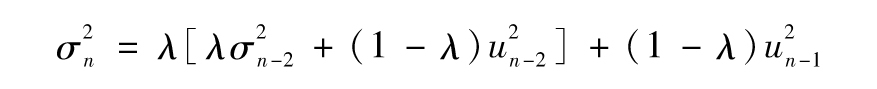
即
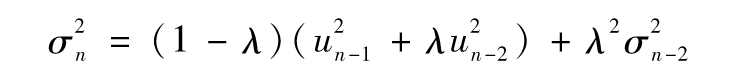
代入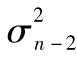 項,我們進一步得出
項,我們進一步得出
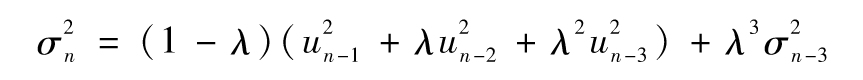
依此類推,我們得出
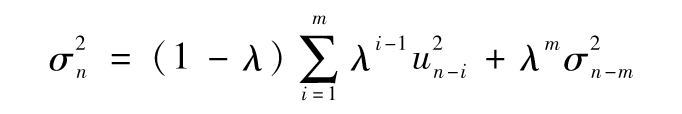
當m很大時,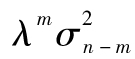 小到可以忽略,所以當αi=(1-λ)λi-1時,式(10-8)與式(10-5)等價。對應於u的權重以λ速度遞減,每一項的權重是前一項權重與λ的乘積。
小到可以忽略,所以當αi=(1-λ)λi-1時,式(10-8)與式(10-5)等價。對應於u的權重以λ速度遞減,每一項的權重是前一項權重與λ的乘積。
【例10-7】 假如λ為0.90,對應於第n-1天由市場變量所估測的波動率為每天1%。在第n-1天,市場變量增加了2%,這意味著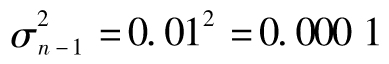 以及
以及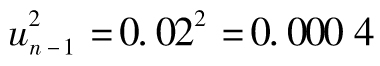 ,由式(10-8),我們得出
,由式(10-8),我們得出
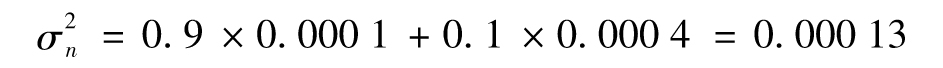
因此,第n天波動率σn的估計為 ,即每天1.14%。注意
,即每天1.14%。注意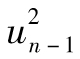 的期望值為
的期望值為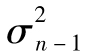 ,也就是0.000 1,這一例子中,
,也就是0.000 1,這一例子中,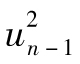 所對應的實際值比期望值要大,因此我們對於波動率的估計會增大。當
所對應的實際值比期望值要大,因此我們對於波動率的估計會增大。當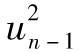 的實際數值小於期望值時,我們對於波動率的估計值會減小。
的實際數值小於期望值時,我們對於波動率的估計值會減小。
EWMA方法的一個非常好的特性是該方法需要的數據相對較少。對於任一時刻,我們只需要記憶對當前方差的估計以及市場變量的最新觀察值。當我們得到市場變量的最新觀察值後,我們可以計算每天價格變化的比例,進而採用式(10-8)更新我們對方差的估計,這時更早的方差估計以及更早的市場變量數據可以被捨棄。
EWMA方法的出發點是對波動率進行跟蹤監測。假定市場在n-1天有一個較大的變化,那麼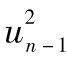 也較大,由式(10-8)可以看出,這時對當前波動率的估計會增加。數值λ決定了當前估算出的日波動率估計對於最新市場變量日百分比變化的靈敏度。在計算σn時,對
也較大,由式(10-8)可以看出,這時對當前波動率的估計會增加。數值λ決定了當前估算出的日波動率估計對於最新市場變量日百分比變化的靈敏度。在計算σn時,對 項,一個較低的λ會對應一個較大的權重。在這種情形下,對接下去幾天的波動率的估計本身就會有很大波動,而當λ較大時(接近於1),估算出的波動率對於新的日百分比變化率信息的反應會較為遲鈍。
項,一個較低的λ會對應一個較大的權重。在這種情形下,對接下去幾天的波動率的估計本身就會有很大波動,而當λ較大時(接近於1),估算出的波動率對於新的日百分比變化率信息的反應會較為遲鈍。
由摩根大通建立並在1994年發佈的RiskMetrics數據庫中,採用λ=0.94來更新每天波動率估計。摩根大通發現對許多市場變量,這一選定的λ值生成的方差預測與實際方差非常接近。[1]2006年以後,RiskMetrics更換了模型,轉而採用一個長記憶模型(long memory model)。相比EWMA模型,在新模型中隨i的增大,賦予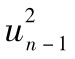 項的權重衰減得要慢。
項的權重衰減得要慢。
[1] See JPMorgan, RiskMetrics Monitor, Fourth Quarter, 1995.在這一章中我們採用另一種方法(最大似然估計)來估計參數,某一天實際的方差是對連續25天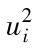 的數據實施等權重平均計算得出的(見作業題10.20)。
的數據實施等權重平均計算得出的(見作業題10.20)。
10.7 GARCH(1,1)模型
我們現在討論由Bollerslev在1986年提出的GARCH(1,1)模型。[1]GARCH(1,1)模型與EWMA模型的不同類似於式(10-5)與式(10-6)的不同。在GARCH(1,1)中,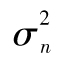 是由長期平均方差VL、un-1及σn-1計算得出的,GARCH(1,1)表達式為
是由長期平均方差VL、un-1及σn-1計算得出的,GARCH(1,1)表達式為

其中γ為對應於VL的權重,α為對應於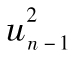 的權重,β為對應於
的權重,β為對應於 的權重,因為權重之和為1,我們有
的權重,因為權重之和為1,我們有
γ+α+β=1
EWMA模型是GARCH(1,1)模型對應於γ=0、α=1-λ及β=λ的特例。
GARCH(1,1)模型中的“(1,1)”代表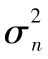 是基於最近的u2的觀察值以及最新的方差的估計而得到的。在廣義的模型GARCH(p,q)中的
是基於最近的u2的觀察值以及最新的方差的估計而得到的。在廣義的模型GARCH(p,q)中的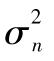 是從最近p個u2的觀察值及q個最新的有關方差的估計而計算得到的。[2]到目前為止,GARCH(1,1)是最流行的一種GARCH模型。
是從最近p個u2的觀察值及q個最新的有關方差的估計而計算得到的。[2]到目前為止,GARCH(1,1)是最流行的一種GARCH模型。
令ω=γVL,我們可以將GARCH(1,1)模型寫成

這種模型的表達形式是為了估計參數。當ω、α及β被估算出後,我們可由γ=1-α-β來計算γ,長期方差VL=ω/γ。為了保證GARCH(1,1)模型的穩定,我們要求α+β<1,否則對應於長期方差的權重會為負值。
【例10-8】 假設某一個由每天觀測數據估算出的GARCH(1,1)模型為
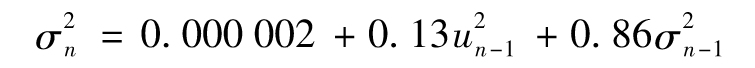
這對應於α=0.13、β=0.86以及ω=0.000 002。γ=1-α-β=0.01,ω=γVL,得出VL=0.000 2。換句話講,由模型隱含出的長期平均日方差平均為0.000 2,對應的波動率為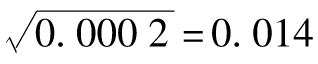 ,即每天1.4%。
,即每天1.4%。
假設對應於n-1天的日波動率估算值為1.6%,因此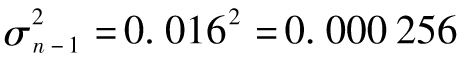 ,又假設n-1天市場價格降低1%,即
,又假設n-1天市場價格降低1%,即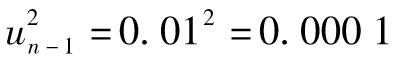 ,因此
,因此
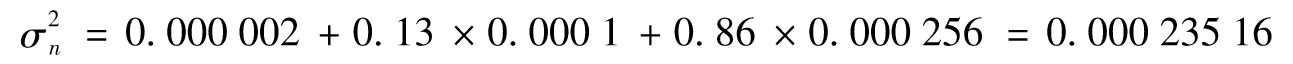
對於波動率的最新估計為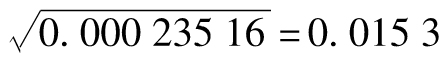 ,即每天1.53%。
,即每天1.53%。
權重
對式(10-10)中的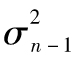 進行替換,我們可得
進行替換,我們可得

即
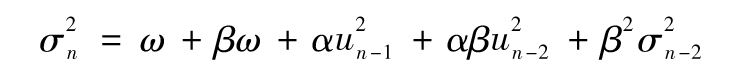
替換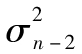 ,我們得到
,我們得到
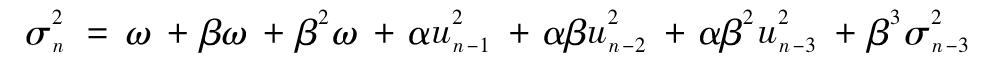
以這種形式繼續下去,我們可以看到對應於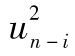 的權重為αβi-1,權重以β指數速度下降,參數β可被解釋為衰減速度(decay rate),這與EWMA中的λ係數近似。在決定最新方差時,此係數決定了不同ui的重要性。例如,如果β=0.9,說明
的權重為αβi-1,權重以β指數速度下降,參數β可被解釋為衰減速度(decay rate),這與EWMA中的λ係數近似。在決定最新方差時,此係數決定了不同ui的重要性。例如,如果β=0.9,說明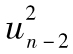 的重要性只是
的重要性只是 的重要性的90%,
的重要性的90%,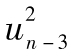 的重要性只是
的重要性只是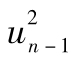 的重要性的81%,依此類推。GARCH(1,1)與EWMA模型類似,其不同之處是在對過去的u2賦予指數衰減權重的同時,對於長期平均波動率也賦予了某種權重。
的重要性的81%,依此類推。GARCH(1,1)與EWMA模型類似,其不同之處是在對過去的u2賦予指數衰減權重的同時,對於長期平均波動率也賦予了某種權重。
[1] See T. Bollerslev, “Generalized Autoregressive Conditional Heteroscedasticity,” Journal of Econometrics 31(1986):307-327.
[2] 有人已經提出反映公司非對稱信息的GARCH模型,在這些模型設計中,σn與un-1的符號有關。在某種意義上,這些模型比GARCH(1,1)更適合股票,這是因為股票的波動率常常與價格有反向關係,因此一個符號為負的un-1比一個符號為正的un-1對於σn的影響更大。關於處理非對稱信息的模型,讀者可參考D. Nelson, “Conditional Heteroscedasticity and Asset Returns: A New Approach,” Econometrica 59(1990):347-370 and R. F. Engle and V. Ng, “Measuring and Testing the Impact ofNews on Volatility,” Journal of Finance 48(1993):1749-1778。
10.8 模型選擇
在實踐中,方差值常常會被拉回到長期平均值水平,這種現象被稱為均值迴歸(mean reversion),我們曾在第7.5節中討論過。GARCH(1,1)模型有均值迴歸的特性,而EWMA沒有均值迴歸特性,從理論上講,GARCH(1,1)比EWMA有更好的特性。
在下一節中,我們將討論如何估計GARCH(1,1)中ω、α、β等的最佳匹配參數。當參數ω為0時,GARCH(1,1)退化為EWMA,在某些場合,最佳匹配參數ω為負,這時對應的GARCH(1,1)模型不穩定,此時採用EWMA模型更為合理。
10.9 最大似然估計法
現在是個很好的時機討論如何應用歷史數據來估計我們以上討論模型的參數,將要討論的方法被稱為最大似然法(maximum likelihood method)。在參數估算過程中,這一方法會涉及選擇合適的參數以使得產生所觀測到的數據的概率達到最大。
為了解釋這個方法,我們引用一個簡單的例子,隨機地抽取某一天10只股票的價格,我們發現其中一隻股票的價格在這一天下降了,而其他9只股票的價格或有所增加或至少沒有下跌,這裡我們要問,當天一隻股票價格下降的概率最好估計為多少?答案是0.1,讓我們看一下這一結果是否就是最大似然估計所給出的結果。
將任意股票價格下降的概率計為p,對應只有一隻股票價格下降,而其他股票價格不下降的概率為p(1-p)9(p對應於一只股票的概率,而其他9只股票中任意一隻股票不下降的概率為1-p),應用最大似然估計法,最好的估計值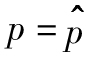 [1]是會使得p(1-p)9取得最大值。將以上表達式對p求導,並令導數為0,我們得出
[1]是會使得p(1-p)9取得最大值。將以上表達式對p求導,並令導數為0,我們得出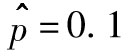 時會使得表達式取得最大值,這說明最大似然估計值正如期望的那樣為0.1。
時會使得表達式取得最大值,這說明最大似然估計值正如期望的那樣為0.1。
10.9.1 估計常數方差
在下一個有關最大似然估計法的例子中,我們考慮如何由服從正態分佈,並且期望值為0的變量X的m個觀察值來估計這一變量的方差。我們假定觀察值為u1,u2,…,um,其對應的期望值為0,將方差記為v。觀察值出現在X=ui的概率等於X的概率密度函數在ui的取值,即
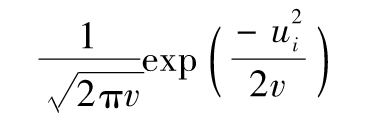
m個觀察值正好為u1,u2,…,um的概率為

應用最大似然法,v的最好估計使得以上表達式達到最大值。
以上表達式的最大化與其對應的對數最大化等價,對式(10-11)取對數並且忽略常數項,我們得出將被最大化的目標函數為

或
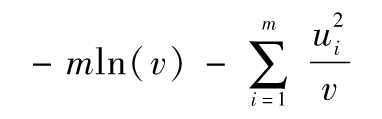
將以上表達式對v求導,並令導數為0,我們可以看到v的最大似然估計量為
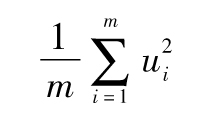
最大似然估計正是式(10-4)的估計式,而獲得無偏差估計值只需要將m替換為m-1。
10.9.2 估計GARCH(1,1)或EWMA模型中的參數
我們現在考慮如何用最大似然法來估計EWMA、GARCH(1,1)或其他波動率的方法中的參數。定義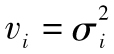 為第i天的方差的估計。假設在方差給定的條件下,ui的條件概率分佈為正態分佈。與上一節類似,我們得出最佳匹配參數應使得以下表達式最大化
為第i天的方差的估計。假設在方差給定的條件下,ui的條件概率分佈為正態分佈。與上一節類似,我們得出最佳匹配參數應使得以下表達式最大化
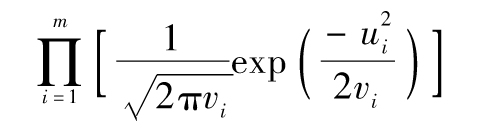
對這一表達式取對數,得出以上表達式最大化與以下表達式最大化等價

除了v被代替為vi,這一表達式與式(10-12)相同,我們可以採用迭代法來求取使得以上表達式達到最大化的解。在模型中迭代地尋找能最大化表達式(10-13)的參數很有必要。
表10-4中所示的計算表顯示出GARCH(1,1)模型中的參數估算過程,這一表格採用了2005年7月18日~2010年8月13日標準普爾500指數的數據。[2]
表中報告的數字是對GARCH(1,1)模型中3個參數ω、α及β的估計,表中第1列對應於日期,第2列對應天數,第3列顯示了在第i天結束時的標準普爾500指數價格Si,第4列顯示了由第i-1天結束時至第i天結束時價格的百分比變化,即ui=(Si-Si-1)/Si-1,第5列是對在第i-1天天末所做的第i天的方差的估計,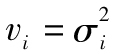 。對於第3天,我們將方差設為
。對於第3天,我們將方差設為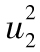 。在接下去的每一天,我們採用式(10-10)來估計方差,第6列顯示了可能性測度
。在接下去的每一天,我們採用式(10-10)來估計方差,第6列顯示了可能性測度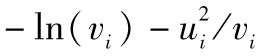 。第5列及第6列中的值是基於參數ω、α及β的當前值計算得出的。我們的目標是如何選取ω、α及β以使得第6列的和達到最大值,這一過程涉及迭代搜索。[3]
。第5列及第6列中的值是基於參數ω、α及β的當前值計算得出的。我們的目標是如何選取ω、α及β以使得第6列的和達到最大值,這一過程涉及迭代搜索。[3]
表10-4 使用2005年7月18日~2010年8月13日標準普爾500指數數據估計GARCH(1,1)模型中的參數
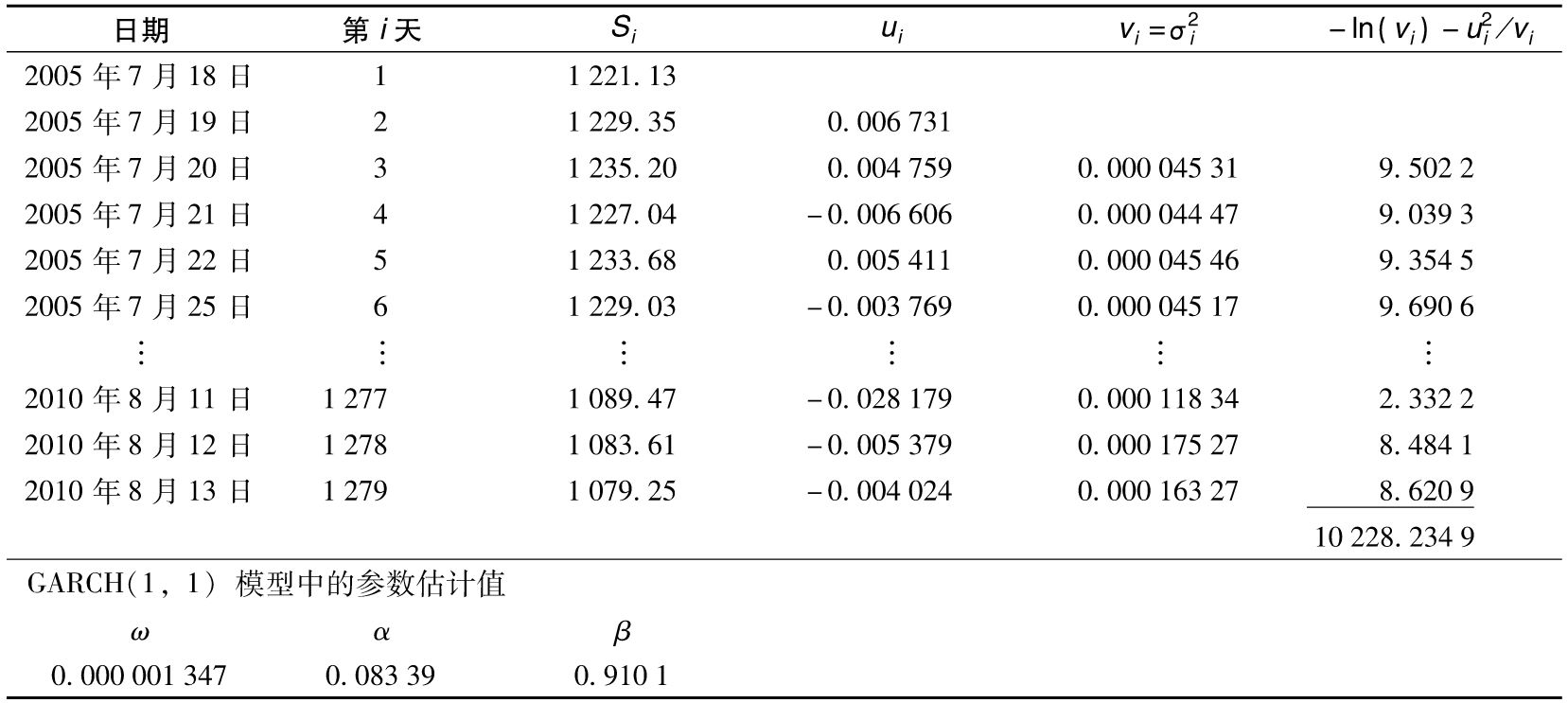
在我們的例子中,參數對應的最佳解為
ω=0.000 001 346 5, α=0.083 394, β=0.910 116
式(10-13)的最大值為10 228.234 9(在表10-4中所顯示的數字對應於參數ω、α及β的最終迭代解)。
在我們的例子中,長期方差VL為
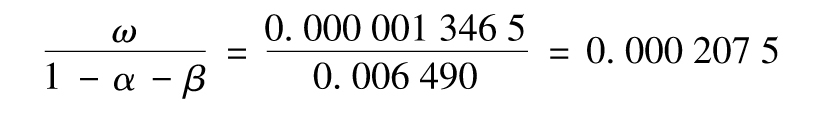
長期波動率為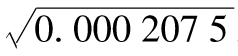 ,也就是每天1.440 4%。
,也就是每天1.440 4%。
圖10-4和圖10-5顯示了該數據涵蓋的5年期內的標準普爾500指數以及由GARCH(1,1)所計算的波動性。在大多數時間,每天的波動率小於2%,但在金融危機期間,某些天的波動率超過了5%(同期VIX指數也顯示了較高的波動率,參見圖10-1)。
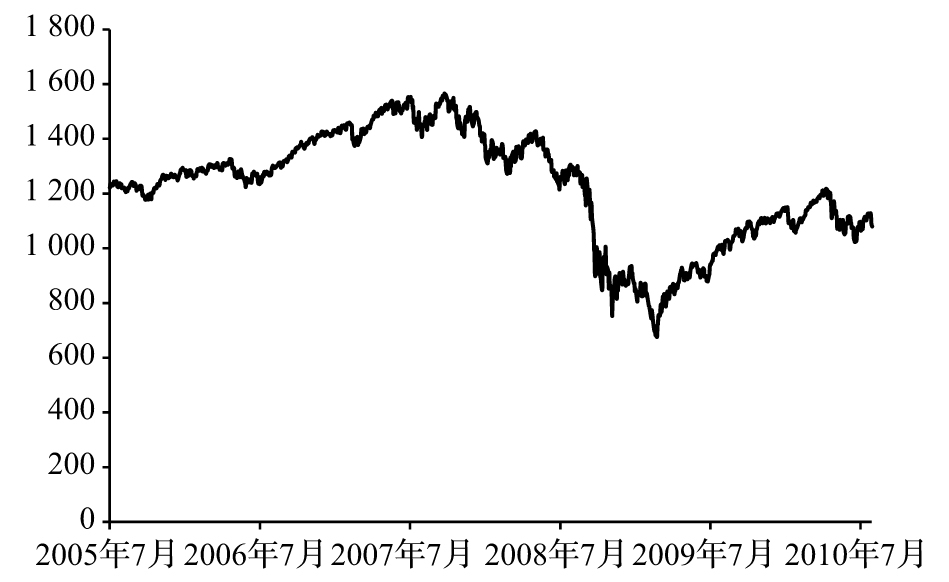
圖10-4 標準普爾500指數,2005年7月18日~2010年8月13日
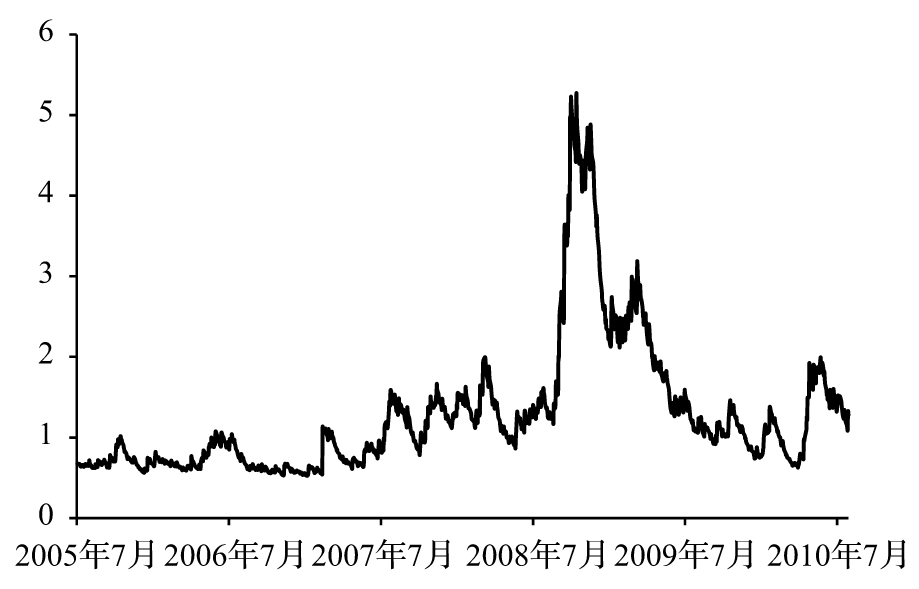
圖10-5 標準普爾500指數的GARCH(1,1)日波動率,2005年7月18日~2010年8月13日
估計GARCH(1,1)參數的另外一種更穩健的方法是所謂的方差目標法(variance targeting)。[4]這種方法將長期平均方差VL設定為由數據計算出的抽樣方差(或其他合理的估計)。因為ω的值等於VL(1-α-β),所以模型只需要估測兩個參數。表10-4的數據所對應的抽樣方差為0.000 241 2,每天的波動率為1.553 1%。令VL等於抽樣方差,我們可以找出使得目標函數式(10-13)達到最大化的α及β,分別為0.084 45和0.910 1,相應的目標函數取值為10 228.194 1,這一數字只是稍稍低於前面計算的極值數據10 228.234 9。
EWMA模型的參數估計過程就相對簡單一些,令ω=0、α=1-λ及β=λ,我們只需要估計一個參數λ,應用表10-4中的數據,使得目標函數式(10-13)取得最大值的λ為0.937 4,對應的目標函數取值為10 192.510 4。
GARCH(1,1)及EWMA模型方法均可以通過Excel軟件中的Solver程序實現,應用Solver,我們可以尋求使得似然函數達到最大的數值解。當計算表格中所尋求的數值解大體在同一水平時,Solver程序的表現令人滿意。例如,在GARCH(1,1)模型中,我們可以將計算表中的單元格A1、A2、A3與數據ω×105、10α及β相對應。然後我們可以使得單元格B1=A1/100 000、B2=A2/10以及B3=A3,我們用B1、B2、B3進行計算,但是讓Solver求解A1、A2、A3的數值以使得似然函數達到最大。偶爾,Solver可能會給出一個局部最優解,因此,有必要多試幾個不同的初始值。
10.9.3 模型表現如何
GARCH模型假設波動率的變化與時間有關。在某一階段波動率較高,而在其他階段波動率較低。換句話說,當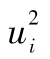 較高時,
較高時,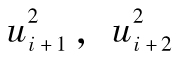 ,…也會較高;當
,…也會較高;當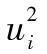 較低時,
較低時,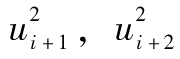 ,…也會較低,我們可以通過計算
,…也會較低,我們可以通過計算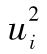 的自相關係數來檢驗這些結論的正確性。
的自相關係數來檢驗這些結論的正確性。
假定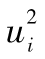 確實有自相關性,如果GARCH模型有效,那麼自相關性就會被剔除。我們通過計算變量
確實有自相關性,如果GARCH模型有效,那麼自相關性就會被剔除。我們通過計算變量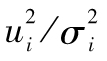 的自相關係數來驗證這一結論,如果計算出的結果顯示自相關性非常小,那麼我們就可以得出結論:有關σi的模型確實解釋了
的自相關係數來驗證這一結論,如果計算出的結果顯示自相關性非常小,那麼我們就可以得出結論:有關σi的模型確實解釋了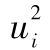 中的自相關性。
中的自相關性。
表10-5顯示的結果是基於以上的標準普爾500指數數據。第1列顯示了計算自相關係數所用的時滯(time lag),第2列對應於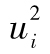 自相關係數,第3列展示了
自相關係數,第3列展示了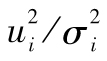 的自相關係數。[5]表中結果顯示出對應於1與15之間的所有時滯,
的自相關係數。[5]表中結果顯示出對應於1與15之間的所有時滯,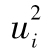 的自相關係數為正,而對於
的自相關係數為正,而對於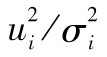 ,有些自相關係數為正,有些為負,這些相關係數的幅度比最初
,有些自相關係數為正,有些為負,這些相關係數的幅度比最初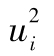 的相關係數要小。
的相關係數要小。
看來GARCH模型對於解釋數據確實做了很好的工作。如果想做一個更科學的檢驗,我們可以採用所謂的Ljung-Box統計方法。[6]當一個數列中有m個觀察值時,Ljung-Box統計量定義為
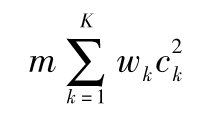
其中ck對應於時滯為k的自相關係數,K為所考慮的所有時滯,再有
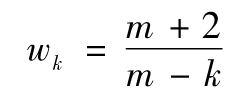
對應於K=15,當Ljung-Box統計量大於25時,我們可以有95%的把握拒絕自相關係數為0這一假設。
基於表10-5中數據,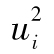 序列的Ljung-Box統計量為1566,這說明自相關性確實存在。關於數列
序列的Ljung-Box統計量為1566,這說明自相關性確實存在。關於數列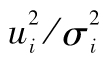 ,Ljung-Box統計量為21.7,這說明GARCH模型確實基本上剔除了數據中的自相關性。
,Ljung-Box統計量為21.7,這說明GARCH模型確實基本上剔除了數據中的自相關性。
表10-5 在採用GARCH模型之前以及之後的自相關係數
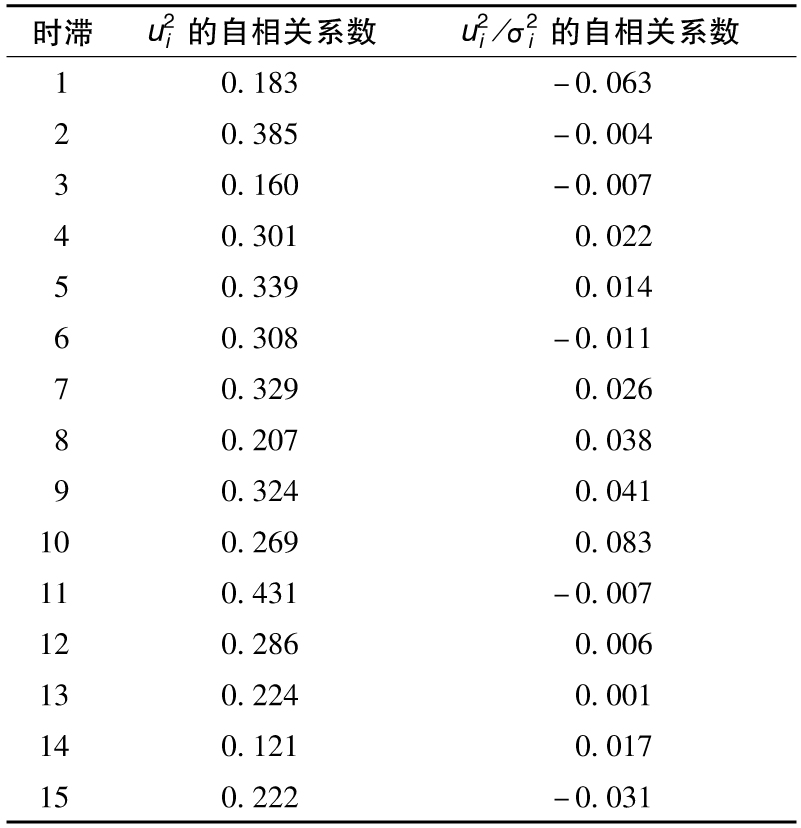
[1] 這裡的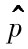 代表估計值,原書採用的符號為p。——譯者注
代表估計值,原書採用的符號為p。——譯者注
[2] 數據和計算過程可以在以下網站上找到:www-2.rotman.utoronto.ca/~hull/riskman。
[3] 就像在後面會討論的那樣,微軟軟件Excel中的廣義求解算法Solver可以用來對問題求解。
[4] See R. Engle and J. Mezrich, “GARCH for Groups,” Risk (August 1996):36-40.
[5] 數列xi對應於時滯k的自相關係數等於xi與xi+k的相關係數。
[6] See G. M. Ljung and G. E. P. Box, “On a Measure of Lack of Fit in Time Series Models,” Biometrica 65(1978):297-303.
10.10 採用GARCH(1,1)模型來預測波動率
採用GARCH(1,1)模型,在n-1天結束時所估算的第n天的方差為
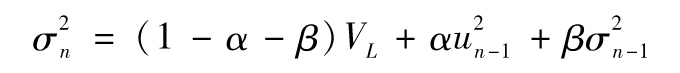
因此
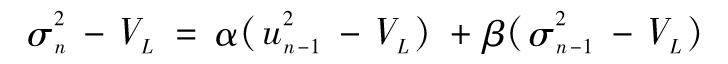
在將來第n+t天,我們有

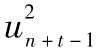 的期望值為
的期望值為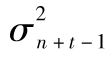 ,因此
,因此
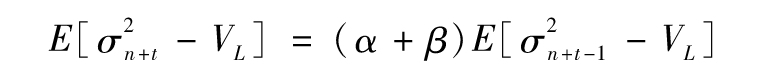
其中E表示期望值。連續應用該式,我們得出

或者

上式採用了在n-1天結束時的所有數據來預測第n+t天的波動率。在EWMA模型中,α+β=1。式(10-14)說明,將來方差的期望值與當前方差相等。當α+β<1時,式中最後一項隨時間增加而逐漸減小。圖10-6顯示出當前方差與VL不同時,預期方差的將來路徑。如上所述,方差具備均值迴歸的性質,均值迴歸水平為VL,迴歸速度為1-α-β。我們對將來方差的預測,會隨著展望時間的延長逐漸趨向於VL,這一分析強調了為保證GARCH(1,1)模型的穩定,我們必須有α+β<1這一條件。當α+β>1時,對應於長期平均方差的權重為負,這時方差不具備均值迴歸特性,事實上,此時的模型具備均值逃離(mean fleeing)特性。

圖10-6 對應於兩種情形預期方差的曲線
在前面考慮的標準普爾500指數數據中,α+β=0.993 5,VL=0.000 207 5。假定我們對於當前方差的估計為每天0.000 3(這對應於日波動率為1.732%),10天之後的方差期望值為
0.000 207 5+0.993 510×(0.000 3-0.000 207 5)=0.0002942
預期波動率為每天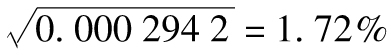 ,這一數值仍然高於長期日波動率(1.44%),但是500天后的預期方差為
,這一數值仍然高於長期日波動率(1.44%),但是500天后的預期方差為
0.000 207 5+0.993 5500×(0.000 3-0.000 207 5)=0.0002110
預期波動率為每天1.45%,這同長期波動率已經非常接近。
10.10.1 波動率期限結構
假定今天為第n天,定義
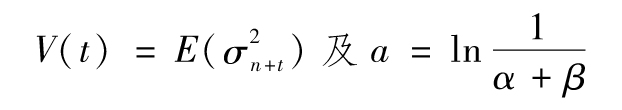
式(10-14)變為
V(t)=VL+e-at[V(0)-VL]
這裡的V(t)是對今後第t天的即時方差(instantaneous variance)的估計,介於今天與時間T之間的日方差平均值為
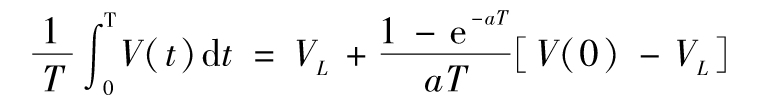
隨著期限T的增大,以上數值會更接近VL。定義σ(T)為GARCH(1,1)模型對於一個期限為T天的期權定價時所採用的每年波動率,假定每年有252天,σ(T)2是每天方差的252倍,因此
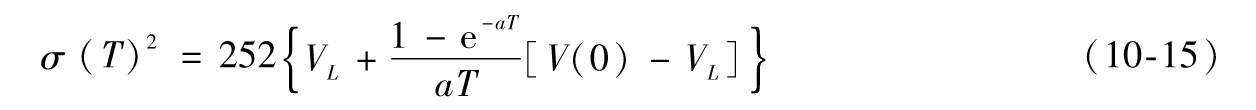
期權的波動率和期權期限之間的關係被稱作波動率期限結構(volatility term structure)。波動率期限結構通常用隱含波動率來求得,但是式(10-15)提供了另外一種途徑,即用GARCH(1,1)來估算。儘管由此所估計的期限結構同隱含波動率的期限結構會有所不同,但這種方法常常被用來預測真正的波動率期限結構如何對波動率的變化做出反應。
在當前波動率高於長期波動率時,GARCH(1,1)模型預測出的波動率期限結構為下降型(downward-sloping),而在當前波動率低於長期波動率時,GARCH(1,1)預測出的波動率期限結構為上升型(upward-sloping)。對標準普爾500指數的實例,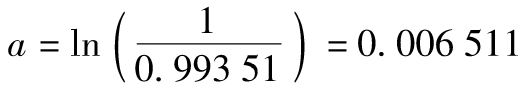 ,VL=0.000 207 5。假定當前的日方差估測為V(0)=0.000 3,由式(10-15)得出
,VL=0.000 207 5。假定當前的日方差估測為V(0)=0.000 3,由式(10-15)得出
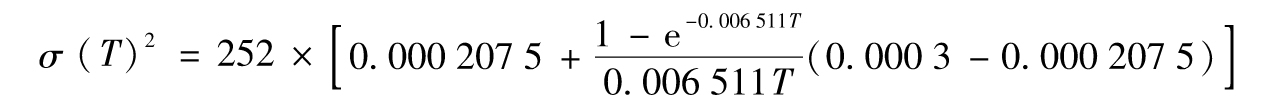
其中時間T以天計。表10-6顯示出對應於不同時間T的每年波動率。
表10-6 由GARCH(1,1)模型預測的標準普爾500指數波動率的期限結構

10.10.2 波動率變化的作用
式(10-15)可以寫為
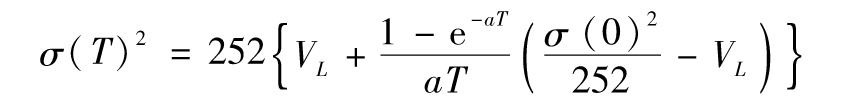
當σ(0)的變化量為Δσ(0)時,相應σ(T)的變化量約為

表10-7顯示了在標準普爾500指數例子中的波動率的變動對於不同期限的期權價格的影響。類似以前的假定,V(0)=0.000 3,因而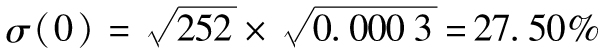 。表中考慮的情形為即時波動率上升100個基點,由27.50%變為28.50%,這意味著Δσ(0)=0.01,即1%。
。表中考慮的情形為即時波動率上升100個基點,由27.50%變為28.50%,這意味著Δσ(0)=0.01,即1%。
表10-7 由GARCH(1,1)模型預測的即時波動率增加1%所帶來的效應

許多金融機構採用這樣的分析來確定其交易戶頭對於波動率變化的敏感性。在計算vega時,我們不是將所有期限的隱含波動率都增加1%,而是將波動率的變化量與期權期限的長短聯繫起來。在表10-7中,10天期權的波動率增加量為0.97%,30天期權的波動率增加量為0.92%,50天期權波動率增加量為0.87%,等等。
小結
在風險管理中,日波動率被定義為每天市場變量的百分比變化的標準差。每天的變化的方差為每天波動率的平方。波動率在交易日要遠高於在非交易日,因此在波動率計算過程中非交易日可以被忽略。每天的市場變化服從正態分佈這一假設很吸引人,但事實並非如此。大多數市場變量變化比正態分佈有更肥的尾部,因此冪律是對我們在日常生活中所遇到的許多分佈的尾部的一個更好的描述。冪律常常被用於描述許多市場百分比變化的尾部分佈。
本章描述瞭如何跟蹤及更新波動率的方法。我們定義ui為第i-1天天末到第i天天末市場變量的百分比變化,市場變量的方差(即波動率的平方)為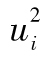 的加權平均。這裡討論的模型的一個主要特性是對應於不同的
的加權平均。這裡討論的模型的一個主要特性是對應於不同的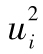 ,模型賦予不同的權重。數據越新,所對應的權重也越大。在EWMA及GARCH(1,1)模型中權重隨著回望期長度以指數速度下降。GARCH(1,1)與EWMA模型的不同之處在於GARCH(1,1)給長期平均方差也賦予了某種權重。EWMA及GARCH(1,1)模型的構造都保證了我們能夠較為容易地預測將來方差的水平。
,模型賦予不同的權重。數據越新,所對應的權重也越大。在EWMA及GARCH(1,1)模型中權重隨著回望期長度以指數速度下降。GARCH(1,1)與EWMA模型的不同之處在於GARCH(1,1)給長期平均方差也賦予了某種權重。EWMA及GARCH(1,1)模型的構造都保證了我們能夠較為容易地預測將來方差的水平。
最大似然法通常被用於估計GARCH(1,1)以及其他基於歷史數據來計算波動率的模型中的參數,這些方法採用數值迭代過程來確定參數,使得歷史數據得以出現的可能性達到最大。當參數確定之後,我們可以從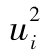 中的自相關性是否被有效地剔除這一指標來驗證模型的好壞。
中的自相關性是否被有效地剔除這一指標來驗證模型的好壞。
我們可以採用GARCH(1,1)模型由歷史數據估算期權波動率,這種分析常常被用於計算波動率的擾動對不同期限期權的隱含波動率帶來的影響。
延伸閱讀
練習題
10.1 某資產的波動率是每天2%,該資產3天后的價格百分比變化的標準差是多少?
10.2 某資產的波動率為每年25%,對應一天的資產價格百分比變化的標準差為多少?假定價格變化服從正態分佈,均值為0,估測在95%的置信度下價格百分比變化的區間為多少?
10.3 為什麼交易員在計算年波動率時採用252天而不是365天?
10.4 什麼是隱含波動率?在實踐中對應於同一資產的不同期權會有不同的隱含波動率,這一結論的含義是什麼?
10.5 假定在過去11天每天交易結束時某匯率數值為0.700 0,0.701 0,0.707 0,0.699 9,0.679 0,0.700 3,0.695 1,0.695 3,0.693 4,0.692 3,0.692 2。請用式(10-2)和式(10-4)估計每天的波動率。
10.6 網站的訪問次數服從式(10-1)給出的冪律分佈,其中α=2。假定有1%的網站每天會受到500或更多次的點擊,則在所有的網站中,日點擊的次數為:(a)1 000;(b)2 000或更多的網站所佔比例為多少?
10.7 請解釋如何用指數加權移動平均(EWMA)模型及歷史數據來估算波動率。
10.8 採用EWMA及GARCH(1,1)對波動率進行更新的不同之處是什麼?
10.9 某一資產的波動率的最新估計值為1.5%,資產在昨天交易結束時的價格為30美元。EWMA模型中的λ為0.94,假定在今天交易結束時資產價格為30.50美元,EWMA模型將如何對波動率進行更新?
10.10 某公司採用EWMA來預測波動率,公司決定將參數λ由0.95變為0.85,請解釋這一變化的影響。
10.11 假定標準普爾500指數在昨天交易結束時的價格為1 040,而在昨天指數的日波動率的估計值為1%。GARCH(1,1)模型中的參數ω=0.000 002、α=0.06以及β=0.92,指數價格在今天交易結束時的價格為1 060,今天新的日波動率的估計值為多少?
10.12 在昨天下午4點,美元/英鎊匯率的波動率的最新估計為每天0.6%,匯率價格為1.5000,在EWMA中參數λ為0.9,假定在今天下午4點匯率價格變為1.4950,今天匯率波動率的最新估計為多少?
10.13 一家公司採用GARCH(1,1)來更新波動率,模型中的參數為ω、α及β。請描述稍稍增加某一參數同時保證其他參數不變的影響是什麼?
10.14 某GARCH(1,1)模型的不同參數為ω=0.000 004、α=0.05以及β=0.92,長期平均波動率為多少?描述波動率會收斂到長期平均值的方程是什麼?如果當前波動率為20%,20天后波動率的期望值為多少?
10.15 假設富時100指數股指(以英鎊計)的每天波動率為1.8%,美元/英鎊匯率的每天波動率0.9%,我們進一步假定富時100指數與美元/英鎊匯率的相關係數為0.4,富時100指數被轉換成美元后的波動率為多少?這裡假定美元/英鎊匯率被表達為1英鎊所對應的美元數量(提示:當Z=XY時,Z所對應的每天百分比價格變化等於X的每天百分比價格變化加上Y的每天百分比價格變化)。
10.16 假定GARCH(1,1)模型中的參數估計為ω=0.000 003、α=0.04以及β=0.94,當前日波動率估計為1%,請估計30天后的日波動率。
10.17 假定GARCH(1,1)模型中的參數估計為ω=0.000 002、α=0.04以及β=0.94,當前日波動率近似為1.3%,在為一個期限為20天的期權定價時,所用的年化波動率應為多少?
作業題
10.18 假定股票在過去連續15天的價格(以美元計)為30.2,32.0,31.1,30.1,30.2,30.3,30.6,30.9,30.5,31.1,31.3,30.8,30.3,29.9,29.8。請用式(10-2)和式(10-4)估計股票價格波動率。
10.19 假定某資產價格在昨天收盤時為300美元,日波動率為1.3%,今天該資產的收盤價為298美元。請採用以下模型來更新波動率:
(a)採用EWMA模型,其中λ=0.94;
(b)採用GARCH(1,1)模型,其中參數選擇為ω=0.000 002、α=0.04以及β=0.94。
10.20 在本書作者的網頁(www-2.rotman. utoronto.ca/~hull/data)上,讀者可以下載一個Excel計算表,其中含有超過900天的不同匯率數據以及股指價格數據。選定某匯率及某種股指,估計EWMA中的λ以使得
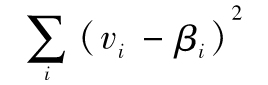
達到最小,其中vi為在i-1天天末對於方差所做的預測,βi是由第i天至第i+25天的數據所計算出的方差,在計算中請採用Excel中的Solver功能,在開始EWMA計算時,令第一天方差的預測值等於第一天收益的平方。
10.21 GARCH(1,1)模型中的參數α=0.03、β=0.95以及ω=0.000 002:
(a)長期平均波動率為多少?
(b)如果當前波動率為每天1.5%,你對20天、40天及60天后的波動率預估為多少?
(c)應採用什麼樣的波動率來計算20天、40天及60天期限的期權價格?
(d)假定有某一事件使得日波動率由1.5%增至2%,請估測這一事件對20天、40天及60天后波動率的影響。
(e)估測這一事件對用於20天、40天及60天期限的期權定價中的波動率的影響。
10.22 使用2005年7月27日~2010年7月27日的歐元兌美元匯率的歷史數據,估算EWMA和GARCH(1,1)模型的參數。數據可以從作者的網頁上下載:www-2.rotman.utoronto.ca/~hull/data。
10.23 投資組合在1個月後損失超出1 000萬美元的概率大約為5%:
(a)假定投資組合價值變化服從正態分佈,均值為0,1個月展望期置信度99%的VaR[1]為多少?
(b)在α=3的冪律假設前提下,1個月展望期置信度99%的VaR為多少?
[1] VaR的概念將在本書第12章中介紹。——譯者注
第11章
相關性與Copula函數
假設一家公司對市場上兩個不同的市場變量有風險敞口。兩個變量之中任意一個變量增加一個標準差,公司會收益1 000萬美元,兩個變量之中任意一個變量減小一個標準差,公司會虧損1 000萬美元。如果這兩個市場變量的變化有很強的正相關性,那麼公司面臨的整體風險很大;如果兩個市場變量的相關性為0,那麼公司面臨的整體風險會小一些,但仍然很大;如果兩個市場變量變化有很強的負相關性,那麼公司面臨的整體風險會大大減小,因為一個變量帶來的損失會被另一個變量帶來的收益中和。這個例子說明,和對市場變量的波動率的監測一樣,風控人員對市場變量變化的相關性進行監測對正確評估市場風險敞口也是至關重要的。
在本章中,我們將要討論如何對相關性進行類似於波動率那樣的監控。這一章也會涉及Copula函數。通過Copula函數我們可以定義兩個或更多變量之間的相關性結構,而這種定義對於任意的概率分佈均適用。Copula函數在風險管理領域有不同形式的應用,利用Copula函數,我們可以較為便利地建立違約相關性,展示如何使用Copula函數來構造一個貸款組合的違約相關性模型。該模型可以被用來計算《巴塞爾協議Ⅱ》中要求的資本金。
11.1 相關係數的定義
變量V1及V2的相關係數ρ被定義為
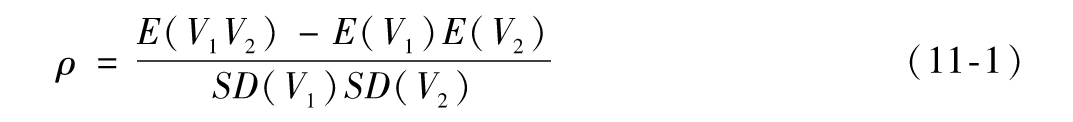
其中E(·)代表期望值,SD(·)代表標準差。如果兩個變量不相關,即E(V1V2)=E(V1)E(V2),因此ρ=0。如果V1=V2,以上表達式中的分子及分母均等於變量V1的方差,此時就像我們期望的那樣ρ=1。
變量V1及V2的協方差被定義為
cov(V1,V2)=E(V1V2)-E(V1)E(V2)
(11-2)
因此相關係數又可以寫為
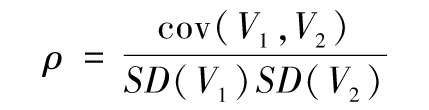
雖然直覺上我們更容易理解相關係數,但是在今後我們將說明協方差才是我們真正需要分析的變量,這類似於第10章的EWMA及GARCH模型,雖然波動率更容易被人理解,但方差才是真正的基礎變量。
相關係數以及關聯性
如果在兩個變量中,其中任意一個變量的信息(觀測值)不會影響另一個變量的分佈,那麼這兩個變量在統計上被定義為相互獨立。精確地講,如果對於所有的x,等式
f(V2|V1=x)=f(V2)
成立,其中f(·)代表變量的概率密度函數,|代表條件概率,變量V1和V2在統計上被定義為相互獨立。
如果兩個變量的相關係數為0,就意味著變量毫無關聯嗎?答案是否定的。這裡舉一個簡單例子來說明問題,假定變量V1的值有三種均等的可能:-1、0及+1。當V1=-1或V1=+1時,V2=1;當V1=0時,V2=0。在這裡我們可以清楚地看到V1和V2有某種關聯性,如果我們觀測到V1的值,我們也可得出V2的值,同時有關V2的信息也會改變我們有關V1的概率分佈。但由於E(V1V2)=0以及E(V1)=0,我們很容易驗證V1及V2的相關係數為0。
這一例子強調相關係數只是用於表達變量之間的某種相關性。這種相關性只是一種線性的關聯關係,而變量之間可以有許多不同形式的關聯關係。我們可以畫出E(V2)與V1的函數圖來顯示V1和V2的關聯特性。圖11-1顯示了幾種不同的關聯形式,圖11-1a顯示了V2的期望值同V1之間有某種線性關係,圖11-1b顯示了V2的期望值同V1之間有一種V形關聯關係(這同我們前面的例子相似,一種對稱的V形的高度關聯關係會造成相關係數為0),圖11-1c顯示了我們經常看到的金融變量之間的關聯性。在這裡V1和V2代表某些市場變量的變化率。當V1正常變化時,V1和V2之間有很弱的關聯性,但V1的極端變化會觸發V2的極端變化(這和市場受壓時,相關性會增加的情況是一致的)。
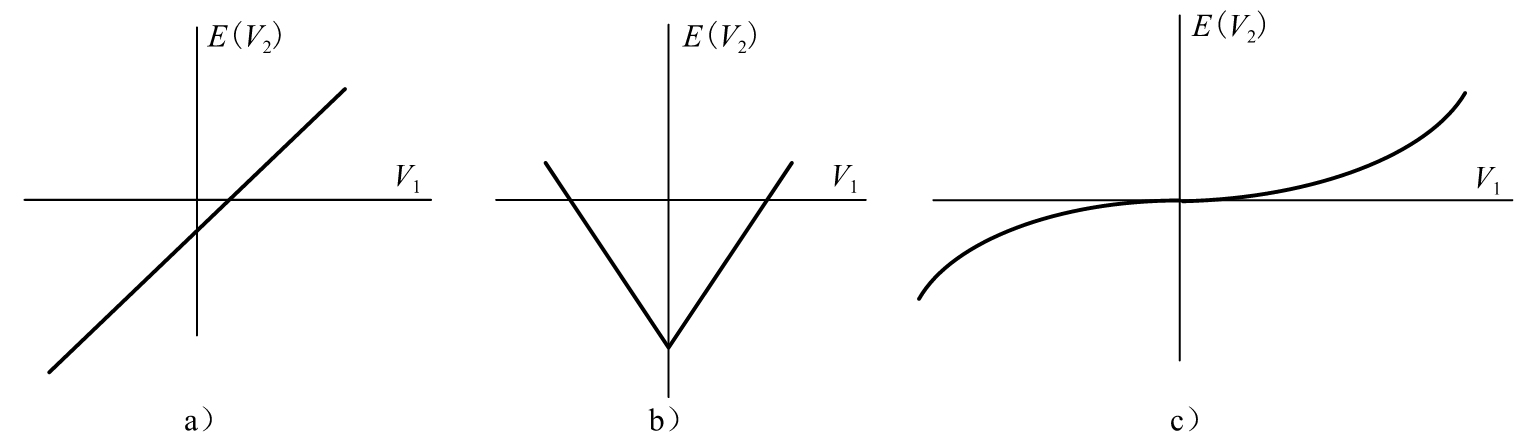
圖11-1 V2依賴於V1的幾種不同形式
我們可以從另一個角度來考察V1和V2的關聯性,即通過檢驗在V1條件下,V2的方差。我們在今後將看到,當V1和V2服從二元正態分佈時,該條件標準差為常數,但在其他情形下,V2的標準差與V1有關。
11.2 測量相關係數
在第10章中我們解釋瞭如何應用EWMA和GARCH模型來監測變量的方差,我們也可以採用類似的方法來監測兩個變量之間的協方差,一個變量每天變化的方差是指這一變量每天收益的方差。類似地,兩個變量每天變化的協方差是指變量每天收益的協方差。
假定變量X和Y在第i天結束時的價值為Xi和Yi,變量X和Y在第i天的收益率為
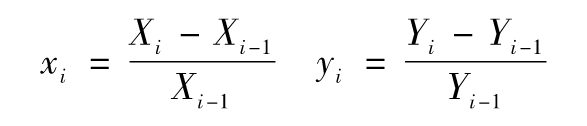
由式(11-2),我們得出變量X和Y在第n天的協方差為
covn=E(xnyn)-E(xn)E(yn)
在第10.5節中我們曾指出風險管理人員在計算每天方差率時常常假定變量的每天預期收益為0,風險管理人員在計算每天協方差時通常需要做出同樣的假設,這意味著變量X和Y在第n天的協方差可以被簡化為
covn=E(xnyn)
對於xi和yi的最近m個觀察值採用同樣的權重,我們得出

採用同樣的權重來估計變量X和Y的每天變化的方差,我們得出關係式
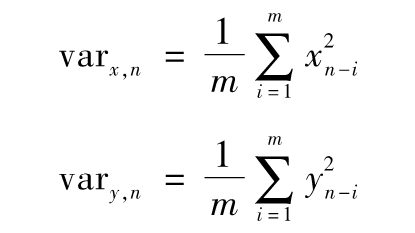
第n天的相關係數的估計值為
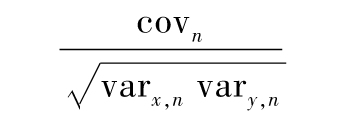
11.2.1 EWMA模型
大多數風險管理人員都同意早期歷史數據的權重應該小於近期歷史數據的權重。在第10章中我們曾討論過應用EWMA模型來預測方差,其中我們看到權重隨著回望期的期限的增大而按指數形式下降,對於協方差,我們可以採用類似的權重形式,一種更新協方差的EWMA模型與式(10-8)相似
covn=λcovn-1+(1-λ)xn-1yn-1
與EWMA模型中的分析相似,我們可以證明對應於數據xn-1yn-1的權重隨著i的增加(也就是隨著回望期的增大)而逐漸降低,λ的值越小,對於近期數據的權重也越大。
【例11-1】 假設λ=0.95,變量X和Y在n-1天的相關係數估計為0.6,同時我們假設變量X和Y在n-1天的波動率估計分別為1%和2%。由協方差及相關係數的關係式,在第n-1天的協方差估計值為
0.6×0.01×0.02=0.000 12
假定變量X和Y在n-1天的百分比變化分別為0.5%和2.5%。在第n天方差及協方差的估計分別為
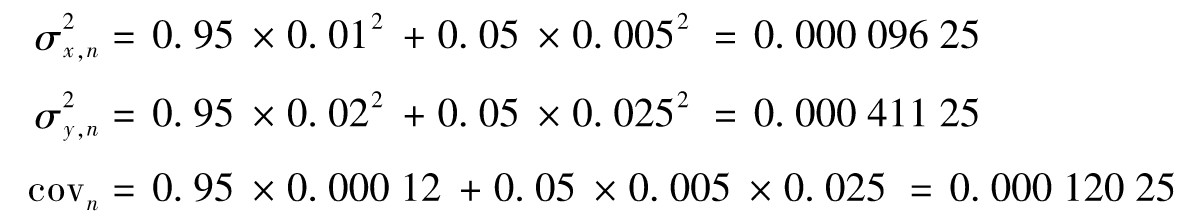
變量X的最新波動率估計值為 ,變量Y的最新波動率估計為
,變量Y的最新波動率估計為 ,X和Y的最新相關係數為
,X和Y的最新相關係數為
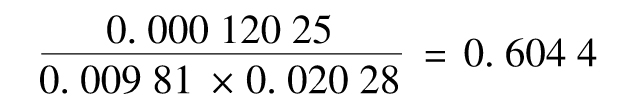
11.2.2 GARCH模型
GARCH模型也可以被用來更新協方差以及預測將來協方差的水平。例如,GARCH(1,1)更新X和Y協方差的表達式為
covn=ω+αxn-1yn-1+βcovn-1
這一公式同更新方差的式(10-10)相似,此公式對於長期平均協方差賦予某種權重,對於最新協方差估計賦予某種權重,對於最新觀測到的協方差數據(也就是xn-1yn-1)也賦予某種權重,長期平均協方差為ω/(1-α-β)。我們可以推導出類似式(10-14)和式(10-15)的表達式來預測未來的協方差,並且計算對應一個未來期限內的平均協方差。
11.3 相關係數和方差-協方差矩陣
計算出多個變量間的方差、協方差和相關係數後,就可以根據這些數據構造出多個變量之間的相關係數矩陣和協方差矩陣。
表11-1是相關係數矩陣,表中的數據是各變量之間的相關係數。因為變量總是與其自身相關,所以相關係數矩陣中對角線上的值都為1。又因為ρij=ρji,所以相關係數矩陣是對稱的。
表11-1 相關係數矩陣

注:ρij是變量i和變量j之間的相關係數。
通常來說,使用方差-協方差矩陣會更加方便。當i≠ j時,矩陣的(i,j)位置元素對應於變量i和變量j之間的協方差;當i=j時,(i,j)位置元素表示變量i的方差(見表11-2)。
表11-2 方差-協方差矩陣

注:covij是變量i和變量j之間的協方差,var=covii是變量i的方差。
協方差的一致性條件
並不是所有的方差-協方差矩陣都滿足內部一致性條件,一個N×N方差-協方差矩陣Ω滿足內部一致性條件的不等式為:對於所有的N×1向量w
wTΩw≥0
(11-4)
其中wT是w的轉置,滿足以上條件的矩陣被稱為半正定矩陣。
為了理解不等式(11-4)為什麼要成立,我們可以假定wT=[w1,w2,…wn],表達式wTΩw為一個組合的方差,其中對第i項資產的投資額是wi。方差自然不能為負,因此不等式(11-4)必須成立。
為了保證矩陣的半正定性,我們在計算方差及協方差時必須保持一致性。例如,如果我們採用最近m個歷史數據並以均等的權重來計算方差,那麼我們在計算協方差時也應採用同樣的數據及權重。如果我們採用EWMA模型,並假定λ=0.94來更新方差,那麼我們在計算協方差時也應該採用同樣的數據。使用GARCH模型來更新方差-協方差矩陣並保證一致性滿足條件比較複雜,涉及使用多變量GARCH模型。[1]
以下方差-協方差矩陣是一個不滿足內部一致性條件的實例

以上任一變量的標準差均為1.0,此時協方差與相關係數相等。第一變量同第三變量高度相關,第二變量同第三變量也高度相關,但是第一變量同第二變量無關,這一現象看起來有些奇怪,令w=(1,1,-1)T,我們可以驗證關係式(11-4)不成立,這因此也證明矩陣不滿足半正定條件。[2]
如果我們對一個含有3個變量的半正定矩陣產生一個很小的擾動(例如,為了計算敏感性),那麼新矩陣往往仍然還是半正定的。但是,對100個變量進行分析時,我們必須要小心,當我們對一個100×100的矩陣產生一個小的隨意擾動時,矩陣的半正定條件就很有可能不再滿足。
[1] 關於其他的方法,見R. Engle and J. Mezrich, “GARCH for Groups,” Risk (August 1996):36-40。
[2] 可以證明一個3×3矩陣滿足內部一致性的條件為 ,其中ρij為變量i與j的相關係數。
,其中ρij為變量i與j的相關係數。
11.4 多元正態分佈
多元正態分佈很容易被理解及應用,在下一節中我們將解釋,多元正態分佈可以被用來描述變量之間的相關性結構,這甚至在每個單一變量不服從正態分佈時也可以做到。
我們首先假定兩個變量V1和V2服從二元正態分佈,假定變量V1的某個觀察值為v1,V2在V1=v1條件下的分佈為正態分佈,期望值為
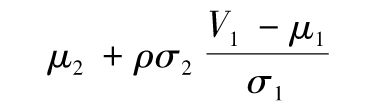
標準差為
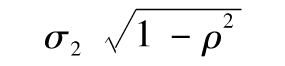
這裡的μ1和μ2分別為V1和V2的(無條件)期望值;σ1和σ2分別為V1和V2的(無條件)標準差,ρ為V1和V2的相關係數。注意V2的條件期望值(條件為V1)與V1有線性關係,這對應於圖11-1a,V2的條件標準差(條件為V1)與V1無關。
用於計算累積雙變量正態分佈的軟件位於作者的網站上:www-2.rotman.utoronto.ca/~hull/riskman。
11.4.1 基於正態分佈來產生隨機抽樣
在大多數計算機語言中都有產生介於0到1之間的隨機數的程序,許多語言也有產生服從正態分佈隨機數的能力。[1]
當我們需要產生二元正態隨機變量的隨機抽樣ε1、ε2(兩個變量的均值均為0,方差均為1)時,我們可以採用如下流程:首先生成兩個服從標準正態分佈(即均值為0且標準差為1的分佈)並且相互獨立的隨機抽樣z1和z2,然後採用以下關係式來生成所需要的隨機抽樣
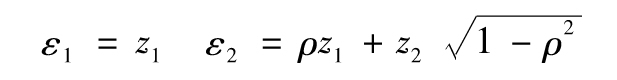
其中ρ為二元正態分佈的相關係數。
接下來我們考慮如何產生n元聯合正態分佈的隨機抽樣(其中所有變量的均值均為0,標準差均為1),這裡變量i與變量j的相關係數為ρij。我們首先生成n個相互獨立並且服從正態分佈的隨機抽樣zi(1≤i≤n)。服從n元聯合正態分佈的隨機抽樣可由下式產生

這裡參數αik的選取需要保證εj之間具有特定的方差和相關性。對於1≤j<i,我們有關係式

以及,對於所有的j<i
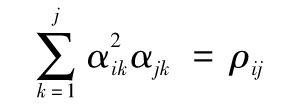
第一個變量的抽樣ε1=z1,所有的α變量可以通過對以上方程求解而得,其中ε2由z1、z2求得,ε3由z1、z2、z3求得,等等。這裡描述的過程被稱為Cholesky分解(Cholesky decomposition)(見練習題11.9)。
如果我們在Cholesky分解中遇到對負數開根號,那麼最初的方差-協方差矩陣一定不滿足內部一致性條件,如同在第11.3.1節解釋的那樣,這就等於是說矩陣不滿足半正定條件。
11.4.2 因子模型
有時服從正態分佈的幾個不同變量的相關係數是由某個因子來決定的。假設U1,U2,…,UN均服從標準正態分佈(期望值為0、標準差為1的正態分佈被稱為標準正態分佈),在單一因子模型中,每個Ui(1≤i≤N)均同一個共同的因子F及另外一個相互獨立的因子有關,準確地講

其中F及Zi均服從標準正態分佈,ai為介於-1與1之間的一個常數,Zi(i=1,…,N)之間相互獨立,每一個Zi同F也相互獨立。選擇Zi的係數使得Ui的均值為0,方差為1。在單一因子模型中,Ui同Uj的相關性起源於共同因子F,變量Ui同Uj的相關係數為aiaj。
單因子模型(one-factor model)的優點是這一模型對於相關結構做了某種假設,使得協方差矩陣總是半正定。在沒有因子模型的前提下,我們必須對N個變量之間的相關性進行估計,這就造成我們需要估計N(N-1)/2個參數,而在因子模型的前提下,我們只需要估計a1,a2,…,aN等N個參數。資本資產定價模型是投資行業單因子模型的一個例子,其中股票的回報包括單一市場變量和單一特殊變量,而這個特殊變量與其他股票回報相獨立,被稱為非系統變量(見第1.3節)。
單一因子模型可以被擴展到2個、3個甚至M個因子,在M個因子模型中
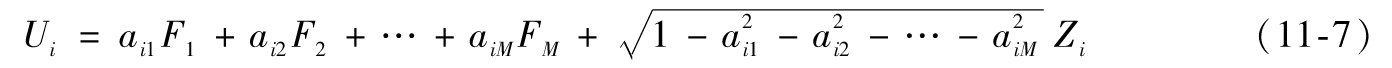
因子F1,F2,…,FM服從標準正態分佈,並且相互獨立,因子Zi之間相互獨立,並且每一個Zi與所有的F因子也相互獨立,這時Ui與Uj的相關係數為
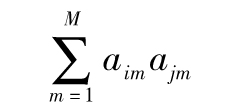
[1] 在Excel中,我們可以採用指令=NORMSINV(RAND())來達到這一目的。
11.5 Copula函數
考慮兩個相互關聯的變量V1和V2。V1的邊際分佈(marginal distribution,有時也被稱為無條件分佈)是指我們在對V2一無所知的情況下V1的概率分佈;類似地,V2的邊際分佈是指我們在對V1一無所知的情況下V2的概率分佈。假定,我們已經對V1和V2的邊際分佈有所估計,我們需要對相關結構做什麼樣的假設來決定變量之間的聯合分佈呢?
當V1和V2的邊際分佈均為正態分佈時,一種方便的做法是假設V1和V2服從二元正態分佈[1](見第11.3節關於相關性的討論)。對於其他邊際分佈,我們也可以做類似的假設。但是通常來講,對於兩個不同的邊際分佈,並沒有一個自然的方式定義相關結構,這就是我們需要引入Copula函數的原因。
以下是一個有關Copula函數的應用的實例,假定V1和V2的邊際分佈為三角分佈,如圖11-2所示,兩個變量均介於0與1之間。V1分佈函數的峰值發生在0.2,V2分佈函數的峰值發生在0.5,兩個分佈函數的最大值均為2.0(因此兩個密度函數下的區域面積均為1.0)。為了應用高斯Copula(Gaussian Copula)函數,我們首先將變量V1和V2映射到U1和U2上,這裡的U1和U2均服從標準正態分佈。這種映射為分位數與分位數(percentile-to-percentile)之間的一一映射。V1分佈上1%的分位數被映射到U1分佈上1%的分位數;V1分佈上10%的分位數被映射到U1分佈上10%的分位數,等等。對於V2,我們也做類似的映射。表11-3顯示了V1的值如何被映射到U1上,表11-4顯示了V2的值如何被映射到U2上。在表11-3中,當V1=0.1時,對應於(求取三邊形面積)0.1的累積概率為0.5×0.1×1=0.05,即5%,V1=0.1的值被映射到標準正態分佈的5%的分位數,其值為-1.64。[2]

圖11-2 V1和V2服從某種三角分佈
表11-3 V1到U1的映射,V1服從圖11-2a中的三角分佈,U1服從標準正態分佈
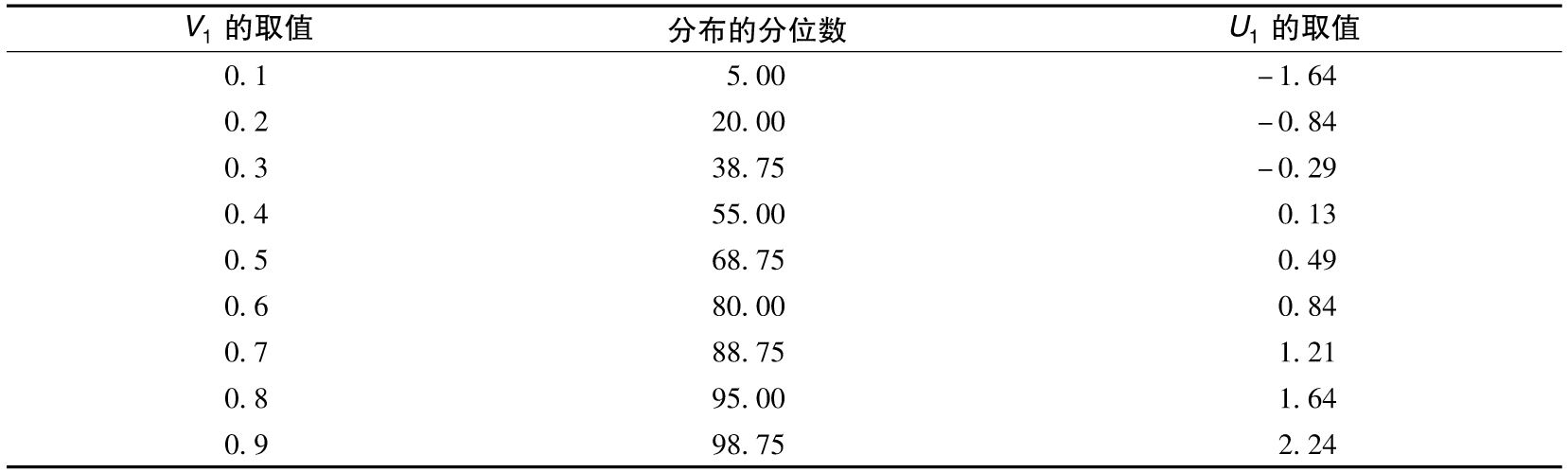
表11-4 V2到U2的映射,V2服從圖11-2b中的三角分佈,U2服從標準正態分佈
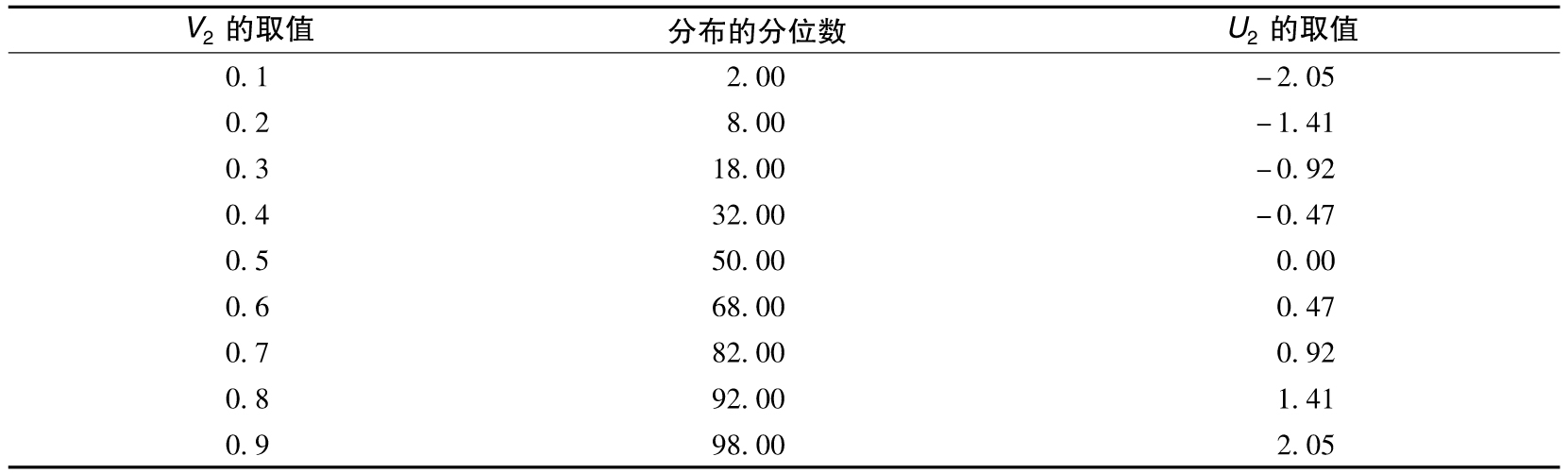
變量U1和U2服從正態分佈,我們假定U1和U2的聯合分佈為二元正態分佈,在這種前提下可以推算出V1和V2的聯合分佈以及相關結構。Copula函數的精髓就在於不直接定義V1和V2的相關性,而是採取一種間接的定義方式。我們將V1和V2映射到性狀較好(well-behaved)的分佈上,而對於這些性狀較好的分佈,我們可以較為容易地定義相關性。
假定U1與U2的相關係數為0.5。表11-5顯示出V1和V2的聯合累積概率分佈。為了說明計算過程,我們首先考慮如何計算V1<0.1和V2<0.1的概率。從表11-3及表11-4出發,我們知道這一概率與U1<-1.64和U2<-2.05的概率相同,通過二元正態分佈,我們可以得出在ρ=0.5的情形下,這一概率數值為0.006[3](在ρ=0的情形下,這一概率僅僅為0.02×0.05=0.001)。
表11-5 在高斯Copula函數模型下V1和V2的聯合概率分佈,相關係數=0.5,表中顯示出V1和V2分別小於某數值的聯合概率
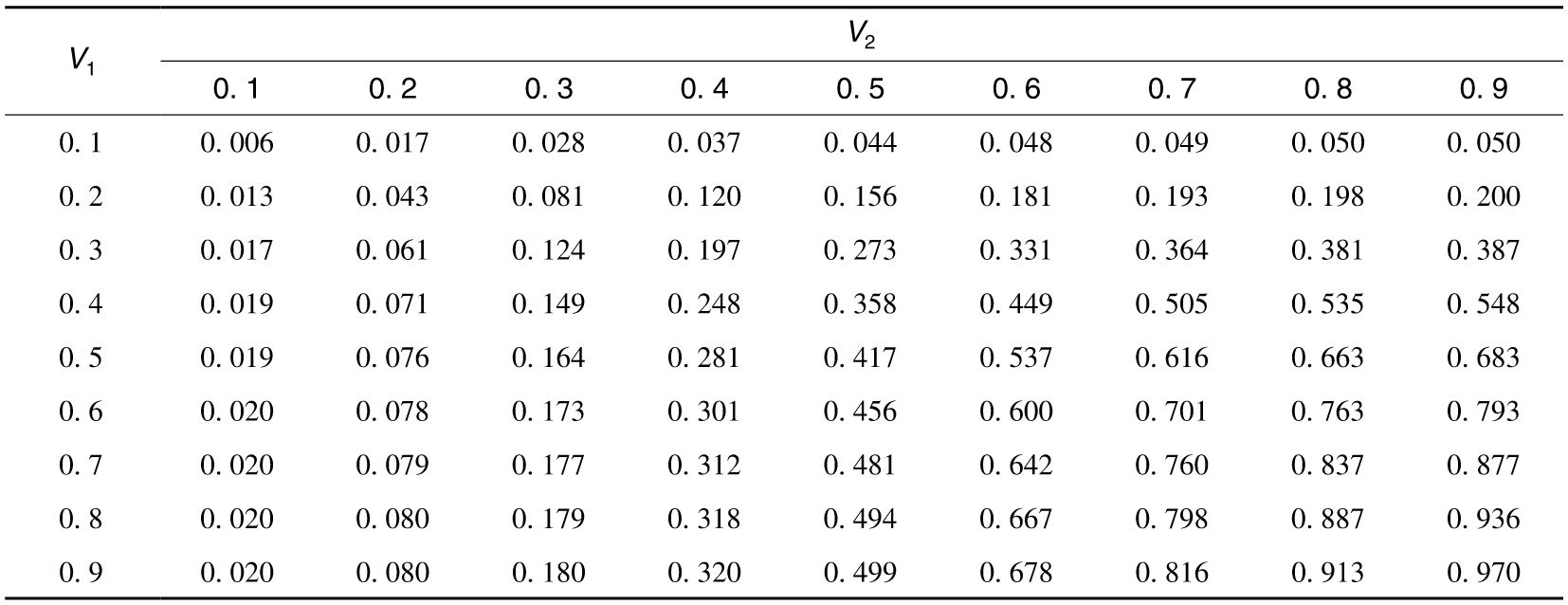
U1和U2的相關係數被稱為Copula相關係數。這一相關係數與通常意義下V1和V2的相關係數不同。U1和U2服從二元正態分佈,U2的條件期望值與U1有線性關係,U2的條件標準差為常數(在第11.4節中曾討論過),但是對於V1和V2,我們沒有類似的結論。
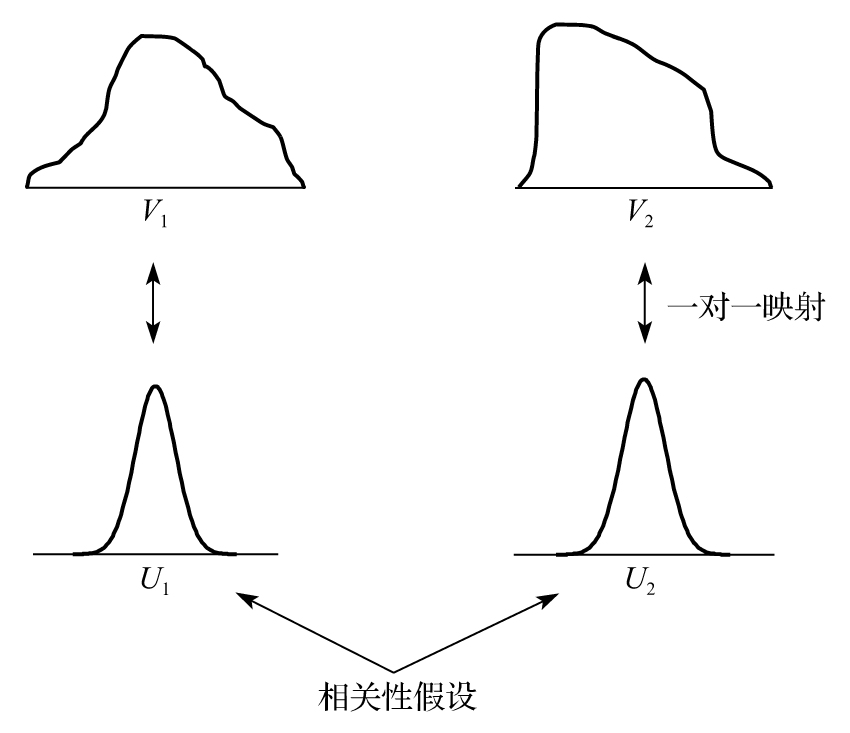
圖11-3 通過Copula函數來定義聯合分佈
11.5.1 Copula函數的代數表達形式
利用Copula模型來定義聯合分佈的方式可由圖11-3來說明。為了能夠以比較正規的形式來描述Copula函數,假定G1和G2分別為V1和V2的累積邊際(即無條件)概率分佈函數,我們將V1=v1映射到U1=u1,V2=v2映射到U2=u2,映射方式如下
G1(v1)=N(u1), G2(v2)=N(u2)
其中N代表累積正態分佈函數,這意味著
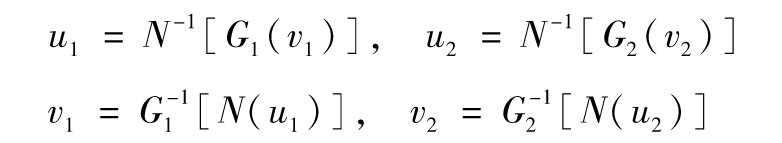
變量U1和U2被假設為服從二元正態分佈,Copula函數的主要特徵就是在定義其相關結構時,V1和V2的邊際分佈沒有任何改變(不管邊際分佈是何種形式)。
11.5.2 其他Copula函數
高斯Copula函數只是定義V1和V2相關性結構的某一種形式,還有許多其他的Copula函數可以用於描述相關性結構。其中一種Copula函數被稱為學生(student)t-Copula函數,這種Copula函數同高斯Copula函數類似,其不同之處只是U1和U2被假定為服從二元學生t-分佈。對於一個有f個自由度,相關係數為ρ的學生t-分佈進行模擬抽樣如下:
(1)在一個逆卡方分佈(inverse chi-square)中進行抽樣,抽樣值為χ(在Excel計算表中,我們可以採用CHIINV函數,第一個變量為RAND(),第二個變量為f);
(2)如第11.4節所述,在一個二元正態分佈中進行抽樣,這裡的相關係數為ρ;
(3)將正態分佈抽樣值乘以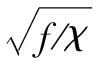 。
。
11.5.3 尾部相關性
圖11-4顯示了二元正態分佈的5000個抽樣。圖11-5顯示了二元學生t-分佈的5000個抽樣,這裡的相關係數均為0.5,學生t-分佈的自由度為4。定義尾部值(tail value)為一個分佈中最左邊或最右邊佔1%區域的尾部所對應的取值。在正態分佈抽樣中,大於2.33或小於-2.33的抽樣值為尾部值。類似地,在t-分佈抽樣中,大於3.75或小於-3.75的抽樣為尾部值,圖中的橫豎線顯示了產生尾部值的情形。圖形顯示在二元t-分佈中兩個變量同時出現尾部值的情形要多於在二元正態分佈中兩個變量同時出現尾部值的情形。換一種說法,二元t-分佈的尾部相關性(tail correlation)要大於二元正態分佈的尾部相關性。我們在前面提到,在極端的市場條件下,變量之間的相關性往往會增加,這說明圖11-1c對相關性的描述往往會比圖11-1a更好,基於這一結果,有些研究人員認為學生t-Copula對市場變量的相關性變化的描述比高斯Copula更好。
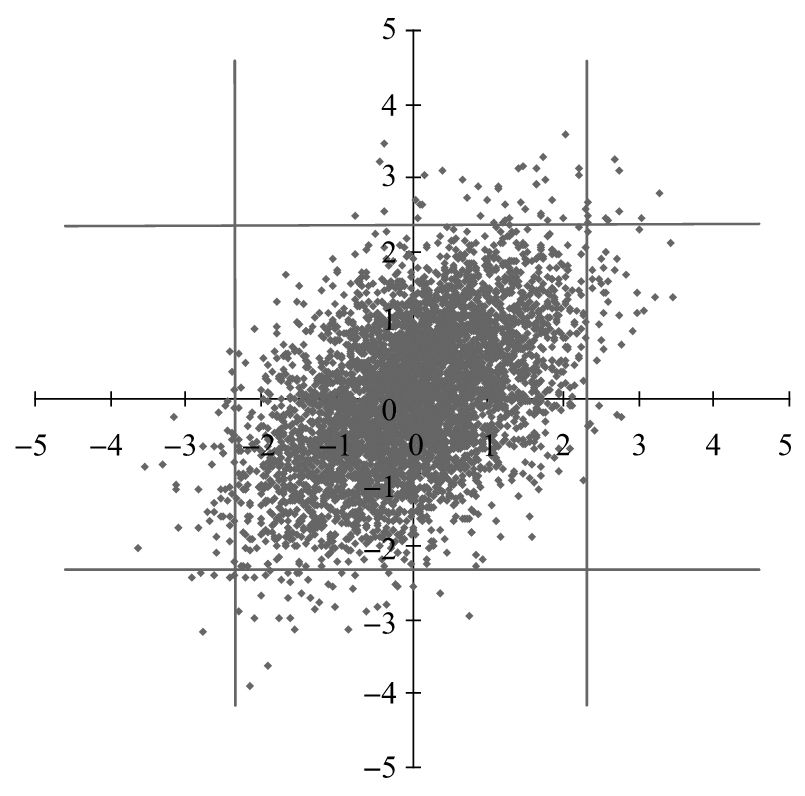
圖11-4 二元正態分佈的5 000個抽樣
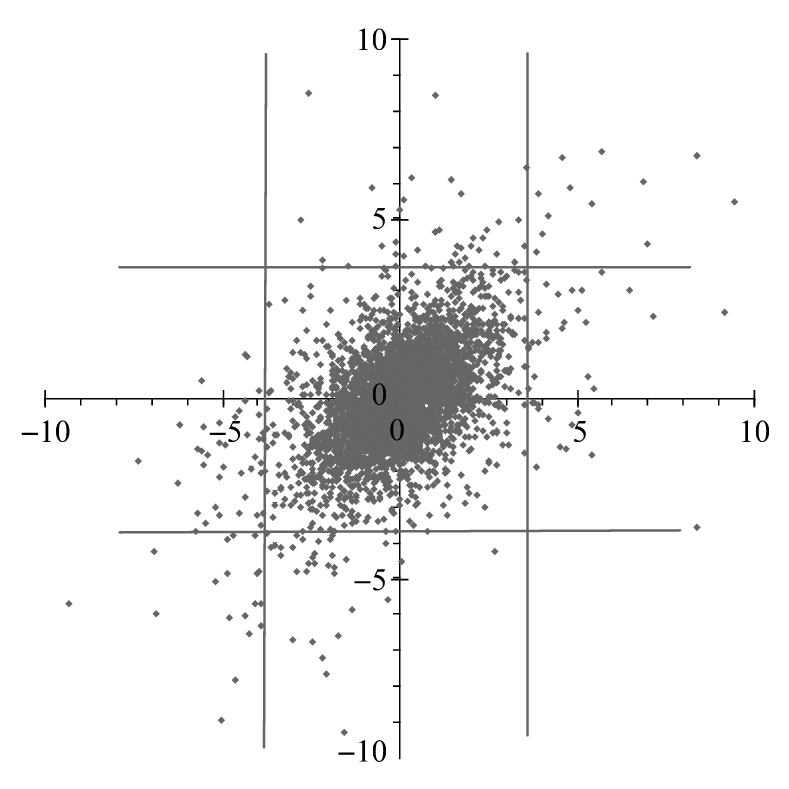
圖11-5 二元學生t-分佈的5 000個抽樣
11.5.4 多元Copula函數
Copula函數可以用於描述多於兩個變量之間的相關結構,其中最簡單的例子就是多元高斯Copula。假定我們已知N個變量V1,V2,…,VN的邊際分佈,對於任意變量i(1≤i≤N),我們將Vi映射到Ui,其中Ui服從標準正態分佈(這裡的映射是分位數之間的一一對應),我們最後假定Ui(1≤i≤N)服從多元正態分佈。
11.5.5 因子Copula模型
在多元Copula模型中,市場分析員常常假定變量Ui之間的相關性由某種因子來決定。在單一因子模型中,由式(11-6),我們得出

其中F和Zi分別服從標準正態分佈,Zi之間相互獨立,Zi與F之間也相互獨立。其他形式的因子Copula模型在選擇因子時也通常要保證F和Zi的期望值為0及標準差為1的條件。我們將在第11.6節中進一步討論與信用風險相關的問題。選擇不同的分佈會影響變量Ui之間的相關性,進而影響Vi變量之間的相關性。
[1] 儘管二元正態分佈是個比較方便的假設,但這一習慣性假設並不是唯一選擇。關於兩個服從正態分佈的變量,我們可以通過許多不同的方式來使得兩個變量相互關聯,例如,我們可以令V2=V1,對應於-k≤V1≤k的情形;V2=-V1,對應於其他情形。練習題11.11是另一個例子。
[2] 在Excel中可採用公式NORMSINV(0.05)=-1.64來計算。
[3] 在作者的網頁(www-2.rotman.utoronto.ca/~hull/riskman)上,讀者可以下載計算二元正態累積分佈函數的Excel計算表。
11.6 將Copula應用於貸款組合:Vasicek模型
在這裡我們將討論一元高斯Copula函數的一種應用,這對於我們理解第15章中的《巴塞爾協議Ⅱ》資本金要求中的公式會有幫助。假定一家銀行有一個鉅額的貸款投資組合。每個貸款每年的違約概率是1%。如果貸款違約是相互獨立的,則每年違約率的期望值大概是1%。但在實際中,貸款的違約不是相互獨立的,它們全都受宏觀經濟的影響。其結果是,在某些年,違約率會比較高,而在其他一些年份,違約率會比較低。表11-6通過統計1970~2016年的違約率證實了這種情況。違約率從1979年最低的0.088%到2009年最高的4.996%不斷變化。其他一些違約率比較高的年份有1970年、1989年、1990年、1991年、1999年、2000年、2001年、2002年、2008年和2016年。
表11-6 1970~2016年所有被評級的公司的年百分比違約率
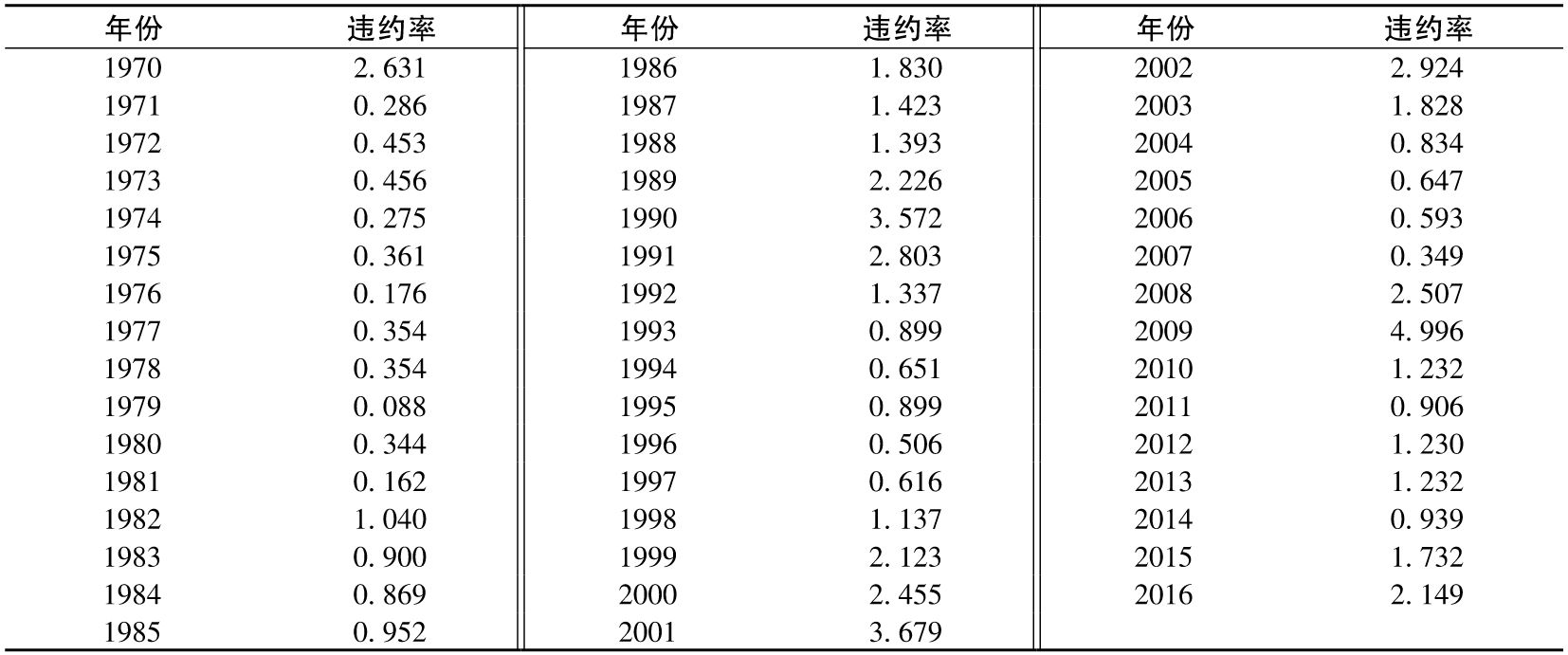
資料來源:穆迪。
為了給組合中貸款的違約率建立模型,定義Ti(1≤i≤N)為公司i的違約時間(這裡暗含的假設是,所有的公司在最終總會破產——只是違約發生的時間會在很久的將來,也許是在幾百年後)。在此我們對問題做一下簡化,假定所有貸款的違約時間的累積概率分佈函數相同,並定義PD為到時間T已發生違約的概率
PD=Prob(Ti<T)
高斯Copula模型可用來描述各貸款之間違約時間的相關結構。按照上面討論的步驟,對每一個i,我們將違約時間變量Ti的累積分佈的分位數與變量Ui的累積分佈的分位數之間進行一一對應的映射,這裡的Ui具有標準正態分佈。我們假定Ui之間的相關結構滿足式(11-8)中描述的因子模型,並且所有的ai都相等,記為a。於是有
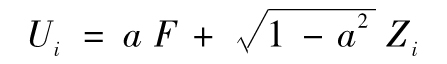
與式(11-8)一樣,變量F及Zi為相互獨立的正態分佈,Zi之間也相互獨立。在這種情況下,每對貸款之間的Copula相關性是相等的,均為
ρ=a2
於是,Ui可以記作

定義最壞情況下的違約率(worst case default rate)WCDR(T,X)為時間T內的違約率(即違約的貸款數與總貸款數的百分比),且該違約率有X%的概率不被超過(在很多情況下,T的時間跨度是1年)。根據我們的假設,我們會得到以下結論
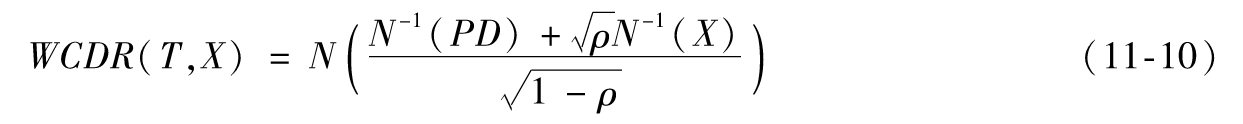
這個結果看上去有些奇怪,但它非常重要。Vasicek在1987最先得出了這個結果。[1]N和N-1是累積正態分佈函數和反累積正態分佈函數,它們可以很容易地由Excel計算表中的NORMSDIST和NORMSINV函數來計算。注意,如果ρ=0,那麼所有貸款的違約是相互獨立的,此時WCDR=PD。隨著ρ的增加,WCDR會隨著增加。
【例11-2】 假如一家銀行對大量零售客戶發放了大量貸款。每筆貸款的年違約概率為2%,在Vasicek模型中,Copula相關係數ρ的估測值為0.1,此時
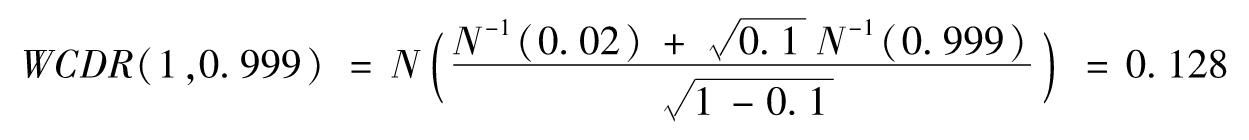
以上計算顯示我們有99.9%的把握肯定違約率不會大於12.8%。
11.6.1 對Vasicek結果的證明
根據高斯Coupula模型的性質,我們有
PD=Prob(Ti<T)=Prob(Ui<U)
其中
U=N-1[PD]
(11-11)
在式(11-9)中,到時間T時違約的概率依賴於因子F。該因子可以被理解成宏觀經濟指數。如果F比較高,則宏觀經濟形勢好,每個Ui趨向較高的值,對應的Ti的值也因此更高,這意味著,在較短時間內發生違約的可能性較低,所以Prob(Ti<T)的值也比較低。如果F比較低,則宏觀經濟形勢差,每個Ui及Ti趨向較小的值,所以在較短時間內發生違約的概率較高。為了進一步說明這一點,我們考慮給定F時違約的條件概率。
由式(11-9)可得出
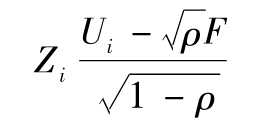
在因子F的值給定的條件下,Ui<U的條件概率為

以上概率與Prob(Ti<T|F)等同,因此
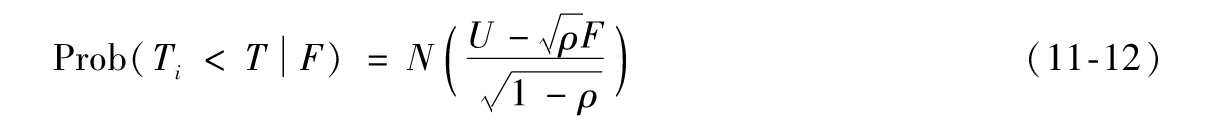
由式(11-11)
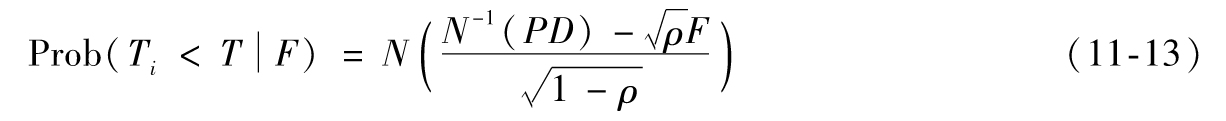
對於一個較大的貸款組合,如果各筆貸款具有相同的違約概率,並且每對貸款之間的Copula相關性為ρ,則以上表達式是對T時刻F條件下貸款組合違約百分比的一種很好的估計,我們將以上表達式定義為違約率(default rate)。
當F減小時,違約率會增加,那麼違約率最壞的狀況會是怎樣呢?F服從標準正態分佈,F<N-1(Y)的概率為Y,因此,存在一個概率Y,使得違約率大於
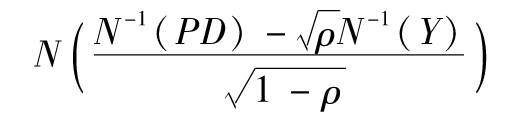
置信度為X%,展望期為T的情況下的違約率可以通過將Y=1-X代入以上表達式得到。因為N-1(X)=-N-1(1-X),所以我們可求得式(11-10)的值。
11.6.2 估計違約概率和相關性ρ
第10章介紹的最大似然估計法可以用來從歷史違約數據中估計違約概率和相關性ρ。我們可通過式(11-10)來計算違約率分佈的高分位數,但實際上,該式對所有的分位數都適用。如果DR為違約率,G(DR)為DR的累積概率分佈函數,由式(11-10)

將該式做變換,可得
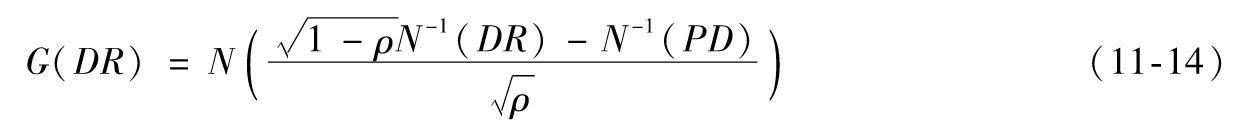
對該式求導,違約概率的概率密度函數為

由歷史違約數據計算違約概率PD和相關性ρ的最大似然估計的步驟如下:
(1)選擇PD和ρ的初始值;
(2)對DR的每個觀察值,計算式(11-15)中概率密度函數的對數;
(3)使用Solver搜索PD和ρ的值使得步驟(2)中各值的和最大。
對錶11-6中的數據使用上述步驟。對ρ和PD的最大似然估計值分別是0.098和1.32%(計算過程見作者的網站上提供的計算表)。違約率的概率分佈如圖11-6所示。第99.9%分位數對應的違約率為
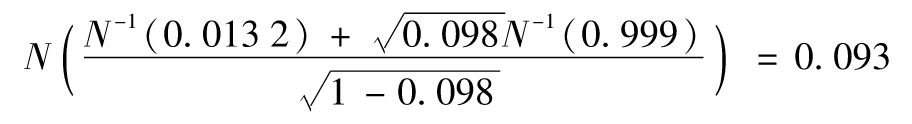
即每年9.3%。

圖11-6 違約率的概率分佈,參數由表11-6所示的數據得出
11.6.3 除高斯Copula以外的其他Copula函數
單因子高斯Copula模型有其侷限性。如圖11-4所示,其得出的尾部相關性很小。這意味著一家公司的意外提早違約和另一家公司的意外提早違約很少同時發生。要找到合適的ρ來擬合數據可能比較困難。例如,如果PD為1%而10年中某年的違約率達到3%,則找不到ρ的值可以跟這種情況保持一致。其他一些具備更強的尾部相關性的單因子Copula模型可以更好地擬合數據。
開發這樣一種模型的方法是為F或Zi選取比式(11-9)中的正態分佈具有更厚尾部的分佈(這些分佈要被放縮,以保證均值為0,標準差為1),然後Ui的分佈再由F和Zi的分佈(可能通過數值方法)決定。式(11-10)變為

其中,Φ、Θ和Ψ分別是Zi、F和Ui的累積概率分佈函數。此時,式(11-14)變為[2]
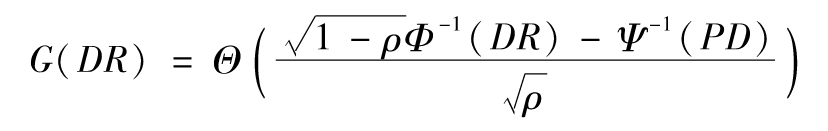
[1] See O. Vasicek, “Probability of Loss on a Loan Portfolio” (Working Paper, KMV, 1987).Vasicek的結果也發表在2002年12月期的Risk雜誌上,文章的標題為“Loan Portfolio Value”。
[2] 在論文“The Risk of Tranches Created from Mortgages”(J. Hull and A. White, Financial Analysts Journal 66, no.5 (September/October 2010):54-67)中,本方法被用於估計由房屋抵押貸款創造的分檔證券的風險。在很多情況下,此方法能更好地擬合曆史數據,但它的缺點在於其中使用的概率分佈相較正態分佈處理起來更復雜,有時需要使用數值方法來確定Ψ和函數g(DR)。
小結
風險管理人員常常採用相關性或協方差來描述變量之間的相互關係。每天的協方差是變量每天變化的相關係數與變量每天波動率的乘積。監測協方差的方法同第10章中監測方差的方法相似。風險管理人員常常跟蹤風險變量的方差-協方差矩陣。
一個變量的邊際分佈是指變量的無條件分佈。風險分析人員在產生邊際分佈後往往還需要描述及估計相關性結構。當變量服從正態分佈時,很自然我們會假設變量之間服從多元正態分佈。在其他情形下,我們需要採用Copula函數來描述相關性結構,這時我們將變量的邊際分佈的分位數以一對一的形式映射到正態分佈(或者其他多元分佈)上,我們尋求的變量之間的相關結構由映射後的變量的相關性結構來確定。
在多變量情形下,分析員常常採用因子模型。因子模型可以用於減少估計相關係數的數量。我們可以假定任意兩個變量的相關係數完全由它們因子之間的相關性決定。公司之間的違約相關性可以通過基於因子的違約時間高斯Copula模型來描述。
對於風險管理人員而言,Copula函數的一個重要用途在於計算貸款組合的違約率分佈。風控人員常常假設不同貸款的違約時間的概率分佈是由單因子Copula模型來確定的。因此,一個大型貸款組合的違約次數分佈的分位數可以通過因子概率分佈的分位數來計算。我們在第15章中將看到,通過採用這種辦法,我們可以計算《巴塞爾協議Ⅱ》所要求的銀行的信用風險資本金數量。
延伸閱讀

練習題
11.1 假定變量之間相關係數已知,你還進一步需要什麼樣的信息來計算協方差?
11.2 相關係數與關聯的不同之處是什麼?假定y=x2,x服從正態分佈,期望值為0,標準差為1,x與y之間的相關係數為多少?
11.3 什麼是因子模型?為什麼可以採用因子模型來描述大量變量之間的相關性?
11.4 矩陣半正定的含義是什麼?一個相關係數矩陣不滿足半正定條件的後果是什麼?
11.5 假定資產A和B的日波動率分別為1.6%和2.5%,資產A和B在上個交易日末的價格為20美元和40美元,該日資產回報相關係數的估計值為0.25,EWMA模型中的λ參數為0.95:(a)計算資產之間當前的協方差;(b)假定在今天交易結束時,資產價格分別為20.50美元和40.50美元,相關係數的最新估計為多少?
11.6 假定資產X和Y的當前日波動率分別為1.0%和1.2%,上個交易日結束時資產價格分別為30美元和50美元,資產回報的相關係數為0.5。在這裡我們採用GARCH(1,1)模型來計算更新相關係數及波動率,GARCH(1,1)模型中的參數估計為α=0.04及β=0.94,在相關係數估計中採用ω=0.000 001,在波動率估計中採用ω=0.000 003,假如在今天交易結束時,資產價格分別為31美元和51美元,相關係數的最新估計為多少?
11.7 假定在練習題10.15中,標準普爾500指數(以美元計)與富時100指數(以英鎊計)的相關係數為0.7,標準普爾500指數(以美元計)與美元/英鎊的匯率的相關係數為0.3,標準普爾500指數的日波動率為1.6%,將富時100指數轉換為美元后與標準普爾500指數的相關係數為多少?(提示:對於3個變量X、Y和Z,X+Y同Z的協方差等於X與Z的協方差加上Y與Z的協方差)。
11.8 假定兩個變量V1和V2服從均勻分佈,此分佈中的數值介於0與1之間,並且所有數值有均等出現的概率。採用高斯Copula函數來定義V1和V2的相關性結構,在這裡Copula相關係數為0.3。將V1和V2的數值分別設定0.25、0.5和0.75,請製作類似於表11-5的表格(在作者的網頁www-2.rotman.utoronto.ca/~hull/riskman中,讀者可以下載計算二元正態分佈的計算表)。
11.9 假定你有3個相互獨立並服從正態分佈的變量z1、z2、z3,你想將這3組變量由Cholesky分解來產生服從三元正態分佈的隨機變量ε1、ε2、ε3,請求出由z1、z2、z3及變量之間的相關係數組成的ε1、ε2、ε3的表達式。
11.10 尾部相關的含義是什麼?如何採用不同的Copula函數來改變尾部相關性?
11.11 假定V1和V2的邊際分佈均為標準正態分佈,請採用自由度為4、相關係數為0.5的學生t-Copula來定義變量之間的相關性,並構造圖表來顯示聯合分佈的抽樣值。
11.12 在表11-5中,在V1<0.1條件下,V2的概率密度函數是什麼?請將這一密度函數同V2無條件分佈進行比較。
11.13 在表11-3及表11-4中,假定V1=0.2,此時V2分佈的中位數為多少?
11.14 假定銀行有一筆大數量的貸款,每筆貸款每年的違約概率為1.5%,違約時的回收率為30%,銀行採用高斯Copula來模擬違約時間。請使用Vasicek模型來估計99.5%置信度下的違約率。假設Copula相關係數為0.2。
11.15 如果過去10年間一個消費貸款組合的違約率為1%、9%、2%、3%、5%、1%、6%、7%、4%和1%。Vasicek模型中參數的最大似然估計是多少?
作業題
11.16 假定在上個交易日結束時某資產X的價格為300美元,價格波動率為每天1.3%,今天X的價格在交易結束時為298美元,假定在上個交易日結束時資產Y的價格為8美元,價格波動率為每天1.5%。Y的價格與X的價格的相關係數為0.8。今天在交易結束時Y的價格同昨天相同,即8美元。請求出最新的X價格及Y價格的波動率及相關係數,在計算中請採用:(a)EWMA模型,參數為λ=0.94;(b)GARCH(1,1)模型,其中模型參數ω=0.000 002、α=0.04及β=0.94。在實踐中,對於X和Y的ω參數是否相同?
11.17 指數分佈的概率密度函數為λe-λx,其中x為自變量,λ為參數,指數分佈的累積概率分佈為1-e-λx。假定變量V1和V2均服從指數分佈,其對應的參數λ分別為1.0和2.0,採用高斯Copula函數來定義V1和V2的相關性結構,其中Copula相關係數為-0.2,製作與表11-5類似的表格,其中V1和V2的值分別為0.25、0.5、0.75、1、1.25及1.5(在作者的網頁www-2.rotman.utoronto.ca/~hull/riskman中,讀者可以下載一個計算累積二元正態分佈的計算表)。
11.18 在Excel計算表中製作一個類似圖11-5的圖形,在圖形中請顯示自由度為4、相關係數為0.5的二元學生t-分佈的抽樣值。進一步,假定V1和V2的邊際分佈分別為自由度為4的學生t-分佈,採用高斯Copula函數來定義V1和V2的相關性結構,Copula相關係數為0.5。請畫出圖形來顯示聯合分佈的抽樣,並比較圖形。
11.19 假定一家銀行有一筆大數量的貸款,每一筆貸款的1年違約概率為1.2%。這家銀行採用高斯Copula來模擬違約時間,求取對應於在99.97%置信度下,貸款損失的最壞數量(99.97% worst case)非常有意義,在這裡請展示對應於不同Copula相關係數,這一最壞損失數量會有什麼樣的不同變化。
11.20 某類貸款過去15年中的違約率為2%、4%、7%、12%、6%、5%、8%、14%、10%、2%、3%、2%、6%、7%、9%。使用最大似然法,計算Vasicek模型中參數的最佳擬合值。違約率的概率分佈是什麼?99.9%置信度下的最壞違約率有多高?
第12章
在險價值和預期虧空
在第8章和第9章中,我們討論了金融機構負責管理某些特定市場變量(例如,股指、利率或大宗商品價格)風險敞口的交易員如何計算delta、gamma及vega等風險指標。金融機構的交易組合往往取決於成百上千個市場變量,交易員每天的分析可能會包括大量計算,雖然這些風險指標對交易員十分重要,但是並不能為金融機構的高管及監管人員提供一個關於整體風險的完整圖像。
在險價值(value at risk,VaR)和預期虧空(expected shortfall,ES)兩項指標都試圖以一個數字來度量金融機構的投資組合面臨的整體風險。其中VaR的概念最先由摩根大通(見業界事例12-1)提出,並已經被企業資產部、基金經理以及金融機構廣泛採用。我們將在第15章和第16章中看到,VaR也是很多監管機構採用的用於計算銀行資本金設定的一種傳統工具,這裡的資本金包括市場風險、信用風險和操作風險資本金。在第18章中我們將會解釋,監管機構正在逐步過渡到ES方法。
業界事例12-1
有關VaR的歷史回顧
在險價值之所以在今天得到廣泛採用應歸功於摩根大通。最初,摩根大通的總裁丹尼斯·韋瑟斯通(Dennis Weatherstone)對他每天收到冗長的風險報告非常不滿意,報告中包含了大量關於希臘值的不同風險敞口的敏感性信息,但對於銀行的整體風險管理意義不大。丹尼斯希望能收到更為簡潔的報告,報告應該闡明銀行的整體交易組合在今後24小時所面臨的風險。最初丹尼斯的下屬認為生成這樣的報告是不可能的事情。但最終,他們還是以馬科維茨交易組合理論為基礎(見第1.1節)做出了在險價值報告,這一報告被稱為4:15報告,因為這一報告要在每天下午4點15分呈現在總裁的辦公桌上。
生成在險價值報告需要大量的工作。風險管理人員需要採集銀行在全世界不同地區的交易數據,這些交易所處的時區往往會不同;同時,他們還要對市場變量波動率及相關性要有一定的估計;另外,他們必須開發出生成報告的系統。摩根大通大約在1990年完成了自己的系統開發工作,這樣的系統帶給銀行最主要的好處是使得銀行高管對於銀行所面臨的風險有了清晰的認識,並能據此更合理地分配資本金。與此同時,其他銀行也紛紛採用類似的方法來計算自己的整體風險。到1993年,在險價值已經成為測定風險的重要工具。
銀行通常對自己開發的模型採取保密措施。1994年摩根大通將自己開發的一個較為簡單的模型RiskMetrics通過網絡公佈於世。RiskMetrics包括了大量市場變量的方差及協方差。RiskMetrics發佈後引起了廣泛的關注,並引發了對各種在險價值模型優缺點的討論。自此之後,在險價值很快得到了金融機構及一些非金融機構的廣泛採用,成為一種標準方法。巴塞爾委員會在1996年公佈了基於在險價值的《巴塞爾協議修正案》。這一修正案在1998年得到了實施(見第15.6節)。後來,RiskMetrics從摩根大通中分離出來,成為一家獨立公司。1997年,這家公司發佈了可用於信用風險管理的CreditMetrics系統,1999年又發佈了可以用於管理非金融機構風險管理的CorporateMetrics系統。
本章將解釋VaR和ES的概念,並對其各自的優勢以及弱點進行討論。在第13章及第14章中,我們將解釋如何計算市場在險價值和預期虧空,在第21章中,我們將討論如何將在險價值用於信用風險管理。
12.1 VaR的定義
當使用VaR來度量風險時,我們希望能夠做出以下陳述:
我們有X%的把握,在T時間段內,我們的損失不會大於V。
這裡的變量V就是交易組合的VaR。VaR是兩個變量的函數:時間展望期(T時間段)及置信區間(X%)。VaR給出了在今後的T天及在X%把握之下,交易損失不會超出的值。
VaR可以由交易組合在T時間內的收益概率分佈得出,也可以由損失的概率分佈得出(對於前者,損失可以認為是負收益;對於後者,收益可以認為是負損失)。例如,當T=5天、X=97時,VaR對應於交易組合在5天后收益分佈中第3個分位數對應的損失;或者,VaR對應於交易組合在5天后損失分佈中第97個分位數對應的損失。在更一般的情況下,當採用收益分佈時,VaR等於圖12-1所示收益分佈的第100-X分位數的負值;當採用損失分佈時,VaR等於圖12-2所示損失分佈的第X分位數的值。

圖12-1 由交易組合在時間T的收益概率分佈中來計算VaR,損失可看作是負的收益,置信度為X%,VaR的大小為V
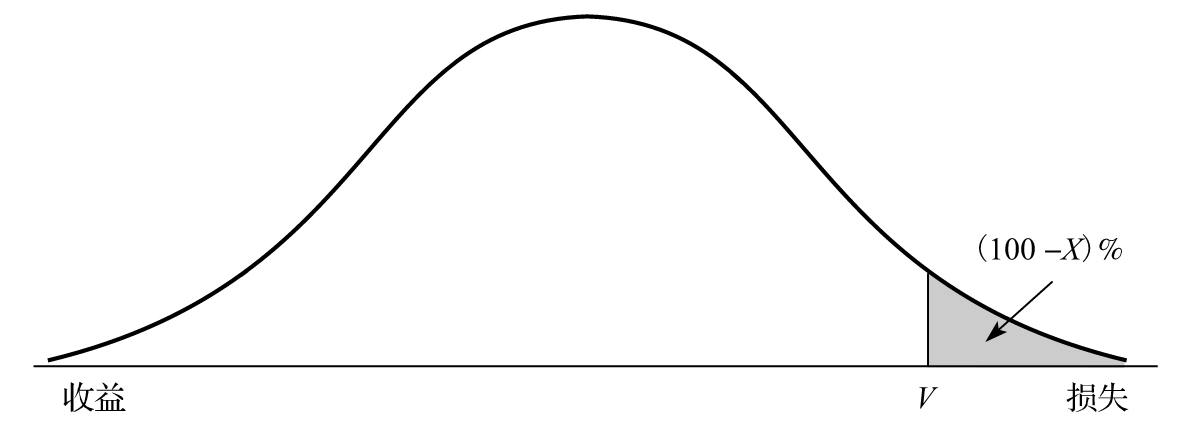
圖12-2 由交易組合在時間T的損失概率分佈中來計算VaR,收益可看作是負的損失,置信度為X%,VaR的大小為V
12.2 計算VaR的例子
在本節中,我們將提供VaR計算的4個例子,在前兩個例子中,收益(損失)分佈為連續形式;在後兩個例子中,收益(損失)分佈為離散形式。
【例12-1】 假定一個交易組合在6個月內的收益服從正態分佈,分佈均值為200萬美元,標準差為1000萬美元。從正態分佈的性質得出,分佈的第一個分位數為2-2.326×10即-2 130萬美元,因此,對於6個月展望期,在99%置信度下的VaR為2 130萬美元。
【例12-2】 假定一個1年項目的最終結果介於5 000萬美元損失和5 000萬美元收益,5 000萬美元損失和5 000萬美元收益之間的任意結果具有均等的可能,這時,項目的最終結果服從由-5 000萬美元到+5 000萬美元的均勻分佈,損失大於4 900萬美元的可能性為1%,因此,對於1年展望期,在99%置信度下的VaR為4 900萬美元。
【例12-3】 假定一個1年項目有98%的概率收益為200萬美元,1.5%的概率損失為400萬美元,0.5%的概率損失為1 000萬美元。損失累計分佈如圖12-3所示,在這一累計分佈下,對應於99%累計概率的點為400萬美元,因此,對於1年展望期,在99%置信度下的VaR為400萬美元。
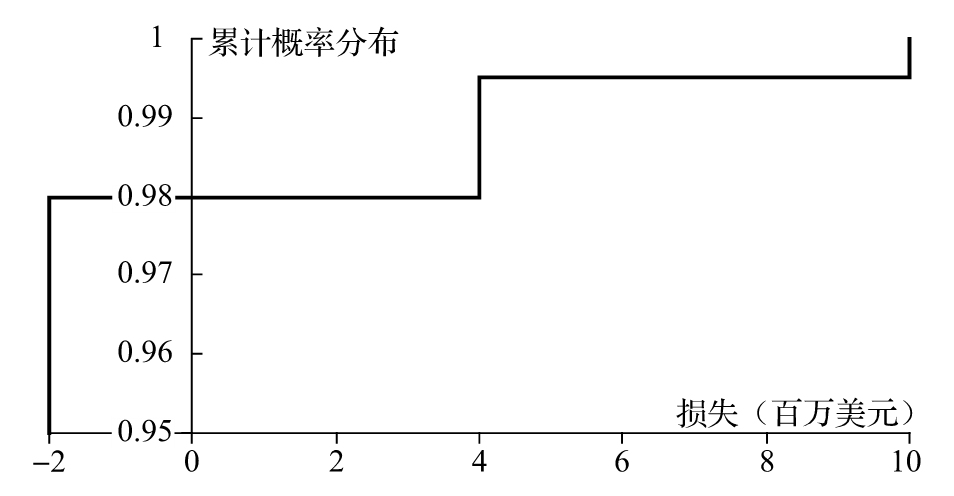
圖12-3 例12-3和例12-4中的累計損失分佈
【例12-4】 考慮例12-3中的情況,假定我們想求得對在99.5%置信度下的VaR,這時,圖12-3顯示,對介於400萬美元和1 000萬美元的任何一點的損失,均有99.5%的把握不會被超出。對於這一區間的任意數值V,損失超出V的概率均為0.5%。VaR在這一情形不具有唯一性,一個合理的選擇是將VaR設定為這一區間的中間值,這意味著,在99.5%置信度下的VaR為700萬美元。
12.3 VaR的缺陷
VaR的概念比較容易理解,因此很受歡迎。在應用VaR時,事實上用戶在問以下簡單的問題:“情況能壞到什麼樣子?”這一問題的答案是所有的高級管理人員都希望知道的。他們很喜歡將交易組合對多個市場變量的不同敏感度壓縮為一個數字的做法。
但是,當採用VaR來設定一個交易員的風險額度時,也可能會產生我們不希望看到的結果。假定一家銀行限定的某交易員的交易組合在一定展望期的99%VaR的額度為1000萬美元,交易員可以構造一個交易組合,該組合有99.1%的可能每天的損失小於1000萬美元,但有0.9%的可能損失為5000萬美元。該交易員滿足了銀行所設定的風險額度,但很明顯,他承擔了銀行不可接受的風險。交易員所追求的收益的概率分佈形狀如圖12-4所示,圖12-4所示的VaR等同於圖12-1所示的VaR,但圖12-4所對應的風險要遠大於圖12-1所對應的風險,這是因為圖12-4所示的分佈更有可能出現大的損失。

圖12-4 時間T內某交易組合價值的概率分佈
注:置信區間為X%,交易組合具有和圖12-1中相同的VaR,但該圖顯示出現大額損失的可能性更大。
我們可以認為,圖12-4所示的概率分佈在實踐中從未發生過。實際上,這並不罕見。許多交易策略有很大的概率得到非常好的收益,但是也存在很小的概率遭受巨大的損失(例如,採用賣出虛值期權這樣的策略,交易員會收到期權費,且在大多數情形下無須為買家支付收益。然而,一旦期權被執行,交易員往往就會遭受很大的損失)。許多交易員喜歡承擔更大的風險,以期得到更高的收益。如果交易員能夠在沒有超出風險額度的情況下承擔更大的風險,他們往往會那樣去做,這裡引用某交易員同作者的一席對話:“我還從來沒有碰到過一種風險控制系統能限制我進行交易。”
12.4 ES
與VaR相比,一種能給予交易員更多動機合理去控制風險的風險測度為預期虧空(ES)。這一測度有時也被稱為條件在險價值(conditional VaR)或條件尾部期望(conditional tail expectation)或尾部損失(tail loss)。VaR測度的目的是回答“情況能壞到什麼樣子”這樣的問題,而ES則要回答“當糟糕的情況發生時,損失的期望值為多大”。像VaR一樣,ES也是兩個變量的函數,即展望期的時間長度T(展望期)以及置信區間的水平X。實際上,為了計算ES,必須首先計算VaR。ES是指在T時間段的損失超出了第X分位數的條件下損失的期望值。例如,假定X=99,T=10天,VaR=6 400萬美元,ES為在今後10天,損失超出6 400萬美元以上的平均損失。
將ES而不是VaR作為交易員的風險額度,會使得交易員進行如圖12-4所示的交易的可能性降低。另外,在下一節中我們將說明,從風險分散的意義上來講,ES要比VaR有更好的性質,因為前者總是能體現風險分散帶來的益處。但是,ES的不利之處在於其複雜性,因此這一風險測度比VaR更難以理解。另外,與VaR相比,對計算ES的過程進行回溯測試(back-testing)更加困難(我們在今後將解釋,回溯測試是利用歷史數據來檢驗風險計量計算方法可靠性的一種途徑)。
12.5 一致性風險測度
假定對應於99.9%置信區間和1年展望期,某交易組合的VaR為5 000萬美元,這意味著在極端條件下(理論上講,每1 000年出現一次),金融機構在1年時損失會超出5 000萬美元,這同時也說明,如果金融機構持有5 000萬美元的資本金,我們會有99.9%的把握,金融機構不會在1年內完全損失自身持有的資本金。
假定我們想設計某種風險測度來確定金融機構應持有的資本金數量,VaR是最好的選擇嗎(在合適的展望期和置信水平下)?Artzner等研究人員對這一問題進行了研究,他們指出理想的測度應滿足以下性質[1]:
(1)單調性(monotonicity):如果在任何情形下,第一個交易組合的回報均低於另一個交易組合的回報,那麼第一個交易組合的風險測度一定要比另一個更大。
(2)平行移動不變性(translation invariance):如果我們在交易組合中加入K數量的現金,那麼交易組合所對應的風險測度要減少K數量。
(3)同質性(homogeneity):假定一個交易組合的內含資產品種和相對比例不變,但內含資產的數量增至原數量的λ倍,此時新的交易組合的風險測度應是原風險的λ倍。
(4)次可加性(subadditivity):兩個交易組合相加所組成的一個新交易組合的風險測度小於或等於最初兩個交易組合的風險測度之和。
以上風險測度的第一個性質顯而易見,如果一個交易組合的回報總是比另一個交易組合要差,那麼第一個交易組合的風險一定會更高;第二個條件也非常合理,如果我們在某個交易組合中加入K數量的現金,那麼該現金可以為損失提供緩衝,相應的額外資本金要求也應該可以減少K數量;第三個條件也很合理,如果我們將某交易組合放大兩倍,那麼相應的資本金要求也應該增大兩倍;[2]第四個條件是在說明風險分散可以降低風險,即我們將兩個交易組合疊加在一起,新的交易組合的風險應該減少,或至少保持不變。
VaR滿足以上討論中的前3個條件,但VaR並不一定永遠滿足第四個條件,這一點將在以下例子中闡明。
【例12-5】 假定兩個獨立貸款項目在1年內均有0.02的概率損失1 000萬美元,同時均有0.98的概率損失100萬美元,任意一個單筆貸款在展望期為1年、97.5%的置信區間下的VaR為100萬美元,將兩個貸款疊加產生一個投資組合,組合有0.02×0.02=0.000 4的概率損失2 000萬美元,並且有2×0.02×0.98=0.039 2的概率損失1 100萬美元,有0.98×0.98=0.960 4的概率損失200萬美元。在展望期為1年、97.5%的置信度下,組合的VaR為1 100萬美元,單筆貸款所對應VaR的和為200萬美元,貸款組合的VaR比貸款VaR的總和高900萬美元,這違反了次可加性。
【例12-6】 我們考慮兩筆期限均為1年、本金均為1000萬美元的貸款。違約的概率由下表所示。

當其中任何一筆貸款違約時,收回本金的數量不定,但我們知道回收率介於0與100%的可能性為均等。當貸款沒有違約時,貸款盈利均為20萬美元。
首先考慮第一筆貸款,違約可能為1.25%,在違約發生的條件之下,損失均勻介於0與1 000萬美元,這意味著有1.25%的概率損失大於0;有0.625%的概率損失大於500萬美元;損失超出1 000萬美元的事件不會發生。損失超出200萬美元的概率為1%(在損失發生的前提下,有80%的概率損失會超出200萬美元,因為損失出現的概率為1.25%,損失大於200萬美元的無條件概率為0.8×0.012 5=0.01,即1%),因此,1年期的99%VaR為200萬美元。同樣的計算也適用於第二筆。
接下來考慮兩筆貸款的組合,違約出現的概率為2.5%。同上,違約所觸發的損失在0與1000萬美元之間均勻分佈。對應這種情況,VaR的估計值為580萬美元,這是因為在兩筆貸款之中有一筆貸款違約的概率為2.5%,在違約發生的條件下,損失超過600萬美元的可能性為40%。因此,損失大於600萬美元的無條件概率為2.5%×40%=1%。當一筆貸款產生違約時,另外一筆貸款會盈利20萬美元,將這一盈利考慮在內,我們得出1年的99%VaR為580萬美元。
將單獨計算的單一貸款所產生VaR相加,我們得出VaR的總和為200萬美元+200萬美元=400萬美元,將兩筆貸款組合在一起得出的VaR比單項VaR的總和580萬美元多180萬美元,這違反了次可加性條件(我們都知道將多筆貸款合成一交易組合會帶來風險分散的效應,但我們看到,兩個交易組合合併之後的VaR可能會大於兩個交易組合VaR的和)。
如果一個風險測度滿足以上所有的4個條件,則這樣的測度被稱為一致性風險測度。例12-5和例12-6說明,VaR不滿足一致性條件。我們可以證明以上討論的預期虧空測度滿足一致性條件,以下例子說明了這一點。
【例12-7】 讓我們考慮例12-5中的情形。每筆貸款的VaR均為100萬美元。為了計算在97.5%的置信區間下的預期虧空,我們注意到,在2.5%的尾部分佈中,有2%的概率損失為1 000萬美元,有0.5%的概率損失為100萬美元(注意,其他97.5%的分佈所對應的損失也為100萬美元),在2.5%的尾部分佈的範圍內,有80%的概率損失為1000萬美元,有20%的概率損失為100萬美元,損失的期望值(以百萬計)為0.8×10+0.2×1,即820萬美元。
將兩個貸款項目結合到一起時,在2.5%的尾部分佈中,有0.04%的概率損失為2 000萬美元,有2.46%的概率損失為1 100萬美元,在2.5%的尾部分佈的範圍內,損失的期望值為(0.04/2.5)×20+(2.46/2.5)×11,即1 114.4萬美元。
因為8.2+8.2>11.144(以百萬美元計),所以我們得出預期虧空滿足次可加性條件。
【例12-8】 考慮例12-6中的情形,我們已經展示了單筆貸款所對應的VaR為200萬美元,將展望期設為1年,在99%的把握之下所對應的預期虧空等於在損失大於200萬美元的條件之下損失的期望值。我們已知損失服從0~1 000萬美元的均勻分佈,如果損失大於200萬美元,那麼預期虧空為200萬美元與1000萬美元之間的中間值,即600萬美元。
例12-6說明,兩筆貸款組成的貸款組合的VaR為580萬美元,貸款組合的預期虧空等於在損失大於580萬美元的條件之下損失的期望值。當一筆貸款違約時,另一筆貸款不可能違約(這一點是由於假設),這時,貸款組合的價值介於20萬美元的盈利(+20)及980萬美元的損失(-980)之間的均勻分佈,損失介於580萬美元與980萬美元之間的期望值為780萬美元。因此,貸款組合的預期虧空為780萬美元。
因為7.8小於2×6(以百萬美元計),所以我們得出預期虧空滿足次可加性條件。
可加性條件並非只是一個理論要求,銀行不難發現,有時將兩個交易組合(例如,將股票交易組合和固定收益投資組合)疊加在一起時,疊加後的組合VaR會升高。
譜函數型風險測度
一個風險測度可以通過其分配給損失分佈的分位數的權重來描述。[3]VaR對第X個分位數設定了100%的權重,而對其他分位數設定了0權重;ES對高於第X個分位數的所有分位數設定了相同比重,而對低於第X個分位數的分位數設定了0比重。我們可以對於分佈中的其他分位數設定不同的比重,並以此定義出所謂的譜函數型風險測度(spectral risk measure)。當譜函數型測度分配給第q個分位數的權重為q的非遞減函數時,該測度一定滿足一致性條件(這種測度滿足次可加性條件)。ES滿足以上要求,但VaR並不滿足以上要求,因為VaR對於高於X的分位數所設定的權重小於對於第X個分位數所對應的權重。研究人員提出了其他形式的風險測度,在這些測度中,第q個分位數的權重隨著q的改變而有較大的變化,其中一種想法是使得第q個分位數所對應的權重與e-(1-q)/γ成比例,這裡的γ為常數,這種權重設定所對應的測度被稱為指數譜函數風險測度(exponential spectral risk measure)。圖12-5展示了當γ為兩種不同的值時,ES及指數譜函數風險測度所對應的不同權重。
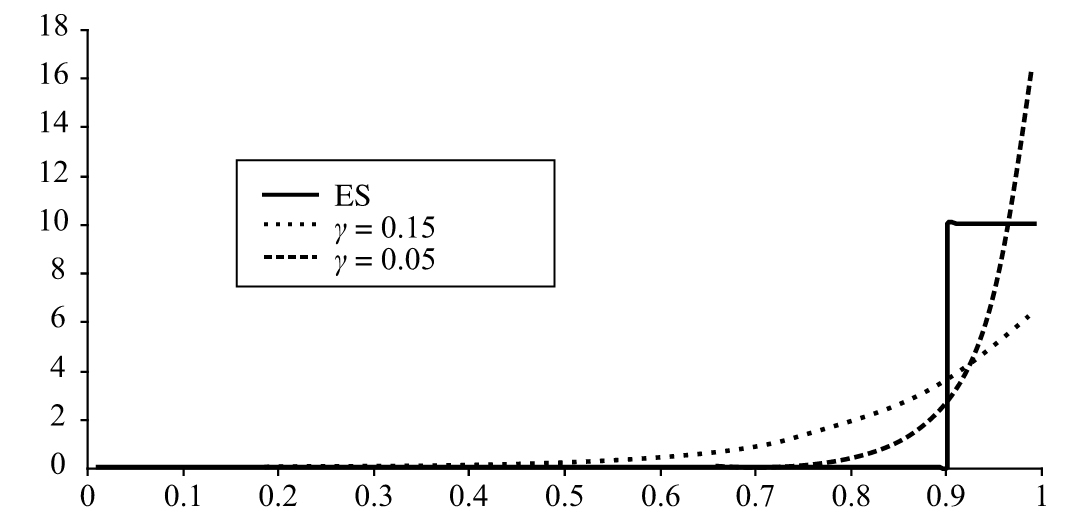
圖12-5 在3種情形中,權重作為分位數的函數
注:a)X=90%所對應的ES;b)γ=0.15所對應的指數譜風險測度;c)γ=0.05所對應的指數譜測度。
[1] See P. Artzner, F. Delbaen, J. -M. Eber, and D. Heath, “Coherent Measures of Risk,” Mathematical Finance 9(1999):203-228.
[2] 在組合規模不大時,這樣認為是沒有問題的。但當組合規模變得十分巨大時,其流動性就受到限制,相應地,資本金的要求可能也會提升。
[3] 這裡的分位數(quantiles)也被稱為百分位數(percentiles)或部分分位數(fractiles)。
12.6 VaR和ES中的參數選擇
用戶在計算VaR或者ES時須設定兩個參數:時間展望期及置信度。一個較為普遍的假設是假定交易組合價值變化在某指定展望期服從正態分佈,但正如我們在第10.3節中討論的,一般來說,這並不是一個好的假設。但是在此,討論一下這個假設下的結果還是有意義的。設交易組合損失的均值為μ,標準差為σ
VaR=μ+σN-1(X)
(12-1)
其中X為置信度,N-1(·)代表累積正態分佈的反函數(在Excel計算表中,這一項的計算可以通過調用函數NORMSINV來實現)。上式顯示出,對於一個相對較短的時間展望期,μ通常被假定為0,且對應於一定的置信度,VaR與σ成正比。
【例12-9】 假定某交易組合在10天展望期上的價值變化服從正態分佈,分佈的期望值為0,標準差為2 000萬美元,10天展望期的99%的VaR為2 000N-1(0.99)=4 650萬美元。
假設損失服從正態分佈,均值為μ,標準差為σ,置信區間為X的ES為

這裡Y是標準正態分佈第X分位數對應的值(即它是均值為0和標準差為1的標準正態分佈上,有1-X概率被超過的點)。從這裡也能看出,如果假設μ的值為0,則ES和VaR類似,也與σ呈正比。
【例12-10】 再次考慮例12-9,10天內組合價值的變化服從一個均值為0、標準差為2 000萬美元的正態分佈。因為標準正態分佈上有1%概率被超過的點為2.326,所以10天展望期、置信度為99%的ES是: (萬美元)。
(萬美元)。
12.6.1 時間展望期
在計算VaR和ES時,時間展望期的選取要因用途而定。當持倉的流動性很好,交易活躍時,則使用較短的(可能僅有幾天)展望期是合理的。當得出的風險測度不可接受時,管理人員應對交易組合及時進行調整。在這種情況下,一個較長展望期的風險測度意義不大,這是因為在一個較長的展望期內,交易組合的成分往往已經發生較大的變化。
養老基金投資組合的管理人員往往會選擇一個較長的展望期。這是因為此類投資組合的交易行為往往不太活躍,而且組合內的某些資產的流動性也不一定很好。當投資組合的流動性從一種工具變化到另一種工具時,可以更改VaR或ES的定義,以使所考慮的變化從一個市場變量到另一個市場變量都不同。例如,考慮一個由IBM的股票和每年交易少於10次的公司債券組成的投資組合。從IBM的價格變化和債券價格的變化計算出一種風險測度是合理的,其中,我們有99%的把握認為IBM的價格變化將在10天之內不會被超過,有99%的把握認為債券價格的變化不會在60天之內被超過。這是監管機構在《交易賬戶的基本審查》中所採用的方法,將在第18章中進行討論。
無論對應於什麼樣的場合,在考慮市場風險時,風險管理人員往往要首先計算1天展望期的VaR或者ES,對於其他的展望期,一個較為常用的假設為
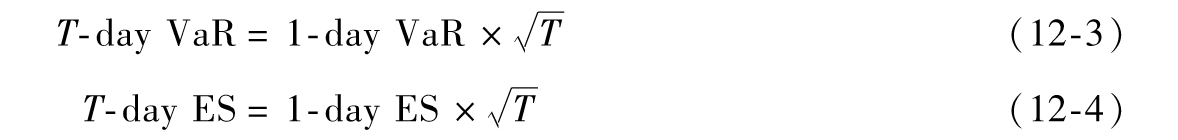
當交易組合價值的日間變化相互獨立,並服從相同的期望值為0的正態分佈時,以上公式完全正確;對於其他情形,這個公式只是一個近似式。以上公式基於式(12-1)和式(12-2)及以下結果事實:
(1)T個相互獨立並具有等同分佈的標準差等於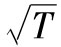 乘以任意一個分佈的標準差;
乘以任意一個分佈的標準差;
(2)多個相互獨立正態分佈的總和仍服從正態分佈。
12.6.2 自相關性的影響
在實際中,投資組合價值每天的變化並不總是相互獨立的,定義ΔPi為交易組合在第i天的價值變化,一個較為簡單的假設是一階自相關,即對所有的i,假定ΔPi與ΔPi-1的相關係數均為ρ。假定對於任意i,ΔPi的方差為σ2,採用兩個變量之和的方差公式,我們得出ΔPi-1+ΔPi的方差為
σ2+σ2+2ρσ2=2(1+ρ)σ2
令ΔPi-j與ΔPi的相關係數為ρj。因此,我們得出以下計算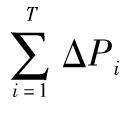 的標準差的計算公式(見練習題12.11)
的標準差的計算公式(見練習題12.11)
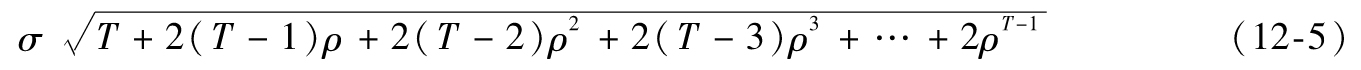
表12-1展示了由1天VaR來計算T天VaR時,自相關性(autocorrelation)的影響。在計算中,我們假設交易組合每天價值變化均服從正態分佈,期望值為0。我們應該注意到T天的VaR(ES)和1天的VaR(ES)的比率與每天波動率σ以及置信度均無關,這一結論是基於式(12-1)、式(12-2)及式(12-5)的性質,即T天標準差與1天標準差成正比。將表12-1中ρ=0情形與其他情形進行比較得出:當自相關存在時,由式(12-3)和式(12-4)所估計的VaR和ES會偏低。
表12-1 當存在一階自相關性時,T天的VaR(ES)同1天的VaR(ES)的比率

注:在計算中,我們假定組合的每天價值變化均服從正態分佈,期望值為0,ρ為自相關參數。
【例12-11】 假定某交易組合的每天價值變化服從正態分佈,均值為0,標準差為300萬美元,每天價值變化的一階自相關係數為0.1,由式(12-5)得出,在今後5天交易組合的價值變化的標準差為
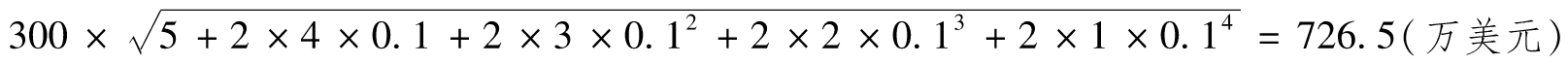
因此5天的95%VaR為:726.5N-1(0.95)=1 195(萬美元);5天的ES為:726.5×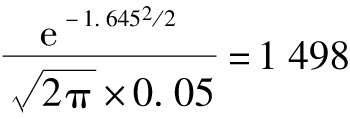 (萬美元)。
(萬美元)。
注意5天價值變化的標準差同1天價值變化的標準差的比率為726.5/300=2.42。在我們的假設之下,VaR及ES均與標準差成正比,這裡的計算正好對應於表12-1中ρ=0.1及T=5的情形。
12.6.3 置信區間
VaR和ES中選用的置信區間與若干因素有關。假定一家銀行想保持自己的AA信用評級,銀行通過計算得出,具有AA信用評級的公司在1年展望期內只有0.03%的破產可能,因此,銀行在內部管理過程中可以採用99.97%置信區間,並且採用1年的展望期來計算資本金。例如,如果對所有敞口,展望期為1年、置信度為99.97%的VaR為50億美元,則意味著如果銀行擁有50億美元資本金,在1年內破產(即將所有股本損失掉)的可能性只有0.03%。銀行也可將這一信息傳達給評級公司,這一信息表明銀行有資格得到AA信用評級。
在實際計算中所採用的置信區間往往比在銀行報告中採用的置信區間要小得多,這是因為對應於高置信區間VaR的估計會非常困難。提高置信區間的一個常用做法是我們將在第13章中介紹的極值理論。如果每天的價值變化服從正態分佈,期望值為0,那麼我們可以採用式(12-1)與式(12-2)來轉換對應於不同置信區間的VaR和ES。例如,假定σ為對應於某展望期交易組合價值變化的標準差,交易組合價值變化的分佈的期望值為0,對應於置信區間為X的VaR估計為VaR(X),預期虧空為ES(X)。由式(12-1)得出
VaR(X)=σN-1(X)
以上公式對不同置信區間X均成立,由此我們可知置信區間為X*的VaR,可以由更低的置信區間X的VaR得出
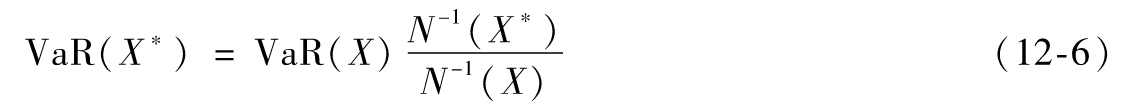
類似地,由式(12-2)

這裡,Y和Y*是標準正態分佈上各有(1-X)和(1-X*)概率被超過的值。
式(12-6)和式(12-7)假定兩個VaR和ES測度具有同樣的展望期,如果我們想同時變換展望期和置信區間,則可以將上述兩式分別與式(12-3)及式(12-4)結合進行計算。
【例12-12】 假定某交易組合1天的95% VaR為150萬美元,1天展望期、95%置信度的ES為200萬美元,同時假定交易組合的價值變化服從正態分佈,均值為0,由式(12-6)得出,1天展望期的99% VaR為: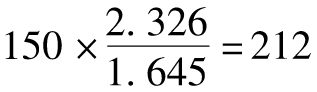 (萬美元)。由式(12-7)可知,1天展望期、99%置信度的ES為:
(萬美元)。由式(12-7)可知,1天展望期、99%置信度的ES為: (萬美元)。
(萬美元)。
12.7 邊際、遞增及成分VaR測度
假定某交易組合由若干子組合(subportfolio)組成。每個子組合對應不同的資產類別(如國內股票、國外股票、固定收益和衍生產品等)。它們可能對應著銀行不同的業務部門(如零售銀行、投資銀行和自營交易),甚至還可能對應著一筆獨立的交易。分析師有時需要計算每個子組合的VaR或ES等測度。
設對第i個子組合的投資額為xi,交易組合對第i個子組合的邊際VaR(marginal VaR)是指交易組合的VaR對子組合i的價值變化的敏感度,即

要估算邊際VaR,我們可以將xi增加一個小的數額Δxi到xi+Δxi,然後重新計算VaR。設ΔVaR是VaR的增量,則我們估計的邊際VaR為ΔVaR/Δxi。對於一個分散度比較好的投資組合,邊際VaR同資本資產定價模型中的Beta係數有密切關係(見第1.3節)。當一個資產的Beta較高時,這個資產所對應的邊際VaR往往也會較高;當一個資產的Beta較低時,這個資產所對應的邊際VaR會很低,在有些情形下,某資產的邊際VaR為負,這說明增加這一資產的權重會減小投資組合的風險。
第i個子交易組合的遞增VaR(incremental VaR)指該子交易組合對VaR的遞增效應,即交易組合包含此子組合時的VaR與不包含此子組合時的VaR的差。交易員通常對新交易的遞增VaR感興趣。
第i個子交易組合的成分VaR(component VaR)定義為

上式的近似表達式為
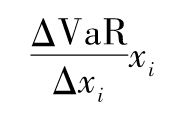
要計算成分VaR,我們可以對第i個子交易組合的投資額進行一個小的相對變化yi=Δxi/xi,然後重新計算VaR。假定ΔVaR為VaR的增量,則成分VaR近似為ΔVaR/yi。在很多情況下,這個近似是合理的。這是因為,如果一個子交易組合的規模相對整個交易組合很小,則我們可以認為邊際VaR在xi減小到0的過程中保持不變。當採用這個假設後,減小xi到0的影響為xi乘以邊際VaR,二者之積就是成分VaR。
邊際預期虧空、遞增預期虧空和成分預期虧空的定義分別與邊際VaR、遞增VaR和成分VaR的定義相仿。
12.8 歐拉定理
由偉大的數學家萊昂哈德·歐拉(Leonhard Euler)很多年前發現的一個結果被證明在將一個風險測度指標由整個投資組合向子組合分配時有重要的作用。令V是一個交易組合上的風險測度,而xi是第i個子組合的大小(1≤i≤M)。假設所有的xi,當xi變為λxi時(即整個交易組合變為原來的λ倍),V變為λV。這對應於第12.5節所述的第三個條件,即線性同質性,這對大部分風險測度是成立的。[1]
基於上述條件,由歐拉定理,下式是成立的

這一結果提供了將V分配到各個子組合中的方法。
當風險測度為VaR時,根據歐拉定理

這裡,Ci是式(12-8)中給出的第i個子交易組合的成分VaR。這一結果表明,一個交易組合的成分VaR的總和等於交易組合的整體VaR。因此,成分VaR可以方便地將整體VaR分配到子交易組合中。如在前一節中解釋的,成分VaR的另一個吸引人的性質是:一個大交易組合的第i個成分VaR與這一成分的遞增VaR近似。
當以ES為風險測度時,歐拉定理同樣顯示交易組合的整體ES是所有成分ES的和:
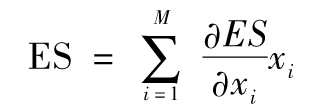
由此,與VaR類似,ES也可以被分配到各個不同的業務部門中。在第26章中,我們會介紹怎樣使用歐拉定理對銀行的經濟資本金在各個業務部門中進行分配。
通過歐拉定理,交易組合的風險可以按組成成分被分解,這對確定所謂的風險預算(risk budgeting)非常有用。風險預算的目的就是在交易組合的不同組成成分之間分配風險。如果通過歐拉分解發現分配給某一成分的風險過高,則交易組合就需要重新調整。
[1] 對一個納入了流動性的風險測度可能不成立。當一個交易組合變得很大時,它的流動性會變差。
12.9 VaR和ES的聚合
有時,風險管理部門可能會使用同樣的展望期和置信區間計算銀行不同業務領域的多個VaR,並希望將這些VaR聚合起來求得整體VaR。以下公式可以達到這一目的
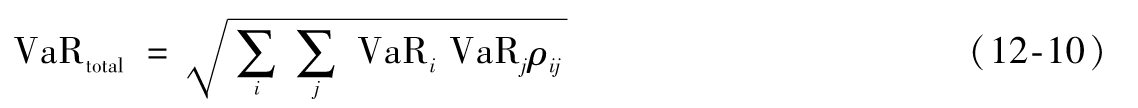
其中VaRi是第i項業務的VaR,VaRtotal是整體VaR,ρij是業務i的損失和業務j的損失的相關係數。上式在損失(收益)期望為0的正態分佈下嚴格成立,並且在其他情況下也提供了很好的估計。將式(12-10)中的VaR替換為ES,所得結果仍然是正確的。
【例12-13】 假設兩個業務部門的ES分別為6 000萬美元和1億美元。損失之間的相關性為0.4,則估計的整體ES為: (百萬美元)。
(百萬美元)。
12.10 回溯測試
回溯測試是一種重要的衡量風險測度在現實中的表現的手段。在回溯測試中,我們會驗證當前採用的風險測度計算過程如果被用於過去,其表現會如何。對VaR的回溯測試會比ES更簡單,這也解釋了為什麼過去監管機構並不情願把用於市場風險的VaR模型轉換為ES模型。在第18章中我們會解釋,監管部門的計劃是在將來,ES模型會被用來計算監管資本金,而回溯測試還是會依賴VaR的測算。
假設我們開發出一個計算1天的99%VaR的模型。在回溯測試中,我們要找出來交易組合在1天內的損失有多少次超出了1天的99%VaR,實際損失超出VaR情形被稱為例外(exception)。如果例外的天數大約佔整體天數的1%,則我們應該對我們的VaR模型表現感到欣慰。但是,如果例外的天數佔整體天數的比例遠大於1%(例如7%),則我們有理由認為VaR的估計偏低。從監管部門的角度來看,由這樣的VaR而得出的資本金數量會太低。此外,如果例外情形發生的頻率遠低於1%(例如0.3%),則我們有理由認為這裡的VaR估計偏高,由此而得出的資本金數量偏高。
在對1天的VaR進行回溯測試時,我們要考慮在日內交易組合本身的變化。對這一問題有兩種處理方式:第一種方式是假定交易組合的構成沒有任何變化,在這一假設之下,我們可以計算交易組合的價值變化,完成計算之後,將VaR與這一理論價格變化(hypothetical changes)進行比較;第二種方式是將VaR同交易組合價值的真實變化進行比較。在VaR的計算過程中,我們必然要假設在展望期內沒有任何新的交易,正因為如此,將VaR同第一種方式中計算所得的理論價格變化進行比較看起來更為合理。但是,在我們的分析過程中,交易組合的實際價格變化才是我們管理的重心。在實踐中,風險管理人員常常將VaR既同理論價值變化進行比較,也同實際價值變化進行比較(事實上,監管機構堅持在回溯測試中,VaR要與交易組合的真實及理論價值變化同時進行比較)。在計算真實價格變化時,一些與市場風險無關的項目必須被剔除出來,這些項目包括手續費收入及一些非市場中間價格的交易(買入與賣出價格的平均)帶來的損益等。
假定VaR的展望期為1天,置信度為X%。如果VaR模型準確無誤,那麼每天的損失超出VaR的概率p=1-X/100。假定我們總共有n個觀察日,在所有的觀察日中有m天損失超出了VaR。假定m/n>p,因為VaR的估計太低,我們在這裡應該拒絕這個模型嗎?將我們的問題表達得更正式一些,我們考慮以下兩種對立假設:
(1)對應任意一天,例外發生的概率為p;
(2)對應任意一天,例外發生的概率大於p。
這裡的例外是指實際損失超出了VaR的估計。從二項式分佈的性質得出,有m或更多天的天數損失超出VaR的概率為
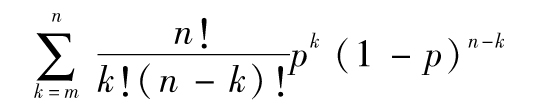
以上計算可通過Excel中的函數BINOMDIST來實現,在統計假設檢驗中,一個經常被選定的置信度為5%,如果在所有觀察日中,有m或更多天實際損失超出VaR的概率小於5%,那麼我們可以拒絕第一種假設,即例外發生的概率為p;當m或更多天實際損失超出VaR的概率大於5%時,我們不能拒絕第一種假設。
【例12-14】 假定我們採用600天的數據來檢測VaR模型,在計算VaR時我們選取了99%的置信區間,在600天觀察數據中我們發現了9個例外,而在這裡我們對例外所發生的個數的期望值為6,這時我們應該拒絕這一VaR模型嗎?通過Excel計算,對應於9個或更多的例外發生的概率為1-BINOMDIST(8,600,0.01,TRUE),以上的計算數值為0.152,因此如果採用5%置信區間,我們不應該拒絕模型。但是假如我們發現例外的個數為12,我們計算出的例外個數為12或更多的概率為0.019,這時我們應該拒絕模型。事實上,當例外個數超出11時我們就應該拒絕模型(例外個數為10或更多的概率大於5%,但例外個數為11或更多的概率小於5%)。
當例外個數m小於例外的期望值時,我們可以採取一個類似的方法來檢驗例外發生的真正概率是否為1%(在這時,我們的對立假設為例外發生的概率小於1%)。此時有m個或更少例外發生的概率為
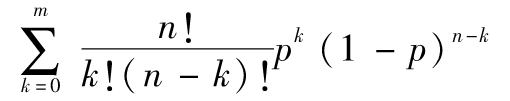
這一數值要與5%閾值來進行比較。
【例12-15】 假定我們採用600天的數據來檢測VaR模型,在計算中我們選用99%的置信程度,在600天觀察數據中我們只發現了1個例外,這一數值遠低於例外的期望值6,這時我們應該拒絕VaR模型嗎?用Excel計算有1個或沒有例外發生的概率為BINOMDIST(1,600,0.01,TRUE)。
以上的計算數值為0.017,因此如果採用5%的置信區間,我們應該拒絕模型,但是,如果例外發生的次數大於或等於2個,那麼我們就不應該拒絕模型。
在這裡我們所考慮的檢驗均為單向檢驗。在例12-14中,我們假定例外發生的概率是1%或者大於1%,在例12-15中我們假定例外發生的概率是1%或者小於1%。Kupiec(1995)開發出一個很有效的雙向檢驗[1](two-tailed test)方法。假定在VaR中例外發生的概率為p,而在n個觀察日中例外發生了m次,變量
-2ln[(1-p)n-mpm]+2ln[(1-m/n)n-m(m/n)m]
(12-11)
應該服從具有一個自由度的chi-平方分佈(chi-square distribution)。當例外發生的次數很高或者很低時,由式(12-11)所計算的統計量會較大。在一個自由度的chi-平方分佈中,統計量大於3.84的概率為5%,因此,當式(12-11)所計算出的值大於3.84時,我們就可以拒絕模型。
【例12-16】 假設在以上兩個例子,我們採用600天的數據來檢驗VaR模型,VaR的置信度仍為99%,當例外出現的次數小於等於1或者大於等於12時,由式(12-11)計算出的統計量大於3.84,因此當2≤m≤11時,我們接受VaR模型,否則,我們拒絕模型。
一般來講,當VaR置信度增大時,回溯測試的難度也會提高。因此,有觀點認為,應使用相對較低的置信區間來計算VaR,以方便進行回溯測試,然後再使用極值理論(見第13章)來得到足夠高的置信度。
聚束狀態
除了例外發生的頻率這個問題外,我們還要討論聚束狀態(bunching)。如果交易組合的每天價值變化是獨立的,那麼例外的發生應該比較均勻地分佈在回溯測試的區間之內。在實踐中,我們發現例外的發生往往聚束在一起,這說明了連續交易日之間的損失分佈並非獨立。一種檢測聚束狀態的方法是採用由Christofferson(1998)提出的統計量[2]
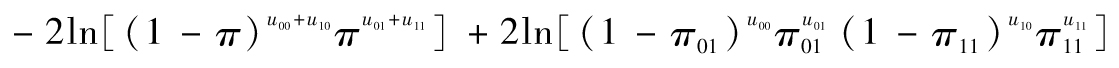
其中uij為在某天我們處在i狀態而在第二天處在j狀態產生的次數。當聚束狀態不存在時,以上定義的統計量服從有一個自由度的chi-平方分佈,這裡狀態0定義為某一天沒有例外發生,而狀態1定義為在某一天有例外發生,再有
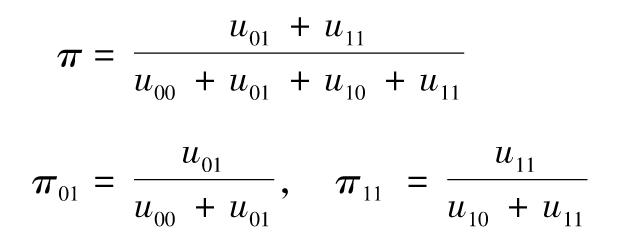
[1] See P. Kupiec, “Techniques for Verifying the Accuracy of Risk Management Models,” Journal of Derivatives 3(1995):73-84.
[2] See P. F. Christoffersen, “Evaluating Interval Forecasts,” International Economic Review 39(1998):841-862.
小結
計算在險價值(VaR)是為了能夠做出以下陳述:“在X%的把握下,在時間段T內,我們的損失不會超出V。”這裡的變量V就是所謂的VaR,X%為置信度,T為展望期。VaR已經成為一個非常流行的風險測度。另外一種更具有良好特性的測度是預期虧空(ES),這一測度的含義為在損失大於VaR的條件之下損失的期望值。在第18章中我們將會解釋,目前監管機構正將市場風險的測度由VaR向ES過渡。
當交易組合價值變化服從正態分佈時,可以很容易地根據T內投資組合價值變化的平均值和標準差來計算VaR和ES。再有,當每天投資組合價值的變化相互獨立並且服從均值為0的正態分佈時,N天的VaR(ES)值可由1天的VaR(ES)乘以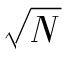 而求得。當每天的變化相互獨立的條件不滿足時,我們可以採用另外一個較為複雜的公式來將1天的VaR轉換為N天的VaR。在實踐中,損失分佈通常比正態分佈具有更肥大的尾部,冪律是一種使用經驗數據對損失分佈的尾部建模的方法,該方法的理論基礎是極值理論,我們將會在第13章中介紹這一方法。
而求得。當每天的變化相互獨立的條件不滿足時,我們可以採用另外一個較為複雜的公式來將1天的VaR轉換為N天的VaR。在實踐中,損失分佈通常比正態分佈具有更肥大的尾部,冪律是一種使用經驗數據對損失分佈的尾部建模的方法,該方法的理論基礎是極值理論,我們將會在第13章中介紹這一方法。
假定一個交易組合由一定數量的子交易組合構成,一個交易組合對於第i個子交易組合的邊際VaR或ES等於交易組合的VaR或ES對於這一子交易組合規模的偏導數。某個子交易組合的遞增VaR或ES等於這個子交易組合對於整個VaR或ES的遞增效應。採用歐拉公式我們可以將VaR或ES按子交易組合的持倉分解為不同成分。成分VaR或ES的總和等於整體VaR或ES。對於一個較大的交易組合,如果每一個成分相對較小,那麼每個成分VaR或ES與遞增VaR近似相等。
回溯測試是風險管理中的一項重要活動。回溯測試是為了檢驗某風險測度應用於歷史數據時表現如何。對VaR的回溯測試較為容易。如果例外發生(即實際發生的損失超出了VaR的值)的比例過高或過低,則意味著VaR模型可能存在缺陷。我們可以利用統計檢驗來判別是否應接受或拒絕某個VaR模型。我們將在第15章中看到,監管機構設定了銀行計算市場風險資本金時所用的VaR乘積因子規則。如果發現銀行的VaR在過去的250天回溯測試中表現欠佳,則監管機構有權增加乘積因子的值。
延伸閱讀

練習題
12.1 VaR與ES的區別是什麼?同VaR比較,ES在理論上的優勢是什麼?
12.2 什麼是譜函數型風險測度?一個譜函數型測度必須滿足什麼樣的條件才可以使得第12.5節中的次可加性條件成立?
12.3 一個基金經理的公告聲明,其管理的基金是1個月展望期的95%的VaR等於投資組合價值的6%,假設你在基金中有10萬美元的投資,你將如何理解基金經理公告?
12.4 一個基金經理的公告聲明,其管理的基金1個月展望期的95%的ES等於投資組合價值的6%,假設你在基金中有10萬美元的投資,你將如何理解基金經理公告?
12.5 假設某兩項投資中的任何一項都有0.9%的可能引發1000萬美元損失,而有99.1%的可能引發100萬美元損失,這兩項投資相互獨立:
(a)對應於在99%的置信水平,任意一項投資的VaR是多少?
(b)選定99%的置信水平,任意一項投資的ES是多少?
(c)將兩項投資迭加在一起所產生的投資組合對應於99%置信水平的VaR是多少?
(d)將兩項投資迭加在一起所產生的投資組合在99%置信水平的ES是多少?
(e)請說明此例中的VaR不滿足次可加性條件,但是ES滿足次可加性條件。
12.6 假定某交易組合的每天價值變化服從正態分佈,分佈的期望值為0,標準差為200萬美元:(a)1天展望期的97.5%VaR為多少?(b)5天展望期的97.5%VaR為多少?(c)5天展望期的99%VaR為多少?
12.7 如果每天價值變化的一階自相關係數等於0.16,對於練習題12.6中(b)和(c)的答案應要進行什麼樣的修改?
12.8 如果某交易組合由若干資產組成,請詳細解釋邊際VaR、遞增VaR以及成分VaR之間的區別。
12.9 假定我們採用1 000個歷史數據來對VaR模型進行回溯測試,VaR所採用的置信度為99%,在觀察日中我們共發現了17個例外,選用5%的置信水平,我們是否應該拒絕模型?在測試中請採用單向檢測。
12.10 請解釋聚束狀態的含義。
12.11 請證明式(12-5)。
12.12 交易組合在1個月內的變化服從正態分佈,均值為0,標準差為200萬美元,計算98%置信度下,3個月展望期的VaR和ES。
作業題
12.13 假定某兩項投資的任何一項都有4%的概率會引發1000萬美元損失,有2%的概率引發100萬美元損失,有94%的概率盈利100萬美元,兩項投資相互獨立:
(a)對應於95%的置信水平,任意一項投資的VaR是多少?
(b)選定95%的置信水平,任意一項投資的ES是多少?
(c)將兩項投資迭加在一起所產生的投資組合對應於95%置信水平的VaR是多少?
(d)將兩項投資迭加在一起所產生的投資組合對應於95%置信水平的ES是多少?
(e)請說明此例的VaR不滿足次可加性條件,但是ES滿足次可加性條件。
12.14 假定一個交易組合的每天價值變化的一階自相關係數為0.12,由1天的VaR乘以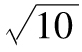 而產生的10天的VaR為200萬美元,將自相關考慮在內時,VaR的最佳估計為多少?
而產生的10天的VaR為200萬美元,將自相關考慮在內時,VaR的最佳估計為多少?
12.15 假設我們採用1 000天數據來對VaR進行回溯測試,VaR所採用的置信水平為99%,在1000天數據中我們觀察到15個例外,在5%置信水平下我們是否應該拒絕VaR模型?在檢驗中請採用Kupiec雙向檢驗。
12.16 交易組合在3個月內的變化服從正態分佈,均值為50萬美元,標準差為300萬美元,計算在99.5%置信度下,3個月展望期的VaR和ES。
12.17 一個交易組合在1個月內損失超過1000萬美元的概率為5%:
(a)假設組合價值變化服從均值為0的正態分佈,1個月展望期的99%置信度的VaR是多少?
(b)假設冪律成立且α=3,1個月展望期的99%置信度的VaR是多少?
第13章
歷史模擬法和極值理論
在這一章中,我們將介紹一種計算市場在險價值(VaR)和預期虧空(ES)最常用的歷史模擬法(historical simulation)。歷史模擬法採用市場變量日間變化的歷史數據來直接估計交易組合從今天到明天的價值變化的概率分佈。
在描述歷史模擬法的機制之後,我們將介紹幾種如何提高計算準確性的方法。我們還會討論壓力VaR(stressed VaR)和壓力預期虧空(stressed ES)。這兩項指標被監管機構用於市場風險監管資本金的計算。最後,我們將討論極值理論。極值理論可以改進對VaR和ES的估計,並用來處理對置信水平要求比較高的情況。
本章講述的所有模型都通過一個由4個股票指數組成的投資組合來講解。這些指數的歷史數據和VaR及ES計算過程可以在本書的網站下載:www-2.rotman.utoronto.ca/~hull/RMFI/VaRExample。
13.1 方法論
歷史模擬法以歷史數據為依據來預測將來。假設,我們採用過去501天的歷史數據來計算1天展望期對應於99%置信水平的VaR(這裡選擇的展望期及置信水平是市場風險管理過程中一種典型的選擇,在實際計算中常常流行採用501天的歷史數據,並由此產生500個情景)。
歷史模擬法的第一步是選定影響交易組合的風險源,這些風險源可能是匯率、股價、利率等,然後我們需要收集這些風險源在過去最近501天的數據,通過這些數據我們可以得出從今天到明天市場變量的500種不同變化情景。我們將數據開始的第1天記為D0(day 0),數據開始的第2天記為D1(day 1),依此類推。情景1(scenario 1)是指由D0到D1所對應數據的變化比率;情景2是指由D1到D2所對應數據的變化比率,依此類推。對於每一個情景,我們可以計算從今天到明天的交易組合的價值變化,由此我們可以得出交易組合日損失(即收益為負)的概率分佈圖,分佈中所對應的99%的分位數是500個計算數值中第5個最壞的損失,VaR的估計值是第99個百分比分位數所對應的損失。[1]假如市場變量的變化是從過去500天提取出來的,這些變量的變化代表從今天到明天變化的不同可能,那麼我們可以有99%的把握肯定,交易組合所對應的損失會小於VaR的估計值。ES是損失分佈中1%的尾部分佈的平均損失。VaR是第5個最大損失值,因此,ES的估計值是比VaR更大的損失的平均值(即第4個最大損失值)。[2]
採用代數符號描述這一過程,我們將某市場變量在第i天所對應的數值記為vi,假定今天為第n天,歷史模擬法產生的市場變量在明天所對應的第i個情景為

對於某些變量,如利率、信用價差和波動率,考慮市場變量的實際變化而不是百分比變化,那麼式(13-1)變為
vn+vi-vi-1
為了簡化討論,在本章的其餘部分中,我們將假設歷史模擬基於潛在市場變量的百分比變化。
13.1.1 過程說明
為了說明計算過程,假定一個投資者在2008年9月25日持有一個價值為1000萬美元的投資組合,組合中有4個股票指數:美國道瓊斯工業指數(DJIA)、英國富時100指數(FTSE 100)、法國巴黎40指數(CAC 40)以及日本日經225指數(Nikkei 225)。每個指數在2008年9月25日的取值如表13-1所示,讀者可以在作者網站上下載含有這4個指數過去501天收盤價格的歷史數據及計算VaR的Excel表單,見www-2.rotman.utoronto.ca/~hull/RMFI/VaRExample,[3]本節中用的計算可以在工作表1~3中找到。
表13-1 用於演示VaR計算過程的投資組合

因為我們考慮的是一個美國的投資者,所以FTSE 100、CAC 40和Nikkei 225這些指數都應該以美元計價。例如2008年8月10日,FTSE 100為5 823.40點,而匯率為1英鎊元兌換1.891 8美元。這意味著,以美元計價的指數為5 823.40×1.891 8=11 016.71。表13-2顯示了以美元計價的指數數據的一部分。
表13-2 採用歷史模擬法計算VaR所需要的股票指數數據 (美元)
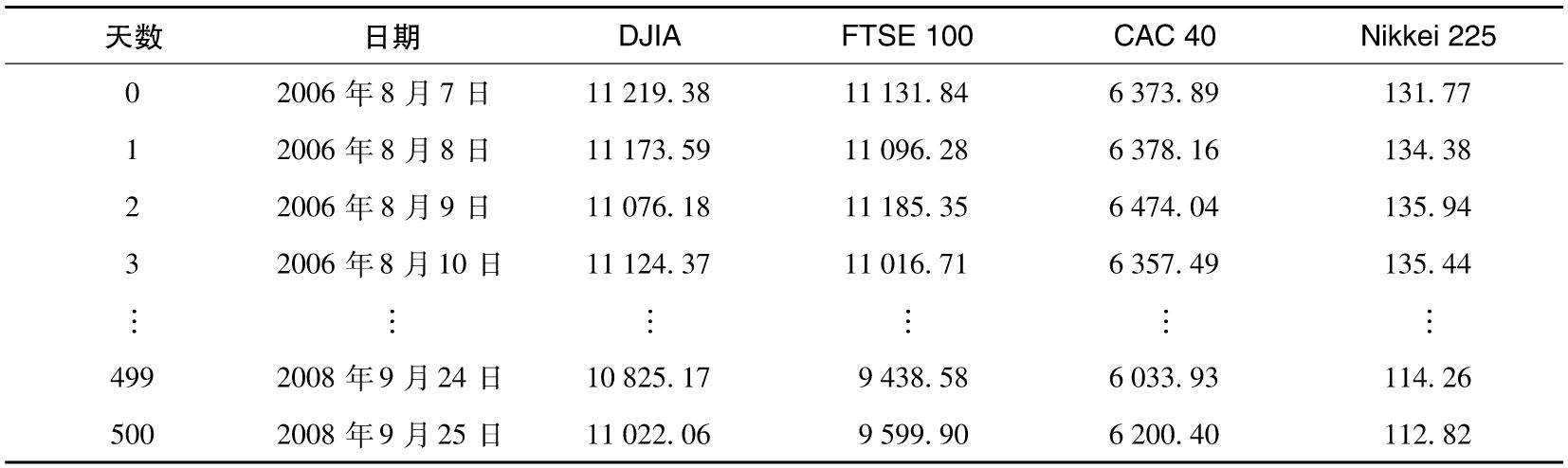
2008年9月25日是檢驗股票投資表現非常有意思的一天。2007年8月開始的信用危機已經持續了1年,股票價格持續下跌了幾個月。在這期間,波動率增大,雷曼兄弟在10天前已經申請破產,美國財政部的7000億美元受困資產救助資金(trouble asset relief program,TARP)還沒有在國會通過。
表13-3顯示了市場變量在2008年9月26日對於選定情景的取值。情景1(表13-3的第1行)是在假定9月25日和26日的市場價格百分比變化等同於2006年8月7日和8日市場價格的百分比變化的情景下,市場變量在2008年9月26日的預測值;情景2(表13-3的第2行)是在假定9月25日和26日的市場價格百分比變化等同於2006年8月8日和9日市場價格的百分比變化的情景下,市場變量在2008年9月26日的另一種預測;依此類推。一般來講,情景i(表13-3的第i行)假定9月25日和26日的市場價格百分比變化等同於歷史數據中第i-1天與第i天的百分比變化(1≤i≤500),情景i定義了市場變量在2008年9月26日的第i種預測。表13-3中的500行就是我們考慮的500個情景。
表13-3 由表13-2的數據所產生的對於2008年9月26日市場變量的不同情景 (所有指數以美元計)
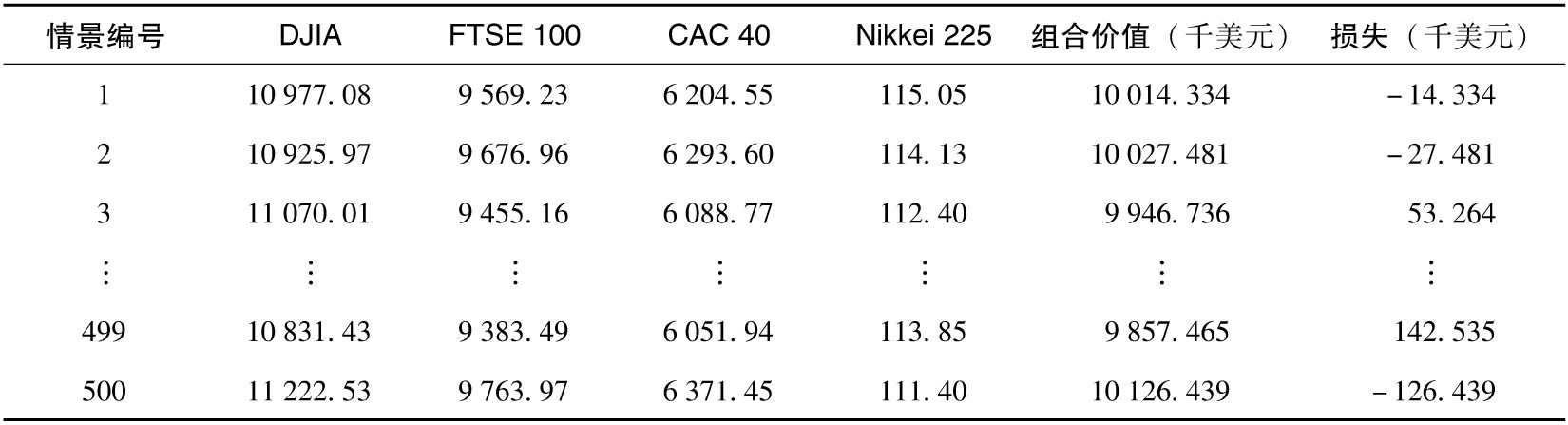
2008年9月25日,DJIA的值為11 022.06,2006年8月7日為11 219.38,2006年8月8日下跌為11 173.59,因此,DJIA在情景1下的預測值為
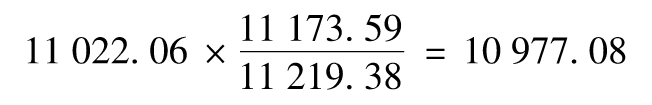
與此類似,在情景1下,FTSE 100、CAC 40、Nikkie 225的預測值分別為9 569.23、6 204.55和115.05。因此在情景1下,組合資產價值為(以千美元計)
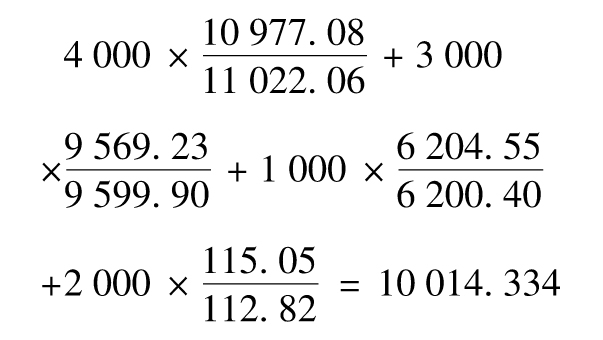
在情景1下,組合收益為14334美元,對於其他情景,我們可以進行類似的運算。在圖13-1中,我們展示了損失分佈的直方圖(柱條代表損失(以千美元為計)出現在450~550、350~450、250~350的次數)。
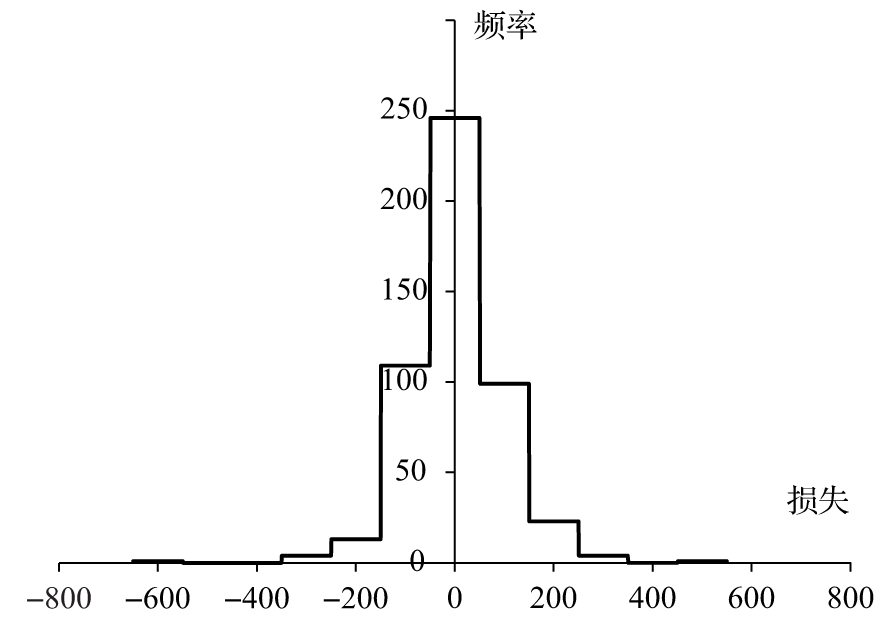
圖13-1 2008年9月25日和26日損失分佈的直方圖(頻率圖)
然後我們將500個不同的損失進行排序,最終結果的一部分被展示在表13-4中,損失最糟糕的情景對應於情景494(其股指變化對應於雷曼兄弟破產那一天的股指變化)。在1天展望期及99%置信區間下,VaR對應於損失中第5個最糟的情景,為253 385美元。
表13-4 對應500個情景損失的排序

如第12.6節所示,10天展望期及99%置信區間的VaR等於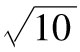 乘以1天展望期及99%置信區間的VaR,10天的VaR等於
乘以1天展望期及99%置信區間的VaR,10天的VaR等於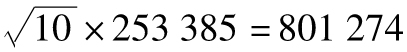 美元。
美元。
在我們的例子中,每天計算VaR時,都應採用最近501天的數據。例如,考慮2008年9月26日(第501天)的情景,我們可以確定所有市場變量所對應的新值,並計算出相應的交易組合的價值。我們可以根據前面描述的過程來求得一個新的VaR。在計算中將採用2006年8月8日~2008年9月26日(第1天到第501天)的數據(我們可以由市場變量的百分比變化來確定500個觀察值,2006年8月7日,即第0天的數據將不再會被使用)。類似地,在下一個交易日,即2008年9月29日(第502天),在計算VaR時,我們將採用2006年8月9日~2008年9月29日的數據;依此類推。
在實際中,一個銀行的交易組合遠比我們在這裡考慮的情形要複雜,銀行的交易組合可能會包括成千上萬的頭寸,銀行的某些頭寸常常是遠期合約、期權和其他衍生產品,而且交易組合本身也在不斷變化。如果一家銀行的交易使得組合變得風險更大,10天展望期的99%VaR一般會增大;如果交易使得組合變得風險更小,10天展望期的99%VaR一般會減小。對於任意一天VaR的計算,我們須假定組合頭寸在兩個交易日之間保持不變。
在計算VaR時,我們考慮的市場變量包括匯率、商品價格和利率等。對於利率,為了能夠對相應的交易組合定價,銀行常常需要不同貨幣的由短期國債、LIBOR和OIS所生成的零息利率期限結構的信息。生成這些期限結構的互換利率和債券收益率就是VaR計算所考慮的市場變量(見附錄B)。任意貨幣的零息曲線都可能會涉及十幾個市場變量。
13.1.2 ES
使用歷史模擬來計算ES時,我們可將觀察到的損失分佈的尾部值取平均。在上面的例子中,最壞的4個情景(以千美元計)是494、339、349和329(見表13-4)。這些情景的平均損失為345630美元,這就是我們對ES的估計。
13.1.3 壓力VaR和壓力ES
前面給出例子中,計算某日的VaR或ES時,我們總是用最近的數據來進行歷史模擬。例如,在第4個例子中,計算VaR或者ES時,我們用到的是最近501天的歷史數據。我們將以此方式計算的VaR和ES稱為當前VaR和當前ES,但實際上,歷史模擬法可採用過去任意時間段的數據。使用波動率較高的時段的數據,預測出的VaR和ES就會較高;使用波動率較低的時段,預測的VaR和ES就會較低。
監管機構已經引入了被稱作壓力VaR和壓力ES的風險測度。要計算這些測度,金融機構首先要尋找一個251天的時間段。在這251天的時間段中,其現有投資組合的VaR或者ES會最大。然後,這251天的歷史數據會扮演前面例子中501天時間段中數據的角色。251天中第0天和第1天之間的市場變化被用來產生情景1,第1天和第2天之間的變化被用來產生情景2,依此類推,這樣總共會生成250個情景。展望期為1天、置信度為99%的壓力VaR是第二大損失和第三大損失之間的中間值。展望期為1天、置信度為99%的ES的估計量是兩個最大損失的平均值。[4]
[1] 在這裡我們有不同的選擇,在這時我們既可以選取第5個最壞或第6個最壞所對應的數值,或者第5個最壞及第6個最壞的平均值,來作為500個抽樣數據中的1%的分位數。在採用Excel計算表的PERCENTILE函數時,假定有n個觀察值,k為某個整數,k/(n-1)分位數是對應於觀察值名列第k+1的數據值,而其他的分位數由線性插值計算求得。
[2] 第1個頁下注指出,可以根據離散數據估算出其他的VaR值。ES也是如此。例如,我們可以對5個最壞的觀察結果取平均值(包括VaR估計值)。另外,我們也可以將第5個最大損失值的權重設為其他4個值權重的一半。這裡提出的建議似乎符合市場慣例。
[3] 為了簡化例子的計算,我們只包括了所有4個股指都開放交易的日期。這解釋了我們為什麼需要2006年8月7日~2008年9月25日這麼長的時間段來提取501個數據。在實際中,在對美國的金融機構進行分析時,我們要對非美國假日的數據進行補充。
[4] 這些不是唯一的方法。VaR可以估計為第三大損失值或第二大損失值(美國聯邦儲備委員會等一些監管機構更喜歡後者)。ES的算法是0.4c1+0.4c2+0.2c3,其中c1、c2、c3是三個最大的損失值,並且c1>c2>c3。
13.2 VaR的精確度
在歷史模擬法中,對於交易組合價值變化分佈的估計是基於過去發生的有限的觀察值,正因為如此,歷史模擬法對分佈的分位數的估計並不是絕對精確的。
Kendall和Stuart(1972)的研究結果給出了由抽樣數據所計算出的概率分佈的分位數的置信區間。[1]假定概率分佈的第q個分位數的估計值為x,這一估計的標準誤差為
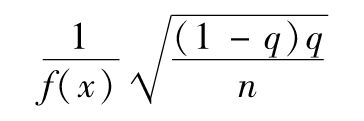
其中n為觀察值的個數,f(x)為對應於損失量為x的損失分佈的密度函數值,這一函數值可以通過將經驗數據與已知分佈進行匹配來估計。
【例13-1】 假如我們採用500個觀察數據來估計損失分佈的99%分位數(第99個分位數),這時n=500,q=0.99。我們可以通過採用某性質已知的標準分佈來對實證數據進行擬合,並由此來求得f(x)的近似值。假定我們選擇正態分佈作為該標準分佈,最佳擬合參數分別為期望值為0,標準差為1 000萬美元。在Excel中,99%分位數所對應數值為NORMINV(0.99,0,1 000)=2 326萬美元,f(x)的取值為
NORMDIST(2 326,0,1 000,FALSE)=2.7
分位數估計值的標準誤差為
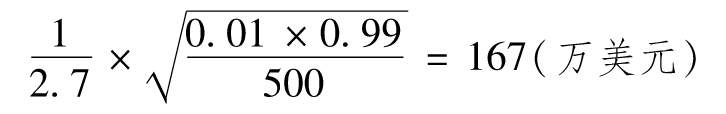
假如採用歷史模擬法所求取的0.99分位數的估計值為2 500萬美元,在95%置信程度下VaR的置信區間為2 500-1.98×167~2 500+1.96×167,即2 170萬~2 830萬美元。
例13-1說明,歷史模擬法所求得VaR的估計的標準誤差較大,隨著置信度的下降,標準誤差也會降低。例如,假定例13-1中VaR所對應的置信程度為95%而不是99%,標準誤差會由167萬美元降至95萬美元。標準誤差隨著抽樣數據數量的增加會有所降低,但標準誤差的大小僅僅與數據量的平方根成反比。如果將例13-1所對應的抽樣數據增加3倍,即由500個增至2 000個,標準誤差僅減小一半,即由167萬美元降至83萬美元。
另外,我們應該認識到歷史模擬法假設市場變量每天變化的聯合分佈是不隨時間的推移而變化的。這一條件在計算VaR過程中往往不完全成立,因此,這對VaR的估計增加了一定的不確定性。
對於表13-1~表13-4的數據,損失的均值(以千美元計)為0.870,標準差為93.698。假定損失服從正態分佈,採用與例13-1類似的計算得出,f(x)為0.000 284,估計的標準誤差(以千美元計)等於

VaR等於253 385美元,相應的95%的置信區間為[220 000美元,280 000美元]。
對於損失估計,採用正態分佈的假設並不一定很好,這是因為損失分佈比正態分佈有更肥大的尾部(表13-1和表13-2中數據的損失分佈的超額峰度為4.2)。要獲得更好的標準誤差估計,f(x)可被假設為服從帕累託分佈(Pareto distribution),我們在第13.5節中將對這一分佈進行討論。
[1] See M. G. Kendall and A. Stuart, The Advanced Theory of Statistics, vol.1, Distribution Theory, 4th ed. (London: Charles Griffin, 1972).
13.3 歷史模擬法的擴展
對非壓力VaR和ES使用歷史模擬法計算的一個關鍵假設是歷史在某種意義上是對將來的一種指導。更為準確地講,即假設由過去幾年數據得出的關於市場變量的實證概率分佈,是對明天市場變量行為的一個指導。不幸的是,市場變量的行為並非平穩的,有時市場波動率會很高,有時會很低。在這一節中,我們將提出第13.1節中的基本歷史模擬法的幾種拓展方法,這些拓展的目的是對歷史數據非穩態的情況進行調整。我們還會介紹一種被稱作自助法的統計方法,該方法可用來確定標準誤差。
13.3.1 對觀察值賦權
在最基本的歷史模擬法中,過去每一天觀察值所對應的權重都相等。更精確地講,當我們採集了n天的日價格變化數據後,我們對於這n個觀察值中任意一個所設定的權重均為1/n。Boudoukh(1998)等建議,對最近的觀察數據應該賦予更大的權重,這可以保證模型充分反映當前市場波動率以及當前市場經濟環境的變化。[1]一種較為自然的權重選擇是使得觀測值的權重隨時間回望期的延伸而呈指數遞減(在第10章中介紹指數加權平均移動模型時,我們曾經對這一方法進行過討論)。情景1所對應的權重(對應於最遙遠的數據)等於λ乘以情景2的權重,情景2所對應的權重等於λ乘以情景3的權重,依此類推。所有權重之和為1,情景i所對應的權重為
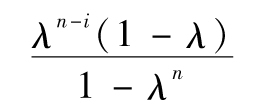
其中n為觀察值的天數。當λ趨向於1時,這一權重趨向於基本歷史模擬法的權重,也就是說權重趨向於1/n(見練習題13.2)。
將所有的觀察值由最壞到最好進行排序,我們可以計算出VaR。由損失最壞的情景開始,我們開始累積計算每一項權重的和,當權重總和達到某指定的分位數界限時,停止計算。例如,假定我們需要計算置信程度為99%的VaR,將觀察數據排序後,我們由最壞的損失開始計算權重和,當權重和剛好超過0.01時,我們停止計算。這時所對應的損失恰恰是置信程度為99%的VaR。對於最佳參數λ的選取,我們可以通過實驗不同的λ,並選擇在回顧檢驗中表現最佳的。與一般的歷史模擬法相比,指數加權方法的缺點在於其應用的有效抽樣的數量較小,但採用一個較大的n是對這一缺陷的補救。事實上,隨著時間的推移,我們並不需要捨棄那些較為陳舊的數據,因此它們對應的權重很低。
表13-5顯示了將這一方法應用到第13.1節中討論的組合所得出的結果,其中λ=0.995(參見作者網站上給出的表單文件中的工作表4和工作表5)。當置信程度為99%時,VaR對應於第3個最糟糕的情景,即282 204美元(而不是第5個最糟情景,即253 385美元),原因是最近的觀察值對應較高的權重,而最大損失的發生時間相對較近。第13.1節的標準計算對所有的觀察值設定的權重為1/500=0.002。最大損失對應於情景494,這一情景所對應的權重為

在損失分佈0.01的尾部中,有0.005 28的概率損失477 841美元,0.002 43的概率損失345 435美元,有0.01-0.005 28-0.002 43=0.002 28的概率損失282 204美元。因此,ES的計算如下

表13-5 對於設有權重的500個情景的損失(由最高到最低排序)
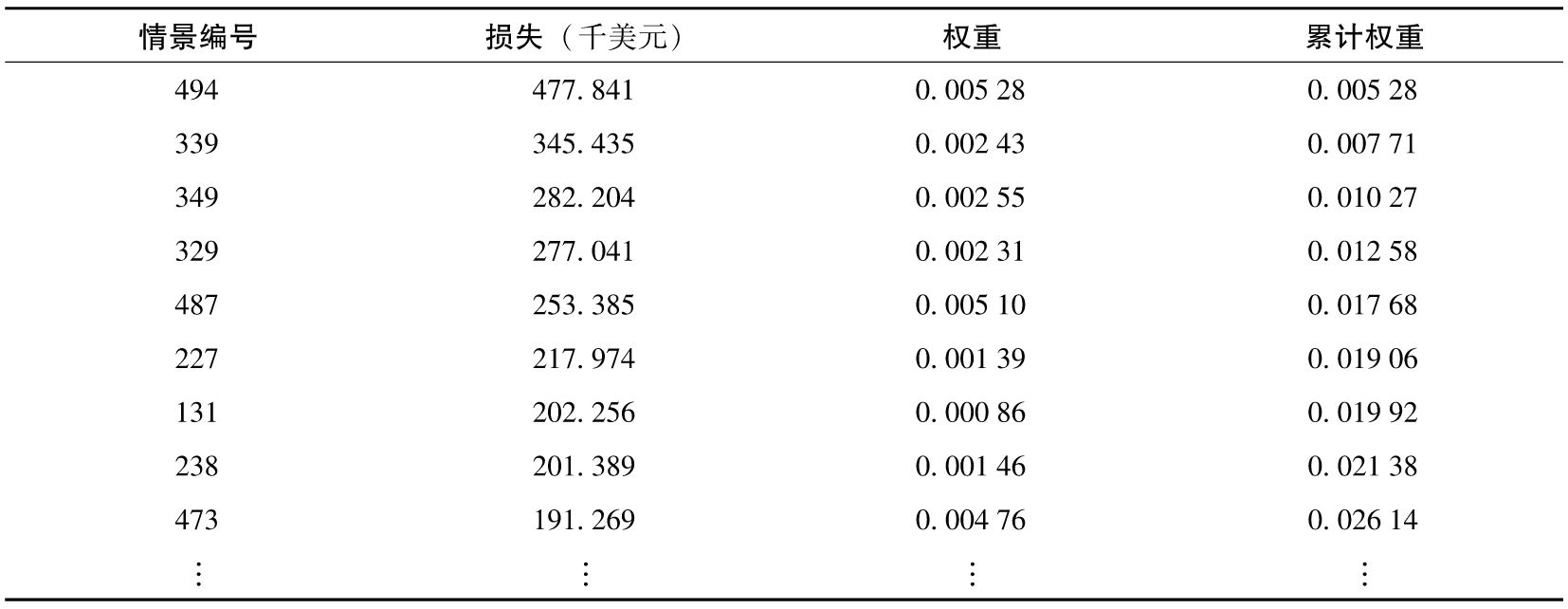
13.3.2 在歷史模擬法中進行波動率的更新
Hull和White(1998)提出了一種在歷史模擬法中引入波動率估計的方法。[2]假定在第i-1天結束時,對於某市場變量的波動率估計為σi,這一數值可以被認為是對第i-1天天末和第i天天末之間的波動率的估計。假定現在為第n天天末,對於市場變量的當前波動率(即今明兩天之間的波動率)估計為σn+1。
假定對某變量,σn+1是σi的2倍。這意味著,我們對某市場變量今天的波動率估計為第i-1天的波動率估計的2倍,因此我們預期今天到明天的變化量也應該是從第i-1天到第i天變化量的2倍。在進行歷史模擬分析時,我們試圖由歷史上第i-1天至第i天的變化,得出由今天到明天變化的一個抽樣,很自然地我們應該將第i-1天至第i天的變化乘以2,一般來講,在實施這一想法時,式(13-1)中的市場變量在第i個情景會變成

在模擬過程中,我們對所有的市場變量均可採取同樣的處理方式。
這一方法很自然及直觀地考慮了波動率的變化,VaR的估計值包括了最新的市場信息,這樣計算出的VaR可能會大於當前交易組合對應於歷史上任意一天情景變化而計算出的損失。Hull和White採用匯率及股指數據證明,這一方法的確比傳統歷史模擬法及指數加權方法要好。
按表13-2中的數據,假定λ=0.94,我們可以使用指數加權移動平均法(EWMA)估計每天的波動率,計算結果被顯示在表13-6中[3](見作者網站提供的表單文件中的工作表6~8)。對於DJIA、FTSE 100、CAC 40和Nikkie 225在2008年9月26日得出的波動率(表中最後一行)與在2008年8月8日得出的波動率(表中第1行)的比率分別為1.98、2.26、2.21、1.15。這些比率作為2006年8月7日~8月8日指數實際變化的乘數因子;類似地,對於以上股票指數,在2008年9月26日得出的波動率(表中最後一行)與在2008年8月9日得出的波動率(表中第2行)的比率分別為2.03、2.33、2.28、1.12,這些比率是作為2006年8月8日~8月9日指數實際變化的乘數因子;其他498天每天變化的乘數因子可以採用類似的方法得出。
表13-6 對於接下來一天,利用EWMA模型計算出的波動率(%每天),λ=0.94
在我們給出的例子中,波動率在歷史數據的結束時達到最高,波動率調整的效果是對500個情景的盈虧增加了變動幅度。表13-7中顯示了將損失由最高到最低進行排序後的部分數據。與表13-4相比,我們看到損失幅度要高得多。1天展望期的99%VaR為602968美元,ES為786855美元。這些值為由標準法計算出的相應值的兩倍多。
表13-7 經波動率調節的500個情景由高到低進行排序後的損失
在這個特例中,股票市場的波動率在2008年餘下的時段仍然很高,1天內指數變化在5%~10%並不少見。在這種情況下,採用波動率調整的方式來計算VaR和ES比標準方法要更好。
13.3.3 調整波動率的更簡便的方法
對我們剛才介紹的方法的一種簡化是使用指數移動加權法對第13.1節標準法中模擬計算出的連續情景下損失的標準差進行監測。表13-3中的最後一列顯示了損失。在作者網頁提供的表單文件中的工作表9和工作表10給出了相關計算。針對第i個場景的調整後的損失等於由標準法計算出的損失乘以第500個場景(最後一行)的標準差的估計值與第i個場景的標準差的估計值的比率。相比對多個市場變量的波動率進行逐一更新,此方法非常簡潔,並且具有將相關性的變化及波動率的變化隱含考慮在內的優點。表13-8顯示了本例中損失的標準差以及經調整後的損失(與以往相同,第一天損失的方差仍然設為整個500天樣本的方差,EWMA模型使用的λ等於0.94)。我們可以看到,較晚期場景的損失的標準差估計遠遠高於早期場景。場景1,2,3,…中的損失分別被乘以2.203,2.270,2.335,…
表13-8 模擬損失的波動率的監測結果
表13-9顯示了經調整後的損失排序後的結果。結果與表13-7中的相似(但得到這裡的結果要簡單得多)。1天展望期的99%置信度的VaR是627 916美元,ES為777 545美元。
表13-9 500個情景經調整後的損失(按從大到小的順序)
13.3.4 自助法
自助法(bootstrap method)是基本歷史模擬法的一種變形,其目的是計算VaR(非壓力VaR或壓力VaR)值本身的置信區間。[4]在這種方法中,我們首先需要按傳統的手段,以歷史數據的變動為基礎,來計算出交易組合的價值變化,然後我們對變化數據進行放回抽樣(sample with replacement),並由此來產生新的抽樣數據。對每一組新的數據,我們都要計算相應的VaR,95%VaR的置信區間估計恰好是介於由新產生數據所計算出的VaR的分佈中第2.5個分位數及第97.5個分位數所界定的範圍。
例如,假定我們有500個數據,我們可以採用放回抽樣的形式,對數據進行抽樣50萬次,由此我們可以產生1000組500天的數據,對於每一組數據我們可以進行VaR運算,並按從小至大的順序進行排列,假如,名列第25位的VaR值為530萬美元,名列第975位的VaR值為890萬美元,因此對應於95%置信水平的置信區間為530萬~890萬美元。通常來講,由自助法所計算出的置信區間範圍要小於由第13.2節中的方法所給出的範圍。
[1] See J. Boudoukh, M. Richardson, and R. Whitelaw, “The Best of Both Worlds: A Hybrid Approach to Calculating Value at Risk,” Risk 11 (May 1998):64-67.
[2] See J. Hull and A. White, “Incorporating Volatility Updating into the Historical Simulation Method for Value at Risk,” Journal of Risk (Fall 1998):5-19.
[3] 方差序列的初始值取決於我們做出的選擇。我們這裡所採用的初始方差等於整個取樣樣本的方差。
[4] See P. Christoffersen and S. Goncalves, “Estimation Risk in Financial Risk Management,” Journal of Risk 7, no.3(2007):1-28.
13.4 計算問題
歷史模擬法牽扯對金融機構整個交易組合的價值的多次重複計算(在我們的例子中是500次),這些計算會相當耗時,當交易組合中的某些產品需要使用蒙特卡羅模擬來估價時更是如此,因為這實際上是嵌套模擬(simulation within simulation):每次對歷史情景的模擬都會再引入蒙特卡羅模擬。
為減少計算時間,金融機構有時會使用delta-gamma近似方法。這一方法在第8章中有過介紹。考慮一個產品,其價格P依賴於單一市場變量S。由S的變化ΔS而引起的P的變化ΔP可近似估計為

其中δ和γ分別是P對於S的delta和gamma。希臘值δ和γ總是已知的,因為每天對產品進行盯市計價時,會計算這些值。因此上式可以在歷史模擬中,近似地計算由於S的變化而引發的交易價值的變化。
當產品的價值依賴於多個市場變量Si(1≤i≤n)時,式(13-3)變為
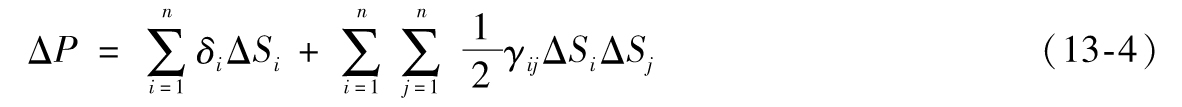
其中δi和γij分別為
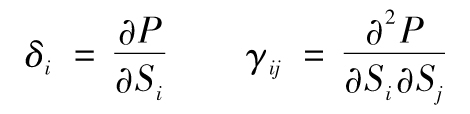
13.5 極值理論
在第10.4節中,我們介紹了冪律,並且解釋了由冪律出發如何對不同分佈的尾部進行估計。在此我們將討論冪律的理論基礎,並且給出比第10.4節更為複雜的估計過程。描述尾部分佈這一學科的理論被稱為極值理論(extreme value theory,EVT)。在這一節中,我們將討論如何應用極值理論來改善我們對於VaR或ES的估計,以及如何將極值理論應用於高置信水平的VaR的估計,極值理論可以使得對實證分佈(empirical distribution)的尾部的外推變得更加光滑。
13.5.1 主要結果
Gnedenko在1943年證明了極值理論的一個主要結論,[1]這一結論可以描述多種概率分佈的尾部的狀態。
假定F(v)為變量v的累積分佈函數(例如,在一段時間內組合的損失),u為v的右端尾部的一個數值,v介於u與u+y(y>0)之間的概率為F(u+y)-F(u),v大於u的概率為1-F(u),定義Fu(y)為在v>u條件下,v介於u與u+y之間的條件概率,即
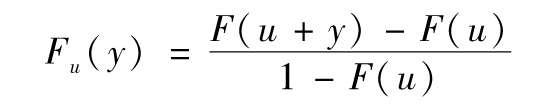
變量Fu(y)定義了右端尾部的概率分佈,即在v>u條件之下,變量v超出u的累積概率分佈。
Gendenko的結果闡明,對於多種概率分佈F(v),分佈Fu(y)(隨著u的增加)趨向於廣義帕累託分佈,廣義帕累託分佈的累積分佈函數為
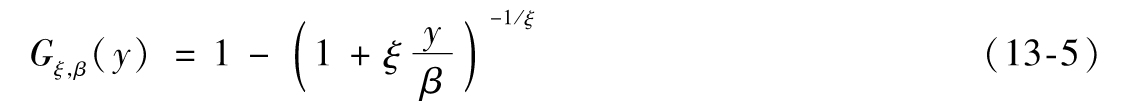
這一分佈中的兩個參數ξ、β必須通過數據來進行估計,參數ξ是有關分佈的形狀,這一參數決定了尾部分佈的肥瘦(heaviness),參數β是分佈的比例因子。
當變量v服從正態分佈時,ξ=0。[2]當尾部分佈變得越來越肥(重)時,對應的ξ值也越來越大。對於大多數金融數據而言,ξ為正並且介於0.1和0.4之間。[3]
13.5.2 參數ξ及β的估計
我們可以採用最大似然法來估計參數ξ及β(見第10.9節),將式(13-5)對y求導,我們可以得出概率分佈的密度函數gξ,β(y),即

首先我們選定數值u(這一數值可與實證分佈中的95%的分位數較為接近),然後將v的觀察值從大到小進行排序,我們要關注的是那些滿足v>u的觀察值。假定在所有觀察值中有nu個抽樣大於u,我們將這些觀察值命名為vi(1≤i≤nu)。根據式(13-6),假定ξ≠0,這裡的似然函數為
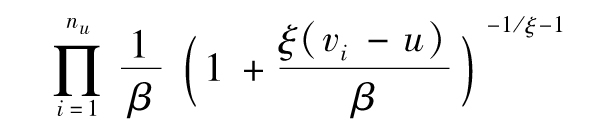
對以上函數求極大值與對其對數求極大值等價,以上函數的對數為
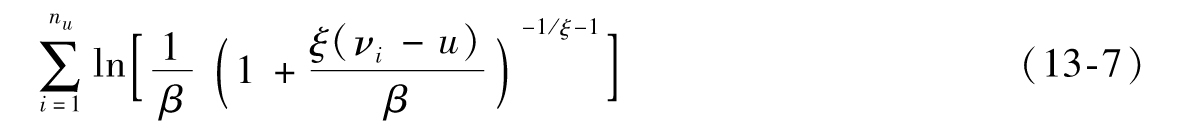
我們可以採用標準的數值程序來求取ξ及β,以使得以上表達式達到極大。Excel提供的Solver程序能給出很好的結果。
13.5.3 對尾部分佈估計
在v>u條件下,v>u+y的概率分佈為1-Gξ,β(y);v>u的概率分佈為1-F(u),因此v>x(x>u)的無條件概率分佈為
[1-F(u)][1-Gξ,β(x-u)]
如果n為觀察值的總數量,由實證數據所得出的對於1-F(u)的估計值為nu/n,因此v>x的無條件概率為

13.5.4 與冪律的等價性
令u=β/ξ,式(13-8)可以簡化為
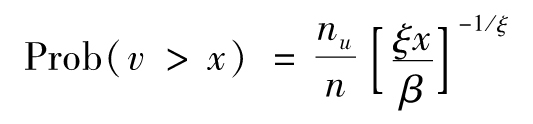
即
Kx-α
其中
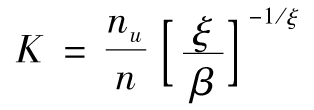
及α=1/ξ,以上過程證明了式(13-8)與第10.4節中的冪律等價。
13.5.5 左端尾部
截至目前,我們只討論了v的概率分佈的右端。如果我們對分佈的左端感興趣,則可以採用-v而不是v來計算。例如,假定一家石油公司已經採集了每天石油價格百分比變化的數據,並想求得1天內、99.9%概率下,石油價格的下跌不會被超出的數量。該數量可以從石油價格增長的左端概率分佈中得出。在分析中,石油公司可以改變每個數據的符號(描述價格增長的數據會變為下跌數據),並採用以上的辦法來進行分析。
13.5.6 計算VaR和ES
為了計算對應於置信水平為q的VaR,我們需要對以下方程求解
F(VaR)=q
因為F(x)=1-Prob(v>x),由式(13-8)得出
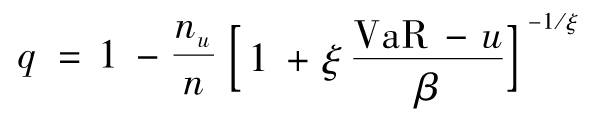
因此
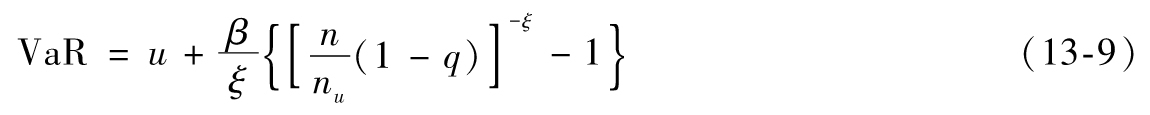
預期虧空如下

[1] See D. V. Gnedenko, “Sur la distribution limité du terme d’une série aléatoire,” Annals of Mathematics 44(1943):423-453.
[2] 當ξ=0時,廣義帕累託分佈形式為Gξ,β(y)=1-exp(-y/β)。
[3] 由式(13-5)所定義的分佈在k≥1/ξ時,v的分佈的k階矩E(vk)為無窮大;正態分佈的所有階矩均為有限;當ξ=0.25時,分佈的矩只有前三階為有限;當ξ=0.5時,分佈的矩只有第一階為有限,等等。
13.6 極值理論的應用
考慮表13-1~表13-4中的數據。當u=160時,nu=22(即有22個情景損失大於160,以千美元計),表13-10顯示了對於β=40和ξ=0.3時的計算。這時,由式(13-7)給出的似然函數的對數為-108.37。
表13-10 對於表13-4的極值理論計算,u=160、β=40及ξ=0.3
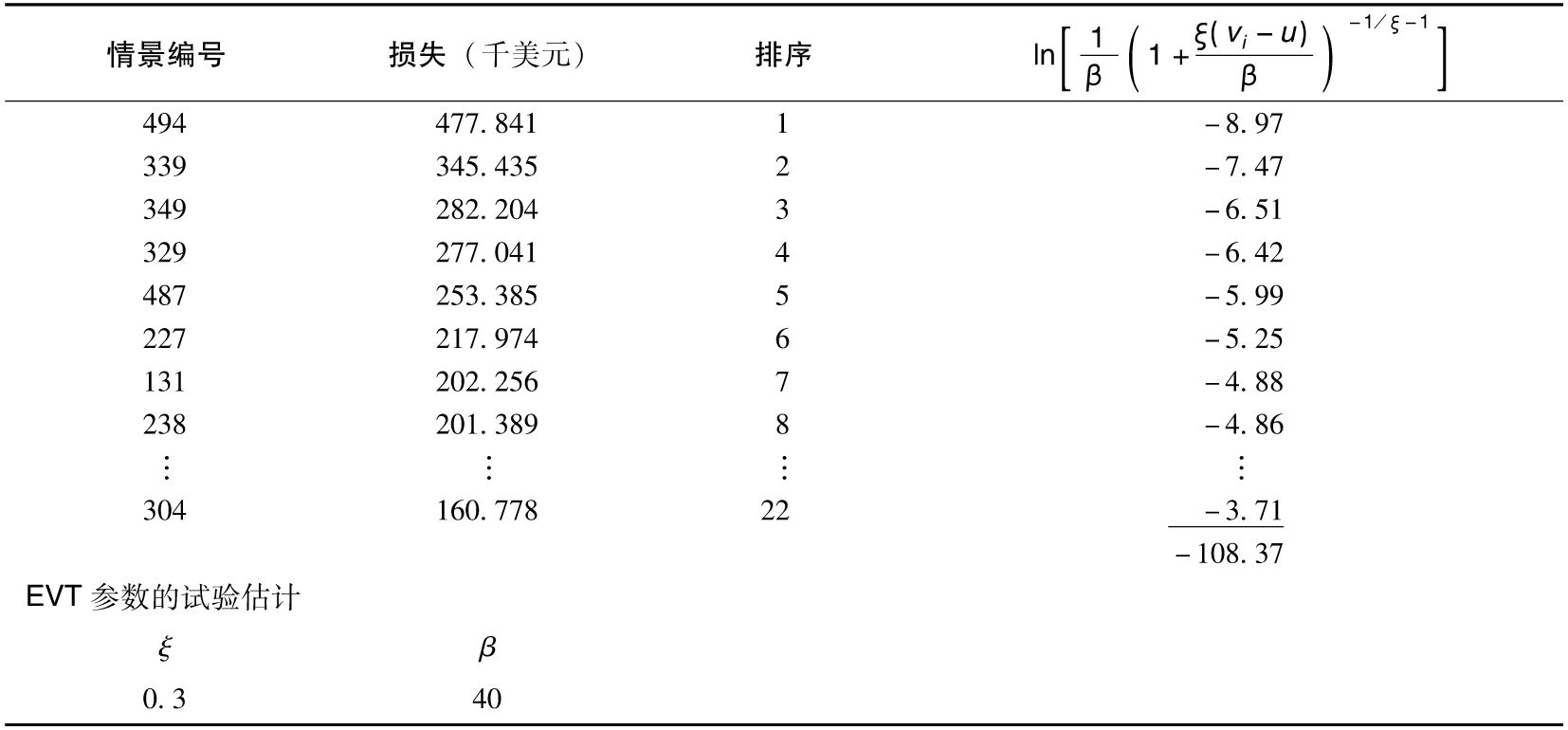
採用Excel計算表中的Solver程序,我們可以求得使得似然函數達到最大值的β和ξ的取值為
β=32.532 ξ=0.436
最大似然函數的對數為-108.21。
假定我們希望估計交易組合在2008年9月25日和9月26日之間,損失大於300 000美元(交易組合價值的3%)的概率,由式(13-8)得出,這一概率為(以下計算式中的金額均以千美元計)
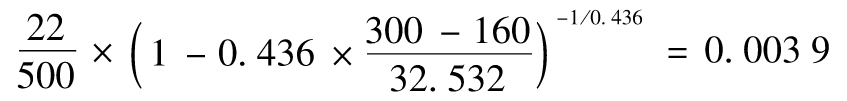
這比從觀察值直接數出來要更為準確。類似地,損失大於500 000美元(交易組合價值的5%)的概率為0.000 86。
由式(13-9)得出,在99%的置信區間下的VaR值為
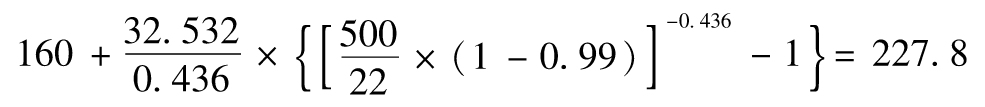
即227 800美元(在本例中,估計的VaR比觀察到的第五大損失少25 000美元)。在99.9%的置信區間下的VaR值為
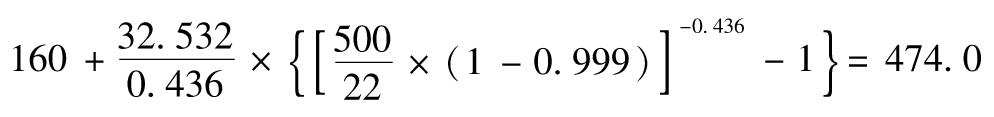
即474 000美元。當置信度進一步增大到99.97%時,VaR值為
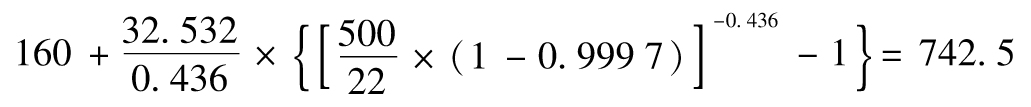
即742 500美元。
式(13-10)可用來提高ES估計的準確度,並可以提升ES估計的置信度。在我們的例子中,當置信水平為99%時,ES為
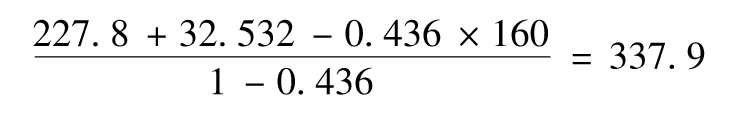
即337 900美元。當置信水平為99.9%時,ES為
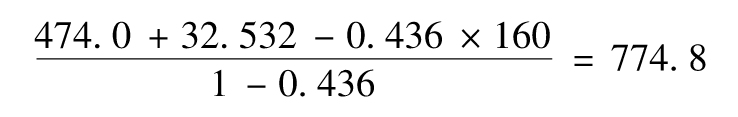
即774 800美元。
極值理論可以用於非壓力或壓力風險測度,也可以比較容易地與第13.3節的波動率調節過程結合起來使用(見練習題13.11)。它還可以與第13.3節討論的數據加權方法結合使用。這時,式(13-7)中的求和部分的每一項必須要乘以賦予不同觀察值的權重。
最後一個應用是對第13.2節中99%置信度的VaR值的置信區間進一步優化。在損失大於160的條件下,取值在VaR水平(227.8)的損失概率分佈的概率密度函數由式(13-6)中的gξ,β(y)給出,其值為
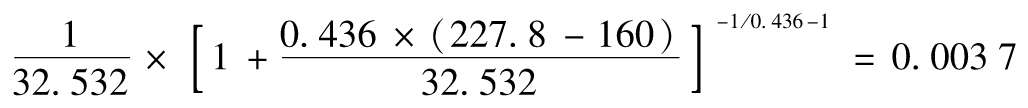
無條件概率密度在VaR水平下的取值為nu/n=22/500與以上數量的乘積,即0.000 16。顯然,這比第13.2節中估計的0.000 284要低,從而使VaR值的置信區間更寬。
有關u的選擇
在計算過程中,我們會遇到一個很自然的問題,那就是如何選定變量u。雖然我們常常發現ξ和β取決於u,但F(x)的估計值大致相同(練習題13.10考慮了我們討論的例子中將u從160變為150的情景),我們希望將u設定為足夠大,來保證確實考慮了尾部分佈的情形,同時我們還希望將u設定為足夠低,來保證使用最大似然估計時的觀測數據不至於太少。在計算中使用更多的數據會提高對於尾部評估的精度,我們在例子的計算過程中應用了500個數據,理想的做法是應用更多的數據。
一個經驗法則是保證u近似等於實證分佈中的95%的分位數(在我們考慮的數據中,實證分佈中的95%的分位數為156.5)。對ξ和β最佳值進行求解時,我們要保證這些參數為正,如果優化程序將ξ設為負值,這可能是由於:①分佈的尾部不比正態分佈更為肥大;②對參數u的選取不當。
小結
歷史模擬法是計算VaR或ES的一種非常常見的方法。在這一方法中,我們需要構造一段期限內市場變量每天變化的數據庫。模擬計算的第一個抽樣假定市場變量的百分比變化等於數據庫所覆蓋的第一天數據的百分比變化,第二個抽樣假定市場變量的百分比變化等於數據庫所覆蓋的第二天數據的百分比變化,依此類推。對於任意的抽樣,我們可以計算出交易組合價值的變化,最後由交易組合的變化值的概率分佈的分位數,我們可以求得交易組合的VaR。將該分佈尾部的價值變化平均,可以得到ES。
對於一般的歷史模擬法有幾種擴展方法。在其中一種方法中,觀測值的權重隨著時間回望期的延伸而呈指數遞減;在另一種方法中,我們會對歷史數據進行調整,以體現波動率的變化。
極值理論可以使通過歷史數據模擬所得出的交易組合損益的概率分佈的尾部變得光滑。通過這一理論,避免了本節相應頁下注中提到的不確定性,我們可以使求得的VaR或ES能反映整個尾部的形狀,而不是隻與尾部的某些個別損失有關。極值理論也可以用來在置信水平較高時計算VaR或者ES。例如,即使我們只有500天的數據,極值理論仍然可以用於對置信水平為99.9%的VaR或者ES進行估算。
延伸閱讀

練習題
13.1 採用500天的歷史數據來計算VaR需要做什麼樣的假設?
13.2 請證明當λ趨向於1時,第13.3.1節中的權重趨向於基本歷史模擬的權重。
13.3 假定我們由1 000個觀察值得出1天展望期的95%的VaR為500萬美元,將觀察值與標準分佈進行擬合,損失分佈對應於95%分位數的概率密度函數值為0.01,請問估算的VaR的標準誤差為多少?
13.4 在第13.1節中計算出的1天展望期的99%的VaR為253 385美元,利用作者網站上的表單來計算:(a)1天展望期的95%的VaR;(b)1天展望期95%的ES;(c)1天展望期的97%的VaR;(d)1天展望期的97%的ES。
13.5 利用作者網站上的表單及第13.1節的基本方法來計算1天展望期的99%的VaR和ES,假定資金是按等量投資於4個指數。
13.6 對於我們考慮的例子,通過第13.3.1節中對觀察值進行加權所得出的1天展望期的99%的VaR等於282 204美元,ES為400 914美元。將計算過程中的參數λ由0.995變為0.99,利用作者網頁上的表單來計算1天展望期的99%的VaR和ES。
13.7 對於我們考慮的例子,通過第13.3.3節中的對波動率進行更新方法所得出的1天展望期的99%的VaR等於627 916美元,ES為777 545美元。將計算過程中的參數λ由0.94變為0.96,利用作者網站上的表單,計算1天展望期的99%的VaR和ES。
13.8 在第13.6節的極值理論應用中,損失大於400 000美元的概率為多少?
13.9 在第13.6節的極值理論應用中,在97%置信區間下的1天展望期的VaR為多少?
13.10 在第13.6節的極值理論應用中,將u由160變為150,這會對最大似然估計的ξ和β產生什麼影響?這將對1天展望期的VaR和ES產生什麼影響?考慮置信範圍分別為:(a)99%;(b)99.9%的情形。
13.11 對錶13-7中經波動率更新程序處理的以及作者網站上的數據進行極值分析,在分析中假定u=400,ξ和β的最佳擬合值為多少?計算1天展望期,置信度分別為99%和99.9%的VaR及ES。損失大於600 000美元的概率為多少?
作業題
13.12 假定由2 000個數據所得出的1天展望期的97.5%的VaR的估計值為1 300萬美元,假定我們觀測到的日價格變化大致服從正態分佈,分佈的期望值為0,標準差為600萬美元,求取VaR值的99%的置信區間。
13.13 假定在第13.1節所考慮的投資組合的資金分配(以千美元計)如下:DJIA為3 000,FTSE為3 000,CAC 400為1 000,Nikkie 225為3 000,利用作者網站上的表單來計算
(a)第13.1節計算的1天展望期的99%的VaR和ES。
(b)利用第13.3.1節討論的對觀察值進行加權的方法,求取1天展望期的99%的VaR和ES,設λ=0.995。
(c)利用第13.3.2節和第13.3.3節討論的對波動率觀察值進行更新的兩種方法,求取1天展望期的99%的VaR和ES,設λ=0.995(使用指數加權移動平均法時,令初始方差等於整個樣本的方差)。
(d)利用第13.6節討論的極值理論,求取1天展望期的99%的VaR和ES,設數據權重相等。
13.14 極值理論對於第13.3.2節中的波動率調整後的結果的影響是什麼?在計算中請將u設定為350。
13.15 對於第13.3.1節中我們考慮的例子,通過對觀察值進行加權所得出的1天展望期的99%的VaR為282 204美元,ES為400 914美元,將計算過程中的參數λ由0.995變為0.99,利用作者網站上的表單來計算1天展望期的99%的VaR和ES。
13.16 對於第13.3.2節中考慮的例子,通過對波動率進行更新所得出的1天展望期的99%的VaR為602 968美元,ES為786 855美元,將計算過程中的參數λ由0.94變為0.92,利用作者網站上的表單來計算1天展望期的99%的VaR和ES。
13.17 在作者網站上,讀者可以下載2006年3月10日之前的1500天的NASDAQ股指數據,採用以下不同方法來計算2006年3月10日的1天展望期的99%的VaR和ES,設交易組合的投資額為1000萬美元。
(a)基本歷史模擬法。
(b)第13.3.1節中的指數加權方法,參數λ=0.995。
(c)第13.3.2節和第13.3.3節中波動率更新方法,參數λ=0.94(使用指數加權移動平均法時,假定方差的初始值等於整個抽樣的標準差)。
(d)極值理論,在計算中變量u被設定為300。
(e)假定日回報率服從正態分佈,均值為0(請分別採用相等的權重及參數λ=0.94的指數加權移動平均法方法來估計日回報率的標準差)。
討論以上不同方法會產生不同結果的原因。
第14章
市場風險:模型構建法
除了歷史模擬法之外,另外一種計算市場風險指標如VaR和ES的方法被稱為模型構建法(model-building method),或者有時也被稱為方差-協方差法(variance-covariance method)。在這一方法中,我們需要對市場變量的聯合分佈做出一定的假設,並採用歷史數據來估計模型中的參數。
模型構建法非常適用於投資組合的價值變化線性依賴於基礎市場變量(股票價格、匯率、利率等)價值變化的情況。在這種情況下,如果假定基礎市場變量的每日變化為多元正態分佈,則其計算速度將比歷史模擬法快得多。本質上,其基礎是馬科維茨(Markowitz)的關於投資組合管理的先驅性理論(見第1.1節)。投資組合價值變化的概率分佈為正態分佈,由投資組合中標的資產的均值和方差以及產品回報的相關性,我們可以計算出投資組合的均值和方差。
當一個投資組合包括期權和其他非線性衍生產品時,該投資組合在短時間內價值變化的概率分佈就不能再被合理地假定為正態分佈。投資組合的gamma風險敞口導致其價值變化的概率分佈呈現偏態。在這種情況下估算VaR或ES的一種方法是蒙特卡羅模擬。然而,模型構建法與第13章中的歷史模擬法一樣耗費計算時間。
本章提供了理解本書後面解釋的兩個重要模型的背景知識:第一個是標準初始保證金模型(SIMM),用於確定雙邊清算的場外衍生產品的初始保證金要求(見第17章);第二個是在交易賬戶基本審查中用於確定資本的標準化方法使用的模型(見第18章)。
14.1 基本方法論
我們先考慮當投資組合只包含單一股票時如何用模型構建法來計算VaR。假定投資組合只包含價值為1000萬美元的微軟公司股票,在計算中我們選擇10天的展望期,同時假定置信水平為99%,在這裡我們要求出投資組合在10天展望期內、99%置信水平下,損失不能超出的數量。在計算過程中我們首先將展望期選定為1天。
我們假定微軟公司股票的波動率為每天2%(對應於每年的波動率32%),[1]交易頭寸的數量為1 000萬美元,投資組合每天價值變化的標準差為1 000萬美元的2%,即200 000美元。
在模型構建法中,我們往往需要假定在展望期內,市場價格變化的期望值為0,這一假設雖然不是絕對正確的,但也還算合理。同標準差相比,市場變量在一個較小的時間區間內價格變化的期望值相對較小。例如,微軟公司的年回報大約是20%,以1天為計,預期回報大約是0.20/252,約等於0.08%,與此對應的每天價格變化的標準差大約為2%。考慮10天的展望期,預期回報大約為0.08%×10,即0.8%,而10天所對應的回報標準差為 ,即6.3%。
,即6.3%。
截至目前,我們得出微軟公司股票每天價格變化的標準差為200 000美元,並且(以近似意義來講)每天價格變化的均值為0。我們假定價格的變化服從正態分佈。[2]因為N(-2.326)=0.01,所以我們得出在正態分佈下,價格下降大於2.326倍的標準差的概率為1%。另外一種等價的說法是,在正態分佈下,我們有99%的把握肯定價格下降程度不會超過2.326倍的標準差,因此,我們得出1 000萬美元微軟公司股票1天展望期的99%的VaR等於
2.326×200 000=465300(美元)
假定微軟公司股票連續每天之間變化相互獨立,我們可以假設10天的收益率標準差為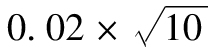 ,10天的收益率為正態分佈,因此微軟公司10天的99%的VaR等於
,10天的收益率為正態分佈,因此微軟公司10天的99%的VaR等於
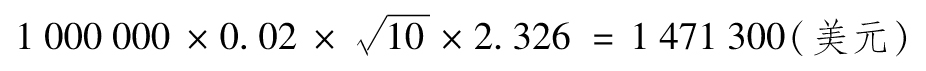
10天的99%的ES可由式(12-2)計算得出,令 ,Y=2.326,且X=0.99。ES的值為1 687 000美元。
,Y=2.326,且X=0.99。ES的值為1 687 000美元。
接下來我們考慮價值為500萬美元的AT&T的股票投資。假定AT&T的每天價格波動率為1%(這對應於每年16%),採用與微軟公司股票類似的計算,我們得出AT&T的每天價格變化的標準差為
5 000 000×0.01=50000
假定價格的變化為正態分佈,1天展望期的99%的VaR等於
50 000×2.326=116 300(美元)
10天展望期的99%的VaR等於
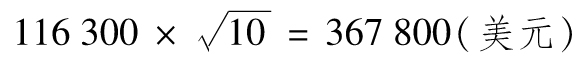
由式(12-2),10天展望期的99%的ES為421 400美元。
14.1.1 兩個資產的情形
接下來我們考慮價值為1 000萬美元的微軟公司股票和價值為500萬美元的AT&T股票的投資組合。我們假定微軟公司及AT&T的股票價值變化服從二元正態分佈,分佈中的相關係數為0.3。由統計學中一個標準的結果得出,如果變量X和Y的方差分別為σX和σY,變量的相關係數為ρ,那麼X+Y的標準差為
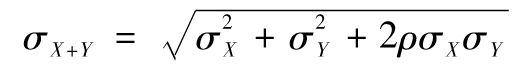
在應用這一結果時,我們令X為微軟公司股票每天的價格變化,令Y為AT&T股票每天的價格變化
σX=200 000, σY=50 000
因此,由兩種股票所組成的投資組合價值的1天變化的標準差為
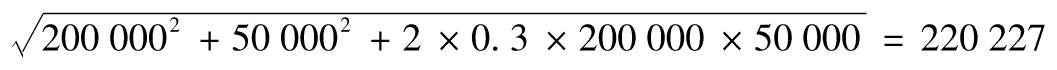
投資組合價值變化的期望值為0,如果我們進一步假設微軟公司和AT&T的收益的聯合分佈是雙變量正態分佈,那麼投資組合的價值變化服從正態分佈。我們得出1天展望期的99%的VaR等於
220 227×2.326=512 300(美元)
考慮10天展望期,σX和σY增加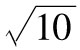 倍,則10天展望期的99%的
倍,則10天展望期的99%的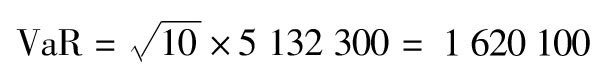 美元。由式(12-2),10天展望期的99%的ES為1 856 100美元,其中
美元。由式(12-2),10天展望期的99%的ES為1 856 100美元,其中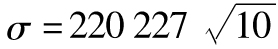 ,Y=2.326,X=0.99。
,Y=2.326,X=0.99。
14.1.2 風險分散的益處
我們以上考慮的例子滿足以下性質:
(1)由單一微軟公司股票組成的投資組合的10天展望期的99%的VaR等於1 471 300美元。
(2)由單一AT&T股票組成的投資組合10天展望期的99%的VaR等於367 800美元。
(3)由微軟公司及AT&T兩種股票組成的投資組合的10天展望期的99%的VaR等於1 620 100美元。
數量(1 471 300+367 800)-1 620 100=219 000美元代表風險分散帶來的好處。如果微軟公司及AT&T的相關係數等於1(完全相關),由微軟公司及AT&T共同組成的投資組合的VaR等於單一微軟公司組合的VaR加上單一AT&T組合的VaR;如果相關係數小於1,就會帶來部分風險的分散化解(diversified away)。[3]同樣的結論對ES也適用。
[1] 如第10.1節所示,在計算VaR時,波動率通常以每天為計量,而在期權定價時,通常以每年為計量,我們可以將每天波動率乘以 ,即大約為16,轉化為每年的波動率。
,即大約為16,轉化為每年的波動率。
[2] 我們可以假定微軟公司股票價格在明天的分佈為對數正態(lognormal),因為1天展望期的時間太短,在這裡對數正態假設與我們以前所做的連續兩天的股價變化服從正態分佈的假設幾乎沒有什麼區別。
[3] 如第12.5節所示,VaR並不一定永遠能帶來風險分散效應。對於非正態分佈,兩個交易組合在合併後所產生的VaR可能會大於兩個交易組合的VaR的總和,而ES沒有此缺點。
14.2 推廣
以上討論的例子是採用線性模型來計算VaR的特例。假定,我們所持有的某投資組合的價值為P,其價值依賴於n個市場變量。根據市場慣例,我們把市場變量稱為風險因子(risk factors),如股票價格、商品價格或匯率(我們會在本章後面考慮利率、信用價差和波動性)。在很大程度上,投資組合的價值變化與風險因子的百分比變化呈線性相關。

其中ΔP為整個投資組合實際的日價值變化,Δxi是一天內第i個風險因子的百分比變化。
參數δi是第8章中解釋的delta風險的變體。持倉頭寸相對於風險因子的delta通常被定義為比率ΔP/ΔS,其中ΔS是風險因子值的微小變化量(所有其他風險因子保持不變),ΔP是投資組合的價值由此產生的變化。我們在這裡使用的參數δi等於ΔP/Δxi,Δxi是第i個風險因子值在百分比上的微小變化(同樣所有其他風險因子保持不變),ΔP是投資組合價值的變化。
如果我們假定式(14-1)中的Δxi服從多元正態分佈,因此ΔP也服從正態分佈。為了計算VaR,我們只需要計算出ΔP的期望值及標準差。基於上一節任意一項Δxi的期望值為0的假設,我們得出ΔP的期望值也為0。
計算ΔP的標準差的方法是前述兩個資產例子的擴展,我們假定σi為第i項資產的日波動率,ρij為資產i及資產j的相關係數,這意味著Δxi的標準差為σi,Δxi和Δxj的相關係數為ρij,將ΔP的方差記為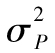 (因為我們考慮的展望期為1天,σi是每天的波動率)。ΔP的標準差是
(因為我們考慮的展望期為1天,σi是每天的波動率)。ΔP的標準差是

該式也可以寫為
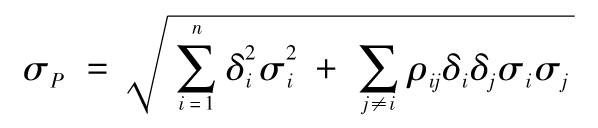
或者
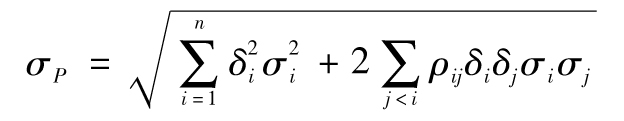
也可以表示為

covij是Δxi和Δxj的協方差,用矩陣形式表示的上式為
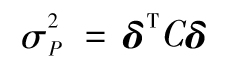
其中,δ是列向量,它的第i個元素是δi,C是方差-協方差矩陣(見第11.3節),δT是δ的轉置。
T天展望期的標準差為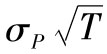 ,因此展望期為置信水平為X%的VaR等於
,因此展望期為置信水平為X%的VaR等於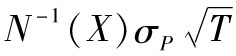 。根據式(12-2),T天展望期、置信水平為x%的ES為
。根據式(12-2),T天展望期、置信水平為x%的ES為
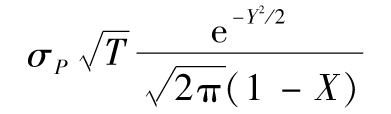
其中Y=N-1(X),且N-1為正態分佈累積函數的反函數(可由Excel中的NORMSINV計算)。
【例14-1】 在前一節所考慮的兩個資產的例子中,投資組合的價值為P,第一個資產(微軟公司)投資了1 000萬美元,第二個資產(AT&T)投資了500萬美元。當以百萬美元計時,δ1=10,δ2=5,並且
ΔP = 10Δx1 + 5Δx2
σ1=0.02,σ2=0.01,ρ12=0.3,則有
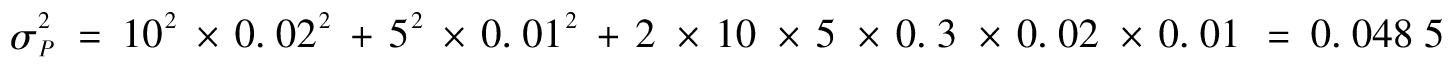
即σP=0.220,這一數量為投資組合每天價值變化的標準差(以百萬美元計),10天展望的99% VaR為 ,即162萬美元,ES為
,即162萬美元,ES為 。
。
也就是186萬美元。這與上一節所計算的結果完全一致。
與馬科維茨的關係投資組合在1天內的回報為ΔP/P,從式(14-2)中得出,組合的日回報的方差為

其中wi = δi/P。當投資組合由n個資產的多頭和空頭頭寸組成,第i個風險因子為第i個資產的價值時,δi是第i個資產的投資價值(如例14-1所示),wi為組合中第i個投資的權重。式(14-2)由馬科維茨的研究給出,直到今天還經常被投資組合經理使用,以將投資組合收益的標準差與單個資產收益的標準差、單個資產收益之間的相關性聯繫起來(請參閱第1.1節)。
14.3 涉及4個投資的例子
根據式(14-2)或式(14-3),我們現在考慮第13.1節中討論的例子。該例涉及一個在2008年9月25日投資400萬美元於道瓊斯工業平均指數(DJIA)、300萬美元於富時100指數(FTSE 100)、100萬美元於巴黎40指數(CAC 40)和200萬美元於日經225指數(Nikkei 225)的投資組合。為了計算,我們採集了截至2008年9月25日500天的歷史數據,讀者可以在作者的網站www-2.rotman.utoronto.ca/~hull/RMFI/VaRExample上下載這些數據和有關計算表單。
表14-1是利用一般方法,即對500個回報數據採用同等權重的方法求得的相關係數矩陣。結果顯示,FTSE 100與CAC 40具有很高的相關性,DJIA與FTSE 100和CAC 40有一定程度的相關性,Nikkei 225與其他指數的相關性較低(甚至與DJIA呈負相關)。表14-2顯示了協方差矩陣。
表14-1 2008年9月25日,對過去500天所有數據設定同等權重所得出的相關係數矩陣

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
表14-2 2008年9月25日,對過去500天所有數據賦予同等權重所得出的協方差矩陣

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
由式(14-3)以及以上方差-協方差矩陣,我們得出投資組合損失的方差為8 761.833(以千美元計),標準差是以上數量的平方根,即93.60,1天的99%的VaR為
2.326×93.60=217.757(千美元)
即217 757美元。1天的99%的ES為
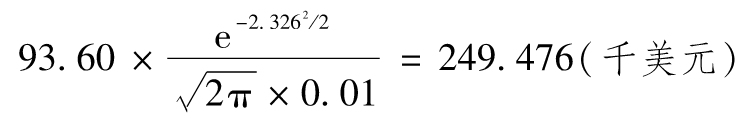
即249 476美元。我們可以將這一結果與由第13章標準歷史模擬法產生的結果(即253 385美元VaR和327 181美元ES)進行比較。
利用EWMA模型
除對所有的市場回報採用同等權重來計算方差-協方差,我們還可以利用指數加權移動平均方法(EWMA),在計算中採用參數λ為0.94。表14-3顯示了通過這種方法得出的方差-協方差矩陣。[1]由式(14-3)以及方差-協方差所給出的組合損失的方差為40 995.765(以千美元計),標準差是以上數量的平方根,即202.474。1天的99%的VaR為
2.326×202.474=471.025
即471 025美元。由式(12-2),1天的ES為539 637美元。以上結果比由等權重所求得結果的兩倍還要高。表14-4和表14-5給出了產生這兩個結果差別的原因。一個由資產多頭頭寸所構成的投資組合的標準差會隨資產回報標準差的增大以及相關係數的增大而增大。表14-4顯示,由EWMA所得出的標準差比由同等權重得出的標準差要高得多。這是因為與緊鄰2008年9月25日前面的一段歷史數據的波動率比500天數據中其他時段的波動率要高得多。比較表14-5和表14-3,我們發現相關係數也比由同等權重得出的相關係數要高得多。[2]
表14-3 利用EWMA模型所求得的2008年9月25日的協方差矩陣,λ=0.94

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
表14-4 利用等權重和EWMA模型所得出的2008年9月25日的波動率(每天%)

表14-5 利用EWMA模型所求得的2008年9月25日的相關係數矩陣

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
[1] 在EWMA方法中,方差最初可以被設定為所有觀察值的方差,但由任意一個合理的初始方差所得出的最終結果都十分接近,而我們只是關心最終的方差結果。
[2] 在市場承壓時,相關性會增大,這一例子說明了這一點。
14.4 對於期限結構的處理
期限結構描述了利率、信用價差和平價波動率等變量。期限結構表明這些變量的值是到期期限的函數。當變量為利率時,期限結構顯示零息利率與其到期期限的關係(有關如何計算零息利率的討論,請參見附錄B)。當變量為信用價差時,期限結構反映了適用於債券或信用違約互換的信用價差與其到期期限的函數關係。當變量為平價波動率時,期限結構顯示了平價期權定價的波動率是其到期期限的函數。[1]
期限結構使模型構建方法更復雜。例如,考慮特定利率的期限結構。公司投資組合中的一種工具可能會在3.32年內產生現金流量,在接下來的短時間內,這一工具的價值變化取決於期限結構上3.32年到期點的情況;另一種工具可能會在4.48年的時點上產生現金流,因此金融機構在期限結構上的該時點也會有風險敞口。3.32年期利率和4.48年期利率將趨於一致,但二者並非完全相關。
顯然,我們不可能對這家金融機構每一種期限的工具都加以考慮。我們將考慮兩種處理期限結構風險的方法:主成分分析和“多重頂點法”(multiple-vertices approach)。對於股票價格、價格和匯率等變量,若變量的值成百分比變化,那麼參數σ就是百分比變化的標準差(如波動率)。在介紹的這兩種方法中,對於這些變量,我們通常考慮實際變化,而不是百分比變化。
14.4.1 主成分分析法
我們在第9.7節中討論了主成分分析法(PCA)的性質。前兩個或三個主因子(PC)說明了在實踐中觀察到的期限結構的大部分變化。第一個因子通常是期限結構的平行移動;第二個因子是期限結構斜率的變化;第三個因子是“彎曲”,即存在期限結構的曲率變化。
處理期限結構的一種方法是,假定1天之內期限結構的變化僅由前兩個或三個主因子引起。我們使用第9章中利率敏感性的例子來說明計算方法。表14-6中的數據是投資組合對利率變動的敏感性。因子載荷和因子得分的標準差在表14-7和表14-8中列出(與表9-6和表9-7相同)。
表14-6 利率1個基點變動所觸發的投資組合價值(以百萬美元計)的變化

表14-7 互換利率的因子載荷
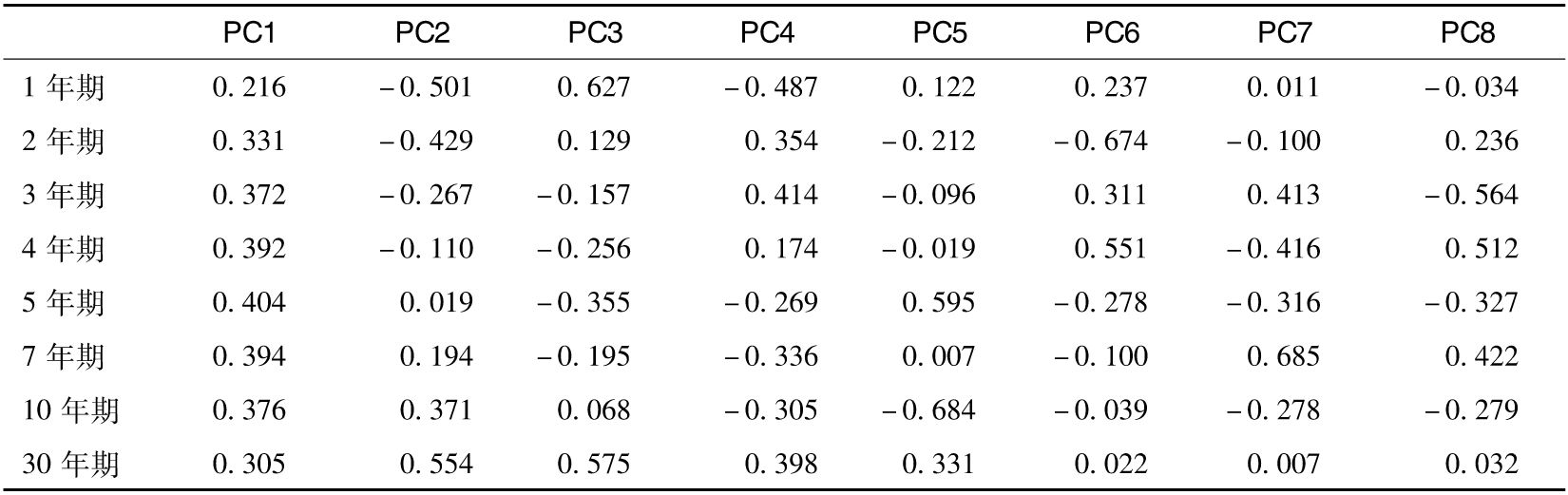
假設前兩個主因子描述了利率變動。投資組合對第1個主因子的敏感度敞口是
10×0.372+4×0.392-8×0.404-7×0.394+2×0.376=+0.05
對第2個主因子的敏感度敞口是
10×(-0.267)+4×(-0.110)-8×0.019-7×0.194+2×0.371=-3.88
均以每個基點的百萬美元為衡量單位。
假設f1和f2是前兩個主因子的因子得分,我們將它們視為每日變化的第一主因子和第二主因子的個數。前兩個主因子導致的投資組合價值在1天之內的變化(以百萬美元計)為
ΔP=0.05f1-3.88f2
主成分分析法中的因子得分相互獨立。表14-8顯示主成分分析法中前兩個因子的標準差分別為17.55和4.77,因此ΔP的標準差為
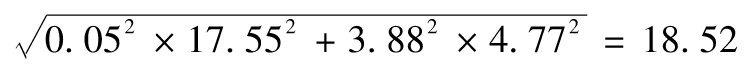
表14-8 因子得分的標準差

假定因子得分服從正態分佈,1天展望期的99% VaR等於18.52×2.326=43.08百萬美元,即4 308萬美元。
注意投資組合對於第1個因子的敏感性較低,而對於第2個因子的敏感性較大。只採用第1個因子(見練習題14.9)進行計算會顯著地低估VaR。
剛才考慮的示例僅對因子載荷表(見表9-7)中的期限有敏感性敞口,可使用內插法計算其他到期期限的敏感性敞口。例如,假設3.5年利率的第1個因子敞口為0.382,第2個因子敞口為-0.188 5,依此類推。
14.4.2 多重頂點法
在度量風險敞口時,衍生工具交易商及其監管者喜歡引入期限結構。我們再次通過利率期限結構來闡述這一點。假設利率期限結構由不同到期期限對應的點構成:3個月、6個月、1年、2年、3年、5年、10年、15年、20年和30年。期限結構是連接這些點的分段線性曲線,如附錄B中所述。通過將一個點移動一個基點,同時保持其他點不變,可以為期限結構上的每個點計算一個delta。我們將以這種方式定義的delta稱為“節點delta”(node delta,使用第9章的術語,又叫“現金局部久期”)。圖14-1顯示了計算5年節點delta時的期限結構變化。其他時點的delta也是類似的計算。當計算最短到期期限(3個月)的delta時,所有小於這一時點的利率都增加一個基點;當計算相對於最長期限(30年)的delta時,所有大於最長期限的利率都增加一個基點(這與附錄B中描述的期限結構的構造方法是一致的)。節點delta的總和為DV01(這是整個期限結構中每個時點的利率平移一個基點的影響)。因此,節點delta是將DV01分為10個組成部分的一種方式。
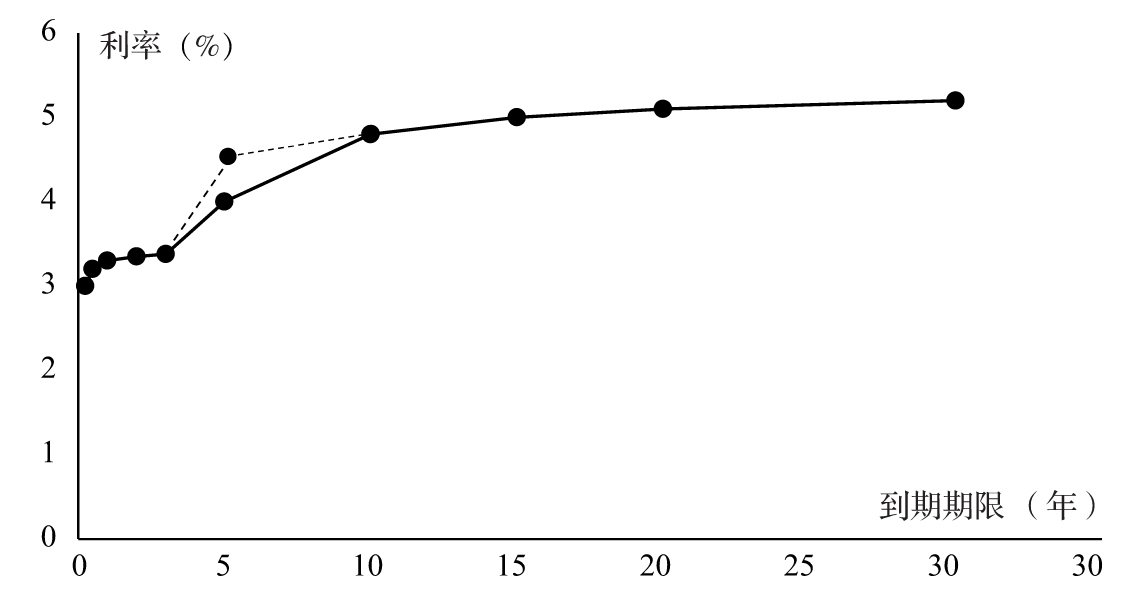
圖14-1 5年期利率隨其他利率不變的變化
考慮一個投資組合,其價值僅取決於一個期限結構。將δi定義為第i個節點delta(當第i個到期期限的利率上升一個基點時,投資組合的價值增加值)。如果σi是第i個節點相對應的1天的利率變化的標準差(以基點為單位),ρij是第i個節點和第j個節點的利率變動之間的相關性,則投資組合在1天之內價值變化的標準差是

任何給定的未來現金流量都具有相對於兩個相鄰到期日的delta。例如,3.5年的現金流相對於3年期利率和5年期利率具有delta,而相對於其他利率則沒有。如果3.5年期利率的一個基點變化的影響為X,那麼3年節點的delta為0.75X,5年節點的delta為0.25X。
注意,式(14-4)與式(14-2)相同。唯一不同的是,式(14-2)考察風險因子的百分比變化(δ變量衡量百分比變化的風險因子對投資組合的影響,σ變量是波動率),而式(14-4)考察風險因子的實際變化(δ變量衡量風險因子實際變化的影響,而σ變量是標準偏差)。式(14-2)和式(14-4)可以擴展到一個考慮某些風險因子的百分比變化和考慮其他風險因子的實際變化的投資組合。
現在假設投資組合P的價值取決於K個期限結構。定義δik、σik、ρijk分別是期限結構k(1≤k≤K)中δi、σi、ρij的值,同時定義
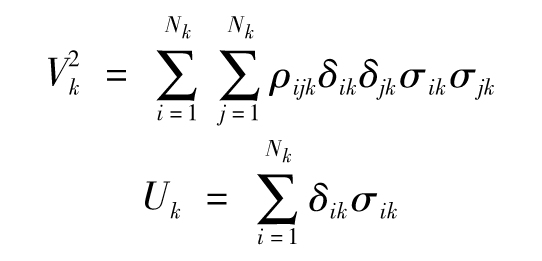
其中Nk是用於期限結構k的頂點數。
通常用一個參數描述兩個期限結構之間的相關性。假設ρ(k1,k2)是期限結構k1和k2之間的相關性。定義它的兩種方法如下:
(1)對於所有i和j,期限結構k1的利率i與期限結構k2的利率j之間的相關性是ρ(k1,k2)。
(2)由於期限結構k1和期限結構k2的變動而導致的投資組合價值的變化之間具有ρ(k1,k2)的相關性。
根據第一個定義可以得到
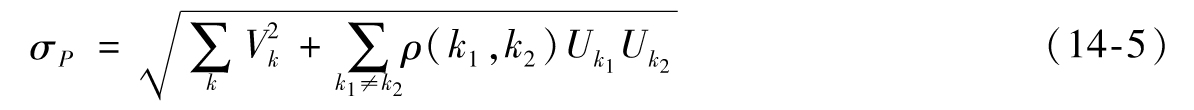
根據第二個定義可以得到
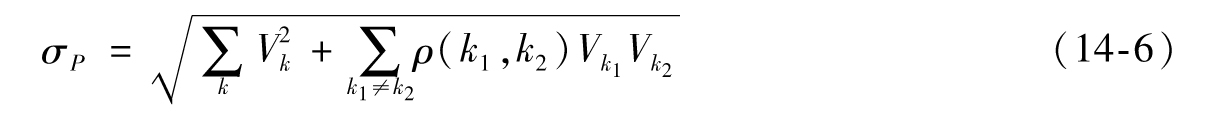
【例14-2】 假設一個投資組合有兩種不同的利率期限結構敞口。表14-9顯示了每天利率變動的標準差以及利率變動的delta敞口。例如,期限結構1的2年期利率每天變化的標準差為5.6個基點(0.056%),而期限結構2的2年期利率每天變化的標準差為11.4個基點。2年期利率的一個基點變化對於期限結構1的影響是8500萬美元,對於期限結構2是6500萬美元。假設兩個期限結構中各節點的相關性ρij都相同,如表14-10所示。期限結構1中的1年期利率變動與期限結構1中的2年期利率變動之間的相關性為0.92。期限結構2也是如此。
表14-9 標準差(以基點為單位)和delta敞口(以每個基點百萬美元計)
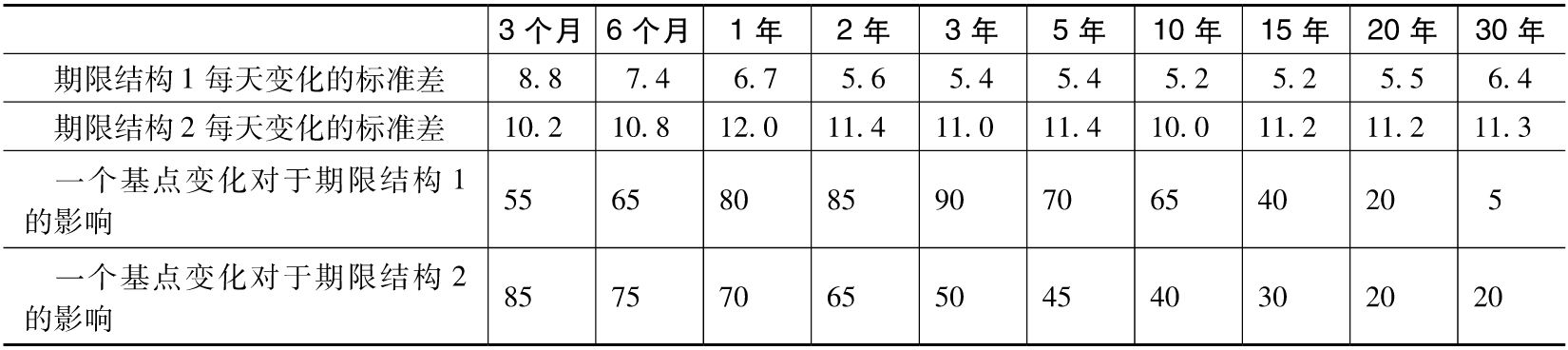
表14-10 不同期限利率之間的相關性
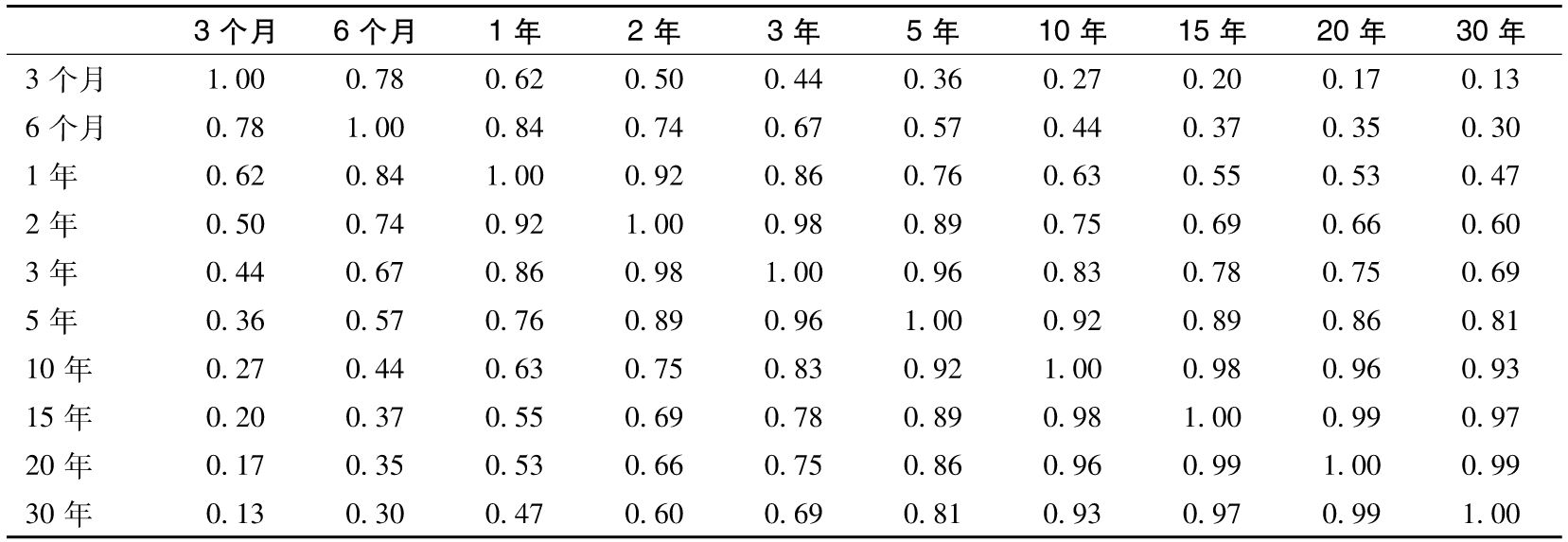
最後,我們假設兩個期限結構之間的相關參數為0.4(以百萬美元計),結果是
U1=3 529 U2=5 501
V1=3 004.9 V2=4 604.3
式(14-5)給出的每天投資組合標準差為6 163.9,式(14-6)給出的每天投資組合標準差為5 980.2。將它們乘以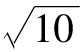 和2.326得到10天的99%VaR。使用式(12-2)計算ES。計算結果顯示在作者的網站上:www-2.rotman.utoronto.ca/~hull/riskman。
和2.326得到10天的99%VaR。使用式(12-2)計算ES。計算結果顯示在作者的網站上:www-2.rotman.utoronto.ca/~hull/riskman。
[1] 正如我們稍後將解釋的那樣,普通期權價格與波動率近似線性相關,因此可以使用式(14-2)處理其對波動率的依賴關係。
14.5 基本步驟的擴展
在本節中,我們繼續探討投資組合與潛在風險因子線性相關的情況,並解釋模型在式(14-2)和式(14-4)中的一些擴展。
14.5.1 受壓度量
假設我們對壓力VaR或壓力ES感興趣。如第13.1.3節所述,這是基於過去一段承壓期的數據而非近期的數據得出的估算值。到目前為止,本章提出的方法都可以使用承壓期的數據來修正波動率和相關性。
14.5.2 非正態分佈
在第12.9節中,我們解釋了聚合n個投資組合的整體VaR的一個近似公式為
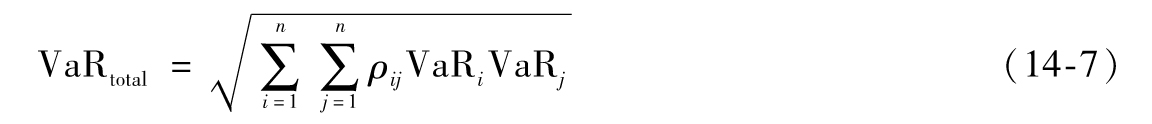
其中VaRi是第i個投資組合的VaR,VaRtotal是整體VaR,ρij是第i個投資組合和第j個投資組合的損失之間的相關性。該公式表明,聚合標準差的方法也可以近似用於聚合百分位數。
結果展示了模型構建方法可以被拓展為允許收益服從非正態分佈的方法。假設基於歷史數據估計出微軟公司的10天收益分佈的1%分位數為-17%,因此向微軟公司投資的1000萬美元的10天99%VaR為170萬美元(而不是在第14.1節中,假設收益服從正態分佈計算得出的1471300美元)。進一步假設,我們估計出AT&T的10天收益分佈的1%分位數為-10%,因此,向AT&T投資500萬美元的10天99%VaR為50萬美元(而不是假設收益服從正態分佈時的估計值367800美元)。使用式(14-7),我們將對微軟公司和AT&T投資組合的VaR估計值調整為
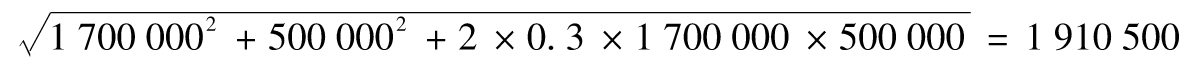
14.6 風險權重和加權敏感性
使用式(14-2)和式(14-4)計算VaR或ES時,要將投資組合中每天變化的標準差乘以一個常數。例如,當計算10天的99%VaR時,將其乘以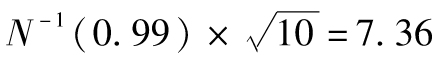 。計算20天的97.5%ES時,將其乘以
。計算20天的97.5%ES時,將其乘以
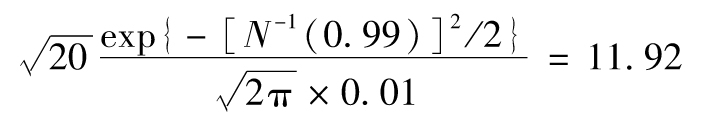
假設β是乘數,則有
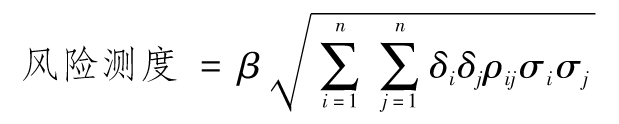
定義Wi=βσi。上式可寫為
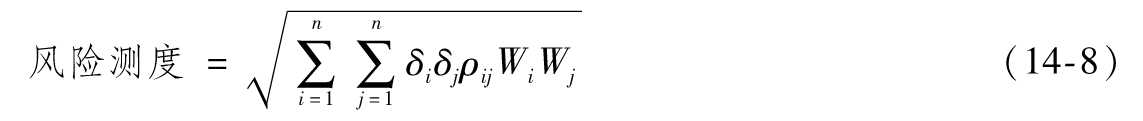
參數W被稱為風險權重,而參數δ稱為加權敏感性。
我們將在後面的章節中看到,該公式用於:
(1)使用標準化方法在交易賬戶基本審查中確定市場風險的資本;
(2)確定雙邊清算交易的初始保證金。
14.7 處理非線性情況
現在我們考察投資組合價值的變化與潛在風險因素的變化非線性相關的情況,包含期權的投資組合就是這種情況。非線性投資組合具有vega和gamma風險敞口。大多數投資組合的波動率近似為線性。因此,如前所述,可以考慮波動率期限結構中的潛在變動來考察vega風險敞口。
衡量gamma風險敞口更困難,因為它會產生二次項。考慮一個由單一期權組成的投資組合,投資組合的價值與資產價格S有關。泰勒級數展開式表明
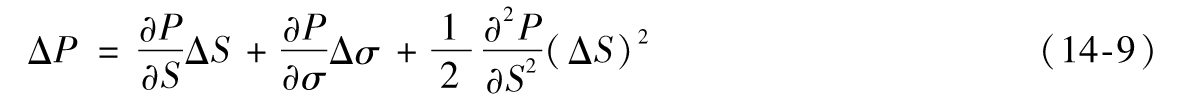
在計算VaR或ES時,不能忽略此擴展中的最後一項。圖14-2顯示了看漲期權多頭的價值同標的資產價格的關係,也能說明這一點。看漲期權多頭是一個具有正gamma產品的例子。如圖所示,當某天標的資產價格的概率分佈為正態分佈時,期權價格的概率分佈具有正偏性。圖14-3顯示了看漲期權空頭價值同標的資產價格的關係。空頭看漲期權的gamma為負。在這種情況下,一天結束時標的資產價格所服從的正態分佈被映射為具有負偏態的期權價值分佈。
一個投資組合的VaR直接取決於投資組合價值概率分佈的左尾。例如,當置信度為99%時,分佈左端小於VaR的數量佔整體分佈的1%。如圖14-2所示,具有正gamma的投資組合與正態分佈相比,左尾分佈較為瘦小,在正態分佈的假設下得出的VaR會偏高。類似地,如圖14-3所示,具有負gamma的投資組合同正態分佈相比,左尾分佈較為肥大,在正態分佈的假設下得出VaR會偏低。
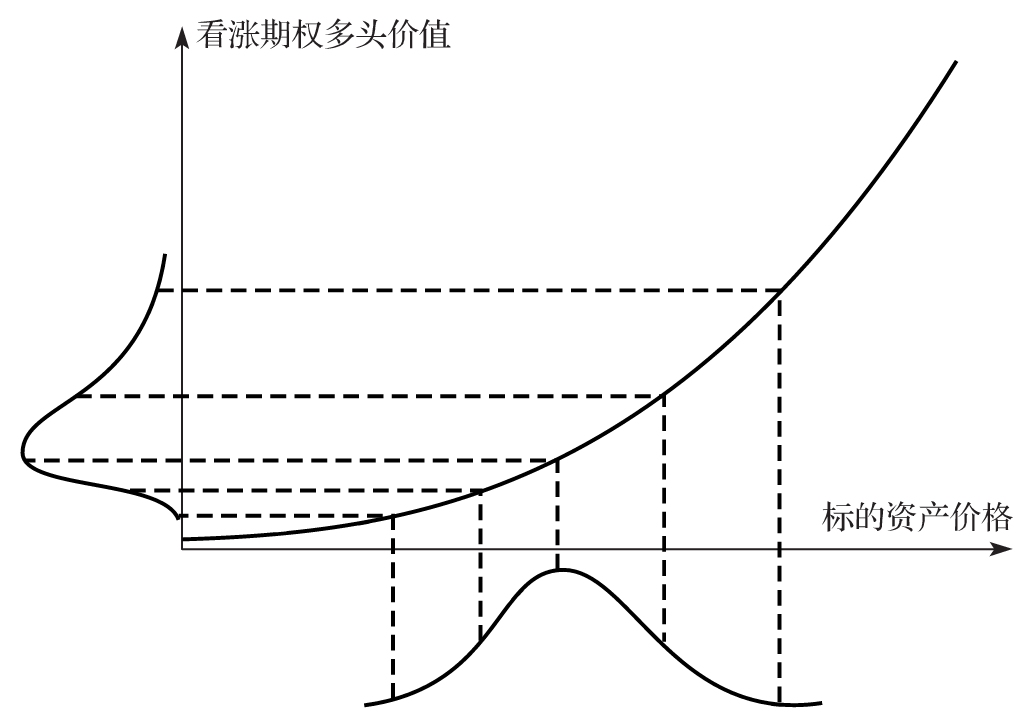
圖14-2 具有正態分佈的標的資產的概率分佈與看漲期權多頭價值的概率分佈的對應關係
圖14-3 具有正態分佈的標的資產的概率分佈與看漲期權空頭價值的概率分佈的對應關係
如果一個投資組合與n個潛在風險因子相關,式(14-1)變為

γij是交叉gamma,其定義為

如果投資組合中的每一個資產只與一個風險因子有關,則不存在交叉gamma。因此,除了i=j時,γij=0。
14.7.1 蒙特卡羅模擬
作為對以上所討論方法的補充,我們可以在實施模型構建法時採用蒙特卡羅模擬(Monte Carlo simulation)來產生ΔP的概率分佈。假設我們要計算投資組合1天展望期的VaR,過程如下:
(1)利用當前的市場變量對投資組合進行定價。
(2)從Δxi服從的多元正態分佈中進行一次抽樣。[1]
(3)由Δxi的抽樣計算出在交易日末市場變量。
(4)利用新產生的市場變量來對投資組合重新定價。
(5)將第4步產生的數值減去第1步的數值,由此產生了ΔP的一個抽樣。
(6)重複第2步~第5步的計算,建立ΔP的概率分佈。
ΔP的概率分佈中的某個分位數就是我們想要求得的VaR或者ES。例如,假如我們由以上方法計算出ΔP的5 000個不同的抽樣,1天展望期的99%VaR對應於抽樣數值從大到小排序中的第50名;1天展望期的99%ES為排序中的第50名,等等。[2]N天展望期的VaR等於1天展望期的VaR乘以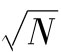 。[3]
。[3]
蒙特卡羅方法的弱點是其計算速度緩慢,計算速度之所以緩慢是因為公司的投資組合(有可能由成百上千的資產所組成)要被定價很多次。一種加速計算的方法是用式(14-10)所描述的ΔP與Δxi的關係,在蒙特卡羅方法中,我們可以由第2步直接跳到第5步,這麼做可以避免投資組合的定價過程,這一技巧被稱為局部模擬方法(partial simulation approach)。
14.7.2 擴展
蒙特卡羅模擬的一個魅力在於,我們不必假設風險因素呈正態分佈。我們可以假設Δxi服從任意的分佈,並使用多元Copula模型定義變量之間的相關性。[4]我們可以採用單因子高斯Copula模型,在以上所描述的5步模擬過程中第2步和第3步之間插入額外的一步,我們可以進行一個新的模擬過程:
(2)由多元概率分佈中提取一次抽樣ui。
(2a)以分位數到分位數的形式將ui映射到Δxi。
14.7.3 柯尼斯-費希爾展開
統計學中柯尼斯-費希爾展開(Cornish-Fisher expansion)由概率分佈的矩入手,來對概率分佈的分位數進行估計。假定μP和σP分別為ΔP的期望值和標準差,即

概率分佈的偏態與第三階矩有關。正偏態性表示概率分佈的右尾比左尾重。負偏態性則相反。ΔP的概率分佈偏態ξP通常定義為
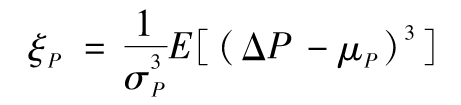
正態分佈的偏態為零。
概率分佈的峰度與第四階矩有關,它衡量分佈尾巴的厚重程度。與偏態相似,ΔP的概率分佈峰度κP通常定義為
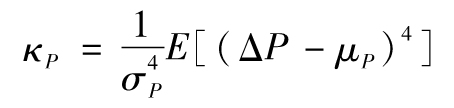
正態分佈的峰度為3。超額峰度(excess kurtosis)衡量的是相對於正態分佈的峰度,定義為峰度減去3。
利用ΔP的前三階矩,柯尼斯-費希爾展開得出的ΔP的第q個分位數為
μP+wqσP
其中
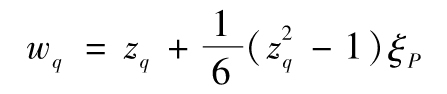
其中zq為標準正態分佈的第q個分位數。當使用更高階矩時,精度會提高。例如,當考慮峰度時,wq的表達式變為
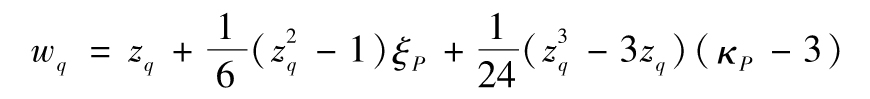
【例14-3】 假定對於某一投資組合我們計算出μP=-0.2,σP=2.2,ξP=-0.4,我們試圖計算分佈1%分位數(q=0.01),對於這一情形,zq=-2.326,假定ΔP的概率分佈為正態,由此得出1%分位數為
-0.2-2.326×2.2=-5.318
換句話講,我們有99%的把握肯定
ΔP>-5.318
對應於q=0.01,採用柯尼斯-費希爾展開並將分佈的偏態考慮在內,我們得出

分佈的1%分位數為
-0.2-2.620×2.2=-5.965
將偏態考慮在內時,投資組合的VaR由5.318變成了5.965。假設我們還知道峰度κP為3.3。對wq的估計改為:
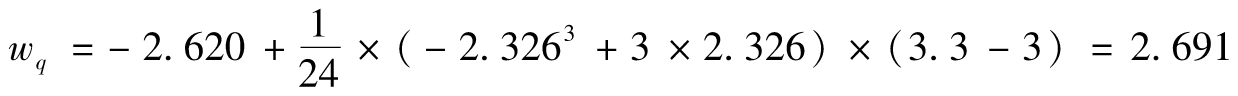
分佈的1%分位數估計為
-0.2-2.691×2.2=6.119
14.7.4 Isserlis定理
為了應用柯尼斯-費希爾展開結果,我們需要計算ΔP的矩。當Δxi服從正態分佈時,原則上可以使用Isserlis定理。定理指出,如果Xi是零均值正態分佈,當n是奇數時
E(X1X2…Xn)=0
當n是偶數時
E(X1X2…Xn)=∑ΠE(XiXj)
∑ΠE(XiXj)的含義為:①列出將X1,X2,…,Xn分成n/2對組合的不同方式;②計算每種方式中每對(XiXj)的期望值E(XiXj),並將它們相乘;③對每組組合的結果求和。
例如
E(X1X2X3X4)=E(X1X2)E(X3X4)+E(X1X3)E(X2X4)+E(X1X4)E(X2X3)
E(X1X2X3X4X5X6)有15種表達形式,其中一種是
E(X1X2)E(X3X4)E(X5X6)
Isserlis定理是一個具有潛在吸引力的結果,因為我們知道一對零均值正態分佈變量的乘積的期望值是標準差σX和σY,它們的協方差為:E(XY)=ρσXσY,其中ρ是σX和σY的相關係數。
當n為奇數時,n個零均值正態分佈變量的乘積為零,因此式(14-10)變為

當只有一個風險因子時,去除下角標σ、ρ、δ和γ,這些等式可簡化為

然而,結構的數量隨著風險因子數量的增加而迅速增加,因此即使風險因子數量並不多,第三階矩的計算也變得非常耗時。
對Isserlis定理的一個變形是(考慮gamma),在計算前二階矩時以VaR或ES為基礎,並且假設沒有交叉gamma。這意味著當i≠j時,γij=0。為簡化公式,我們設γii=γi

由Isserlis定理可得
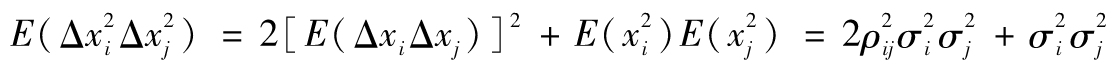
因此可得ΔP的標準差是
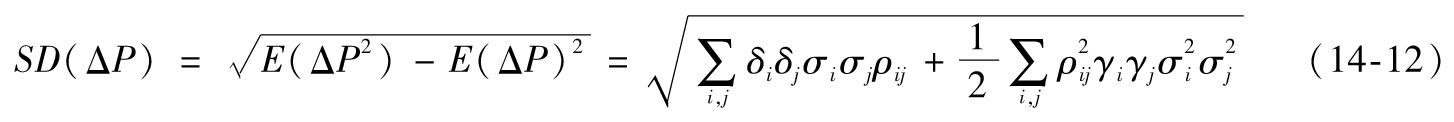
我們在第17章中討論標準初始保證金模型(SIMM)時將應用到這個定理。
[1] 一種做法在第11.4.1節中給出了。
[2] 就像在歷史模擬法中那樣,極值理論可以用來對尾部分佈進行光滑處理,在處理之後我們可以得出極端分位的更好估計。
[3] 當交易組合中包含期權時,這一假設只是一個近似,但這種近似被大多數實際操作採用。
[4] See J. Hull and A. White, “Value at Risk When Daily Changes Are Not Normally Distributed,” Journal of Derivatives 5, no. 3 (Spring 1998): 9-19。
14.8 模型構建法與歷史模擬法的比較
在第13章和本章中,我們討論了兩種計算VaR的方法:歷史模擬法和模型構建法。模型構建法的優點是計算速度快,並且這一方法可以與第10章和第11章討論的波動率及相關性的更新法較為容易地結合到一起(在第13.3節中我們曾指出,波動率的更新法也可以用於歷史模擬法之中,但這種並用是一種非常牽強的做法)。模型構建法的主要缺點是,只有當投資組合價值的變化與風險因子每天的百分比變化或實際變化呈線性相關時,才能產生快速的結果,並假定風險因子的每天變化為多元正態分佈。實際上,風險因子每天變化的分佈往往與正態分佈不同(例如,見表10-1)。模型構建法的使用者可以使用第14.5.2節中的方法,寄希望於存在某種形式的統計中心極限定理,從而使一個龐大的投資組合整體每天的盈虧服從正態分佈,即便在投資組合各組成成分本身的變化並不服從正態分佈的情況下。
實際上,模型構建法往往可被用於投資組合(畢竟這一方法同流行的馬科維茨的期望值-方差法理論較為接近)。考慮到gamma的複雜性,對金融機構的交易活動很少用這一方法來計算VaR。可以認為,gamma對VaR或ES的影響遠小於delta的影響。然而,通常情況並非如此,如第8章解釋的那樣,金融機構往往喜歡對衝頭寸以將自身的delta敞口調整到接近於0的水平。
小結
歷史模擬法利用歷史數據來決定市場變量每天變化的聯合分佈,而模型構建法假定分佈為某種特殊形式,最為流行的選擇是假定市場變量的百分比變化服從多元正態分佈。當投資組合價值變化與市場變量百分比變化呈某種線性關係時,VaR和ES的準確值可以很快被計算得出。其他情形較難處理,一種實現模型構建法的方法是採用蒙特卡羅模擬(可容納任何投資組合),但是這種方法在計算上要慢很多。
模型構建法常常被用於投資組合,因為難以對gamma進行建模,所以它很少被用於金融機構的投資組合。
延伸閱讀

練習題
14.1 假定某投資組合由價值為100 000美元資產A的投資以及價值為100 000美元資產B的投資構成,假定兩種資產的日波動率均為1%,兩項投資回報的相關係數為0.3,投資組合5天展望期的97%的VaR和ES為多少?
14.2 當利用模型構建法來計算VaR時,請描述3種處理利率產品的不同方法。
14.3 假設在12年利率中,每增加一個基點,投資組合的價值就增加5萬美元,並且沒有其他敏感因素。採用多頂點法對3個月、6個月、1年、2年、3年、5年、10年、15年、20年、30年的頂點進行建模。投資組合對期限結構每個頂點的一個基點增長的敏感度是多少?
14.4 一家金融機構擁有一個標的變量為USD/GBP匯率的期權投資組合,投資組合相對於匯率變化百分比的delta為3.9,如果匯率每天變化的波動率為0.7%,請問10天展望期、99%置信度的VaR為多少?
14.5 假定在練習題14.4中投資組合的gamma為4.3(根據百分比變化計算),gamma的變化將如何影響投資組合價值變化與匯率變化的關係式?
14.6 投資組合有2年期利率和5年期利率的風險敞口。2年期利率每增加一個基點,會使投資組合的價值增加10 000美元。5年期利率每增加一個基點,投資組合的價值就會減少8 000美元。2年期利率和5年期利率的每日標準差分別為7個基點和8個基點,兩者之間的相關係數為0.8。當置信水平為98%、展望期為5天時,投資組合的ES是多少?
14.7 解釋在建立模型的方法中如何使用風險權重和風險敏感性。
14.8 假定某投資組合的每天價值變化與由主成分分析(PCA)法所計算出的兩個因子呈很好的線性關係,投資組合對於第一個因子的delta為6,對於第二個因子的delta為-4,兩個因子的標準差分別為20及8,投資組合5天展望期的90%的VaR為多少?
14.9 表14-6所對應的實例中假定了兩個因子,當你假定有:(a)一個因子;(b)三個因子時,計算結果會分別有什麼樣的變化?
14.10 一家銀行擁有某資產的多個期權投資組合,期權組合的delta為-30,gamma為-5,對這些數字應如何進行解釋?資產的價格為20,每天價格變化的波動率為1%,採用Isserlis定理計算投資組合價值變化的前三階矩。結合柯尼斯-費希爾展開分別採用:(a)前二階矩;(b)前三階矩來計算1天展望期的99%的VaR。
14.11 假設練習題14.10中投資組合的vega為-2,這一vega對應於年波動率的1%的變化,請導出投資組合每天價值變化與delta、gamma及vega的關係式的模型。
14.12 請解釋為什麼線性模型對包含期權的投資組合的VaR僅僅是提供了一個近似估計?
14.13 假定在過去的某一時間,某家公司進入了一項遠期合約,合約約定這家公司在將來某時刻以100萬英鎊買入150萬美元,這一遠期合約在6個月後到期,6個月零息英國債券的每天波動率為0.06%(價格在轉換成美元后),6個月期限零息債券的波動率為0.05%,兩個債券回報的相關係數為0.8,當前的匯率為1.53。請計算遠期合約1天(以美元計)價值變化的標準差,並計算10天展望期的99%的VaR。在計算中假定英鎊及美元6月期的利率為5%,這裡的利率為每年連續複利利率。
14.14 在第14.3節的計算中,投資於DJIA、FTSE 100、CAC 40及Nikkei 225的資金分別為400萬美元、300萬美元、100萬美元及200萬美元。如果我們投資於每個指數的資金均為250萬美元,計算出的VaR和ES將如何改變?對以下情形進行計算:(a)波動率及相關性是由等權重模型得出;(b)利用參數λ=0.94的EWMA模型得出。請利用作者網站上的表單進行計算。
14.15 將第14.3節中EWMA計算中的參數λ由0.94換為0.97將發生什麼?利用作者網站上的表單進行計算。
14.16 說明存在多個頂點時,使用單個相關參數定義兩個期限結構之間相關關係的兩種替代方法。
作業題
14.17 某投資組合由價值為300 000美元的黃金投資及價值為500 000美元的白銀投資構成,假定以上兩種資產變化每天的波動率分別為1.8%及1.2%,並且兩種資產回報的相關係數為0.6,請問投資組合10天展望期的97.5%的VaR和ES為多少?投資分散效應所減小的VaR和ES為多少?
14.18 考慮對於某標的資產的期權投資組合,假定投資組合的delta為12,標的資產價格為10美元,標的資產每天價格變化的波動率為2%,相對於百分比變化的delta是多少?請由delta來估計投資組合1天展望期的95%的VaR。
14.19 假定作業題14.18中投資組合的gamma為-2.6(同樣是根據實際變化來衡量的),相對於成比例變化的gamma是多少?請導出投資組合價值變化同標的資產價格每天變化的二次關係式並:
(a)計算投資組合的前三階矩。
(b)利用前二階矩並假定投資組合的每天價值變化為正態分佈,計算投資組合1天展望期的95%的VaR。
(c)利用第三階矩及柯尼斯-費希爾展開來對(b)的答案進行修正。
14.20 一家公司持有2年期和3年期債券的多頭及5年期債券的空頭,每一項債券投資的面值為1億美元,債券每年支付5%券息,請計算公司投資對於1年、2年、3年、4年及5年利率的風險敞口,採用表14-7和表14-8的數據及以下不同的有關利率變化的假設來計算20天展望期的95%的VaR,利率變動分別由(a)一個因子;(b)兩個因子;(c)三個因子來解釋。在計算中假定零息債券收益率保持在5%。
14.21 一家公司持有債券投資組合的價值為600萬美元,投資組合的修正久期為5.2年,假定利率曲線的變化只有平行移動形式,並且我們假定利率曲線變動的標準差為0.09(利率以百分比計),利用久期模型來估測20天展望期的90%的VaR,請詳細解釋這裡的VaR計算方式的缺點,給出兩種更為準確的計算方法。
14.22 一家銀行賣出了標的資產為某股票的看漲期權,同時又賣出了標的資產為另一家股票的看跌期權,看漲期權的標的資產股票價格為50,期權執行價格為51,標的資產變化波動率為每年28%,期權的到期日期為9個月;看跌期權的標的資產股票價格為20,執行價格為19,標的資產變化波動率為每年25%,期權的到期日期為1年。兩種股票均不支付股息,無風險利率是每年6%,兩種股票回報的相關係數為0.4,請採用以下方式計算銀行投資組合的10天展望期的99%的VaR:(a)只採用delta;(b)採用局部模擬法;(c)採用整體模擬法。
14.23 在第14.3節的計算中,投資於DJIA、FTSE 100、CAC 40及Nikkei 225的資金分別為400萬美元、300萬美元、100萬美元及200萬美元。如果我們將投資於指數的資金數量變為300萬美元、300萬美元、100萬美元及300萬美元,計算出的VaR將如何改變?對以下情形進行計算:(a)波動率及相關性由等權重模型得出;(b)利用EWMA模型得出。如果將EWMA模型中的參數λ由0.94換為0.90,會發生什麼變化?請利用作者網站上的表單進行計算。

第15章
《巴塞爾協議Ⅰ》《巴塞爾協議Ⅱ》及《償付能力法案Ⅱ》
《1988年巴塞爾協議》的發佈標誌著銀行監管標準國際化時代的開始。自那以來,銀行監管規則不斷演化。儘管規則本身不斷推陳出新,但原有的很多方法得以保留下來。因此,為了更好地理解當前的監管環境,我們有必要回顧一下監管規則的發展歷史。本章介紹了2007年信用危機前監管環境的變遷。第16章將介紹自2007年危機以來的新變化。
在本章的開始,我們首先回顧一下20世紀80年代到2000年之間銀行監管規則的進化。我們將解釋《1988年巴塞爾協議》(即《巴塞爾協議Ⅰ》(Basel Ⅰ))、淨額結算規定(netting provision)和《1996年修正案》(1996 Amendment)。隨後我們將討論《巴塞爾協議Ⅱ》(Basel Ⅱ),這一協議是對前一個版本協議的巨大修訂,世界各地的很多銀行在2007年左右已經實施了該協議。在最後,我們將討論《償付能力法案Ⅱ》(Solvency Ⅱ),該法案類似於《巴塞爾協議Ⅱ》,但針對的對象是保險公司,2016年,這一法案在歐盟地區實施。
15.1 對銀行業進行監管的原因
對銀行業進行監管的主要出發點是確保銀行持有足夠的應對自身風險的資本金。完全消除銀行破產的可能性是不切實際的,但政府想做到的是保證任何一家銀行破產的概率要達到極小,並因此提供一個穩定的經濟環境,來確保個人及企業對銀行系統的信心。
一些人推崇以下觀點:“對銀行進行監管沒有什麼太多的必要,即使不設定監管條例,銀行仍然會謹慎地管理其面臨的風險,並且保證自身資本金水平與自身面臨的風險一致。”不幸的是,從歷史的角度來看,以上的觀點並不正確。毫無疑問,銀行監管條例對於增加銀行資本金起了非常重要的作用,政府的監管使得銀行對自身所面臨的風險有了更好的認識。
如第2.3節所示,政府對存款提供保護的目的是保護存款人的利益。如果沒有存款保險,相對自己的資本金來說,承擔了過多風險的銀行會有困難來吸引存款人。但與此同時,存款保險制度的存在令存款人不需要精心地挑選存款銀行。銀行在承擔鉅額風險時也無須擔心會失去存款客戶群體。[1]政府最不願意看到的是存款制度造成銀行承擔過多的風險。因此,存款保險制度應與資本金制度相伴,以確保金融系統的穩定。
監管人員一個最大的擔心是系統性風險,該風險是指某家大銀行的倒閉會造成其他大銀行的倒閉,從而觸發整個金融系統崩潰的可能。業界事例15-1描述了系統性風險的產生過程。一家大型銀行或金融機構出現生存危機時,政府會左右為難,如果不出手相救,則銀行破產可能會將整個系統拖垮;如果出手相救,則可能是給市場發出了錯誤信號。這樣做會使一些大的金融機構對其所面臨的風險喪失應有的警惕性,因為它們會自認為可以“大而不倒”(too big to fail),當運作出現問題時,政府總會來救助。
業界事例15-1
系統風險
系統性風險是指由某一家金融機構違約而促成的連鎖反應(ripple effect)。一家銀行的違約可能會引發其他銀行的違約,從而對整個金融系統的穩定性產生威脅。這是因為銀行之間存在著大量的場外交易。當銀行A破產時,銀行B會因為與銀行A之間的交易而蒙受損失,這些損失可能會造成銀行B破產,銀行C可能同銀行A及銀行B之間都有交易,因此銀行C也可能會遭遇巨大損失,從而給自己的運作帶來巨大的困難。這種連環反應可能進一步持續下去發生。
金融系統成功地經歷了1990年的德崇證券(Drexel)、1995年的巴林銀行和2008年的雷曼兄弟等違約事件的考驗,但監管人員仍然憂心忡忡。在2007~2008年的金融動盪中,許多大型金融機構得到了政府救助,這正是因為政府考慮到要防止系統性風險。
在2008年的市場震盪中,美國和歐洲政府出面拯救了許多大型金融機構,卻在2008年9月讓雷曼兄弟破產。美國政府這麼做可能是想告訴市場,政府救助不是總會有的。政府放任雷曼兄弟破產的做法也受到了抨擊,因為這麼做確實使得危機更加惡化。
[1] 如第3章所討論的,這一現象類似於保險公司面臨的道德風險,即保險條約的存在會改變投保人的行為。
15.2 1988年之前的銀行監管
在1988年之前,一個國家內部的銀行監管機構通過設定資本金佔整體資產的最低比率來達到監管目的,但是不同的國家間對於資本金以及資產比率的定義也往往不同。有些國家對於監管規則的要求比其他國家更為嚴格。隨著銀行業國際化的發展,那些在監管規則較為寬鬆的國家運營的銀行被認為相對於那些在監管規則更嚴格的國家運營的銀行享有更多的競爭優勢。另外,一些國際性銀行給某些不發達國家,例如,墨西哥、巴西、阿根廷發放了大量貸款,因此產生了巨大的風險敞口,而且針對這些敞口,銀行有時還會鑽不同會計制度的空子(見業界事例2-3)。這些現象,使監管機構對銀行的資本充足率提出了質疑。
另外一個問題是銀行進行的交易變得越來越複雜。場外衍生產品,例如,利率互換、外匯互換以及匯率期權等產品發展迅猛,這些產品增加了銀行的信用風險的敞口程度。例如,我們考慮一個利率互換合約,當互換合約對於銀行有正的市場價值,即對交易對手有負價值時,如果對手違約,則銀行會遭受損失,但是這些因衍生產品交易產生的潛在未來敞口(potential future exposure)並未被反映在銀行所報告的資產中,這意味著這些產品對銀行報告中的資產額沒有影響,因此這些產品對銀行持有資本金的數量也不會產生影響。對於監管機構來講,總資產額不再能準確地反映銀行整體風險的大小。由此可見,制定一個較為完善的管理方法,而不是僅僅簡單地設定一個資本金同資產負債表內資產的最低比率就非常有必要。
巴塞爾委員會(Basel Committee on Banking Supervision)成立於1974年。委員會由來自以下國家的代表組成:比利時、加拿大、法國、德國、意大利、日本、盧森堡、荷蘭、瑞典、瑞士、英國及美國。該委員會定期在瑞士的巴塞爾國際清算銀行(Bank for International Settlements)召開會議。這些會議的第一個主要成果就是產生了《關於統一國際銀行資本計算和資本標準的協議》(International Convergence of Capital Measurement and Capital Standards),這一協議也被稱為《1988年巴塞爾協議》(The 1988 BIS Accord)或被簡稱為“協議”(Accord),近來這一協議也被稱為《巴塞爾協議Ⅰ》。
15.3 《1988年巴塞爾協議》
《1988年巴塞爾協議》是監管部門第一次嘗試以風險為基礎來定義資本充足率的國際性條約。條約產生之後,有人曾指出這一條約過於簡單隨意,但事實上這一條約是一個偉大的成就。所有12個巴塞爾委員會的參與國均簽署了這一協定,這一條約大大增強了銀行的自身風險管理意識,同時也大大提高了銀行對於風險管理的投入。協議中引入的庫克比率(Cooke ratio)[1]被認為是一個關鍵創新。
15.3.1 庫克比率
庫克比率將資產負債表內及表外所有的信用風險敞口都納入了考慮範圍。它建立在被稱作風險加權資產(risk-weighted assets,有時也被稱為風險加權總量(risk-weighted amounts))的概念上。這一指標被用來測定銀行的整體信用風險敞口。
信用風險敞口可以分為三類:
(1)對資產負債表內的資產的敞口(排除衍生產品);
(2)對資產負債表外的項目的敞口(排除衍生產品);
(3)對場外交易的衍生產品的敞口。
首先讓我們考慮第一類。表內每一項資產都對應於一個權重,這一權重反映了資產所對應的風險。在表15-1中,我們展示了協議中某些資產的權重。現金及OECD(經合組織)政府債券被認為是沒有風險的資產,因此其對應權重為0,企業債券的權重為100%,OECD銀行的貸款及政府管理部門所對應的權重為20%,無抵押房屋貸款的權重為50%。表內資產的整體加權平均總和為
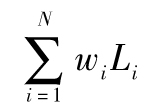
其中Li為面額數額,wi為風險權重。
表15-1 表內資產風險加權權重

【例15-1】 某銀行的資產包括1億美元的企業貸款、1 000萬美元的OECD政府債券及5 000萬美元的住房貸款,風險加權資產的總和為(以百萬美元計)
1.0×100+0.0×10+0.5×50=125
即12 500萬美元。
現在考慮第二類風險。表外項目包括銀行承兌票據(banker’s acceptance)、保函(guarantee)和貸款承諾(loan commitment)等。對這些產品的本金乘以一個轉換因子,就可以得到所謂的等價信用量(credit equivalent amount)。從信用的角度來看,與貸款信用風險類似的產品,例如銀行承兌票據的轉換因子為100%。其他產品,如票據發行便利(note insurance facilities,即銀行同意擔保某家企業在將來某一時間以某些既定條款來發行短期債券)的轉換因子會低一些。
接下來我們考慮第三類。對於場外衍生產品,例如利率互換或遠期合約等,等價信用量的計算方式為
max(V,0)+aL
(15-1)
其中V為衍生產品合約的當前價值,a為附加因子,L為面額。以上表達式的第一項為當前風險敞口,如果對手今天違約,而V為正,則合同對於銀行是資產,所以就會損失V;如果對手今天違約,而V為負,則合同對於對手是資產,所以銀行沒有損失,也無收益。因此,銀行的風險敞口為max(V,0)(有關在雙邊清算的場外衍生產品市場中如何處理違約的更多詳細信息,請參見第17章和第20章)。第二項附加項aL是為了應對風險敞口在未來增加而進行的補充。表15-2列舉了附加因子a的數值。式(15-1)被稱為現期敞口法(current exposure method,CEM)。在1998年以後的幾年中,對附加因子進行了修訂和擴展。
表15-2 衍生產品附加因子(面額的百分比)和剩餘期限

【例15-2】 一家銀行持有面額為1億美元的利率互換,剩餘期限為4年。利率互換的當前價值為200萬美元,在這一情形下,附加因子為0.5%,因此等價信用量為200+50=250萬美元。
在計算風險加權資產時,第二類、第三類風險敞口的等價信用量還要和與對手有關的風險加權因子相乘,這裡的風險加權因子與表15-1中的因子相似,其不同之處是此處企業所對應的風險加權因子為0.5而不是1.0。
【例15-3】 考慮例15-2中的銀行,當利率互換的對手為企業時,風險加權資產為250×0.5=125萬美元,而當交易對手為OECD銀行時,風險加權資產為250×0.2=50萬美元。
綜上所述,我們得出,假如一家銀行有N項表內資產及M項表外資產,風險加權資產的總和為

其中Li為第i項表內資產的面額,wi為第i項資產的加權因子;Cj為第j項表外資產的等價信用量,wj*為與交易對手有關的風險因子。
15.3.2 資本金要求
協議要求銀行持有的資本金至少是風險加權資產的8%,資本金的構成包含兩項內容:
(1)第一類資本,這類資本包含股本(除去商譽(goodwill)價值)和非累積永續優先股[2](noncumulative perpetual preferred stock)(商譽從權益中減去[3])。
(2)第二類資本,這類資本為附加資本(supplementary capital),它包括累積永續優先股[4](cumulative perpetual preferred stock),一定類型的99年期限債券以及發行期限大於5年的次優先級債券(優先級次於貸款)。
股權資本是最重要的資本類型,因為它可以吸收損失。如果股權資本大於損失,銀行就可以持續經營下去。如果股本低於損失,銀行就陷入資不抵債的境地。在後一種情況下,第二類資本就可以發揮作用,為存款人提供保護。如果銀行在耗盡了第一類資本後清盤,額外的損失首先由第二類資本承擔,只有在第二類資本也耗盡的情況下,存款人才會遭受損失(見第2.2節)。
協議要求銀行資本金中第一類資本不得低於50%(即風險加權資產的4%)。另外,協議要求普通股應占風險加權資產的2%(在《巴塞爾協議Ⅲ》中,委員會更新了第一類資本金的組成內容和對普通股的定義)。
有些國家的監管機構要求銀行持有的資本金高於巴塞爾委員會的最低要求,而有些銀行自身設定的資本金管理目標也會高於監管機構所設定的標準。
[1] 這一比率以當時英格蘭銀行(Bank of England)的彼得·庫克(Peter Cooke)來命名。
[2] 非累積永續優先股的期限為無限長,股息為某一指定比率,沒有付出的股息不累積(即某年年末付的股息不延續到第二年)。
[3] 當一家公司收購另一家公司時就會產生商譽,它等於購買價格減去資產的賬面價值,代表獲得的無形資產。
[4] 在累積永續優先股中,沒有付的股息必須在普通股(common stock)付股息之前付清。
15.4 G30政策建議
1993年,一個由衍生產品用戶、交易商、學術界人士、財會專家及衍生產品律師組成的工作小組推出一個報告。該報告給衍生產品交易商以及用戶提出20項有關衍生產品的管理的建議,同時該報告也給立法機關、監管及督查機構提出了4項建議。這一報告是基於對全球80個交易商及72個產品用戶的調查結果,在調查中採用了問卷及採訪形式。該報告雖然不是監管條例,但報告的推出直接影響了風險管理實踐的發展進程。報告的內容簡介如下:
(1)一家公司的風險管理政策應在公司的高層,最好是董事會層面得以確認及通過。公司不同層次的管理層必須貫徹執行風險管理政策。
(2)衍生產品應在每一天盯市計價(即每天通過與市場價格相一致的模型對產品重新定價)。
(3)衍生產品交易商必須採取一致性的風險管理測度。例如,利用在險價值VaR來度量市場風險。對持有的市場風險必須設定額度。
(4)衍生產品交易商必須採取壓力測試來求得在極端的市場條件下所面臨的風險。
(5)公司必須建立與交易部門相獨立的風險管理部門。
(6)衍生產品交易的信用風險的評估必須基於現有交易當前的重置價值(replacement value)以及未來潛在的重置成本。
(7)對某一交易對手的信用風險敞口,應通過可執行的淨額結算協定實現聚合(在下一節中我們將討論淨額結算這一概念)。
(8)公司設定信用風險額度的管理人員必須獨立於交易人員。
(9)交易商及用戶必須謹慎評估如抵押品(collateralization)及降級觸發(downgrade trigger)等信用風險緩釋策略的成本和收益。特別是,交易商及用戶必須評估自身及交易對手是否有能力支付降級觸發的現金流要求(降級觸發將在第20章中討論)。
(10)只有具備合適背景及經驗的人員才能承擔與衍生產品交易、交易監督及後臺管理等相關的責任。
(11)公司必須建立足夠完善的系統來採集交易數據,處理交易,進行結算並且生成相關報告。
(12)交易商及用戶應明確記錄用來進行風險管理的衍生產品,以確保這些產品以及它們所管理的風險在收入處理上的一致性。
15.5 淨額結算
場外衍生產品交易市場的參與者傳統上會為交易簽署一個國際互換和衍生產品協會(International Swaps and Derivatives Association,ISDA)的主協議。淨額結算(netting)一詞的含義來源於主協議中的一個條款,該條款聲明,如果違約發生,則所有的交易都被當作是一筆交易。這意味著如果交易的一方在簽署了主協議的一筆交易中違約,則該交易對手所有簽署了主協議的交易都被認為違約。
淨額結算和ISDA主協議將在第17章和第20章中討論。目前,我們只需明確淨額結算的直接效應是大幅減少信用風險。假定一家銀行與某一個交易對手有3筆互換交易,對於銀行而言,這3筆合約的價值分別為+2 400萬美元、-1 700萬美元及+800萬美元,假如交易對手因為賬務困難而不能履行義務。對於交易對手而言,三個合約的價值分別為-2 400萬美元、+1 700萬美元及-800萬美元。在沒有淨額結算的情況下,交易對手會對第一個合約違約,保存第二個合約,對第三個合約違約,此時銀行損失為3 200萬美元(=2 400+800)。在有淨額結算的情況下,交易對手在違約時也一定對第二個合約違約,因此銀行的損失只有1 500萬美元(=2 400-1 700+800)。
更一般地,假如一家金融機構與某交易對手有N筆交易,第i筆交易的當前價值為Vi,在沒有淨額結算的情況下,交易對手違約時引發的損失為

在有淨額結算的情況下,交易對手違約引發損失為
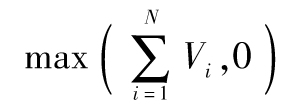
在沒有淨額結算情況下,風險敞口類同於期權的投資組合,而在有淨額結算的情況下,風險敞口類同於投資組合的一個期權。
《1988年巴塞爾協議》沒有考慮淨額結算的效果,由式(15-1)得出,對於某交易對手的等價信用量為
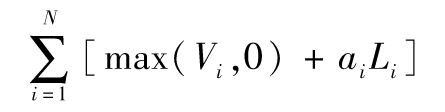
其中ai為第i個交易的附加因子,Li為第i個交易的面額。
截至1995年,淨額結算在許多國家的法庭得到了認可。因此,1988年的條約被修改,當交易可能實施雙邊淨額結算時,銀行可以採用淨額結算來降低其等價信用風險量,這樣做首先要計算淨替換比率(net replacement ratio,NRR),這一比率等於有淨額結算的敞口與無淨額結算後敞口的比率,即
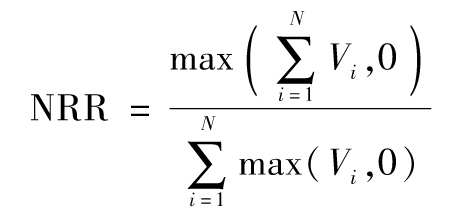
等價信用量的計算被修改為
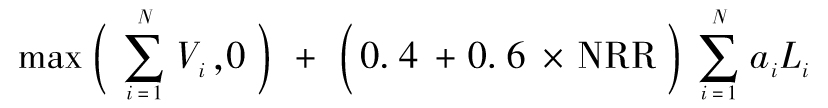
【例15-4】 考慮表15-3中的例子。表中顯示某家銀行與某交易對手有3筆衍生產品合約。表中第3列顯示合約的當前市場價值,第4列顯示由表15-2得出的附加因子。在有淨額結算的情況下,當前敞口為-60+70+55=65,而在無淨額結算的情況下,當前敞口為0+70+55=125。
因此淨替換比率為
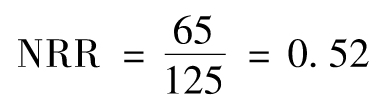
表15-3 與某一交易對手進行的衍生產品交易組合

所有附加量總和為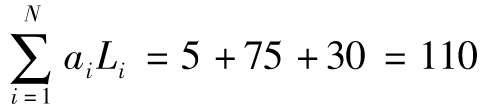 。在有淨額結算的情況下,等價信用量為65+(0.4+0.6×0.52)×110=143.32。在無淨額結算的情況下,等價信用量為125+110=235。假定交易對手為某OECD銀行,其對應風險權重為0.2,這意味著在有淨額結算的情況下,風險加權資產為0.2×143.32=28.66;在無淨額結算的情況下,風險加權資產為0.2×235=47。
。在有淨額結算的情況下,等價信用量為65+(0.4+0.6×0.52)×110=143.32。在無淨額結算的情況下,等價信用量為125+110=235。假定交易對手為某OECD銀行,其對應風險權重為0.2,這意味著在有淨額結算的情況下,風險加權資產為0.2×143.32=28.66;在無淨額結算的情況下,風險加權資產為0.2×235=47。
15.6 《1996年修正案》
1995年,巴塞爾委員會對1988年的協議提出了一個修正案,這一修正案在後來被稱為《1996年修正案》,並在1998年實施,所以有時這一修正案也被稱為“BIS 1998”。修正案包括了對交易行為涉及的市場風險設定的資本金。
盯市計價(marking to market)是指利用經當前市場價格校準的模型,每天對資產和負債進行重新定價的措施。這一做法也被稱為公允價值會計制度(fair-value accounting)。對於持有的以交易為目的的資產和負債,銀行必須採用公允價值會計制度。這些產品包括大部分衍生產品、可變賣權益類證券、外匯和商品。這些產品構成了銀行的交易賬戶。對於那些一直會被持有到期滿的投資資產,銀行不需要實行公允價值會計制度,這些資產包括貸款及某些債券,這些產品構成了銀行的銀行賬戶(banking book)。
在《1996年修正案》中,巴塞爾委員會在1988年所提出的信用風險資本金對交易和銀行賬戶中的表內及表外資產仍然適用,但對交易賬戶中的以下頭寸存在例外:①債券及股票類證券交易;②大宗商品及外匯交易。另外,在《1996年修正案》中,對於交易賬戶中的所有項目均設定了市場風險資本金。[1]
《1996年修正案》提出了一種計算市場風險資本金的標準方法。標準法對於不同種類的債券、股票、外匯、商品及期權等產品均設定了不同的資本金要求,但沒有考慮不同產品之間的相關性。較為先進並且具備完善風險管理功能的銀行可以採用內部模型法(internal model-based approach)來計算市場風險資本金。內部模型法採用在險價值及在《1996年修正案》中給出的公式來計算市場資本金數量。大部分規模較大的銀行都希望採用內部模型法,因為採用該方法可以充分反映分散風險帶來的好處,因此內部模型法計算出的市場資本金數量往往低於標準法。
在內部模型法中,計算在險價值VaR要求的設定為10天展望期和99%置信度。其含義是10天內有1%的可能性,損失會超出的數字。資本金要求是
max(VaRt-1,mc×VaRavg)+SRC
(15-3)
其中mc為乘積因子,SRC是指特定風險資本金(specific risk charge)數量。變量VaRt-1是前一天的在險價值,VaRavg是過去60天在險價值的平均值。因子mc的最小值為3,當監管部門發現銀行的內部模型有缺陷時,該值也可能會更大。稍後我們會對這一點做進一步的解釋。
式(15-3)中的第一項覆蓋了主要市場變量的變動帶來的風險,如利率、匯率、股票指數和大宗商品價格等。第二項SRC則反映了與某特定企業相關的風險,如公司股票價格或信用價差的變動。
考慮第一項並假設mc=3。在大多數情況下,最近的VaR,即VaRt-1,會小於過去60天VaR的均值的3倍。因此,在大多數情況下,應對大部分市場變量變動的資本金要求為
3×VaRavg
計算VaR的最常見方法是第13章中介紹的歷史模擬法。如在第12章中介紹的,幾乎所有的銀行都會首先計算1天99%的VaR。監管機構在制定《1996年修正案》時,明確說明了10天99%的VaR可由1天99%的VaR乘以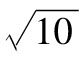 得出。也就是說,當按照資本金要求計算mc倍的10天99%的VaR的均值時,其本質是計算
得出。也就是說,當按照資本金要求計算mc倍的10天99%的VaR的均值時,其本質是計算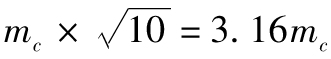 乘以1天99%的VaR的均值。如果mc=3,也就是1天VaR均值的9.48倍。
乘以1天99%的VaR的均值。如果mc=3,也就是1天VaR均值的9.48倍。
接下來考慮特定風險資本金。一種可以帶來特定風險的金融產品為企業債券。企業債券包含兩種風險:利率風險及信用風險。利率風險已經反映在式(15-3)的第一項中,而信用風險則由SRC來捕捉。[2]《1996年修正案》提出了計算SRC的標準方法,但同時也允許銀行在取得監管機構批准以後,採用內部模型法。
採用內部模型計算SRC同樣採用10天展望期、99%的置信度。監管資本金的計算也要將在險價值乘以一個因子(類似mc)。這一因子的最小值為4,而且最終求得的資本金不得低於標準方法給出的資本金的50%。第21.5節給出了計算SRC的一種方法。
在完成實施《1996年修正案》後,銀行(實施內部模型的銀行)的整體資本金包括:①等於風險加權資產(RWA)8%的信用風險資本金;②本節介紹的市場風險資本金。為了方便起見,針對市場資本金,RWA等於12.5乘以由式(15-3)計算所得的數量。這意味著信用及市場資本金的總和為
整體資本金=0.08×(信用風險加權資產+市場風險加權資產)
(15-4)
對於應對市場風險的資本類型,銀行有更多選擇。銀行可以採用第一類資本及第二類資本,甚至還可以採用第三類資本。第三類資本包括原始期限至少為2年的次優先級無抵押並無付款拖欠的短期債券(第三類資本在《巴塞爾協議Ⅲ》中被取消了)。
回溯測試
BIS修正案要求銀行在計算1天99%置信度的VaR以後,要通過過去250天的歷史數據進行回溯測試。如第12.10節所示,測試過程中需要將銀行目前計算VaR的程序應用到過去最近250天的情景。如果在某一天的實際損失超出了計算出的當天的VaR,這一天就被稱為例外。進行計算時,通常考慮兩種情況:①針對所考慮的某一天,計算中包括交易組合在當天的變化;②計算中假定交易組合在這一天沒有變化(監管機構通常對前一種情景更加關心)。
如果在過去250天內,例外天數小於5,則因子mc通常被設定為3;如果例外天數為5、6、7、8、9,則mc分別被設定為3.4、3.5、3.65、3.75、3.85。銀行監管當局通常有權來決定是否要實施更高的係數。當根據例外次數可以確認模型確實有缺陷時,監管當局往往會選取更高的參數來作為懲罰。在例外是由交易組合的變化所引發的情況下,監管當局可以考慮選取更高的mc,但並不一定要實施。當例外發生的原因完全是由於運氣差時,修正案並沒有給監管當局提出建議。當例外天數為10天或更多時,修正案要求係數等於4。練習題15.18從我們在第12.10節討論的統計檢驗的角度,對以上指導意見進行了討論。
[1] 如果某些非交易賬戶中的頭寸是為了對衝交易賬戶中的風險敞口,這些交易也需要包括在市場資本金的計算中。
[2] 如前所述,根據《1996年修正案》1988年信用風險資本金不適用於交易賬戶中的債券。
15.7 《巴塞爾協議Ⅱ》
《1988年巴塞爾協議》顯著地改善了資本金的計算方法,但仍存在許多明顯的弱點。在《1988年巴塞爾協議》中,銀行對所有企業的貸款權重均為100%,只要貸款金額相同,所需求的資本金也相同。也就是說,從資本金的角度,銀行對一個信用等級為AAA的企業發放貸款的處理方式與對一個信用等級為B的企業發放貸款的處理方式是相同的。[1]另外,《1988年巴塞爾協議》沒有考慮對違約相關性進行建模。
1999年6月,巴塞爾委員會提出了一個新提案,這一提案被稱為《巴塞爾協議Ⅱ》,並在2001年1月及2003年4月得到了修正。經過一系列的定量影響測算(quantitative impact studies,QIS)後,協議的制定人員初步驗證了協議的可應用性,並對協議所要求資本金的數量有了一定的認識。[2]2004年6月,協議最後一部分條款得到了所有參與成員的共識。2005年11月提案又得到了進一步更新。再經過又一輪的定量影響測算後,該協議在2007年得到實施。
《巴塞爾協議Ⅱ》對於活躍的大型國際銀行較為適用,而對於美國許多地區性小銀行,美國的監管部門認為《巴塞爾協議Ⅱ》對它們並不適用(對這些小銀行監管部門採用與《巴塞爾協議Ⅰ》類似的《巴塞爾IA協議》)。在歐洲,銀行無論大小都必須採用《巴塞爾協議Ⅱ》,另外,歐盟規定證券公司也像銀行那樣採用《巴塞爾協議Ⅱ》。
《巴塞爾協議Ⅱ》基於三個“支柱”:
(1)最低資本金要求;
(2)監督審查過程;
(3)市場紀律。
在第一支柱中,《巴塞爾協議Ⅱ》對於銀行賬戶中的信用風險計算採用了新的計算方式,這一方式體現了對手(借款方)的信用風險。對於市場資本金,《巴塞爾協議Ⅱ》相對於《1996年修正案》沒有改變。《巴塞爾協議Ⅱ》增加了操作風險資本金的內容。在《巴塞爾協議Ⅰ》中,銀行持有的資本金數量(至少)為風險加權資產(RWA)的8%,《巴塞爾協議Ⅱ》對這一要求保持不變。如果對於某一風險的資本金是直接計算的,而不是通過RWA,那麼我們要將資本金乘以12.5,將其轉換為與RWA等價的量。因此,我們得出以下關係式
整體資本金=0.08×(信用風險RWA+市場風險RWA+操作風險RWA)
(15-5)
第二支柱是關於監督審查過程,這部分包括了銀行風險管理手段中定量和定性兩個方面的內容。監管部門有責任確保銀行建立了可靠的流程,以保證資本金水平能夠維持。協議指出,銀行的資本金水平應高於監管規則指定的最低標準,以應對資本金要求的起伏以及在短期內增加資本金時可能面臨的困難。協議允許不同國家的監管機構對協議的實施方式採取一定的靈活性(以更好地適應當地的情況),但要求協議條款的實施具有總體上的一致性。第二支柱更加強調監管部門在問題發生時要儘早介入。監管部門所做的工作不應僅侷限於確保銀行的資本金達到最低要求,還應包括鼓勵銀行開發和採用更好的風險管理手段,並對這些手段進行評估。監管部門還應對《巴塞爾協議Ⅱ》第一支柱中沒有涉及的風險(如集中風險)進行評估,並且在發現不足時與銀行開展積極的對話。
第三支柱是關於市場紀律,這一支柱要求銀行需要更多的披露資本金分配以及所承擔風險的信息。這一支柱的根本出發點是使股東或潛在股東獲得更多有關風險管理決策的信息,這種透明度的增加會促使銀行在做出這些決策時更加嚴謹。
[1] 信用等級劃分已在第1.7節中討論。
[2] 定量影響測算忽略了在新協議實施以後,銀行可能調整其投資組合結構來使得資本金需求量達到最小這一事實。
15.8 《巴塞爾協議Ⅱ》中的信用風險資本金
關於信用風險資本金的計算,在《巴塞爾協議Ⅱ》中,銀行有以下三種選擇:
(1)標準法;
(2)基礎內部評級(internal rating based,IRB)法;
(3)高級內部評級法。
但是,美國(如上所述,只對大銀行實行《巴塞爾協議Ⅱ》)決定只採用基礎內部評級法。
15.8.1 標準法
如果某些銀行的管理在監管部門看來還不夠成熟,沒有達到採用內部評級法的程度,這些銀行可以採用標準法來計算資本金。標準法與《巴塞爾協議Ⅰ》類似,其不同之處在於風險權重的不同,[1]表15-4是對某些新規則的一個總結。將表15-4同表15-1進行比較,我們看到一家銀行所在的國家是否擁有OECD身份在《巴塞爾協議Ⅱ》中已經不重要。對於一個主權國家的風險敞口的權重範圍為0~150%,而對於一家銀行或企業的風險敞口的權重範圍為20%~150%。在表15-1中,OECD國家銀行的信用風險被認為小於企業風險,OECD銀行的風險權重為20%,企業的風險權重為100%,而表15-4對於銀行及企業的處理方式較為接近。表15-4有一點非常有趣,如果一個國家、企業或銀行的信用評級很差,其風險權重可能比沒有信用評級的情況還要差,監管機構允許銀行對自己註冊地的國家或國家央行的敞口採用更低的風險權重(20%對應於50%,50%對應於100%,100%對應於150%)。
表15-4 《巴塞爾協議Ⅱ》標準法中關於國家、銀行及企業的風險權重(面額的比率)與信用級別有關

①包括對國家央行的風險敞口。
②國家監管機構有選擇權。
在《巴塞爾協議Ⅱ》的標準法中,住房抵押貸款的風險權重為35%,其他零售貸款的風險權重為75%。如果是針對銀行的風險敞口,那麼計算規則會更加複雜。除了採用由表15-4給出的風險權重,國家監管部門可以選擇根據銀行註冊國的主權評級來確定資本金要求。如果銀行註冊國的評級介於AAA及AA-之間,那麼風險權重為20%;如果註冊國的評級介於A+與A-之間,那麼風險權重為50%;如果註冊國的評級介於BBB+與B-之間,那麼風險權重為100%;如果註冊國的評級低於B-,那麼風險權重為150%;如果註冊國沒有評級,那麼權重為100%。另外一個複雜之處是如果國家監管部門採用表15-4定義的規則,則對於期限小於3個月的貸款處理可能更有利,當借款方信用級別介於AAA與BBB-之間時,權重為20%;當借款方信用級別介於BB+與B-之間時,權重為50%;當借款方信用級別低於B-時,權重為150%;對應於無信用級別的情形,權重為20%。
2017年12月,巴塞爾委員會創建了一個更加細化的標準化方法,用於確定信用風險敞口的風險權重。在某些情況下,它還限制了高級IRB法的使用。如第16.4節所述,修訂後的標準化方法將為確定總資本要求提供依據。
【例15-5】 假定一家銀行資產的構成為貸款方信用評級為A級的1億美元貸款、1 000萬美元信用評級為AAA級的政府債券及5000萬美元房屋貸款。《巴塞爾協議Ⅱ》標準法所計算的風險加權資產總和為(以百萬美元計)
0.5×100+0.0×10+0.35×50=67.5
即6 750萬美元,而《1988年巴塞爾協議》所計算的風險加權資產總和為12 500萬美元(見例15-1)。
15.8.2 對於抵押品的調節
關於抵押品,銀行可以採用兩種辦法來調整其風險權重。第一種方法被稱為簡單法(simple approach),這一方法同《1988年巴塞爾協議》中的方法類似;第二種方法被稱為綜合法(comprehensive approach)。對於銀行賬戶中的資產,銀行有權在兩種方法中任選其一,而對於交易賬戶中的資產,在計算交易對手信用資本金時,銀行只能採用綜合法。
在簡單法中,對應於抵押品所覆蓋的風險敞口部分,交易對手的風險權重被抵押品的風險權重所代替(這裡的敞口是通過淨額結算所得),對於抵押品不覆蓋的部分,仍然採用交易對手所對應的風險權重。抵押品所對應的最小權重為20%,[2]抵押品的價格必須要每6個月重新定價一次,抵押品的期限一定要大於風險敞口的期限。
在綜合法中,銀行要向上調整風險敞口的計算以反映將來市場變化可能造成的風險敞口的增大,同時銀行應減少抵押品的估值以反映市場變化可能造成的抵押品價格的下降[3](具體調整的幅度與敞口及抵押品價格變化的波動率有關)。在進行調節後,新的風險敞口等於調整以後的風險敞口超出調整後的抵押品價值的餘額,然後,我們將交易對手所對應的風險權重用於新的風險敞口得出風險加權資產。對於風險敞口及抵押品價值的調整,銀行可採用《巴塞爾協議Ⅱ》中所設定的規則來進行計算,或者在經過監管部門批准之後,採用內部模型進行計算。當存在淨額結算約定時,風險敞口及抵押品價值的淨額結算要分開進行,各調節量的計算中要進行加權平均。
【例15-6】 假定一家銀行對於某交易對手的風險敞口為8 000萬美元,對應的抵押品的價值為7000萬美元。抵押品由信用評級為A的一家公司的債券組成,交易對手的信用級別為B+。對應於交易對手的權重為150%,而對應於抵押品的權重為50%,在簡單法下銀行的頭寸所對應的風險加權資產為
0.5×7 000+1.5×1 000=5 000(萬美元)
考慮綜合法,假定風險敞口在今後可能會增加10%,而抵押品價值可能會減少15%,因此經過調整後的風險敞口為1.1×8 000-0.85×7 000=2 850萬美元,對應於這一敞口的風險權重為150%,我們得出風險加權資產為4 275萬美元。
15.8.3 內部評級法
圖15-1顯示了內部評級法模型的基本思路。監管機構將資本金建立在在險價值(VaR)的基礎上,而在險價值的計算要選定1年展望期及99.9%的置信區間。它們認識到金融機構在產品定價時往往已經考慮了預期損失(例如,銀行貸款利率的設定要能夠覆蓋貸款預期損失),資本金應等於在險價值減去預期損失。
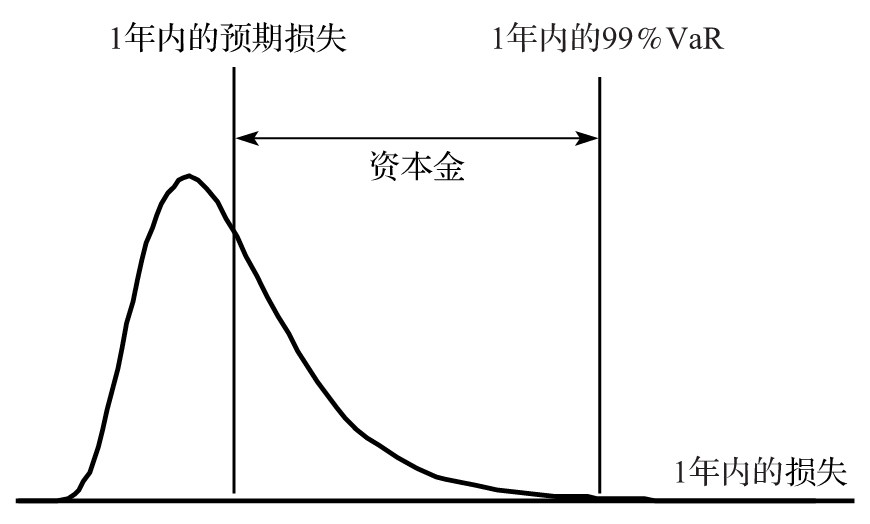
圖15-1 損失概率密度函數以及金融機構所需要的資本金
這裡VaR的計算基於第11.6節中的違約時間單因子高斯Copula模型。假定某銀行的債務人很多,每個債務人在1年內的違約概率均為PD,債務人之間的Copula相關係數均為ρ。[4]如第11.6節所示,我們定義
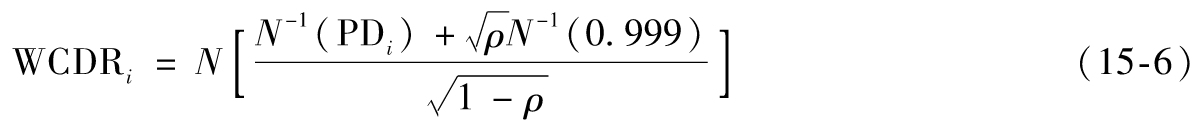
其中WCDRi為“最壞情況下的違約概率”(worst-case default rate),即銀行有99.9%的把握,下一年第i個交易對手的違約可能性不會超過該數。Gordy(2003)[5]的研究表明,對一個大的交易組合(貸款、貸款承諾、衍生產品等),如果相關性ρ相同,則1年展望期、99.9%置信度的VaR近似於
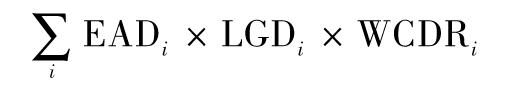
其中EADi為第i個交易對手在違約時的風險敞口,LGDi為第i個交易對手違約的情況下的損失率。變量EADi是一個貨幣量,是指在違約發生時,第i個交易對手欠款的數量。變量LGDi是相對EADi的一個比例值,是指在違約時損失所佔EADi的比率。例如,在債務人違約時,如果一家銀行能收回貸款的30%,則LGDi=0.7。
違約造成的預期損失為
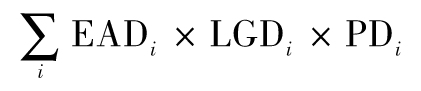
圖15-1所示的資本金等於99.9%置信度所對應的最壞損失減去預期損失,即
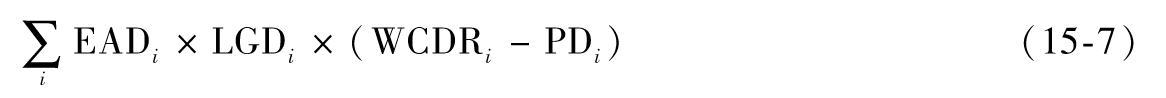
現在我們去掉下標,對一個交易對手,定義:
PD——交易對手在1年內違約的概率(表示為小數);
EAD——違約時的敞口(貨幣值);
LGD——當違約損失率或違約發生時,敞口中損失的比例(表示為小數)。
表15-5顯示了在高斯Copula模型中,WCDR與PD及ρ有關。當ρ=0時,因為資產之間沒有相關性且每一年的違約率相等,所以WCDR=PD;當ρ增加時,WCDR也會隨之增加。
表15-5 1年期、99.9%置信區間的WCDR與PD及ρ的關係

15.8.4 違約風險敞口
在基礎IRB法中,對衍生產品的EAD的計算通常基於《巴塞爾協議Ⅰ》[6]中的CEM方法。在高級IRB法中,銀行可以使用其內部模型來計算EAD。
使用內部模型的第一步是計算未來若干時間內每個交易對手的預期風險敞口(EE,通常涉及蒙特卡羅模擬和第20章討論的方法)。在未來時間t的有效預期風險敞口(有效EE)是時間0到時間t之間的最大EE。EAD設置為有效預期正風險敞口的1.4倍,該值是第一年有效EE的平均值。[7]
15.8.5 對企業、主權國家及銀行的風險敞口
對於企業、主權國家及銀行的風險敞口,《巴塞爾協議Ⅱ》根據實證研究結果,假定相關係數ρ與違約概率之間存在如下關係式[8]
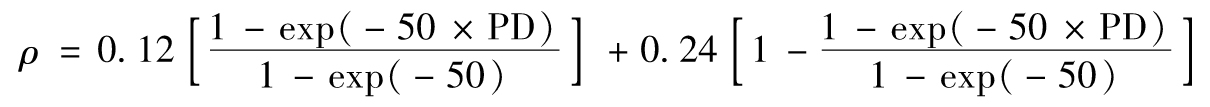
因為數量exp(-50)非常小,所以這一公式實際可以近似為
ρ=0.12(1+e-50×PD)
(15-8)
當PD增加時,ρ會減小。造成這種PD與ρ之間的反向關係的原因如下:當某家企業信用惡化時,企業所對應的PD會增大,此時公司的違約概率會變得更加獨立,市場整體情況對該企業違約概率的影響會變得越來越小。
結合式(15-8)與式(15-6),我們得出表15-6,該表展示了WCDR與PD的關係。如同我們預計的那樣,WCDR是PD的一個遞增函數,但是,如果我們假定ρ與PD無關時,WCDR增長速度並不快。
表15-6 企業、政府和銀行的WCDR與PD的關係

對一個交易對手,資本金的計算公式為
EAD×LGD×(WCDR-PD)×MA
(15-9)
以上公式中前三項的含義已經在關於式(15-7)的討論中解釋過,變量MA是針對期限的調節,這一數量由如下公式決定

其中
b=[0.118 52-0.054 78×ln(PD)]2
M為敞口的期限。針對期限的調整是因為考慮以下情況:當產品的期限大於1年時,1年的信用風險敞口可能會因為對手信用評級降低或違約而增加(當M=1時,MA=1,此時期限調整無任何效果)。如第15.7節所述(見式(15-5)),風險加權資產(RWA)等於12.5乘以資本金
RWA=12.5×EAD×LGD×(WCDR-PD)×MA
因此,資本金等於RWA的8%,其中4%應為第一類資本。
在基礎IRB法中,銀行提供參數PD,而其他參數LGD、EAD及M是由巴塞爾委員會來設定的。針對銀行和企業的風險敞口,需要設置PD的下限0.03%。對於高優先級索賠(senior claims),LGD被設定為45%,而對於次優先級索賠(subordinated claims),LGD被設定為75%。當存在抵押品時,為了應用前述綜合法,我們首先需要將LGD下調,下調的比例等於經調整後的抵押品價值與經調整後的風險敞口的比例。經調整的風險敞口及抵押品的價值都需要以綜合法進行計算。對衍生產品,EAD的計算與《1988年巴塞爾協議》中計算衍生產品等價信用量的方法類似(即當前敞口加附加項),計算中應考慮淨額結算的效應,在大多數情況下M=2.5。
在高級IRB法中,對企業、主權國家及其他銀行的敞口,銀行均提供自己對PD、LGD、EAD及M等參數的估計。信用風險緩釋措施,例如降級觸發,會減小PD的數值(對於PD,有一個與基礎IRB法類似的要求,那就是PD的下限不能低於0.03%)。影響LGD的兩個主要因素為債券的優先級別及抵押品。在計算EAD時,銀行可以在取得監管機構的批准後使用自己的模型。當涉及衍生產品時,模型往往會使用蒙特卡羅模擬來決定在未來1年內,預期敞口(考慮了淨額結算及抵押品以後)會如何變化。
由式(15-9)給出的資本金是用於覆蓋在1年內、99.9%置信度之下非預期損失不會超過的數量(如前面所述,預期損失應該已經包含在銀行對產品的定價中)。WCDR對應於(理論上)千年一遇的違約概率。巴塞爾委員會保留了當由式(15-9)所得出的資本金過高或過低時,對其施加某乘積因子的權利(這裡的乘積因子可能大於1,也可能會小於1),這一因子通常為1.06。
【例15-7】 假定某銀行的資產構成為企業貸款,貸款的總面額為1億美元,借款方的信用等級為A,對於企業的PD的估計為0.1%,LGD為60%,貸款的平均期限為2.5年,這意味著
b=[0.118 52-0.054 78×ln(0.001)]2=0.247
因此

由表15-6,我們得出WCDR為3.4%,在《巴塞爾協議Ⅱ》基礎IRB法中,對於企業貸款的風險加權資產的總量為
12.5×100×0.6×(0.034-0.001)×1.59=39.3(百萬美元)=3 930(萬美元)
《巴塞爾協議Ⅰ》所對應的資本金為1億美元,而由《巴塞爾協議Ⅱ》標準法所計算的數量為5 000萬美元(見例15-1及例15-5,這裡的1億美元貸款只是以上例子中投資組合的一部分)。
15.8.6 零售貸款敞口
零售貸款的資本金計算方法與對企業、政府及銀行敞口的資本金計算方法相似,其不同之處在於這時基礎IRB法與高級IRB法合併成了一個方法。每家銀行都可以對參數PD、EAD及LGD進行估計。在計算中沒有對於期限的調節,計算資本金的公式為
EAD×LGD×(WCDR-PD)
風險加權資產為
RWA=12.5×EAD×LGD×(WCDR-PD)
其中WCDR由式(15-6)計算得出。對於住房抵押貸款,ρ被設定為0.15;[9]對於合格滾動貸款,ρ被設定為0.04;計算其他零售敞口的WCDR所採用的ρ由以下公式得出

因為exp(-35)的數量很小,所以以上公式與以下公式基本等同於
ρ=0.03+0.13e-35×PD
(15-11)
將式(15-11)同式(15-8)進行比較,我們得出對於零售貸款所採用的相關性要比其他貸款低得多。類似於表15-6,表15-7顯示了零售貸款的WCDR與PD的關係。
表15-7 關於零售貸款,1年期、99.9%置信區間的WCDR與PD之間的關係

【例15-8】 假定某銀行資產由5 000萬美元貸款組合構成,其中PD的估計值為0.005,LGD的估計值為20%。對於這一情形,ρ=0.15及
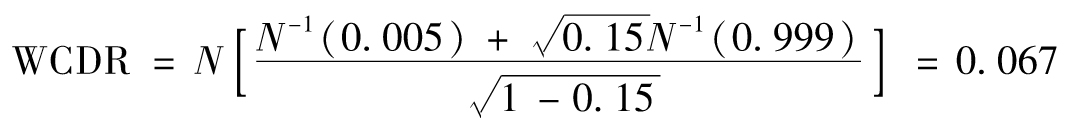
風險加權資產為
12.5×50×0.2×(0.067-0.005)=7.8(百萬美元)
與此相對照,《巴塞爾協議Ⅰ》所對應的風險加權資產為2 500萬美元,《巴塞爾協議Ⅱ》標準法所對應的風險加權資產為1750萬美元(見例15-1及例15-5,這裡討論的5 000萬美元房屋貸款只是投資組合結構的一部分)。
15.8.7 信用擔保以及信用衍生產品
傳統上巴塞爾委員會對於信用擔保和信用衍生產品(如信用互換)所採用的處理方法為信用替換方法。假定一家信用評級為AA級的公司給一個信用評級為BBB級的借款方提供貸款擔保。在計算資本金時,信用擔保方的信用級別(AA級)而不是借款方的信用級別(BBB級)被用於計算資本金,因此,這筆貸款看上去好像是貸給了一家AA級的公司。然而這種計算方式仍然誇大了信用風險,因為只有當擔保方及借貸方同時破產時才會造成貸款損失(而且擔保方要在借款方破產之前就已經破產)。[10]巴塞爾委員會對這一問題做了處理。2005年7月,委員會對《巴塞爾協議Ⅱ》中的雙重破產問題發表了一個報告,這一報告對於雙重破產做了特殊處理。[11]這一方法代替了信用替換方法,銀行首先在風險敞口沒有任何擔保的假設下進行資本金的計算,完成計算後將資本金再乘以0.15+160×PDg,其中PDg 為擔保人的1年期的違約概率,最後的計算結果即為最終的資本金數量。
[1] 採用新權重計算的比率有時被稱為麥克唐納比率,即以巴塞爾委員會主席威廉·麥克唐納(William McDonough)來命名。
[2] 當抵押品為與敞口相同幣種的現金或政府債券時,這一規定並不成立。
[3] 對於貸款,這一調整並不是十分必要的,而對於場外型的衍生產品,就十分有必要,該調整是在附加因子之上的額外調整。
[4] 注意,巴塞爾委員會的文件對Copula相關係數採用的符號為R,而不是ρ。
[5] See M. B. Gordy, “A Risk-Factor Model Foundation for Ratings-Based Bank Capital Ratios,” Journal of Financial Intermediation 12(2003):199-232.
[6] 正如將在16.4節討論的那樣,此規定是根據被稱為SA-CCR的法規變更進行修訂的。
[7] 見巴塞爾銀行監管委員會,“The Application of Basel II to Trading Activities and the Treatment of Double Default Effects,” July 2005。
[8] See J. Lopez, “The Empirical Relationship between Average Asset Correlation, Firm Probabilityof Default, and Asset Size,” Journal of Financial Intermediation 13, no.2(2004):265-283.
[9] 根據我們從金融危機所觀察到的,這個值有可能過低了。
[10] 第19章將要討論的信用違約互換(CDS)為違約提供了保險,對於CDS的處理方式與對信用擔保處理方式類似。
[11] See Bank for International Settlements, “The Application of Basel II to Trading Activities and the Treatment of Double Defaults,” July 2005,這一文獻可在www.bis.org上下載。
15.9 《巴塞爾協議Ⅱ》對於操作風險的處理
除了對銀行計算信用風險資本金的方法進行了改進,對於操作風險,《巴塞爾協議Ⅱ》也提出了資本金要求。操作風險源於多個方面,包括銀行內部的流程出現失誤及銀行外部突發的不良事件(比如關鍵設施發生火災)等。
監管機構允許銀行採用以下三種方法來計算操作風險資本金:
(1)基本指標法;
(2)標準法;
(3)高級計量法。
具體採取以上的哪一種方法取決於銀行管理的先進程度。三種方法中最簡單的是基本指標法,該方法下所需要的資本金等於銀行過去3年毛收入的平均值乘以0.15。[1]標準法與基本指標法較為接近,兩種方法的不同之處在於,在標準法中,不同的業務類別所對應的計算因子會有所不同。在高級計量法中,銀行採用自己的內部模型來求得在1年展望期及99.9%置信度下所對應的損失。類似於用於計算信用風險資本金的內部評級法,操作風險資本金等於該損失減去預期損失。採用高級計量法的一個好處在於,這一方法在一定條件下允許銀行考慮保險措施所帶來的風險緩解效應。我們將在第23章中進一步討論操作風險。
如第23章所述,監管機構認為高級計量法並不成功,因此在2016年提出一種新的、更簡單的方法替代它。
[1] 毛收入等於淨利息收入加上非利息收入,淨利息收入等於貸款利息收入與存款以及其他支撐貸款產品利息支出的差值。負毛收入的年份在計算中應該忽略。
15.10 第二支柱:監督審查過程
《巴塞爾協議Ⅱ》中的第二支柱是關於監督審查過程。對此,《巴塞爾協議Ⅱ》提出了4項重要原則:
(1)銀行必須根據自身的風險特徵,建立評估自身資本金充足狀況的過程,並且制定維持資本充足的戰略。
(2)監管機構必須審查和評估銀行內部的資本充足率評估系統,以及銀行監控並保證資本充足率合規的能力。監管機構如果對檢查結果不滿意,應採取適當的監管措施。
(3)監管機構應期望銀行在實際運營中所持的資本金高於最低的監管資本金要求,同時監管機構應該具有要求銀行持有超額資本金的能力。
(4)監管機構在發現問題時應儘早介入,以防止銀行持有的資本金低於支撐其風險特徵的最低資本金水平;如果資本充足率沒有維持或者回升,則監管機構應督促銀行及時採取補救措施。
巴塞爾委員會建議,各國監管部門對於銀行賬戶上的利率風險、信用風險及操作風險要特別注意。信用風險管理的關鍵點包括銀行所用的壓力測試、違約的定義、信用風險集中度,以及與使用抵押品、信用擔保及信用衍生產品相關聯的風險等。
巴塞爾委員會還強調監管機構的監督審查過程應透明並落實責任。當監管機構在審查過程中需要酌情做出自己的判斷或者設定的資本金要求高於《巴塞爾協議Ⅱ》規定的最低資本金要求時,這一點顯得尤其重要。
15.11 第三支柱:市場紀律
《巴塞爾協議Ⅱ》的第三支柱是關於要求銀行增加風險評估過程及資本充足率的信息披露。監管機構對信息披露的強制性程度在不同國家也各不相同。但是,銀行一般不會忽視監管機構的建議,因為監管機構可以使銀行管理人員的日子很難過。有時銀行為了能夠被准許採用特別的模型來計算資本金,必須披露更多的管理信息以增加透明度。
監管部門所要求的信息披露同財務信息披露可能不同,監管部門要求披露的信息並不一定出現在年度報告中,銀行有權決定什麼樣的信息是相關且重要的,應予披露。這些信息應包括:
(1)銀行的什麼部門實施了《巴塞爾協議Ⅱ》,對不實施《巴塞爾協議Ⅱ》的部門進行了什麼樣的調整;
(2)資本金構成產品的期限及條件;
(3)構成第一類資本的產品類型以及每種類型產品在第一類資本金中的佔有比率;
(4)第二類資本的數量;
(5)對應於信用、市場及操作風險的各項資本金的數量;
(6)銀行面臨的其他風險以及對不同風險的評估方法的信息;
(7)風險管理部門的結構以及運作方式。
15.12 《償付能力法案Ⅱ》
如第3.11節所述,當前對於保險公司監管還沒有一個國際標準。在美國,保險公司的監管是各州的職責。美國保險監理官協會(NAIC)對各州的監管提供一定的協助。在歐洲,保險公司的監管是由歐盟來負責的。在歐洲已經延續多年的監管框架,即《償付能力法案Ⅰ》在2016年被《償付能力法案Ⅱ》替代。《償付能力法案Ⅰ》中的資本金計算僅僅考慮了保險承保風險,而在《償付能力法案Ⅱ》中,投資風險和操作風險也被考慮進來。
《償付能力法案Ⅱ》與《巴塞爾協議Ⅱ》有許多相似之處。《償付能力法案Ⅱ》也有三個支柱,第一支柱是關於資本金計算以及資本金的種類;第二支柱是關於監督審查過程;第三支柱是關於面向市場的風險管理信息披露。因此,我們可以看到這三個支柱類似於《巴塞爾協議Ⅱ》的三個支柱。
《償付能力法案Ⅱ》的第一支柱闡明瞭最低資本要求(minimum capital requirement,MCR)和償付能力資本要求(solvency capital requirement,SCR)。如果保險公司的資本金低於SCR的水平,那麼保險公司至少要向監管當局提交一個計劃,闡明如何將資本金恢復到SCR水平之上。監管機構也許會要求保險公司採取特殊措施來改善資本金現狀。MCR是保險公司資本金水平的絕對最低限度,如果資本金低於MCR水平,那麼監管當局可以要求保險公司不再承接新業務。這可能會造成保險公司破產清算,並將保單轉移給其他公司。MCR通常為SCR的25%~45%。
對於SCR,有兩種計算方式:一種是標準法,二是內部模型法。在內部模型法中,VaR的計算要採用1年展望期和99.5%的置信度(這裡採用的置信度低於《巴塞爾協議Ⅱ》中99.9%置信度的要求)。保險公司可以採用更長的時間段以及較低的置信度,只要資本金提供的保護是相當的。SCR包括投資風險、承保風險和操作風險。投資風險可以被細分為市場風險和信用風險;承保風險可以進一步以風險來源分類,即來自人壽保險、非人壽保險(即財產及意外傷害險)以及健康保險業務。
資本金可以用於抵禦重大不利事件,在定量影響測算中,這些不利事件包括:
(1)全球股市32%的下跌;
(2)房屋市場20%的下跌;
(3)匯率20%的變化;
(4)一些影響財產及意外傷害險的償付的特定災難情景;
(5)醫療健康服務的費用增長為歷史費用標準差的某個倍數;
(6)死亡率增加10%;
(7)死亡率減小25%;
(8)承保費用增加10%。
保險公司的內部模型要滿足三個測試。第一個測試是統計質量測試(statistical quality testing),這一測試是關於計算VaR的數據和方法的合理性;第二個測試是校正測試(calibration test),這一測試用來檢驗對風險的評估是否與一般的SCR目標準則一致;第三個測試是使用測試(use test),這一測試用來檢驗模型是否真正與風險管理人員切實相關,並被他們所使用。
《償付能力法案Ⅱ》的資本金有三種。第一類資本由股權資本、留存收益和其他等價的資金來源構成;第二類資本由優先級低於投保人保單的借貸組成,這些借貸要滿足在不利條件(wind-down scenarios)下的可獲得性;第三類資本也由優先級低於投保人保單的借貸組成,但這些借貸不需要滿足以上的可獲得性條件。類似於《巴塞爾協議Ⅱ》,《償付能力法案Ⅱ》也闡明瞭SCR中第一類、第一類+第二類、第一類+第二類+第三類資本金構成比例的限制。
小結
這一章是對全球範圍內銀行所面臨的資本金要求的一個綜述。自20世紀80年代以來,監管機構對銀行所持有的最低限度資本金計算方法的要求發生了巨大變化。1988年以前,監管機構通常按資本金同資產的最低比率或資產同資本金的最高比率來設定資本金要求。20世紀80年代末,銀行監管機構以及銀行業自身都認識到對資本金計算方法進行變革的必要性。衍生產品交易的迅猛發展以及銀行在全球範圍內業務競爭的需要,促使監管機構頒佈一個全球性的、統一的銀行管理條約,以保證公平競爭。
《1988年巴塞爾協議》對錶內及表外的信用風險敞口都設定了資本金要求。計算過程中對錶內項目,都要計算風險加權資產。對一筆表內貸款,其對應的風險加權資產數量等於貸款本金乘以借貸方所對應的風險權重。而對於互換等衍生產品,銀行首先要計算等價風險量,最終的風險加權資產等於等價風險量乘以交易對手的風險權重。銀行持有的資本金數量不能低於整體風險加權資產的8%。1995年,巴塞爾委員會對信用風險量的計算進行了修改,在計算中允許淨額結算。1996年,作為一個新的修正案,對市場風險也設定了資本金要求。具有先進管理水平的銀行可以採用在險價值來計算資本金。
1999年,巴塞爾委員會又提出了《巴塞爾協議Ⅱ》。協議已在2007年左右被很多銀行實施。《巴塞爾協議Ⅱ》中關於市場風險資本金的條款沒有改動,但信用風險資本金的計算變得較以前更加複雜,這樣做的目的是反映借貸人的信用評級或銀行內部結合監管機構指定的相關參數對違約概率的估計。另外,在《巴塞爾協議Ⅱ》中增加了對操作風險資本金的要求。
《償付能力法案Ⅱ》是關於保險公司的監管框架,2016年在歐盟地區實施。這一法案對投資風險、承保風險和操作風險都設定了最低資本金要求。《償付能力法案Ⅱ》的整體框架與《巴塞爾協議Ⅱ》類似。
延伸閱讀

練習題
15.1 “當一家鋼鐵企業破產時,其他在同一行業的企業可能會受益,因為這時競爭對手少了一個。但是當一家銀行破產時,其他銀行並不一定受益。”請解釋這一觀點。
15.2 “存款保險制度使得銀行資本金監管制度變得更為重要。”請解釋這一觀點。
15.3 一個簡單利率互換涉及固定利率及浮動利率的互換,固定利率及浮動利率所對應的面額相等,在互換到期時本金不互換。當一家銀行進入一個期限為5年的利率互換時,互換面額為1億美元,銀行所面臨的信用風險的特徵是什麼?這裡假定在互換開始時,利率互換的價值為0。
15.4 在貨幣互換交易中,一個幣種的本金要同另一個幣種的本金進行交換,請說明為什麼貨幣互換交易的信用風險要大於利率互換中的信用風險。
15.5 某筆4年期的利率互換對於某金融機構有負價值,在交易中金融機構是否面臨信用風險?請對你的結論做出解釋。利用《巴塞爾協議Ⅰ》,計算對資本金的要求數量。
15.6 請採用《巴塞爾協議Ⅰ》來計算持有以下交易(交易對手為某企業)的一家銀行資本金的數量(計算中沒有淨額結算協議):
(a)一個9年期的利率互換,面額為2.5億美元,當前市價為-200萬美元;
(b)一個4年期的利率互換,面額為1億美元,當前市價為350萬美元;
(c)一個6個月期的商品衍生產品交易,面額為5 000萬美元,當前市價為100萬美元。
15.7 採用1995年對於《巴塞爾協議Ⅰ》有關淨額結算的改進,重新計算練習題15.6中的資本金數量。
15.8 某銀行與一個企業客戶之間的所有衍生產品合約的價值對銀行來說都為正值。在與該客戶簽署的主協議中,淨額結算條款會帶來什麼樣的價值?
15.9 請解釋為什麼在《巴塞爾協議Ⅱ》中最終計算要將信用風險(IRB)、市場風險及操作風險所對應的數值乘以12.5?
15.10 銀行的交易賬戶與銀行賬戶的區別是什麼?一家銀行當前持有一筆給某客戶的本金為1 000萬美元的貸款,在貸款結束時,客戶不再借貸,而是希望將自己的債券賣給銀行,這一變化會如何改變銀行監管資本金的數量?
15.11 在《巴塞爾協議Ⅰ》下,銀行不願意借錢給信用好的企業,而是希望幫助企業發行債券,這樣做是為什麼?你認為《巴塞爾協議Ⅱ》關於貸款的規定會影響銀行的行為嗎?
15.12 銀行有時會利用監管套利來降低資本金數量,這裡監管套利的含義是什麼?
15.13 式(15-9)給出了《巴塞爾協議Ⅱ》關於資本金的計算公式,這一公式將4項乘到一起,請解釋公式中每一項的含義。
15.14 請解釋因抵押品對資本金進行調整時,簡單法與綜合法的不同之處。
15.15 請解釋在《巴塞爾協議Ⅱ》中,計算信用風險資本金的標準法、IRB法及高級IRB法之間的差別。
15.16 請解釋在《巴塞爾協議Ⅱ》中,計算操作風險資本金的基本指標法、標準法及高級計量法之間的差別。
15.17 假定某銀行資產包括2億美元的零售貸款(並非住房抵押貸款),其PD為1%,LGD為70%,《巴塞爾協議Ⅱ》中IRB法所對應的風險加權資產為多少?對於第一類及第二類資本的需求為多少?
15.18 在第12.10節,我們討論瞭如何採用統計檢驗的方式來接受或拒絕一個VaR模型;在第15.6節,我們討論了銀行監管機構在計算監管資本時,如何設定乘數因子mc。在這一節中,我們指出在250個抽樣中,如果例外次數為5或更大,相應的乘數因子會增大,當VaR模型表現良好時,例外為5次或更多的概率為多大?
作業題
15.19 對於衍生產品,《巴塞爾協議Ⅰ》所要求附加量是什麼?“如果其中有關附加量的規定使附加量與合約的市場價格掛鉤,《巴塞爾協議Ⅰ》會更加完善。”你將如何說明這一觀點。
15.20 請採用《巴塞爾協議Ⅰ》來計算某銀行所持有的資本金,這家銀行同另一家銀行之間有以下合約(無淨額結算協定):
(a)一個期限為2年的遠期外匯合約,合約市價為200萬美元,合約要求銀行以5 000萬美元價值買入某數量外幣;
(b)一個期限為6個月的期權的多頭頭寸,期權標的資產為標準普爾500指數,面額為2 000萬美元,期權當前價值為400萬美元;
(c)一個期限為2年的石油商品互換合約,合約的面額為3 000萬美元,當前市值為-500萬美元。引入淨額結算條款會對以上計算產生什麼影響?
15.21 某銀行與某信用級別為AA的企業有以下交易:
(a)一個期限為2年的互換合約,面額為1億美元,當前價值為300萬美元;
(b)一個期限為9個月的外匯遠期合約,面額為1.5億美元,當前價值為-500萬美元;
(c)一個期限為6個月的期權的多頭頭寸,期權標的資產為黃金,面額為5 000萬美元,當前價值為700萬美元。
採用《巴塞爾協議Ⅰ》及無淨額結算協議所計算的資本金為多少?加入淨額結算協議對計算結果的影響是什麼?《巴塞爾協議Ⅱ》標準法所對應的資本金數量為多少?
15.22 假如一家銀行的資產包含給信用級別為BBB級的企業的5億美元貸款,貸款企業的PD估計值為0.3%,平均期限為3年,LGD的估計為60%,《巴塞爾協議Ⅱ》高級IRB法所對應的風險加權資產為多少?所需的第一類及第二類資本分別為多少?這與《巴塞爾協議Ⅱ》標準法及《巴塞爾協議Ⅰ》所計算的資本金數量有什麼不同?
第16章
《巴塞爾協議Ⅱ.5》《巴塞爾協議Ⅲ》及其他後危機修訂
《巴塞爾協議Ⅱ》的最終實施時間大體上和2007年金融危機的開始時間一致,此次危機是自20世紀30年代以來金融市場經歷的最大危機,這種巧合對《巴塞爾協議Ⅱ》的名聲來講是一個不幸。市場上有些觀點認為《巴塞爾協議Ⅱ》是造成危機的一個因素。這些觀點指出,正是因為銀行有自主權來計算PD、LGD和EAD等參數的值,將整個行業引入了自我監管的階段。然而,指責《巴塞爾協議Ⅱ》是不公平的,如第6章所述,在《巴塞爾協議Ⅱ》實施之前,危機的種子已經撒下。[1]
在本章的開始,我們首先討論《巴塞爾協議Ⅱ.5》。在目睹了銀行業在危機中遭受的慘重損失後,巴塞爾銀行監管委員會(Basel Committee on Banking Supervision)對市場風險資本金的計算進行了改進。《巴塞爾協議Ⅱ.5》是對這些改進的彙總,其實施期限是2011年12月31日。
本章的第二部分內容是《巴塞爾協議Ⅲ》,該版協議是對銀行監管條例的一項重大改進。《巴塞爾協議Ⅲ》發佈於2010年12月,其中包括一系列關於增加銀行信用風險資本金的規定,並且對合格資本金的定義進行了加強。另外,《巴塞爾協議Ⅲ》的一個重要新特點是對銀行面臨的流動性風險進行了闡述。該版本協議會在較長時段內逐步實施,最終實施完成的日期為2019年。
本章還將討論2008年來作為對巴塞爾委員會工作的補充所引入的其他監管規定,其中包括奧巴馬總統在2010年7月21日簽署的《多德-弗蘭克法案》,以及歐盟和英國設立的一些新的規定。
[1] 事實上,美國在《巴塞爾協議Ⅱ》實施方面曾落後於其他國家。如果在危機開始時,美國完成了對《巴塞爾協議Ⅱ》的實施,那麼美國諸多銀行的資本金比危機開始時的實際數量還要低。
16.1 《巴塞爾協議Ⅱ.5》
在信用危機中,市場參與者認識到巴塞爾協議框架下的市場風險資本金計算方法要進行調整。如上所述,這些調整在最後被歸結成《巴塞爾協議Ⅱ.5》。實施日期為2011年12月31日。[1]這些調整包括:
(1)壓力VaR的計算;
(2)加入了增量風險計提;
(3)對信用相關性產品設立的綜合風險計量。
這些措施極大地增加了大型銀行需要持有的市場風險資本金的數量。
16.1.1 壓力VaR
1996年提出的對《巴塞爾協議Ⅰ》的修正案首先引進了針對市場風險的資本金,其計算是基於10天展望期、99%置信度的VaR。大部分銀行採用基於歷史模擬的計算方法。我們已在第13章中對這一方法進行了闡述。在銀行採用1996年引入的規則前,歷史模擬法的假設是市場變量在某個交易日接下來一天的百分比變化可從該變量在過去的1~4年中,日百分比變化的歷史數據中隨機抽樣產生。2003~2006年市場變化的波動率較低,因此利用這一區間的數據所得出的市場在險價值從監管資本金的角度來看也偏低。另外,在危機開始後的一段時間內,VaR仍然持續偏低,因為此時用來計算VaR的大部分歷史數據仍然來自波動率較低的時期。
以上觀察到的現象促使巴塞爾委員會引入了壓力VaR的概念。如在第13.1.3節中介紹的,壓力VaR是基於市場在受壓的條件下的250天(即12個月),而不是僅由過去1~4年的變動數據求得的。當採用歷史模擬法計算壓力VaR時,市場變量在下一個交易日中的百分比變化量是從市場受壓條件下的250個交易日的日百分比變化量中抽樣得出的。
《巴塞爾協議Ⅱ.5》要求銀行計算兩個VaR值,其中之一是一般的VaR(即基於過去1~4年的市場變量變動數據),另一個就是壓力VaR(由市場受壓區間內的250個交易日的數據得出)。在計算了兩個VaR之後,銀行要對其進行彙總。計算資本金總量的公式為
max(VaRt-1,mc×VaRavg)+max(sVaRt-1,ms×sVaRavg)
其中VaRt-1和sVaRt-1分別為前一天的VaR和壓力VaR(基於10天展望期和99%置信度);VaRavg和sVaRavg分別為過去60天的平均VaR和壓力VaR(同樣是基於10天展望期和99%置信度)。參數mc和ms由銀行監管部門決定,其下限為3。如第15.6節解釋的那樣,在《巴塞爾協議Ⅱ.5》之前,資本金要求為
max(VaRt-1,mc×VaRavg)
由於壓力VaR不會小於正常的VaR值,以上公式說明(當mc=ms),在《巴塞爾協議Ⅱ.5》框架下,資本金數量至少是以前的兩倍。事實上,資本金要求提高兩倍的情況並不罕見。
起初,從業者普遍認為2008年的市場數據給壓力VaR的計算提供了很好的為期1年的樣本。後來大家才認識到,1年承壓期的選擇應該反映銀行本身的風險狀態。因此,現在銀行在計算壓力VaR時,要選取某個長度為1年的時間段,在該時間段內,銀行當前的投資組合會表現得非常差,因而不同銀行選擇的承壓期很有可能是不同的。
16.1.2 增量風險計提
2005年,巴塞爾委員會發現交易賬戶上的頭寸敞口要求的資本金低於銀行賬戶上的類似敞口並對此產生了擔憂。以一個債券為例,如果將債券放在交易賬戶上,如第15.6節所述,資本金數量等於以10天展望期和99%置信度計算的VaR再乘以一個係數;如果將此債券放在銀行賬戶上,如第15.8節所述,資本金數量等於以1年展望期和99.9%置信度計算的VaR值。交易賬戶所對應的資本金數量遠遠小於銀行賬戶所對應的資本金。由於這個原因,銀行往往更願意將與信用有關的產品放在交易賬戶上。[2]
於是,監管機構在2005年提出了增量違約風險計提(incremental default risk charge,IDRC)的概念。其中,資本金數量是以1年展望期和99.9%置信區度為基準。這一計提針對交易賬戶中對違約風險有敏感性的產品而設定。如果實施這一規則,這些產品的資本金要求會等於使用交易賬戶計算方法得出的資本金和使用銀行賬戶計算方法得出的資本金中的較大者。2008年,當巴塞爾委員會發現2007年和2008年信用市場危機時,大部分損失來自信用風險級別的變化、信用價差的增大以及市場流動性的消失,而不僅僅是違約的結果。因此委員會對前面的提案進行了修訂,以反映這些風險,於是IDRC演化為今天的增量風險計提(incremental risk charge,IRC)。[3]
增量風險計提要求銀行在計算與信用有關的產品資本金時,展望期為1年,置信度為99.9%。在計算過程中,銀行不僅要考慮違約可能性,還要考慮信用評級變化。與IDRC一樣,增量風險計提將資本金要求設定為利用交易賬戶計算和利用銀行賬戶計算獲得的資本金的最大值。因為增量風險計提是針對交易賬戶,假定銀行在1年的展望期中可以對投資組合進行調整,所以違約風險由此可以得到緩解。因此,銀行必須要對增量風險計提所覆蓋的產品的流動性展望期進行評估。流動性展望期(liquidity horizon)是指在市場受壓的情況下,銀行對產品進行平倉或對所有重大風險進行對衝所需要的時間。
假定一個信用等級為A級的債券的流動性展望期為3個月,當計算1年展望期的VaR時,銀行可以假定在第3個月的最後,如果債券評級發生改變或債券已經違約,銀行可以利用另一個類似的A級債券取代最初持有的A級債券。在第6個月和第9個月結束時可進行類似的操作。這一假設被稱為風險水平恆定假設(constant level of risk assumption)。
風險水平恆定假設造成的影響是違約的可能性會降低。但與此同時,為應對債券評級下降而對持倉進行調整會產生規模較小的損失。一般來說,風險水平恆定假設會使1年展望期、99.9%置信區間的VaR值變小。[4]巴塞爾委員會指定在計算增量風險計提時,採用的最小流動性展望期為3個月。
綜上所述,增量風險計提框架對於信用產品在1年展望期、99.9%置信度內的違約和信用等級變化風險提供了度量手段,同時考慮了單一資產或投資組合的流動性展望期。
16.1.3 綜合風險計量
綜合風險計量(comprehensive risk measure,CRM)概念的引入是考慮到相關性賬戶(correlation book)存在的風險。這類投資組合包含諸如資產支持證券(asset backed securities,ABS)和擔保債務憑證(collateralized debt obligations,CDO)等對不同資產違約風險的相關性敏感的金融工具。我們在第6章中對這類產品進行了討論。假設一家銀行持有一個ABS的AAA級分檔。在正常的市場環境下,該分檔資產遭受損失的可能性很小。但是在相關性增大,市場受壓的情況下,此分檔遭受損失的可能性大大提高,正如我們在2007~2009年的金融危機中看到的一樣。
對於與相關性有關的產品,CRM取代了增量風險計提和特定風險資本金。表16-1給出了《巴塞爾協議Ⅱ.5》中計算CRM的標準方法。經歷了金融危機中證券化的慘痛教訓(見第6章),監管機構對再證券化產品(如ABS CDO)設定的資本金要比一般證券化產品(如ABS)的資本金數量高。對此我們不應該感到意外。在表16-1中提到的資本減除(deduction)是指從資本金數量中直接減除了相應的面額數量,也就是說,相對面額設定了100%的資本金。
表16-1 針對相關性產品的標準資本金

《巴塞爾協議Ⅱ.5》闡明,在監管當局批准的前提下,對於一些無評級的產品,銀行可以採用內部模型計算CRM。而為獲得監管機構的批准,銀行所開發的模型必須要相當完善。例如,模型應能夠捕捉多個違約的累積效應、信用價差風險、隱含相關性的波動率、信用價差和隱含相關性的關係、回收率的波動率、對衝失效的風險以及調整對衝狀態所需的潛在費用等。同時銀行還必須定期進行嚴格的壓力測試。採用內部模型法計算出的資本金還受到由標準法計算出的資本金的某一下限的限制。
[1] 見巴塞爾銀行監管委員會,“Revisions to the Basel Ⅱ Market Risk Framework”,2011年2月。
[2] 如第6章所述,如果一家銀行由銀行賬戶的貸款來產生資產支持證券,然後將所有由此產生的份額全部買進,並將這些資產放置於交易賬戶,那麼銀行所需的監管資本金數量將下降,雖然銀行的風險敞口並沒有實質變化。這也是銀行願意將貸款證券化的原因之一。
[3] 見巴塞爾銀行監管委員會,“Guidelines for Computing Capital for Incremental Risk in the Trading Book”,2009年7月。
[4] 對風險水平恆定假設的討論見C. Finger,“CreditMetrics and Constant Level of Risk”,MSCI 2010。
16.2 《巴塞爾協議Ⅲ》
在2007~2009年金融危機以後,巴塞爾委員意識到對於《巴塞爾協議Ⅱ》必須進行大幅改進。《巴塞爾協議Ⅱ.5》增加了市場風險資本金,同時委員會還希望進一步提高股本資本要求。另外,對於股本資本的定義必須加強,對於流動性風險也要增設監管規則。
巴塞爾委員會在2009年12月提出了一個提案,在徵求了銀行的意見、一輪定量影響研究及幾輪國際性會議以後,《巴塞爾協議Ⅲ》在2010年12月終於發佈。[1]協議包括6個部分:
(1)資本金定義及要求;
(2)資本金留存緩衝;
(3)逆週期緩衝資本;
(4)槓桿比率;
(5)流動性風險;
(6)對手信用風險。
《巴塞爾協議Ⅲ》的實施是一個漸進過程,期限為2013~2019年。
16.2.1 資本金定義及要求
在《巴塞爾協議Ⅲ》框架下,銀行的資本構成如下:
(1)第一類股權資本;
(2)附加第一類資本;
(3)第二類資本。
第三類資本不復存在。
第一類股權資本(也被稱作核心第一類資本)包括股權資本和留存收益,但不包括商譽及延遲稅務資產。第一類股權資本在固定收益養老金計劃出現赤字的情況下要進行下調,但在固定收益養老金盈餘的情況下不能向上調節(見第3.12節有關養老金計劃的討論)。出於監管目的,證券化交易對留存收益的影響不計入第一類資本。另外,由於金融機構自身的信用等級變化產生的留存收益變化也不能計入第一類資本(這對應於我們將在第20章中討論的DVA)。對於納入少數股東權益(minority interest)和合並報表的子公司(consolidated subsidiaries)的資本,《巴塞爾協議Ⅲ》也進行了相關規定。附加第一類資本包括原先被計入第一類資本,但並非普通股的項目,如非累積優先股等。第二類資本包括優先級低於存款、最初發行期限超過5年的債券。
普通股權資本在《巴塞爾協議Ⅲ》中被稱作持續經營資本金(going-concern capital),這是指銀行處於持續經營狀態時(也即股權資本為正時),普通股權資本可用於承擔損失。第二類資本被稱作破產清算資本(gone-concern capital),這是指銀行不能再持續經營時(也就是股權資本為負時),第二類資本承擔損失。在破產過程中,第二類資本優先權低於存款人。如果在銀行破產時,第二類資本為正,則從理論上講,存款人可以收回全部存款。
協議對資本金要求如下:
(1)第一類股權資本金在任何時刻均不得低於風險加權資產的4.5%。
(2)整體第一類資本金(第一類股權資本金上附加第一類資本金)在任何時刻均不得低於風險加權資產的6%。
(3)整體資本金(整體第一類資本金加第二類資本金)在任何時刻均不得低於風險加權資產的8%。
《巴塞爾協議Ⅰ》要求第一類股權資本不低於風險加權資產的2%,整體第一類資本金不得低於風險加權資產的4%。《巴塞爾協議Ⅲ》的要求更加嚴格,表現在以下兩點:第一,第一類股權資本和整體第一類資本佔整體風險加權資產的比例更高;第二,用於滿足監管資本金要求的股權資本的定義更加嚴格。但是第一類和第二類資本的總和佔整體風險加權資產的比率仍與《巴塞爾協議Ⅰ》和《巴塞爾協議Ⅱ》的要求相同。
《巴塞爾協議Ⅲ》下資本金的過渡性安排是到2013年1月1日,第一類股權資本金和整體第一類資本金的比率分別要達到3.5%和4.5%;到2014年1月1日,分別要達到4%和5.5%;到2015年1月1日,新的資本金要求要全部滿足,而關於合格資本金構成的實施則延遲到2018年1月1日。
巴塞爾委員會對於系統重要性(systemically important)銀行要求更高資本金持有率。對於這一點,我們在本章後面的內容將做進一步討論。
16.2.2 資本金留存緩衝
除以上提及的資本金,《巴塞爾協議Ⅲ》還要求金融機構在正常情況下持有第一類股權資本緩衝,數量等於風險加權資產的2.5%。巴塞爾委員會設計這個規定是為確保銀行在正常市場情況下能將資本金提高到一定程度,而在金融市場出現困難的情況下用這些緩衝來吸收損失(建立資本金留存緩衝做法的依據是銀行在正常的市場條件下比在受壓的情況下能更為容易地吸納資本),如果銀行的資本金留存緩衝被全部或部分消耗,則在資本金緩衝被補充完畢前,銀行的股息發放要受到限制。表16-2中給出了關於股息的規定。例如,當第一類股權資本佔風險加權資產的比率為5.5%時,留存的收益要佔80%。因此,派發的股息佔收益的比率不能超過20%。在某種程度上,4.5%的基本股權資本金要求和7%的股權資本金要求之間的差異,類似於《償付能力法案Ⅱ》中的MCR與SCR之間的差異(見第15.12節)。
表16-2 資本留存緩衝造成的股息限制
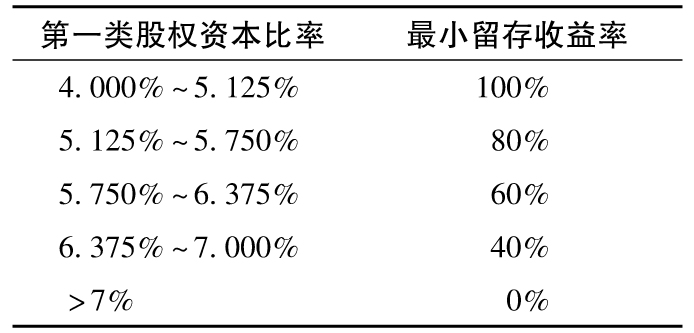
《巴塞爾協議Ⅲ》對資本金留存緩衝做出的規定意味著在正常市場條件下(這裡不包括系統性重要銀行額外持有的資本金),銀行持有的第一類股權資本金至少是風險加權資產的7%;整體第一類資本金至少是風險加權資產的8.5%;第一類和第二類資本金至少是風險加權資產的10.5%。如果以上這些比率在市場受壓條件下(因為損失的緣故)分別下降到4.5%、6%和8%,那麼銀行會在監管部門的壓力下,將資本金持有率提升回規定的水平。《巴塞爾協議Ⅲ》提高資本金比率的一個後果就是銀行很難再取得1990~2006年的資本回報率,然而,銀行的股東會因為銀行持有額外的資本金從而降低了股票風險而感到欣慰。
資本金存留緩衝的實施時間是2016年1月1日至2019年1月1日。
16.2.3 逆週期緩衝資本金
除了以上提及的資本金留存緩衝,《巴塞爾協議Ⅲ》還制定了逆週期資本金緩衝。該緩衝與留存資本緩衝類似,但其在各個國家的實施程度取決於各國監管機構自己的決定。逆週期緩衝資本金是對銀行盈利情況的週期性提供保護,該緩衝佔風險加權資產的比率可以為0~2.5%,其構成必須全部為第一類股權資本。
表16-3 在設定資本留存緩衝和2.5%逆週期緩衝資本後對股息發放的限制
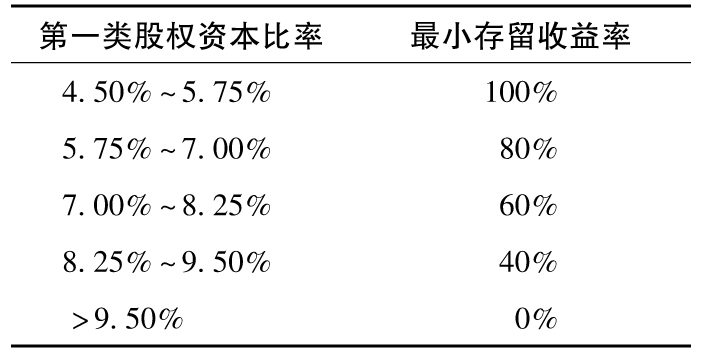
對於逆週期資本緩衝不為0的國家,表16-2要被修改。例如,當逆週期資本緩衝比率為2.5%時,表16-2被表16-3取代。類似於留存資本緩衝,逆週期資本緩衝的實施時間也為2016年1月1日至2019年1月1日。
16.2.4 槓桿比率
除了設定基於風險加權資產的資本金比率外,《巴塞爾協議Ⅲ》還設定了一個最小槓桿比率,為3%,[2]其定義為資本金佔風險敞口的比率。這裡的資本金是指一類整體資本。風險敞口是以下幾項的加總:①資產負債表內敞口;②衍生產品敞口;③證券融資交易敞口;④資產負債表外項目。對各個項目加總時,不進行風險加權調整。資產負債表內敞口包括表內所有的資產。衍生產品敞口的計算方式為“重置成本加附加項”(replacement cost plus add-on),類似於《巴塞爾協議Ⅰ》中的規定(見第15.3節)。證券融資交易敞口包括不涉及表內資產的回購協議、證券借入/借出交易等。表外項目包括貸款承諾、貸款替代品、承兌及信用證等。經過過渡期後,於2018年1月引入槓桿比率。
一些國家的監管機構表示它們認為3%的標杆比率太低。2014年10月,美國監管機構提議將美國最大的8家銀行控股公司的槓桿比率提高到5%(我們稍後將會提到,這8家銀行控股公司被稱作G-SIB),並將這8家控股公司旗下受FDIC保護的子公司的比率提高到6%。2014年10月,英國金融政策委員會(England’s Financial Policy Committee)將英國銀行的槓桿比率提高到了4.05%,並且在市場旺盛時有可能提高到4.95%,以防止過度借貸。在中國,標杆比率被設定為4%。
為什麼巴塞爾委員會要引入槓桿比率?其原因是監管機構認為銀行在計算風險加權資產時的靈活度太高了,而計算總敞口(total exposure)時的靈活度就小得多。需要說明的是,這並不意味著監管機構不再重視以風險加權資產為依據的資本金要求。它們要求銀行同時滿足:①本章前面提到的資本與風險加權資產的比率;②這裡介紹的資本與非風險加權的敞口之間的槓桿比率要求。
這兩種資本比率中的一種可能是銀行的關鍵比率(即最接近不符合監管要求的比率)。如果風險加權資產比率是關鍵因素,那麼可以說,槓桿比率是合理的,因為它為監管機構提供了有用的額外信息。但如果槓桿比率是關鍵因素(有證據表明,對於美國的一些銀行來說,槓桿比率一直是關鍵因素),可能會鼓勵銀行持有風險資產,因為它們對槓桿比率的影響與安全資產相同,但提供更高的預期收益。這可能會給監管機構帶來意想不到的不利後果。
16.2.5 流動性風險
在危機之前,《巴塞爾協議》一直將重點集中於銀行是否有足夠多的資本金來應對風險。但金融危機表明,危機帶給很多金融機構的問題並非源自資本金的充足與否,而是因為銀行承受的流動性風險。
流動性風險的根源是銀行往往採用短期資金(例如商業票據)來為期限更長的資產提供資金支持。當市場認為銀行的財務狀況很健康時,這樣的融資方式不是一個問題。[3]假定一家銀行採用發行90天的商業票據所得資金來支持其業務行為,當90天票據期滿時,銀行要發行新的票據來進行再融資,並重復此模式,即對融資進行展期。當銀行出現運作困難時(或市場認為其運作有困難時),以上模式就難以為繼。這是因為銀行很難再對其商業票據進行展期。這裡所說的問題就是造成英國北巖銀行及美國雷曼兄弟倒臺的原因。
《巴塞爾協議Ⅲ》為確保銀行能夠承受流動性壓力引入了兩個流動性比率:
(1)流動性覆蓋比率(liquidity coverage ratio,LCR);
(2)淨穩定融資比率(net stable funding ratio,NSFR)。
LCR側重於描述銀行在流動性受困的情況下,30天內的生存能力。其定義為

在計算流動性覆蓋比率的30天區間內要包括銀行資金受到劇烈衝擊的情形,其中包括銀行的信用級別被下調3個等級(例如從AA-級下調到A-級)、部分喪失存款、批發市場的資金來源全部喪失、資產減記比率提高(即以抵押品所獲資金與抵押品的價值比率下降)以及信用額度被提取等。《巴塞爾協議Ⅲ》要求流動性覆蓋比率至少為100%,這是為了保證銀行有足夠多流動性優良的資產來應對流動性壓力。
淨穩定融資比率(NSFR)側重於1年期流動性管理,其定義為

NSFR的分子等於每項可得資金(資本金、機構存款、零售存款等)乘以一個可得穩定資金(available stable fund,ASF)因子,再求和。這裡的ASF因子反映了資金的穩定性。如表16-4所示,機構存款的ASF因子小於零售存款的ASF因子,而零售存款的ASF因子又小於第一類資本金和第二類資本金。NSFR分母根據需要資金支持的項目得出。每一項資金需求均要乘以一個所需穩定資金(required stable funding,RSF)因子,該因子反映了所需資金的持續性。表16-5顯示了這些因子的數量。
表16-4 為淨穩定融資比率設定的ASF因子

表16-5 為淨穩定資金比率設定的RSF因子
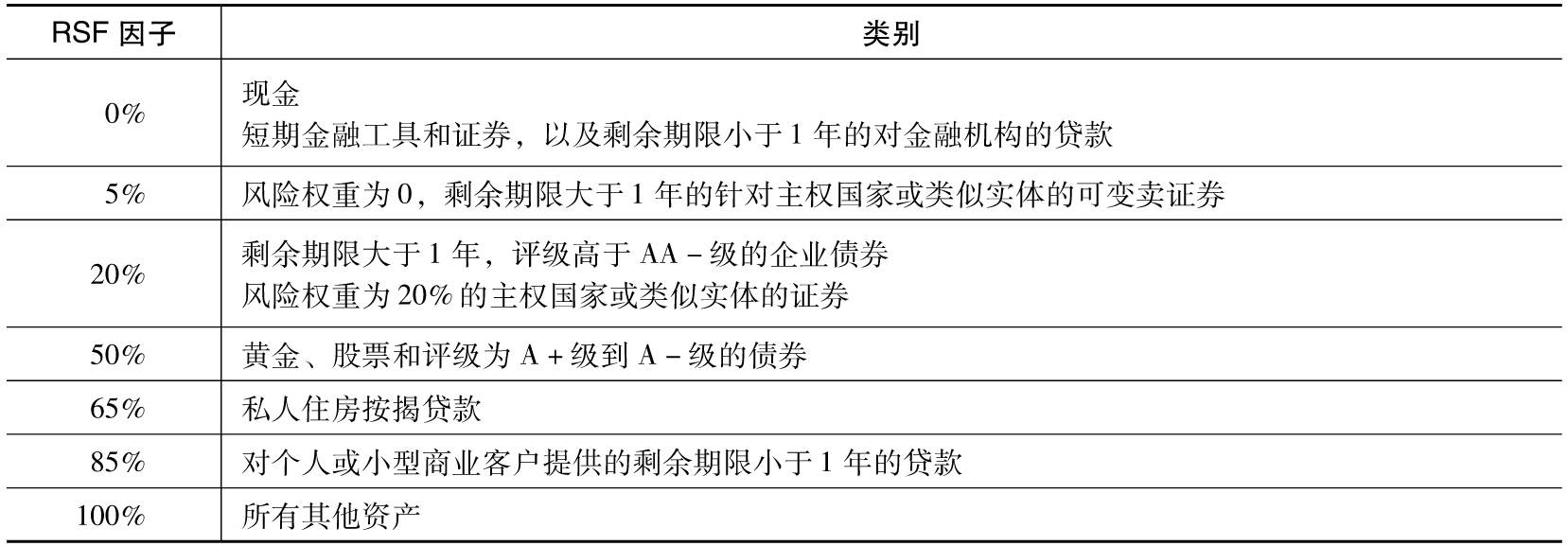
《巴塞爾協議Ⅲ》要求NSFR的下限為100%,這是為了保證計算得出的可獲得穩定資金供應量高於必需的穩定資金需求量。
【例16-1】 一家銀行的資產負債表如下。
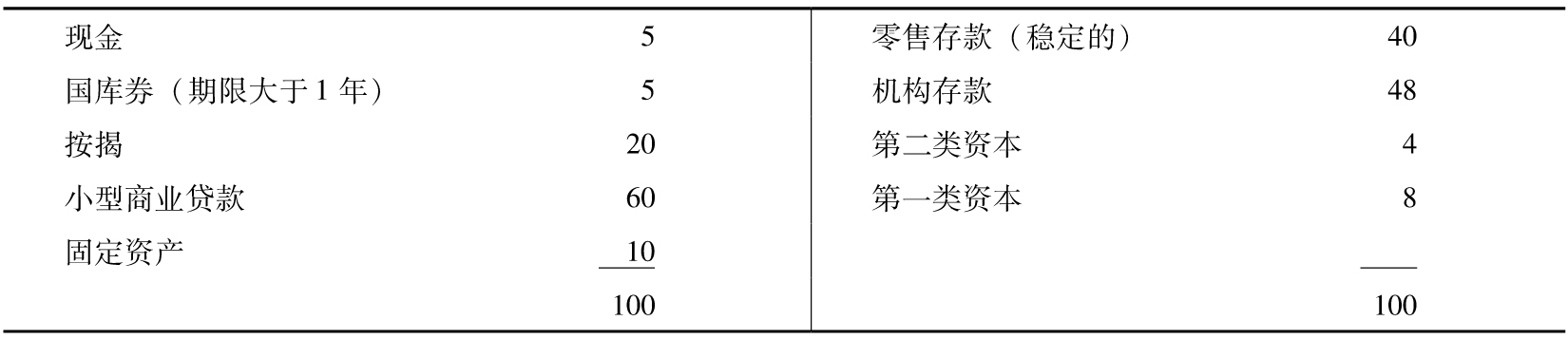
穩定資金供應量為:40×0.9+48×0.5+4×1.0+8×1.0=72
穩定資金需求量為:5×0+5×0.05+20×0.65+60×0.85+10×1.0=74.25
NSFR比率為72/74.25=0.970或97%,因此該銀行沒有達到NSFR的要求。
《巴塞爾協議Ⅲ》的新規定較為嚴格,並且有可能對銀行的資產負債表產生極大影響。根據2014年9月的估計,要滿足這些規定,美國的銀行將不得不持有額外的1000億美元高流動性資產。LCR的計劃實施時間為2015年1月1日至2019年1月1日(但美國的監管機構要求必須在2017年1月1日前全面實施),NSFR的計劃實施時間是2018年1月1日。
16.2.6 對手信用風險
對每個衍生產品的交易對手,銀行要計算信用價值調整量(credit value adjustment,CVA)。CVA是由於對手存在違約的可能而造成的預期損失。計算CVA的方法將在第20章中討論。在報告利潤時,所有交易對手的CVA要從利潤中扣除。
我們將在第20章中看到,針對某一交易對手的CVA的變化可能來自兩個方面:①與對手進行的交易所涉及的市場變量發生變化;②用於對手借貸的信用價差發生變化。《巴塞爾協議Ⅲ》要求由對手信用價差變化引發的CVA風險要計入市場風險的VaR計算中。我們還將在第20章中看到,一旦CVA被計算出來,我們可以較容易地對交易對手的信用價差的期限結構曲線進行平行移動來求得CVA的敏感度,即delta和gamma。這些敏感度可以被用來計算相應的市場風險指標。
2015年,巴塞爾委員會提議對CVA風險的資本計算進行修改。[4]一個主要目的是,允許那些對衝信用價差變化和CVA風險因素變化的影響的銀行,在計算監管資本時兼顧這兩個因素。如果沒有這種變化,對衝風險因素的變化將增加資本費用。
16.2.7 全球系統性重要銀行(G-SIB)、系統性重要金融機構(SIFI)和國內系統性重要銀行(D-SIB)
在2007~2009年金融危機期間,政府不得不對多家大型的、系統性重要金融機構實施救助,因此,監管機構對這類金融機構能否持有足夠的資本金,從而避免重蹈覆轍尤為關注。
G-SIB是全球系統性重要銀行(global systemically important bank)的簡稱,而SIFI指的是系統性重要金融機構(systemically important financial institution),包括銀行和非銀金融機構。對SIFI,一種廣泛流行的看法是它們“大而不倒”,也就是說,如果這些機構出現了財務困難,政府將不得不對它們進行救助。
一家銀行或其他金融機構的系統性重要程度取決於萬一其倒閉,會對全球金融體系造成多大影響,而這又取決於這家機構的經營活動以及它與全球其他金融機構之間簽署的合同。巴塞爾委員會用了一種打分的辦法來評估哪些銀行是G-SIB。一些研究人員還嘗試採用網絡理論的方法來回答這一問題。
2013年,巴塞爾委員會發表了要求G-SIB提高一類股權資本金比例的規定的最終版本。[5]G-SIB將按照額外股權資本佔風險加權資產的1%、1.5%、2%、2.5%或3.5%歸類。新的規定於2016年1月起生效。
每年金融穩定委員會都會發布G-SIB名單。2017年11月,名單上有30家銀行。這些銀行中,17家歸於1%的類別,8家歸於1.5%的類別,4家歸於2%的類別,1家(摩根大通)歸於2.5%的類別。3.5%的類別為空。[6]G-SIB被要求持有至少佔風險加權資產4.5%的第一類股權資本金,另加2.5%的資本留存緩衝,再加上我們上面剛剛討論的額外資本金。假設總資產是風險加權資產的X%。根據第16.2.1節,所有一級資本(CET1+AT1)必須至少為風險加權資產的(X+1.5)%,一級資本與二級資本之和必須至少為風險加權資產的(X+3.5)%。
2014年11月,金融穩定委員會發布了針對G-SIB的關於總損失吸收能力(total loss-absorbing capacity,TLAC)的提案。該提案是對2013年聖彼得堡G20領袖峰會一項呼籲的迴應,並諮詢了巴塞爾銀行監管委員會的意見。TLAC由可以吸收損失並在違約情況下保護存款人的金融工具組成。所用到的工具包括股本、優先股和次級債。從2019年1月1日起,G-SIB的最低TLAC將佔風險加權資產的16%,到2022年1月1日將增至18%。不遵守TLAC規定可能會妨礙銀行發放股息的能力。
有些國家對資本金的要求高於《巴塞爾協議Ⅲ》和金融穩定委員會設定的最低標準或者要求提前實施新的標準。例如瑞士就對本國的兩家大銀行提出了更高的資本金要求,這兩家銀行是瑞銀和瑞信,均為G-SIB。瑞士之所以這樣做的原因不難理解,這兩家銀行對其整體經濟的影響很大,任何一家銀行破產都會給國家帶來嚴重後果。
各國的監管機構將一些沒有被認作為G-SIB的銀行歸類為國內系統性重要銀行(D-SIB)。這些銀行可能被要求持有比最低標準更高的資本金、披露額外的信息或進行更加嚴格的壓力測試(見第22章)。2016年美國有8家銀行被認作為G-SIB,這8家銀行是美國銀行、紐約梅隆銀行(Bank of New York Mellon)、花旗集團、高盛集團、摩根大通、摩根士丹利、道富銀行(State Street Corp)和富國銀行(Wells Fargo),其他資產規模大於500億美元的銀行被認作D-SIB。
[1] 見巴塞爾銀行監管委員會,“Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems,”2011年6月;見巴塞爾銀行監管委員會,“Basel III: International Framework for Liquidity Risk Measurement Standards and Monitoring,”2010年12月。
[2] 見國際清算銀行,“Basel III Leverage Ratio Framework and Disclosure Requirements,”2014年1月。
[3] 當短期資金被用於支持長期固定利率貸款時,如果利率升高,淨息差就會受到擠壓,但是這一風險可用利率互換這樣的金融工具進行對衝(見例5-1)。
[4] 見巴塞爾銀行監管委員會,“Review of Credit Valuation Adjustment Risk Framework”,2015年10月1日。
[5] 見巴塞爾銀行監管委員會,“Global Systemically Important Banks: Updated Assessment Methodology and the Higher Loss Absorbancy Requirement,”2013年7月。
[6] 金融穩定委員會發布的2016年名單中,G-SIB銀行總數仍為30家,各類別中的數量也沒有變化,但花旗集團取代匯豐被歸於2.5%的類別。其他類別中的銀行名單也發生了一些變化,2014年名單中並不包括任何一家來自中國的銀行,而在2016年名單上,中國工商銀行被歸於1.5%的類別,中國銀行、中國農業銀行和中國建設銀行歸於1%的類別。——譯者注
16.3 未定可轉換債券
在金融危機後,銀行發展出一種很有意思的籌措資本金的方式,即所謂的未定可轉換債券(contingent convertible bonds,CoCo)。傳統上,可轉換債券發行後,在一定情形下,債券持有者可按事先約定的兌換比例將債券換成股份。一般來講,債券持有者會選擇公司表現較好、股票價值比較高的時機來進行轉換。未定可轉換債券和一般可轉換債券有所不同,這些債券在某些條件滿足時會自動轉換。一般來講,這些條件會在金融機構遭遇財務困難時滿足。
未定可轉換債券對銀行具有吸引力,這是因為在正常情況下,這些債券以債務的形式存在,銀行因而可獲得較高的資本回報率。而在銀行遭遇困難出現虧損時,這些債務轉換成股份,因而銀行可繼續維持一定的股本緩衝,以避免破產。從監管當局的角度而言,未定可轉換債券也具有潛在的吸引力。因為這樣可避免在金融機構陷入困境時,政府被迫進行救助。實際上,未定可轉換債券也被稱為“自救”(bail-in)的一種方式。當金融機構出現危機時,私有領域的債券投資者會注入新的股權資本,這樣就避免了公共部門的介入。
設計未定可轉換債券的一個關鍵因素是如何制定轉換的觸發條件和設定轉換的比率(即1份債券可轉換的股權數量)。在已發行的這類債券中,一種較為流行的觸發條件是第一類股權資本與風險加權資產的比率低於一定水平;另一種可能的觸發條件是股票的市值與資產的賬面價值的比率低於一定水平。
勞埃德銀行(Lloyd’s Banking Group)、荷蘭合作銀行(Rabobank Nederlands)和瑞信是第一批發行未定可轉換債券的金融機構。業界事例16-1描述了瑞信在2011年發行的此類債券。這些債券在公司的第一類股權資本低於風險加權資產的7%時,或者瑞士監管當局認為瑞信需要政府救助時,會自動轉換成股份。據估計,在2010~2020年的10年中,世界各地的銀行會發行大約1萬億美元的未定可轉換債券,這些債券將幫助銀行應對《巴塞爾協議Ⅲ》中關於資本充足率的新的監管要求。
業界事例16-1
瑞信的未定可轉換債券
2011年2月14日,瑞信公佈將發行未定可轉換債券,並將這些債券與兩家中東投資者卡塔爾控股(Qatar Holding LLC)和奧拉揚集團(Olayan Group LLC)的現有投資進行交換。當以下兩個條件中的任意一個被滿足時,該未定可轉換債券都將自動轉換為股權:
(1)第一類股權資本低於風險加權資產的7%;
(2)瑞士監管當局認為瑞信需要政府救助,以避免破產。
以上消息公佈後,瑞信在2011年2月17日公開發行了20億美元的未定可轉換債券。這些債券的條款和中東投資者已經持有的債券條款相似,惠譽給出的債券評級為BBB+。債券到期日為2041年,在2015年8月以後,債券可以被贖回。債券券息為7.875%。隨著這次發行,事先對此類債券在市場上是否受歡迎的懷疑被一掃而光,因為市場上對債券的預訂量是發行量的11倍。
瑞信已經聲明,它計劃用以上描述的債券來滿足非股權資本金要求的1/3,其餘的2/3將以另外發行的未定可轉換債券來滿足,其轉換條件是第一類股權資本低於風險加權資產的5%(而不是7%)。
如果轉換條件為第一類股權資本與風險加權資產的比例等於5.125%或更高,則轉換前的CoCo債券可計入附加第一類資本;否則可作為第二類資本。
16.4 標準化方法和SA-CCR的使用
2017年12月,巴塞爾委員會宣佈,從2022年開始,所有資本計算都將採用標準化方法。銀行的總資本要求將是下列兩種方法計算的最大值:①在使用批准的內部模型之前計算得出的;②標準化方法給出的一定百分比。到2022年,這一比例將達到50%,到2027年將升至72.5%。
2022年適用的市場風險資本的標準化方法將在第18章中說明。如第23章所述,操作風險資本將完全基於標準化方法。信用風險的標準化風險權重是對第15.8.1節中《巴塞爾協議Ⅱ》的權重的修訂。
在《巴塞爾協議Ⅰ》中,CEM計算衍生產品違約風險敞口(EAD)的標準化方法已通過SA-CCR得到改進。[1]
EAD=1.4×(RC + PFE)
其中RC為重置成本,PFE為潛在風險敞口。對於沒有提交擔保品的交易,RC計算為
RC=max(V,0)
對於受保證金協議約束的交易,調整為
RC=max(V-C, D, 0)
其中C為交易對手提交的抵押物的淨值(銀行提交的抵押物被認為是負數)。V為淨額結算組合衍生產品的盯市價值,D是在沒有收到任何額外擔保物的情況下V可能發生的變化(例如,因為擔保品協議中規定了最低的轉讓金額)。它反映了擔保品協議的條款。例如,如果V=C=50,並且在沒有收到任何額外的擔保品的情況下V可以增加到51,則D=1,RC=1。對於非現金擔保物,要在計算C時削減。
PFE是一種計算總附加敞口的相對複雜的方法。要考慮兩個因素:
(1)當交易對手提交了超額抵押物時,風險就會降低,並且風險的降低程度隨著抵押物數量的增加而增加。
(2)當沒有抵押物時,信用風險隨著V變得更負而減小,V為輕微負值時的總附加敞口,應高於V是高度負值時的總附加敞口。
[1] 見巴塞爾銀行監管委員會,“The Standardized Approach for Measuring Counterparty Credit Risk Exposures,”,2014年4月。
16.5 《多德-弗蘭克法案》
《多德-弗蘭克法案》在2010年7月正式成為法律,其目標是防止美國政府將來再次被迫對金融機構進行大規模救助,並同時保護消費者,該法案的要點如下。
(1)成立兩個新的政府實體:金融穩定監管委員會(Financial Stability Oversight Council,FSOC)及金融研究辦公室(Office of Financial Research,OFR)。目的是對系統性風險進行監管並對經濟狀況進行研究,這些機構的任務是識別威脅美國金融系統穩定的風險,推行市場紀律並維持投資者信心。
(2)聯邦存款保險公司(Federal Deposit Insurance Corporation,FDIC)的有序清算(orderly liquidation)職權被擴大了,而聯邦儲蓄機構管理局(Office of Thrift Supervision)則被撤銷。
(3)FDIC的存款保險金額上限被永久性地增加到25萬美元(原有的25萬美元的受保金額上限是臨時措施)。
(4)對於大型對衝基金和類似的金融中介機構引入了監管條款,這些機構必須在美國SEC註冊,並披露其業務行為。
(5)成立聯邦保險辦公室(Federal Insurance Office),該辦公室要與各州的監管機構協作,對保險行業進行全方位監管。
(6)對吸收貸款的金融機構的自營及類似交易進行限制。此項規定最初是由美聯儲前主席保羅·沃爾克提出,因此被稱為“沃爾克法則”(Volcker Rule)。
(7)有些經營高風險的交易部門要分離成為資本獨立的實體。
(8)標準場外衍生產品的交易必須通過電子平臺互換執行設施(SEF)來執行。SEF的功能類似於交易所,人們希望藉此增加場外交易的市場透明度。金融機構之間的標準衍生產品交易必須通過中心清算機構(Central Clearing Party,CCP)進行清算(見第17章關於CCP的進一步討論)。商品期貨交易委員會(Commodity Futures Trading Commission,CFTC)被賦予了監督CCP和SEF活動的職責。
(9)美聯儲要為從事支付、結算和清算等行為的系統性重要金融設施設定風險管理標準。
(10)加強了對投資者的保護,完善了對證券的監管。
(11)要求評級機構對其採用的評級方法和所用的假設增加透明度,而且其潛在的法律責任也有所增大。SEC設立了一個信用評級辦公室(Office of Credit Rating),對評級機構進行監督。
(12)外部信用評級不能再被用於金融機構的監管過程(此項規定直接與巴塞爾委員會的規定產生衝突。我們在本章和第15章中均已看到,《巴塞爾協議》中確實採用了外部評級信息)。
(13)在美聯儲內成立金融保護局,其職責是保證消費者在購買諸如按揭貸款和信用卡一類的金融產品時能得到清晰、準確的信息。
(14)發行證券化產品的機構須持有所發行的各個產品的5%(關於此項規定,有一些例外)。
(15)聯邦銀行監管機構應制定監管規則,防止金融機構採用那些可能帶來過高風險的薪酬方案(例如,那些只與僱員短期表現掛鉤的薪酬方案)。對於高管的薪酬,方案賦予了股東無約束力的投票權(non-binding vote),並要求董事會薪酬委員會應由獨立董事構成。
(16)按揭貸款提供商應對借貸人的還款能力做合理的可信度鑑定(reasonable good faith determination),這些鑑定要基於經過驗證並存檔的信息。不進行該鑑定可能會導致喪失(在借貸人斷供時)拍賣房屋的權利。
(17)大型金融機構的董事會中至少應包含一名具有大型複雜金融機構風險管理經驗的專家。
(18)FDIC在金融機構陷入破產時,可對其進行接管,並變賣其資產。財產損失將由其股東和債權人承擔,而破產費用將由金融行業來承擔。
(19)在第1點中提到的對監督系統性風險負有責任的兩家機構FSOC和OFR,負責識別系統性重要金融機構(SIFI)。
(20)美聯儲和FDIC要求所有系統性重要金融機構都準備一份“遺囑”(living will)。遺囑中要說明在危機發生時,機構將如何融資;在發生破產時,如何進行清算。
《多德-弗蘭克法案》並沒有闡述房利美和房地美將來的角色,而這兩家機構在美國按揭市場上起著關鍵作用。2008年9月,美國政府接管了這兩家機構。
特朗普表示,他打算廢除《多德-弗蘭克法案》的某些部分,沃爾克法則和消費者金融保護局(Customer Financial Protection Bureau)是最有可能的目標。
16.6 其他國家的法案
大型銀行是名副其實的全球性機構。當世界各地的監管環境有差異時,銀行很有可能將其部分甚至全部業務從一個監管區域轉移到另外一個監管區域。雖然世界不同地區均採用《巴塞爾協議Ⅲ》的監管規則,但各地的監管機構在規則的使用上還是擁有一些靈活度,各國的立法也不盡相同。2011年,瑞銀曾提出要將其投行的總部從蘇黎世轉移到倫敦、新加坡或紐約。這項提議成了報紙的頭版消息,瑞銀之所以這麼做是為了規避瑞士監管當局所提出的較高的資本金要求,當然瑞銀最終沒有這麼做。
上一節討論了美國立法當局引入的法律條款,其他國家對於其中一些議題也進行了立法。英國成立了一個由約翰·維克斯爵士(Sir John Vickers)任主席的獨立委員會,處理銀行業面臨的問題,並通過了《2013年金融服務(銀行改革)法案》(Financial Services(Banking Reform)Act 2013)。歐盟則於2011年11月成立了一個由埃爾基·利卡寧(Erkki Liikanen)領導的委員會,並於2012年發表了一個報告。
英國、歐盟和其他一些國家的法規及建議與美國的法律要求有很多相似之處。例如《多德-弗蘭克法案》要求美國的證券化產品發起人須持有所有資產的5%(見上面第14點),歐盟發佈的資本要求指令2(Capital Requirement Directive 2,CRD2)也有類似的規定。[1]多數國家的立法機關都認為標準場外衍生產品交易應通過中央清算中心進行清算(見上面第8點),而不是進行雙邊清算。
有時,不同國家的規定相近,但不完全相同。《多德-弗蘭克法案》規定標準衍生產品交易應在互換執行設施(見第8點)上進行。歐盟引入了類似的交易平臺,被稱為有組織交易設施(OTF),但是並沒有教條地要求所有標準產品的交易都必須使用OTF。
《多德-弗蘭克法案》中最有爭議的部分可能就是沃爾克法則了(見第6點)。該法則禁止銀行進行自營交易,並對銀行及其附屬機構投資對衝基金和私募股權公司進行了限制。引入該規則的動機是合理的:銀行不應該拿儲戶的錢去投機,因為這些資金是受FDIC保險保護的。但這條規則實施起來可能有難度,因為對有很大交易組合的銀行來說,很難辨別一筆新加入的交易是為了對衝風險還是為了投機。[2]儘管如此,很多美國銀行還是關閉了自營交易部門,很多原來在這些部門工作的員工離開銀行,加入了對衝基金。英國的維克斯委員會也意識到保護儲戶資金的重要性,雖然並沒有採取禁止自營交易這樣的嚴厲手段,但要求零售銀行業務到2019年進行所謂的“圍欄”(ring-fenced)改革,實現與交易及投行等風險更高的業務的隔離。歐盟的利卡寧委員會也提出了類似的要求,將銀行核心業務與自營交易及其他高風險活動分離。
大部分國家的監管機構都認為“遺囑”(見第20點)對SIFI很重要,並因此給SIFI施加了很大的壓力,促使它們制定遺囑。出於稅務及監管的考慮,SIFI往往具有非常複雜的組織結構。新的監管要求可能導致SIFI的組織結構簡化,使同一機構下的不同業務彼此分離成為資本獨立的法律實體,這樣一來,當一家SIFI面臨破產需要救助時,就不必救助其所有的實體。如果SIFI制定的遺囑不能令監管機構滿意,監管機構有權強令其部分甚至全部剝離某些業務。監管機構不希望2008年雷曼兄弟破產時造成的恐慌和跨境訴訟重演。同時監管部門還認為,如果雷曼兄弟和它的ISDA主協議在結構上能使其衍生產品組合在公司破產後的幾天內仍然存活以有序地平倉,則圍繞其衍生產品組合清盤而進行的經年累月的法律官司就可以避免。
僱員薪酬也是一個重要問題。在危機以前,許多交易員及其他一些僱員的年度獎金是他們薪酬的主要部分。這導致了他們中很多人在進行決策時,更注重短期效益。獎金髮放以後如果出現損失,僱員並不一定要退回獎金。許多銀行已經認識到這個問題,並主動將獎金延期到3~5年內支付,而不是在1年內就全部支付。如果一個交易員在某一年的業績很出色,而在接下來一年卻很糟糕,那麼業績好的一年的獎金中被延遲的部分會在業績不好的那一年被收回。《多德-弗蘭克法案》關於金融企業薪酬制度的規定還算相對溫和。當金融機構接受“受困資產救助項目”(Troubled Asset Relief Program,TARP)的資金援助時,僱員的薪酬會受到限制。但當資金被償還後,銀行在支付薪酬方面馬上就恢復了自由。[3]
另外一些國家對薪酬進行了限制。有些限制是臨時性的。例如2009年,英國曾經對超出25000英鎊的獎金施加了一次性“超級稅”(supertax),但另一些限制則是永久性的。例如,2013年4月,在歐盟引入的資本要求指令4(CRD 4)中,對銀行員工獎金進行了封頂。在新的指令下,銀行員工獎金與固定薪金的比例最大為1(有一定靈活性,可提高到2,但需要股東批准),但英國的銀行希望能夠繞開這一規定。[4]
[1] 德國將持有比率從5%提高到了10%。
[2] 對此,華爾街上流行一個笑話,說銀行必須僱一些心理學家或者心理醫生,來診斷交易員在交易前到底在想什麼。
[3] 事實上,這正是TARP資金被儘快償還的重要動機。
[4] 隨著2016年英國退出歐盟,英國銀行可能不必再受到來自歐盟的這方面的“困擾”。英國金融監管當局也應該具有了更大的獨立性。——譯者注
小結
2007年開始的金融危機是世界很多地區自20世紀30年代以來經歷的最嚴重的危機。危機中有些金融機構破產了,另外一些機構必須靠接受納稅人的資金救助才得以生存下來。巴塞爾委員會和世界不同地區的監管者試圖對金融機構監管中的漏洞進行修補,這麼做確實是非常有必要的。
《巴塞爾協議Ⅱ.5》對銀行持有的市場風險資本金進行了上調。該協議明確了資本金除了應該反映正常情況下市場變量的變動,也應該反映市場受壓情況下的波動率和相關性的變化;該協議還填補了另外一些漏洞,以避免銀行通過將資產由銀行賬戶轉移到交易賬戶的手段來降低資本金要求;該協議還對依賴信用相關性的衍生產品提出了特殊資本金要求。眾所周知,這些產品是金融危機的焦點。
《巴塞爾協議Ⅲ》較大幅度地增加了銀行的股權資本金。巴塞爾委員會也意識到,危機期間銀行遇到的很多困難源自流動性問題,因此協議對金融機構的流動性引入了新的監管規定。
各國政府也引入了針對金融機構的新的監管規定。在美國,《多德-弗蘭克法案》有許多條款是為了保護消費者和投資者,避免將來的政府救助,同時對金融系統的監督也會變得更加謹慎。其他國家也通過了與此類似但並不完全相同的法規。
《巴塞爾協議Ⅲ》以及諸如《多德-弗蘭克法案》一類的國家立法將如何實施仍有很多不確定性,這也是銀行面臨的重大風險之一。當這些新的措施付諸實施後,效果會如何呢?在一段時間內,我們還沒有答案。監管當局面臨的一個問題是那些意想不到的後果。《巴塞爾協議Ⅰ》產生的意想不到的後果是金融機構不願為優質企業發放貸款,因為此類貸款的風險權重為100%,而《1996年修正案》和信用衍生產品市場的發展則鼓勵銀行將信用風險由銀行賬戶轉移到交易賬戶,以此降低資本金要求。毫無疑問,《巴塞爾協議Ⅲ》及全球各國的其他相關立法也一定會產生這類意料之外的後果。我們希望新的條款給金融系統帶來的益處可以彌補那些意想不到的後果所產生的副作用。
延伸閱讀

練習題
16.1 《巴塞爾協議Ⅱ.5》的3個重要組成部分是什麼?
16.2 《巴塞爾協議Ⅲ》的6個重要組成部分是什麼?
16.3 採用傳統方法計算的VaR和壓力VaR有哪些不同?
16.4 解釋增量風險計提的計算方法,巴塞爾委員會為什麼要引入該條款?
16.5 在標準法下,面值為1億美元的AAA級的資產抵押債券(ABS)與同樣面值和評級的ABS CDO所需的資本金有什麼不同?
16.6 與《巴塞爾協議Ⅰ》和《巴塞爾協議Ⅱ》相比,《巴塞爾協議Ⅲ》將第一類股權資本金(包括資本緩衝)增加了多少?
16.7 假定一家銀行的第一類股權資本金比率為6%,銀行可支付的最大股息在以下兩種情況下分別為多少?(a)在沒有逆週期資本緩衝的情況下;(b)在逆週期資本緩衝比率為2.5%的情況下。
16.8 解釋槓桿比率與通常監管當局要求的資本比率有何不同。
16.9 解釋流動性覆蓋比率和淨穩定資金比率的定義。
16.10 如果例16-1中的機構存款有一半被穩定的零售存款代替,淨穩定資金比率將如何變化?
16.11 什麼是CVA?在《巴塞爾協議Ⅲ》下,有關CVA的監管規則是什麼?
16.12 解釋未定可轉換債券的運作方式,對於(a)銀行和(b)監管當局而言,這些證券有什麼吸引力?
作業題
16.13 試各舉一例,說明《多德-弗蘭克法案》的內容與以下規定存在衝突之處:(a)巴塞爾國際監管規則;(b)其他國家引入的監管規則。
16.14 某銀行的資產負債表如下。
(a)淨穩定資金比率是多少?
(b)如果銀行為滿足《巴塞爾協議Ⅲ》的要求,決定吸引更多(穩定的)零售存款,並用新增存款購買國庫券,則銀行需再吸引多少存款才能達到目的?

第17章
OTC衍生產品市場的監管
在第5章中,我們區分了場外交易市場(OTC)和交易所交易市場。交易所交易市場是在交易所開發的交易平臺上買賣交易所開發的產品的市場。市場參與者的交易必須由交易所清算中心的成員進行結算。交易所清算中心要求其會員繳納保證金(也可以是擔保品),而會員則要求他們所結算的經紀人繳納保證金。反過來,經紀人要求他們的客戶繳納保證金。
OTC市場是金融機構、基金經理和企業財務主管可以直接進行交易的市場,不受交易所的限制。在2007~2008年的信用危機之前,OTC交易市場基本上不受監管。兩個市場參與者可以參與他們喜歡的任何交易。他們可以提供擔保品,也可以不提供擔保品;他們可以直接進行清算交易,也可以通過第三方。此外,他們沒有義務向任何人透露交易的細節。
自金融危機以來,OTC交易市場受到了大量的監管。本章將解釋這些規定,並說明監管壓力正在導致OTC市場變得更像交易所交易市場。
17.1 OTC市場清算
首先,我們將介紹OTC交易是如何進行清算的。主要有兩種方式:中央清算和雙邊清算。如圖17-1所示(這是簡化的假設,即只有8個市場參與者和1箇中央對手方)。在雙邊清算中,市場參與者相互清算交易。在中央清算中,由中央對手方(CCP)的第三方進行清算交易。
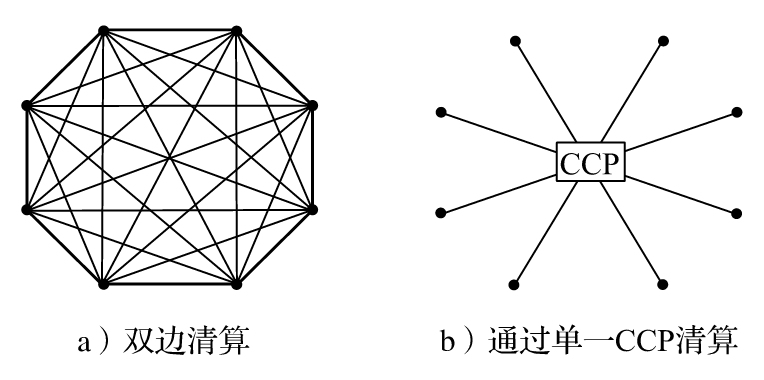
圖17-1 雙邊清算和中心清算
17.1.1 保證金
在進一步詳細描述雙邊清算和中央清算之前,我們先回顧一下保證金賬戶的操作。保證金(margin)是指用來描述OTC交易市場和交易所交易市場的擔保品。
變動保證金(variation margin)是反映衍生工具投資組合價值變化的抵押物。考慮到A與B進行交易的情況,擔保協議規定雙方必須繳納變動保證金(起點金額或最低轉讓金額)。[1]這意味著,如果未平倉合約的價值在1天內發生變化,從而對A的價值增加了X美元(對B的價值下降了X美元),B需要向A提供一個與X美元價值相當的抵押物。變動保證金的累積效應是,如果未償付的衍生產品在某一特定時間對A的價值增加了V美元,對B的價值減少了V美元,那麼在那之前,B應該向A提交了V美元價值的擔保品。[2]
變動保證金提供了一些防止交易對手違約的保護。在以下的理想情況中,它能提供全面保護:①交易對手在違約時未欠下任何變動保證金;②一旦交易對手違約,所有未平倉頭寸都可以以市場中間價進行替代交易。實際上,違約的交易方通常會在違約的前幾天停止提供擔保品,而未違約方通常會因替代交易受到買賣價差的影響。[3]考慮到投資組合價值在違約前一段時間內的不利變動,當沒有繳納保證金時,市場參與者除了要提交變動保證金外,有時還要求繳納初始保證金。請注意,在這種情況下,不利的市場變動是指投資組合對非違約方的價值增加,而不是減少。這是因為在未繳納變動保證金的一段時間內,投資組合價值的增加導致了重置成本的增加。[4]初始保證金可以隨著未平倉投資組合和相關波動率的變化而隨時間變化,它反映了由於不利的市場狀況和替代交易的成本所造成虧損風險。[5]
大多數變動保證金是以現金形式,但現行的協議可能會規定,證券能替代現金,這些證券可能會折價出售。這意味著證券的市場價值會被降低,以確定它們的保證金價值。例如,美國國債可能會有10%的折減,這意味著,如果它的市場價值是100美元,它將只能滿足90美元的保證金要求。
現金保證金應賺取利息嗎?這在期貨市場和OTC交易市場存在差異。期貨交易所清算所要求會員提供初始保證金和變動保證金。會員從初始保證金中獲得利息,但他們不收取變動保證金的利息,因為期貨合約採用每天結算制度,變動保證金不屬於會員。在OTC交易中,由於交易不是每天結算的,所以所有的現金保證金通常都會產生利息。
17.1.2 中央清算
在中央清算中,由中央對手方(CCP)負責交易清算。CCP的運作方式和場內清算所很類似。假設有兩家公司A和B同意進行一筆場外衍生產品交易。它們可以將交易提交給CCP清算。如果CCP接受了清算請求,就會充當交易雙方的中間人,與A和B分別進行一筆方向相反的交易。
例如,假設原來的交易是一個利率互換,面額為1億美元,為期5年,其中A向B支付5%的固定利率,而B向A支付LIBOR利率,由此會生成兩筆交易。其中,在公司A與CCP之間的交易中,A按1億美元面額,支付5%固定利率,接收LIBOR利率;在公司B與CCP之間的交易中,B按1億美元面額,支付LIBOR利率,並接收5%的固定利率。A和B之間不再有對彼此的信用敞口。圖17-2對此進行了說明。如果交易中有一方不是CCP的會員,那麼它可以通過一家會員進行清算。
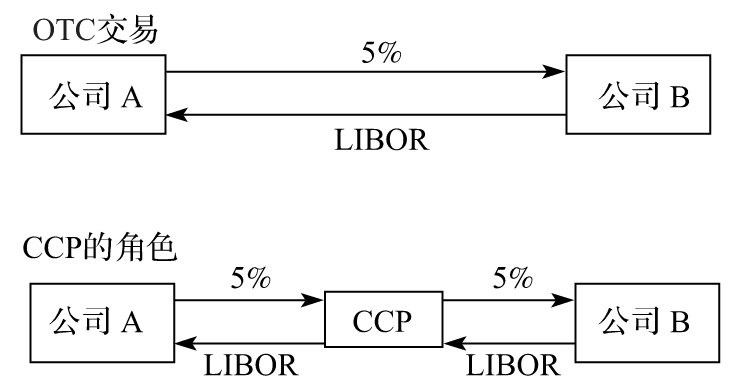
圖17-2 CCP在OTC市場扮演的角色
3家大型的CCP是:
(1)SwapClear(倫敦LCH Clearnet的一部分);
(2)ClearPort(芝加哥商業交易所集團的一部分);
(3)ICE Clear Credit(洲際交易所的一部分)。
CCP要求會員為經其清算的交易提供初始和變動保證金。一般來說,初始保證金的數額應足以覆蓋5天展望期、99%置信度下的市場變動。這保護了中央對手方清算所在平倉或替換違約成員的頭寸時免受損失。
考慮圖17-2中的互換。如果該交易是交易雙方通過CCP清算的唯一交易,那麼CCP可能要求雙方均提供50萬美元的初始保證金。如果在交易後的第一天,利率下降導致交易對公司A的價值下降了10萬美元,則公司A可能會被要求提供10萬美元變動保證金,而CCP也需要對公司B支付相等的數額。CCP確定的初始保證金要求也可能發生變化。如果所要求的變動保證金不能被滿足,則交易會被CCP以該價位平倉。通常現金和國債可用來作為保證金。一般來說,支付給保證金餘額的利率通常會接近於美元的隔夜聯邦基金利率(也接近於其他貨幣的隔夜利率)。
在實踐中,每個市場參與者通常與CCP同時存在多筆交易。對某市場參與者來說,初始保證金要求反映了其與CCP之間所有頭寸總價值的波動。CCP在OTC市場扮演著場內清算所在場內交易中相似的角色。二者之間的主要區別在於,經由CCP清算的交易通常不如場內清算所清算的交易那麼標準化,因此在計算保證金要求時,前者往往更加複雜。
通過CCP清算交易的關鍵優勢在於,在經由場內清算所清算的期貨交易中,交易雙方不必擔心彼此的信用狀況。因為由CCP充當了雙方的直接對手方,而CCP要求的變動保證金和初始保證金可用來處置違約風險。
CCP會員需要繳納清算基金(如果交易的一方或雙方均不是CCP會員,它們就需要經過會員來清算。同時,他們需要向會員繳納保證金)。如果某會員不能按時足額提供保證金,該會員就會被認為違約,其交易會被平倉。在平倉過程中,可能會產生損失。一個瀑布型的結構定義了承擔損失的先後順序:
(1)違約會員的初始保證金;
(2)違約會員繳納的清算基金;
(3)其他會員繳納的清算基金;
(4)CCP的股本。[6]
正如我們在前面提到的,這跟場內清算所處理違約事件的機制非常相似。
17.1.3 雙邊清算
在雙邊清算中,每對市場參與者都要簽訂一份協議,協議中規定了他們之間未來所有交易的清算方式。通常由ISDA主協議來規範(ISDA是國際互換和衍生產品協會的簡稱)。該協議的信用支持附件(CSA)規定了擔保安排,如交易雙方應該提供的擔保品(如果有的話)、可以作為擔保品的資產以及證券的折減等事項。協議的主體規定了一方違約時會發生的情況(例如,宣佈破產,未能按時支付衍生產品款項,不能按要求提供擔保品)。我們稍後將更詳細地討論這個問題。
17.1.4 淨額結算
我們在第15.5節中討論過《巴塞爾協議Ⅰ》中關於淨額結算的內容。淨額結算也是ISDA主協議以及CCP與其會員之間協議的重要內容。淨額結算意味著在下述情況下,交易雙方所有的交易會被作為一個交易來處理:①計算擔保品數額時;②因為發生違約而造成提前終止事件。正如我們在第15.5節中解釋的,淨額結算減少了信用風險。因為有了此項規則,違約的一方就不能選擇只對虧損的交易違約,而保留盈利的交易。
淨額結算還可以節省初始保證金。假設A方與CCP有兩個不完全相關的交易,投資組合的初始保證金很可能低於兩筆交易的保證金。
17.1.5 如何處理違約
當發生違約或破產時,衍生產品交易的處置和其他交易的處置是不同的。例如,在ISDA主協議中,也有類似的提前終止條款。條款規定,如果發生“違約事件”,在一定的短時間內,[7]非違約方有權利終止與違約一方的所有交易。違約事件包括宣佈破產、在到期時不能及時履行支付義務、不能按要求提供擔保品等。[8]非衍生產品合約不一定總能以這種方式終止。衍生產品和非衍生產品交易的另一個重要區別是,衍生產品交易中一旦發生違約,非違約方可以立即將違約方提供的擔保品留置,而無須再經過法院的指令。
如果交易雙方簽署有ISDA主協議,當違約發生後,非違約方會計算現有交易的市場中間價,然後可以對這個價格做出有利於非違約方的適當調整。調整量通常是買賣價差的一半,將調整以後的價格作為結算價格。這個價格調整可以看作是一種補償,因為非違約方必須與另外一家交易商進行一筆同樣的交易,以重置違約的交易。而在進行新交易時,會有買賣價差。假設一筆交易對非違約方的市場中間價是2000萬美元,市場上該交易的買入價是1800萬美元,賣出價是2200萬美元。結算時,該交易的定價應為2200萬美元,因為這是非違約方重置該交易的費用。如果非違約方在交易中處於另一個方向,即市場中間價為-2000萬美元,結算時該交易的定價應為-1800萬美元。在這種情況下,我們會假設第三方只願意出價1800萬美元來從違約方手中接手該交易。
[1] A和B可能是兩個衍生產品交易商或一個衍生產品交易商及其客戶之一,A和B中的一個也可以是CCP。閾值是指在要求追加保證金之前投資組合對一方的最小价值,最低保證金是必須提交保證金所需的最小投資組合價值變動。
[2] 在這種情況下,請注意,如果A以1萬美元從B手中購買期權,則必須向B支付1萬美元,但B必須將這1萬美元作為變動保證金返還給A。
[3] 如後面所述,非違約方可向違約方索賠其在替代交易時所產生的與買賣價差有關的成本。
[4] 市場參與者擔心交易價值的增加可能看起來很奇怪,但是,假設與違約交易對手的交易被與另一交易對手進行的另一筆交易對衝(通常是這種情況),那麼與另一方的交易可能會造成損失,而不會對違約交易產生任何補償性收益。
[5] 如前所述,允許非違約方將違約方所繳納的保證金維持在合法要求的數額之內。
[6] 在某些情況下,如果有違約發生,未違約成員需要繳納額外的清算基金。額外繳納的數額會有一個上限(這種制度對場內清算所和 CCP都適用)。
[7] 非違約方不一定要履行這個權利。通常在交易中處於浮虧狀態的一方會認為不終止是最好的選擇。
[8] 新的違約解決機制已經被提出。在保證金/擔保品能繼續被提供的前提下,即使一方已申請破產,交易也能夠被保留一定時間而不是終止。這種機制可以使破產方的衍生產品組合以一種有序的方式出清。
17.2 危機後的監管改革
許多人認為,OTC衍生產品市場對2008年信用危機負有部分責任。2008年金融危機爆發後,20國集團(G20)領導人於9月在匹茲堡會晤,他們希望通過監管OTC市場來降低系統性風險。領導人會後發表聲明達成共識:
所有標準化的OTC衍生產品合約應通過交易所或電子交易平臺進行交易,在合適的情況下,應採用中央對手方的方式清算,改革最遲於2012年年底完成。OTC衍生產品應向交易倉庫報告。不採用中央清算的OTC衍生產品交易合同應適用更高的資本要求。我們要求金融穩定委員會及其相關成員評估實施情況及其是否足以提高衍生產品市場的透明度,降低系統性風險,防止市場濫用。
這引起OTC衍生產品的三個主要變化:
(1)要求所有標準化OTC衍生產品通過中央對手方進行清算。標準化衍生產品包括普通利率互換(佔OTC衍生產品交易的絕大部分)和信用指數違約互換。這個要求的目的是降低系統性風險(見業界事例15-1)。它導致衍生產品交易商之間的信用敞口減少,從而降低了金融機構間的內在聯繫導致金融體系崩潰的可能性。
(2)要求標準化的OTC衍生產品合約在電子平臺上交易。這一舉措是為了提高透明度。如果有一個電子平臺來撮合買賣雙方,那麼所有市場參與者都應能隨時獲得產品交易的價格。[1]這些平臺在美國被稱為互換執行設施(SEF),在歐洲被稱為有組織交易設施(OTF)。在實踐上,標準化OTC衍生產品一旦在這些平臺上進行交易,就會被自動轉交給CCP。
(3)要求OTC市場上的所有交易都報告給中央交易數據倉庫。這一要求為監管機構提供了有關OTC交易市場參與者所承擔風險的重要信息。這在一定程度上是對美國國際集團(AIG)慘敗的迴應。在AIG請求紓困之前,監管機構並不知道AIG的一家子公司所承擔的巨大風險。
前兩項規定僅適用於兩家金融機構間的交易(或一家金融機構與一家因OTC衍生產品交易規模而具有系統性重要非金融公司之間的交易)。因此,衍生產品交易商可以繼續以危機前的方式,與許多非金融公司客戶進行交易。
約25%的OTC交易在危機前通過中央交易方清算,其餘75%通過雙邊清算。由於新規定的出現,這些比例發生了反轉,現在約75%的OTC交易通過中央交易方清算,25%的交易通過雙邊清算。
17.2.1 未清算交易
在2011年舉行的另一場G20會議之後,針對非標準OTC衍生產品的監管有所收緊。這些衍生產品不包括在上一節提到的規則中。它們適用於雙邊清算而不是集中清算,被稱為未清算交易(uncleared trade)。監管(在2016~2020年實施)規定兩家金融機構(或一家金融機構與一家被認為具有系統性重要非金融企業)之間的未清算交易必須遵循保證金規定。在此之前,雙邊清算的吸引力之一是,市場參與者可以自由協商其ISDA主協議的任何信用支持附件。
法規規定,對於未清算交易,交易雙方都必須繳納初始保證金和變動保證金。在金融危機前的OTC市場交易中(特別是在衍生產品交易商之間的交易中),變動保證金相當普遍,但很少要求繳納初始保證金。當與信譽不高的交易對手進行交易時,衍生產品交易商可能會堅持要求對手提供初始保證金。但在雙邊清算市場上,需要繳納初始保證金的情況極為鮮見。
變動保證金通常是直接由交易一方轉交給另一方,但初始保證金不能這樣處理。例如,如果A將100萬美元的初始保證金轉給B,B又將100萬美元的初始保證金轉給A,那麼初始保證金就不能達到預期的目的,因為雙方間的保證金會相互抵消。因此,法規要求初始保證金必須轉給第三方,由第三方託管。
17.2.2 初始保證金的確定:SIMM
對於未清算交易的新規定,ISDA主協議的雙方必須就變動保證金和初始保證金達成一致。變動保證金要求就未完成交易的估值達成協議,並已制定解決任何分歧的程序。初始保證金的計算比交易價值的計算更為複雜,不同的模型能給出截然不同的結果。因此,人們一直試圖制定一個行業標準。
在雙方未清算交易組合規則中有明確規定,在壓力市場條件下,初始保證金有99%的概率不會超過10天的價值收益。需要注意的是,初始保證金是在險價值的一個標誌。當計算在險價值時,就是在確定損失分佈的極限百分位數,而當計算初始保證金時,是在確定收益分佈的極限百分位數。這是因為風險敞口隨著投資組合無抵押價值的增加而增加。
巴塞爾委員會提出了一種計算初始保證金的方法,它規定了不同類型交易的初始保證金佔交易額的百分比。這不是一種主流的方法,因為它沒有考慮淨額結算。如果市場參與者在第1天和第5天的兩筆交易幾乎相抵,那麼即使對交易對手的淨風險敞口接近於0,第5天的初始保證金也幾乎是第1天的2倍。ISDA提出了標準初始保證金模型(SIMM)來克服這一問題。這個模型現在已經得到了監管機構的批准。
SIMM使用第14章描述的模型構建法,[2]delta與vega風險使用式(14-8)的加權敏感性和風險權重進行處理
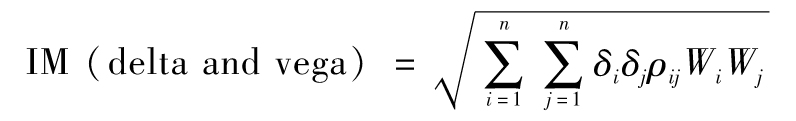
其中Wi為風險因子i的風險權重(由監管機構指定),δi為所持頭寸對風險因子i的敏感性(由銀行決定),ρij為風險因子i與j的相關性(由監管機構規定)。在置信度為99%、10天展望期的情況下,計算Wi的一個公式是

其中σi是在受壓的市場條件下第i個風險因子的每日波動率(或標準差,如利率、信貸息差和波動率)。
為計算初始保證金gamma風險的增量效應,SIMM首先考慮了所有delta為0且沒有交叉gamma的情況。由式(14-11)和式(14-12)可知,1天內投資組合價值變化的均值和標準差分別為
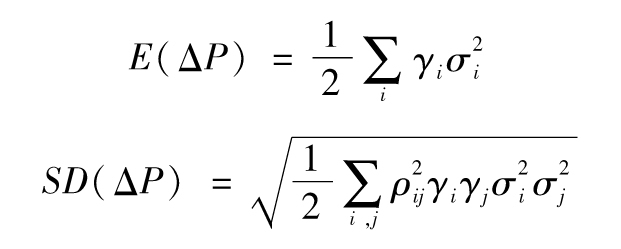
其中γi是對於第i個風險因子的gamma風險。
將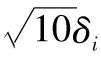 代入δi,可以獲得10天內投資組合變化的平均值和標準差的估計值。定義
代入δi,可以獲得10天內投資組合變化的平均值和標準差的估計值。定義
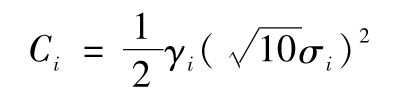
則10天變化中的平均值m,標準差s分別為
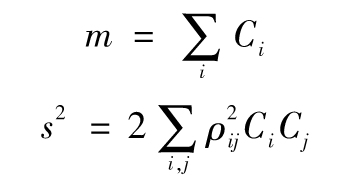
SIMM模型中假設
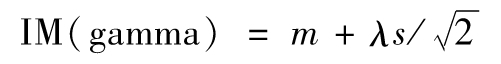
式中參數λ(見作業題17.14)定義為
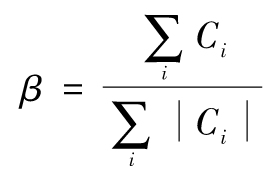
如圖17-3所示。這種關係產生的結果具有正確的性質,並與使用蒙特卡羅模擬進行的測試密切相符。
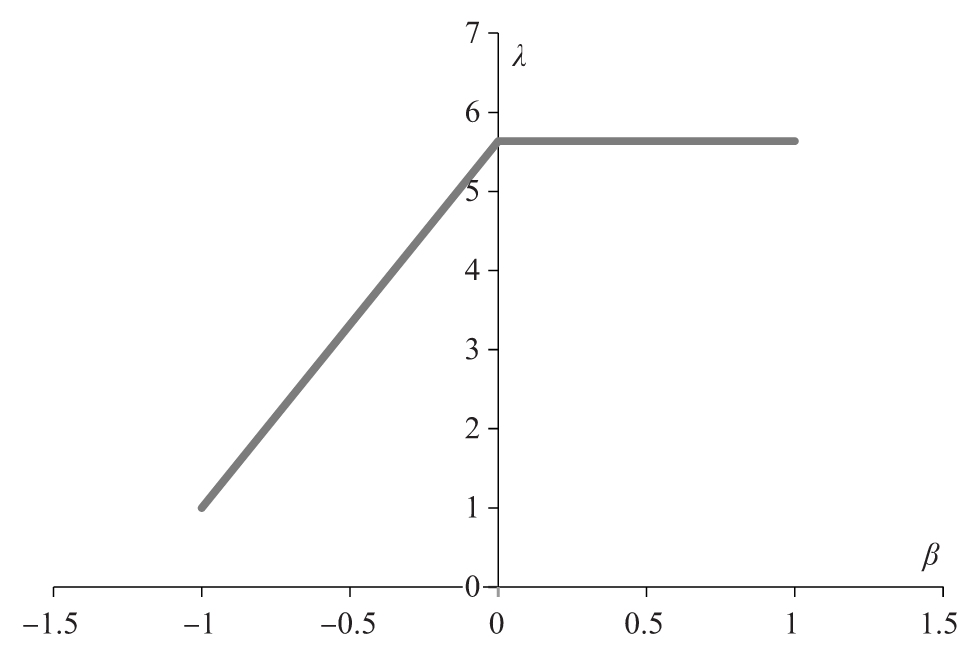
圖17-3 λ和β的關係
SIMM中還有很多其他的細節。為簡化計算,gamma由使用兩種持有歐式期權的vega計算得來。風險因子被分成幾組,一些風險因子涉及帶有頂點的期限結構,按第14章中描述的進行處理。按照規定的規則計算組內與組間的相關性ρij。
[1] 這裡的一個問題是,適用於互換的電子平臺類型可能與交易所使用的電子平臺類型不同。互換交易是間斷性的,有大量的名義本金,而交易所中期貨和期權交易的規模通常要小得多。
[2] See “ISDA SIMM: From Principles to Model Specification,” ISDA, March 3, 2016.
17.3 OTC交易新規定帶來的影響
實行新的監管規則後,OTC衍生產品交易所需的擔保品數量上升了。在危機前,大部分OTC衍生產品是經過雙邊清算的,而初始保證金在大部分情況下是不需要的。在新的規定下,大部分交易將會通過CCP清算,並且雙方都需要支付初始和變動保證金。更進一步,金融機構之間雙邊清算的交易,也需要支付與經過CCP清算的交易相類似的保證金。
有研究指出(Duffie and Zhu,2011),新規定下的巨大擔保品要求可能會得到部分的中和。在中央清算的機制下,有可能進行更多的淨額結算。在圖17-1中,在雙邊清算機制下,市場參與方有很多不同的淨額結算集合,每個集合對應一個不同的交易對手。在中央清算下,則只有一個淨額結算集合。例如,銀行A可以將與銀行B的對手交易和與銀行C的對手交易淨額結算,只要與銀行B和銀行C的交易都經過同一個CCP清算。
但是圖17-1只是一種簡化情況。它假設我們只能在兩種可能性中做出選擇:要麼是100%的雙邊清算,要麼是所有交易都通過唯一的CCP清算。實際的情況是:①會有很多不同的CCP,而這些CCP之間可能並不會相互協調以降低對初始保證金的要求;②有些交易將繼續使用雙邊清算。因此,現實中的衍生產品清算機制將會是圖17-1相結合的方式。
另外,在使用CCP清算的新規定下,淨額結算在某些情形下有可能減少而不是增加。對此,圖17-4做出了說明。圖中給出了有三個市場參與者和一家CCP的情況。圖中虛線代表的是標準化的交易,這些交易可以採用中央清算方式。實線代表的是非標準化交易,這些交易不能使用中央清算方式。例如,在銀行B與銀行A的交易中,非標準交易對於銀行B而言,價值為100,對於銀行A而言,價值為-100;標準交易對於銀行A而言,價值為50,對於銀行B而言,價值為-50。
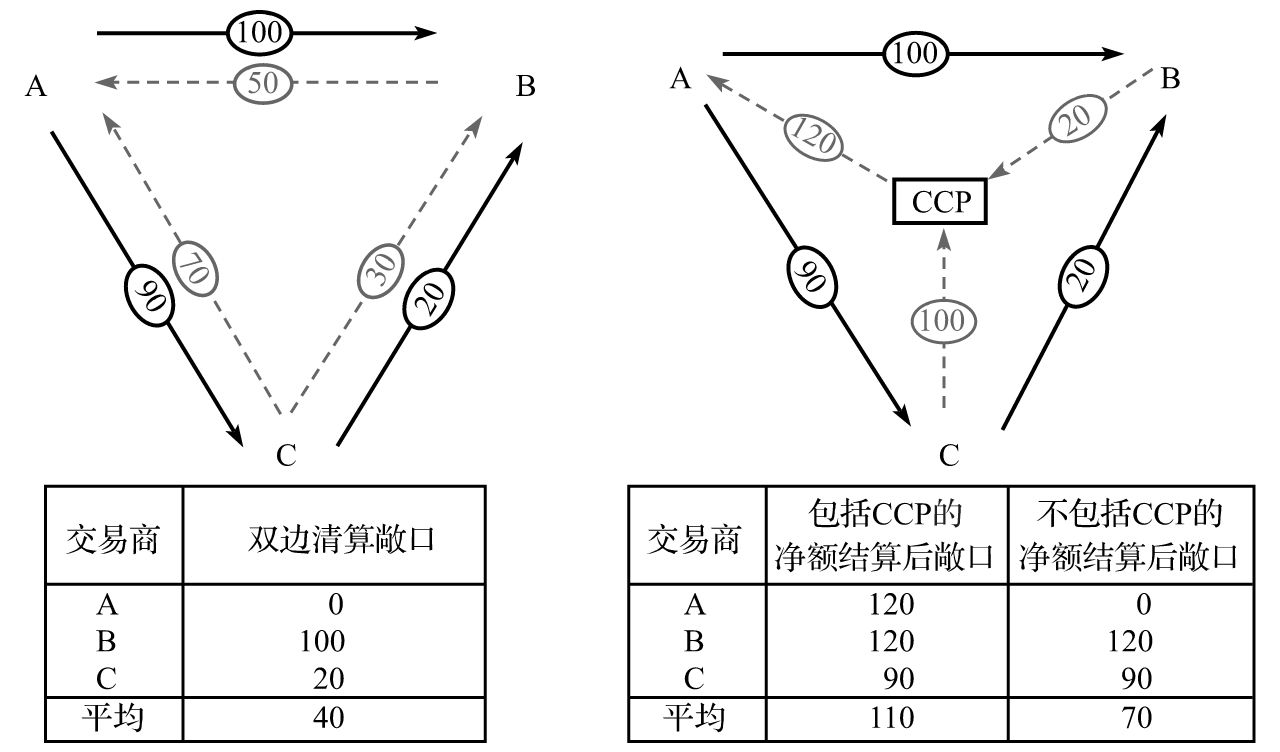
圖17-4 三個市場參與者、一家CCP、兩類交易的例子,其中一種交易可通過中央清算,而另一種不行
在沒有中央清算的情況下,三方所面臨的風險敞口平均值為+40;在引入CCP以後,包括CCP在內的信用風險敞口平均值為110,不考慮CCP的信用風險敞口平均值為70。在這種簡單的情形下,中央清算有可能增加了市場參與者的保證金負擔。這是因為在沒有中央清算規定的情況下,標準交易和非標準交易是可以相互淨額結算的,但在中央清算的制度下,這種淨額結算不再被允許了。
大部分專家認為,儘管淨額結算會增加,但整體上新的規定還是會大規模地增加對擔保品和保證金的要求。在危機前,很少有OTC衍生產品交易會引入初始保證金。在危機後,大部分OTC衍生產品交易有初始保證金要求。另外,隨著越來越多的交易通過CCP清算,金融機構被清算基金佔用的資金量也會上升。
17.3.1 流動性
新監管規定下的擔保品大多數必須是現金或政府債券。因此,對所有衍生產品市場參與者來說,流動性是一個日益重要的問題。在任何時候,不僅已經交出的擔保品會造成流動性的流失,而且銀行還必須在手頭準備足夠的高流動性資產,以應對可能的保證金催付(來自CCP的保證金催付必須即刻被滿足)。我們在第16章中看到,《巴塞爾協議Ⅲ》已經意識到流動性的重要性並提出了兩項銀行必須遵守的新的流動性比率。傳統上,資本金是決定銀行內部各業務部門和不同項目盈利能力的關鍵衡量指標。在將來,包括資本金和流動性的二維衡量指標可能會得到廣泛使用。通常在資本金和流動性之間要進行權衡,因為一個從資本金角度具有吸引力的項目往往在流動性方面不那麼吸引人,反之亦然。
17.3.2 再抵押
另外一項危機後引入的變革也可能會增加流動性壓力。在危機爆發前,在很多國家和地區(特別是英國),再抵押是很通行的做法(見業界事例17-1)。所謂再抵押(rehypothecation),就是交易商用收到的來自某對手方的擔保品去滿足另一對手方的擔保品要求。據估計,在危機前,衍生產品交易所需的擔保品大約有4萬億美元,但由於再抵押的存在,只有約1萬億美元是新的擔保品。[1]換句話說,每項擔保品平均被使用了4次。在巴塞爾委員會及國際證監會組織(International Organization of Securities Commissions,IOSCO)正在制定的新規定中,再抵押的使用受到限制。這些新規定允許初始保證金在滿足某些條件的情況下可再抵押一次。變動保證金可以被再抵押,但越來越多的交易商自己對再抵押施加限制,因為他們不想像雷曼兄弟的一些交易對手那樣處於不利地位(見業界事例17-1)。
業界事例17-1
再抵押
擔保品管理中再抵押的應用可能會引起麻煩。如果A方給B方提供了擔保品而且擔保品是允許再抵押的,那麼B方可以用收到的擔保品來滿足C方對擔保品的要求,C方再用其滿足D方對擔保品的要求,依此類推。據估計,2007年美國銀行系統中有擔保品4萬億美元,但這是由1萬億美元的原始擔保品加再抵押製造出來的。在英國,再抵押更為常見,而且擔保品的所有權會隨之轉移。
2008年8月雷曼兄弟宣佈破產後,客戶(特別是歐洲的對衝基金客戶)發現他們交給雷曼兄弟的擔保品很難收回,因為這些擔保品很多都被再抵押出去了。有了這樣的教訓,現在市場參與者在再抵押問題上比以前更加謹慎,信用支持附件(CSA)中也加入了相應的條款來禁止或限制再抵押的使用。
17.3.3 OTC和場內交易市場的統一
上述發展已經使OTC衍生產品交易和場內交易的界限變得模糊。現在很多OTC交易已經在類似於交易所的平臺上進行,並且通過與場內清算所相似的機構來清算。隨著時間的推移,標準OTC交易的比例會進一步上升,這些交易的處理都會類似場內交易。另外,即使金融機構之間雙邊清算的交易也會越來越像場內交易。這是因為初始保證金必須交給第三方機構託管,我們預計為這些業務服務的機構也會相應地建立起來(類似場內清算所)。
從另外一個方面講,交易所也在逐步努力向機構投資者提供非標準化的產品,以儘量從OTC市場多佔份額。從結果來看,在OTC市場向場內市場方向靠攏的同時,場內市場也在相向而行,朝著OTC市場的方向推進。很多CCP和交易所的所有權已經統一,將來也會在保證金要求和業務實踐等領域開展合作。一單交易是通過交易所或是CCP來清算在將來可能變得不再重要了,因為它都會經由同一個組織,以同樣的方式進行處理。
[1] See M. Singh and J. Aitken, “The (Sizable) Role of Rehypothecation in the Shadow Banking System,” Working Paper, International Monetary Fund, 2010.
17.4 CCP倒閉的風險
監管機構的一個核心目標是降低系統性風險。有些評論者批評新的監管規則將原來“大而不倒”的銀行替換成了“大而不倒”的CCP。對金融體系而言,如果像倫敦清算所(LCH Clearnet)或芝加哥商業交易所清算中心(CME Clearing)這樣的清算機構倒閉,確實意味著重大的災難。正如赫爾(Hull,2012)指出的,雖然在理論上我們可以設計出CCP與會員之間的合約,使CCP的倒閉變得基本上不可能發生,[1]但在實踐中,CCP保持適度的風險敞口是合理的,這樣可以促使它們有動機對關鍵問題做出嚴謹的決策,如是否接收某個新會員、如何設置初始保證金等。
用“大而不倒”的CCP替代大而不倒的銀行的合理性在於:相比銀行,CCP的組織架構要簡單得多,因此對CCP進行監管要比對銀行進行監管容易很多。本質上,監管機構只需保證CCP在實務中做好以下幾點工作:①選擇會員;②交易定價;③確定初始保證金和清算基金份額。但要監管銀行,就必須監控銀行很多非常複雜的業務活動。因此對監管機構來說,確保CCP不把業務擴展到衍生產品交易中介這一核心職能以外,避免其成為更加複雜的組織,是非常重要的。
[1] See J. Hull, “CCPs, Their Risks, and How They Can Be Reduced,” Journal of Derivatives 20, no.1(Fall 2012):26-29.
小結
在2007~2009年的信用危機之前,OTC衍生產品市場大體上是沒有監管的。市場參與者可以達成任何符合雙方意願的交易,然後以雙方認可的方式進行交易的清算。他們也可以自由地選擇擔保品的處理方式,但這種情況已經不復存在了。現在,在世界範圍內,OTC衍生產品市場都受到大量的監管。OTC衍生產品市場對金融危機有多大的責任並沒有定論,但是監管法規的變化對該行業的影響是各經濟門類中最大的。
金融機構間大部分標準的OTC衍生產品必須通過中央對手方CCP來進行清算,這和場內清算機制很類似。交易雙方都需要提交初始保證金和變動保證金。金融機構間的非標準交易可以繼續採用雙邊清算。但自2015年開始,監管規則也要求為這些交易提供擔保品。特別地,金融機構間的交易需要初始保證金(與其他資產隔離)和變動保證金(當交易價值變化時,資金會由交易的一方轉入另一方)。
15~20年後,衍生產品市場將會是什麼狀況?目前的趨勢表明,OTC市場和場內市場正在相互融合,二者之間的區別逐漸模糊。但需要說明的是,我們並不能保證這樣的趨勢一定會持續下去。在金融危機前,OTC市場對大型金融機構來說,利潤非常豐厚。金融機構很可能會不斷地嘗試擺脫監管法規帶來的影響,從而逐步找到重建新的衍生產品市場的方法,回到與金融危機前相仿的狀況。監管機構的決心和銀行的創造性之間將會展開一場較量。
延伸閱讀

練習題
17.1 清算OTC衍生產品時,使用ISDA主協議和使用CCP之間有什麼不同?
17.2 試著解釋在2007~2008年金融危機後引入的新的監管規定,這些規定要求:(a)某些交易必須通過CCP清算;(b)對某些雙邊清算的交易,有額外的保證金要求。
17.3 為什麼在2007~2008年金融危機後引入的監管規定會給某些金融機構帶來流動性問題?
17.4 解釋一下擔保品協議中“折減”的含義。
17.5 解釋一下ISDA主協議中“違約時間”和“提前終止”的含義。
17.6 在圖17-4中用到了CCP,假設A和B之間用實線表示的交易中的一半轉入了CCP,那麼該變化對三方的平均敞口有何影響?考慮兩種情況:(a)計算中包括對CCP的敞口;(b)計算中不包括對CCP的敞口。
17.7 一家公司成為CCP會員並通過CCP進行交易清算後,其面臨的信用風險是什麼?
17.8 “淨額結算會影響交易方需要提供的擔保品以及在出現提前終止事件時的結算。”試著解釋這句話的含義。
17.9 什麼是再抵押?
17.10 為什麼對CCP實施監管要比對銀行實施監管更簡單?
17.11 在ISDA主協議下,如果出現了提前終止事件,非違約方求償的數額如何計算?
作業題
17.12 “預計新規的某些方面將增加衍生產品擔保品的數量,有些方面可能會減少。”解釋這句話的含義。
17.13 在圖17-4中用到了CCP。假設A和C之間發生了一筆額外的交易,交易對A價值140,交易採用雙邊清算。這筆交易對圖17-4中的交易商的敞口有何影響?
17.14 考慮單個資產的delta中性頭寸,其gamma(相對於資產的百分比變化)為γ(γ> 0)。假設資產的10天收益率服從均值為0、標準差為σ的正態分佈。
(a)假設隨機樣本服從標準正態分佈,寫出在10天內投資組合價值變化ΔP作為γ、σ的函數的表達式。
(b)標準正態分佈的平方是具有一個自由度的卡方分佈。根據這樣的卡方分佈和C,將(a)中ΔP的表達式寫為隨機樣本的函數,其中C=γσ2/2。
(c)具有一個自由度的卡方分佈的第99個分位數為6.63(參閱Excel中的CHISQ.INV)。試說明ΔP的第99個分位數為6.63C。
(d)一個自由度的卡方分佈的均值和方差分別為是1和2。試說明該結果與圖17-3和第17.2.2節中IM(gamma)的公式一致。
(e)說明當γ<0時,ΔP的第99個分位數小於0,因此圖17-3中的IM(gamma)=0。
第18章
交易賬戶基本審查
2012年5月,巴塞爾銀行監管委員會發布了一份諮詢文件,提議對市場風險監管資本的計算方式進行重大修改。這種方法被稱為“交易賬戶基本審查”(FRTB)。[1]巴塞爾委員會在收到市場參與者的意見,並進行了定量影響研究(QIS)後修改了提案,[2]且於2016年1月公佈了最新版的文件,[3]同時要求各銀行自2019年起實施新規。但是在2017年12月,實施時間又被推遲到了2022年。
FRTB確定市場風險資本金的方法比監管機構以前使用的方法複雜得多,本章將概述其主要內容。
[1] 見國際清算銀行,“Consultative Document: Fundamental Review of the Trading Book”,2012年5月。
[2] QIS由銀行計算以評估擬議的監管改革對資本金要求的影響。
[3] 見國際清算銀行,“Minimum Capital Requirements for Market Risk”,2016年1月。
18.1 背景
《巴塞爾協議Ⅰ》對市場風險資本的計算是基於10天展望期、99%置信水平計算出的在險價值(VaR)。VaR能夠反映當前的情況,因為計算是基於最近一段時間(通常是1~4年)市場變量的變現。《巴塞爾協議Ⅱ.5》要求銀行除計算現有的VaR指標外,還應計算壓力VaR。正如第13.1節和第16.1節所描述的,這是基於市場變量在市場受壓狀況下的250天期間內的表現計算的VaR。為了確定承壓期,銀行需要通過回溯來查找一個銀行的當前投資組合表現會非常差的250天的時間段。
FRTB提出改進用於確定市場風險資本金的計算方法,以97.5%置信水平的預期虧空(ES)取代現有的99%置信水平的VaR。與計算壓力VaR的情況類似,97.5%置信水平下ES的計算是基於對市場受壓時市場變量變動的觀測。
在正態分佈中,99%置信水平的VaR和97.5%置信水平的ES的計量結果幾乎完全相等,假設損失服從均值為μ、標準差為σ的正態分佈,99%的VaR為μ+2.326σ,而97.5%的ES為μ+2.338σ(見練習題18.2)。[1]對於具有比正態分佈尾部更肥大的分佈而言,97.5%的ES可能遠大於99%的VaR。
FRTB進一步建議對《巴塞爾協議Ⅰ》與《巴塞爾協議Ⅱ.5》中使用的10天展望期進行更改,以反映交易涉及的市場變量因其流動性不同而變化的事實。FRTB要求市場變量的變化量(也被稱作擾動(shocks))應為其在市場受壓情況下某一時段內發生的改變量。這些市場變量則可稱為風險因子(risk factors),這樣的時間段被稱為流動性展望期(liquidity horizons)。有5個不同的流動性展望期將被採用:10天、20天、40天、60天與120天。表18-1顯示了這些流動性展望期內風險因子的分配情況。
表18-1 市場變量在不同流動性展望期上的分配
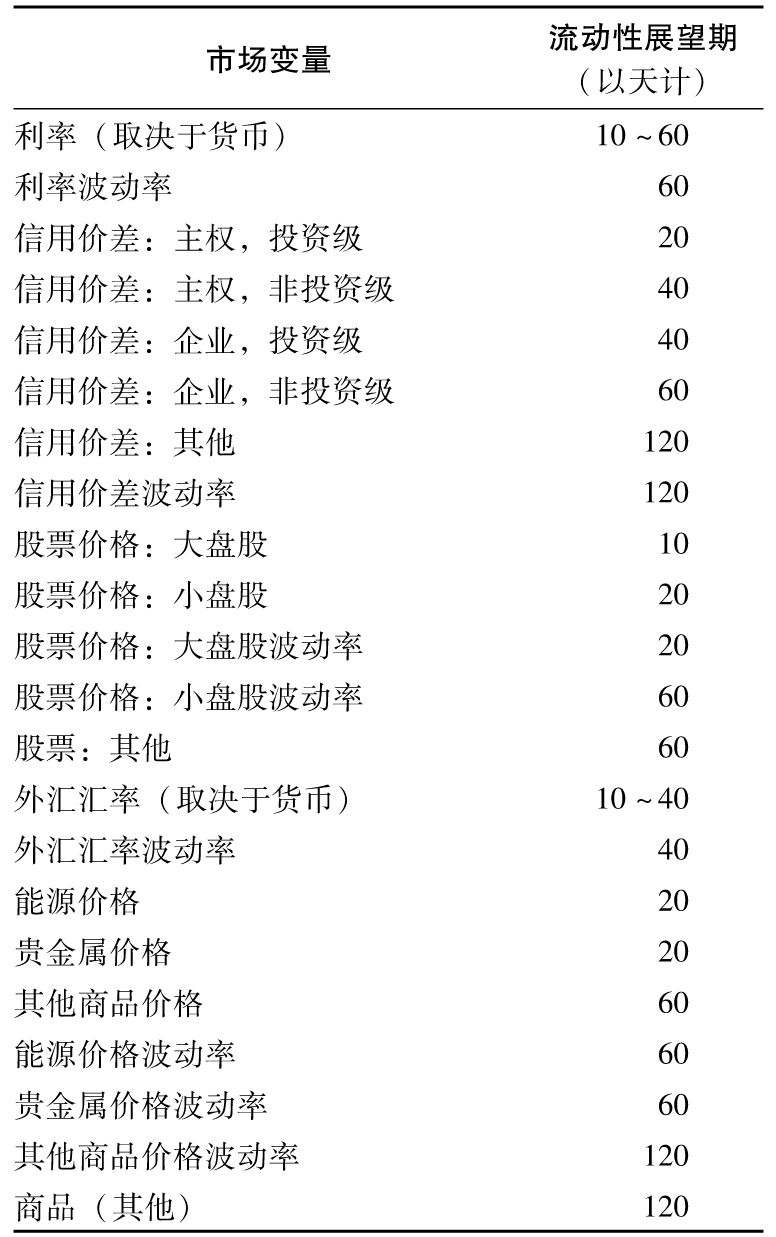
FRTB規定了計算市場風險資本金時要採用標準法和內部模型法,即使銀行已經獲得批准使用內部模型法,監管機構仍然要求它們計算兩種方法下的所需資本金。這與巴塞爾委員會要求使用標準法為計算資本金要求提供一個下限的安排相一致,正如第16.4節所述,2017年12月,巴塞爾委員會公佈了一項規定,要求銀行的總資本金至少達到標準法算出的資本金的72.5%,計劃將以5年為一個階段分步實施,於2027年前實現這一目標。這是巴塞爾委員會自2008年危機以來的一種變化趨勢,減少對內部模型法的依賴,並使用標準法為計算資本金提供參考。
FRTB與以往市場風險監管要求的區別在於,大多數計算都是在交易部門進行的。此外,使用內部模型法的權限是按部門分配的。因此,可能在某一特定時間點,一家銀行的外匯交易部門獲准使用內部模型法,而股票交易部門卻沒得到批准。
前面幾章說明了交易賬戶和銀行賬戶計算資本金方式的不同,當銀行為了最小化資本金而選擇將產品分配到交易賬戶或者銀行賬戶時,可能會導致監管套利。在《巴塞爾協議Ⅱ.5》中,增加的風險費用降低了這種做法的收益。FRTB通過更明確地定義兩個賬戶間的差異來消除監管套利。
[1] 根據式(12-2),一個均值為μ、標準差為σ的正態分佈的ES的為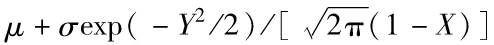 ,其中X是置信水平,Y是標準正態分佈上有1-X的概率被超過的點,故ES也可以為μ+σ2f(VaR)/(1-X),其中f是損失的概率密度函數。
,其中X是置信水平,Y是標準正態分佈上有1-X的概率被超過的點,故ES也可以為μ+σ2f(VaR)/(1-X),其中f是損失的概率密度函數。
18.2 標準法
標準法規定資本金由三個部分組成:利用風險敏感分析衡量的風險費用、違約風險費用和剩餘風險附加費用。
回顧第18.1節的內容,定義了7個風險類別:利率風險、外匯風險、商品風險、股權風險和三種信用價差風險。在每個風險類別中,分別計算delta風險費用、vega風險費用和曲率風險費用。
每個風險類別中的delta風險費用根據第14.6節描述的風險權重和加權敏感性方法計算
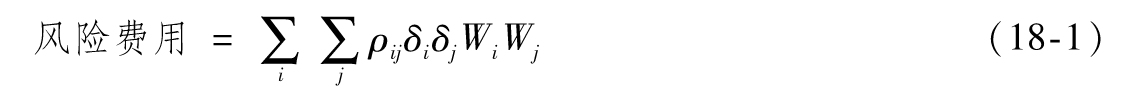
在這個公式中,將風險類別中所有的風險因子進行加總。風險權重Wi和風險因子相關係數ρij都是由巴塞爾委員會決定的。[1]加權敏感性δi(或delta)由銀行決定的。如第14章所述,就股票價格、匯率或商品價格等風險因子而言,delta度量投資組合對這些變量百分比變化的敏感性。例如,如果商品價格上漲1%,就會使投資組合的價值增加3000美元,delta就是3 000/0.01=300 000。在利率和信用價差等風險因子方面,delta是用絕對變化來定義的。例如,如果利率上升一個基點(0.000 1)會使投資組合價值減少200美元,則對這一利率的delta為-200/0.000 1=-2 000 000。
思考監管機構如何設定風險權重Wi。首先,假設所有的風險因子都來自股票價格、匯率或商品價格,delta對百分比變化十分敏感。如果Wi設定為風險因子i的日波動率,則式(18-1)中的風險費用就等於投資組合每天價值變動的標準差。這與第1章和第14章討論的馬科維茨結果相一致。如果將Wi設為風險因子i在壓力市場情況下的日波動率(受壓日波動率),根據式(18-1)能計算出壓力市場條件下投資組合每天價值變化的標準差。實際上,Wi被設定為受壓日波動率的倍數,以反映監管機構要求的流動性展望期和置信度水平。假設風險因子i的受壓日波動率估計為2%,且風險因子有20天的流動性展望期,風險權重可設定為0.02×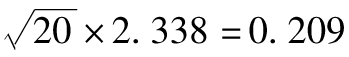 (注意,乘數2.338是在假定損失服從正態分佈時,為得到97.5%置信度的ES,標準差必須乘以的數字)。
(注意,乘數2.338是在假定損失服從正態分佈時,為得到97.5%置信度的ES,標準差必須乘以的數字)。
現在假設風險因子是利率和信用價差,delta是對於以基點衡量的實際變化的敏感性。風險因子i的風險權重Wi設為壓力日標準差的倍數。如果倍數為1,公式將給出組合在1天中的標準差。在實際操作中,確定乘數是為了反映流動性展望期和置信度水平。
計算vega風險的方法類似於delta風險,[2]使用式(18-1)計算每個風險類別的vega風險費用。假定風險因子(由i和j表示)為波動率,對風險類別中的所有波動率進行求和。參數δi實際上就是vega,表示投資組合價值對波動率i微小變化的敏感性。[3]參數ρij是波動率i和波動率j間的相關性,而Wi是波動率i的風險權重。後者的確定類似於delta風險權重,反映波動率i的波動性、流動性展望期和置信度水平。
假設在不同風險類別的風險因子之間,同一風險類別內的vega風險和delta風險之間均不存在風險分散效應。到目前為止,資本金最終的計算結果是7個風險類別的delta風險費用與7個風險類別的vega風險費用之和。
18.2.1 期限結構
在風險因子為利率、波動率和信用價差的情況下,通常存在一個由若干個點定義的期限結構。例如,利率期限結構通常由10個點確定,分別是期限為3個月、6個月、1年、2年、3年、5年、10年、15年、20年和30年的零息利率。正如第14章所討論的,期限結構的每個頂點都是一個獨立的風險因子。投資組合對於期限結構中一個頂點的基點移動的delta風險,是通過在保持其他點不變的情況下對該頂點增加一個基點計算得來的。巴塞爾委員會規定了期限結構的每個頂點的風險權重以及同一期限結構中各頂點之間的相關性。
當確定了不同期限結構上各點之間的相關性時,可以採用一種簡化方法,即假設期限結構1上的點A與期限結構2上的點B之間的相關性對於所有A和B都是相同的。這是第14章中考慮的備選辦法之一,見式(14-6)。
18.2.2 曲率風險費用
曲率風險費用是在標準法下銀行gamma風險敞口的資本費用。為了考察投資組合對第i個風險因子的風險敞口,銀行需要通過改變風險權重Wi來檢測增加風險因子和降低風險因子的影響。如果投資組合與風險因子線性相關,風險因子增加Wi對投資組合的影響為Wiδi。同樣地,降低風險因子的Wi對投資組合的影響為-Wiδi。為了評估delta效應的淨曲率的影響,標準法計算了:
(1)Wiδi減去因風險因子的Wi增加所帶來的影響;
(2)-Wiδi減去因風險因子的Wi減少所帶來的影響。
風險因子的曲率風險費用是這兩者中的較大者。如果delta效應的淨曲率的影響為負值,則定義為0。如圖18-1中所示的計算。在圖18-1a中,O點為投資組合目前的價值。如果沒有曲率,風險因子的Wi的增加將使投資組合價值移到C點,而風險因子的Wi的降低將使投資組合價值移到A點。由於曲率的存在,Wi的增加使投資組合價值增加到D點,而Wi的降低使投資組合價值增加到B點。又由於AB>CD,所以風險費用為AB。在圖18-1b中,因為曲率實際上增加了在增加和減少風險因子情況下所持頭寸的價值(相對於delta增加和減少的結果),所以風險費用為0(圖18-1a對應於期權中的空頭頭寸,圖18-1b對應於期權中的多頭頭寸)。
當存在多個風險因子時,每個因子的處理方式類似於圖18-1。如果存在期限結構(例如,利率、信用價差和波動率),為了計算曲率的影響,所有的點都有相同的移動量(最大的Wi)。在利率期限結構中,對應於3個月期的點的Wi往往是最大的,因此,期限結構會出現向上和向下的平行變化。通過使用δi,可以使期限結構上的每個點都消除delta效應。
將不同風險因子的曲率風險費用組合起來,可以確定總曲率風險費用。當存在風險分散效應時,聚合公式大致與巴塞爾委員會規定的用於計算相關性的delta公式相似。
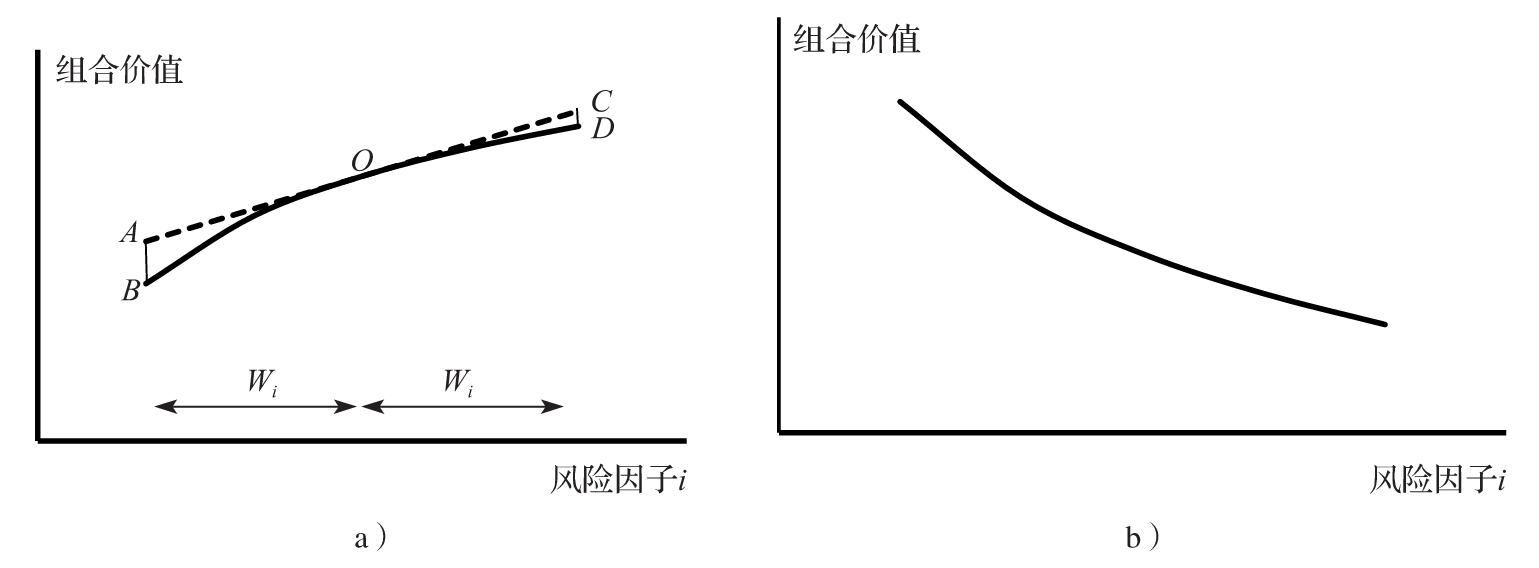
圖18-1 計算風險因子的曲率風險費用
注:在圖18-1a中,曲率風險費用為AB;在圖18-1b中,曲率風險費用為0。
18.2.3 違約風險費用
在FRTB中,與交易對手信用價差變化相關的風險和與交易對手違約相關的風險將會被分別處理。在標準法中,信用價差風險通過前述的delta/vega/曲率方法處理。而違約風險,有時被稱為突發違約(jump-to-default,JTD)風險,將收取單獨的違約風險費用,這是通過將每個風險敞口乘以給定的違約損失(LGD)和違約風險權重計算得出的。LGD和風險權重均由巴塞爾委員會規定。例如,高級債務的LGD被指定為75%,評級為A級的對手方的違約風險為3%。對於股票頭寸,需要支付LGD=100%的違約風險費用。這些設定風險敞口的規則都由監管機構明確規定。
18.2.4 剩餘風險附加
剩餘風險附加主要用於處理前述的delta/vega/曲率方法無法處理的風險,其中包括不與普通期權成線性組合時的奇異期權。附加額通過將交易的名義金額乘以巴塞爾委員會指定的風險權重計算得來。奇異期權中的風險權重為1%。
18.2.5 一種簡化的方法
在本節中,我們描述了巴塞爾委員會要求所有大銀行使用的標準法。值得注意的是,2017年6月,巴塞爾委員會發表了一項諮詢文件,概述了針對小型銀行的一種簡化的標準法,[4]在多個方面進行了簡化,例如,無須考慮vega和gamma風險。這將使FRTB更適用於美國等有許多小銀行的國家,因為這些銀行往往只進行相對簡單的交易。
[1] 銀行需要將巴塞爾委員會規定的相關係數分別乘以1.25、1.00和0.75,然後設定資本費用為所獲得結果的最大值。
[2] 如第14章所述,這種方法很有效,因為在許多情況下,大多數衍生產品的價值近似線性地取決於波動率。
[3] 銀行可以選擇是考慮波動率的百分比變化還是實際變化。
[4] 見巴塞爾銀行監管委員會,“Simplified Alternative to the Standardized Approach to Market Risk Capital Requirements”,2017年6月。
18.3 內部模型法
內部模型法要求銀行估計置信水平97.5%下的壓力ES,但FRTB並沒有為此規定一個具體的方法。在通常情況下,很可能採用第13章所描述的歷史模擬法。如表18-1所示,風險因子被賦予了不同的流動性展望期,定義:
·類別1:展望期為10天的風險因子;
·類別2:展望期為20天的風險因子;
·類別3:展望期為40天的風險因子;
·類別4:展望期為60天的風險因子;
·類別5:展望期為120天的風險因子。
所有的計算都是基於風險因子在10天內的變化量。《巴塞爾協議Ⅰ》和《巴塞爾協議Ⅱ.5》規定,銀行可以通過考慮風險因子1天的變動來計算1天的VaR,然後將該VaR放大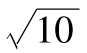 倍得到10天展望期的VaR。在FRTB中,銀行還要考慮在過去一個壓力時期裡10天內發生的變化。計量經濟學家自然傾向於在用歷史模擬法估計VaR或者ES時使用非疊加時間段,因為他們希望觀測到的損失是相互獨立的。然而,由於要考慮到10天的變化,所以這種方法不可行,因為這需要一段很長的歷史時期。FRTB要求銀行基於重疊的10天週期進行估算。在第一個模擬試驗中,假設未來10天內所有風險因子的百分比變化與承壓期第0~10天的百分比變化量相同;在第二次模擬實驗中,假設未來10天內所有風險因子的百分比變化與承壓期第1~11天的百分比變化量相同,依此類推。
倍得到10天展望期的VaR。在FRTB中,銀行還要考慮在過去一個壓力時期裡10天內發生的變化。計量經濟學家自然傾向於在用歷史模擬法估計VaR或者ES時使用非疊加時間段,因為他們希望觀測到的損失是相互獨立的。然而,由於要考慮到10天的變化,所以這種方法不可行,因為這需要一段很長的歷史時期。FRTB要求銀行基於重疊的10天週期進行估算。在第一個模擬試驗中,假設未來10天內所有風險因子的百分比變化與承壓期第0~10天的百分比變化量相同;在第二次模擬實驗中,假設未來10天內所有風險因子的百分比變化與承壓期第1~11天的百分比變化量相同,依此類推。
銀行需要首先計算所有風險因子均採用10天變化量的情形下的預期虧空(我們將此記為ES1)。然後,對類別1中的變量保持不變,對類別2及其以上類別的其他所有變量進行10天展望期的變動,再次計算預期虧空(我們將其記為ES2)。接下來,對類別1和類別2中的變量保持不變,對類別3、4和5中的所有變量進行10天展望期的變動,以此計算出的預期虧空記為ES3。然後,保持類別1、2、3中的變量不變,對類別4和5中的變量進行10天展望期的變動,將計算出的預期虧空記為ES4。最後,對類別5中的變量進行10天展望期的變動,而所有其他變量保持不變,計算出預期虧空記為ES5。
最終計算出的經流動性調整的ES為
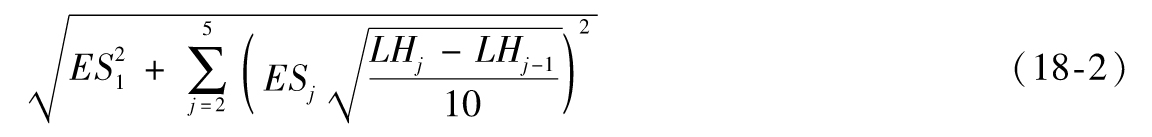
其中LHj為類別j的流動性展望期。為更好地理解式(18-2),首先假設所有的風險因子都包含在類別1和類別2中,計算ES1和ES2。假設所有風險因子在10天內的變動獨立於類別2中風險因子在10天內的變動。根據第13章所述的平方根法則,經流動性調整的ES為
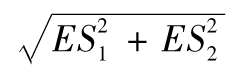
假設還存在類別3中的風險因子,如果第3類風險因子的流動性展望期是20天而不是40天,則表達式 是正確的。假設在額外的20天內,類別3的風險因子的變動獨立於已經考慮過的所有風險因子的變動。更進一步,假設第3類風險因子在20天內的ES等於10天內ES的
是正確的。假設在額外的20天內,類別3的風險因子的變動獨立於已經考慮過的所有風險因子的變動。更進一步,假設第3類風險因子在20天內的ES等於10天內ES的 倍。流動性調整的ES變為
倍。流動性調整的ES變為
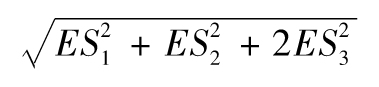
依此類推,得到式(18-2),這是計算ES的級聯方法(cascade approach,也可用於計算VaR)。
對每一個交易部門的ES都要進行計算,如果有6個部門,就需要像上面那樣通過內部模型法進行5×6=30次的ES計算。使用重疊的時間段並不是一個太理想的選擇,因為相鄰的歷史模擬試驗中用到的變化量不是相互獨立的。這並不會給結果帶來偏差,但降低了有效的樣本數量,產生的結果與使用非重疊時間段數據的結果相比,帶有更多的噪聲。
FRTB代表了一種趨勢,不再以1天的變化量作為計算基礎。巴塞爾委員會認為,儘管觀察數據缺乏獨立性,但基於10天變化量的計算得出的結果會比使用1天變化量的結果提供更多相關的信息。即使在相鄰幾天內的變化量不是相互獨立的,也可以合理地假定在相鄰10天期間的變化量之間相互獨立。
銀行需要尋找過去它們當前投資組合表現非常差的一個時間段(需要回溯到2007年)來計算受壓VaR或受壓ES。當實施《巴塞爾協議Ⅱ.5》時,銀行有時很難使用所有風險因子去尋找過去的承壓期,因為一些風險因子可能沒有足夠的歷史數據。因此,無法知道這些風險因子在過去250天的承壓期內是如何表現的。FRTB允許使用風險因子的子集來做承壓期的計算(風險因子子集對ES的貢獻要達到75%),然後計算結果要按照使用所有風險因子計算出的最近12個月的ES與使用風險因子子集計算出的最近12個月的ES的比例進行放大(這可能使ES計算的數量增加一倍,從30個增至60個)。
除了計算投資組合整體的ES外,銀行還需要計算每個交易部門的ES,這樣的ES被稱為分項ES。計算分項ES時,我們需要對相應交易部門中的相應風險因子進行擾動,同時保持其他所有部門的風險因子不變。分項ES的總和總是大於投資組合的整體ES。我們所說的加權ES(WES)是基於投資組合整體的ES和各分項ES的總和的加權平均。具體地說
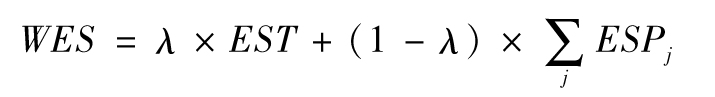
其中EST為投資組合整體的ES,ESPj為第j個交易部門的分項ES,參數λ由巴塞爾委員會設定為0.5。
一些風險因子被歸類為不可建模的(non-modelable)風險因子。特別地,如果在連續觀測的1年或者超過1個月的時間內,對某個風險因子的觀測值少於24個,則該風險因子是不可建模的。這些風險因子需要通過包含壓力測試的特殊規則來處理。
第t天的總資本金要求為
max(WESt-1+NMCt-1,mc×WESavg+NMCavg)
其中WESt-1為第t-1天的加權ES,NMCt-1為第t-1天的不可建模的風險因子的資本費用,WESavg為前60天的平均加權預期虧空,NMCavg為前60天的不可建模的風險因子的資本費用,參數mc的最小值為1.5。
18.3.1 回溯測試
FRTB沒有對內部模型法下用於計算的資本金要求的壓力ES進行回溯測試,有兩個原因:其一,ES比VaR更難進行回測;其二,根本不可能對壓力VaR和壓力ES進行回測。壓力測量所基於的壓力數據都是極端數據,從統計學上講,這些數據在未來被觀測到的頻率不會與在壓力期間內相同。
通過對每個交易部門在使用1天展望期和最近12個月曆史數據計算得出的VaR都進行回溯測試,FRTB能回測銀行的模型,測試中使用的置信水平為99%和97.5%。如果計算出的99%的VaR有超過12個結果,或97.5%的VaR有超過30個結果,交易部門就需要使用標準化方法計算資本金,直到這兩種情況都消失。
監管機構還可能要求銀行進行其他回溯測試,其中一些可能涉及計算每天損益的p值,即觀測利潤小於實際利潤或者損失大於實際損失的概率。如果模型運行良好,得到的p值應該是均勻分佈的。
18.3.2 損益歸因
監管機構使用的另一種測試方法是損益歸因。銀行須將一天的實際損益與模型預測的損益進行比較,用以下兩項衡量指標進行比較

其中,U代表實際損益與模型預測的損益之間的差額,V表示一天的實際損益[1]。監管機構預計第一個指標在-10%到10%之間,而第二個指標小於20%。如果在12個月內有4個或更多的比率超出了這個範圍,交易部門就必須使用標準化方法來確認資本金。
18.3.3 信用風險
正如前面所說,FRTB區分了公司的兩種信用風險敞口。
(1)信用價差風險。這是公司信用價差發生變化帶來的風險,會導致該產品的盯市價值發生變化。
(2)突發違約風險。這是公司直接違約的風險,通常會導致銀行立即產生損失或收益。
在內部模型方法下,信用價差風險的處理方式與其他市場風險類似。表18-1顯示,信用價差的流動性展望期從20天到120天不等,信用價差波動的流動性展望期為120天。違約風險的處理方式與銀行賬戶中的違約風險相同。在內部模型方法中,資本金是通過VaR計算出的資本計提,具有1年的時間展望期和99.9%置信水平。
18.3.4 證券化產品
《巴塞爾協議Ⅱ.5》引入了綜合風險度量(CRM)費用,以涵蓋如資產支持證券和債務抵押債券等證券化產品的風險(見第16.1節)。CRM規則允許銀行(經監管部門批准)使用內部模型法。但巴塞爾委員會認為,由於不同銀行對同一投資組合計算的資本金差異太大,使用內部模型法的結果並不讓人滿意。因此,在FRTB下,必須對證券化產品使用標準化方法計算資本金。
[1] “實際”損益應為如果一天內沒有交易將發生的損益,有時又叫假設損益。
18.4 交易賬戶和銀行賬戶的對比
交易賬戶的基本審查討論了應將資產分配在交易賬戶還是銀行賬戶中的問題。一般來說,交易賬戶包含那些銀行計劃用來交易的產品,銀行賬戶包括預計將持有至到期的資產。銀行賬戶中的產品會計入信用風險資本金,而交易賬戶中的產品則計入市場風險資本金。這兩種資本金的計算方法完全不同,在過去曾造成了監管套利。例如,正如我們在前面的章節中提到的那樣,銀行通常選擇在交易賬戶中持有與信用相關的產品,因為這樣做需要的監管資本金比把這些產品放在銀行賬戶上要少。
FRTB試圖使交易賬戶和銀行賬戶之間的區別更清晰,以減少主觀因素的影響。要將產品計入交易賬戶中,僅僅有交易的意向是不夠的,銀行還必須能夠在交易專櫃上交易和管理產品的潛在風險。每日的價值變動應影響到銀行股本,並通過償付能力風險體現出來。FRTB為不同類型的金融工具提供了更客觀的規則,以確定應該使用交易賬戶還是銀行賬戶。
重要的一點是產品在最初一旦被分配到銀行賬戶或交易賬戶後,有嚴格的規則阻止其隨後在兩類賬戶之間移動。從一類賬戶轉移到另一類賬戶只能在非常特殊的情況(比如交易專櫃的關閉,以及有關公允價值認定的會計準則發生變更)下才被允許。因在兩類賬戶之間移動資產而帶來的任何資本金收益將被禁止。
小結
FRTB是對市場風險資本金計算方式的重大變化。在使用了20年的基於10天展望期和99%置信水平的VaR後,監管者將使用不同展望期和97.5%置信度的ES測度來確定市場風險資本金。時間展望期可能長達120天,旨在將流動性納入資本金的計算中。在計算資本金時,要對市場變量進行擾動,擾動的幅度取決於市場受壓的情況下的流動性展望期。
巴塞爾委員會規定了標準化方法和內部模型法。即使監管機構批准銀行使用內部模型法,銀行也必須實施標準化方法。標準化方法下監管資本金的計算基於涉及交易賬戶的delta、vega和gamma風險的公式。內部模型法下的監管資本金基於壓力ES來計算。要對每個交易櫃檯分別進行計算。
延伸閱讀

練習題
18.1 總結一下以下監管規則中市場風險資本金計算的不同之處:(a)《巴塞爾協議Ⅰ》;(b)《巴塞爾協議Ⅱ.5》;(c)FRBT。
18.2 根據本章第4個腳註,驗證當損失服從均值為μ、標準差為σ的正態分佈時,97.5%的ES為μ+2.338σ。
18.3 解釋為什麼FRTB提出的使用帶重疊的10天展望期觀察到的市場數據變化不是相互獨立的。
18.4 相比VaR,ES有何優點?
18.5 交易賬戶和銀行賬戶之間有什麼不同?為什麼在FRTB中,監管機構會認為確定一個金融產品放在交易賬戶還是銀行賬戶很重要?
18.6 FRBT中與信用相關的交易是如何處理的?
作業題
18.7 假設某投資者在2014年9月30日持有如表13-1所示的價值1000美元的投資組合。當天的DJIA、FTSE 100、CAC 40和Nikkei 225的值指數分別為17042.90、6622.7、4416.24和16173.52,匯率分別為1.6211USD/GBP、0.7917EUR/USD、109.64JPY/USD。假設截至2008年9月9日的250天為該組合的歷史承壓時間段。結合歷史模擬法和級聯方法,通過重疊時段方法計算97.5%的ES。指數的相關數據見於作者的網站(請參閱“Worksheets for Value at Risk Example”)。在本題中,假設DJIA和FTSE具有10天的流動性展望期,CAC 40具有40天的流動性展望期,Nikkei 225具有20天的流動性展望期。對於承壓期內的每一天,思考變量在該天后10天的變化量。

第19章
估測違約概率
如第15章所述,監管部門多年來一直要求銀行計提資本金來應對信用風險。在《巴塞爾協議Ⅱ》下,銀行在得到監管部門批准後可以採用自有模型來估測違約概率,並計算應計提的資本金數量。《巴塞爾協議Ⅱ》的要求促使銀行投入更多的人力和物力來開發更好的估計違約率的方法。
本章將討論估測違約概率的不同方法,並解釋風險中性違約概率與真實世界違約概率的差別。本章討論的內容將在第20章中得到進一步的應用,屆時我們將介紹如何對雙邊清算的場外衍生產品的價格進行交易對手信用風險調節,而在第21章中,我們將討論信用在險價值的計算方法。
19.1 信用評級
如第1.7節中介紹過的,穆迪、標準普爾及惠譽等評級機構對企業債券的信用狀況提供評級。[1]因為信用評級反映了有關信用質量的信息,所以人們可能往往認為公司的信用級別會隨市場上的消息或好或壞而經常被調整。事實上,公司信用級別的變化並不是很頻繁。評級公司在評定信用級別時,其中一個目標是保證級別的穩定性。例如,評級機構不想看到某家公司在被降級的幾周後又得到升級。只是在有理由相信某公司的長期信用狀況有所改變時,信用評級機構才會調整這家公司的信用級別。這主要是因為債券交易員往往是信用評級的主要用戶,在很多情況下交易員持有的債券頭寸的信用級別必須服從某些交易規則的限制(例如,只能投資於投資級別的債券)。如果信用級別變化太頻繁的話,交易員必須進行頻繁交易(並付出較大的交易費用)以滿足有關信用級別的要求。
另外,信用評級機構在評級時往往要貫穿經濟週期(rate through the cycle)。如果宏觀經濟形勢變差,可能會使某家公司在今後6個月內的違約概率增大,而對這家公司在今後3~5年的違約概率影響很小。這時評級機構往往不會改變這家公司的信用評級。
穆迪KMV和Kamakura等公司會根據其股票價格和其他變量來估計公司違約的概率。這種估測值是不穩定的,而且對市場信息的反應往往比信用評級更快。我們將在第19.8節中討論這個用於估計違約概率的模型。
19.1.1 內部評級
大部分銀行都建立了針對企業及個人客戶的信用狀況評級過程。這麼做非常有必要。因為評級機構一般只公佈較大的企業的評級結果,這類企業發行公募債券。由於這個原因,評級機構往往不能覆蓋中小企業。如在第15章中解釋的那樣,《巴塞爾協議Ⅱ》中的內部評級法(IRB)允許銀行採用自己的模型來計算違約率(PD)。
採用內部評級法來估計PD時往往需要對某些財務指標進行估測,例如資產回報率(return on asset),以及資產負債表中的一些指標,例如流動比率(current ratio)以及負債與股本的比率(權益負債率,debt-to-equity ratio)等。認識到公司持有的現金(而不是盈利)才能真正反映其償還能力,因此銀行常常將公司提供的財務信息轉換成現金流報告,通過現金流報告銀行可以估計貸款人償還貸款的能力大小。
19.1.2 Altman Z評分模型
愛德華·阿特曼(Edward Altman)最先提出以公司的財務指標比率來預測違約率。1968年他開發出著名的Z-score模型(Z-score model)。[2]通過採用統計學中的判別分析(discriminant analysis)方法,阿特曼試圖從企業的5個財務比率入手來預測違約率:
X1——流動資金/總資產(working capital/total asset);
X2——留存收益/總資產(retained earning/total asset);
X3——息稅前利潤/總資產(earning before interest and tax/total asset);
X4——股票市值/負債賬面總額(market value of equity/book value of total liabilities);
X5——銷售收入/總資產(sales/total assets);
對於上市的製造業企業,Z-score模型由以下公式給出
Z=1.2X1+1.4X2+3.3X3+0.6X4+0.999X5
(19-1)
當一家公司的Z-score大於3.0時,這家公司違約可能性不大;當一家公司的Z-score介於2.7與3.0之間時,這家公司的信用處於警戒(on alert)狀態;當一家公司的Z-score介於1.8與2.7之間時,這家公司有一定的違約可能;當Z-score小於1.8時,這家公司違約的可能性很大。式(19-1)來自對66家製造業上市公司進行的採樣。在這66家公司中有33家公司在1年內違約,而另外33家得以倖免。Z-score模型對樣本外預測(test out of sample)(即預測那些產生式(19-1)中係數的樣本以外的公司的違約率)非常準確。模型的第一類錯誤(type Ⅰ error,即模型預測公司不會違約,而事實上卻違約了)及第二類錯誤(type Ⅱ error,即模型預測公司會違約,而事實上卻沒有)均很小。[3]後來在原始模型的基礎上,研究人員又開發出了用於非上市製造業企業以及非製造業企業的Z-score模型。
【例19-1】 考慮一家公司,其流動資金為170 000,總資產為670 000,息稅前利潤為60 000,銷售額為2 200 000,股票市值為380 000,總負債為240 000,留存收益為300 000,與以上數據對應的各項比率為X1=0.254,X2=0.448,X3=0.089 6,X4=1.583,X5=3.284,Z-score模型為
1.2×0.254+1.4×0.448+3.3×0.089 6+0.6×1.583+0.999×3.284=5.46
這一得分顯示這家公司在近期不會有違約的危險。
自45年前阿特曼提出最初的Z-score方法以來,該方法得到了修訂和擴展,現在已可用於《巴塞爾協議Ⅱ》框架下的違約概率估計。
[1] 理論上講,信用級別應該對應於某給定的債券而不是某家公司,但是在大多數情況下,某公司發行的所有債券往往具備同樣的信用級別,因此信用級別也就成了公司的某種特徵。
[2] See E. I. Altman, “Financial Ratios, Discriminant Analysis, and the Prediction of Corporate Bankruptcy,” Journal of Finance 23, no.4(September 1968):589-609.
[3] 很顯然第一類錯誤所觸發的貸款損失要遠大於第二類錯誤所觸發的損失。
19.2 歷史違約概率
表19-1是由評級公司公佈的一組典型數據,這些數據顯示了公司的信用隨時間推移而出現的不同變化。例如,表19-1顯示某債券的初始穆迪信用級別為Baa,這家公司有0.177%的概率在1年內違約,並且有0.461%的概率在2年內違約等。債券在一個指定的年份違約的概率可由這一表格計算得出。例如,初始信用級別為Baa的公司在第2年違約的概率為0.461%-0.177%=0.284%。
表19-1 1970~2016年的平均累積違約率 (%)
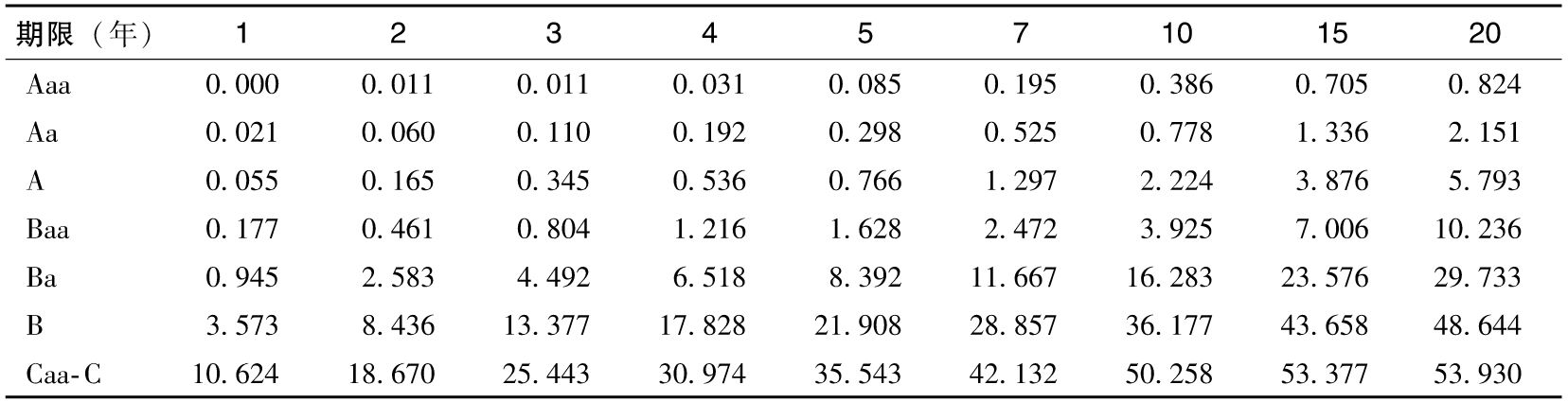
資料來源:穆迪。
表19-1顯示具備投資級別的債券在某年內違約概率隨著期限的增大而有所增大(例如,Aa級債券在第1~5年的違約概率分別為0.021%、0.039%、0.050%、0.082%及0.106%)。這是因為在最初發行時,債券的信用狀況較好,但隨著時間的推移,信用出現問題的可能性也會增大,而對於最初的信用級別較差的債券,每年的違約率常常是時間期限的一個遞減函數(如Caa級別的債券在第1~5年的概率分別為10.624%、8.046%、6.773%、5.531%、4.569%)。產生這一現象的原因是,對信用較差的債券,今後一兩年是企業能否生存下去的關鍵期,如果企業能夠度過這個階段,則說明其財務狀況很可能已得到改善。
違約密度
由表19-1我們可以計算出Caa級別的債券在第3年的違約概率,即25.443%-18.670%=6.773%。這一違約概率被稱為無條件違約概率(unconditional default probability)。此概率是今天,即在0時刻,所看到的第3年的違約概率。Caa債券一直到第2年年底都不會破產的概率為100%-18.670%=81.330%,因此我們得出在前2年沒有違約的條件下,公司在第3年違約的概率為6.773%/81.330%=8.33%。
這裡計算出的違約概率8.33%對應於1年的觀察期。通過考慮在時間t之前沒有違約的條件下,違約發生在t與t+Δt之間的概率,我們可以求得對應於時間t的違約密度(default intensity),這一違約密度也被稱為風險率(hazard rate)。時間t的違約密度λ(t)的含義是指在從0時刻到t時刻違約沒有發生的條件下,違約發生在t與t+Δt之間的概率為λ(t)Δt。如果V(t)是從今天到時間t公司仍然生存的累積概率(就是說直到時間t違約仍沒有發生),那麼t與t+Δt之間的無條件違約概率為V(t)-V(t+Δt),在時間t之前沒有違約的前提下,違約發生在t與t+Δt之間的條件概率為[V(t)-V(t+Δt)]/V(t),因此
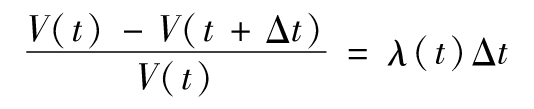
或
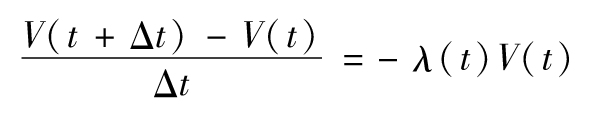
對以上公式求極限得出
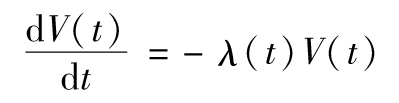
因此
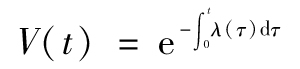
定義Q(t)為時間t之前的違約概率,我們得出
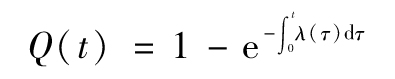
或者

其中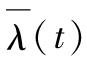 為介於0與時間t之間的平均風險率(違約密度)。
為介於0與時間t之間的平均風險率(違約密度)。
【例19-2】 我們假定違約密度為常數,每年為1.5%,截至第1年年末違約概率為1-e-0.015×1=0.014 9;截至第2年年末違約概率為1-e-0.015×2=0.029 6;截至第3年、第4年、第5年年末違約概率分別為0.044 0、0.058 2、0.072 3。第4年的無條件違約概率為0.058 2-0.044 0=0.014 2,在前3年沒有違約的前提下,在第4年違約的條件概率為0.014 2/(1-0.044 0)=0.014 9。
19.3 回收率
當一家公司破產時,公司的債權人會對公司的資產進行追索。[1]有時公司會進行重組,而債權人會同意接受債務的部分償付;在其他的情形下,公司資產會被清算變賣,所得資金最大限度地用於償還債務。在債務追索過程中,有些債權具有優先權,能拿回更多的償付。
債券回收率(recovery rate)是指在違約大約30天后,債券市場價值與債券面值的比率。正如我們在第15章中看到的那樣,《巴塞爾協議Ⅱ》的公式是以違約損失率來表達的,債券回收率等於1減去違約損失率。
表19-2給出了美國不同種類型債券的歷史平均回收率。這一數表顯示,一級留置權資產的回收率可以達到52.8%,更次級債券的回收率僅為23.2%。
表19-2 1983~2016年企業債券和銀行貸款的回收率

資料來源:穆迪。
回收率對違約率的相關性
在第6章中,我們看到2007~2008年信用危機的教訓之一是,抵押貸款的平均回收率與抵押貸款違約率呈負相關。隨著抵押貸款違約率的上升,喪失抵押品贖回權會導致更多的房屋被出售,房價下跌,這反過來又導致了回收率下降。
回收率同違約概率有很強的負相關性。[2]在債券的違約率較少的年份,經濟狀況通常良好,違約債券的平均回收率可能高達60%;在債券的違約率很高的年份,經濟狀況通常很差,違約債券的平均回收率可能低至30%。這種負相關性的結果是,在違約率很高的年份,貸款人的情況會變得雪上加霜,因為此時回收率往往也會很低。
[1] 在美國,債券持有者的索賠包括債券的本金以及應計利息。
[2] See E. I. Altman, B. Brady, A. Resti, and A. Sironi, “The Link between Default and Recovery Rates: Theory, Empirical Evidence, and Implications,” Journal of Business (November 2005):2203-2228.這一相關性在穆迪的投資者服務出版物中也有討論。研究發現,1年中的平均回收率和非投資級別債券的違約率高度相關。
19.4 信用違約互換
信用市場上一種非常重要的衍生產品為信用違約互換(credit default swap,CDS)。如業界事例19-1所示,這種產品的市場在2007年之前一直快速增長,然後下降。作為一種金融工具,形式最簡單的CDS給信用保護的買入方提供了對某家公司違約的保險。這裡所涉及的公司被稱為參考實體(reference entity),而這家公司的違約事件被定義為信用事件(credit event)。在CDS中,保險的買入方在信用事件發生時有權利將違約公司的債券以債券面值作價賣給保險的賣出方。[1]可賣出的所有債券的面值總額被稱為CDS的面值(notional principal)。
業界事例19-1
CDS市場
在1998年和1999年,國際互換與衍生產品協會(International Swaps and Derivations Association,ISDA)制定了關於場外交易市場信用違約互換的標準條款。自從標準條款建立以後,CDS市場增長迅猛。國際清算銀行從2004年12月開始統計信用衍生產品市場的數據。在當時,未平倉的合約的面值估計有6萬億美元。2007年12月,面額達到頂峰,有58萬億美元並開始回落。到2016年12月,這一數字已降至10萬億美元左右。銀行和其他一些金融機構在CDS交易中既買入信用保護,也賣出信用保護。但就整體來看,銀行是信用保護的淨買入方,保險公司是信用保護的淨賣出方。CDS(以及其他信用衍生產品)流行的一個後果是,承擔貸款風險的金融機構往往不再是最初的發放貸款並進行最初信用查證的銀行。
在2007年8月開始的信用危機中,監管機構對系統性風險非常擔心(對系統性風險的討論見業界事例15-1)。毫無疑問,這種擔心部分來自AIG保險公司遭受的損失。AIG賣出了大量由按揭貸款所產生的AAA級證券的信用保護(見第6章)。因賣出信用保護,AIG付出了慘重代價。如果AIG破產,將會波及金融系統的其他機構,造成巨大損失。美國政府不得不在2008年9月對AIG實施救助。
CDS在歐洲主權債務危機中也備受詬病。一些立法機構認為,CDS市場上的投機行為加劇了一些國家(比如希臘)的債務問題,因此對主權信用的CDS裸露頭寸(即在沒有對參照實體信用風險敞口的情況下買入CDS)在2013年被禁止。
2007~2008年,許多信用衍生產品的交易銷聲匿跡,但提供對單一參照實體信用保護的普通CDS交易仍十分活躍(不出意料,利差相比危機前有戲劇性增長),同其他衍生產品相比,CDS的運作十分簡單,而其他衍生產品(例如,由按揭產生的證券化產品ABS和CDO,見第6章)就沒有這麼高的透明度。但是,正如業界事例19-2中指出的那樣,這種結構中的缺陷正在顯現,這可能是其受歡迎程度下降的原因。
當雷曼兄弟在2008年9月破產時,市場上存有大量以雷曼兄弟為參考實體的CDS合約。雷曼兄弟破產所對應的回收率(由拍賣過程決定)僅為1美元收回8美分,違約賠償支付為面值的92%。市場上曾有人預言,某些信用保護賣出方可能不能承擔支付義務,因而會有更多的破產發生。但在清算日(2008年10月21日)到來時,一切都進行得很順利。
CDS的買入方必須向賣出方定期付款,直到CDS到期或者信用事件發生。付款日期通常在每個季度末尾。
以下的實例可以幫助我們理解CDS的結構。假如某兩家公司在2018年12月20日進入了一個5年期的CDS。假定CDS的面值為1億美元,CDS的買入方費率為每年90個基點(支付時間為每季度的結束)。買入方因此得到了對某參考實體的信用保護。
圖19-1展示了該CDS交易。如果參考實體沒有違約(也就是沒有信用事件發生),信用違約互換的買入方就不會得到任何回報,且需在2019~2023年每年的3月20日、6月20日、9月20日和12月20日向賣出方支付大約225 000(=0.25×0.009 0×100 000 000)美元。[2]當有信用事件發生時,賣出方須向買入方支付一筆可觀的賠償。假定在2021年5月20日(即第3年的第5個月),CDS的買入方通知賣出方有信用事件發生,如果合約闡明交割的方式為實物交割,CDS買入方可以以1億美元的價格向CDS的賣出方賣出面值為1億美元的參考實體發行的債券;如果合約闡明交割的方式為現金交割(這種方式現在更為普遍),則會在違約發生後的幾天內,採用一個兩階段式的拍賣過程以確定最便宜可交割債券(cheapest deliverable bond)的市場中間價。假定拍賣顯示最便宜可交割債券的價格為100美元面值合35美元,這時CDS賣出方必須向買入方支付6 500萬美元。

圖19-1 信用違約互換
當信用事件發生後,信用保護的買入方向賣出方進行的支付會終止。但是,付款準確時間為每個時間區間的末段,因此通常買入方必須向賣出方支付最後的應計累積款(accrual payment)。在我們的例子中,當違約事件發生在2021年5月20日時,買入方必須向賣出方支付由2021年3月20日到2021年5月20日的應計款(大約為150 000美元),在這之後,買入方不需要再支付任何其他費用。
信用保護買入方每年所付出的費用與面值的百分比為CDS利差(CDS spread,在我們的例子中,CDS利差是90個基點)。市場上有若干家大銀行是CDS的做市商。對於某家公司(參考實體)的一個5年期CDS利差的報價,有的做市商可能給出250個基點的買入價、260個基點的賣出價,這意味著該做市商準備以每年250個基點(每年支付面額的2.5%)買入該公司的信用保護,同時也準備以每年收入260個基點(每年收入面額的2.6%)來賣出該公司的信用保護。
許多公司和國家是CDS交易中的參考實體。5年期CDS合約最為常見,其他期限(例如1年、2年、3年、7年和10年)也有交易。通常合約的到期日為3月20日、6月20日、9月20日和12月20日。這種安排的結果是合約實際到期期限可能並不一定完全等於合約中指定的年限。假定你在2018年11月15日通知交易商你想買入一個5年期信用保護,合約的到期日是2023年12月20日。你的第一個付款日期為2018年12月20日,付款數量對應於2018年11月15日到2018年12月20日這一時間段。[3]在此之後,就是每季度付款。
CDS合約的一個關鍵點是關於信用事件(即違約)的定義。通常信用事件包括不能按期付款、債務重組或破產。在北美採用的合約中,重組事件有時候被排除在外,特別是在參考實體公司的債券收益率非常高的情況下。CDS市場存在一個信息不對稱問題,業界事例19-2對此做了說明,這可能是市場熱度下降的原因。
業界事例19-2
CDS市場是一種公平遊戲嗎
CDS同其他衍生產品有一個很重要的不同,那就是其他衍生產品通常與利率、匯率、股指價格、商品價格等變量有關,對於這些變量我們沒有理由相信某個市場參與者會比其他市場參與者具有更好的信息。
某家公司的CDS利差與將來某個時間段內這家公司的違約率有關。因此,有些市場參與者對參照實體的違約概率的估計可能比其他人更好。如果某家金融機構同一家公司業務來往頻繁,並向這家公司提供業務諮詢、貸款,且幫這家公司發行新債券,那麼該金融機構對這家公司的信用的瞭解肯定要好於與這家公司毫無來往的其他金融機構。經濟學家將這種情形命名為信息不對稱(asymmetric information)問題。
2018年1月11日的《金融時報》報道了對CDS市場的公然濫用。美國房屋建築商Hovnanian從對衝基金GSO Capital Partners中獲得了誘人的資金,並同意將不支付利息,從而技術性違約(technical default)。GSO購買了Hovnanian的信用保護,並獲得了可觀的回報。假設這是一項法律安排,則可能導致CDS(目前的結構)完全消失。
19.4.1 最便宜可交割債券
通常CDS合約中會規定,在違約發生時有哪幾種債券可以用於交割。可交割債券的優先級往往相同,但在違約剛剛發生後,債券價格與本金的比率可能會不同。[4]這樣一來,CDS就為信用保護的買入方提供了一個最便宜可交割債券的選項。如前面所述,當違約發生後,一個拍賣過程會被用來確定最便宜可交割債券的價格,進而決定信用保護的買入方的收益。
附錄K討論瞭如何確定CDS利差以及如何對CDS交易進行定價。
19.4.2 信用指數
信用市場上的參與者已經開發出用於跟蹤CDS利差的指數。早在2004年,市場上多個指數的產生方就達成了一個協議,促成了不同指數間一定程度上的合併。現在用於生成指數的兩個重要的標準組合是:
(1)CDX NA IG指數,該指數用於跟蹤北美125家投資級公司的CDS利差;
(2)iTraxx歐洲指數,該指數用於跟蹤歐洲125家投資級公司的CDS利差。
指數中包含的參照實體在每年的3月20日和9月20日會被更新。當一家公司不再是投資級時,就會被移出組合,由其他投資級的公司取而代之。[5]
假設某做市商對CDX NA IG 5年指數報出的買入價為165個基點,賣出價為166個基點,這意味著投資者可以對指數內的每家公司以每年166個基點的價格,買入指數中125個參照實體的信用保護。如果對每個參照實體要求保護的面額均為800 000美元,則投資者的費用為0.016 6×800 000×125,即每年1 660 000美元。同時投資者也可以賣出關於這125個實體的每個面額為800 000美元、為期5年的信用保護,投資者的收入為每年1 650 000美元。當某個參照實體違約時,信用保護的買入方會收到通常的CDS違約賠償,每年為信用保護所付的費用減少1 660 000/125=13 280美元。對於期限是3年、5年、7年和10年的CDS指數,市場上的買入和賣出都很活躍。這類合約的到期日通常是12月20日和6月20日(這意味著,“5年”合約的實際期限介於4.75年與5.25年之間)。大體上講,指數的利差是構成指數的參照實體的CDS利差的平均值。[6]
19.4.3 固定息票的使用
為了滿足交易的需要,CDS和CDS指數合約的實際運作方式比這裡描述的更為複雜一些。在真正的市場上,CDS和CDS指數交易類似於債券交易。對每一種交易的標準合約,都要標明固定的息票(coupon)和回收率。用於購買信用保護的定期付款數額等於息票數額。CDS利差(類似於債券的收益率)可以從市場報價中得到。在進行交易時,要用一個特定的過程來計算交易期限內,使用CDS利差得出的付款額的貼現值與使用息票率得出的付款額的貼現值之間的差。如果利差的報價低於息票,在交易開始時,信用保護的賣出方須向買入方支付這一差價。如果利差的報價高於息票,在交易開始時,信用保護的買入方須向賣出方支付這一差價;在此之後,信用保護的買入方定期向賣出方支付的費用等於息票率乘以到目前為止指數組合中尚未違約的公司所對應的總面額。
[1] 債券的面值(face value或par value)是指債券發行人在不違約情形下應償還的本金數量。
[2] 因為天數計算慣例的影響,所以每次支付的數量並不完全等於225 000美元。
[3] 如果當前時間距第一個付款日少於一個月,那麼第一次支付通常會挪到第二個付款日進行,否則應在第一個付款日支付。
[4] 有幾個原因會造成這種現象,違約時對於債券的追索往往包括面值和應計利息,應計利息高的債券在違約時的價格往往會比較高。同時,市場也會判斷重組事件發生之後,公司的決定會對哪些債券的持有者更為有利。
[5] 2014年9月20日,市場定義了iTraxx歐洲22系列(Series 22 iTraxx European)以及CDX NA IG 23系列(Series 23 CDX NA IG),這些序列號說明,截至2014年9月,iTraxx歐洲組合已被更新21次,CDX NA IG系列已被更新22次。
[6] 更為準確地講,指數本身的利差取值比指數中所包含的公司的CDS利差的平均值要稍低一些。為了解釋這一點,我們考慮兩家公司,假定一家公司的CDS利差為1 000個基點,另一家公司的CDS利差為10個基點。買入這兩家公司的信用保護所對應的平均利差應該稍稍低於505個基點。這是因為支付1 000個基點的利差的預期時間會短於支付10個基點的利差的時間,因此1 000個基點的利差的權重應較小。關於CDX NA 1G的另外一個複雜的情況是,指數上違約事件的定義包含重組,而構成指數的公司的CDS合約中不包含重組事件。這種情況不存在於iTraxx歐洲指數中。
19.5 信用價差
信用價差是投資者因為承擔某種信用風險而每年索取的額外回報。從上一小節中,我們已經看到CDS利差提供了度量信用價差的一種手段。另外一種手段是採用債券收益率利差。該利差等於企業債券收益率高出無風險利率的那部分。我們接下來將說明以上兩種利差應近似相等。
19.5.1 CDS利差與債券的收益率
CDS可以用來對企業債券風險進行對衝,假設某投資者買入了一個5年期的企業債券,債券收益率為每年7%,同時投資者又進入了一個5年期CDS合約,在此合約中買入針對債券發行企業的違約保護。如果CDS利差為每年200個基點(即2%),這裡CDS的作用是將企業債券轉換為無風險債券(至少在近似意義上)。如果債券發行人不違約,則投資者的收益率為每年5%(企業債券收益率減去CDS的利差),投資者在違約發生前的收益回報率為5%;如果債券發行人違約,投資者在違約發生前仍獲得5%的收益率。違約發生後,按照CDS條款,投資者可以將手中的債券換回本金,然後在餘下的期限內,將這些資金投資於無風險資產,直至5年期滿。
以上討論說明,n年期CDS利差應該大約等於n年企業債券的平價收益率與n年無風險債券收益率的差價。[1]如果CDS利差遠小於企業債券收益率與無風險債券收益率的差價,那麼投資者通過買入企業債券及買入信用保護而得到的收益率(近似於無風險)會大於無風險利率;如果CDS利差遠大於企業債券收益率與無風險債券收益率的差價,那麼投資者可以賣空企業債券及賣出信用保護而得到比無風險利率更低的貸款利率。在後面的內容中,我們將會討論,上面描述的套利並不完美,在實際中能否使用這些策略,受到流動性限制以及其他一些考慮的影響。
19.5.2 無風險利率
CDS利差是對信用價差的一個直接估算。為了通過債券收益率來估計信用價差,我們必須對無風險利率做出假設。當交易員對債券收益率利差給出報價時,具有某個期限的無風險利率一般是對應於類似期限的國債利率。例如,債券交易員對某企業債券收益率的報價可能是國庫券收益率加上250個基點。
若干研究人員比較了債券收益率與CDS利差,並以此來推算無風險利率。為了做到這一點,必須將CDS的期限與債券期限進行匹配,並通過上述套利策略得出無風險利率,例如,假定5年期債券的收益率為4.7%,5年期CDS利差為80個基點,5年期隱含無風險利率為3.9%。
如第9.2節所示,傳統上,交易員在衍生產品定價時,往往將LIBOR/互換曲線作為對無風險利率的近似。研究結果顯示這一做法也被延續到信用市場。市場隱含無風險利率與LIBOR/互換曲線的差別遠遠小於與國債利率的差別。一項測算顯示,隱含無風險利率在平均意義上大致等於LIBOR/互換利率減去10個基點。[2]這一估計似乎是合理的。在第9.2節中我們曾指出,利率互換交易中的信用風險可類比為信用等級為AA級公司的一系列短期貸款的信用風險,信用級別為AA級的短期產品含有10個基點的違約風險利差是較為合理的。
19.5.3 資產互換
資產互換(asset swap)為信用市場交易員提供了方便的參照物,這是因為資產互換價格中的利差是對企業債券收益率與LIBOR/互換收益率之間的差價的直接估計。
為了解釋資產互換的機制,我們假定對於某債券的資產互換的利差報價為150個基點,對應於這一報價有三種可能:
(1)債券價格等於票面價值(par value),即100美元。資產互換的一方(公司A)支付債券的息票,而另一方(公司B)支付LIBOR+150個基點。[3]
(2)債券價格低於其票面價值,假定債券價格為95美元。在資產互換中,除了指定的息票以及浮動利率,在互換協議開始時,A方首先對每100美元的面值支付5美元,然後,在資產互換中A方支付債券的息票,B方支付LIBOR+150個基點。
(3)債券價格高於其賬面價格,假定債券價格為108美元。在互換開始時,B方首先對每100美元的面值支付8美元,然後,在資產互換中A方支付債券的息票,B方支付LIBOR+150個基點。
以上三種不同方式均可使資產互換的利差(我們例子中為150個基點)的貼現值等於無風險債券的價格超出類似企業債券的差價,這裡的無風險利率被假定為LIBOR/互換曲線(見練習題19.16)。
19.5.4 CDS-債券基差
一家公司的CDS-債券基差(CDS-bond basis)等於這家公司CDS的利差與這家公司債券收益率利差的差,即
CDS-債券基差=CDS利差-債券收益率利差
債券收益率利差是通過公司債與LIBOR/互換基準利率的差得出的,通常可認為是資產互換利差。
根據前面討論的關於CDS利差與債券收益率的套利策略得出,以上基差應接近於0。但事實上,有若干原因導致這個基差不為0,例如:
(1)債券的交易價格可能與面額之間有很大的不同(價格高於面額的債券的基差往往為正,價格低於面額的債券的基差往往為負)。
(2)CDS的交易對手可能會違約(這會帶來基差為負的傾向)。
(3)在CDS合約中,暗含一個支付最便宜債券的期權(這會帶來基差為正的傾向)。
(4)CDS收益中不包括用於交割債券的應計利息(這會帶來基差為負的傾向)。
(5)CDS合約中的重組條款(restructuring clause)可能會觸發在無違約(破產)情況下的賠償支付(這會帶來基差為正的傾向)。
(6)市場認為LIBOR利率高於無風險利率(這會帶來基差為正的傾向)。
在2007年市場危機之前,CDS-債券基差基本為正。例如,De Witt估計在2004~2005年,基差大約為16個基點。[4]在2007年8月開始的信用危機中,基差變為很大的負值。但正如Bai和Dufresne(2011)在研究中揭示的那樣,因為缺乏流動性和其他一些考慮,金融機構很難在債券和CDS之間套利。[5]自金融危機以來,CDS-債券基差(有時為正,有時為負)已經大大減小了。
[1] n年期債券的平價收益率是指債券價格等於其面值時所對應的息票率。
[2] See J. Hull, M. Predescu, and A. White, “The Relationship between Credit Default Swap Spreads, Bond Yields, and Credit Rating Announcements,” Journal of Banking and Finance 28 (November 2004):2789-2811.
[3] 注意,這裡交換的是息票。無論債券是否違約,A、B雙方都必須支付條款中規定的款項。
[4] See J. De Witt, “Exploring the CDS-Bond Basis,” Working Paper no.104, National Bank of Belgium, 2006.
[5] See J. Bai and P. Collin-Dufresne, “The CDS-Bond Basis,” Working Paper, 2013, SSRN-id2024531.
19.6 由信用價差來估算違約概率
我們現在討論如何用信用價差來估計違約概率。
19.6.1 近似計算
某個5年期信用價差(CDS利差、債券收益率利差或資產互換利差)為240個基點,預期回收率為40%。這意味著違約帶給企業債券持有者損失的期望值為240個基點(或每年2.4%)。粗略地說,我們可以認為信用價差大致相當於平均損失率。回收率為40%,我們得出在沒有前期違約的條件下,5年內平均每年的條件違約密度為0.024/(1-0.4)=4%,一般來講條件違約概率滿足

其中s(T)是期限為T的信用價差(以連續複利計算),R為回收率,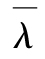 為從時間0到時間T之間的平均違約密度(風險率)。
為從時間0到時間T之間的平均違約密度(風險率)。
假定已知若干不同期限的信用價差,我們可以通過利差剝離方法(bootstrap)來求得違約密度的期限結構(至少在近似意義上講),以下我們舉例說明計算過程。
【例19-3】 假定3年期、5年期、10年期的CDS利差分別為50、60和100個基點,違約回收率為60%,3年期平均違約密度近似為0.005/(1-0.6)=0.0125;5年期平均違約密度近似為0.006/(1-0.6)=0.015;10年期平均違約密度近似為0.01/(1-0.6)=0.025。由此得出,3年期與5年期之間的違約平均密度為(5×0.015-3×0.0125)/2=0.01875;5年期與10年期之間的違約平均密度為(10×0.025-5×0.015)/5=0.035。
19.6.2 更加準確的計算
以上計算對CDS利差較為適用,當標的債券價格接近於面值時,以上計算對於債券收益率利差和資產互換利差也可以給出比較好的近似。我們接下來給出一個更加準確的計算,這一方法對債券價格不接近於面值時也適用。
假設面值為100美元的某企業5年期債券的息票率為每年6%(每半年付息一次),收益率為每年7%(連續複利)。類似的無風險債券的收益率為5%(連續複利)。由收益率隱含得出的企業債券價格為95.34美元,無風險債券的價格為104.09美元,因此,未來5年內,由違約引發的預期損失為104.09-95.34,即8.75美元。為了簡單起見,假定企業債券每年的違約率為Q,並且違約只會發生在0.5年、1.5年、2.5年、3.5年及4.5年時,即剛好發生在支付息票之前。對所有的期限,假定無風險利率均為5%(連續複利),債券預期回收率為40%(這一分析可以擴展到違約發生更頻繁的情況)。
表19-3計算了與違約率Q有關的預期損失。為了說明計算過程,我們考慮表19-3中對應3.5年的一行,在3.5年時,不考慮違約的債券價格的期望值為(在計算中利用遠期無風險利率)
3+3e-0.05×0.5+3e-0.05×1.0+103e-0.05×15=104.34(美元)
表19-3 由債券每年的違約概率Q來計算違約損失
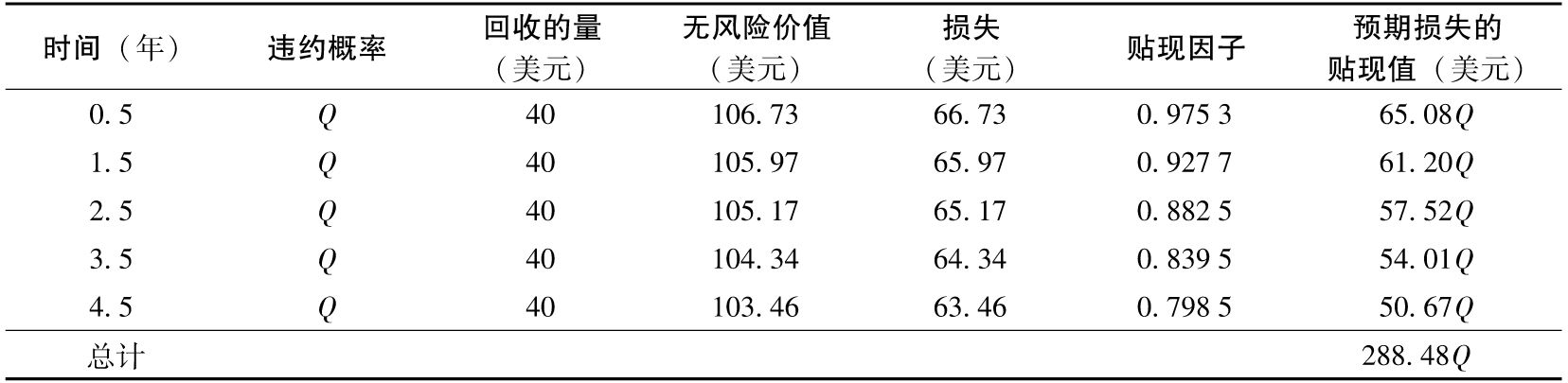
注:本金=100美元。
由第19.3節回收率的定義得出,違約發生時債券的回收價值為40美元,因此違約觸發的損失為104.34-40=64.34美元,這一損失所對應的貼現值為54.01美元,因此違約預期損失為54.01Q。
表19-3顯示預期損失的總和為288.48Q,該預期損失等於前面計算出的8.75美元的預期損失,因此Q的值為8.75/288.48,即3.03%。我們在計算中假定每年的違約概率相等,而且每年只能發生一次違約。我們可以把計算擴展到違約發生頻率更高的情況。同時,我們也可以假設違約密度為一個常數,或者違約概率隨時間呈現一定的模式,而不是假定一個不變的無條件違約概率。使用幾隻不同的債券,我們可以估計關於違約概率期限結構的多個參數。例如,假定有期限分別為3年、5年、7年和10年的4只債券,並且違約概率服從一個階躍函數(step function)。我們可以利用第1只債券來估計前3年中每年的違約概率,利用第2只債券來估計第4年和第5年的違約概率,利用第3只債券來估計第6年和第7年的違約概率,利用第4只債券來估計第8年、第9年和第10年的違約概率(見練習題19.15和練習題19.24)。這一方法和附錄B中給出的用券息剝離法計算利率的期限結構的過程很類似。
19.7 違約概率的比較
現在,我們比較一下由歷史數據得出的違約概率以及由信用價差推算出的違約概率。表19-4顯示了:
·不同信用等級的公司7年的平均累積違約概率,數據由穆迪發佈。與表19-1中7年期違約率所在的列是一致的。
·1996年12月~2007年6月,不同信用等級的公司的平均信用價差。這些數據取自美林發佈的債券收益率數據,其中使用的假設是無風險利率比同期互換利率低10個基點(關於無風險利率的近似見第19.5.2節)。債券的平均期限在7年左右。
表19-4 累積違約概率與信用價差的比較
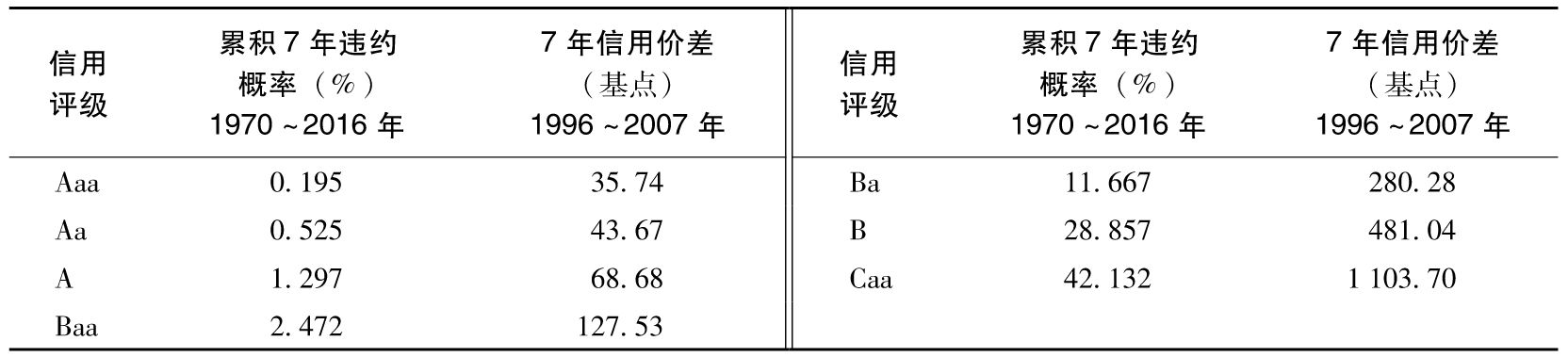
表中考慮的數據截至金融危機爆發之前。在金融危機中,信用價差暴漲。我們會看到由信用價差推算出的違約密度要高於由歷史數據統計得出的違約密度。如果這種非常時期也被包括進來,那麼這一結果會變得更加顯著。
表19-5顯示了7年平均風險率。[1]7年曆史違約密度(風險率)的計算與表19-4中的累積違約率一致。假設Q為7年累積違約概率。由式(19-2)
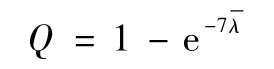
表19-5 7年平均違約密度
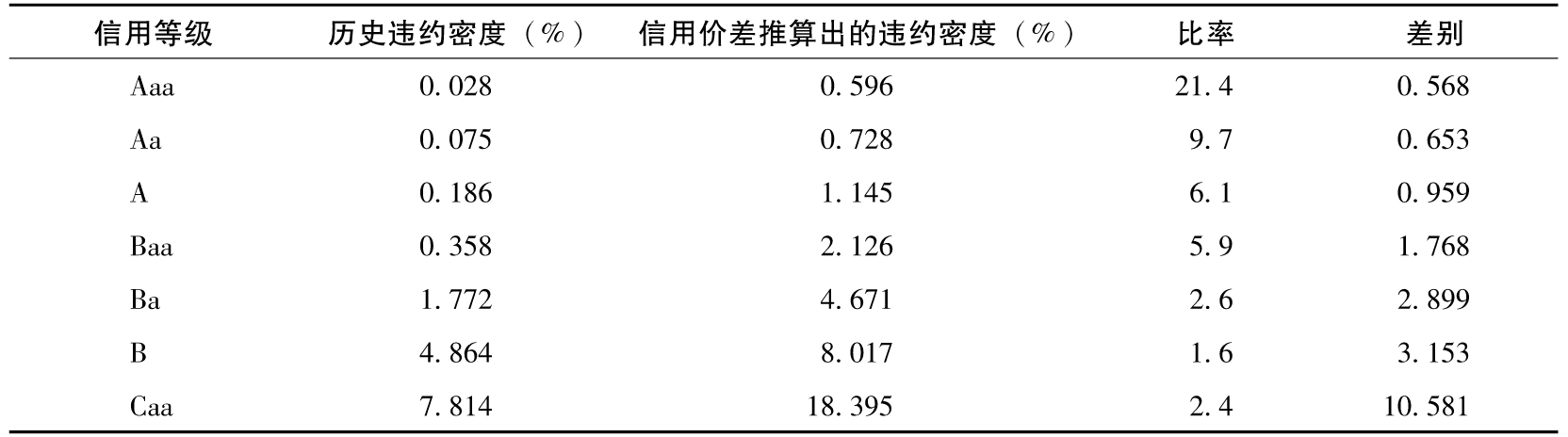
其中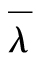 為平均風險率,並且
為平均風險率,並且
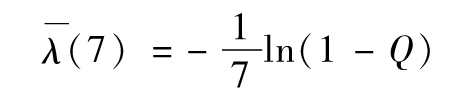
例如,對於信用級別為A的公司,7年累積違約率為1.217%或0.012 17,因此7年違約密度的平均值為
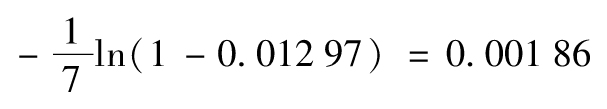
即0.186%。表19-5所示的由信用價差所得出的違約密度基於式(19-3),使用的回收率為40%。再次考慮一個評級為A的債券。表19-4中給出的平均的7年信用價差為68.68基點或0.006 868,因此平均的7年違約密度為
0.006 868/(1-0.4)=0.01145
表19-5顯示,在金融危機前,由信用價差推出的違約密度比通過長期歷史數據得出的要高。債券的信用等級越高,由債券價格倒推出來的違約密度與由歷史數據得出的違約密度之比就越大,隨著信用質量的下降,這個比率也隨之降低。與之相對,兩種違約概率的差隨著信用級別的降低而增加。[2]
表19-6是對這些結果的另一種解釋。此表顯示出投資者從不同信用級別的債券獲得的超出無風險利率之上的投資回報(這裡的無風險利率仍然等於7年互換利率減去10個基點)。我們還是考慮A級債券,這種債券的收益率超過7年國債收益率的平均利差為111個基點,這111個基點中的42個基點是我們選取的無風險利率近似與7年國債收益率的利差。補償預期違約需要11個基點(這一數值等於由表19-5中的歷史違約密度算出的1年違約概率乘以1減去回收率0.4)。最終我們得出額外預期回報(在考慮了預期違約後)為58個基點。[3]
表19-5及表19-6顯示,當兩種違約概率的百分比差距較大時,債券的額外預期回報相對較小。對於Aaa級債券,兩種違約概率的比率為21.4,但額外預期回報只有34個基點。預期額外回報隨著信用級別的降低而有所增加。
表19-6 債券的額外預期回報

表19-6中的額外回報並不總為常數。信用價差(及由此導致的額外回報)在2001年、2002年及2003年的前半年很高,之後一段時間很低,一直到2007年年中信用危機開始後,額外回報和信用價差急劇增加。
19.7.1 真實世界與風險中性概率比較
在第7.2節中,我們解釋了風險中性定價方法。通過這一方法,我們可以假設所有投資者在風險中性的前提下,對現金流進行定價(也就是說,投資者並不因承擔風險而索取超額收益)。採用風險中性定價,我們可以求得產品價格,計算出的價格無論是在真實世界或風險中性世界中均適用。
第7.2節已經解釋了風險中性違約概率的理論基礎。這些違約概率(有時也被稱作隱含違約概率)就是由信用價差推導出的違約概率。與此相對,由歷史數據得到的違約概率為真實世界違約率(有時也被稱作物理違約率)。表19-6中的額外預期回報直接來自真實世界及風險中性世界違約概率的差異,當沒有額外預期回報時,真實世界違約率會等同於風險中性違約率,這一結論反過來也成立。
為什麼真實世界中的違約概率與風險中性世界中的違約概率會相差甚遠呢?就像我們剛剛討論的那樣,這一問題等同於,為什麼企業債券交易員的平均收益要高於無風險利率?
一個原因是企業債券的流動性較差,債券交易員會因此而索求更高的回報,但這隻佔整體額外回報的一小部分。在正常市場情況下,這一說法大概可以解釋表19-6所示的額外回報中的25個基點。另外一個可能的原因是債券交易員的主觀違約率假設可能比表19-1中給出的違約率要高得多。交易員所假想的蕭條情景可能比他們所用的數據中出現的真實情形更差。但是,以上說法很難解釋額外回報中的大部分。[4]
目前為止,造成表19-5及表19-6中結果的最主要原因是債券違約並不是相互獨立的(也就是說,金融市場上的違約是有相關性的)。每年違約率的顯著變化就是證據。穆迪在1970~2016年的統計結果顯示(見表11-6),在對所有被評級的公司中,1979年的違約率最低,僅為0.088%,而2009年的違約率最高達4.996%。這種債券違約率的年度變化會引發系統性風險(即不能通過風險分散而消除的風險)。債券交易員因承擔風險自然會索取回報。從這個角度,債券交易員和股票交易員並沒有什麼不同,後者因承擔系統性風險而每年獲得5%或6%的額外回報。從表19-6中我們可以看到,交易高質量債券的交易員獲得的額外回報遠小於這個數字。但是,隨著債券信用質量的下降,額外回報會增加,接近股票的回報。
是什麼導致了違約的相關性進而引發系統性風險?一個解釋是宏觀經濟。好的宏觀經濟形勢會減少所有公司的違約概率,壞的宏觀經濟形勢會增加所有公司違約的可能(在第11章中討論的Vasicek模型中,可以認為因子F代表了經濟的健康情況)。另一種解釋被稱作“傳染”(contagion)效應。業界事例19-3討論了這一現象。
業界事例19-3
傳染效應
信用危機傳染效應是世界經濟中一個領域的問題引發其他不相關領域的問題的過程。1998年,俄羅斯國債違約引發了安全投資轉移現象,所有債券的信用價差都增大了。在2007年開始的信用危機中,存在類似的安全投資轉移現象,信用價差再次加大。隨之而來的衰退造成了2009年違約公司的數量創下紀錄。2011年,希臘的債務問題使得投資者不願購買其他國家(如西班牙、愛爾蘭、葡萄牙和意大利等)的國債,結果這些國家發行的國債的信用價差大幅增加。
造成信用危機傳染效應的原因在研究人員中存在爭議。系統性風險(見業界事例15-1)可能是傳染的原因之一。也可能是投資者在一個行業遭受損失後,對風險變得更加厭惡。還可能是一個行業出現問題後,導致投資者對其他不相關的行業也變得悲觀。不論原因是什麼,不同行業的實體都會發現為自己的業務活動融資變得更加困難,並因此增加了違約的可能性。
除了我們剛剛討論的系統性風險,每一個債券還會伴有非系統性(或特殊(idiosyncratic))風險。當我們討論股票時,我們認為投資者可以選取一個股票組合,例如,由30個股票構成的股票組合來對非系統性風險進行分散,因此投資者對承擔非系統性風險不應要求額外風險利差(risk premium)。對於債券,我們就沒有這麼清晰的結論。債券收益具有非常大的偏態性(highly skewed),而且上漲的幅度有限(例如,對於單一債券可能在1年內有99.75%的概率收益率為7%,而有0.25%的概率收益率為-60%。第一個情形對應於有沒有違約發生,第二個情形對應於有違約發生)。這類風險難以分散,[5]我們必須持有成千上萬的債券才能將風險分散。在實際中,許多債券組合與完全風險分散相去甚遠。因此,和前面一段提到的因承擔系統性風險而要求額外回報一樣,債券交易員對於自身所承擔的非系統性風險也應要求額外回報。
19.7.2 究竟應該採用哪種估計
到這一步我們自然會問,在信用風險分析中應該採用真實世界的違約率還是風險中性世界的違約率?這個問題在第7章中有更常規的討論。對這一問題的回答取決於分析目的,當對衍生產品定價或者分析違約對產品價格的影響時,應該採用風險中性違約概率,這是因為在分析中會涉及計算將來預期的現金流的貼現值,在計算中會不可避免(有意或無意)地採用風險中性定價理論。當採用情景分析法來估測因違約而觸發的損失時,應該採用真實世界的違約率。例如,在計算監管資本金時採用的違約概率即為真實世界的違約概率。
[1] 這裡分析類似J. Hull, M. Predescu, and A. White, “Bond Prices, Default Probabilities, and Risk Premiums,” Journal of Credit Risk 1, no.2(Spring 2005):53-60。
[2] 其他一些研究也已注意到了兩種方法估算出的違約概率的不同,例如J. S. Fons, “The Default Premium and Corporate Bond Experience,” Journal of Finance 42, no.1(March 1987):81-97, and E.I. Altman, “Measuring Corporate Bond Mortality and Performance,” Journal of Finance 44, no.4(September 1989):909-922。
[3] 為了簡便起見,我們在計算過程中沒有考慮複利頻率對利差、回報和違約密度的影響。
[4] 除了基於1970~2016年時間段的表19-1以外,穆迪也產生了一個基於1920~2016年時間段的數據表。採用這一較長時間段的數據,我們發現對應於表19-5中的投資級債券的歷史違約密度有所增加,但是,非投資等級債券的違約密度有所下降。
[5] See J. D. Amato and E. M. Remolona, “The Credit Spread Puzzle,” BIS Quarterly Review (December 2003):51-63.
19.8 利用股價來估計違約概率
當採用類似表19-1中的數據來估計公司真實世界的違約率時,必須依賴公司的信用評級,不幸的是公司信用評級的更新較慢,因此有些人認為股票價格為估測違約概率提供了更為及時的信息。
1974年,默頓(Merton)提出了一個模型,在模型中公司的股票被當作公司資產的期權。[1]為了便於討論,假設公司僅發行一個零息債券,債券到期時間為T,定義
V0——公司資產的當前價值;
VT——公司資產在時間T的價值;
E0——公司股票的當前價值;
ET——公司股票在時間T的價值;
D——在時間T公司發行債券的本息的總和;
σV——資產波動率(假設為常數);
σE——股票的瞬時波動率。
當VT<D時,公司會對自己發行的債券違約(至少在理論上如此),此時公司的股價為0;當VT>D時,公司會支付自己在時間T的負債,在時間T,股票價值為VT-D。在默頓模型中,公司在時間T的股價為
ET=max(VT-D, 0)
以上公式顯示出公司的股票可以看作是對公司資產的看漲期權,期權的執行價格為債券應償還的本息總量。布萊克-斯科爾斯公式(見本書附錄E)給出了這一期權的當前價格
E0=V0N(d1)-De-rTN(d2)
(19-4)
其中
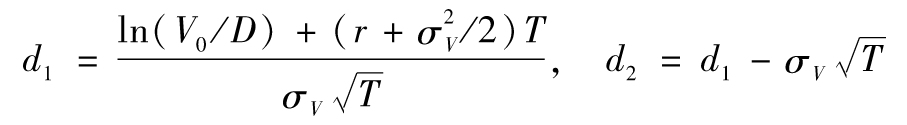
其中N(·)代表累積正態分佈函數。
在默頓模型中,如果期權不被行使,則意味著公司違約。公司在時間T的違約風險中性概率為N(-d2)。為計算這一數量,我們需要V0及σV,這兩個變量都不能在市場上直接觀察。如果公司是一家上市公司,我們可以觀察到E0,這意味著式(19-4)是V0及σV必須遵守的一個等式,我們此時也可以估計σE,由隨機微積分中的伊藤引理(Ito’s Lemma),我們得出
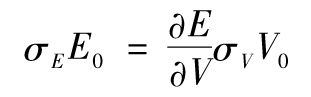
這裡∂E/∂V為股票的delta。由附錄E得出,delta=N(d1),因此
σEE0=N(d1)σVV0
(19-5)
上式是V0及σV必須遵守的另一個等式。式(19-4)及式(19-5)給出了一組關於V0及σV的方程組,由這兩個方程我們可以求得V0及σV的解。[2]
【例19-4】 假如一家公司的股價市值為300萬美元,股價變化的波動率為80%。公司在1年後必須償還的債務為1 000萬美元,無風險利率為每年5%。對應這一情形:E0=3,σE=0.80,r=0.05,T=1及D=10。對式(19-4)及式(19-5)求解,我們得出(以百萬計)V0=12.40及σV=0.212 3,變量d2=1.140 8,公司違約概率為N(-d2)=0.127,即12.7%。債券的當前市價為V0-E0,即9.40。債券預期付款的貼現值為10e-0.05×1=9.51。債券的預期損失為(9.51-9.40)/9.51,為債券不違約時價值的1.2%。
19.8.1 基本模型的擴展
我們接下來將說明基本默頓模型在哪幾個方面可以得到擴展。例如,一種擴展形式是假定每當資產價格低於一定的障礙值時,就會觸發違約;另外一種擴展方式是假定債券可以分期償還。許多研究人員發現公司發行股票的隱含波動率是反映公司違約率的一個很好的指標(隱含波動率越大,違約概率也越高)。赫爾等(2004)的研究證明了這一結果與默頓模型的一致性。[3]這項研究給出了採用兩個股票隱含波動率來實現默頓模型的方法,結果顯示這種擴展的模型與最初的實現方式結果非常接近。
19.8.2 模型的表現
由默頓模型及其擴展形式所產生的違約概率與實際違約概率有多麼接近呢?這一問題的答案是:在風險中性及真實世界中,默頓模型及其擴展形式均對違約概率提供了較好的排序。這意味著通過建立某種單調性關係,我們可以將由默頓模型產生的違約概率映射為真實世界或風險中性世界的違約率。穆迪KMV和Kamakura公司提供一項服務,將默頓模型的違約概率轉換為真實世界的違約概率。CreditGrades採用默頓模型來估計信用價差,這一信用價差與風險中性違約概率密切相關。在理論上,違約概率N(-d2)為風險中性違約概率。這使得穆迪KMV和Kamakura用它來估計真實世界的違約率的做法有些牽強。根據以上描述的校正過程,我們在分析計算中所採用的一個根本假設是:風險中性世界的違約概率、真實世界的違約概率以及由默頓模型估算的違約概率在排序上是一致的。
19.8.3 真實世界與風險中性世界的違約概率的比較
默頓模型有助於我們理解為什麼風險中性世界中的違約概率會高於真實世界。在風險中性世界中,公司資產的預期增長率是無風險利率。在真實世界中,公司資產的預期增長率通常高於無風險利率(反映出市場所要求的風險溢價)。因此,在風險中性世界中,未來資產價值跌到債務價值以下的概率也會比在真實世界中更高。
19.8.4 違約距離
違約距離(distance to default)用來描述默頓模型的輸出結果。這是指要在將來T時刻引發違約所需的、以標準差計算的資產價格的變化量。違約距離的公式為
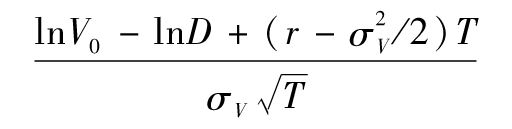
當違約距離降低時,公司違約的可能性會加大。在例19-4中,1年的違約距離為標準差的1.14倍。
[1] See R. Merton, “On the Pricing of Corporate Debt: The Risk Structure of Interest Rates,” Journal of Finance 29(1974):449-470.
[2] 為了對兩個非線性方程F(x,y)=0及G(x,y)=0求解,我們可以採用Excel中的Solver程序,通過求取[F(x,y)]2+[G(x,y)]2的極小值來達到目的。
[3] See J. Hull, I. Nelken, and A. White, “Merton’s Model, Credit Risk, and Volatility Skews,” Journal of Credit Risk 1, no.1(2004):1-27.
小結
對風險管理人員而言,估計違約概率及回收率是一個很重要的業務事項。如果一家公司公開發行債券,那麼信用評級是一個重要信息來源。對於被評級的公司,穆迪等評級機構都提供了大量有關其違約率的統計數據。回收率是指違約發生不久以後,債券的市場價格與其面值的比率。對於不同種類的債券,評級機構也提供關於回收率的統計數據。
我們也可以通過多種方法來估計違約概率,信用違約互換(CDS)就是其中一個信息來源。在一個CDS合約中,一家公司從另外一家公司買入參考實體(即第三方公司或國家)對其義務違約的保險。CDS利差是為買入信用保護每年需要支付的費用與受保面額的比率。信用價差的另外兩個來源分別是公司發行的債券的收益率高出無風險利率的超額收益率以及資產互換利差。基於一定的回收率假設,風險中性世界的違約概率可以通過信用價差計算出來。
基於歷史數據的違約概率,例如由評級公司所產生的違約概率,被稱為真實世界或物理世界的違約概率。由CDS、債券和資產互換得出的違約概率被稱為風險中性違約概率。風險中性違約概率會高於真實世界中的違約概率。在對資產進行定價時,應使用風險中性違約概率,而真實世界的違約概率應用於情景分析。這兩種概率都可以通過默頓在1974年提出的模型來估計,前提是模型能得到恰當的校正。
延伸閱讀

練習題
19.1 穆迪對於還沒有違約的公司提供多少個信用評級?這些信用級別分別都是什麼?
19.2 標準普爾對於還沒有違約的公司提供多少個信用評級?這些信用級別分別都是什麼?
19.3 利用表19-1中的數據來計算評級為B的公司在第1年的平均違約概率。
19.4 利用表19-1中的數據來計算評級為Ba的公司在第3年的平均違約概率。
19.5 某信用違約互換每半年支付一次利息,CDS利差為60個基點,信用違約互換的面額為3億美元,交割方式為現金形式。假設違約發生在第4年零2個月,而交易價值計算代理人(calculation agent)所提供的最便宜可交割債券在剛剛違約時的價格等於面值的40%,請從信用保護賣出方的角度,陳述此合約所涉及的現金流以及時間安排。
19.6 請說明信用違約互換的兩種交割方式。
19.7 請解釋風險中性概率與真實世界違約概率的差別。
19.8 哪一個公式建立了CDS回報與CDS面值及回收率的關係?
19.9 某家企業3年期債券的收益率與類似無風險債券的收益率的利差為50個基點,假定回收率為30%,請估計3年內每年平均違約密度。
19.10 某家企業5年期債券的收益率與類似無風險債券的收益率的利差為80個基點,假定回收率為40%,請估計5年內每年平均違約密度,如果企業3年期債券的利差為70個基點,計算結果顯示第4年到第5年的平均違約密度為多少?
19.11 對於以下情形,研究人員應採用真實世界還是風險中性違約概率?
(a)計算信用在險價值;
(b)因違約而造成的價格調整。
19.12 回收率通常是怎麼定義的?
19.13 請驗證:(a)表19-5中第2列結果與表19-4中第2列的一致性;(b)表19-6中第4列結果與表19-5的一致性,在計算中假設回收率為40%。
19.14 一個4年期企業債券的息票率為每年4%,每半年付息一次,以連續複利表示的收益率為5%。假設無風險收益率曲線水平為3%(以連續複利為計),假定違約事件僅僅發生在年末(在付息或償還本金之前)並假設回收率為30%,假定風險中性違約率在今後每年均相同,請使用表19-3中的方法估計風險中性違約率。
19.15 假定某公司發行了3年期及5年期債券,兩隻債券每年均支付4%息票,每半年付息一次。債券的收益率(連續複利)分別是4.5%和4.75%。對所有的期限,無風險連續複利利率是3.5%。債券回收率為40%,違約事件均發生在每年的正中間。從第1年到第3年的每年風險中性違約率為Q1,從第4年到第5年的為Q2,估計Q1及Q2的值。
19.16 考慮某資產互換,B為對應於1美元單位面值的債券價格,B*為對應於1美元單位面值的無風險債券價格,V為對應1美元單位面值的資產互換利差的貼現值,請證明V=B*-B。
19.17 證明第19.8節中默頓模型中的T年期限零息債券的信用價差等於
-ln[N(d2)+N(-d1)/L]/T
其中L=De-rT/V0。
19.18 某公司的股票市價為200萬美元,股票價格變化的波動率為50%,1年後債券償還數量為500萬美元,無風險利率為每年4%,採用默頓模型計算違約概率(提示:Excel中的Solver程序可以對問題中的方程求解)。
19.19 某交易員在2013年6月20日進入一個5年信用違約互換,合約要求每季度付款,利差為每年400個基點。面值為1億美元。違約發生在第4年零2個月。拍賣過程確定的最便宜可交割債券的價格為其面值的30%。請列出信用違約互換賣出方的現金流及其時間。
19.20 “在信用違約互換中買入方的頭寸與持有某個無風險債券的多頭及某個企業債券的空頭的組合相似。”請解釋這一觀點。
19.21 為什麼在信用違約互換中存在信息不對稱問題?
19.22 假定LIBOR/互換曲線水平為6%(以連續複利計),5年期息票率為5%(每半年付息一次)的債券價格為90.00,無風險債券的價格是多少?違約預期損失的貼現值是多少?對應於這一債券的資產互換應如何構造?此時資產互換的利差應如何計算?
作業題
19.23 假定一個企業債券每年支付7%的息票,每半年付息一次,收益率為5%(以每半年複利計)。所有期限的無風險債券的收益率為每年4%(以每半年複利計)。假設違約事件每半年發生一次(剛好在券息付出日之前),回收率為45%。請在以下假設下估計違約概率:(a)在每個可能違約的日期,無條件違約概率均相同;(b)在每個可能的違約日期之前無違約的條件下,發生違約的條件概率均相同。
19.24 某公司發行了1年期和2年期債券,均提供8%的息票,每年付息一次。債券收益率(以連續複利計)分別是6%和6.6%。對應於所有期限的無風險利率均為4.5%,回收率為35%。違約事件均發生在年正中間,請估計每年的風險中性違約率。
19.25 某公司的股票市價為400萬美元,股票變動的波動率為60%。2年後需償還的債券的數量為1 500萬美元,無風險利率為每年6%。採用默頓模型來估測違約預期損失、違約概率及違約時的回收率(以無違約值的百分比表示),請解釋為什麼默頓模型會給出一個較高的回收率(提示:Excel中的Solver程序可以對問題中的方程求解)。
第20章
CVA和DVA
如在第17章中討論過的,場外衍生產品的清算有兩種方式:通過中央清算方(CCP)進行清算或進行雙邊清算。根據金融危機後引入的新的監管規則,金融機構間進行的標準衍生產品交易必須通過CCP清算。金融機構間的非標準衍生產品合約進行雙邊清算,但是新引入的監管規則要求雙方提供大量的擔保品,使得信用風險基本被消除。在本章中,我們將重點討論雙邊清算的場外衍生產品交易中的信用風險。這其中包括與非系統重要性終端用戶的交易,以及在新規則實施前與其他交易對手已經達成的交易。
對衍生產品交易的信用風險進行評估的複雜性要遠遠超過對貸款中的信用風險進行評估,這是因為衍生產品交易中將來的風險敞口(即在違約發生時的損失數額)並不是已知的。如果一家銀行為客戶提供了一筆本金為1 000萬美元、無抵押、期限為5年的貸款,本金在到期時償還,則銀行基本明確,這5年間的風險敞口大約為1 000萬美元。但如果銀行與客戶進行了一筆5年期的利率互換交易,則銀行面臨的風險敞口就不再像貸款的敞口那樣容易確定,這是因為利率互換的價值與將來的利率變化有關。如果對於銀行而言,利率互換價值為正,則銀行面臨的風險敞口等於互換的價值(即如果對手違約,銀行將損失該數量);如果價值為負,則銀行面臨的風險敞口為零(因為在這種情況下,如果對手違約,銀行將沒有任何損失)。
本章將討論信用價值調整量(credit valuation adjustment,CVA)和債務價值調整量(debit valuation adjustment,DVA)。CVA是衍生產品交易商遭受的因交易對手可能違約而帶來的預期損失,DVA是衍生產品交易商獲取的因自身可能違約而帶來的預期收益(即交易對手的預期損失)。
20.1 衍生產品的信用敞口
首先我們簡要地討論一下衍生產品交易所產生的風險敞口的特性。先考慮最簡單的情況,即在衍生產品交易商與某對手之間只存在一個衍生產品交易的情況。我們假設交易採用雙邊清算,雙方都不需要向對方提供擔保品。
總共會有以下三種可能:
(1)該衍生產品永遠是交易商的負債;
(2)該衍生產品永遠是交易商的資產;
(3)該衍生產品既可能是交易商的資產,也可能是交易商的負債。
以上第一種情形的實例是期權的空頭頭寸,第二種情形的實例是期權的多頭頭寸,第三種情形的實例是遠期合約或利率互換。
對於交易商來講,第一種情形中的衍生產品交易不會產生交易對手信用風險。當交易對手違約時(例如,因為破產),交易就終止了。[1]如在第17.1.5節中解釋的,在其後的清算過程中,交易商需要支付衍生產品的價值(如果該交易的價值對交易商為負。定價時要考慮買賣價差,以反映交易商替換該交易的成本)作為破產的交易對手的財產。因此交易商不會在對手的破產中受損,也不會從中獲利。
在第二種情形下,對交易商而言,對手信用風險敞口始終存在。如果交易對手破產,則交易商往往會遭受損失。對交易對手而言,交易商實際上成為一個無抵押債權人,債務的面值即為衍生產品的價值(同樣,對價值也要進行買賣價差調整,以反映交易商的替換成本),損失數量與對手違約時的衍生產品價值有關。
第三種情形更為複雜,交易商對於交易對手的信用風險敞口在將來可能存在也可能不存在。如果衍生產品對於交易商的價值為正時交易對手違約,則交易商可能會遭受損失;如果交易對手違約時衍生產品對於交易商的價值為負,則交易商不會有任何損益,正如第一種情況。
在計算自己面對的敞口時,交易商通常不會將第18.2節中介紹的買賣價差調整量考慮在內。因此,在我們上面考慮的這個簡單例子中,交易商的淨敞口是
max(V, 0)
其中變量V是衍生產品在違約時的市場價值。
當交易商和交易對手之間存在很多交易時,根據交易商和交易對手之間的雙邊協議,這些交易會進行淨額結算(見第15.5節)。在任意時刻,如果沒有擔保品,交易商的淨敞口為max(V,0),其中V等於所有交易市場價值淨額結算後的淨值。
在計算其信用風險時,交易商既關心其當前的信用風險敞口,也關心未來的信用風險敞口。監管機構已經意識到這一點。如第15.3節所述,《巴塞爾協議Ⅰ》採用了CEM方法,其中貸款等價敞口為當前風險敞口加上附加額。此版本用於計算《巴塞爾協議Ⅱ》中的違約風險敞口(EAD),並在SA-CCR中進行了修訂(見第16.4節)。在《巴塞爾協議Ⅱ》的高級IRB方法中計算EAD的程序涉及有效預期正風險敞口的計算(見第15.8.4節)。
在本章中,我們將重點討論CVA和DVA的計算方法,估計可能的違約造成的預期損失。
[1] 注意,衍生產品對於對手而言是一個資產,因此當對手破產時,造成破產的原因一定與該衍生產品無關。
20.2 CVA
在場外衍生產品交易中,對每一個進行雙邊清算的交易對手,交易商都要計算一個信用價值調整量(CVA)。[1]這一數量是對交易對手違約所帶來的預期損失的估計。CVA會導致衍生產品的價值下降。在某個時間段內,CVA總值的提高(或降低)會導致同期利潤的降低(或提高)。
假定T代表與某交易對手的所有衍生產品交易中最長的期限,為了計算CVA,我們將0~T的區間化成若干小的時間段(例如,從現在到1個月,從1個月到3個月,等等)。
假定第i個時間區間起始為ti-1,結束為ti(t0=0),假定時間段的數量為n,定義
qi——交易對手在第i個時間段內的風險中性違約概率;
vi——如果在第i個時間段內發生違約,在該時間段中點上交易商對交易對手淨預期風險敞口(考慮擔保品以後)的當前價值;
R——交易對手違約時,交易商作為無抵押債權人的回收率。
假定淨風險敞口與對手違約概率無關,對手在第i個時間段違約所產生的預期損失的當前值為
(1-R)qivi
整體預期損失為

變量qi是風險中性違約概率(這是因為CVA的計算涉及對未來現金流的定價。如第7章所示,在定價時,應使用風險中性違約概率而不是真實世界的違約概率)。qi的值可以由對手的信用價差來進行估計,如第19.6節所示。假定si為交易對手對應於時間ti的信用價差的估計,根據式(19-3),時間0~ti的平均風險率(hazard rate)為

時間0~ti的不違約的概率為
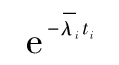
因此
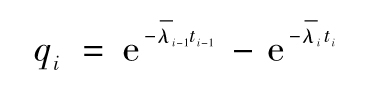
或者

vi通常是通過蒙特卡羅模擬計算得出的,即在風險中性世界,從時間0到T,我們要對市場變量進行模擬,這些模擬變量決定了交易商與交易對手的交易價值。在每次模擬抽樣中,對於每個小的時間段的中點,我們要計算交易商對於交易對手的風險敞口,然後求得這些敞口的均值,vi等於對應於第i個區間的均值的貼現。在實踐中,交易商可能與數千個對手存在交易,因此要計算對所有對手的風險敞口vi對計算量的要求非常大。
20.2.1 擔保品和補救期
在計算vi的過程中,我們需要考慮擔保品協議。交易雙方達成的擔保品協議通常是信用支持附件(CSA)或ISDA主協議的一部分。協議中會指明交易雙方提交的擔保品計算細節,以及對非現金擔保品價值的折減量。假設違約發生時,交易對手提交的擔保品的價值為C(如果C為負值,則-C為交易商向交易對手提交的擔保品的價值)。在任意情況下,交易商對交易對手的風險敞口為
E=max(V-C, 0)
(20-4)
這裡V是所有現有交易對交易商的市場價值的總和。
式(20-4)說明了一個簡單的事實:當交易的價值-V對交易商來說是正值時,交易對手提供的擔保品可以用來降低(某些情況下甚至消除)由此產生的風險敞口。如果交易商向對手提供了擔保品(C<0的情況),當對手發生違約時,這部分價值不會被返還,而如果-C>-V,則超出的部分也變成了敞口的一部分。前面提到過,在CVA和DVA的計算中,對敞口的考慮一般採用交易的市場中間價(在第17.1.5節中,我們曾展示過一個類似的結果:當違約發生時,需要對市場中間價進行調整,調整幅度為買賣價差的一半,以得出索償的數額)。
在實踐中,從交易對手停止提供擔保品到交易被平倉通常會有一段時間,這段時間被稱為補救期(cure period),也被稱作風險邊際期(margin period of risk)。這段長時間的長度通常介於10到20天之間。補救期的存在意味著當違約發生時,擔保品的價值並不反映違約時刻的交易組合的價值,而是10~20天之前的價值。
假定第i個區間的中間值為ti*,即ti*=(ti-1+ti)/2,c為補救期。在進行蒙特卡羅模擬計算vi時,計算過程既要考慮到與對手的交易組合在ti*的價值,也要考慮到其在ti*-c的價值(i=1,2,…,n)。在每次模擬過程中,交易在ti*-c的價值與CSA條款結合起來,用來確定在ti*時刻持有的擔保品的價值,然後通過式(20-4)得出ti*時刻敞口的值。[2]例20-1對計算過程進行了說明。
【例20-1】 假設一家銀行和某個客戶之間的協議要求雙邊、零起點金額提供擔保品。設其中一方為A,另一方為B。這意味著在任意交易日,A方提供給B方的擔保品的數量應等於max(V,0),即所有未清償交易對另一方的價值。補救期為20天。這意味著當有違約發生時,A方提供給B方的擔保品的價值等於max(V,0),而V為交易組合20天前對B的價值。假設時刻τ為銀行計算CVA時使用的時間段的中點值。
(1)在某次模擬試驗中,τ時刻未清償交易組合對銀行的價值為50,而20天前的價值為45。當對手在τ時刻違約時,銀行持有的擔保品的價值為45。因此,銀行的敞口為5,即衍生產品交易價值中未被擔保的部分。
(2)在某次模擬試驗中,τ時刻未清償交易組合對銀行的價值為50,而20天前的價值為55。因此,在這種情況下,我們認為銀行持有足夠的擔保品,風險敞口為零。
(3)在某次模擬試驗中,τ時刻未清償交易組合對銀行的價值為-50,而20天前的價值為-45。在這種情況下,當對手在τ時刻違約時,銀行提交給交易對手的擔保品價值低於50。因此,銀行的敞口為零。
(4)在某次模擬試驗中,τ時刻未清償交易組合對銀行的價值為-50,而20天前的價值為-55。在這種情況下,當對手在τ時刻違約時,我們會認為銀行20天前提交給交易對手的價值55的擔保品不會被返還。因此,銀行的敞口為5,即擔保品價值超出衍生產品價值的部分。
20.2.2 峰值敞口
除了計算CVA,交易商通常還會計算在每個時間段中點上風險敞口的峰值(peak exposure)。該峰值對應於蒙特卡羅模擬的高分位數,例如,我們設定了97.5%的分位數,蒙特卡羅模擬的次數為10000次。時刻ti*的敞口峰值為在10000個抽樣值中,該時刻對應敞口值按由大到小順序排序的第250個值。最高峰值(maximum peak exposure)對應於所有ti*峰值中的最大值。
這裡有一個常常被忽略的理論問題。為了計算CVA,我們要在風險中性世界對市場變量進行模擬,並且在計算中使用的貼現利率為無風險利率(如第7章所述,對衍生產品進行定價時,我們通常這樣做)。但在計算峰值敞口時,我們是在進行情景分析。實際上我們是在問:“將來我們對交易對手的敞口在最壞的情況下有多大?”要回答這個問題,如第7章中討論過的,我們理論上應該是在真實世界而不是風險中性世界中對市場變量進行模擬。[3]
20.2.3 降級觸發
淨額結算和擔保品協議是雙邊清算的衍生產品交易中降低信用風險的重要手段。有時,ISDA主協議的信用支持附件(CSA)中還會包含降級觸發條款。該條款會申明,如果交易中一方的信用評級下滑到某一級別時,另一方有權索取更多的擔保品或將交易終止。
AIG事件為降級觸發條款的運作提供了一個實例,許多AIG的交易申明,當AIG的信用高於AA級時,AIG無須為交易支付擔保品,而當AIG的信用低於AA時,交易對手就會要求AIG提供擔保品。2008年9月15日,AIG被三家評級公司降級到AA以下,這導致了擔保品的催付而AIG無力支付,AIG最終只有憑藉政府的大規模援助才得以倖存。
其他深陷降級觸發條款困境的公司還有安然(Enron)、施樂(Xerox)和安巴克(Ambac)。如果發生跳躍性降級(例如由AA級直接降至違約),降級觸發條款對被降級公司的交易對手並不能提供保護。另外,某公司的交易對手,只有在有限度的適用針對此公司的降級觸發條款時,才能對自身提供有效的保護。假如一家公司在與許多對手的交易中都設定了信用降級觸發條款,當該公司的信用評級低於一定級別時,會出現類似AIG的情形,造成該公司對現金的需求猛增,如果現金不足,則會迅速導致破產。
[1] 關於CVA的更多內容,可參閱J. Hull and A. White, “CVA and Wrong Way Risk,” Financial Analysts Journal 65, no.5(September/October 2012):5869; E. Canabarro and D. Duffie, “Measuring and Marking Counterparty Risk,” Chapter 9 in Asset/Liability Management for Financial Institutions, ed. L. Tilman (New York: Institutional Investor Books, 2003); E. Picault, “Calculating and Hedging Exposure, CVA, and Economic Capital,” in Counterparty Credit RiskModeling, ed. M. Pykhtin(London: Risk Books, 2005); and J. Gregory, Counterparty Credit Risk: The New Challenge for Financial Markets, 2nd ed. (Hoboken, NJ: John Wiley & Sons, 2012)。
[2] 這裡的結論基於一些簡化假設,即擔保品的支付是一個不間斷的過程,而且沒有最小支付數量的限制,為了反映真實情形,這些假設可以被放鬆。
[3] 當對不遠的將來的峰值敞口進行計算時,使用真實世界進行模擬和使用風險中性世界進行模擬所得的結果差別很小。
20.3 新交易的影響
當交易商與一個交易對手商談一筆新的衍生產品交易時,這筆新交易對CVA的附加效應會影響到交易的條款。如果這筆新增交易的價值與交易商和該對手之間已有的其他交易的價值是正相關的,則該筆新交易會使CVA增大;如果相關性是負的,則該筆新交易會使已有CVA減小。
例如,假設交易商和交易對手之間只有一筆交易,即一個5年期的外匯遠期合約。在合約中,交易對手將買入外匯。如果交易對手有興趣再進行一筆3年期的同幣種外匯遠期交易,則交易商給出的價格的競爭性將與新增交易中交易對手是買入外匯還是賣出外匯有關。如果交易對手希望買入外匯,則新增3年期交易會使交易商的CVA增大(這樣會降低交易商的收入,因此新交易對交易商的吸引力會降低);反過來講,如果交易對手希望賣出外匯,則新增交易會與已有交易淨額結算,從而降低交易商的CVA(這樣新交易對交易商會更具吸引力)。這些CVA和淨額結算考慮說明,當交易進行雙邊清算並且沒有完全擔保時,如果一家企業希望進行一筆新的衍生產品交易,那麼對該企業而言,一個與它已經有未清償交易的交易商給出的價格往往會比另一家沒有與其交易的交易商給出的價格更為有利。
CVA的計算量一般會很大,一家交易商同一個交易對手之間往往會有成百上千個交易。[1]通過重新計算整體CVA的方式來計算一個新交易的CVA增量通常不是一個合乎實際的做法。好在對於CVA增量的計算,我們有了一個比較高效的做法。
在第20.2節描述的CVA計算過程中,由模擬產生的市場變量的路徑以及交易組合在每個路徑上的價值可以被儲存起來。[2]當考慮一個新交易時,我們可以採用已經被記錄下來的市場變量取值,並基於這些市場變量,來對新增交易的將來價值進行計算。這樣一來,對未來任意時刻,我們都可以求得在之前產生的蒙特卡羅模擬路徑上,新增交易對於交易組合將來價值的附加效應。在此基礎上,我們也可以得出在每條蒙特卡羅路徑上,新交易對未來敞口的附加效應。由此,對於風險敞口的附加效應的均值也可以計算出來,再利用式(20-1),我們就可以求得對CVA的附加效應。
為了說明計算過程,假定某交易商與一個交易對手的交易組合的價值只與黃金價格有關。在計算CVA的模擬過程中,對應於第2.5年時間節點,在第545次抽樣中,黃金價格為每盎司1572美元,此時投資組合對交易商的價值為240萬美元。假定沒有擔保品,此價值也就對應於風險敞口。如果第2.5年也對應於第20個時間段的中間值,則意味著v20等於在第2.5年的價值(即240萬美元)的貼現,假設貼現值為230萬美元。
如果在完成CVA計算不久,交易商要與此交易對手進行一筆新的交易,交易價值同樣僅與黃金價格有關。對於這筆交易,在所有的關於黃金價格的模擬路徑上,我們要對新增交易進行定價。假定在第545次模擬路徑上,在第2.5年(黃金價格為1572美元時),新增交易的價值為-420萬美元。這意味著在第545次的模擬路徑上,在2.5年時間節點上,交易組合價值在加入了新交易以後,將最初的230萬美元減至-190萬美元,因此風險敞口也減至0,新的v20的取值也為0,從而新交易的效果是將v20的值減小了230萬美元。對於所有的模擬和時間節點,我們可以進行類似的計算。定義Δvi為所有模擬路徑中vi變化的均值,新增交易對於既存交易組合的附加效應也可以由下式估算得出

[1] 雷曼兄弟在破產時,總共與超過8 000個交易對手之間進行了150萬筆交易。
[2] 準確地講,在每次計算CVA時,市場變量在節點ti*和ti*-c的值(1≤i≤n)要被儲存起來,交易組合在這些節點的市場價值也要被儲存起來(直到下一次計算CVA時,這些數據才可以被清除)。
20.4 CVA風險
對於每個交易對手,交易商都要計算CVA,這裡的CVA本身也可以被看作衍生產品,而且是一種比較複雜的衍生產品。事實上,對任意交易對手的CVA,都比與此交易對手之間已有的任何其他交易要更加複雜,這是因為CVA的大小取決於交易商與交易對手之間的所有交易的淨值。
CVA增大(減小),交易商報告的淨收益會減小(增大)。正因為此,許多交易商也會像對待其他衍生產品那樣,謹慎地對CVA進行對衝。這也意味著交易商要採用第8章討論的方式,對CVA的希臘值(delta、gamma、vega)進行計算。
決定vi數量的市場變量包括利率、匯率、商品價格等,針對這些變量來計算希臘值會很花費時間。例如,在計算CVA對於匯率的敏感性(delta)時,我們要對匯率進行擾動,然後重新計算CVA。一項被稱作聯合差分(adjoint differentiation)的方法可以用來減小計算負擔。[1]
決定qi的變量為交易對手的不同期限上的信用價差。由式(20-3)得出
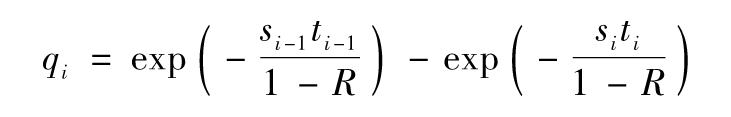
由式(20-1)

利用delta/gamma近似,當信用價差的期限結構有一個平行移動Δs時(假定其他與vi數量有關的市場變量不變),相應的CVA變化為

在vi已知的情況下,以上計算非常簡單。
《巴塞爾協議Ⅲ》中要求交易商利用上式,將信用價差變化帶來的風險納入市場風險資本金的計算中。最初,這種由市場變量變化引起的並能影響Vi的風險不包括在市場風險資本金計算中。這使得交易商不願對衝與Vi相關的風險,因為對衝會增加而不是減少為計算資本金時評估的市場風險。巴塞爾委員會於2015年解決了這個問題。[2]
[1] See for example M. Giles and P. Glasserman, “Smoking Adjoints: Fast Monte Carlo Greeks,” Risk 19, no.1(2006):88-92, and M. Henrard, “Adjoint Algorithmic Differentiation: Calibration and the Implicit Function Theorem,” Journal of Computational Finance 17, no.4(2014):37-47.
[2] 見巴塞爾銀行監管委員會,“Review of Credit Valuation Adjustment Risk Framework,”2015年10月1日。
20.5 錯向風險
截至目前,我們一直都在假定交易對手的違約概率與風險敞口無關。有時以上兩個因素有一定相關性,也就是說,當交易商對於對手的風險敞口較高(較低)時,對手違約可能性也較大(較低)。這種現象被稱作錯向風險(wrong-way risk);類似地,當交易商對於對手的風險敞口較高(較低)時,對手違約可能性較低(較高),這種現象被稱作正向風險(right-way risk)。
與交易對手進行交易時,交易商對於錯向風險或者正向風險的主觀判斷取決於交易商對於對手業務,尤其是交易對手所面臨的風險的特質的瞭解程度。要做出正確判斷還取決於對對手與其他交易商進行的其他交易的瞭解。針對這一點的準確信息較難取得。
錯向風險可能發生的一種情形是,某個交易對手利用信用違約互換,向交易商賣出信用保護(AIG就是眾所周知的例子)。當交易商從一個交易對手買入了信用保護,而該保護所針對實體的信用價差增大時,該信用保護對於交易商的價值為正。然而,因為不同公司的信用價差具有相關性,此時交易對手的信用價差很有可能也增大了,並導致計算得出的違約概率增大。類似地,正向風險往往發生在一個交易對手從交易商買入信用保護的情形。
當一家公司試圖投機並因此與一個或多個交易商進行了大量的相似交易時,對這些交易商來說,也可能引入錯向風險。這是因為對手公司的財務狀態決定了,當交易價值走向對其變得不利時,公司違約的可能性會變大。
當公司進行交易的目的是部分對衝既存風險時,這在理論上對交易商而言,會是正向風險。這是因為當交易價值走向變得對對手公司不利時,公司可以從沒有被對衝的風險敞口中獲益,因此其違約概率會相對較小。[1]
一種錯向風險的處理方法是針對vi和qi相互無關的模型,引入某一個乘數因子,該因子被稱作alpha乘積因子(alpha multiplier)。這樣可以通過該因子來增大最終CVA的數量。《巴塞爾協議Ⅱ》將alpha設定為1.4,但也允許銀行使用自己的錯向風險模型,但其中alpha因子的下限不得低於1.2。這意味著,CVA的最終數量也會比假定vi和qi相互無關的模型產生的結果至少高出20%;如果銀行沒有自己的模型來處理錯向風險,則必須負擔高出40%的數量。銀行通過內部模型計算公佈的因子值通常介於1.07和1.10之間。
目前也已經有一些模型被開發出來,用以捕捉風險敞口與違約概率之間的相關性。例如,Hull和White在2012年提出了一個簡單模型,其中在任意時刻t的風險率與此時刻觀測到的變量值有關。[2]在該模型中,描述相關程度的參數既可以主觀估計,也可以通過歷史數據,將交易對手過去的信用價差與當前交易組合在過去市場狀況下的價值進行關聯來進行估計。只需要對第20.2節的計算進行一些微調,我們就可以實現這個模型。
[1] 當交易對手出現流動性困難時,是以上結論的一個例外,在此時即使被對衝的資產價值有所提高,交易對手卻沒有能力為對衝交易提供擔保品,見業界事例24-2關於Ashanti Goldfields案例的討論。
[2] See J. Hull and A. White, “CVA and Wrong Way Risk,” Financial Analysts Journal 68, no.5(September/October 2012):58-69.
20.6 DVA
債務價值調整量(DVA)[1]是CVA的鏡像。CVA是交易商由於交易對手可能違約而遭受的損失的預期,而DVA是交易對手因為交易商可能違約而造成的損失的預期,也就是交易對手的CVA。如果DVA對交易對手而言是一項成本,那麼它對交易商而言應該是收益(這是因為衍生產品交易是一項零和遊戲,一方的收益就是另一方的損失)。能夠產生這項收益是因為,如果交易商違約了,那它就不必再向對手支付未清償衍生產品的價值(如果未違約,支付要照常進行)。財會規則已經納入了CVA和DVA。與交易對手的未清償衍生產品的賬面價值計為
fnd-CVA+DVA
其中,fnd是不考慮任何一方的違約可能性時衍生產品組合的價值。
我們可以採用與計算CVA同樣的方式來計算DVA。將式(20-1)中交易對手違約時的回收率R替換為交易商本身違約時的回收率,我們就可以採用同一公式來計算DVA,其中vi是在第i個區間中點上交易對手對交易商的風險敞口的當前價值,qi為交易商在第i個區間的違約概率。採用類似於計算交易商對於交易對手的淨風險敞口的方法,在考慮了交易商繳納的擔保品以後,我們也可以求得交易對手對於交易商的淨風險敞口。
DVA效用的出人意料之處在於,當衍生產品交易商的信用價差增大時,DVA會增加,由此造成交易商持有的衍生產品的賬面價值增大,交易商的盈利也因此增加。有些銀行在2011年第三季度報告的利潤額因此曾增加了幾十億美元。這引起了監管機構的擔憂,並因此決定,在計算監管資本金時,DVA的損益要從普通股本的定義中剔除。
[1] DVA有時也被稱作“debt value adjustment”。
20.7 一些簡單例子
為了進一步說明本章的內容,我們在此給出一些簡單例子。
20.7.1 價值為正的單筆交易
首先我們假設某交易商與一個交易對手進行了一筆衍生產品交易,交易對於交易商的價值一直為正,對交易對手的價值一直為負(例如,交易商從對手處買入期權)。我們假設在交易中沒有擔保品,為了簡單起見,我們還假定此衍生產品交易的支付只發生在產品的最終到期日。
在將來任意時刻,交易商對交易對手的風險敞口等於交易的價值。因此,在ti時刻的預期風險敞口的貼現值(被計為vi)等於交易在ti時刻預期價值的貼現值。我們假定在交易期滿之前沒有任何支付,交易在ti時刻預期價值的貼現值總是等於產品的當前價值。
因此,式(20-1)變為
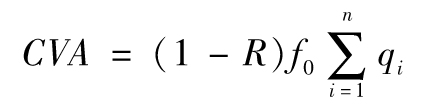
其中f0是在假設交易對手不會違約的情況下的衍生產品價值,假定f0*為將對手違約可能考慮在內的衍生產品價值
f0*=f0-CVA
或者

這意味著在這一情形下,對手違約對於衍生產品的價值的影響是將其價值按一定比率減小,這裡的比率如式(20-6)所示,等於累計風險中性違約概率與1減去回收率的乘積。
我們現在考慮一個由交易對手發行的無抵押零息債券。債券在T時刻支付1 000美元。定義B0為無違約風險時的債券價格,B0*為債券的實際價格。假定在違約時,債券的索償優先權與衍生產品索償的優先權等同。因此,違約時衍生產品的回收率等於債券的回收率,類似於式(20-6),我們可以得出
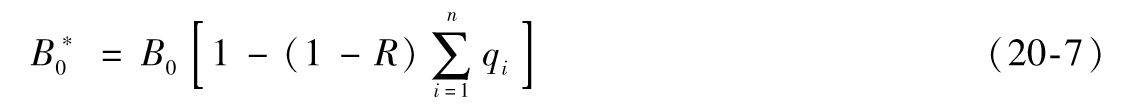
由式(20-6)和式(20-7)得出

如果y為在T時刻到期的無風險零息債券的收益率,y*為在T時刻到期的由衍生產品交易對手發行的零息債券收益率,即B0=e-yT與B0*=e-y*T,由式(20-8)得出
f0*=f0e-(y*-y)T
(20-9)
上式說明,衍生產品的價格等於無風險的衍生產品價格以y*-y進行貼現。
【例20-2】 考慮公司X在場外交易市場賣出的一個2年期的期權,在無違約前提下期權的價值為3美元。假定由公司X發行的2年期零息債券的收益率比相應的無風險利率高1.5%,期權的實際價值為
3e-0.015×2=2.91
即2.91美元。
20.7.2 利率互換與貨幣互換
我們接下來考慮交易商進行了一對與不同交易對手的互換交易,交易之間相互抵消(也被稱作背靠背交易)。圖20-1比較了當互換交易分別為匯率互換和利率互換時,將來的整體預期風險敞口。利率互換的預期風險敞口的起始值為零,然後隨時間變化會增加,最後又會下降;匯率互換的預期風險敞口與之形成對比,隨時間變化會持續增加。利率互換和匯率互換的預期風險敞口不同的主要原因是在匯率互換中,會有最終本金的互換,而進行本金互換時的匯率有很大的不確定性。當利率互換到期時,雙方需要互換的金額很小。因此我們可以得出,匯率互換交易的對手違約風險的影響要遠大於利率互換交易。對兩類互換,式(20-1)中交易商計算的交易對手的違約概率qi是相同的,但是匯率互換的vi一般來說會更大。
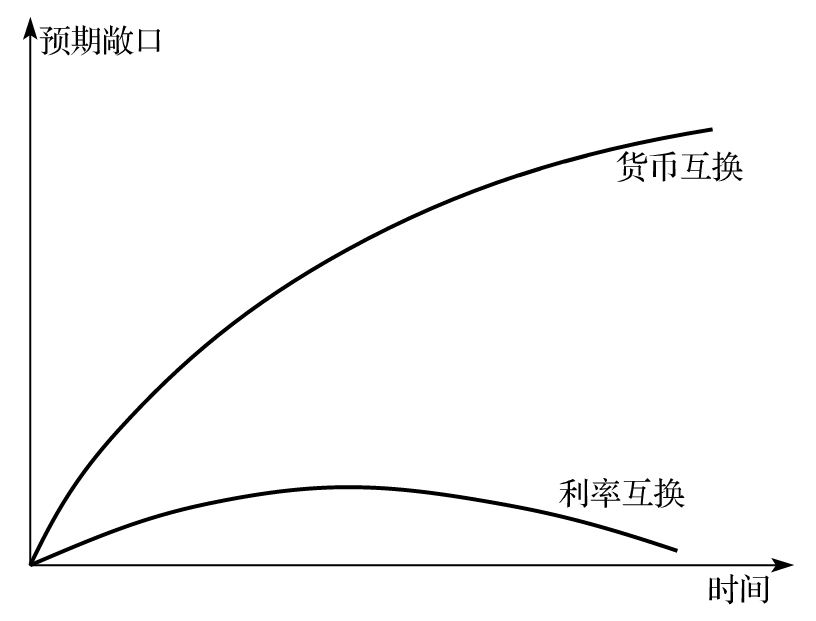
圖20-1 一對背靠背的利率互換和一對背靠背的匯率互換的預期敞口對比
20.7.3 單一遠期交易
下面一個例子是交易商與交易對手之間進行了一筆遠期交易,其中交易商要在將來時間T以特定價格K買入資產。假設在交易中沒有擔保品,資產在今天的遠期價格為F0(在今天為已知),在時間t(t≤T)的遠期價格為Ft(在今天為未知)。如附錄C所示,遠期價格在時間t的價值為
(Ft-K)e-r(T-t)
其中r為無風險利率(假定為常數)。
在時間t的風險敞口為
max[(Ft-K)e-r(T-t),0]=e-r(T-t)max[(Ft-K),0]
(20-10)
風險敞口的當前價值等於在時間t支付回報max[(Ft-K),0]的衍生產品的貼現值,該衍生產品是關於遠期價格的期權,由附錄E的期權公式得出,該衍生產品的價值為
e-rt[F0N(d1)-KN(d2)]
其中
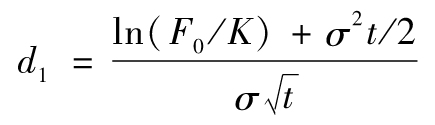
以及

其中σ是資產遠期價格的波動率。由式(20-10)我們可以得出,在時間t的風險敞口的當前值為
e-rt[F0N(d1)-KN(d2)]
因此式(20-1)中的vi滿足
vi=e-rT[F0N(d1,i)-KN(d2,i)]
(20-11)
其中
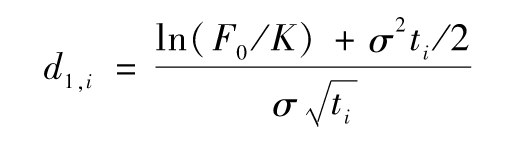
以及
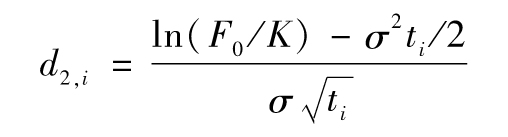
【例20-3】 假定某銀行和一家礦業公司進行了一筆關於黃金的遠期交易,交易規定在兩年後銀行將以每盎司1 500美元的價格買入100萬盎司黃金,黃金的遠期價格為每盎司1 600美元。礦業公司在第1年的違約概率為2%,在第2年的違約概率為3%,假定礦業公司違約的時間發生在每年的年正中,無風險利率為每年5%,金融機構預測礦業公司違約回收率為30%,在黃金遠期合約兩年期滿時,遠期價格的波動率為20%。
在這一情形下,按式(20-11)
v1=e-0.05×2[1600N(d1,1)-1500N(d2,1)]
其中
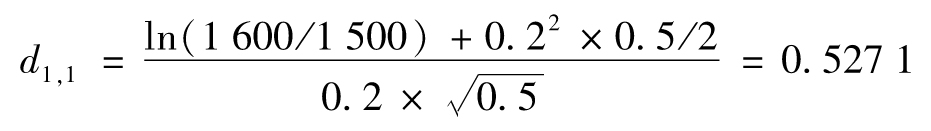
以及

由此得出v1=132.38。同理
v2=e-0.05×2[1600N(d1,2)-1500N(d2,2)]
其中

以及
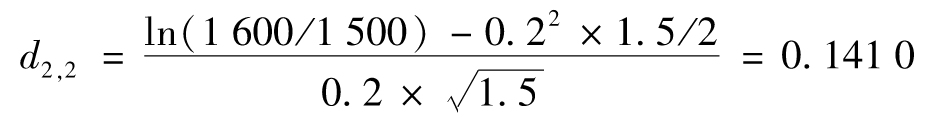
由此得出v2=186.65。
其他變量的取值為q1=0.02、q2=0.03以及R=0.3,因此
CVA=(1-0.3)×(0.02×132.38+0.03×186.65)=5.77
在沒有違約的假設下,遠期合約的價值為(1 600-1 500)e-2×0.05=90.48,將對手違約考慮在內,遠期合約的價值為
90.48-5.77=84.71
我們可以將該例擴展到礦業公司的違約發生時間更為頻繁的情形(見作業題20.13和作業題20.14)。
小結
衍生產品交易商與某交易對手之間雙邊清算的衍生產品的信用價值調整量(CVA)是交易對手未來可能違約而造成的損失的當前價值。一般來說,交易商會建立一個系統,計算針對所有進行雙邊清算的交易對手的CVA。系統對與交易的市場價值有關的變量進行模擬,由此來決定在將來違約發生時,交易商面臨的淨風險敞口。計算中還要考慮淨額結算和擔保品協議。一個簡單假設是風險敞口與違約概率相互無關。考慮錯向風險(風險敞口與違約正相關)和正向風險(二者負相關)的模型也可以被開發出來。
CVA本身是一種比較複雜的衍生產品,許多交易商也像管理其他衍生產品那樣,對CVA風險進行對衝。CVA相關的風險有兩類:交易對手信用價差的變化以及與交易相關的市場變量本身的變動。CVA計算出來以後,對前一種風險,計量起來較為簡單,並且在《巴塞爾協議Ⅲ》中,監管機構要求交易商計提針對這一風險的資本金。計算CVA對其他基礎市場變量變動的敏感性更加困難。對這部分風險,監管機構目前沒有要求資本金計提。
交易商針對雙邊清算的衍生產品交易對手的債務價值調整量(DVA)是交易商本身在將來可能的違約給交易對手造成的預期損失的當前價值。對交易商來說,DVA是盈利。DVA可與CVA同時計算。
延伸閱讀

練習題
20.1 銀行與交易對手進行一筆新交易,該交易可能降低也能增大銀行對該交易對手的信用風險敞口,請解釋為什麼。
20.2 一家公司提議使用該公司本身的股票作為擔保品。你該如何迴應?
20.3 假設一家金融機構與兩個不同的交易對手X和Y分別進行了一筆交易,以下哪些正確說法?
(a)在1年時,兩筆交易迭加的預期風險敞口等於與X交易的預期風險敞口加上與Y交易的預期風險敞口。
(b)整體違約損失的當前值等於交易對手X的違約損失的當前值加上交易對手Y的違約損失的當前值。
(c)在1年時,整體風險敞口的第95%分位數等於與交易對手X的風險敞口的第95%分位數加上與交易對手Y的風險敞口的第95%分位數。
解釋你的答案。
20.4 “在沒有擔保品和其他交易的情況下,遠期合約多頭頭寸的信用敞口等於一個無違約風險看跌期權空頭與一個有違約風險看漲期權多頭的信用敞口的總和。”請解釋這一觀點。
20.5 假定一家公司發行的3年期零息債券的收益率與3年期無風險零息債券的收益率的利差為120個基點。這家公司賣出的由布萊克-斯科爾斯-默頓模型定價的標準期權的價格被高估了多少?假定公司和其對手之間只有一筆交易,交易中沒有擔保品。
20.6 降級觸發條款會增大違約風險嗎?解釋你的答案。
20.7 給出發生:(a)錯向風險;(b)正向風險的兩個例子。
20.8 什麼是“補救期”?
20.9 “淨額結算規定意味著CVA不能按交易逐筆計算。”請解釋為什麼。
20.10 “在銀行財務遭遇困難時,DVA可以讓公司的賬面利潤看上去更漂亮一些。”請解釋為什麼。
20.11 《巴塞爾協議Ⅲ》包括了CVA風險中的哪一部分?
20.12 某交易商與其交易對手的CSA規定,雙方都必須提交擔保品而且起點金額為0。如果補救期為15天,在什麼情況下,交易商的CVA模型會產生損失?
作業題
20.13 將例20-3的計算進行擴展,假定違約可以發生在每個月的中間點上,第1年每個月發生違約的概率為0.001 667,第2年每個月發生違約的概率為0.002 5。
20.14 使用例20-3中的數據計算銀行的DVA。假設銀行可能在每個月的中點違約。兩年內違約概率為每月0.001。假設銀行違約時,交易對手能得到的回收率為40%。
20.15 考慮某歐式看漲期權,期權標的資產為某不付股息的股票,股票的價格為52美元,期權執行價格為50美元,無風險利率為5%,波動率為30%,期權期限為1年,假定回收率為0,無擔保品,無其他交易,並且違約概率與期權價格無關,計算:
(a)假定無違約風險,期權價值為多少?
(b)假定期權承約商在期權到期時有2%的違約概率,期權的價格為多少?
(c)假如期權買入方不是在交易開始時付費,而是在期權到期時付費(包括應計利息),如果期權承約人在期權到期時有2%的違約概率,那麼以上期權費的時間安排將如何降低期權購買方的違約損失?
(d)假如在(c)中期權買入方有1%的違約概率,這對期權賣出方的風險是什麼?請討論這一情形下違約的兩面性,對於交易雙方期權的價格分別為多少?
20.16 假定一家銀行發行的3年期零息債券的收益率與3年期無風險零息債券的收益率的利差為210個基點,由布萊克-斯科爾斯-默頓公式得出的期權價格為4.10美元,如果你從銀行買入期權,你願意支付的實際價格為多少?
第21章
信用在險價值
在險價值(VaR)是測算監管資本金的關鍵,也是金融和非金融企業風險管理實踐的核心內容。在本章中,我們將討論計算信用風險VaR的一些方法。
信用風險VaR的定義與市場風險VaR類似,是在某一展望期內,在一定的置信度下,信用損失不會超出的數量。有些信用風險VaR模型僅考慮由違約造成的損失;其他一些不僅考慮違約,還考慮由於降級和信用價差變化造成的損失。
銀行通過計算信用風險VaR來求得監管資本金和經濟資本金。監管資本金要求已經在第15章和第16章中討論過。經濟資本金是金融機構對自身承擔的風險的自我估計,並用來計算各業務部門的資本回報率。我們將在第26章中對經濟資本金做進一步討論。有時,銀行選擇用來計算其信用風險經濟資本金的VaR模型可能不同於用來計算監管資本金的VaR模型。
VaR是一種情景分析的方法。因此,依照我們在第7章中的解釋,對用來生成不同展望期的場景的違約概率的估計應該來自真實世界。然後再使用風險中性估計來計算組合在VaR展望期內的價值。在第19章中,我們還曾討論過真實世界中的違約概率小於風險中性世界中的違約概率。
信用風險VaR採用的展望期通常比市場風險VaR長。計算市場風險VaR的展望期通常是1天,然後在計算監管資本金時再延展到10天。而對於信用風險VaR,當持有的產品是出於非交易目的時,採用的展望期通常為1年。歷史模擬法是計算市場風險VaR的主要工具(見第13章),而信用風險VaR的計算通常需要更加複雜的模型。
任何信用風險VaR模型面臨的一個核心問題是信用相關性。不同公司的違約(或降級或信用價差變化)事件的發生並不是彼此獨立的。在經濟衰退時,大部分公司都會受到不利的影響,變得更可能違約。當經濟形勢趨好時,情況相反。這種違約率和經濟形勢之間的關係是產生信用相關性的重要原因。如果信用相關性增加(就像在市場受壓的情況下發生的那樣),投資組合有信用風險敞口的金融機構面臨的風險就會增大。
21.1 信用評級遷移矩陣
金融機構採用的計算信用風險VaR的模型中經常會用到信用評級遷移矩陣(rating transition matrices)。這些矩陣揭示了在某一段時間內,公司的信用等級從一個級別遷移到另一個級別的概率。這些概率基於歷史數據得出。信用等級可以是金融機構內部產生的,也可能是由穆迪、標準普爾或惠譽等專業評級機構發佈的。表21-1給出了由穆迪發佈的1年期信用評級遷移矩陣,該矩陣通過追蹤1970~2016年擁有穆迪評級的公司的表現得出。例如,該矩陣表明一家初始評級為A的公司,在1年後有90.90%的概率仍然擁有A評級;有2.64%的概率會升級為Aa;有5.67%的概率會降級成Baa,依此類推。這類公司1年內違約的概率為0.06%,或者說每10000家中會有6家違約。
表21-1 1970~2016年1年期信用評級遷移矩陣
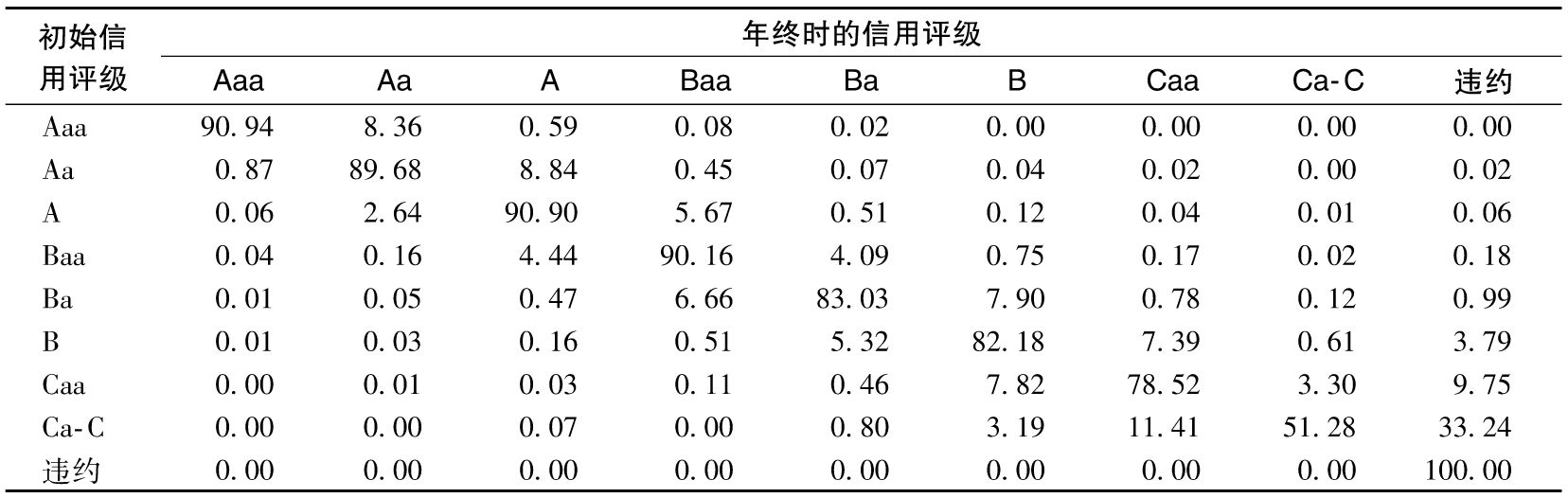
注:概率以百分數表示,並對跳轉到無評級的情況進行了調整。
資料來源:穆迪。
假設在一定時間段內信用評級的變化獨立於其他時間段,表21-1可用來計算1年期限以上的評級遷移矩陣。例如,2年期矩陣可以將兩個1年期矩陣相乘。如表21-2所示,5年期遷移矩陣是1年期遷移矩陣的5次方。由表21-2我們可以顯而易見地看出,一家公司在5年中維持同一評級的概率大大低於在1年中維持該評級的概率,5年中違約的概率也大大高於1年中違約的概率。
表21-2 由表21-1計算出的5年期信用評級遷移矩陣,概率以百分數表示
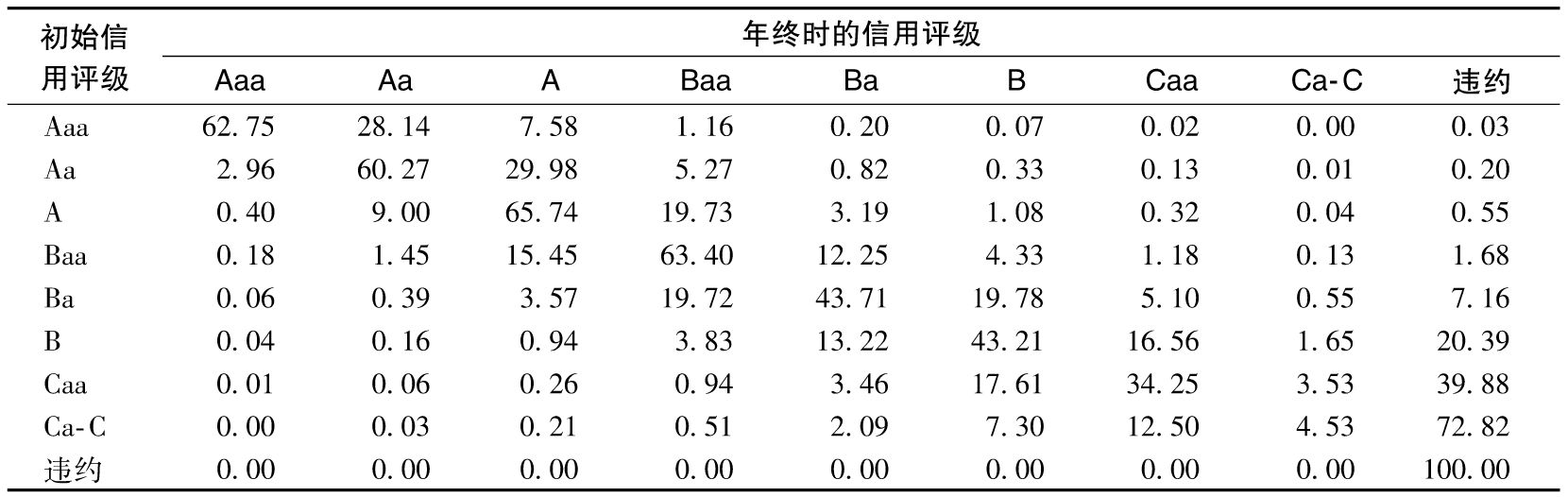
在小於1年的期限中計算信用評級的變化不太容易。例如,估計6個月期信用評級遷移矩陣要將表21-1中的矩陣開方,估計3個月期信用評級遷移矩陣需要開4次方,依此類推,附錄J介紹了計算方法,在作者的網頁上可下載計算工具。
表21-3顯示了由表21-1得出的1個月期信用評級遷移矩陣。正如我們預想的,一家公司在1個月中信用評級不變的概率非常高。
表21-3 由表21-1計算出的1個月期信用遷移矩陣,概率以百分數表示

表21-2和表21-3中的結果假設在一定時間段內信用評級的變化是獨立於其他時間段的,這並不完全符合實際情況。如果一家公司最近被降級,那麼它在接下來一段時間再次被降級的可能性很高。[1]這種現象有時被稱作評級衝量(ratings momentum)。但是對大部分的情況,獨立性假設並非很不合理。[2]
[1] 對這一點的討論,見E. Altman and D. Kao, “The Implications of Corporate Bond Rating Drift,” Financial Analysts Journal (May-June 1992):64-75, and D. Lando and T. Skodeberg, “Analyzing Rating Transitions and Rating Drift with Continuous Observations,” Journal of Banking and Finance 26(2002):423-444。
[2] 當我們將表21-2中的5年期信用遷移矩陣和穆迪發佈的實際5年期信用遷移矩陣做比較時,發現二者是非常接近的。表21-2中的違約概率比實際中的略小,這符合評級衝量現象。
21.2 Vasicek模型
《巴塞爾協議Ⅱ》中內部評級法(IRB)對銀行賬戶的信用風險資本金要求是基於Vasicek的高斯Copula模型(見第11.6節和第15.8節)。該方法用於計算貸款組合違約率分佈的高分位數。如第11章所示,我們定義WCDR(T,X)為時長為T的區間內,違約率分佈的第X個分位數。注意,WCDR代表最壞違約率。Vasicek模型將WCDR(T,X)與違約概率PD以及用來描述信用相關性的參數ρ建立了聯繫。第11.6節中給出了其公式
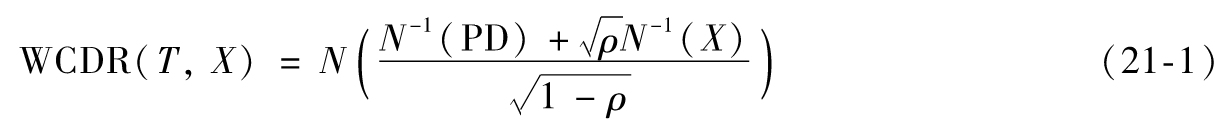
對單筆貸款,令EAD代表違約時的風險敞口,LGD為違約損失,損失分佈的第X個分位數大致為
WCDR(T, X)×EAD×LGD
Gordy的研究結果使我們能夠將上式進行擴展。[1]假定我們有一個由n筆貸款組成的貸款組合,其中每筆貸款相比整個組合來說都很小。損失分佈的第X個分位數大致為
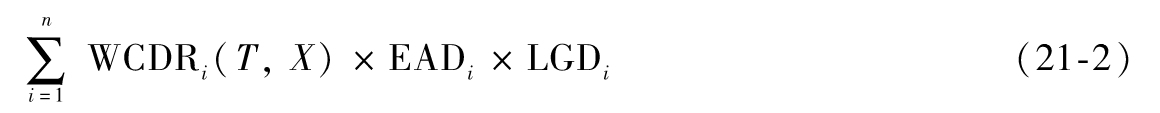
其中,WCDRi(T,X)、EADi和LGDi分別是組合中第i筆貸款的WCDR、EAD和LGD。
如第15章中討論的那樣,銀行賬戶中的監管資本金等於式(21-2)在展望期T為1年、置信水平X為99.9%時的值。有時式(21-2)中求和的各項需乘以一個期限調整因子MAi。這是考慮到以下的情況:如果貸款i的期限長於1年,其信用質量可能僅僅是逐漸下降而不是一下違約。在IRB的基礎方法中,銀行估計PD的值,EAD、LGD和MA的值由《巴塞爾協議Ⅱ》的規則設定。在IRB高級方法中,上述各值全部由銀行估計。但在兩種方法中,參數ρ均由《巴塞爾協議Ⅱ》的規則設定。
當Vasicek模型用來確定經濟資本金時,銀行可以自行估計ρ值。第19.8節中討論的結構化模型表明,兩家公司的ρ應該大致等於它們資產回報率之間的相關性。[2]作為一種近似,這和它們的股票回報率之間的相關性應該是相等的。因此,通過計算一組公司股票回報率之間的相關性,我們可以確定出對這組有公司風險敞口的投資組合的相關性(ρ)。如果這些公司不是上市公司,我們可以使用與之類似的上市公司進行估計。另外一種途徑是第11.6.2節中介紹的最大似然法。
我們在第11章中曾經指出,Vasicek模型的缺點是它對尾部相關性的考慮不夠充分。採用其他Copula模型來取代高斯Copula模型可以對這一點進行修正(其他Copula模型參見第11.6.3節)。
[1] See M.Gordy, “A Risk-Factor Model Foundation for Ratings-Based Capital Rules,” Journal of Financial Intermediation 12, no.3(July 2003):199-233.
[2] See for example, J. Hull, M. Predescu, and A. White, “The Valuation of Correlation Dependent Derivatives Using a Structural Model,” Journal of Credit Risk 6, no.3(Fall 2010):99-132.
21.3 Credit Risk Plus
1997年,瑞士信貸(Credit Suisse)金融產品小組開發了一個計算信用VaR的模型,這一模型被命名為Credit Risk Plus,[1]該模型使用了保險行業中一種被廣泛採用的解析近似法。
假定一家金融機構有n筆某類型的貸款,每筆貸款在1年時間內違約的概率為q,整個交易組合的違約數量的期望值為qn。假定違約事件之間相互獨立,根據二項分佈可得出有m筆貸款違約的概率是
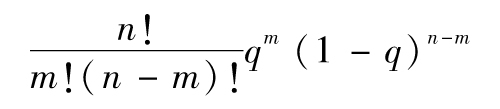
如果q的值較小而n值很大,我們可由泊松分佈(Poisson distribution)給出上式的近似
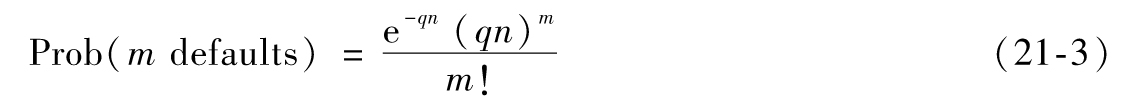
即使各貸款之間的違約概率不相等,上式仍然基本上是正確的,只要所有貸款的違約概率都很小,且q等於未來一年中貸款組合中貸款的平均違約概率。
在實際中,我們並不能確定未來一年內的違約概率q。如表11-6顯示的,不同年份的違約率可能相去甚遠。一個比較方便的假設是預期的違約數量qn服從一個gamma分佈,分佈的均值為μ,標準差為σ。
這樣,式(21-3)中的泊松分佈變成了一個負二項分佈
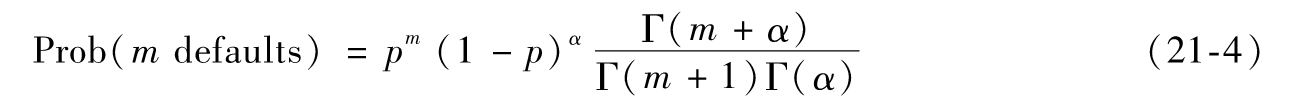
這裡α=μ2/σ2,p=σ2/(μ+σ2),Γ(x)為gamma函數。[2]
表21-4給出了當μ=4時,不同σ下各違約數的概率分佈。第1列(σ=0)通過式(21-3)得出,其他列由式(21-4)得出。從表中可以看出,當σ趨向於0時,式(21-4)中的負二項分佈得出的各違約數的概率分佈趨向泊松分佈。隨著σ增加,發生極端情況即出現大違約數的概率會增加。假設違約產生的損失是常數,如表中最後一行顯示的,當σ=0時,即違約率不存在不確定性時,99.9%的VaR損失對應11個違約。當σ=10時,即違約率的不確定性很大時,99.9%的VaR變得非常大,其對應發生98個違約時的損失。
表21-4 當預期違約數為4時,違約數的概率分佈
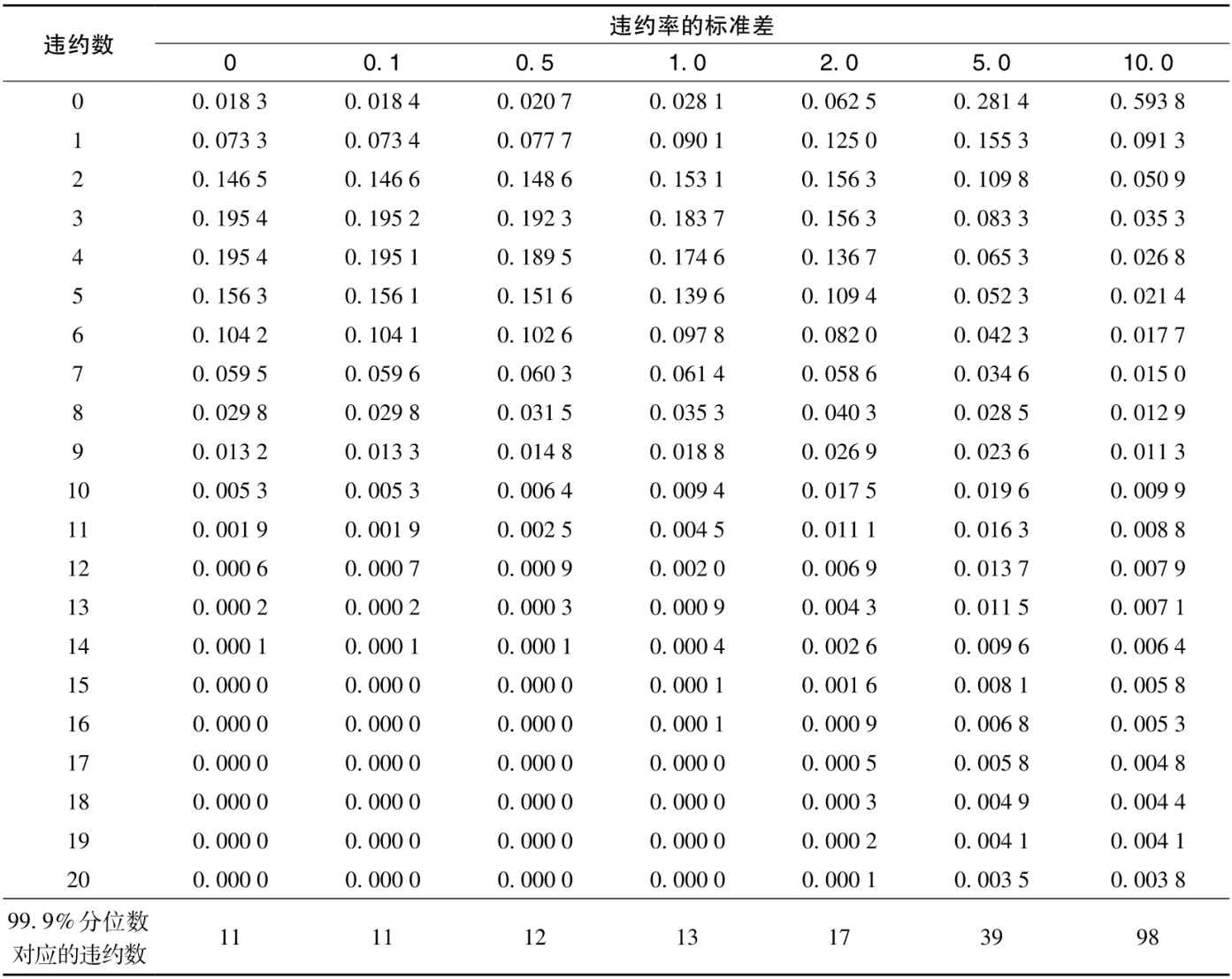
在實際中,違約損失具有不確定性,而且銀行的風險敞口也有很多類別,各類別的違約率也各不相同。我們可以更深入地運用解析方法,但是一種更靈活的方法是使用蒙特卡羅模擬。模擬過程如下:
(1)在整體違約率中進行抽樣。抽樣中使用的數據樣本可以來自類似表11-6的數據源。
(2)開發將各類別的債務人的違約率與整體違約率相關聯起來的模型。一個簡單的做法是建立整體違約率與各類別違約率的迴歸模型。
(3)對各類別的債務人的違約事件進行抽樣。
(4)對各類別的每一違約事件的違約損失進行抽樣。
(5)計算所有違約造成的整體損失。
(6)重複以上(1)~(5)的計算,求得整體損失的概率分佈。
(7)由整體損失概率分佈來計算所要求的VaR。
有多種方法可以進一步改進蒙特卡羅模擬的結果。對錶11-6中的數據的分析表明,某年中的違約概率與前一年的違約概率存在相關性,這說明由表11-6中的數據直接對違約率隨機取樣以決定下一年內的違約率可能不是最好的辦法。開發一個模型,能夠將下一年的違約率與前一年的違約率或其他宏觀經濟因素關聯起來,可能是個不錯的選擇。
需要注意的是,違約率的不確定性在分析中佔有重要地位。如果沒有這個不確定性,就不會有違約相關性,並且如表21-4所顯示的,產生大量違約事件的概率是很小的。隨著違約率不確定性的升高,違約相關性也會增加,大量違約事件出現的概率也會增加。出現違約相關性的原因在於,所有公司都具有相同的違約率,違約率或高或低。沒有違約相關性,損失的概率分佈會很對稱。當存在違約相關性時,損失會呈現正偏態,如圖21-1所示。
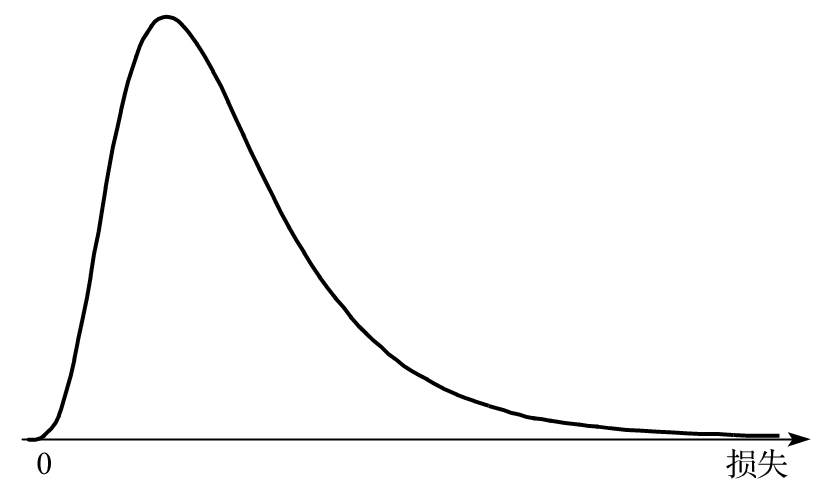
圖21-1 違約損失概率分佈的一般形態
[1] 見瑞士信貸金融產品小組的報告,“Credit Risk Management Framework”,October,1997。
[2] 在Excel中,GAMMALN函數可以返回gamma函數Γ(x)的自然對數。當x為整數時,Γ(x)=(x-1)!。
21.4 CreditMetrics
Vasicek模型和Credit Risk Plus模型僅估算由違約引起的損失的概率分佈,降級引發的影響沒有被考慮在內。[1]我們現在討論能處理降級和違約兩種情況的CreditMetrics模型。該模型最先由摩根大通在1997年提出,基於類似於表21-1中所示的某種信用遷移矩陣。評級可由內部產生(由銀行自己的歷史數據)或由評級機構發佈。
計算一個包含有很多對手方的組合1年展望期的信用VaR需要進行蒙特卡羅模擬。在每一條模擬路徑上,每個對手方在一年後的信用等級要被確定下來(我們在稍後會解釋如何做到這一點)。針對每一個交易對手的信用損失由此也可以算出來。如果在一年後某交易對手的信用評級不是違約,那麼我們就要在一年後這個時間點上對與該交易對手進行的所有交易重新定價,然後求出信用損失。如果一年後的信用等級為違約,信用損失等於違約時的敞口乘以1減去回收率。[2]
計算過程需要用到每個信用等級的信用價差期限結構。一種簡單的假設是,該期限結構與目前市場上觀察到的是一樣的。另外一種假設是存在一個信用價差指數,指數服從某概率分佈,而所有信用價差都與該指數具有某種線性關係。
當與某交易對手的交易中包含衍生產品時,我們需要對第20章中描述的CVA計算進行擴展。回憶一下,對每個交易對手,計算CVA時需要將從目前開始一直到與該對手進行的期限最長的交易結束時為止的這一時間段劃分為n個區間。我們定義qi為第i個區間內發生違約的概率;vi為區間i的中點上預期淨敞口的貼現值,其中考慮了擔保品;R為回收率。在當前看來,一年以外違約造成的預期損失為
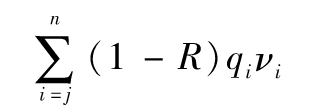
這裡假設第j個區間就是自一年後開始的區間。
在CreditMetrics的每次模擬試驗中,如果在第一年沒有違約,那麼根據式(20-3),一年時的信用價差期限結構會給出一年以後的各區間上的違約概率。假設qi*為某次模擬試驗中第i個區間(i≥j)的違約概率。此次試驗中的信用損失為

注意,如果對手的信用評級在年內得到改善(即使保持不變),這一違約損失有可能變成負值。
如果某次模擬試驗中,第一年內發生了違約,會對違約時間進行抽樣,以確定違約時的敞口。該值會被乘以1減去回收率,得出違約損失。
CreditMetrics蒙特卡羅模擬的結果會生成一個包括所有交易對手的違約以及降級造成的總損失的概率分佈。所需的信用VaR可由這個分佈得出來。
相關性模型
在確定信用損失的抽樣過程中,我們不應假設不同交易對手的信用評級變化是相互獨立的。高斯Copula模型可以用來構造信用評級變化的聯合概率分佈(見第11.5節有關Copula模型的討論),兩家公司信用遷移的Copula的相關性一般被設定為等於股票回報的相關性(第1章中介紹的資本資產定價模型提供了一個股票回報的單因子模型。類似第11.4.2節所討論的,此模型可以用來生成具有內部一致性的相關性矩陣)。
假設我們需要對一個A級債券及一個B級債券的信用變化進行模擬。模擬中採用的信用遷移矩陣如表21-1所示。假如兩家公司股票回報的相關性為0.2,在每一個抽樣過程中,我們對兩個服從標準正態分佈的變量xA及xB進行抽樣,並保證xA及xB的相關性為0.2。變量xA決定A級公司的新的信用等級,變量xB決定B級公司的新的信用等級。由表21-1,一家評級為A的公司變為Aaa,Aa,A,…的概率分別是0.000 6,0.026 4,0.909 0,…,因為
N-1(0.000 6)=-3.238 9
N-1(0.000 6+0.026 4)=-1.926 8
N-1(0.000 6+0.026 4+0.909 0)=1.522 0
當xA<-3.238 9時,A級公司信用級別上升為Aaa級;當-3.238 9<xA<-1.926 8時,A級公司信用級別變為Aa;當-1.926 8<xA<1.522 0時,A級公司級別保持不變;依此類推。類似地,表21-1同樣顯示了一家評級為B的公司變為Aaa,Aa,A,…的概率分別是0.000 1,0.000 3,0.001 6,…,因為
N-1(0.000 1)=-3.719 0
N-1(0.000 1+0.000 3)=-3.352 8
N-1(0.000 1+0.000 3+0.001 6)=-2.878 2
當xB<-3.719 0時,B級公司信用級別上升為Aaa;當-3.719 0<xB<-3.352 8時,B級公司信用級別變為Aa;當-3.352 8<xB<-2.878 2時,B級公司信用級別變為A;等等。A級公司在xA>N-1(0.999 4)時違約,對應於xA>3.238 9;B級公司在xB>N-1(0.962 1)時違約,對應於xB>1.775 6。圖21-2是此例的圖形顯示。

圖21-2 CreditMetrics相關性模型
注:一家A級公司和一家B級公司在一年後信用轉移的可能,圖中xA和xB分別服從標準正態分佈,其相關性等於A級公司及B級公司股票回報的相關性。
有一點值得說明的是,如果CreditMetrics和Credit Risk Plus都使用同樣的一組假設,那麼在理論上它們應產生相同的長期違約損失分佈,主要的區別在於損失發生的時間。例如,假設某組合中包含一筆貸款。在第1年,借貸方的評級從A降到了BBB;在第2年,又從BBB降到了B。我們可以假設在第1年和第2年沒有損失,而在第3年計算損失(Credit Risk Plus的方法)。另外一個方法是,我們可以通過重新定價,分別計算第1年、第2年、第3年的損失(CreditMetrics方法)。第二種方法計算出的各年損失相加後應等於第一種方法計算的損失。
[1] 但是在用於監管資本金的Vasicek模型實現中,期限調整因子可以用來考慮降級。
[2] 回收率通常會從一個經驗數據集中抽樣。
21.5 信用價差風險
交易賬戶上大部分對信用敏感的產品都嚴重依賴信用價差。因此,計算信用風險VaR或ES時需要考慮信用價差的可能變化。一種可能的手段是,類似於市場風險VaR,用歷史模擬法計算出展望期為1天、置信度為99%的信用風險VaR。由1天的VaR,放大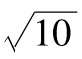 倍,可得10天展望期的VaR。為此,需要統計所有相關企業過去500天內(或其他區間)信用價差的變化。第一個歷史模擬場景假設所有公司的信用價差的百分比變化等於第1天的變化,第二個歷史模擬場景假設信用價差的百分比變化等於第2天的變化;依此類推。但是,這個方法有一個顯而易見的問題,如果某家公司在當前還存在,那它過去就沒有違約過,因此該方法實際上假設以後沒有違約的可能性。[1]另一個問題是,並不是所有企業的信用價差都是每天更新的,因此數據的質量可能不高。
倍,可得10天展望期的VaR。為此,需要統計所有相關企業過去500天內(或其他區間)信用價差的變化。第一個歷史模擬場景假設所有公司的信用價差的百分比變化等於第1天的變化,第二個歷史模擬場景假設信用價差的百分比變化等於第2天的變化;依此類推。但是,這個方法有一個顯而易見的問題,如果某家公司在當前還存在,那它過去就沒有違約過,因此該方法實際上假設以後沒有違約的可能性。[1]另一個問題是,並不是所有企業的信用價差都是每天更新的,因此數據的質量可能不高。
另一種辦法是採用CreditMetrics中用到的一種方法。第21.1節給出了計算10天期限的信用評級遷移矩陣的方法。該矩陣給出了一家公司的信用等級在10天內發生各種變化或者違約的概率。信用評級變化的歷史數據定義了與各個信用等級有關的10天后信用價差變化的概率分佈,然後採用蒙特卡羅模擬。在每次模擬中,從遷移矩陣中產生一個抽樣,以決定該公司是維持原評級、遷移到一個新的評級還是發生違約。對信用價差變化的概率分佈同樣進行抽樣,以決定每個信用等級10天后的信用價差,由此我們可得到10天后整個組合的價值並由此進一步得到VaR。
信用相關性可以通過兩種途徑引入。第一種:採用第21.4.1節中介紹的方法,使用高斯Copula模型,將各企業信用評級的變化關聯起來。第二種:各信用等級信用價差的變化可假設為完全(或近似完全)相關,因此當一個評級為A的產品的信用價差上升時,其他信用等級的產品的利差也會上升。
【例21-1】 為說明上述方法,讓我們考慮下面一個簡單例子。假設某公司有一個2年零息債券,面值為1 000美元。無風險利率為3%,當前信用價差為200個基點,因此,債券的收益率為5%(均為年複利)。當前的債券價格為1 000/1.052=907.03美元。假設債券現在的評級為Ba,近似於表21-3中的數據,在下個月,債券評級上升到Baa的可能性為0.6%,有98.5%的可能性評級保持不變,有0.8%的可能性評級會下降到B,還有0.1%的可能性會違約。如果違約,債券的價格將變為400美元。對每一個可能的信用等級,有三個可能性均等的信用價差,按基點計算,這些利差分別為:對Baa級別的80、100和120;對Ba級別的160、200和240;對B級別的400、450和500。
很明顯,最壞的情況是違約。違約發生的可能性為0.1%,將導致的損失為907.03-400=507.3美元。第二壞的情況是評級被降為B,同時利差變為500基點。這種情況發生的可能性為0.8/3=0.267%。因為債券還有1.917年到期,其價格將變為1 000/1.081.917=862.85,損失為907.03-862.85=44.17美元。表21-5顯示了所有可能發生的情況的概率及其帶來的損益。
表21-5 例21-1中的結算結果
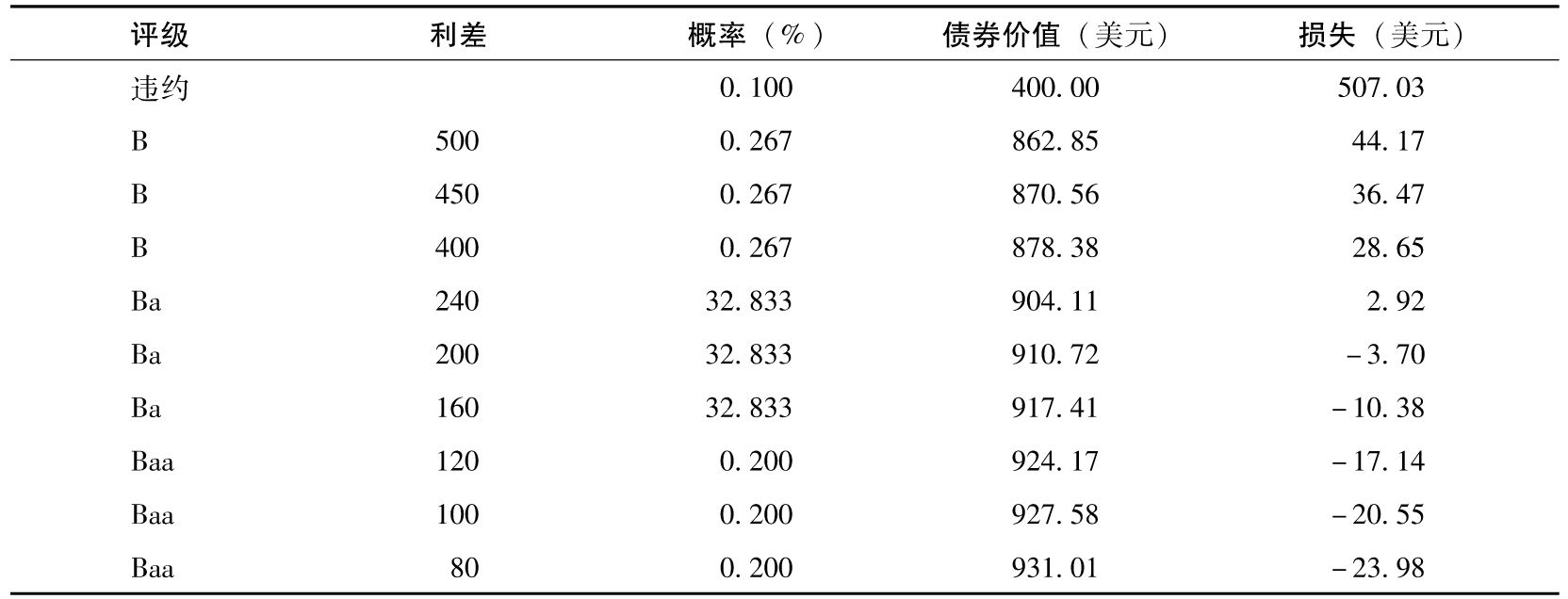
該表表明,如果置信度高於99.9%,得出的VaR為507.03美元;如果置信區間在99.9%和99.633%之間,VaR為44.17美元;依此類推。當置信度為99%時,VaR為2.92美元。
風險水平恆定假設
在計算VaR或ES時,銀行有時會做出一個恆定的風險水平假設,它們假設一個投資組合會週期性地重新平衡,將風險恢復到最初的水平。
例如,假設一家公司投資於Baa級債券,並正在考慮兩種替換交易策略:
(1)持有債券1年,然後賣出債券(“買入並持有”策略)。
(2)在每個月月底進行再平衡,以便如果債券不再是Baa級,它們將被賣出,並被Baa級債券取代(“恆定風險水平”策略)。
表21-1中Baa列的數值是第一種策略的結果,而在第二種策略的情況下,表21-3中Baa列的結果重複12次。
考慮第一次違約的情況,根據表21-1,買入並持有策略下的違約概率為0.001 8。根據表21-3,每月違約概率為0.000 121 5。[2]因此,當使用恆定風險水平策略時,一次違約的概率是
12×0.000 121 5×0.999 878 511=0.001 456
這比買入並持有策略下的違約概率低19%。兩次或兩次以上違約的概率暫不考慮。
接下來考慮債券評級下降至C的概率。根據表21-1,在買入並持有策略下這一概率為0.001 7。而在恆定風險水平策略下,一次降級為C的概率為
12×0.000 127 7×0.999 872 311=0.001 530
這比買入並持有策略下的概率減少了10%。不止一次降級為C的概率暫不考慮。
最後,考慮降級為Ba的概率。根據表21-2,在買入並持有策略下,這一概率為0.040 9。在恆定風險水平策略下,一次降級為Ba的概率為
12×0.003 873 5×0.996 126 511=0.045 505
這比買入並持有策略下降級為Ba的概率增加了10%。恆定風險水平策略下多次降級的概率約為0.001。
計算結果表明,買入並持有策略比恆定風險水平策略將導致更大的違約損失和債券更大幅度的降級,但小幅度評級變動帶來損失的可能性更小。因此,當使用恆定風險水平策略時,VaR和ES通常較小。
[1] 解決這一問題的方法之一是假設當信用價差超過某一水平時,即發生違約。另一種方法是將跳躍式違約(jump-to-default)的風險分開另外處理。
[2] 注意,這些結果是基於比表21-3中小數點後更多的數字得出的,可在作者的網站上看到結果。
小結
信用風險VaR的定義方式與市場風險VaR類似,是在一定時間展望期內和置信度下,信用損失不會被超出的數量。
巴塞爾監管規定要求計算展望期為1年、置信度為99.9%的信用風險VaR。對出於經濟資本目的的計算,可能使用不同的置信度。我們介紹了三種計算銀行賬戶VaR的方法:Vasicek模型、Credit Risk Plus和CreditMetrics。Vasicek模型基於組合中涉及的企業的違約時間的單因子高斯Copula模型,該方法被用來計算監管資本金。Credit Risk Plus採用類似保險業中常用的步驟,通過設定單家公司的違約分佈來計算違約損失。CreditMetrics與以上二者不同,其將違約和降級兩種情況都考慮在內。該方法將高斯Copula模型和信用遷移矩陣結合起來使用。
為確定交易賬戶的信用風險VaR,一種方法是收集公司信用價差變化的歷史數據,並使用與計算市場風險VaR類似的歷史模擬法。另一種方法是建立針對公司的信用等級遷移和各信用等級的平均信用價差的模型。
延伸閱讀

練習題
21.1 解釋Vasicek模型、Credit Risk Plus和CreditMetrics在以下幾個方面的不同:(a)信用損失的認定;
(b)違約相關性的處理。
21.2 請解釋風險水平恆定假設的含義。
21.3 使用表21-1中的信用評級遷移矩陣,計算2年期的信用評級遷移矩陣。一家評級為Aaa的公司在兩年內保持Aaa評級的概率是多少?被降級為Aa的概率是多少?
21.4 使用表21-1中的信用評級遷移矩陣和作者網頁上的計算工具,計算6個月期的信用評級轉移矩陣。一家評級為Aaa的公司在6個月內保持Aaa評級的概率是多少?被降級為Aa的概率是多少?
21.5 如何使用歷史模擬法來計算交易賬戶上債券的信用風險VaR?其中展望期為1天,置信度為99%。該方法的缺點是什麼?
21.6 某銀行持有100筆期限為1年的貸款,每筆貸款的違約概率是1%。至少有6筆貸款違約的概率是多少?(假設每筆貸款的違約事件是獨立的。)
21.7 假設每筆貸款的違約率可能是0.5%或1.5%,這兩種情況的可能性相等。重複練習題21.6中的計算。
21.8 解釋表11-6(數據也可在作者網站上的計算表中找到)中違約率的自相關性,其對Credit Risk Plus模型有何影響?
作業題
21.9 請詳細解釋真實世界概率與風險中性世界概率的不同。這兩個概率中的哪個會更高一些?某銀行進入了一個信用衍生產品合約,合約規定如果某公司的信用從A級降為Baa級或更低時,銀行將支付100美元。1年的無風險利率為5%,採用表21-1來估計衍生產品的價格,在計算中你需要什麼樣的假設?你對衍生產品的價格可能是高估了還是低估了?
21.10 假設某銀行有某類總值為1 000萬美元的風險敞口,但單筆敞口都很小。1年的違約概率為1%,回收率為40%,Copula相關係數為0.2。使用Vasicek模型計算展望期為1年、置信度為99.5%的VaR。
21.11 使用表21-1中的信用評級遷移矩陣和作者網站上的工具計算為期1.25年的信用評級遷移矩陣。

第22章
情景分析和壓力測試
壓力測試(stress testing)的目的是評估極端情況的影響,這些情況有發生的可能性,但又沒有被在險價值(VaR)或預期虧空(ES)模型所考慮。如果我們要從2007年夏天開始的金融危機吸取一個教訓的話,那就是我們應該更加重視壓力測試,而不應只是機械地應用VaR/ES模型。VaR/ES模型很有用,但這種模型不可避免地受到歷史回望的侷限,而風險管理應當更關心今後將會發生什麼。
本章將討論產生壓力測試情景的不同方法,以及如何應用得到的結果。我們將說明為什麼2007~2008年的金融危機會促使銀行監管機構要求銀行進行更多的壓力測試,而且監管機構本身也越來越多地親自操刀定義壓力場景以保證銀行持有足夠的資本金應對市場突變。
22.1 產生分析情景
計算VaR/ES最為流行的方法是在第13章中所討論的歷史模擬法。在這一方法中,我們假定過去幾年的歷史數據為我們提供了在今後1~10天內市場變化的指導。如果某種事件在歷史數據所覆蓋的時間內沒有發生,那麼在基本計算方法中,這一事件不會對計算出的VaR有任何影響。
我們已經討論過幾種改進的計算VaR/ES的方法,這些方法不再簡單地假設市場變量在未來短期內的變化僅僅是以往情景的隨機抽樣,特別地:
(1)當市場變動很大時,對波動率進行更新(第13.3節)可以產生更多的極端結果。
(2)極值理論(第13.5節)可以對從歷史數據中獲取的損失分佈的尾部進行外延。
(3)壓力VaR或壓力ES(見第13.1節)選取投資組合表現非常差的250天曆史數據,以計算這一特定時間段產生的影響。
但是,VaR/ES計算方法的本質是回望型的,那些將來可能會發生但又不能在歷史數據中體現的情形是不能在VaR/ES中體現出來的。壓力測試就是為了克服VaR/ES測度中的這一弱點。
壓力測試包含估測金融機構的投資組合在極端市場條件下的表現。有時,極端市場變化以標準差來度量,如我們在表10-1中討論過的匯率的例子。如果日變化量是正態分佈的,那麼5個標準差所對應的事件將會每7000年才發生一次。但在實際中,平均每5年左右就會發生一次5個標準差的市場變動(這一事實說明在風險管理過程中,市場變化服從正態分佈並不是一個好的假設)。
壓力測試的關鍵是如何選擇情景,我們接下來考慮不同的選擇方法。
22.1.1 對單一變量進行壓力測試
一種方法是使用假設某一變量有很大變化而其他變量保持不變的情景。對於這類情形,有時會考慮下面的例子:
(1)收益率曲線平行移動(上或下)100個基點;
(2)假定某資產的隱含波動率會由當前水平上下波動50%;
(3)股指上下變動10%;
(4)一個主要貨幣的匯率上下變動6%;
(5)一個非主要貨幣的匯率上下變動20%。
如在第8章中所討論的那樣,市場變量的一個微小變化所產生的影響可由delta來描述。市場變量的一個較大變化所產生的影響可由delta及gamma組合來描述。在以上所描述的情景中,市場變化量太大,用希臘值來估計產品組合價值的變化很可能不再可靠。
22.1.2 涉及多個變量的情景
通常當一個市場變量有劇烈變化時,其他變量也會變化。為應對這種情況,金融機構鬚生成涉及多個變量同時變化的情景。一種流行的做法是採用市場變量在歷史上曾出現過的極端變化情景。例如,為了檢驗美國股票價格的劇烈變化,某公司可以假設所有市場變量的百分比變化等於1987年10月19日的變化(在這一天,標準普爾500指數變化幅度達22.3個標準差)。如果認為這一變化太過極端,可以採用1988年1月18日的市場變化(這一天市場變化幅度為6.8個標準差)。其他可以選擇的股市劇烈變化的日子為2001年9月11日(這一天恐怖分子襲擊了紐約的世貿中心)和2008年9月15日(這一天雷曼兄弟宣告破產)。為了檢驗英國利率劇烈變動的效應,金融機構可以假定所有市場變量的百分比變化等於1992年4月10日的變化(這一天10年期債券收益率的變化為8.7個標準差)。
另外一種方法是把過去發生的變化量放大。例如,我們可以選取一個市場趨向不利但變化比較溫和的時期,然後將這一時期的實際變化幅度放大3~5倍。這樣做的一個問題是,在市場受壓的情況下,相關度會增加,但將所有市場變量同時放大一定的倍數,不會增大相關性。
有些歷史情景對應於一天市場變化的幅度,而其他一些情景,尤其是涉及信用及流動性的變量,其變化對應於若干天、若干星期甚至若干個月。在情景中考慮市場變量的波動率十分重要。一般來講,當利率及匯率有劇烈變動時,其隱含波動率以及其他很多變量的波動率也會大幅增加。有些情景可能會涉及大宗商品價格的劇烈變化,例如2014年下半年,石油價格大幅下跌。還有另外一些情況導致安全投資轉移以及與之相伴的流動性短缺和信用價差擴大。1998年8月俄羅斯國債違約以及2007年8月投資者對由次貸生成的證券化產品喪失信心時都出現了這類情況(見第6章)。
22.1.3 由管理人員所產生的情景
歷史絕對不會一成不變地重複,其中的部分原因是交易員對過去的危機有一定了解,並引以為鑑以避免重蹈覆轍。美國按揭貸款市場導致了2007年開始的金融危機。將來的信用危機不太可能仍是由於按揭信用審批制度的鬆懈而導致,但無論如何,今後仍有可能會出現信用危機。
從多方面來看,壓力測試中最有用處的情景是由金融機構的高管或經濟研究團隊所提出的。公司高管和經濟研究團隊可以綜合他們對市場、世界政治、經濟環境以及當前全球市場的不確定性來產生合理的、會造成巨大損失的情景。有時管理人員產生的某些情景是基於歷史事件,但往往根據當前金融及經濟狀況對這些事件進行了調節。
一種產生壓力測試情景的方法是由高管組成一個委員會,定期召開會議,並通過頭腦風暴(brainstorm)的形式來回答以下一個簡單問題:“市場會出現什麼預想不到的情景?”Clemens和Winkler(1999)對這種委員會的最佳構成進行了研究,[1]他們的結論是:①委員會應由3~5個成員組成;②委員會成員的背景應各不相同;③委員會成員之間應有一個健康的交流渠道。為了能對整個宏觀狀況有全面的把握,委員會成員必須能跳出他們日常工作的窠臼,這一點非常重要。
在產生有價值的情景方面,高管的想法有時並不一定要十分有創意。在2005年及2006年,許多金融評論員認識到美國住房市場正在經歷一場泡沫,而這些泡沫遲早會破。當然我們現在很容易做事後諸葛亮,但在當時壓力測試委員會要是能提出一個全國範圍內房價會下跌20%~30%的情景,也是很合理的要求。
公司高管及董事會都要理解壓力測試的重要性,做到這一點十分重要。公司高管與董事會成員要以壓力測試為依據來做出戰略決策。由公司高管來提出分析情景的一大好處是,這能使高管更容易接受壓力測試的重要性。而由公司中層管理人員所產生的情景往往不會得到嚴肅的對待。
22.1.4 核心變量和周邊變量
當對單個市場變量產生受壓情景或情景是由管理層產生時,這些場景可能只涉及幾個核心變量(core variable)的變動,因而不夠完善。一種進行壓力測試的方法是將沒有被檢驗的周邊變量(peripheral variable)的變化設為0,但這種方法往往不令人滿意。另外一種方法是首先假定核心變量產生了劇烈變動,並建立周邊變量對核心變量的迴歸(regression),這種迴歸可以預測周邊變量的變化程度與核心變量變化程度的關係,最後將這些預測(以預測點或概率分佈的形式)用於壓力測試之中。
這種壓力測試方式被稱為條件壓力測試(conditional stress testing),最初由Kupiec(1999)提出。[2]Kim和Finger(2000)進一步將這一想法推廣到所謂的“斷箭”(broken arrow)壓力測試方法中。在該方法中,他們假設核心變量與周邊變量之間的相關性是以受壓市場為基準的,而不是以過去的平均值為基準。[3]
22.1.5 完善壓力測試情景
管理人員應該仔細檢查壓力測試情景,以盡力確保所有的不利情景均已被考慮在內。這些情景不但要包括市場劇烈變化對金融機構自身投資組合的即時效應(immediate effect),同時還要考慮來自其他眾多金融機構的連帶效應(knock-on effect),因為這些金融機構往往受到相同的衝擊,並做出相同的反應。許多人聲稱,他們認識到美國住房市場的泡沫會在2007年破裂,但是他們並沒有認識到泡沫破裂的嚴重後果,也沒有充分認識到許多金融機構會同時蒙受損失,從而造成市場的安全投資轉移現象以及隨之而來的流動性問題和信用價差的巨幅增大。
另外一個關於連帶效應的例子是1998年長期資本管理公司(LTCM)的失敗(見業界事例22-1)。LTCM的業務模式是持有流動性差的證券,同時賣空流動性好的證券。LTCM的破產是由於俄羅斯國債違約而引發的安全投資轉移現象。許多投資者只想買入流動性好的證券。流動性好的與流動性差的證券間的利差顯著增加。LTCM認為自身已經進行了壓力測試檢驗,並對1998年之前所發生的安全投資轉移現象的衝擊有了一定認識。但不幸的是,其中恰恰沒有考慮連帶效應。1998年,許多對衝基金交易策略都在追隨LTCM的交易策略。所以當安全投資轉移現象出現後,它們也幾乎在同時試圖將各自的交易平倉。平倉即意味著要變賣流動性差的證券,同時買入流動性好的證券,這進一步加重了投資安全轉移的幅度,使其比以前發生過的同類現象更為嚴重。
業界事例22-1
LTCM的巨大損失
20世紀90年代中期成立的對衝基金公司LTCM在其交易中一直採用證券抵押融資的方法。該對衝基金的投資策略被稱為收斂套利(convergence arbitrage)。這一策略的簡單例子如下:假如X及Y是同一家公司發行的兩個債券,X及Y具有相同的回報,但X的流動性比Y要差(X的交易沒有Y活躍),市場對於差的流動性要求一定的補償,因此X的價格比Y要低一些。LTCM在交易中首先對X持多頭,並對Y持空頭,之後LTCM等待在將來某個時刻兩個債券的價格趨向一致,這樣LTCM可能達到套利的目的。
當利率增長時,LTCM預計X及Y債券價格下降的數量基本相同,因此對於X債券付出的擔保品與Y債券收回的擔保品基本相等;類似地,當利率下降時,LTCM預計X及Y債券價格上漲的數量也會基本相同,因此由X收回的擔保品和對Y支出的擔保品應大致相等,所以因擔保合約造成的資金外流不應該很大。
1998年8月,俄羅斯國債違約,因此造成了資本市場的安全投資轉移現象。這一現象導致投資者對流動性好的產品的定價遠高於平時,從而使得LTCM投資組合中流動性好的產品與流動性差的產品的差價急劇增大。LTCM買入的債券價格大幅下降,而LTCM賣空的債券價格急劇增長。這時LTCM無論是對多頭還是空頭交易都必須注入更多擔保品。公司的財務又處於高槓桿狀態(高負債比率)。LTCM因不能滿足交易合約中擔保品的要求,必須對交易進行平倉,從而造成了40億美元的損失。假如其財務並不處於高槓桿狀態,LTCM也許能夠承受安全投資轉移現象所帶來的壓力,從而有機會等到流動性好的產品價格及流動性差的產品價格趨向一致。
壓力測試情景最好能動態變化,以考慮進行壓力測試的金融機構以及其他金融機構對劇烈變化的反應。例如,考慮一家賣出期權的金融機構,這裡的期權依賴某標的產品,金融機構在交易中保持delta中性。標的資產價格的大幅上升(或下降)會馬上觸發期權交易的損失(見第8.1節)。為了保持delta中性,金融機構需要買入(或賣出)大量的標的資產。因此,delta對衝費用與資產價格的波動率有關。通常,在資產價格回穩之前,由於波動率較高,進行delta對衝的成本也會很高。
22.1.6 逆向壓力測試
逆向壓力測試(reverse stress testing)是指通過一定的計算步驟,尋找會導致金融機構蒙受重大損失的情景。逆向壓力測試已經成為風險管理中的一個重要工具,很多銀行監管機構要求銀行建立逆向壓力測試機制。
【例22-1】 作為逆向壓力測試的一個例子,我們考慮以下情景,假定某金融機構持有4份某資產的歐式看漲期權,資產價格為50美元,無風險利率為3%,波動率為20%,資產本身不提供任何收入。下表給出了交易頭寸、執行價格、期限等信息。當前頭寸的價值為-25.90美元(以千美元計)。很多程序可以用來搜索可造成最大損失的日內資產價格以及波動率變化。在分析中我們需考慮變化的邊界值。在此,我們假設資產價格將介於40美元與60美元之間時,波動率將介於10%與30%之間。

採用歐式期權的計算公式(見附錄E)以及Excel的Solver程序,我們可以確定最差情景,即波動率降至10%,資產價格降至45.99美元時,最大損失為2.893 8億美元。於是通過逆向壓力測試,我們得出該金融機構的最大損失發生在資產價格下跌8%而且波動率急劇下降的情景。
這個情景看起來不太合理。當資產價格下跌8%時,波動率不太可能會急劇下降。我們在使用Solver時可以將波動率的下限設定為20%而不是10%,這樣我們就可以求得一個新的最差情景,即波動率為20%,資產價格下跌至42.86美元時,相應的最大損失為8719萬美元。
在實際應用中,如例22-1一般對金融機構有風險敞口的每一個市場變量進行搜索因計算量過大而不切實際。一種做法是,識別出5~10個關鍵的市場變量,並假定其他變量的變化依賴於這些變量的變化。
另一個簡化搜索過程的辦法是將搜索問題結構化。主成分分析法(見第9.7節)可以應用於市場變量(比較理想的情況是數據應來自受壓市場條件),然後進行搜索以確定會造成重大損失的主成分變化量。這一方法會降低搜索空間的維數,而且會減少不合理的情景的產生。
另一個方法是風險管理人員可以將情景結構化。例如,管理層可能對過去發生的某個情景感興趣,在這一情景中,利率升高、股價下跌,某些匯率下滑。根據這樣的要求,風險分析師可以找出應該對歷史上觀測到的變量的變化幅度做多少倍的放大,才能使損失達到某種程度。例如,我們可能發現,如果2008年的信用危機重現,一家金融機構可以生存下來,但是如果市場的變化量再增大50%,可能就會出現大麻煩。
逆向壓力測試可以作為一個工具,輔助壓力測試委員進行頭腦風暴。在壓力測試委員會召開會議之前,分析人員可以通過逆向壓力測試來求得幾種會給金融機構帶來災難的情景,這些情景和委員會成員產生的情景將在會議上討論,委員會成員可以憑藉自己的判斷來排除那些分析員給出的不合理情景,並對其他一些情景進行修改來使其合理,然後對這些情景進行更深入的研究。
[1] See R. Clemens and R. Winkler, “Combining Probability Distributions from Experts in Risk Analysis,” Risk Analysis 19, no.2(April 1999):187-203.
[2] P. Kupiec, “Stress Testing in a Value at Risk Framework,” Journal of Derivatives 6(1999):7-24.
[3] See J. Kim and C. C. Finger, “A Stress Test to Incorporate Correlation Breakdown,” Journal of Risk 2, no.3(Spring 2000):5-19.
22.2 監管條例
巴塞爾委員會要求當銀行採用內部VaR模型計算市場風險資本金時,要同時伴有“嚴格以及全面”的壓力測試。與此類似,銀行採用《巴塞爾協議Ⅱ》中的內部評級法(高級法和基礎法)來計算信用風險資本金時,也必須同時通過壓力測試來檢驗模型假設的合理性。
2009年5月,巴塞爾委員會發表了關於壓力測試在實踐中的應用以及監管機構如何對其進行監督的最終建議。[1]建議強調了壓力測試在確定銀行為吸收市場巨大變動所需的資本金變量方面發揮的重要作用,並且特別指出,當溫和的市場條件持續相當長的一段時間之後,壓力測試尤其重要,因為在這種情況下,市場參與者容易產生麻痺自滿情緒。
建議強調公司最高管理層以及董事會在壓力測試中應扮演重要角色,特別是最高管理層及董事會應該積極參與壓力測試管理,並積極參與制定壓力測試的目標、定義壓力測試情景、討論壓力測試結果以及對潛在應對措施進行評估,從而做出決策。建議還指出,那些在2007年金融危機中表現好的銀行的高級管理層都積極參與了壓力測試的開發以及實施,並以壓力測試結果為基礎制定銀行的戰略發展策略。壓力測試必須涵蓋銀行的所有業務領域,而不是每個領域單獨進行自己的壓力測試。
巴塞爾委員會的建議還指出,2007年以前壓力測試的情景大多是基於歷史數據,變化的幅度比市場上真正的變化幅度要低很多。具體的建議包括以下幾個。[2]
(1)壓力測試應成為一家銀行整體治理和風險管理文化的組成部分。壓力測試應具備可操作性,壓力測試的相關分析結果應當被用於管理決策,包括董事會和高管層做出的戰略性業務決策。董事會和高管層的參與對壓力測試的有效實施至關重要。
(2)銀行應通過開展壓力測試,促進風險識別和控制,彌補其他風險管理工具的不足,改善資本和流動性管理,加強內部與外部的溝通與交流。
(3)壓力測試應綜合考慮銀行內部各方的意見並從一系列不同的視角和技術出發加以考慮。
(4)銀行應制定書面的壓力測試政策和流程。對項目的實施應進行適當的文檔記錄。
(5)銀行應有一個穩健、強有力的基礎設施,該設施應具備足夠的靈活性以便適當開展不同精細度的、不斷變化的壓力測試。
(6)銀行應定期維護和更新其壓力測試框架,並定期由獨立部門評估壓力測試項目主要構成部分的有效性和主要環節的穩健性。
(7)壓力測試應覆蓋全銀行範圍內各類風險和各個業務領域。銀行應能有效地整合各類壓力測試活動,以提供一個全銀行全面風險情況的描述。
(8)壓力測試應該涵蓋包括前瞻性壓力情景在內的一系列情景,並充分考慮和體現整個系統的相互作用與反饋效應。
(9)壓力測試應能產生不同嚴重程度的場景,包括那些能導致嚴重後果的事件,無論這些後果是因為損失的規模還是因為銀行的聲譽受到傷害而導致。壓力測試方案也應確定哪些情景會影響銀行的生存能力(逆向壓力測試),從而可以發現潛在風險以及風險之間的相互作用。
(10)銀行在整體壓力測試方案中,應考慮同時來自資金和資產市場的雙重壓力以及市場流動性下降對風險敞口估值造成的影響。
(11)風險緩釋技術的有效性應接受系統性的檢驗。
(12)壓力測試方案應明確包括複雜和定製產品(bespoke product),例如,證券化產品敞口。針對證券化資產開展的壓力測試應考慮標的資產、受系統因素影響的風險敞口、相關合同安排、內嵌的觸發條款以及槓桿的影響,特別是與發行結構中的優先次序有關聯時,這些尤為重要。
(13)壓力測試方案應包括進行中(pipeline)風險和庫存(warehousing)風險。[3]銀行應在壓力測試中包括這類風險,而不考慮其被證券化的可能性。
(14)銀行應改進壓力測試的方法以反映聲譽風險的影響。銀行應將表外業務(off-balance-sheet)和其他相關實體的風險整合到其壓力測試方案中。
(15)銀行應改進其針對高槓杆交易對手的壓力測試方法,考慮這些高槓杆交易對手對特定資產類別或市場變動的脆弱性,並評估與風險緩解有關的潛在的錯向風險。
對銀行監管當局的建議如下所示。
(1)監管當局應該定期綜合評估銀行的壓力測試方案。
(2)當發現壓力測試方案存在嚴重不足或者決策程序中沒有充分考慮到壓力測試結果時,監管當局應要求銀行管理層採取整改措施。
(3)針對那些能對銀行整體風險產生影響的情景,監管當局應當評估其影響範圍和危害程度,而且在必要時對銀行進行質詢。監管當局可以要求銀行在特定場景下使用特定投資組合或參數進行敏感度分析,或對銀行的生存產生威脅的情景(逆向壓力測試情景)進行評估。
(4)在《巴塞爾協議Ⅱ》框架的第二支柱(監管審查過程)下,監管當局應當把檢查銀行壓力測試的結果作為銀行內部資本充足性評估和流動性管理審查工作的一部分。監管當局在評估資本和流動性充足與否時,應考慮前瞻性壓力測試的結果。
(5)監管當局應考慮實施基於通用情景的壓力測試。
(6)監管當局應與其他公共部門及銀行業開展建設性對話,識別出系統的薄弱環節。監管當局還應具備評估銀行壓力測試方案的能力和技巧。
監管當局選擇的場景
銀行監管機構要求銀行要考慮極端情景,並且確保在不同情景下都有足夠多的資本金。很明顯,銀行希望監管資本金越低越好,所以銀行管理人員不會有強烈的意願主動考慮那些會引發監管資本金大幅上升的極端情景。正是由於這個原因,銀行會很自然地傾向於在分析過程中使用那些被淡化過的、相對溫和的情景。
一種克服這一弊端的方法是由銀行監管機構親自提供壓力情景(巴塞爾委員會給出的第18條和第20條建議)。很多國家和地區的監管部門(包括英國、歐盟和美國)現在已經常規性地進行這類壓力測試,以確保自己監管範圍內的銀行持有充足的資本金以應對極端不利事件。如果銀行不能通過這類壓力測試,就會被要求提升資本金水平並且可能在股利分派方面會有所限制。
美聯儲從2009年開始,對總資產超過500億美元的銀行(即全球系統性重要銀行(G-SIB)和區域系統性重要銀行(D-SIB))進行年度壓力測試。從2011年起,這一測試被稱為全面資本評估與評審(Comprehensive Capital Analysis and Review,CCAR)。銀行要求提交資本計劃(包括股票分紅計劃)。美聯儲產生的情景是類似1973~1975年、1981~1982年和2007~2009年經濟蕭條的情景。這些情景包括對25個變量的預測,包括宏觀經濟變量,如國內生產總值(GDP)增長率、失業率、股票指數和房價指數等。
總資產超過100億美元的美國銀行需要進行《多德-弗蘭克法案》壓力測試(Dodd-Frank Act Stress Test,DFAST)。DFAST中考慮的情景和CCAR中的類似,但是銀行不必提交資本計劃,而是假設銀行的資本管理建立在一套標準的設定上。CCAR和DFAST都承擔了銀行的大量工作,其中包括數千頁證明所使用模型的合理性的文件。
監管機構通過親自選定情景,可以使銀行關注的重點集中到經濟衰退的情景中,而這些情景是監管機構最關切的。如果監管當局發現許多銀行進行風險相近的交易,它們可以要求這些銀行考慮同一組特殊的情景,來分析其對這些交易所帶來的不良影響。由監管當局提出壓力情景也有缺點,監管當局之所以花費很多精力來親自生成壓力測試情景,部分原因是希望藉此鼓勵金融機構在場景的生成上也投入更多的精力,並對不良後果有更多關注。如果壓力情景完全由監管部門來制定,那麼監管部門的這一目的可能就不能完全達到,因為銀行的關注重點可能全部集中到了監管制定的場景中。在一個理想的監管環境中,對銀行管理層制定的場景和監管部門制定的情景都應該進行評估。
存在一種危險,即金融機構可能採取一些措施,使自己能夠通過壓力測試,但這些措施不能使自己變得更加安全。業界事例22-2給出了一個比較極端的例子。當監管機構給丹麥的人壽保險及養老基金公司制定了主要情景以後,有些公司選擇針對監管使用的情景進行對衝,並且是僅對這些情景進行對衝。[4]這不是監管當局的初衷。壓力測試中的每一個情景都應該被看作可能會發生的一系列事件的代表。金融機構不僅應該確保自己持有的資本金足以應對某一特定情景,而且在其他類似或相關的場景中也能保證充足。現在監管機構已經對這類問題有了非常好的認識,並且建立相關的程序保證銀行不能通過上述方式鑽監管制度的空子。
業界事例22-2
交通燈期權
2001年6月,丹麥金融監管局(Danish Financial Supervisory Authority,DFSA)引入了一套交通燈(traffic light)式償付能力壓力測試系統。在這一系統下,人壽保險及養老基金須每半年提交一個報告來說明事先定義的市場變動對於自身的影響。紅燈情景(red light scenario)對應於利率70個基點的下降、股票價格12%的下跌以及房地產市場8%的下跌,如果在這種情景下,某家公司的資本金低於一定的水平,這家公司就被分類為紅燈狀態(red light status),要受到更為頻繁的審查,公司每個月都需要提交報告。黃燈情景(yellow light scenario)對應於利率100個基點的下降、股票價格30%的下跌以及房地產市場12%的下跌,如果在這種情景下,某家公司資本金低於一定的水平,這家公司就被分類為黃燈狀態(yellow light status),須每個季度提交報告。如果公司的資本金無論是在紅燈情景還是在黃燈情景下都高於一定的水平,則稱為處於綠燈狀態(green light status),公司只需每半年提交一次報告。
衍生產品經紀商開發了一類特殊產品,幫助人壽保險及養老基金維持綠燈狀態。這些產品被稱為交通燈期權(traffic light option)。在交通燈情景下,這些產品能產生回報,因此能夠在這些情景下提升金融機構的表現。交通燈期權僅在市場變動接近監管定義的紅燈和黃燈情景的情況下才會產生回報。這類期權通常比較便宜。
[1] See “Principles for Sound Stress-Testing Practices and Supervision,” Basel Committee on Banking Supervision, May 2009.
[2] 在本節的翻譯過程中,譯者參考了中國銀監會(2018年已和中國保監會合併為中國銀保監會)發佈的《穩健的壓力測試實踐和監管原則》。——譯者注
[3] “進行中風險和庫存風險”是指已準備被證券化,但受限於市場條件,最終不一定會被證券化的資產相關的風險,這些風險在危機中導致了損失。
[4] 業界事例22-2的信息來自P. L. Jorgensen, “Traffic Light Options,” Journal of Banking and Finance 31, no.12(December 2007):3698-3719。
22.3 如何應用結果
壓力測試一個最大的問題就是如何有效地應用測試結果。一種非常普遍的現象是壓力測試結果常常被高管忽略。一種典型的態度是:“對呀,總有一兩種情景會給我們帶來災難,但我們無法在所有可能發生的情況下都能保護自己。”一種避免這種迴應的做法是(如前所述)讓高管提出壓力情景。來自高管的另外一種更積極的迴應是:“與這些情景相關的風險是否可以接受?如果不能接受,讓我們分析一下應該如何進行交易或者採取其他措施,以保證風險被控制在可以被接受的範圍之內。”
高管及風險管理人員所面臨的難題是,對可能出現的不利情況,他們要面對兩份不同的風險報告:一份報告是通過VaR或ES模型生成的,另一份報告是通過壓力測試生成的。管理人員的決策應基於哪一份報告呢?
22.3.1 壓力測試與VaR計算的結合
Berkowitz(2000)指出,如果能做到將壓力測試的結果與VaR計算結合起來,那麼壓力測試會得到更多重視。[1]為了達到這一目的,我們可以給每個情景賦予一定概率。假定某金融機構考慮了ns數量的壓力測試情景,而這些情景所對應的總概率為p,進一步假定有nv數量的VaR情景是通過歷史模擬來生成的,從而共有ns+nv數量的情景,其中ns數量的壓力情景的概率為p,nv數量的歷史情景的概率為1-p。
不幸的是,人類並不擅長估計極端事件出現的概率。為了使壓力測試委員會能夠完成這一任務,一種合理的做法是對壓力情景進行分類,對每一個分類,事先賦予一個概率。可以如下分類:
(1)概率=0.05%,極端事件,每2000個情景中出現一次。
(2)概率=0.2%,非常事件,但其權重應該與具有500個情景的歷史模擬法中每個情景的權重相同。
(3)概率=0.5%,小概率事件,但其權重應該大於具有500個情景的歷史模擬法中每個情景的權重。
【例22-2】 假定在第13.1節的例子中採用5個極端情景,這些情景所對應的損失(以千美元計)分別為235、300、450、750及850。對於每個情景所設定的主觀概率分別為0.5%、0.2%、0.2%、0.05%及0.05%,因此全部壓力情景所對應的概率為1%,這意味著我們將對由歷史模擬所產生的情景設定99%的概率。如果採用相同的權重,每個歷史模擬情景所對應的概率為0.99/500=0.019 8。表13-4也因此被表22-1取代,將損失由最差到最好進行排序,每個情景所對應的概率也從最差情景開始進行累積,[2]當置信水平為99%時,VaR等於累積概率大於0.01的第一個損失量,在我們的例子中,為282 204美元。
表22-1 損失由最高到最低進行排序
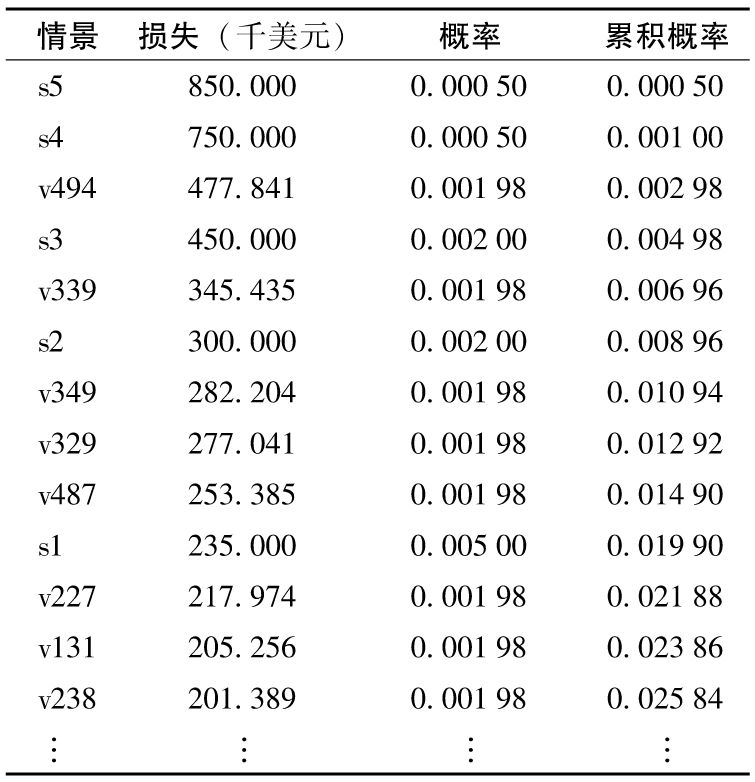
注:對於例22-2,s1、s2……為壓力情景;v1、v2……為VaR歷史模擬情景。
Rebonato在2010年提出了一個更加精細的估計場景概率的方法。該方法用到了統計學中廣為人知的貝葉斯定理(Bayes theorem)和貝葉斯網絡(Bayersian network)。[3]一個包含兩個事件的場景的概率等於第一個事件發生的概率乘以在第一個事件發生的前提下第二個事件發生的條件概率。類似地,一個包含三個事件的場景發生的概率等於第一個事件發生的概率乘以在第一個事件發生的前提下第二個事件發生的條件概率,再乘以在第一個和第二個事件發生的前提下第三個事件發生的條件概率,Rebonato的方法提供了估測條件概率的一種方法。
22.3.2 客觀概率與主觀概率
對概率的估計有兩類:客觀估計和主觀估計。客觀概率(objective probability)是通過進行若干次實驗來觀察某個事件出現的頻率從而得出的概率。一個很好的例子是假設某個罐子中有紅球和黑球,紅球和黑球的比例未知,我們想求得從罐子中抽取任意一球為紅球的概率。為此,我們可以從罐子中隨意抽取一球,並觀察顏色,然後將球放回罐子中;然後我們再隨機抽取一球,並觀察顏色,再將球放回罐子中;我們可以持續地進行100次這樣的實驗,實驗後發現有30次為紅球,70次為黑球,我們由此估計出抽取紅球的概率為0.3。不幸的是,對實際生活中的大多數客觀概率的估計要遠比這個例子困難,因為實際生活中事件的概率在每次抽樣中並不等同,同時抽樣之間可能並不獨立。
主觀概率(subjective probability)是依據某個人對某一特定事件發生機會的判斷而得出的概率。主觀概率估計不基於歷史數據,這一概率反映了一種信念程度。對於同樣事件,不同的人可能會給出不同的主觀概率。
歷史模擬中的概率為客觀概率,而我們給壓力測試情景所設定的概率為主觀概率。許多分析員不喜歡主觀概率,因為這些概率並不是基於數據得出的。還有一個問題在於,往往出於政治方面的考慮,金融機構也更偏重於歷史數據。假定你採用歷史數據進行管理,如果管理出現失誤,你可以將過錯怪罪於數據;但是,假定你採用由一些人估計的主觀概率,如果管理出現失誤,那些提供主觀概率的人就要承擔責任。
但是,如果所有的概率估計僅僅是侷限於客觀概率,風險管理無疑只能拘泥於歷史,這樣就不能充分利用高管的判斷及專長。金融機構高管的職責就是要對機構本身的運作進行把控,從而設法避免災難性風險。
[1] See J. Berkowitz, “A Coherent Framework for Stress Testing,” Journal of Risk 2, no.2(Winter 1999/2000):5-15.
[2] 這種做法與歷史模擬法中設定場景權重的做法相同(見第13.3節的表13-5)。
[3] See Riccardo Rebonato, Coherent Stress Testing: A Bayesian Approach to Financial Stress (Chichester, UK: John Wiley & Sons, 2010).
小結
壓力測試是風險管理過程的重要組成部分。壓力測試促使金融機構考慮那些被VaR或ES模型所忽略的但時有發生的極端情景。一旦合理情景被審定後,金融機構可以採取措施,來減緩不利情況對於自身的影響。全面壓力測試的好處是金融機構可以通過測試結果來了解自己產品組合中的風險特性。
我們可以採用幾種不同方式產生壓力測試情景。一種做法是假定某個市場變量會有劇烈變化,而其他變量保持不變;另外一種做法參照過往市場發生極端變動時變量的變化幅度。最好的方法是由高管和經濟學家成立專門的委員會,利用他們的判斷和經驗來產生合理的極端情景。有時金融機構要進行逆向壓力測試,即利用計算機算法來搜索會導致大幅損失的情景。情景的設定要儘量全面,並且要考慮連帶效應以及市場變量最初的變化發生後造成的後繼影響。2007年夏天開始的市場波動說明,連帶效應有時可能會非常嚴重,甚至會導致安全投資轉移現象的產生、信用價差的增大以及市場流動性的枯竭。
監管人員要求銀行要持有充足的資本金以應對壓力情景。美國、歐盟和英國的監管機構會定期設計壓力場景,供所有大型金融機構使用。這有可能導致一些金融機構不得不提高資本金並發現與系統性風險有關的問題。
如果對極端情景設定主觀概率,我們可以將壓力測試與VaR模型結合到一起,雖然這一想法很好,但2009年5月巴塞爾委員會公佈的壓力測試指導意見中並沒有包括這一做法。
延伸閱讀

練習題
22.1 解釋3種不同的產生壓力測試情景的做法。
22.2 什麼是逆向壓力測試?如何應用?
22.3 為什麼監管環境會導致金融機構低估其採用壓力情景的嚴重性?
22.4 什麼是交通燈期權?其缺點是什麼?
22.5 為什麼高管要參與壓力測試?
22.6 由銀行監管機構制定壓力測試情景的優缺點各是什麼?
22.7 解釋主觀概率及客觀概率的不同。
22.8 在第13.1節的例子中,考慮7個壓力情景,這些情景所觸發的損失(以千美元計)分別為240、280、340、500、700、850以及1050,這些情景對應的主觀概率分別為0.5%、0.5%、0.2%、0.2%、0.05%、0.05%及0.05%。採用第22.3節中討論的做法,計算新的展望期為1天、置信度為99%的VaR。
22.9 假定例22-1中的4個期權頭寸被改為200、-70、-120及-60。用Solver程序來求取對於一天內盈利變化的最差情況。假定資產價格變化介於40美元與60美元之間,波動率變化介於10%與30%之間。
作業題
22.10 以下變化對於例22-1中的最差情景有什麼影響?(a)期權為美式期權,而不是歐式期權;(b)期權為障礙期權,其中當資產價格達到65美元時,期權被敲出。用Solver程序來求取盈利變化的最差情景。假定資產價格變化介於40美元與60美元之間,波動率變化介於18%與30%之間。
22.11 採用第13.3節中的指數加權平均移動模型來對於不同情景設定權重,例22-2中的VaR結果會有什麼不同?
第23章
操作風險
在1999年頒佈的《巴塞爾協議Ⅱ》中,銀行監管機構增加了有關操作風險資本金的內容。這一舉動受到了來自銀行的阻力。某著名國際性銀行的總裁兼CEO曾對監管部門的計劃有這樣一種評述:“這是我看到的最昏頭昏腦的事情。”但是隨著《巴塞爾協議Ⅱ》實施日期的臨近,監管部門並沒有從原有立場上退縮。因為它們知道,過去10年裡,銀行遭受的許多重大損失都是操作風險損失,而不是信用風險損失或市場風險損失。
自1999年協議實施以來,操作風險也導致了一些重大損失。我們在業界事例5-5中討論了法國興業銀行無賴交易員導致的損失以及2011年UBS發生的類似事件。我們將在業界事例25-1中討論2012年摩根大通的倫敦鯨事件。2014年,法國巴黎銀行(BNP Paribas)被迫向美國政府支付90億美元的罰金(約為銀行一年的利潤),該銀行被控代表蘇丹、伊朗、古巴等受美國製裁的國家的客戶,通過美國的銀行進行以美元計價的交易。除此以外,該銀行還被禁止一年內在美國從事某些業務。
對銀行來說,網絡風險變得日趨重要。銀行部署了先進的安全系統防衛網絡攻擊,但攻擊手段也在不斷進化。另外,銀行對計算機和互聯網的使用越來越倚重,這也為網絡欺詐提供了更多機會。銀行的客戶和員工必須不斷地接受教育與培訓,以維護銀行的數據安全。對犯罪分子而言,對銀行發動網絡攻擊是很有吸引力的,因為正如美國著名的銀行搶劫犯Willie Sutton所說,“那裡是錢之所在”(that’s where the money is)。對恐怖分子而言,銀行也是高價值目標,因為攻擊銀行可以破壞一個國家的經濟和社會生活。
一些監管機構已經把操作風險視作銀行面臨的最重要風險。美國貨幣監理署(Office of the Comptroller of the Currency,OCC)署長托馬斯(Thomas J.Curry)在2012年曾說:“面對目前如此複雜的銀行市場以及在底層對其進行支撐的複雜技術,OCC認為操作風險很高並且還在增加是理所當然的。事實上,我們監管下的機構應把它列為事關安全性和穩健性的頭等大事之一。”他進一步認為操作風險的重要性已經超過了信用風險。[1]大多數銀行原本已經制定了對於操作風險的一些管理框架,但是監管當局對於操作風險資本金新的要求促使銀行加大了對操作風險度量及監督等方面的投入。
同信用風險及市場風險相比,操作風險更加難以量化,風險管理的難度也更大。對於信用風險及市場風險,銀行是有意識地承擔一定量的風險,在市場上有很多產品可以幫助銀行降低這些風險。與市場及信用風險不同的是,操作風險註定是銀行業務運作中的一部分。在操作風險管理過程中最重要的任務就是首先對風險類型進行識別,然後是有的放矢地制定管理措施。在業務操作過程中,我們不可避免地會面臨事先(exante)沒有預見到的某種操作風險,而這些操作風險所帶來的損失也往往是巨大的。
有些人可能認為諸如法國興業銀行遭受的損失(見業界事例5-5)是由市場風險導致的,因為是市場因素的變化使得銀行損失慘重。但是我們應該把這類事件歸咎於操作風險,因為這涉及了內部詐騙(傑洛米·科維爾構造了虛假的交易,以隱瞞自己的豪賭)。假定沒有詐騙行為,如果銀行政策允許自己的交易員承擔巨大風險,那麼此損失可以被歸為市場風險。如果銀行的政策不允許交易員承擔如此巨大的風險,但交易員利用風險控制過程中的漏洞進行交易,那麼這些損失應該被歸類為操作風險。法國興業銀行的例子表明操作風險損失通常與市場變化有關。假如市場變化對科維爾有利,那麼科維爾的交易不會引發損失。科維爾的詐騙行為以及法國興業銀行風險控制中的漏洞也許永遠不會被發現。
操作風險損失與保險公司的損失有某種可比性。保險公司面臨的一些風險事件具備小概率大損失的特性,這些事件包括颱風、地震及其他自然災害。與此類似,銀行面臨的操作風險也具備小概率大損失的特性。但這兩種風險之間有一個很大的不同:當保險公司因為某種自然災害遭受了很大損失時,這一自然災害可能影響了保險業中所有的公司,下一年的保險費可能會飛漲,以彌補損失,而操作風險可能隻影響某一家銀行,因為行業競爭激烈,銀行在下一年度往往不敢增加服務收費以彌補上一年的損失。
[1] 見托馬斯於2012年5月16日在財政俱樂部(Exchequer Club)的演講。
23.1 操作風險的定義
操作風險的定義多種多樣,有人喜歡將操作風險定義為剩餘風險(residual risk),也就是說操作風險是除市場風險及信用風險之外的銀行面對的所有其他風險。為了對操作風險進行估計,我們可以研究一下金融機構的財務報告並在營收中扣除:①信用損失的影響;②由市場風險敞口而帶來的損益。扣除這兩項後的收入波動應歸咎於操作風險。
大多數人認為這種操作風險的定義太寬了。這種定義囊括了諸如進入某一新市場、開發某種新產品以及經濟環境等不同因素。而另外的一種定義是,所謂操作風險,正如它的名字所稱的,是因為業務操作而造成的風險。這種定義包括交易處理、支付等過程中出現錯誤而帶來的風險。但這種定義方式又太狹隘了。這種定義不包含諸如無賴交易員(如傑洛米·科維爾)等重要風險。
操作風險分為內部風險及外部風險。內部風險是公司可以控制的那部分風險,公司可以選擇自己的僱員,可以選擇計算機系統,可以建立自己的風險控制政策,等等。有人將操作風險定義為所有的內部風險。這樣一來,操作風險包含的內容比僅僅是由業務操作而造成的風險要廣泛,還包括諸如無賴交易員及其他僱員詐騙等許多內控措施不力所引發的風險。
監管機構對於操作風險的定義不僅僅只是包括內部風險,它們認為由外部事件引發的風險也應是操作風險的一部分。這些外部事件包括某種自然災害(例如,影響銀行運作的火災及地震等)、政治及監管風險(例如,一家公司在某個國家被勒令停業)、保安體系被侵犯等。以上列舉的不同操作風險均被包含在巴塞爾銀行監管委員會在2001年給出的操作風險的定義中:
因內部措施、人員或系統不足或失效,以及外部事件引發損失的風險。
這種定義包括法律風險,但不包括聲譽風險以及業務策略所造成的風險。
有些操作風險可能會造成銀行運營費用的增加或者銀行利潤的降低,還有一些操作風險與信用及市場風險有互動關係。例如,如果某個貸款文件中有錯誤,損失往往只發生在對手違約的時候;當某個交易員超出了自己的交易額度並且錯誤地報告了自己的頭寸時,此時只有在市場變動對交易員不利時才會造成損失。
23.2 操作風險的分類
巴塞爾銀行監管委員會將操作風險分成7類,[1]它們是:
(1)內部詐騙(internal fraud):這類行為包括涉及至少一個內部方的旨在詐騙、挪用財產、逃避法律條款及規定以及公司政策的行為(不包括涉及多元化和歧視事件)。例如,風險頭寸報告做假、僱員偷竊、利用僱員賬戶來進行內部交易(insider trading)和流氓交易等。
(2)外部詐騙(external fraud):指第三方意圖詐騙、挪用財產以及規避法律的行為。例如,搶劫、偽造證件、支票連續透支以及計算機黑客等。
(3)僱用實務以及工作場所的安全性(employment practices and workplace safety):這類行為包括因違反僱用、健康以及安全協議等造成的人員傷亡賠償,或與多元化及歧視有關的賠償。這類行為的實例包括工人薪酬的索賠、違反僱員健康和安全制度、有組織的工會行為、反歧視行為的索賠以及一般的索賠事件(例如,某個客戶在某分行滑倒後受傷而引起的索賠)。
(4)客戶、產品以及業務實踐(clients,products,and business practices):因不經意或粗心大意而無法兌現對客戶應盡的專業義務,或使用了不恰當的產品或業務實踐。這類行為的實例包括違反誠信、濫用託管保密信息、銀行賬戶的不合法交易、洗錢行為以及銷售未經批准的產品,等等。
(5)對於有形資產的破壞(damage to physical assets):自然災害或其他事件而造成的有形資產的損失或破壞。例如恐怖分子襲擊或破壞分子打砸搶燒、地震、火災及水災等事件。
(6)業務中斷以及系統故障(business disruption and system failures):這類事件的實例包括計算機硬件及軟件的失效、通信故障以及停水、停電等。
(7)交易的執行、交付以及過程管理(execution,delivery,and process management):這一類風險包括與交易對手和供應商有關的交易過程、管理的失效以及因此造成的爭議。實例包括輸入數據錯誤、擔保品管理錯誤、法律文件不完整、未經批准進入客戶賬戶、非客戶交易對手的不當行為以及與供應商的爭端等。
銀行中有8種業務類別:
(1)企業融資;
(2)交易與銷售;
(3)零售銀行;
(4)商業銀行;
(5)支付及交割;
(6)代理服務;
(7)資產管理;
(8)零售經紀。
將7類操作風險與8種業務類別相結合,我們可以得出一家銀行共有7×8=56個潛在的操作風險來源。
[1] 見巴塞爾委員會關於銀行監管的報告,“Sound Practices for the Management and Supervision of Operational Risk,” Bank for International Settlements, July 2002。
23.3 《巴塞爾協議Ⅱ》下的監管資本
我們現在討論如何通過《巴塞爾協議Ⅱ》來確定監管資本金。正如我們將在第23.4節看到的,巴塞爾委員會已表示,打算完全改變其用以確定操作風險監管資本的程序。它特別指出,將放棄使用高級計量法(AMA),該方法是一種用於確定操作風險損失基於1年展望期和99%置信水平的VaR的複雜程序。然而,許多銀行已經投入了大量資源來實施AMA,這種情況不大可能馬上轉變。實際上,一些國家的監管機構表示,支持它們的銀行繼續使用AMA方法。因此,我們將在本節中回顧AMA方法。
根據《巴塞爾協議Ⅱ》,銀行可以採用三種不同的方法來計算操作風險監管資本金。最簡單的方法被稱為基本指標法(basic indicator approach)。在這種方法中,操作風險資本金等於過去3年毛收入平均值的15%。這裡的毛收入等於淨利息收入與非利息收入的和。[1] [2]另外一種較為複雜的計算操作風險資本金的方法被稱為標準法(standardized approach)。在標準法中銀行業務被分成8個不同業務類別:企業融資、交易及銷售、零售銀行、商業銀行、支付及交割、代理服務、資產管理以及零售經紀。我們首先計算以上列舉的每一業務類別在過去3年中毛收入的平均值與該業務部門相應的“beta因子”乘積,然後我們對以上計算結果求和,最終結果即為操作風險資本金。表23-1展示了不同業務類別所對應的beta因子。計算操作資本金的第三個方法被稱為高級計量法(advanced measurement approach,AMA),在這一方法中銀行可以採用自己設定的定量及定性標準來計算操作風險監管資本金。[3]與信用風險資本金類似,其基於1年展望期、99.9%置信度的VaR。
表23-1 標準法中的beta因子
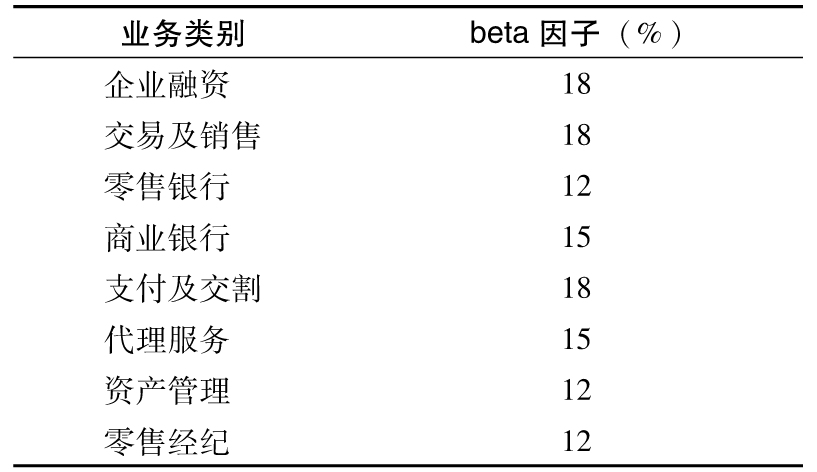
銀行採用AMA方法來計算操作風險資本金的目的可以與銀行對信用風險進行定量化管理的目的進行類比。其最終的目標是產生一個類似圖23-1中的損失分佈,如果銀行可以使監管人員相信它們計算出的操作風險的預期成本已被包含在產品價格之中,那麼資本金自然也就是用來覆蓋非預期成本的。在計算時所採用的置信水平為99.9%,展望期為1年。非預期損失等於展望期為1年、置信水平為99.9%的VaR與展望期為1年ES的差。
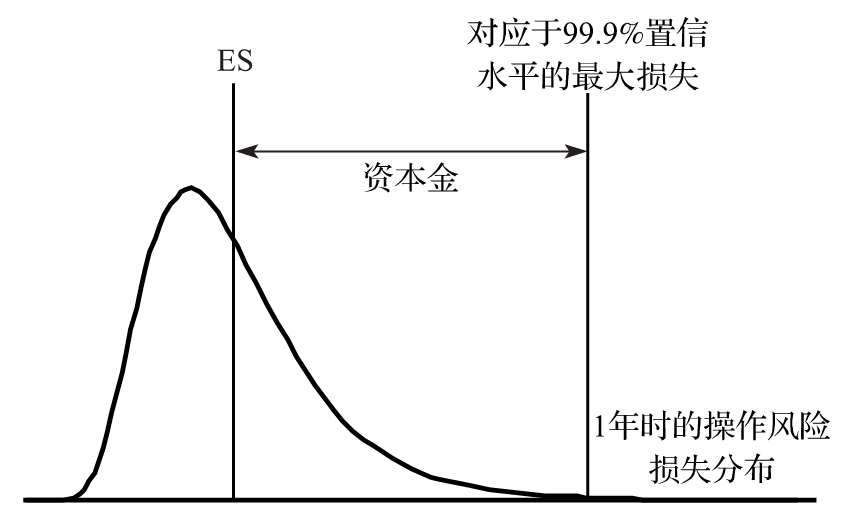
圖23-1 計算操作風險的VaR
如前所述,考慮有8種業務類別,一共有7×8=56(7種風險類別和8種業務類別)種風險與業務類別的不同組合。使用第12.9節描述的方法,對每一個組合,銀行須估計1年期、置信度99%的VaR,然後再將它們彙總起來,以產生一個單一的操作風險VaR測度。
23.3.1 損失程度及損失頻率
有兩個分佈對估計操作風險的損失非常重要:一個是損失頻率分佈,另一個是損失程度分佈。損失頻率分佈(loss frequency distribution)是在某個時間段(通常是一年)內觀察到的損失出現的次數,而損失程度分佈(loss severity distribution)是指在損失事件出現後損失量的大小。通常我們假設損失頻率分佈與損失程度分佈相互獨立。
對於損失頻率,一個比較自然的概率分佈是泊松分佈,在這一分佈中,損失在各個時間段內隨機發生,並且在任意一個Δt的時間段內,損失出現的概率為λΔt。在時間T有n個損失出現的概率為
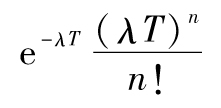
參數λ為每一個單位時間內損失出現的平均次數。例如,假如在10年時內損失出現了12次,對應的λ為每年1.2次,或每個月0.1次。泊松分佈具有一個特性,即損失頻率的期望值等於損失頻率的方差。[4]
我們通常假定損失程度分佈服從對數正態分佈。這一概率分佈中的參數分別為損失的對數的期望值以及方差。
對於每一個業務類別和損失類型的組合,損失頻率分佈與損失程度分佈必須結合在一起以產生整體損失分佈。計算過程可採用蒙特卡羅模擬方法。[5]我們曾提到,通常假定損失程度與損失頻率相互獨立,對於每一次模擬抽樣,我們進行以下計算:
(1)在頻率分佈中進行抽樣,以決定損失事件的數量(=n)。
(2)在損失程度分佈中進行n次抽樣以決定每次損失事件所對應的損失數量(L1,L2,…,Ln)。
(3)計算整體損失(=L1+L2+…+Ln)。
進行多次抽樣後,我們可以得出所考慮的損失類型的整體損失分佈。接下來可以確定分佈的99.9分位數。
圖23-2顯示了這個計算過程。在這一實例中預期損失頻率為每年3次,而損失程度為某種對數正態分佈,每個損失的對數的期望值被假設為0,損失對數的標準差被假設為0.4,這裡的計量單位為百萬美元,讀者可以在作者網頁上下載產生圖23-2的Excel計算表。
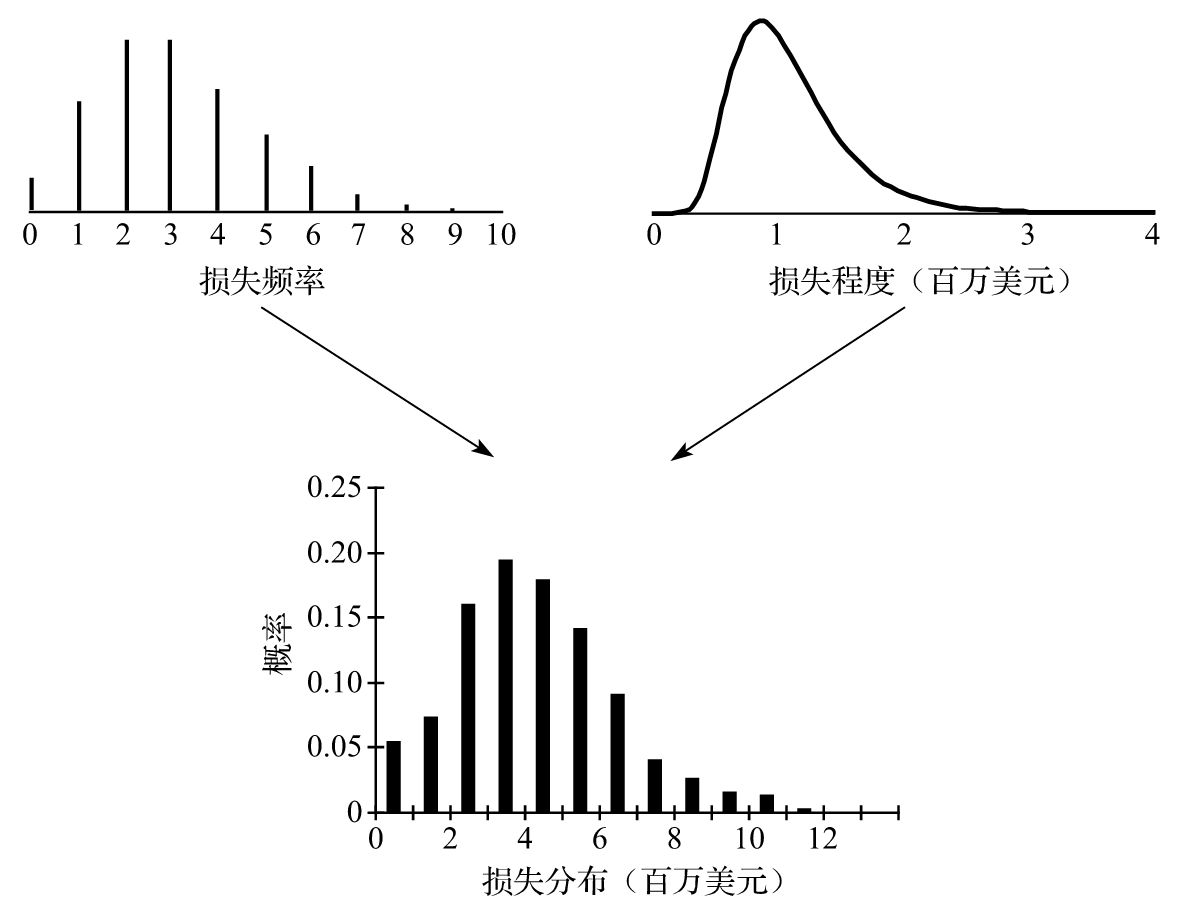
圖23-2 由損失頻率分佈以及損失程度分佈來計算損失分佈
巴塞爾委員會要求AMA的實現中要包含4個要素:內部數據、外部數據、情景分析以及業務環境和內部控制因素。[6]下面我們將對每一個展開詳細討論。
23.3.2 內部數據
不幸的是,銀行內部可以用來估測某一風險種類的損失程度以及損失頻率分佈的歷史數據往往比較少。許多銀行根本就沒有保存自己以往的操作風險損失數據。現在銀行開始收集這些數據,但要採集到合理水平的數據量還需要一些時間。從這個角度,將信用損失數據同操作風險數據進行比較,我們會發現許多有趣的地方。傳統上銀行對於信用風險的記錄要比對操作風險所做的好得多。另外,對於信用風險,銀行可以依賴信用評級公司公佈的大量數據來估測違約概率以及違約損失。銀行對操作風險數據的採集在過去遠沒有像採集信用風險數據那麼系統化。
通常,操作風險損失可以歸為兩類:高頻低額損失(high-frequency low-severity loss,HFLSL)和低頻高額損失(low-frequency high-severity loss,LFHSL)。前一類損失的例子是信用卡詐騙造成的損失,後一類損失的例子是無賴交易員造成的損失。銀行應關注的重點應該是低頻高額損失。這些損失構成了損失分佈的尾部。整體損失分佈的某個分位數可以通過整體低頻高額損失分佈的相應分位數加上整體高頻低額損失的均值來估計。關注低頻高額損失的另一個原因是,高頻低額損失通常已經被考慮在產品定價當中。
按照定義,低頻高額損失發生的頻率低。即使損失數據記錄完整,僅靠內部數據也難以滿足要求,因此需要外部數據和情景分析來彌補。正如我們所講的,外部數據可以用來確定損失嚴重性的分佈。損失頻率分佈僅限於用銀行內部數據和情景分析估算出來。
23.3.3 外部數據
外部數據的來源主要有兩個:一個是數據聯盟,即為銀行提供數據共享服務的公司(保險行業中的數據共享機制由來已久,現在銀行業也開始這麼做);另一個是數據提供商,這些公司採用系統化的手段採集公開發布的數據。外部數據增加了銀行可用來估算損失的數據量,它的另一個好處是,銀行可以藉此將那些沒有發生在自己內部但已經發生在其他銀行中的損失納入考慮範圍。
無論是利用內部數據還是外部數據都要對通貨膨脹進行調節。另外,對於外部數據,銀行還必須進行比例調整。假如一家銀行的銷售額為100億美元,而對應的操作風險損失為800萬美元,這一數據應如何被應用於銷售額僅為50億美元的另一家銀行呢?一個自然假設是當銷售額為50億美元時,操作風險損失就應該是400萬美元。這種估計可能低估了操作風險損失。Shih等(2000)的研究結果顯示公司的規模和損失的規模呈非線性關係。[7]他們估計的模型是
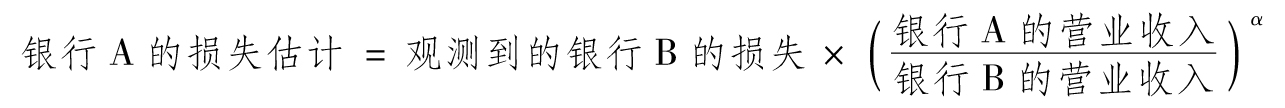
其中α=0.23,這意味著我們例子中銷售額為50億美元的銀行的相應損失估計大約為8×0.50.23=6.82(百萬美元)。在進行恰當的比例調整後,我們可以將其他銀行的共享數據同本銀行的數據進行合併,由此可以得出一個損失程度分佈的更大的數據庫。
數據提供商的數據來自公開發布的數據源,如報紙和交易期刊。數據提供商給出的數據不同於內部數據和銀行業共享數據,因為含有一定的偏差。例如,只有較大的損失才會被披露,而且損失越大,被公開報道的可能性就越高。
外部公開數據對於確定相對損失程度非常有用。假如,一家銀行對本行公司財務部門發生的內部詐騙案所造成損失的期望值及標準差有很好的估計,但是對涉及公司財務的外部詐騙以及發生在交易及銷售部門的內部詐騙所造成的損失沒有太好的數據。如果銀行估計公司財務部門內部詐騙的期望及標準差分別為5 000萬美元及3 000萬美元,進一步假設外部數據顯示公司財務部門外部詐騙損失程度的期望值是內部詐騙損失程度的期望值的兩倍,而外部詐騙損失程度分佈的標準差是內部詐騙的1.5倍。在沒有更好的選擇的情況下,銀行可以假定公司財務部門因為外部詐騙所造成損失程度的期望值為2×5 000=10 000萬美元,標準差為1.5×3 000=4 500萬美元。與此類似,如果外部數據顯示交易及銷售部門內部詐騙損失分佈的期望值及標準差分別是公司財務部門內部詐騙損失分佈的期望值及標準差的2.5倍及2倍,銀行就可以假定本行交易及銷售部門因內部詐騙所造成的損失分佈的期望值為2.5×5 000=12 500萬美元,標準差為2×3 000=6 000萬美元。
23.3.4 情景分析
在AMA中,情景分析是一個評估操作風險的關鍵工具。情景分析的目的是生成能夠全面覆蓋各種可能的低頻高額損失事件的情景。這些情景有可能來自銀行本身的經歷,也可能是基於其他銀行遭受的損失,還有一些可能是諮詢人員建議的,或由風險管理團隊和高管以及業務部門經理一起產生的。巴塞爾委員會估計,在很多銀行內部,經考慮過的可能導致1 000萬歐元以上損失的情景的數量是內部實際發生的、達到這一數字的損失的數量的20倍。
一個由風險管理團隊和公司高管所組成的委員會應該負責估計這些場景中的損失程度和損失頻率的參數。如第23.4節中解釋的,對數正態分佈常常被用來產生損失程度分佈,而泊松分佈常常被用來產生損失頻率分佈。來自其他銀行的數據可能對估計損失程度有幫助。損失頻率應能反映銀行已實施的控制措施的效果和從事的業務類型。它們還應反映操作風險委員會成員的觀點。與第22.3節類似,不同類別的損失頻率可定義如下:
(1)平均千年一遇的情景(λ=0.001);
(2)平均百年一遇的情景(λ=0.01);
(3)平均50年一遇的情景(λ=0.02);
(4)平均10年一遇的情景(λ=0.1);
(5)平均5年一遇的情景(λ=0.2)。
委員會可以將產生的每一個情景劃分給以上任意一個類別。
這裡的情景分析與第22章中的分析有一個差別,我們在這裡並沒有用來確定損失的模型,而且如果無法獲取數據,損失程度分佈的參數應由委員會來估計。一種方法是由委員會來估計平均損失並確定在99%的置信度下,不會被超出的高額損失數量。然後我們可以使用一個對數正態分佈來擬合已有的估計。
幸運的是,操作風險的環境變化不會像市場風險和信用風險環境變化那麼快,因此產生操作風險情景並持續更新的工作量不會像產生市場風險和信用風險情景那麼繁重。但無論如何,高管需要對以上描述的管理過程投入大量的時間。一家銀行採用的情景通常與其他銀行的相關情景類似。行業內的諮詢顧問和行業協會可能會開發出一些標準情景,從某種意義上講,這會減輕操作風險管理委員會的負擔。但是,對損失頻率的估計應該與銀行的特定情況有關,並反映銀行風險控制現狀以及當前的業務狀況。
類似於市場和信用風險壓力測試,基於高管的判斷來產生操作風險壓力情景的優點是,這一方法可以生成金融機構從來沒有經歷過,但可能會出現的損失情景。情景分析可以促使管理人員以更主動和更有創造力的方式來管理將來可能發生的不利事件。這樣做會帶來許多好處。對於有些情景,銀行可以事先制定政策以保證在不利事件發生時如何將損失程度控制到最小,而對於另外一些情景,銀行可以主動提出預防措施來減小不利事件發生的概率。
無論是採用情景分析法還是內部/外部數據法,每個特定損失種類的分佈都必須合併起來以產生最終的整體操作風險損失分佈。各操作風險類別間的相關性假設可能導致算出的1年展望期、99.9%置信度的VaR的結果有很大不同,因此最終的AMA資本金也會不同。基於第12.9節中的材料,第26章給出瞭如何利用相關性來合併包括市場風險、信用風險和操作風險在內的經濟資本金。同樣的方法也可被用來合併不同類型的操作風險資本金要求。人們常常認為操作風險損失之間基本上沒有相關性,而且有實證研究結果支持這一主張。如果假設相關性為0,我們就可以簡單地採用蒙特卡羅模擬的方法,從各個情景的分佈中抽樣來得到整體風險損失的分佈。
23.3.5 業務環境和內部控制因素
在估計損失程度和損失頻率時,業務環境和內部控制因素(business environment and internal control factor,BEICF)應被考慮在內。這些因素包括業務部門的複雜程度、採用的技術的先進程度、變化的快慢、監管的力度、員工更換的頻率等。例如,影響對無賴交易員這一情景的估計的因素可能包括:對交易員的監管力度、對交易的監控程度以及中臺和後臺系統的長處和缺點。
[1] 淨利息收入等於由貸款所帶來利息與支撐貸款的產品的應付利息之差(見第2.2節)。
[2] 如果某年的毛收入為負,則被0取代。——譯者注
[3] 巴塞爾委員會在2016年3月正式公告,將操作風險的AMA從監管資本金體系中刪除。理由是該方法過於複雜,在實踐中缺乏統一標準,容易造成銀行的風險加權資產不合理波動。委員會提出了新的標準計量法(standardized measurement approach,SMA)以取代AMA。——譯者注
[4] 如果期望值大於方差,選擇二項分佈(binomial distribution)可能更為合理。如果期望值小於方差,選擇負二項分佈(negative binomial distribution,也即混合泊松分佈)可能更為合理。
[5] 將損失程度與損失頻率分佈進行結合在保險業中是個十分常見的問題。除了蒙特卡羅法,另外兩個方法也較為流行,一個方法是Panjer算法,另一個方法是快速傅立葉變換(fast Fourier transforms),見H.H. Panjer, “Recursive Evaluation of a Family of Compound Distributions,” ASTIN Bulletin 12(1981):22-29。
[6] See Basel Committee on Banking Supervision, “Operational Risk: Supervisory Guidelines for the Advanced Measurement Approach,” June 2011.
[7] See J. Shih, A. Samad-Khan, and P. Medapa, “Is the Size of an Operational Loss Related to Firm Size?” Operational Risk Magazine 2, no.1(January 2000).Shih的結果是否適應於法律風險非常有爭議,我們常常看到一些大的法律糾紛的賠償數量通常與銀行的承受力有關。
23.4 標準計量法
巴塞爾委員會一直致力於使各銀行在實施其監管時保持一致。如果不同的銀行根據同樣的數據計算出截然不同的資本金,巴塞爾委員會認為這樣的基本監管沒有奏效。這就是採用AMA所面臨的情況。巴塞爾委員會希望,AMA的靈活性最終會使得各銀行監管趨於一致性。但實際上,AMA的內在複雜性和內部建模法的廣泛性導致了資本金的高度不確定性。
2016年3月,巴塞爾委員會發布了一項諮詢文件,指出它將用一種新的方法——標準計量法(standardized measurement approach,SMA),取代以往所有用於確定操作風險資本金的方法。[1]在實施AMA過程中,大量投資的銀行感到惱火是可以理解的,如前所述,某些國家的監管機構很可能會允許它們繼續使用AMA方法。
SMA比AMA簡單。它首先定義了業務指標(BI),這是一個用於衡量銀行規模的指標,類似於《巴塞爾協議Ⅱ》中基本指標方法使用的總收入(Gross Income,GI)。關鍵區別在於:
(1)雖然負收入(例如,來自貿易)將會降低GI,但不會降低BI。
(2)BI包括了一些在GI中省略,但會產生操作風險的項目。
(3)操作費用會降低GI,但因為它們會導致操作風險,所以BI會增加。
銀行的BI成分是根據其BI值使用表23-2所示的分段線性關係計算出來的。隨著銀行規模的擴大,BI每增加1美元,BI成分也隨之增加。對於BI在0~10億歐元的小型銀行來說,該比率是0.11;對於BI在10億~30億歐元的銀行來說,該比率將上升到0.15;對於BI在30億~100億歐元的銀行來說,該比率是0.19;對於BI在100億~300億歐元的銀行來說,該比率為0.23;對於BI高於300億歐元的銀行來說,該比率為0.29。
表23-2 根據BI計算BI成分

對BI超過10億歐元的銀行需要計算如下損失
損失成分=7X+7Y+5Z
其中X為操作風險導致的年平均損失總額,Y為僅包含1 000萬歐元以上損失的年平均損失總額,Z為僅包含1億歐元以上損失的年平均損失總額。這些損失數據應該是平均超過10年的高質量數據。[2]根據巴塞爾委員會的估計,損失成分和BI成分的計算結果表明,對於一家普通銀行來說,損失成分等於BI成分。
內部損失乘數計算公式為

其中,e是指數常數2.718,這樣計算的目的是使銀行平均的內部損失乘數為1。平均損失高於(低於)行業平均水平的銀行,其內部損失乘數將大於(小於)1。可能的最小內部損失乘數為ln 1.718,即0.514。
最後,可以計算出SMA的資本要求。對於BI小於10億歐元的小銀行,SMA資本金等於其BI成分(因此這些小銀行都被視為“平均”)。對於其他銀行,SMA資本金的計算方式(以百萬歐元計)為
SMA資本金=110+(BI成分-110)×內部損失乘數
[1] 見巴塞爾銀行監管委員會,“Consultative Document: Standardized Approach for Operational Risk”,2016年3月。
[2] 在過渡時期,沒有10年高質量損失數據的銀行可以使用至少5年的數據。
23.5 操作風險損失的預防
到目前為止,為了確定資本金,我們一直側重於對操作風險的度量。操作風險經理工作的關鍵是未雨綢繆,在損失發生之前加以防範,儘量避免損失。現在我們探討一些可以做到這一點的方法。
一種途徑是跟蹤其他銀行的損失並從中吸取教訓。2002年,當7億美元的無賴交易員損失發生在愛爾蘭聯合銀行的巴爾的摩(Baltimore)子公司時,世界不同地區的風險管理人員應仔細分析此案例並且自問:“這種情況會發生在我們身上嗎?”業界事例23-1講述的是發生在20世紀80年代末的一個關於英國執法機關的故事。這一事件發生後,所有銀行立即開始著手建立程序,以檢查交易對手是否有資質進行衍生產品交易。
業界事例23-1
哈默史密斯和富勒姆的故事
1987~1989年,英國倫敦地區的哈默史密斯和富勒姆(Hammersmith and Fulham)進行了600個左右總面值大約為60億英鎊的利率互換以及相關交易。這些交易的目的看起來不是對衝風險而是投機,對這些交易負有直接責任的兩位僱員對這些產品的交易風險及運作方式知之甚少。
到1989年,由於利率的變化,哈默史密斯和富勒姆因為這些利率互換交易損失了數以百萬計英鎊。對與哈默史密斯和富勒姆進行交易的銀行而言,這些交易價值連城。但此時銀行對信用風險產生了擔憂。因為為了對衝利率風險,這些銀行已經與其他交易對手進行了反方向的利率互換交易,如果哈默史密斯和富勒姆違約的話,銀行仍必須兌現在這些反方向交易中承擔的義務,從而會蒙受損失。
但真正發生的事情並不是違約。哈默史密斯和富勒姆的審計部門認為這些利率互換交易無效,因為哈默史密斯和富勒姆沒有權力交易這些產品。英國法庭也支持了這一決定。這一糾紛後來被一直上訴到英國的上議院(House of Lords),即英國的最高法院。上議院最後裁決認為哈默史密斯和富勒姆沒有權利交易這些互換產品,議會同時又裁定將來如果是因為風險管理的需要,哈默史密斯和富勒姆有權利進行利率互換交易。無論如何,同哈默史密斯和富勒姆進行交易的銀行對於這些合約被法庭中止而感到無比的憤怒。
23.5.1 因果關係
操作風險管理人員應該試著定義自己的業務決策與操作風險損失間的因果關係。銀行應準備回答以下問題:僱員平均教育水平的提高是否可以減少將來交易處理過程中的錯誤?一個新的計算機系統是否可以減少系統故障而帶來的損失?操作風險是否和僱員離職率有關?如果這兩者確實相關的話,我們是否可以通過減少僱員離職率來降低操作風險的程度?我們是否可以通過清楚地劃分僱員的職責以及改善交易員的獎勵機制來降低無賴交易員風險?
一種定義因果關係的方式是通過統計方法,如果我們檢驗了一家銀行在12個開展業務的不同地區並且發現銀行後臺僱員的教育與交易處理中的錯誤有一個較強的負相關性,這時我們要進行一個以提高這些地區後臺僱員教育背景為目的的成本效益分析(cost benefit analysis)。在某些場合,一個較為詳細的損失分析也許能夠使管理人員對問題有一個更深刻的認識。例如,如果有40%計算機故障可以歸咎於硬件的落後,這時我們應做一個硬件更新的成本收益分析。
23.5.2 風險控制自我評估以及主要風險指標
風險控制自我評估(risk and control self-assessment,RCSA)是銀行試圖瞭解操作風險敞口的一個重要方式。RCSA過程要求業務部門的管理人員對自己面臨的操作風險進行識別,有時要採用由高級管理層或諮詢人員設計的問卷(questionnaires)或計分卡(scorecard)的形式。
通過度量與理解操作風險,我們很可能會進一步制定主要風險指標(key risk indicators,KRI)。[1]風險指標是管理操作風險的重要工具,最重要的風險指標是前瞻性的。這些指標對公司各個環節存在的操作風險提供了前期預警(early warning)。適用於某些特定情況的風險指標的例子如下:
(1)僱員離職率;
(2)交易過程失敗的次數;
(3)臨時僱員的數量;
(4)管理人員和工作人員的比例;
(5)空缺職位的數量;
(6)過去12個月內,沒有連續休假10天以上的僱員的比例。
管理層希望通過這些關鍵指標發現問題並能夠及時採取改正措施,以避免損失。銀行對操作風險進行量化非常重要,但更重要的是銀行必須採取措施來對這些操作風險進行管理以及控制。
23.5.3 電子郵件和電話
降低操作風險的一個重要途徑是教育僱員仔細斟酌他們在電子郵件中寫下的文字以及當他們在交易大廳工作時在電話中的通話內容。針對金融機構僱員不當行為指控的法律訴訟以及監管調查是重要的操作風險源。當一樁訴訟或投訴被髮起以後,金融機構最先要做的事情之一就是提供所有的相關通信記錄。這類記錄常常讓金融機構陷入很難堪的境地,從而難以為自己辯護(業界事例27-3中給出的法布里斯·圖爾的電子郵件就是讓人尷尬的一個生動例子)。在發出一封電子郵件或撥打一通要被錄音的電話前,僱員應考慮這樣一個問題:“如果通信的內容被公眾所知,會不會對我的僱主造成傷害?”
[1] 有時也被認為是業務環境和內部控制因素(BEICF)。
23.6 操作風險資本金的分配
操作風險資本金分配方式的出發點是鼓勵業務部門積極地增強自身的操作風險管理能力。在第12.8節和第26.6節中,我們討論了資本金的分配。如果一個業務部門能證明通過自身採取的措施減小了操作風險出現的頻率以及損失程度,那麼該部門的資本金就應該有所降低。這樣一來會提高該業務部門的資本回報率(因此也會提高該部門管理人員的獎金)。
我們應注意到有時無限制地降低操作風險對於管理過程來講並不一定是最優的。有時為降低風險而付出的代價可能大大超過資本金減少所帶來的好處,從而降低資本回報率。銀行應該鼓勵業務部門恰當地計算和確認所承擔的操作風險,以優化資本回報率。
對操作風險的評估以及操作風險資本金的分配要達到使業務部門更深切地體會到管理操作風險的重要性。操作風險管理應成為每一個管理人員日常工作重要的一部分。成功的操作風險管理制度中的一個重要組成部分是來自高級管理層的支持。巴塞爾銀行監管委員會已充分意識到了這一點。委員會建議銀行的董事會應參與風險管理制度審批並對制度的落實進行定期檢查。
23.7 冪律的應用
在第10.4節中,我們介紹過冪律。該定律闡明對於許多變量,以下關係式成立
Prob(v > x)=Kx-α
其中v代表變量的值,x是v所取的一個較大數值,K及α均為常數。在第13.5節中討論極值理論時,我們曾討論過冪律的理論基礎以及最大似然估計的過程。
DeFontnouvelle等(2003)採用由外部供應商給出的數據證明了銀行所經歷的大額損失服從冪律。[1]這一結果使計算高置信度(如99.9%)的VaR變得更加簡單。應用內部及外部數據和情景分析,我們可以通過第13章所介紹的最大似然估計法估計冪律中的參數。損失分佈中第99.9%百分位數可以由式(13-9)估算得出。
當我們對損失分佈進行迭加時,具有最肥尾部的分佈往往會最顯著,這意味著具有冪律中最低的α值的損失會決定整體損失分佈的尾部極值。[2]因此如果在計算中我們僅僅是對整體操作損失的尾部極值感興趣,那我們僅需考慮一到兩個業務類別與損失類型不同的組合。
[1] See P. de Fontnouvelle, V. DeJesus-Rueff, J. Jordan, and E. Rosengren, “Capital and Risk: New Evidence on Implications of Large Operational Risk Losses,” Journal of Money, Credit and Banking 38, no.7(October 2006):1819-1846.
[2] 在第13章中,參數ξ與1/α相等,因此具有最大ξ值的損失分佈會決定尾部的極值。
23.8 保險
操作風險管理人員需要做的一個重要決策是要在多大程度上對操作風險進行投保。對於不同形式的風險如火災損失及無賴交易員損失等,保險公司都可以提供保險產品。在保險公司的資產負債表滿足一定條件下,採用AMA計算資本金的銀行可以通過在某家保險公司投保來降低資本金計提量。在第3.7節中我們討論了保險公司在設計保險產品時要面臨的道德風險和逆向選擇,在這一節中我們將從操作風險的角度再次討論這些問題。
23.8.1 道德風險
保險公司對銀行的操作風險承保時面臨的風險之一是道德風險(moral hazard),這種風險是指銀行持有保險合約時與沒有投保時相比行為會發生變化,這種行為的變化會增加保險公司的風險。例如,一家銀行對搶劫進行了投保,保險合約的存在可能會使銀行對自身安保工作有所鬆懈。銀行對安保工作的懈怠會使搶劫案件相比投保之前更容易發生。
傳統上保險公司採用多種不同的方式來應對道德風險,通常的做法是保險公司在保險合約中會註明一定的免賠額(deductible),免賠額的存在意味著銀行必須首先要承擔一定的損失。保險公司有時也會採用“共保條款”(coinsurance provision)來應對道德風險,在這種方法中,保險公司只承擔超出免賠額以上損失的一個比例(小於100%)。另外幾乎所有保險合約都有一個保單限額(policy limit),即保險公司應付賠償款的上限。讓我們再次考慮為搶劫投保的那家銀行,因為免賠額,共保協議以及保單限額的存在會使銀行對自己分行的安保不再掉以輕心。業界事例23-2討論了無賴交易員保險中的道德風險問題。
業界事例23-2
無賴交易員保險
無賴交易員保險反映了道德風險的獨特之處。一家貪圖利益的銀行可以買入這種保險來保護自己,同時放鬆對交易風險額度的控制,如果一個交易員超出交易額度但是獲得了盈利,那麼這種結果對銀行有利;如果交易員的交易帶來損失,那麼銀行可以通過向保險公司索賠無賴交易員賠償金來彌補損失。將免賠額、共保條款以及保單限額等若干條件考慮在內以後,保險所帶來的收益會小於交易員所造成的損失,但是無賴交易員超額交易所帶來的可能的損失有可能要遠小於可能的盈利,對於銀行來講這種超額交易仍然很划算。
考慮到以上問題,我們也許會對有些保險公司仍願意為無賴交易員承保感到奇怪。提供這類保險的保險公司會特別注重銀行如何管理交易額度,而且往往要求銀行不要向交易人員洩露保險條款的存在。保險公司通常保留對損失事件進行調查的權利。
從銀行的角度來看,上面提到的放鬆對交易額度的管理是目光短淺的做法。銀行可能發現無賴交易員索賠造成了今後所有保險價格的顯著增長。另外,一個大額度無賴交易員損失(即使在投保後)也會給銀行聲譽造成巨大損害。
23.8.2 逆向選擇
保險公司面臨的另外一個問題是逆向選擇(adverse selection),這是指保險公司無法分辨低風險投保人與高風險投保人。如果保險公司給每個人提供的保險價格都一樣,那麼這樣不可避免會吸引更多的高風險投保人。例如,不具備良好的內控系統的銀行往往會購買無賴交易員保險;同樣的道理,沒有良好的外部風險控制措施的銀行常常會購買外部詐騙保險。
為了應對逆向選擇問題,保險公司必須瞭解銀行的風控過程以及銀行過去的損失。在做過最初風險評估以後,對於同樣的保險合約,針對不同的投保銀行,保險公司會給出不同的報價。隨著時間的推移,保險公司會收集到更多的有關銀行操作風險損失的信息,這時保險公司對保單的收費有可能增加也可能減少。這一做法同保險公司賣出汽車保險時的做法沒有什麼不同,在汽車保險剛剛開始時,保險公司會盡量收集有關駕駛員的信息,隨著時間的推移,保險公司可以收集到更多有關駕駛員風險(車禍次數、超速罰款次數等)的信息,然後保險公司能夠以這些信息為基準來對保險價格進行修正。
23.9 《薩班斯-奧克斯利法案》
美國政府在2002年通過了《薩班斯-奧克斯利法案》(Sarbanes-Oxley Act),這一法案的通過在很大程度上是由於安然公司的垮臺而直接導致的。該法案給美國的金融機構以及非金融機構在操作風險管理方面又提供了一個新的指導方針。法案要求公司董事會成員要花更多的精力在公司的日常運作上,董事會必須對公司的內控進行監督並保證風險能得到評估和恰當處理。
該法案對上市公司董事會的構成提出了規定,並闡述了公司董事會的職責。SEC被賦予了對董事會進行審查以及促使董事會承擔更多責任的權力。法案規定,為某家公司提供審計服務的公司不能再給這家公司提供任何重大的非審計服務。[1]審計公司必須採取輪換制。董事會中的審計委員會必須要了解不同的財會處理方式。發佈審計報告時,要附帶公司CEO以及CFO對財務報告準確性的保證。如果公司的年終報告出現嚴重錯誤而被調整,公司CEO及CFO則必須退還自己的獎金。法案的其他條款對內部人交易、信息披露、給公司高管的個人貸款、公司董事的投資交易報告以及董事對公司內控措施的監督都做出了相應規定。
[1] 安然公司的審計公司安達信(Arthur Anderson)除了為安然公司提供審計外,還為該公司提供許多其他服務,在安然公司倒臺時,安達信也沒有幸免。
小結
1999年,銀行監管機構提出設定操作風險資本金的意向,作為《巴塞爾協議Ⅱ》的一部分,這種意向促使銀行對於操作風險的評估以及管理進行了認真思考。監管機構定義了7種不同的操作風險類型和8個不同的業務類別,並鼓勵銀行對這56種業務及風險類型組合提供量化管理。
從理論上講,某一特定類型的操作風險損失的處理方式同保險精算中損失的處理方法非常類似。在量化過程中首先需要估計操作風險損失頻率分佈以及損失程度分佈,然後這兩個分佈被結合在一起來產生整體損失分佈。當採用《巴塞爾協議Ⅱ》中的高級計量法(AMA)時,銀行需使用內部數據、外部數據、情景分析以及業務環境和風險控制因素來估計這些分佈。
2016年,巴塞爾委員會宣佈,AMA的表現不如預期,並表示計劃要求銀行採用新的方法——標準計量法(SMA)。作為SMA的一部分,巴塞爾委員會制定了業務指標,以衡量銀行的規模,這與銀行潛在的操作風險敞口相關。將該指標與銀行過去10年的平均損失經驗相結合,可以確定操作風險監管資本金。
操作風險經理的一部分工作是提高員工對操作風險的認識,從而防止造成損失。他們還應明白產生操作風險損失的原因,並制定關鍵風險指標以跟蹤機構不同部門的操作風險水平。
在對操作風險資本金進行估算後,我們還應該將資本金在不同業務類別中進行合理分配,分配方式要儘量做到在不過分提高管理成本的前提下鼓勵業務部門降低操作風險。
第10章所討論的冪律可以被用於描述操作損失分佈。冪律能夠從實證數據出發並利用極值理論(見第13章)來估算損失分佈的尾部狀態。將幾種損失分佈進行迭加時,尾部最肥的分佈最為突出,這一性質可以簡化整體操作風險VaR的計算過程。
對許多操作風險類別,銀行可以買入保險。然而許多保險合約包括免賠額、共保條款以及保單限額等條款,因此銀行在購買保險以後仍需承擔一定的風險。再有,隨著時間的推移,保險費會根據保險理賠次數以及保險公司對投保機構操作風險管理狀況的評估指標的掌握髮生變化。
銀行對於操作風險(資本金)的度量、管理以及分配過程仍然處在較為初級階段。隨著時間的推移,會積累更多的關於操作風險的數據,更為精確地描述操作風險的方法也會逐漸產生。一個核心問題是,操作風險有兩個重要類型:高頻低額損失以及低頻高額損失。對於前者,我們比較容易量化,但高級計量法(AMA)產生的操作風險VaR往往取決於後者。
監管機構已經較為成功地使銀行意識到操作風險的重要性。從許多角度來看我們都可以這麼講:操作風險管理過程給銀行帶來的好處不只是最後產生的那個操作風險計量數字,而是產生這個數字的過程本身。如果這一過程實施得當,將使銀行管理人員對操作風險更加關注,並對這一風險產生新的認識。
延伸閱讀
練習題
23.1 監管機構對於操作風險的定義都包括哪些風險?哪些風險不在定義之內?
23.2 假定一個外部數據顯示的一家年收入為10億美元的銀行的操作損失為1億美元,假定你所在的銀行的年收入為30億美元,你所在的銀行由外部數據隱含推算出的操作損失的估計為多少?(使用Shih的結論。)
23.3 假定一種操作損失的數量不超過2 000萬美元的概率為90%,冪律參數α為0.8,損失不超過以下數量的概率分別為多少?(a)4 000萬美元;(b)8 000萬美元;(c)2億美元。
23.4 請討論道德風險以及逆向選擇問題在汽車保險中是怎樣被處理的。
23.5 請列舉《薩班斯-奧克斯利法案》對上市公司CEO的兩個影響。
23.6 在什麼情況下交易損失可劃歸市場風險?在什麼情況下應劃歸操作風險?
23.7 請討論在人壽保險合約中是否有:(a)風險道德;(b)逆向選擇問題。
23.8 什麼是外部損失數據?這些數據是如何取得的?如何應用這些數據來決定一家銀行的操作風險?
23.9 哪些分佈被經常應用於描述損失頻率及損失程度?
23.10 請列舉兩個被銀行中央操作風險管理部門監控的主要風險指標的例子。
23.11 在作者網頁上可以下載生成圖23-2的計算表。損失分佈的期望值及標準差分別等於多少?改變模擬數據來找出損失頻率由3變為4對於損失分佈的影響。
23.12 根據標準計量法(SMA),決定監管資本的關鍵投入因素是什麼?
23.13 有兩家BI成分為3億歐元的銀行。在過去的10年間,A銀行已經遭受了10次2 000萬歐元的操作風險損失,而B銀行只發生了一次2億歐元的操作風險損失,請問SMA下兩家銀行的操作風險監管資本各是多少?
作業題
23.14 假定某銀行操作風險損失小於1000萬美元的概率為99%,請採用冪律求出當α分別等於以下數值時:(a)0.25;(b)0.5;(c)0.9;(d)1.0,對應於99.97%概率的最壞操作損失為多少。
23.15 考慮以下兩個事件:(a)某銀行因為與某交易對手的交易造成突如其來的法律糾紛,法律糾紛帶來的損失為10億美元;(b)由於得克薩斯州突如其來的颶風使某家保險公司損失了10億美元。假如你同時持有這家銀行及這家保險公司的相同數量的股票,這時你對於哪個損失會更為介意?為什麼?
23.16 在作者網頁上可以下載生成圖23-2的計算表,如果損失程度為beta分佈,則損失分佈會發生怎樣的變化?這裡beta分佈參數上限等於5,下限等於0,其他參數均等於1。
23.17 一家銀行有55億歐元的BI,在過去的10年裡,它發生了8次操作風險損失,損失的金額分別為3、7、15、65、85、150、250和300(以百萬歐元為單位)。在SMA下,銀行的操作風險監管資本是多少?
第24章
流動性風險
對金融機構和監管人員來講,在2007年中期開始的信用危機突出了流動性風險管理的重要性。當投資者喪失對金融機構的信心時,許多依賴於機構儲蓄來取得資金的銀行的運營遭遇了危機。金融機構進而發現,它們持有的許多曾具有良好流動性的產品,在危機中只能以大甩賣的價格出售。
區分償付能力(solvency)與流動性(liquidity)的不同十分重要。有償付能力是指公司的資產大於負債,因此公司的淨值為正;流動性是指在指定付款日,銀行有足夠的現金進行支付。有償付能力的銀行有時可能會因為流動性問題而破產。考慮一家銀行,其資產大部分是由流動性不好的按揭貸款構成的。假如資產融資的90%來自存款,10%來自股權,銀行有良好的償付能力。但如果市場上出現擠兌現象,假如有25%的存款人突然抽取資金,這很有可能會造成銀行破產。在這一章中,我們將討論英國一家經營按揭貸款的銀行——北巖銀行因流動性問題而破產的過程。
金融機構應謹慎管理流動性風險,這一點顯然很重要。金融機構的流動性需求常常帶有不確定性,因此必須對流動性最差的情況進行評估,並確保在這種情況下,仍能通過將資產轉換為現金,或通過外部拆借的形式來取得現金以確保機構的存續。
在交易過程中,確保流動性也非常關鍵。一個流動性好的資產頭寸是指在短時間內可以變賣的頭寸。當一個資產的流動性變差時,因為買賣價差的增大,交易員往往會蒙受損失。對於期權和其他衍生產品,非常重要的一點是衍生產品的標的資產市場應具有良好的流動性,因為只有在這個前提下,交易員才能進行日常交易,以維持自身的delta中性(見第8章)。
本章將討論流動性風險的不同方面。我們會考慮交易流動性風險(liquidity trading risk)以及融資流動性風險(liquidity funding risk),還將討論所謂的“流動性黑洞”。流動性黑洞(liquidity black holes)是指由市場的震盪所造成的流動性枯竭的現象。
24.1 交易流動性風險
假定一家金融機構持有100份、1 000份、10 000份甚至100 000份IBM股票,這時流動性不會是一個大問題,因為紐約股票交易所每天有數以百萬計的IBM股票交易,市場給出的報價與金融機構可以賣出的價格沒有太大的不同。但是,並非所有的資產均可以輕易地轉換為現金。例如,想要在一天內以市場價格出售價值1億美元的一家非投資級美國公司債券,就不太容易,新興市場的公司股票和債券可能會更加難以變賣。
一個特定資產的出售價格取決於以下因素:
(1)資產的中間價格,或對其價值的估計;
(2)資產被出售的數量;
(3)資產被變賣的速度;
(4)經濟環境。
當一家做市商給出一個金融資產的買入價和賣出價時,金融機構能夠以該買入價來買入或以該賣出價來賣出一定小數量的資產。但是,做市商給出的價格只適用於一定數量。在此數量之上,做市商會提高買賣價差。這是因為,當交易數量增大後,對風險敞口的對衝也會變得更加困難。
當一個金融產品沒有做市商時,市場上仍會有一個隱性的買賣價差。如果一家金融機構想同另外一家金融機構進行交易(也許是中間商),那麼產品交易價格取決於金融機構是希望買入還是賣出。買賣價差可能介於資產中間價的0.05%~5%,甚至高達10%。
買賣價差與交易量有關,買入報價及賣出報價與交易數量的關係如圖24-1所示。當交易數量增大時,買入價會逐漸降低,賣出價會逐漸升高。對於某種產品,如果市場上存在做市商,在交易量不超過做市商交易容量限制的情況下,買入價和賣出價不會發生變化,一旦超出做市商的額度,買入價和賣出價就會逐漸分離。

圖24-1 買入價和賣出價作為交易數量的函數
圖24-1描述了大型金融機構之間的市場運作。有趣的是零售市場的買賣價差會出現與圖24-1相反的圖形。例如,有人想在某銀行的支行買入外匯或將資金投資90天,當交易數量增大時,他也許會拿到更好的報價。
一個資產所能實現的價格取決於資產變賣的速度和市場條件。假如你想賣出你的住房。有時房地產市場是賣方市場(seller’s market)。當你剛剛將房屋投入市場,你可能就會馬上收到幾個報價,也許你在一週內就能將房子賣掉。而在其他市場上,也許你要花6個月或更長時間才能將房子賣掉。在第二種情形中,如果你想馬上將房子賣掉,也許你所能得到的價格會遠遠低於市場的估價。
金融資產與房地產有非常相似之處,有時市場流動性很差(例如,1998年俄羅斯國債違約後,或2007~2008年次債危機後),這時即使變賣很小數量的資產也會花很長時間,甚至根本賣不出去。但在市場流動性很好的其他情形下,即使賣出較大數量的資產也不會出現什麼問題。
出售數量巨大的資產可能會淪為“掠奪性交易”(predatory trading)的受害者。情況通常發生在這樣的情形下:某市場參與者(假設為公司A),持有數量巨大的類資產,而其他市場參與者猜測公司A將被迫在短期內將這些資產平倉,此時這些市場參與者就會與公司A進行同樣的交易,以試圖從中牟利。比如,如果市場預期公司A將必須出售大量的某隻股票,其他的參與者就會事先做空這隻股票,以期在股價下跌時獲利。如果發生這種情況,公司A就難以用比較有競爭力的股價,從自己的持倉中脫身。為避免遭遇這種境地,金融機構都要求自己的員工對本機構的持倉和未來的交易計劃嚴格保密。在2012年發生的“倫敦鯨”事件(見業界事例25-1)以及德國金屬公司的案例(見業界事例24-3)中,掠奪性交易都扮演了重要角色。而在長期資本管理公司(見業界事例22-1)的案例中,基金所持頭寸在美聯儲的監督下緩慢平倉,從而避免了成為掠奪性交易的獵物。
金融資產市場的另一個問題是,當某家金融機構出於某種原因希望將某頭寸平倉時,常常其他金融機構也想做出類似舉動,因此正常市場存在的流動性可能會瞬間蒸發,隨之會產生流動性黑洞,我們在本章後面的內容中將對這一現象進行討論。
24.1.1 透明度的重要性
市場參與者從2007年的信用危機中所得到的教訓之一是透明度對流動性的重要意義。如果一個資產具有不確定性,那麼該資產的流動性也不會持續很久。
如第6章所示,在2007年以前,市場上非常流行建立次級按揭貸款和其他資產的組合,並通過證券化、再證券化甚至再再證券化將其中的信用風險生成金融工具。有些金融工具比第6章介紹的還要複雜,因為有時ABS CDO中包含了非按揭貸款,甚至是其他ABS CDO中的分檔。在2007年8月以後,市場參與者意識到自己對交易的這些產品的風險實際上知之甚少。更糟糕的是,要取得這方面的信息也很困難。當市場參與者意識到自己錯誤地用信用評級取代了對產品的真正理解時,為時已晚。
2007年8月以後,由次級按揭貸款所生成的債券流動性消失,金融機構沒有能力對自己幾個月前還爭先買入的投資進行盯市計價。它們意識到自己買入了高度複雜的信用衍生產品,而且沒有有效的工具給出其實際的價值。它們既缺少必要的模型,也沒有足夠關於衍生產品標的投資組合的信息。
與此相對照的是其他機制完善的信用衍生產品(例如信用違約互換),在2007年信用危機後一直在市場上進行交易。由此我們得出的教訓是:市場有時會被一些不透明的產品迷惑,但是一旦醒悟過來,這些產品的流動性會隨即消失。當這些複雜產品再次交易時,價格可能很低而且買賣價差可能會很高。如第6章所述,美林曾在2008年7月以每美元面值僅合22美分的價格賣給Lone Star Funds總額達306億美元的ABS CDO分檔(這些產品曾經的信用評級為AAA級)。
24.1.2 市場流動性的度量
某資產的買賣價差可以用貨幣值(dollar value)來衡量,也可以用與資產價格的比率來衡量。當以貨幣值衡量時,買賣價差為
p=賣出價-買入價
買賣價差比率(proportional bid-offer spread)的定義為

分母中的市場中間價等於買入價與賣出價的平均值。在有些情況下,使用貨幣值p可能會更方便,而在另外的情況下,使用差價比例s可能會更方便。
市場中間價可以被視為公允價值。當對某資產的頭寸進行平倉時,金融機構支付的費用為sα/2,其中α為頭寸的貨幣價值(市場中間價),這反映出市場交易並非以市場中間價格成交這一事實,而是買入交易以買入價格執行,而賣出交易以賣出價格執行。
一種度量交易賬戶流動性的手段是計算在一定的時間段,在正常市場條件下,對交易賬戶中的頭寸進行平倉的成本。假定si為某金融機構持有的第i個產品的買賣價差比率,αi為相應頭寸的貨幣價值,因此
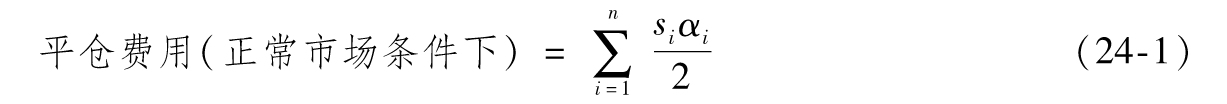
其中n為頭寸的總數量。注意,雖然產品的多元化會減少市場風險,但多元化並不一定會自動降低交易流動風險。如前所述,隨著第i個頭寸的增大,si會有所增大。持有許多小的頭寸而不是一個大的頭寸,會減小流動性風險。設定頭寸的限額(position limit)是減小交易流動風險的一種手段。
【例24-1】 假定一家金融機構買入1 000萬股某公司的股票,同時買入了5 000萬盎司某種商品。股票價格的每股買入價為89.5美元,賣出價為90.5美元;每盎司商品的買入價為15美元,賣出價為15.1美元。股票頭寸的市場中間價為90×1 000萬=9億美元;大宗商品頭寸的市場中間價為15.05×5 000萬=7.525億美元。股票的買賣價差比率為1/90,即0.011 11;大宗商品的買賣價差比率為0.1/15.05,即0.006 645,正常市場的平倉費用為(以百萬美元計)
900×0.011 11/2+752.5×0.006 645/2=7.5
即750萬美元。
另外一種檢驗流動性的方法是:計算在一定時間區間內,在受壓市場條件下的平倉費用。定義μi和σi為買賣價差比率的均值和標準差,因此
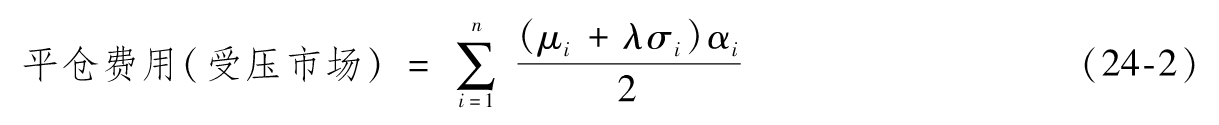
參數λ定義了差價的置信區間。例如,如果我們想求得在“99%的最差情形”下的平倉費用(即買賣價差僅有1%的概率會被超出的情況),假定價差服從正態分佈,那麼對於所有的i,λ=2.326。
【例24-2】 假定在例24-1中股票的買賣價差的均值和標準差分別為1.0及2.0,商品的買賣價差的均值和標準差均為0.1。股票的買賣價差比率的均值和標準差分別為0.011 11及0.022 22,商品的買賣價差比率的均值和標準差均為0.006 645。假定差價均服從正態分佈,在99%的置信程度下,平倉費用不會超過以下數額(以百萬美元計)
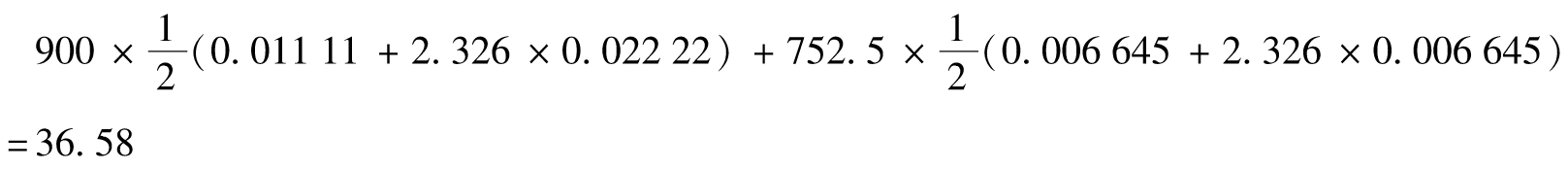
即3 658萬美元。這一費用幾乎是正常市場條件下平倉費用的5倍。
在實踐中,買賣價差並不服從正態分佈,參數λ需要被加以修正以便反映實際分佈。例如,對於某類金融產品,如果我們發現99%的分位數與均值的差距等於3.6倍的標準差,那麼這些產品的λ應被設定為3.6。
式(24-2)假設所有產品的價差之間有完美的相關性(即完全相關),這一假設看起來有些過分保守,但實際情況常常如此。當流動性較差,買賣價差較大時,所有產品差價均趨向於高度相關。對於金融機構而言,通過式(24-1)及式(24-2)的方式來定期監控流動性的變化非常有意義。正如我們看到的那樣,買賣價差與平倉的速度有關,因此式(24-1)及式(24-2)定義的測度應該是平倉時間長度的一個遞減函數。
24.1.3 經流動性調整的VaR
我們在第12~14章中討論的VaR是為了估算銀行交易賬戶在盯市計價前提下,對應於“最差情況”下的損失程度。式(24-1)和式(24-2)是為了計算當市場價格不變時,對交易組合進行平倉所需的費用。雖然VaR及流動性風險測度是為了度量不同的風險,但有些研究人員還是建議應該將它們結合起來,形成經流動性調整的VaR(liquidity adjusted VaR)。對這一概念的一種定義方法是由常規VaR加上正常市場平倉交易組合的費用。由式(24-1)出發,得出
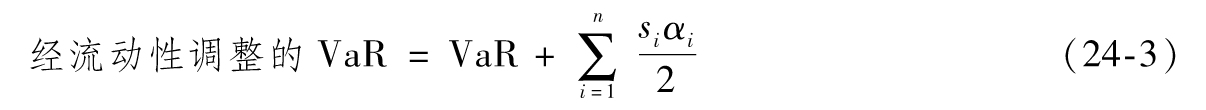
另外一種做法是,將其定義為常規VaR加上在受壓市場下平倉交易組合的費用,由式(24-2)出發,得出[1]
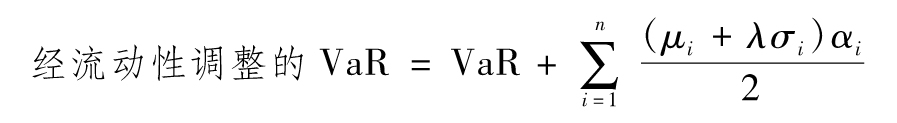
24.1.4 優化平倉
交易員想將一個持倉數量較大的金融產品平倉,一定要做出最佳交易決策。如果平倉太快,交易員將面臨很大的買賣價差,但因為平倉時間短,市場中間的變化不會太大;如果由交易員決定花幾天時間來將交易平倉,其面臨的買賣價差將會低一些,但是,由於中間市場價格變動而造成的潛在損失會大一些。
Almgren和Chriss(2001)在他們的文章中討論過這一問題。[2]假定某交易員想在n天內將V個單位數量的頭寸平倉。定義在一天內,交易員交易q單位數量債券的買賣價差為p(q)(以每單位美元價格計量),qi為在第i天的交易量,xi為第i天天末交易員的頭寸,1≤i≤n。由此得出,xi=xi-1-qi,1≤i≤n,其中x0等於最初的頭寸數量V。
每筆交易的費用為買賣價差的一半,買賣價差帶來的費用總共為
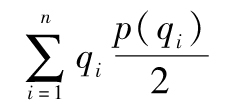
假設市場中間價格的變化服從正態分佈,每天變化標準差為σ,且交易均發生在每天的開始,交易員頭寸在第i天變化的標準差為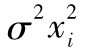 。假定在連續日期的價格變化是獨立的,因此對尚待平倉的頭寸,價格變化的標準差為
。假定在連續日期的價格變化是獨立的,因此對尚待平倉的頭寸,價格變化的標準差為
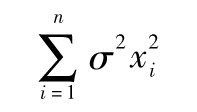
在考慮交易費用後,交易員可能對VaR進行極小化。被極小化的目標函數與式(24-3)定義的經流動性調節的VaR有些相似,交易員的目標是選擇qi,並在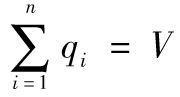 的條件下,使
的條件下,使
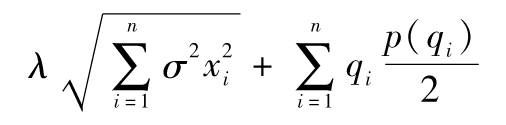
取得極小值。如上所述,xi通過V和qi來求得,參數λ給出了VaR估計值中的置信區間。例如,在每天價格變化服從正態分佈的假設前提下,考慮99%的置信水平,即λ=2.326。一旦估計出函數p(q),我們可以採用Excel中的Solver程序來對目標函數進行優化。
【例24-3】 假設某交易員希望在5天內將1億單位的某資產頭寸平倉,假定以貨幣值計,買賣價差與每天交易量的函數關係為
P(q)=a+becq
其中a=0.1,b=0.05,c=0.03,這裡q(以百萬計)為交易數量。
每天價格變化的標準差為0.1,在作者網頁(www-2.rotman.utoronto.ca/~hull/riskman)上,讀者可以下載一個計算優化交易策略的計算表。當置信區間設定為95%時,第1~5天的交易量分別為48.9、30.0、14.1、5.1、1.9(以百萬計)。當VaR置信度減小時,每日交易量變化的幅度也會變小。例如,當置信度設定為90%時,每日交易量分別為45.0、29.1、15.6、7.0、3.3(以百萬計);當置信度設定為75%時,每日交易量分別為36.1、26.2、17.7、11.6、8.4(以百萬計)。對於置信度小於50%的極限情形,交易員只對預期費用感興趣,而不再關心費用的標準差,這時,交易員每天需要交易2 000萬單位的資產。
這一例子說明,當頭寸需要在n天內平倉時,有超過1/n的資產需要在第一天內交易,這是因為持有頭寸的期限越長,市場朝不利方向變化所帶來風險也會越大。
24.1.5 度量市場流動性的其他方法
到目前為止,我們的討論集中在買賣價差這一度量市場流動性的指標上,還有很多其他的度量指標也已經被提出來。每日交易量(即每天發生在某資產上的交易次數)也是一個重要的指標。當一個資產流動性很差時,每日交易量常常為零。每筆交易的規模對價格的影響幅度是另外一個度量指標。Amihud(2003)[3]提出了一個與此類似,但計算更加簡便的指標。該指標是所考慮的時間段內,以下值的日平均值

這個指標現在已被研究人員廣泛採納。Amihud的研究表明某一資產的預期回報會隨著流動性的下降而上升,換句話說,投資者會為持有流動性差的資產而要求額外補償。
[1] A. Bangia, F. Diebold, T. Schuermann, and J. Stroughair, “Liquidity on the Outside,” Risk 12(June):68-73.
[2] See R. Almgren and N. Chriss, “Optimal Execution of Portfolio Transactions,” Journal of Risk 3(Winter 2001):5-39.
[3] See Y. Amihud, “Illiquidity and Stock Returns: Cross-Section and Time Series Effects,” Journal of Financial Markets 5(2002):31-56.
24.2 融資流動性風險
我們接下來考慮融資流動性風險,這種風險與金融機構在出現現金需求時,是否能夠滿足這種需求有關。在本章開篇部分中,我們曾指出流動性不同於償付能力,一個有償付能力(即股權值為正)的金融機構因為流動性困難也可能會破產。英國的一家按揭貸款商北巖銀行的破產就說明了這一點(見業界事例24-1)。
業界事例24-1
北巖銀行
英國北巖銀行由此前的北巖建築協會(Northern Rock Building Society)於1997年在倫敦股票交易所上市而創立。到2007年,北巖銀行已經成為英國前五大按揭貸款提供商。當時北巖銀行已有76家分行,其提供的服務包括存款賬戶、儲蓄賬戶、貸款和住房及財產保險。這家銀行在1997~2007年發展迅猛,其發行的部分按揭貸款通過其在開曼群島註冊的子公司Granite進行了證券化。
北巖銀行主要依靠出售短期債券來融資。自2007年8月次債危機後,銀行發現很難再通過發行新債券來替換已到期的債券,這是因為機構投資者不願意借出資金給那些在按揭業務中涉足太深的銀行。當時,銀行資產足以償還負債,因此北巖銀行沒有喪失償還能力。英國金融服務監管局(Financial Services Authority,FSA)在2007年指出“FSA斷定北巖銀行具有償付能力,資本金持有量超出監管資本金的要求,並且其貸款組合的質量很好”,但北巖銀行無法籌措資金,這給其運作帶來了嚴重困難。北巖銀行在2007年9月12日向英格蘭銀行求助,並在接下來幾天內,向三方監管部門(Tripartite Authority)——英格蘭銀行、英國金融服務監管局以及英國財政部(HM Treasury)借入了30億英鎊的資金。
2007年9月13日,英國廣播公司(BBC)的商務欄目編輯羅伯特·佩斯頓(Robert Peston)發佈消息,聲稱北巖銀行已經向英格蘭銀行尋求緊急救助。9月14日,星期五,北巖銀行出現了擠兌現象,數以千計的北巖銀行客戶排長隊提取存款,這是150年來首次出現的英國銀行擠兌現象。北巖銀行的某些客戶持有“純網絡”(internet-only)賬戶,因為嘗試登錄網絡的客戶過多,導致很多客戶不能夠訪問自己的賬戶。9月17日,星期一,憂心忡忡的存款人繼續提取存款。據估計,從2007年9月12日到9月17日客戶提取的資金總量達20億英鎊。
英國存款保險對儲戶2000英鎊以內的存款有100%的保障,對2000~33000英鎊的存款有90%的保障。在2007年9月17日晚間,英國財務大臣阿利斯泰爾·達林(Alistair Darling)宣佈,英國政府和英格蘭銀行將保證北巖銀行客戶全部存款的安全。在這一消息公佈後,英國報紙進行了大量宣傳,北巖銀行分行外的長隊才逐漸消失。在達林先生的消息公佈之後,北巖銀行股票自2.67英鎊回升了16%,而在當年年初,其股價為12英鎊。
在2007年9月12日以後的幾個月內,北巖銀行尋求的緊急救助資金大幅增加。英格蘭銀行堅持對北巖銀行的資金施以懲罰性利率,這樣做是想告誡其他銀行不要承擔過多風險。北巖銀行通過變賣資產籌措了一些資金,但到2008年2月為止,緊急救助資金的需求已高達250億英鎊。這時英國政府宣佈將北巖銀行國有化,銀行的管理團隊也被更換。銀行被拆分成北巖公共有限公司(Northern Rock plc)和北巖資產管理(Northern Rock Asset Management)。銀行的壞賬由北巖資產管理繼承。2011年11月,由帶有傳奇色彩的企業家理查德·布蘭森(Richard Branson)爵士領導的維珍集團(Virgin Group)以7.47億英鎊的價格從英國政府手中收購了北巖公共有限公司。
北巖銀行的故事說明流動性問題可以使一家銀行在短時間內陷入崩潰邊緣。如果這家銀行管理得更保守一點,更注意確保自己能夠獲得融資,則它可能會存活下來。
金融機構中融資流動性問題來源於以下方面:
(1)宏觀經濟環境造成的流動性壓力(例如,2007~2009年金融危機期間的安全投資轉移)。投資者不願意為任何有信用風險的資產提供資金。
(2)過於激進的融資決策。所有的金融機構都有用短期工具支持長期資金需求的傾向,並因此造成流動性錯配。金融機構需要問自己一個問題:“多少錯配才算多?”
(3)財務表現欠佳,造成信心缺乏,由此可能導致儲蓄流失以及滾動融資困難。
通常,當一家公司遭遇嚴重的流動性問題時,上述三種情況是相伴發生的。管理流動性風險的關鍵是預測現金需求並保證在不利情況下也能滿足這些需求。有些現金需求可以被較好地預測到,例如一家銀行發行了債券,銀行知道息票的支付時間。對於其他的情況,例如零售客戶提取存款,或企業使用銀行提供的信用額度時,流動性的可預測性則相對較小。而隨著金融機構交易的產品越來越複雜,對現金需求的預測也會變得越來越困難。例如信用觸發條款(見第20.2.3節)、金融機構提供的擔保以及衍生產品中交易對手的破產均會對現金來源產生難以預料的影響。
24.2.1 流動性的來源
金融機構的流動性主要來源如下:
(1)持有的現金和隨時可以變現的短期國債;
(2)變賣交易賬戶中頭寸的能力;
(3)在短時間內拆借現金的能力;
(4)在短時間內通過有利的條款以吸引零售和批發存款的能力;
(5)在短時間內將資產(例如貸款)進行證券化的能力;
(6)由中央銀行借入資金。
下面我們逐一討論這些項目。
1. 現金和國債
現金和國債是非常好的流動性來源。現金理所當然地可以隨時用來滿足流動性要求,而諸如由美國和英國政府發行的國債通常可以在短時間內很容易地變現。但是現金和國債作為流動性來源,是比較昂貴的。在資產所提供的流動性與其所提供的收益之間通常需要做一定的權衡。為了能夠盈利,金融機構必須投資於諸如企業貸款一類的資產。相對於國債,這些資產帶來的收益較高。因此,金融機構合理地持有的現金和國債是有一定限制的。
2. 變賣交易頭寸
在第24.1節中,我們曾討論過融資流動性風險與交易流動性風險是相關的,因為金融機構滿足融資流動性的一種手段是變賣交易賬戶中的部分頭寸。因此,對金融機構而言,對交易賬戶的流動性進行量化,進而把握使用交易賬戶來籌措現金的能力是非常重要的。金融機構要保證自己能在市場受壓的情況下存活下來,在這種市場狀況下,通常流動性是短缺的。因此,對流動性的分析應基於受壓市場條件,而不是正常市場條件。這也是上一節所討論的流動性測度要考慮受壓市場條件下的買賣價差的原因。
3. 拆借現金的能力
在市場狀況正常時,信用良好的銀行拆借現金通常是沒有什麼困難的。但在市場承壓的狀況下,市場上對風險的厭惡程度會上升。這就導致貸款的利率更高,期限更短,甚至在有些情況下貸不到款。金融機構應監控那些可以在短時間內轉換為貸款擔保品的資產的狀況。金融機構可以通過從其他金融機構獲得授信額度(當然有一定成本)的辦法,來降低自身的融資流動性風險。例如美國的一家抵押貸款發行商Countrywide,有一筆115億美元的財團貸款便利(loan facility)。在2007年的金融危機中,該便利被用來救急(儘管如此,Countrywide還是遭遇了嚴重的問題,於2008年1月被美國銀行收購)。如業界事例24-1討論的,英國一家類似的住房貸款提供商北巖銀行則沒有做到這一點。
4. 零售和批發存款的能力
相比零售存款,批發存款是變動幅度更大的資金來源,在市場受壓的情況下,可能迅速枯竭,但即便是當今的零售存款也不像從前那樣穩定。現在存款人可以很容易地比較不同金融機構提供的存款利率,並可以通過互聯網來轉移資金。然而,流動性不是隻影響一兩家金融機構的問題,而是整個市場所面臨的問題。當一家金融機構因為流動性問題而試圖吸納更多的批發及零售存款時,其他金融機構往往也有類似的需求,因此增大存款市場份額的願望並不十分容易實現。
5. 證券化
如第2章所述,銀行發現發起-分銷的經營模式確實很具吸引力。銀行與其將流動性不好的資產保留在資產負債表上,不如將這些資產進行證券化。我們曾在第6章中討論了證券化的過程。在2007年8月以前,證券化是銀行一個很重要的流動性來源。但是在2007年8月後,投資者發現證券化產品風險太大,使得這種資產的流動性在瞬間消失,發起-分銷模式難以為繼。銀行不得不為發放的貸款提供資金支持,因此銀行變得不再那麼願意發放貸款。
證券化還導致了2007年8月後的其他流動性問題。很多銀行有為資產支持商業票據(asset-backed commercial paper,ABCP)提供流動性支持的安排。這些票據被用來為證券化之前的債務類產品如按揭貸款提供資金支持。當投資者不再願意購買資產支持商業票據時,銀行就不得不將這些票據收入自己賬下。有時為了避免聲譽受到不良影響,即使在沒有法律責任的情況下,銀行也不得不對參與證券化的“管道”(conduit)公司及其他資產負債表外機構進行財務支持。
6. 由中央銀行借入資金
中央銀行(例如美國的美聯儲、英國的英格蘭銀行及歐洲中央銀行)常常被認為是最後貸款人(lenders of last resort)。當金融機構面臨財務困難時,為了保證金融系統的安全,央行往往會向出現危機的機構提供資金支持。借入資金的銀行必須提供擔保品,央行通常要對擔保品折價,即借出資金的數量會低於抵押品的價值,且中央銀行通常會收取很高的利息。2008年3月,在貝爾斯登(後來被摩根大通收購)出現問題時,美聯儲為投行及商業銀行延長了拆借便利,[1]後來這些便利也向房利美及房地美(二者在2008年9月被美國政府接管)開放。
不同央行的拆款規定各不相同。在2007年8月信用危機後,歐洲中央銀行(European Central Bank,ECB)的折價率比其他中央銀行更小。因此有些英國銀行更希望從ECB借入資金,而不是從英格蘭銀行借入資金。有一種說法是,甚至北美一些銀行也考慮在愛爾蘭開設分行來取得歐洲中央銀行的資金。截至2008年9月,ECB共借出了4670億歐元資金。在這之後,ECB宣佈它將實行更高的折價率。
銀行一般對自己從央行借入資金的舉動保持低調。因為從央行舉藉資金的行為可能被市場解讀為銀行運作出現困難,從而導致喪失其他流動性的來源。如業界事例24-1所示,關於北巖銀行需要緊急救助資金的消息導致了儲蓄客戶的擠兌行為,進一步加劇了流動性問題。
7. 對衝問題
當一家公司利用有保證金要求的合約來對衝流動性差的資產時,往往會出現流動性問題。如業界事例8-1所示,金礦公司往往採用與金融機構簽署的在2~3年內賣出黃金的遠期合約來對衝風險。在遠期合約中金礦公司要支付保證金,而且保證金的數額是每日計算的,以反映遠期合約的價值。如果黃金價格上升很快,遠期合約價值就會快速下降,這會造成金融機構向金礦公司催收鉅額保證金的局面。遠期合約的損失會被尚未開掘的黃金價格的上升所抵消,但是地下的黃金不具備流動性。如業界事例24-2所示,Ashanti Goldfields公司在黃金價格急速上漲而不能滿足保證金催收時,不得不對公司進行了一個大的改組。
業界事例24-2
Ashanti Goldfields
Ashanti Goldfields是一家位於加納(Ghana)的西非金礦公司,該公司在1999年因為對衝而面臨運營困難。最初,為了保證其股東在黃金價格下跌時不受損失,公司決定使用遠期合約來對衝風險。在遠期合約中,Ashanti Goldfields以固定價格賣出黃金。在1999年9月26日,歐洲中央銀行突然宣佈它們將在接下來的5年中對黃金的出售保持克制,這個消息令市場感到意外。消息公佈後,黃金價格一下上漲了25%。Ashanti Goldfields不能滿足遠期合約中的保證金催收要求,不得不進行大的改組,其中包括出售一個礦井、稀釋股東權益以及重新建立對衝頭寸等。
另外一個因為對衝帶來融資流動性困難的極端例子源自一家德國公司——德國金屬公司(Metallgesellschaft,MG)。最初,這家公司與客戶之間簽署了協議,在協議中該公司以固定價格向其客戶提供石油及天然氣(見業界事例24-3)。Ashanti Goldfields和德國金屬公司的事例並不是說公司不能使用遠期或期貨合約來對衝風險,而是公司在進入合約時,應確保自身有足夠的資金來應對在緊急情形下的資金需求。
業界事例24-3
德國金屬公司
20世紀90年代初期,德國金屬公司(MG)以高出市場價6~8美分的固定價格向客戶售出了大筆5年及10年期的取暖油以及汽油合約。為對衝這些敞口,這家公司買入短期期貨並對這些短期期貨進行滾動展期。但在這麼做了以後,油料價格下降,期貨合約中的多頭觸發了增補保證金的要求。雪上加霜的是,MG的交易量特別大,而且能夠被其他市場參與者所預見,因此交易變得愈加困難。
MG的短期現金流承受了巨大的壓力。MG對衝策略的設計者認為短期資金外流會被長期固定合約的正收益所補償,但是MG的高管及為其提供服務的銀行對鉅額的現金流出產生了擔憂。結果是,公司決定將所有的對衝交易平倉,並且與那些持有固定價格合約的客戶達成協議,將合約取消。最終這些事件造成了MG 13.3億美元的損失。
24.2.2 準備金要求
有些國家存在準備金制度,要求銀行將存款的一部分以現金的形式存放在銀行的金庫或存入央行賬戶。準備金的要求只適用於交易存款(transaction deposits,實際上就是存入支票賬戶的存款)。對於美國大銀行而言,目前準備金的要求為10%。而某些國家(例如加拿大和英國)沒有強制的準備金要求,另外一些國家的準備金要求要高於美國。
除了用來確保銀行有最起碼的流動性,準備金要求還會影響市場的貨幣供應。當準備金要求為10%時,100美元的存款只有90美元可用於貸款,而這些貸款又會給金融系統帶來90美元的存款,從而又產生了81美元可用於貨款,這個過程會一直持續。隨著這個過程進行下去,市場上的總貨幣供應量(M1)[2]為90+81+72.9+…,即900美元。當準備金的要求為20%時,100美元的存款可以產生80美元的貸款,進而產生64美元貸款等,這時整體M1貨幣供應量為400美元。大多數國家並不採用調整準備金率的方式來管理貨幣供應量,但中國是一個例外。中國對準備金的要求經常發生變化。
24.2.3 監管規則
如在第16章中介紹過的,《巴塞爾協議Ⅲ》引入了兩個流動性風險要求:流動性覆蓋比率(LCR)和淨穩定融資比率(NSFR)。
對LCR的要求是

計算LCR時考慮的30天期限要包含嚴重受壓的情景,如信用評級被下調3個等級(例如從AA+降到A+)、失去部分存款、喪失全部批發融資渠道、抵押品折價率升高和信用額度提取完畢等。LCR在2015~2019年執行(2015年要求的比率為60%,2019年要求的比率為100%)。
對NSFR的要求是

其中分子數量等於每項可得資金(資本金、機構存款、零售存款等)乘以一個可得穩定資金因子(ASF因子)再求和,其中ASF因子反映了不同種類資金的穩定性(見表16-4)。分母由需要資金支持的資產和表外項目計算得出,每一項要乘以一個所需穩定資金因子(RSF因子),該因子反映了資金需求的穩定性(見表16-5)。這一要求計劃在2018年1月1日起實施。[3]
在2007年流動性危機之後,銀行監管部門修改了關於銀行管理流動性的規則,[4]這些規則可以總結如下。
(1)各銀行必須承擔穩健管理流動性風險的責任。銀行須制定流動性風險管理框架來保證維持足夠的流動性。其中包括通過持有不受限的、高流動性資產來建立流動性風險緩衝,以應對極端受壓情況,如部分或全部喪失擔保和非擔保融資渠道。銀行監管部門應該對銀行的流動性風險管理框架和流動性資產持有水平進行評估,確保其滿足要求。在銀行不能滿足其中任何一項要求時,監管部門要迅速採取行動,以保護存款人並避免對整個金融系統產生衝擊。
(2)銀行必須明確地闡明自身的流動性風險容忍度,並確保其容忍度與其業務戰略相符,同時也要與銀行本身在金融系統中所扮演角色相符。
(3)銀行的高管必須制定與風險容忍度相符的流動性風險管理戰略、政策和實施措施,並保證銀行持有足夠的流動性。高管應時刻注意銀行流動性水平的變化並定期向公司董事會報告。銀行董事會應至少每年審查和批覆以上戰略、政策和措施,並保證高管對流動性風險的管理是有效的。
(4)在所有重要的業務活動中,銀行都應將與流動性相關的成本、收益和風險引入內部定價、績效評估和新產品核准過程中,不論這些活動是在資產負債表內還是表外。由此,可使各個業務部門的風險激勵(risk-taking incentive)與其業務活動在整個銀行層面帶來的流動性風險保持一致。
(5)銀行應該具備識別、度量和監控流動性風險的完善過程。這一過程應包括一個健全的框架,以預測銀行的資產、負債以及資產負債表外項目在一個合理的時間跨度內、不同情形下所產生的現金流。
(6)銀行應主動地監控其所有的法律實體(即分公司)、業務部門和貨幣種類內部以及彼此之間的流動性風險敞口與融資需求,並考慮到與流動性轉移有關的法律、監管規則和操作等方面的限制。
(7)銀行應建立適當的融資戰略,以保證資金來源以及期限的多元化。在其選定的融資市場上,銀行應保持業務的連續性,並和資金提供者建立密切的聯繫,以提升資金來源的多樣性。銀行應經常性地調整自己從不同的渠道快速獲取資金的能力,識別會影響這種快速融資能力的關鍵因素,並對這些因素進行密切監控,從而保證預估的融資能力是真實有效的。
(8)銀行應主動地管理其日間流動性頭寸(intraday liquidity position)及風險,並保證在正常及受壓市場條件下均能及時滿足付款及交割義務,並以此對金融體系中支付和交割活動的平滑運作做出貢獻。
(9)銀行應該積極地管理其擔保品頭寸,對有擔保負擔的資產(encumbered asset)和無擔保負擔的抵押資產(unencumbered asset)區別對待。銀行應對持有擔保品的法律實體和其所在地理位置進行監控,以備不時之需。
(10)銀行要定期進行壓力測試。測試應涵蓋短期和長期不同時間跨度、與金融機構自身有關的特定情景以及整個市場均處於受壓狀態的情景。通過單獨的情景或綜合眾多情景,識別會造成流動性枯竭的原因,並保證當前的風險敞口處於銀行確立的流動性風險容忍度之內。壓力測試結果應被用於調整銀行的流動性風險管理策略、產品頭寸及開發有效的預案。
(11)銀行應制定正式的融資計劃預案(contingency funding plan,CFP),其中須明確緊急情況下應對短期流動性的策略。預案應明確針對不同受壓環境的政策,建立清晰的問責制度,還應包括請求協助及向上彙報的過程。對預案應進行定期測試,以保證其具備良好的可操作性。
(12)為了能夠應對不同的流動性受壓情景(如全部或部分喪失無擔保和通常情況下有擔保的資金來源),銀行應該持有一定數量的、具有高流動性並無擔保責任的資產作為緩衝。在使用這些資產來取得資金時,不應該有任何關於法律、監管及操作方面的障礙。
(13)銀行要定期公開披露自己的信息,以使市場參與者能對其流動性風險管理框架和流動性資產持倉水平的可靠性做出有依據的判斷。
對監管部門的建議是:
(14)監管部門應該定期對銀行的整體流動性風險管理框架和流動性資產持倉水平進行全面評估,以判斷銀行對流動性風險是否有足夠的應對措施,並與銀行在金融系統中所扮演的角色相符。
(15)監管部門在對銀行的流動性風險管理框架和流動性資產持倉水平進行評估時,還應綜合考察銀行的內部報告和市場信息。
(16)如發現銀行的流動性風險管理過程或流動性資產水平存在不足之處,監管部門應要求銀行及時採取相應的補救措施。
(17)國內和國際監管部門之間以及公共職能部門(如央行)之間應相互交流,在對流動性風險管理的監督和審查過程中相互合作。這種交流在平時應定期進行,而在市場受壓時,交流的深度和頻率都應相應加強。
[1] 中央銀行擔心投資銀行破產會引發系統性風險(見業界事例15-1)。投行與其他投行及商業銀行之間簽有衍生產品交易,這些衍生產品交易數量很大。危險的是,因為銀行之間的鉅額交易,一家投行破產可能會引發金融行業內的連鎖反應,進而可能導致商業銀行的破產。
[2] 即狹義貨幣。——譯者注
[3] 因為NSFR對銀行影響較大,有些國家的監管機構將其實施期限延後。例如加拿大將NSFR的實施時間從2018年1月1日推後了1年到2019年1月1日。——譯者注
[4] See Bank for International Settlements, “Principles for Sound Liquidity Risk Management and Supervision,” September 2008.
24.3 流動性黑洞
人們有時認為,科技及其他領域的進步已經改善了金融市場的流動性,這種說法值得商榷。市場上的買賣價差確實呈下降的趨勢,但也確實出現了在同一時刻幾乎所有的市場參與者都想進行同樣交易的傾向。這也就產生了所謂的流動性黑洞現象,並且這一現象產生的頻率在逐漸增加。[1]流動性黑洞是指,在某一市場上,幾乎所有人都希望買入(而不希望賣出)或賣出(而不買入)而造成的市場流動性枯竭現象。這種現象有時也被稱作“出口擁堵”(crowded exit)。[2]
在一個運作良好的市場上,因為新的信息出現,市場參與者可能會改變他們對某個資產價格的觀點。但在這樣的市場,價格變化不會對新信息過分敏感。如果價格下跌幅度太大,市場參與者就會馬上行動買入資產,這時一個新的均衡價格會被建立;當一個資產的價格大幅度下跌時,造成更多的市場參與者都想賣出,從而導致價格遠低於其平穩成交價格時,就會產生流動性黑洞。在市場大量拋售資產時,流動性會枯竭,這時資產只能以大甩賣的價格賣出。[3]
24.3.1 正反饋和負反饋交易員
金融市場的流動性變化取決於市場交易員的行為。市場上存在兩類交易員:提供負反饋(negative feedback)的交易員和提供正反饋(positive feedback)的交易員。[4]負反饋交易員在價格下跌時買入資產,而在價格上漲時賣出資產;正反饋交易員在價格下跌時賣出資產,而在價格上漲時買入資產。
在一個具有流動性的市場裡,負反饋交易員佔據交易的主導地位。當一個資產的價格低於合理價格時,交易員會買入資產,從而造成了市場需求,使得資產價格回升到一個較為合理的價位;類似地,當一個資產價格上升太大時,交易員會出售資產,這時會產生資產供應,使資產價格回落到一個更為合理的價位。以上過程促使資產價格在買方和賣方之間實現平衡,從而使市場具有良好的流動性。
當正反饋交易員主導交易時,資產的價格會趨向於不穩定,市場會變成單邊市場,流動性會變差。這時資產價格下跌會導致交易員變賣資產,從而造成價格進一步下跌和更多的資產被出售;資產價格上漲會促使交易員買入資產,使得資產價格進一步上漲,這又會造成更多的資產被買入。
市場上存在正反饋交易有若干原因,例如:
(1)趨勢交易(trend trading):趨勢交易者試圖識別資產價格的趨勢。他們在資產價格上漲時買入,在資產價格下跌時賣出。一個相關的策略是突破交易(breakout trading),指當資產價格超出一個確定的範圍之外時的交易。例如,如果一隻股票在過去6個月的交易價格在25~30美元,交易員可能傾向於在價格高於30美元時買入,在價格低於25美元時賣出。
(2)止損規定(stop-loss rules):交易員通常受制於損失額度的規定。當某資產價格下跌到一定水平時,他們要自動賣出資產以限定損失的幅度,這些規定就是所謂的止損規定,這也是正反饋的來源之一。市場上總是存在這一現象。
(3)動態對衝(dynamic hedging):在第8章中,我們討論了期權交易員可以採用動態對衝來保持投資組合的delta中性狀態。表8-2及表8-3說明了交易員如何在20周內對一個期權空頭進行對衝。要對(看漲或看跌)期權空頭進行對衝,我們需要在價格上漲時買入標的資產,並在價格下跌時賣出標的資產。該類對衝所產生的交易具有正反饋效應,有可能降低市場流動性(與之相對,對一個(看漲或看跌)期權的多頭進行對衝需要在價格上升時賣出資產,並在價格下跌時買入資產,這種交易具有負反饋效應,因此不會對市場的流動性產生負面作用)。當銀行持有大量期權空頭時,又可能會造成市場的不穩定性和低流動性。如業界事例3-1所示,銀行曾經向英國保險公司賣出了大量的長期限的利率期權,當銀行對衝自身風險時,英國的長期利率的變化受到了嚴重影響。
(4)產生合成期權(creating options synthetically):對期權的空頭進行對衝,與以合成的方式產生期權的多頭頭寸是等價的。正是這個原因,金融機構可以進行市場交易來生成合成期權,就如同對期權空頭進行對衝那樣。合成期權交易會導致正反饋交易的產生,從而會影響市場的穩定性,並導致流動性惡化。1987年10月的股票市場大跌就是一個經典實例。在大跌的前一段時間,股票市場表現良好,這時有越來越多的投資組合經理採用商業軟件,以合成的形式產生所持投資組合的看跌期權。軟件會提醒投資組合經理在價格下跌時賣出組合資產的一部分,並在價格上漲時馬上買入組合資產的一部分。如業界事例24-4所示,投資組合經理的交易行為在1987年10月19日造成了流動性黑洞的產生。當時,股票價格暴跌。相對來講,1987年的流動性黑洞現象是短期的,市場在4個月後恢復到暴跌前的水平。
業界事例24-4
1987年股票暴跌
1987年10月19日,星期一,道瓊斯工業平均指數下跌幅度超過20%。在這次下跌中,組合保險策略起了關鍵的作用。1987年10月,有超過600億美元的股票資產被用於組合保險策略。這一保險策略以合成的形式構造了組合的看跌期權,即在股市下降時,賣出股票(或賣出指數期貨);在股市上升時,買入股票(或買入指數期貨)。
在1987年10月14日星期三至1987年10月16日星期五這段時間,市場下跌了近10%,其中大部分跌幅發生在星期五的下午。由此,由交易組合保險策略程序顯示至少有120億美元的股票或股指期貨需要被出售。然而事實上,當天交易組合保險持有者在當天只來得及賣出價值40億美元的資產。在接下來的一週,保險持有者需要繼續賣出大筆的資產以達到他們的模型所要求的數量。據估計,10月19日由三家交易組合保險持有者所賣出的股票數量佔整個紐約股票交易所成交量的10%,而整個交易組合保險策略所產生的交易佔到了整個股指期貨交易的21.3%。其他投資者預見到交易組合保險持有者會大筆拋出股票,這些投資者也紛紛將自己的股票拋出,這可能也進一步加劇了股票市場的下跌幅度。
股票市場下跌造成了整個交易市場的超負荷運作,許多組合保險持有者不能夠及時完成模型所要求的交易,因此組合保險也沒有帶來預定的效果。不管怎麼說,1987年後,交易組合保險策略不再受人青睞。這一事件說明當所有市場參與者都在從事某種交易時,如果我們也進行類似策略(即使是對衝策略),則可能會非常危險。在這裡我們引用Brady關於暴跌的報告:“當所有的投資者同時出現在某類交易的同一側時,小額交易市場流動性的充足會使人產生錯覺,認為在大量交易的情況下,市場也具備流動性。具有諷刺意味的是,正是這個錯覺,使很多具有相似動機的投資者(例如,組合資產保險的投資者)採用的交易策略所需要的流動性遠遠超出了市場所能提供的流動性。”
(5)保證金:當市場變量有一個大幅度變化,特別是當交易員的頭寸具有很高的槓桿時,可能會造成保證金催付。這時交易員可能沒有足夠多的資金來滿足保證金催付要求,而不得不將交易平倉。這會進一步導致市場變量朝某個方向移動。波動率很可能會增加,並使得形勢進一步惡化,因為交易所會因此增加保證金要求。
(6)掠奪性交易:這在第24.1節中提過。如果交易員事先知道某企業遇到了麻煩,將被迫大量拋售某資產,他們就會知道該資產的價格很可能會下跌。因此,他們會賣空該資產。而這將加劇價格的下滑,且下滑的幅度會比沒有賣空行為時更大。為避免成為掠奪性交易的受害者,對大量資產的平倉要緩慢進行。
(7)LTCM:業界事例22-1所描述長期資本管理公司(LTCM)的失敗就是一個正反饋效應的實例。LTCM交易中的一類交易為“相對價值固定收益”(relative value fixed income)。在這類交易中,LCTM持有流動性較好的債券的空頭頭寸,並同時持有與之類似,但流動性較差的債券的多頭頭寸。LCTM持有這些頭寸的目的是等待兩類債券的價格在將來趨於一致。1998年俄羅斯國債違約後,相對於流動性好的債券,流動性較差的債券價格開始下跌。LTCM(及與LTCM持有類似頭寸的公司)的頭寸具有高槓杆,它們不能滿足保證金催付的要求,只能將交易平倉。而平倉交易需要買入流動性好的債券並同時賣出流動性差的債券,這些交易會進一步加重安全投資轉移現象,進一步造成不同流動性的債券之間價格的偏離。
24.3.2 槓桿化和去槓桿化
槓桿化和去槓桿化是市場上的常見現象。圖24-2及圖24-3描述了這兩個過程。當銀行具有充足的流動性(例如,銀行能夠對資產進行證券化或存款水平比一般情況更高)時,銀行會比較容易地給企業、投資者及消費者提供更多的信用,這時信用價差會降低。而當信用的獲取變得更加容易時,市場對金融及非金融資產的需求也會隨之增大,從而使得資產價格上揚。資產常常被用作貸款的擔保品,而貸款又被用作買入資產的資金。當資產價格上升時,作為貸款擔保品的資產價值(以市場價格計)也會增加,使得貸款額度可以進一步增加。這就造成更多的資產會被買入,並由此循環下去。這種循環會造成經濟生活中產生更多的貸款,因此被稱為槓桿化(leveraging)。
圖24-2 槓桿化
圖24-3 去槓桿化
去槓桿化(deleveraging)與槓桿化過程正好相反。因某種原因銀行發現流動性不足(例如,市場對證券化產品的需求下降),這時,銀行不願意再提供貸款,信用價差會增大,市場對金融資產及非金融資產的需求會下降,資產價格會下跌,用於支撐貸款的擔保品價值也會下跌,銀行會因而減少信用額度,這會進一步造成資產的拋售,也會加劇資產價格的下跌。
世界不同地區的經濟形勢在2007年之前均呈現槓桿化的特徵。在這一期間,信用價差下降。不管是為了做什麼,貸款人都可以較為容易地取得貸款。但自2007年年中開始,形勢發生了變化,由圖24-3所示的去槓桿化現象開始出現,信用價差開始增大,在市場上不再那麼容易取得貸款,資產價格開始下跌。[5]
對衝基金受到槓桿化和去槓桿化週期的影響尤其顯著。考慮一家對衝基金,該基金可以借入的資金是自身股本的20倍。2007年下半年開始,對衝基金經理可能會從其機構經紀那裡得到警示需要降低槓桿。假定槓桿需要被減至5倍,對衝基金只有變賣資產才能達到目的,這家對衝基金及其他類似的對衝基金的做法會使資產價格下跌。對衝基金的股本價值也會下跌,從而必須賣出更多資產。
24.3.3 非理性繁榮
1996年12月,美聯儲前主席艾倫·格林斯潘在談到股票市場時提出了“非理性繁榮”(irrational exuberance)這一說法。格林斯潘說道:“我們怎樣才能知曉非理性繁榮何時過分地推高了資產價格呢?”(“非理性繁榮”這一詞彙一直被市場參與者銘記在心,因為在格林斯潘演講之後,全球股市全線下跌。)大多數的流動性黑洞可以歸根於各類不同的非理性繁榮。非理性繁榮的產生是因為受僱於很多不同金融機構的交易員,對於某種資產或某個市場變量進行了不理性的追捧,造成金融機構的資產負債表過多地累積了對該資產或該變量的風險敞口,而且這種過程會不斷地自我強化。當許多金融機構決定進入某個特定的頭寸時,與之有關的資產價格會上升,這使得金融機構的頭寸看起來會帶來利潤,而這又會使金融機構有更大的慾望進入更多類似的頭寸以從中獲利。金融機構中的風險管理人員應該對機構所承擔的風險表示疑義(也許他們會這樣做的),但大多數時候金融機構的高級管理人員可能會對這些質疑採取置之不理的態度,因為這些高風險業務線還在賺錢。正如花旗銀行的前CEO查克·普林斯(Chuck Prince)在2007年7月10日指出的那樣:“如果將流動性比作音樂,當音樂停止時,事情會變得複雜,但只要音樂還在演奏,你就必須起來跳舞。我們到現在還一直在跳舞。”
最終,在某個時刻,市場的泡沫總會破裂。許多交易員會同時試圖平倉,這會引發流動性的消失,從而造成鉅額損失。波動率的增大以及金融機構採用的風險管理步驟(例如,由歷史數據來計算市場VaR)會導致許多金融機構同時對某個較大規模的風險頭寸進行平倉。這有可能引發進一步損失,並造成更加嚴重的流動性問題。一些銀行可能會破產或受到破產謠言的打擊。多數銀行可能會經歷流動性融資困難,因此會收緊貸款的發放。
關於以上討論的一個經典實例就是2007年開始的次債危機。其他例子包括1987年的股票市場的暴跌、1994年債券市場的暴跌、1997~1998年的亞洲金融危機和1998年長期資本管理公司的破產。非理性繁榮是人類的特性之一。從某種意義上講,這一現象不可避免。如第6章所述,交易員薪酬制度進一步促成了非理性繁榮的產生。我們知道交易員薪酬中的一大部分是年終獎金,年終獎金與交易員當年的表現有關。一個交易員的頭腦可能十分清醒,意識到市場上出現了非理性繁榮,並且遲早會調整。但是,如果交易員判斷市場調整很可能要明年才會發生,那麼他仍會有動機繼續建立自己的頭寸,以圖短線回報最大化。
24.3.4 監管規定的影響
從許多方面我們都已經看到建立全球統一的政策來確保世界各地的銀行遵循同樣的監管規定是監管部門的一個重要目標,這一點是值得稱道的。像我們在第15章中解釋的那樣,在《巴塞爾協議Ⅰ》之前,世界上不同國家對於資本金的要求和執行力度各不相同。銀行必須在全球範圍內競爭,那些受較低資本金制約或者所受的監管規定執行不夠嚴格的銀行就能更容易地承擔風險,並因而在對某些產品的定價方面享有競爭優勢。
但是,打造一致的監管環境是需要代價的。所有銀行對外部事件的反應會比較一致。以市場風險為例,波動率及相關性的變大會造成市場VaR數量和市場資本金的增大,因此銀行會盡量減小自己的風險敞口。銀行所持交易比較類似,不同銀行會做出類似的交易舉動,這時流動性黑洞也會因此產生。
信用風險管理過程中也有類似的問題。當經濟週期處於最低點時,違約概率會相對較高,因此由《巴塞爾協議Ⅱ》中內部模型法所測算的用於貸款的資本金要求也比較高。這時銀行不太願意借錢給客戶,因此造成中小企業融資困難。而當經濟週期處於高點時,違約概率相對較低,這時金融機構發放貸款的意願有可能過高(這與圖24-2和圖24-3的現象類似)。巴塞爾委員會意識到了這一問題,因此《巴塞爾協議》要求在進行參數估計時,違約概率應該是一個包含了整個經濟週期的平均違約概率,而不應該只是針對某一時刻所做的估計。
其他金融機構,如保險公司、養老基金和主權財富基金,是否應該接受和銀行一樣的監管呢?也許我們會傾向於回答“是”,因為我們不想讓某家金融機構享有對其他金融機構的政策優勢,但正確的答案是“否”。這些金融機構的交易時間跨度比銀行大,它們不應該因為交易非流動性的資產而受到懲罰。另外,當波動率和相關性增大時,這些金融機構也不應該被要求對它們的投資組合進行調整。這些參數都有迴歸均值的趨勢,因此會逐漸回落。
24.3.5 多元化的重要性
經濟學模型通常假設市場參與者的行為是相互獨立的。但我們曾指出,事實上並非如此。正是由於參與者之間不是相互獨立的,才會產生流動性黑洞。為不同金融機構工作的交易員往往會在同樣的時間做同樣的交易。為了解決流動性黑洞問題,我們需要將金融市場多元化。建立多元化的一種辦法是,意識到不同種類的金融機構承受的風險是不同的,因此對它們的監管規則也應該是不同的。
對衝基金已經成為市場的主要參與者,它們基本不受監管的制約,並可以採用任何自己喜歡的交易策略。從某種意義上講,對衝基金增強了市場的多元化(也增強了流動性),但是,如上所述,對衝基金往往具有高槓杆性。當流動性變差時,例如在2007年,所有的對衝基金同時都想對交易進行平倉,這反而會使市場流動性更加惡化。
從我們的討論中得出的一個結論是:逆向投資策略有一定的好處。如果市場因為以上原因反應過激,投資者可以在流動性惡劣、其他人大量拋售資產的時候買入,並從此獲利。但是,當以短期VaR為基準的風險測度成為風險管理標準時,金融機構很難做到這一點。
[1] See A.D. Persaud, ed., Liquidity Black Holes: Understanding, Quantifying and Managing Financial Liquidity Risk (London: Risk Books, 1999).
[2] See for example J. Clunie, Predatory Trading and Crowded Exits: New Thinking on Market Volatility (Petersfield, UK: Harriman House, 2010).
[3] 流動性黑洞往往與資產價格下跌密切相關,但有時這一現象也會產生於資產價格上漲的情形。
[4] 這一假設是對真實世界的簡化,這樣做是為了幫助我們理解市場的動態過程,有些交易員的交易策略要比正負反饋這一假設更為複雜。
[5] 顯然這裡描述的去槓桿化的情況並不適用於中國和加拿大等國家。即使從全球範圍內來看,這種情況也僅持續了較短的時間。伴隨著主要央行的貨幣寬鬆政策,各類資產的價格在過去的幾年間普遍大漲。——譯者注
小結
市場上存在兩類流動性風險:交易流動性風險和融資流動性風險。交易流動性風險針對的是交易賬戶上的頭寸平倉的難易度。資產的交易流動性風險與資產的特點、交易數量、交易的速度和經濟環境有關。2007年的信用危機強調了透明度的重要性。沒有被投資者理解或定義不明確的資產的流動性往往不會持久。在某一特定時刻,資產的流動性能夠以買賣價差比率來測算。這一比率等於買入價與賣出價的差除以買入價和賣出價的平均值。一個頭寸的平倉費用與資產價格的比,等於買賣價差比率的一半。金融機構應監控在正常及受壓市場條件下,平倉全部交易賬戶資產的費用。
當交易員要對一個較大的資產頭寸進行平倉時,需要在市場風險及買賣價差之間進行權衡。快速的平倉會引發較高的買賣價差,但同時市場風險也會較低;緩慢的平倉的買賣價差較低,但市場風險較高。最優交易策略與以下因素有關:①買賣價差的貨幣價值,該價值與每天的交易數量有一定的函數關係;②每天資產價格變化的分佈。對於任意給定的平倉策略,交易員可以選擇一定的置信區間,並且計算出在不超出置信區間的前提下的平倉費用。由此,我們可以得出一個將費用最小化的平倉策略。
融資流動性風險與金融機構在有需要時能否獲得足夠的資金有關。金融機構要在正常及受壓市場條件下,對現金需求進行預測,並有相當大的把握能夠滿足現金要求。這樣做對金融機構而言至關重要。金融機構對現金的需求與儲蓄客戶提取存款、貸款客戶使用信用額度的多少、金融機構的擔保承諾、交易對手違約等因素有關。現金來源可以是易於轉化為現金的產品、批發市場的拆借、資產證券化、吸收新的存款、自有現金及由央行貸入的資金(從央行貸入現金往往是最後一種手段)。2008年6月,銀行監管機構公佈了銀行流動性管理應遵循的17條原則。監管機構指出,將來它們會更加謹慎地監控銀行的流動性風險管理流程。
最為嚴重的流動性風險來自被稱為流動性黑洞的現象。這種現象之所以會發生,是因為市場上的交易員都希望在同一時刻進入同樣的交易。交易員之所以會這麼做可能是因為他們持有相同的頭寸或採用相似的方法來管理風險。還有一種可能性是,由於交易員之間所產生的盲目追捧心理,導致某一風險的過分集中。為了避免流動性黑洞,投資者需要建立多元化的投資策略。具有長期投資目標的交易員應該儘量做到不受短期市場變化的影響。
延伸閱讀

練習題
24.1 2007年次債危機時的透明度問題是什麼?
24.2 某個資產的買入價為50美元,賣出價為55美元,這些報價的含義是什麼?買賣價差比率為多少?
24.3 假定某投資者持有價值5 000美元的公司A股票的空頭,並持有價值3000美元的公司B股票的多頭,公司A股票的買賣價差比率為0.01,公司B股票的買賣價差比率為0.02,投資者平倉自己的頭寸的費用為多少?
24.4 假設在練習題24.3中,兩家公司的買賣價差均服從正態公佈,公司A的買賣價差的均值為0.01,標準差為0.01;公司B的買賣價差的均值為0.02,標準差為0.03。在95%的置信度下,投資者的平倉費用為多少?
24.5 一位交易員想在今後10天內將一個價值6 000萬美元的頭寸平倉。買賣價差的貨幣值作為每天交易量q的函數可以被寫為a+becq,其中a=0.2、b=0.1以及c=0.08,q以百萬計。價格每天變化的標準差為0.1美元,在95%的置信度下,使平倉費用極小化的最優交易策略是什麼?
24.6 解釋流動性覆蓋比率(LCR)和淨穩定融資比率(NSFR)的區別。
24.7 依賴批發市場取得資金來進行運作,為什麼會有風險?
24.8 Ashanti Goldfields和德國金屬公司的融資風險的特性是什麼?
24.9 (a)正反饋交易和(b)負反饋交易的含義是什麼?哪類交易會造成流動性問題?
24.10 經流動性調節的VaR的含義是什麼?
24.11 流動性黑洞是如何產生的?請解釋為什麼監管規定也會導致流動性黑洞。
24.12 為什麼遵從一個多元化的交易策略會給市場的流動性帶來好處?
作業題
24.13 討論對於市場流動性而言,對衝基金帶來的好處和壞處。
24.14 假設某交易員買入了某些流動性差的股票。其中包括公司A的100股,買入價為50美元,賣出價為60美元;公司B的200股,買入價為25美元,賣出價為35美元。這些頭寸的買賣價差比率為多少?在平倉時,一個高的買賣價差對交易費用的影響是什麼?如果買賣價差服從正態分佈,均值為10美元,標準差為3美元,在99%的置信度下,交易費用與交易組合價值的比率最高是多少?
24.15 一個交易員想在8天之內將一個200 000單位的資產頭寸平倉。買賣價差作為每天交易量q的函數可以被寫為a+becq,其中a=0.2、b=0.15以及c=0.1,q以千單位計。每天價格變化的標準差為1.5美元。在99%的置信度下,使交易費用極小的最佳交易策略是什麼?在賣出資產前,交易員的平均等待時間為多少?隨著置信度的變化,平均等待時間如何變化?
第25章
模型風險
金融機構對模型的使用正在快速增長。模型被用於制定信用決策、流動性管理、信用風險評估、衍生產品估值、在險價值(VaR)和預期虧空(ES)等風險度量的計算、客戶金融資產投資組合的管理、資本充足率的評估、客戶關係管理、欺詐檢測、識別洗錢,等等。融入先進分析技術(例如機器學習)的複雜模型,使得一些以往由人們進行的活動自動化(參見第28章關於機器學習的討論)。現在人們意識到,大型金融機構需要具備模型風險管理功能,以確保模型適合其預期目標,並以正確的方式使用。
我們可以利用模型來模擬現實世界。建立一個為某金融產品定價的模型的藝術在於該模型能夠捕獲產品的重要特性,同時又不會複雜到難以使用。模型幾乎總是依賴於對所建模的現象的一些假設。重要的是要理解這些假設,並知道什麼時候這些假設不適用。
以往,定量分析師可以在電子表格中創建模型,並在極少監督下使用。現在情況已經不同了,必須對模型進行充分的記錄和定期審查,以確定它們是否仍然合適和按預期運行。模型的更改通常需要得到批准。模型風險管理的這些方面通常不受模型構建者的歡迎。他們往往喜歡模型開發的創造性方面,不喜歡花時間證明他們的模型和記錄它們。
在前面,我們已經指出,自2007~2008年金融危機以來,監管機構已不再那麼熱衷於利用內部模型來確定資本金要求了。它們更加關注金融機構內部將模型用於其他目的的方式。模型風險是操作風險的一個組成部分。監管者希望銀行有一個管理模型風險的系統,模型必須由該系統開發、驗證和使用。
本章首先回顧了模型風險管理的監管要求,描述了模型驗證小組的角色,比較模型在金融領域的應用方式與其在物理學家以及其他科學領域的應用方式的不同。在此之後,本章重點放在模型的評估和風險管理上,並探討了一些可以從該領域所犯的錯誤中吸取的教訓。
25.1 監管要求
2011年4月,美國聯邦儲備系統理事會發布了SR 11-7,為銀行提供了有效的模型風險管理指導。[1]事實證明,這份文件的影響力非常大,因此美國銀行將確保其行為與文件中概述的原則一致。其他地方的銀行監管機構表示,它們希望有類似的系統性方法來理解和管理模型風險。如果銀行監管機構認為銀行的模型風險管理系統不完善,則可能會要求銀行持有更多的資本金。
SR 11-7將模型風險定義為“基於不正確或誤用的模型輸出和報告的決策可能產生的不良後果”。產生模型風險主要有以下兩個原因。
(1)從其目標的角度來看,該模型可能存在根本性錯誤。這些錯誤可能與它使用的數據、計算方式、數值過程、假設等有關。
(2)模型可能被不正確或不恰當地使用。瞭解模型的侷限性是很重要的。一個模型可能是基於一組特定的市場條件或一種特定類型的客戶行為而開發的。當條件改變時,模型可能不再適用。
金融機構應確定模型風險的來源及其嚴重程度。與簡單模型相比,複雜模型通常會導致更大的模型風險。當模型是相互聯繫的,或者多個模型基於相同的基本假設集時,模型風險的程度就會更大。監控模型性能很重要,以便儘早確定模型是由於何種原因而沒有實現預期的效果。
25.1.1 模型創建
在開發模型時要做好存檔工作,這麼做有幾個原因。如果模型開發人員離開了開發小組,並且沒有做好存檔,其他人可能很難承擔繼續完成模型的責任,開發人員可能會因此丟失工作。其次,監管機構在評估金融機構使用的程序時,經常會要求查看模型文檔。此外,如果模型有良好的文檔記錄,那麼模型驗證和定期評審也會變得更加方便。
模型文檔的一個重要方面是闡述模型的目的、基礎理論、行業實踐的評估和已發表的研究的回顧。重要的是,文檔中必須清楚地解釋基本的數學、使用的數值計算過程和做出的假設等。文件應該足夠詳細,以便新手能夠理解已經完成的工作。如前所述,整理模型文檔對於模型開發人員來說常常被視為無聊的工作。但是在實踐中,這一個有用的規程,迫使模型開發人員後退一步,以前所未有的方式來思考他們的工作。有時還會改變模型的結果。
模型應該儘可能徹底地進行測試。這應該包括仔細測試計算機代碼的所有部分,並評估模型在輸入一系列數據時的表現。測試應該確定模型運行良好和運行不良時的情況。這可以通過逐漸輸入極值並觀察模型的性能來實現。在某些情況下,將所提出的模型的輸出結果與更精細的模型的輸出結果進行比較是合適的,因為後者的計算速度太慢,無法在實踐中使用。
測試模型性能的方法取決於模型的性質。根據歷史數據開發的模型應該在樣本外進行測試。例如,如果制定貸款決策的模型是從特定時期收集的特定數據集開發的,那麼顯然不適合再使用這些數據對其進行測試。同樣,如果消費者的投資組合管理策略是通過分析某個特定時期的資產價格行為而開發的,那麼應該使用另一個時期的數據對其進行測試。
我們在前面的章節中已經討論瞭如何回測VaR模型,它也可以用於其他情況。假設一個基於特定假設集的模型被用來為障礙期權定價。這可能可以確定它在過去的運行情況,但使用該模型的用戶會平均獲利嗎?如果能獲利,利潤是否足以補償所承擔的風險?
在實踐中使用模型時,金融機構應收集信息,以確定其是否反映了經濟和商業現實,是否按照預期的方式運行。模型的存在可能會帶來行為改變的危險。例如,用於管理客戶關係的模型可能導致客戶行為的不同;潛在的洗錢者在瞭解(也許通過反覆試驗)這種模型是如何運作的並相應地調整自己的行為之前,用於檢測洗錢的模型可能會很有效。甚至使用模型的用戶也可能找到調整模型輸入或模型使用方式的方法,以使自己使用的模型結果看起來更好。
25.1.2 模型驗證
人們越來越關注模型風險管理,由此組成了模型驗證小組,這些小組負責驗證組織使用的所有模型是否按預期執行。他們檢查模型開發人員的工作,並嚴格審查了所生成的模型以及模型是如何執行的。
負責驗證模型的人員應該獨立於模型開發者和模型用戶。確保驗證的獨立性對於模型風險管理功能的成功至關重要。應選擇採用報告的方式和激勵措施來促進獨立性。模型驗證功能的成功與否,應該通過模型評審的客觀性、提出的問題以及管理層為解決問題而採取的行動來評判。企業文化很重要。如果不鼓勵客觀思考和決策的挑戰性,那麼模型驗證過程很可能是無效的。監管機構可能會要求查看模型,以及經過模型驗證並適當修改後的模型的應用實例。
在進行初始驗證之前,模型有時會在小範圍內被非正式地使用。然而,在金融機構正式運行模型之前,進行第一次驗證非常重要。驗證的範圍和嚴格程度應取決於模型提出的風險。考慮已經開發出一個使數十億美元的貸款決策自動化的模型的情況。此時,模型的驗證非常必要。即使模型運行良好且符合其目標,模型驗證小組也應該分階段實施對模型的密切監控,以減少模型風險。
在模型被批准使用後,模型驗證也應該持續進行,以監控市場和商業慣例的變化對模型性能的影響。SR 11-7建議驗證組至少每年審查一次模型。模型的用戶(特別是與開發人員不同的用戶)可以輸入參數,驗證組可以使用最近的數據來檢驗模型的性能是否與首次使用可用數據驗證的模型性能一樣好。模型的應用結果(如信用決策的制定、使用該模型的投資回報、防止的欺詐企圖)都應該記錄在案,並將其與預期結果進行比較。
業界事例25-1描述了倫敦鯨事件,這是模型驗證組在壓力下批准模型的一個例子。這是因為,當一種產品的巨大頭寸與一種類似產品的相反頭寸對衝時,該模型為降低在險價值,進而降低監管資本金提供了理由。如果模型驗證組有更多的時間,他們就會對模型進行更仔細的檢查。可能有人會認為這兩種產品的相關性過大,還可能會有人指出,對小頭寸有效的對衝策略,並不總是對大頭寸有效。銀行對規模大的頭寸使用該模型,有可能導致掠奪性交易,從而降低對交易產品價格的歷史比較的相關性。
業界事例25-1
倫敦鯨事件
這裡所說的“倫敦鯨”是指摩根大通(JP Morgan Chase,JPM)首席投資辦公室(Chief Investment Office,CIO)的一名交易員布魯諾·伊克希爾(Bruno Iksil)。伊克希爾因為在CDX和iTraxx指數上的信用違約互換的巨大頭寸而得到了這個綽號(如第19.4節解釋的,這些信用違約互換產品提供了對一組公司的違約事件的保護)。
CIO的職責是將銀行的富餘現金進行投資。截至2011年年末,CIO在信用指數上的頭寸雖然比較大,但還算合理,而且是淨多頭(也就是說CIO買進的違約保護多於賣出的違約保護)。這一淨多頭為CIO在固定收益產品上的頭寸提供了對衝。JPM希望降低其風險加權資產,以滿足新的《巴塞爾協議》的監管要求,同時在經濟狀況改善的展望下,也希望將自己在信用指數上的頭寸變得更加中性。但是如果將手中的信用指數產品平倉,就會導致損失。這主要是因為這些產品的盯市計價結果是負的,另外還因為JPM在這些產品上的頭寸太大,如果平倉,市場就會朝不利於自己的方向移動。出於這些考慮,CIO採取的對策是賣空與手中持有的指數不同的信用指數來進行對衝。
CIO的如意算盤是自己持有的多頭和空頭能夠彼此抵消。但實際上,這種情況沒有發生。其他市場參與者意識到,有人持有巨大的頭寸(像其他機構一樣,JPM當然竭力為自己的頭寸保密。但是其他市場參與者意識到市場上潛伏著一條“鯨魚”,隨著事態逐漸明朗,大家發現這條鯨魚正是來自JPM的交易員)。意識到這些頭寸將來必將被平倉,並且將引發市場較大的調整,部分市場參與者實施了掠奪性交易策略,即建立與JPM相反的頭寸。其結果是,市場朝不利於JPM的方向發展,JPM預想的多頭和空頭價格會緊密相關的情況沒有出現。
CIO進一步加大了頭寸。這樣做一方面是出於技術對衝的原因,另一方面也是為保護自己避免成為掠奪性交易的受害者。理論上,CIO的巨大頭寸平衡得很好(也就是說,模型顯示頭寸價值不會因信用價差變動而受到任何較大的影響)。CIO持有CDX投資級(investment grade,IG)和CDX高收益(high yield,HY,即非投資級)指數的多頭與空頭。舉例來說,CIO賣出了大量10年期CDX IG9指數,買入了大量5年期CDX IG9指數(這是2007年9月生成的包含125個參照實體的信用指數。儘管不是現在市場上最新的CDX IG指數,但其交易還算活躍。125個參照實體中的121個尚未違約)。不幸的是,指數價格的走向沒有按照CIO所預期的那樣發生。2012年4月和5月,JPM承認蒙受了60億美元的損失。CIO僱員的延遲分紅被收回,JPM主席兼CEO吉米·戴蒙(Jamie Dimon)當年也被減薪。美國政府部門還對CIO交易組合價值誤報的指控進行了調查,其結果是JPM又被罰款10億美元。
為什麼CIO會被允許持有這麼大的風險?2012年1月,CIO超出了自己的VaR限額,而且因為CIO的巨大交易頭寸,整個銀行的VaR限額也被超出,但是一個新的VaR模型被開發出來。這個模型是在2012年1月的下半月完成的,並被模型檢驗部門匆匆批准。該模型將CIO的VaR降低了50%。因此,在1月前報告的VaR值又回到了限額以內。2013年1月,JPM關於倫敦鯨事件的內部報告顯示,在這一過程中存在多處錯誤。開發模型的量化人員以及模型檢驗部門都面臨很大的壓力,必須完成模型的開發和審批。CIO交易員手下的量化人員以及模型檢驗部門僅對模型進行了非常有限的回望測試。2012年5月,這個模型又被重新檢驗,發現其中存在多個嚴重錯誤,並就此停止使用。
這個事件強調了模型驗證功能的重要性,以及模型驗證為什麼需要獨立進行。
SR 11-7認為全面的驗證應該包括三個核心要素:
(1)對概念合理性的評估,包括文檔記錄;
(2)持續監控,包括過程驗證和基準測試;
(3)結果分析,包括回溯測試。
一個良好的模型開發過程應該產生有據可查的記錄文檔來支持所有的模型假設。有一種危險是,模型開發人員偏向於特定類型的模型,或者甚至會通過開發一個不必要的複雜模型來展示其量化技能。驗證工作應該確保這種情況不會發生。穩定性是模型的一個重要屬性。如果輸入參數時的一個微小變化會導致輸出的較大變化,那麼該模型可能不穩定且不適用於其預定用途。模型驗證應包括模型應力測試,即對模型輸入極端參數以測試其適用性範圍。
如前所述,持續監測是模型驗證的核心部分。這包括確保對模型所做的所有更改都經過了驗證並存檔記錄。如果模型用戶和模型開發人員是同一個人(有時是這樣的情況),那麼模型用戶就有可能調整代碼以提高模型性能。這不能令人滿意,並可能導致模型只不過是一組沒有統一理論的調整而已。如果一個模型沒有達到它所能達到的效果,就應該對其進行審查,並開發出一個基礎更好的新模型。對於模型驗證功能來說,重要的是調查不使用模型的情況,因為經理認為輸出與他們的經驗和判斷不一致。這可能表明改進模型或使用新方法是必要的。
結果分析(如回測)對於監控模型的性能非常重要。其中的一些工作應該由模型開發人員進行,並形成記錄文檔。這項工作應該由模型驗證小組持續進行檢查,並分析預期結果與實際結果之間存在差異的原因。例如,一個特定的流動性管理模型可能在低利率環境下運行良好,但在利率上升時表現不佳,經過這種類型的分析可以改進模型。
25.1.3 供應商模型
並非所有的模型都是內部開發的,有些模型是從供應商那裡購買的。有時,購買模型的目的是對內部開發的類似模型進行基準測試。此時,供應商模型可能是一個有用的驗證工具。在實踐中,金融機構也可以使用供應商模型,因為它比內部開發類似模型便宜。在這種情況下,供應商模型應該與內部模型受到相同的驗證。然而,這對模型驗證組提出了特殊的挑戰,因為建模專家是組織的外部人員,模型的某些方面可能是專有的。
金融機構應該有選擇供應商模型的流程,應要求供應商提供說明模型設計、測試結果和模型侷限的文檔。金融機構應堅持要求供應商進行持續的績效監控和結果分析,並將結果提供給客戶。
驗證組應負責批准金融機構使用供應商模型。他們可能無法訪問計算機代碼,但仍可以針對模型對各種輸入參數產生的結果進行廣泛的分析。驗證小組應該要求供應商提供關於用於開發模型的數據的完整信息。對於供應商停業或決定停止提供模型的情況,應該有一個應急計劃。這裡的一個辦法是將計算機代碼和所有其他專有資料置於託管狀態,並在供應商不再能夠提供支持的情況下提供給客戶。
[1] 參見聯邦儲備系統理事會,貨幣監理署,“Supervisory Guidance on Model Risk Management”,SR 11-7,2011年4月。
25.2 物理和金融模型
現在,有許多物理專業的工作人員從事金融模型開發工作。金融領域的一些模型在結構上與物理領域的模型類似。例如,著名的布萊克-斯科爾斯-默頓期權定價模型所對應的微分方程是被物理學家應用了多年的熱交換方程。然而,正如Derman所指出的,物理學家採用的物理模型和金融模型有一個重要的區別。[1]在物理學中,模型用於描述物理現象,具有很高的精確性。而同物理模型相比,金融模型是為了描述市場變量,而這些變量同人類的舉止行為有關(如客戶、借款人的行為),因此這些模型不過是對市場變量的儘可能好的估計。
物理模型和金融模型的一個重要區別在於模型參數。物理模型參數通常是不變的常數。例如,地球表面的引力始終為32英尺每二次方秒。[2]而金融模型中的參數每天都在變化,一個期權的波動率在某一天可能是20%,第二天可能是22%,第三天又可能是19%。實際上,我們將在後面看到,在某一日,金融模型參數的取值通常要儘量與當日市場上觀測到的價格相匹配,這一匹配模型參數的過程被稱為校正。
[1] 見E. Derman, My Life as a Quant: Reflection on Physics and Finance, Wiley, 2004; E. Derman, “Model Risk”, Risk, 9, 2(May 1996):139-145。
[2] 物理學家可能不能同意這一說法。重力加速度是隨緯度而變化的。——譯者注
25.3 簡單的模型:代價高昂的錯誤
不一定只有複雜的模型才可能導致損失。業界事例25-2說明了一個簡單的模型也能引起風險的例子。基德-皮博迪(Kidder Peabody)公司的計算機系統沒有準確計算線性產品中的融資成本,其後果是模型將交易員的巨大損失錯誤地報告為一筆可觀的利潤。基德-皮博迪公司使用的模型應該經過獨立的驗證後再使用。即使沒有解決模型的理論問題,模型價格和市場價格之間的差異也會向模型驗證組表明模型存在嚴重錯誤。
如果基德-皮博迪公司能夠質疑交易員的操作,那麼模型的錯誤會很容易被識別。事實上,政府債券部門的風險經理巴里·芬納(Barry Finer)曾經指出在一個與美國同樣高效的市場上很難獲取鉅額套利利潤,但他的擔憂並沒有引起重視。
業界事例25-2
基德-皮博迪公司的低級錯誤
通過將帶息國債的本金和利息現金流作為兩個獨立的證券賣出,投資銀行可以用帶息國債生成零息債券,這種零息債券被稱作本息分離債券(strip)。一位為券商基德-皮博迪工作的名叫約瑟夫·杰特(Joseph Jett)的交易員有一個非常簡單的交易方式,其做法是買入本息分離債券,然後將其在遠期市場出售。遠期市場上本息分離債券的價格總是高於現市價格,因此表面上看來這位交易員發現了印鈔機!事實上遠期市場同現市的差別僅僅是因為購買債券的融資費用而造成的。例如,假定3個月期的利率為每年4%,本息分離債券的市價為70美元,3個月期本息分離債券的遠期價格應該是70e0.04×3/12=70.70美元。這是因為,對於想在3個月後持有本息分離債券的人來說,遠期合約節約了0.70美元的融資成本。
基德-皮博迪公司的計算機系統顯示杰特的每一筆交易的盈利都等於遠期價格同現市價格的差(我們的例子中為0.70美元)。通過不斷將每一筆遠期進行滾轉,杰特得以逃避應計的融資費用。最後系統顯示杰特的交易盈利1億美元(他也因此拿到了一筆可觀的分紅),但實際上損失了3.5億美元。這一事例說明一家大的金融機構也可能會犯簡單低級的錯誤。
有時模型開發人員會做出錯誤的假設,但不如基德-皮博迪公司的模型那樣容易識別。利率互換市場就是一個例子。在第5.5.3節中我們指出,對於一個簡單的標準利率互換,我們可以假設遠期利率等於將來的實際利率,附錄D對於這一方法進行了陳述。例如,當計算利率互換的價格時,如果在第2年和第2.5年時間段的遠期利率是4.3%,我們就可以假定在浮動利率與固定利率進行互換時,這一時間段所採用的浮動利率為4.3%。這一結果看上去很容易被誤認為:所有將來交換現金流的互換合約都可以基於遠期利率將成為實際利率這一假設來定價,但事實並非如此。例如,在LIBOR置後互換(LIBOR-in-arrears swap)合約中,浮動利息的支付與利息的確定發生在同一天(而不是像在一般利率互換中有一個計利期(accrual period)的延後)。LIBOR置後互換所採用的假設應該是今後實際發生的利率等於遠期利率加上一個“凸性調整”(convexity adjustment)。如業界事例25-3所示,這一性質在20世紀90年代中期給那些對凸性調整不瞭解的金融機構造成了損失。
業界事例25-3
發現競爭對手模型中的弱點
LIBOR置後互換是一種利率互換合約,在這種合約中,浮動利率支付日與觀察日相同,而不是在一個計利期之後。在一般的標準互換合約中,我們可以假定將來的利率等於遠期利率,而在LIBOR置後互換定價中,我們應該假設將來的利率等於遠期利率再加上一個“凸性調整”項。
20世紀90年代中期,一些較為成熟的金融機構掌握了利率置後互換合約的正確定價方式,一些不太成熟的金融機構仍然採用“遠期利率等於將來利率”這一天真假設。由此,這使那些成熟老到的公司便可以從那些不太成熟的公司那裡贏得可觀的利潤。
在衍生產品市場上,交易員一旦發現了交易對手模型中的弱點,是不會心慈手軟的。
利率期貨市場也提供了類似的例子。在大多數情況下,可以合理地假設期貨價格等於相應的遠期價格。例如,一年內交割黃金的期貨合約的期貨價格應該與同期交割黃金的遠期價格非常接近。這兩份合同有一些不同之處。例如,期貨合約每天結算,空頭寸方對確定準確的交割日期有一定的靈活性,但這些區別並沒有在期貨價格和遠期價格之間產生實質性的差異。20世紀90年代中期,許多市場參與者選擇假設利率期貨合約的期貨利率與相應的遠期利率相同。事實上,大多數對期貨合約價格近似等於遠期價格的假設並不適用於利率期貨合約,這是因為利率期貨合約持續的時間長,每日結算制度都會造成影響。同樣,在利率相等的情況下,期貨和遠期在不同的時間結算。期貨在期初按基礎利率結算,而遠期則在期末結算。[1]
交易檢測模式
我們剛才概述的情況表明,在產品估值中識別模型風險的一個重要方法是交易檢測模式。特別是,金融機構內部的風險管理職能人員應跟蹤以下內容:
(1)金融機構與其他金融機構之間的交易類型;
(2)在競標不同類型的結構性交易時,競爭的激烈程度;
(3)從不同產品的交易中獲得的利潤。
對某一特定類型的業務投資過多,或從相對簡單的交易策略中賺取鉅額利潤,都可能是一個警告信號。如果金融機構發現自己的價格與市場脫節,就必須調整估值程序,使之與市場接軌。
杰特在基德-皮博迪公司的交易中獲得高額利潤(參見業界事例25-2),這應該說明出了問題。同樣,在20世紀90年代中期,如果某個金融機構的風險管理團隊發現交易員與其他金融機構正在進行大量收到固定利息而支付浮動利息LIBOR置後互換(參見業界事例25-3),他們就可以警示模型開發人員模型存在潛在的問題,並指示暫時停止互換交易。
[1] 見J. Hull, Options, Futures, and Other Derivatives, 10th edition (Upper Saddle River, NJ: Pearson, 2017),可供更詳細的討論。
25.4 標準產品的模型
如果某些產品在市場上交易活躍,我們就不需要採用模型來對這些產品定價,市場交易價格就是實際價格。假設市場上某種交易活躍的股指期權,做市商報出的買入價為30美元,賣出價為30.5美元。我們對這一期權的最佳估價為其中間價30.25美元。
場外交易市場一種普遍的情況是儘管被定價的產品是一種標準產品(比如期權),但該產品與市場交易的產品並不完全相同。例如,被定價產品是一種期權,但其執行價格或者期限(或者兩者)與市場上可以直接觀察到的期權有所不同。此時模型被用來保證該產品的定價方式與市場上可觀察到的類似產品的價格一致。布萊克-斯科爾斯-默頓模型在實際中的應用方式為我們提供了一個很好實例(關於布萊克-斯科爾斯-默頓模型,見附錄E)。
布萊克-斯科爾斯-默頓模型之所以有效,是因為它的所有輸入參數(除了一個參數以外)都已知,模型中唯一一個不能被觀察到的變量即是波動率,這意味著價格和波動之間存在一對一的對應關係。當指定了期權的波動率時,就可以計算價格。同樣,如果市場上存在該資產的期權,就可以確定與市場價格相符的波動率。與期權價格保持一致的資產波動率被稱為隱含波動率(implied volatility)。負責對某一特定資產進行投資的交易員會跟蹤所謂的波動率曲面,這一曲面顯示了期權波動率同期權執行價格以及期限的函數關係。
表25-1顯示了一個匯率期權的波動率曲面(為簡單起見,我們假設當前匯率接近1)。注意,如果布萊克-斯科爾斯-默頓模型確實是對市場假設的一個準確描述的話,那麼表中的波動率應該為常數,不會隨時間而變化。針對不同的執行價格和期限,期權的隱含波動率是不一樣的,並且它們會隨著時間而變化(對於所有資產的期權都是如此)。交易員的工作是瞭解當前的波動率曲面以及其隨時間的變化情況。
表25-1 波動率曲面 (%)
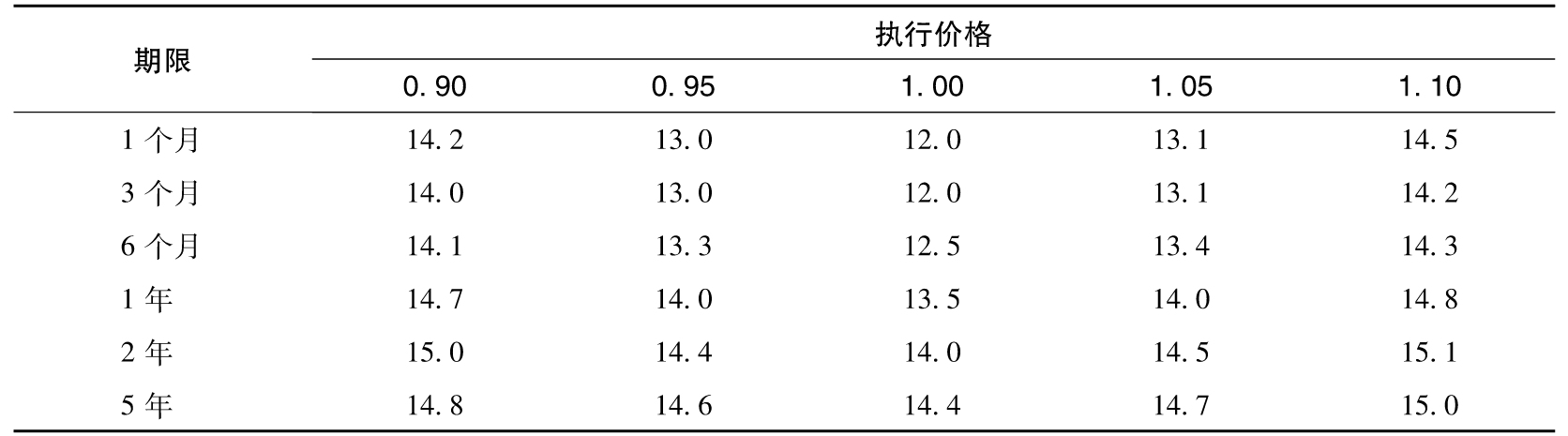
注:不同執行價格和期限的波動率以年百分比的形式給出。
假設某交易員想要為一個9個月期限和執行價格為1.05的期權進行定價(見表25-1)。具有此行權價的6個月期限的期權的波動率為13.4%,1年期限的期權的波動率為14.0%。交易員可以對13.4%及14.0%進行插值,作為對波動率估計,插值結果為13.7%。這一數據可以用於布萊克-斯科爾斯-默頓模型,從而評估波動率為13.7%的期權的價值。假設期限和執行價格都與表中不同,我們可採用二維插值。首先在執行價格之間插入,然後在期限之間插入(如果先在到期期限之間插值,然後在執行價格之間插值,也會得到相同的答案。見練習題25.12)。考慮執行價格為0.92和期限為1.5年的期權。具有此行權價的1年期限的期權的插值隱含波動率為14.42%,2年期限的期權的插值波動率為14.76%,因此1.5年期權的插值波動率為14.59%。
25.4.1 標準產品的模型風險來源
模型驗證組面臨的一個問題是,對活躍交易產品價格的確定是否取決於所使用的模型。如果在剛剛考慮的例子中,我們用另一個模型代替布萊克-斯科爾斯-默頓模型,價格會是相似的嗎?這個問題的答案是,當被估值產品的性質與活躍交易的產品完全相同時(即只有執行價格和期限等參數不同),該模型通常不會對價格產生實質性影響。[1]這是因為這個模型僅僅被用作一個複雜的插值工具,如果另一種合理的模型使用的方式類似於布萊克-斯科爾斯-默頓模型,那麼兩個不同的模型通常會給出相似的交易活躍產品價格。
在極端情況下容易產生模型風險,模型驗證組應該對此進行檢查。例如,當波動率曲面在執行價格或期限維度上非常陡峭時,應該檢查不同模型的運行情況。此外,模型驗證組應該檢查市場上可用的定價數據的可靠性,以及當可用數據比通常少時模型如何工作。
25.4.2 對衝
對於交易活躍的產品,主要的模型風險是對衝。正如我們所討論的,使用不同的模型通常不會對價格產生太大的影響,但會對對衝業績產生影響。
我們應該區分模型內對衝(within-model hedging)以及模型外對衝(outside-model hedging)。模型內對衝是指對模型內已假設具有不確定性的變量來進行對衝,模型外對衝是指對在模型內被假設為常量(或者非隨機變量)的變量來進行對衝。以布萊克-斯科爾斯-默頓模型為例,採用該模型對股票價格的變化進行對衝(delta及gamma對衝)是模型內對衝,這是因為模型假定標的資產價格變化具有不確定性,但是對波動率對衝(vega對衝)是模型外對衝,這是因為模型本身假定波動率為常數。
在實踐中,交易員幾乎總會同時進行模型外對衝和模型內對衝。如我們以前的解釋,這樣做的原因是在參數校正過程中,波動率(在模型中被假設為常數)等參數每天都會發生變化。一個好的交易員在對交易賬戶的風險進行監控時,會關心交易賬戶對於市場常見的波動率曲面移動的敏感性。[2]
如果一個模型給出的產品價格與市場價格一致,並且對每天會產生變化的變量都進行對衝(這裡的參數包括模型中假設的常量以及隨機變量),那麼理論上對衝後會使交易員頭寸的價值保持恆定。事實上,這並不一定成立。再次考慮布萊克-斯科爾斯-默頓模型來評估匯率期權中的頭寸價值。每個期權價格都是匯率、其隱含波動率和期限的確定性函數,[3]這意味著交易員對投資組合中所有期權的匯率和隱含波動率都有風險敞口。通過外匯交易,可以很容易地對衝匯率風險,這被稱為delta對衝,通常至少進行一次(參見第8章)。對衝波動率變化的風險並不那麼容易,這需要在其他期權(可能是昂貴的)上進行交易,並且基於波動率曲面會隨時間變化的假設。[4]因此,波動率對衝不可能像delta對衝那樣有效。
在實踐中,delta對衝往往是交易員唯一定期進行的對衝。期權頭寸的delta取決於所使用的模型,這意味著交易員採取的對衝頭寸因模型而異。模型驗證組的一項重要工作是測試用於替代模型的delta對衝的有效性。
25.4.3 損益分解
可以進行的一種分析稱為損益分解(P&L decomposition)。風險經理將投資組合每天價格的變化分解成以下成分:
(1)沒有被對衝的風險所帶來的變化;
(2)由於對衝模型的不完善所帶來的變化;
(3)每一天新的交易所帶來的變化。
如果某天價格變化變得不可接受,損益分析就會指出在哪些方面我們應花更多精力。好消息是,平均來講,根據錯誤模型進行對衝導致總損失或總收益通常很小,這是因為在一家較大的金融機構中,不完美對衝所帶來的風險通常會被不同的交易組合分散。
[1] 這在S. Figlewski, “Assessing the Incremental Value of Option Pricing Theory Relative to an Informationally Passive Benchmark,” Journal of Derivatives (Fall 2002):80-96中已經說明。
[2] 我們可以採用第9章描述的主成分分析方法。如果風險敞口對每個主要成分的敏感性都很小,則敞口對實際中觀察的移動的敏感性也會很小。
[3] 為簡化例子,假設利率和股息收益率恆定。
[4] 如果可以完全對衝波動率曲面的波動,那麼delta對衝的差異將被波動率對衝的差異所抵消,但這在實踐中並不能完美實現。
25.5 非標準產品的模型
衍生產品定價的一般步驟是建立一個模型,然後根據市場上可以觀察到的標準產品的價格來確定模型的參數。圖25-1展示了某一金融產品常用定價的方法。選擇某種或某幾種其價格在市場上可以直接觀察到的產品作為“校準產品”(calibrating instruments),選擇這些產品的依據是它們應與目標產品相似。由校正產品我們可以得出模型參數,這些參數可用於對目標產品的定價。
圖25-1 如何應用模型對金融產品定價
當這種方法用於交易活躍的標準產品時,其價格沒有太高的不確定性。對於非標準產品則不一樣,模型風險會更大,因為模型的選擇對於定價及對衝均會有較大的影響。業界事例6-1中給出了結構化產品定價中的模型風險的例子。這個例子說明,在對資產支持證券(ABS)和擔保債務憑證(CDO)分檔定價時,認為ABS的BBB分檔類似於BBB級債券的假設並不可取。
需要注意的重要一點是,我們幾乎總是關注所謂的相對估值(relative valuation),目的是使金融產品的價值與市場上可以觀察到的其他類似金融產品的價值一致。使用模型給出的絕對值價格對衍生產品進行估值非常罕見。這是金融模型和物理模型之間的另一個區別。
金融機構不應該僅僅依賴單一模式為非標準產品定價,而應該儘可能使用多種模型。通過採用不同的模型,我們會得到產品價格的分佈區間,並且有助於我們更好地理解面臨的模型風險。
假如金融機構要將某產品出售給客戶,三種不同的模型顯示該產品的價格分別是600萬美元、750萬美元和850萬美元。即使金融機構認為第一種模式是最好的,並計劃以這一模型作為每天定價和對衝的正式模型,但金融機構給客戶的報價至少應該是850萬美元。此外,金融機構對自己的賬面盈利應持保守態度。如果產品以900萬美元的價格出售,這時將賬面盈利記為300萬美元會很誘人(900萬美元減去被認為是最好的模型計算出的價格600萬美元)。然而,這種做法過於激進。另外一個更好也更保守的做法是,將這300萬美元盈利記入一個準備金賬戶,將這些盈利在產品的整個期限中逐漸釋放出來。[1]
加權蒙特卡羅模擬法
當使用多種模型時,這些模型都應該根據市場上觀察到的交易活躍的標準產品的價格進行校驗。例如,在對一個障礙期權進行定價時,測試模型給出的普通看漲期權和看跌期權的價格應等於市場上觀察到的價格。我們不應滿足於測試少數幾個不同的模型,而是應該通過嚴密的分析,嘗試回答這樣一個問題:“那些能夠對活躍交易正確定價的模型給出的模型價格區間有多大?”如果能正確地進行這種分析,那麼對非標準產品,我們能得到一個最佳的價格和一個最差的價格。有一種方法被稱為加權蒙特卡羅模擬法(weighted Monte Carlo simulation)。[2]在該方法中,我們先對正式模型進行蒙特卡羅模擬,然後對每次取樣賦予不同的權重。權重的分配有一定限制,需保證加權後的蒙特卡羅模擬結果與市場上觀察到的標準產品的價格相匹配。在這一限制下,我們可以通過一個優化過程來搜索分別使得非標準化產品價格最高和最低的權重分配。
[1] 這麼做也會保證交易員的分紅制度更為合理。
[2] See, for example, A. Elices and E. Gimenez, “Weighted Monte Carlo,” Risk (May 2006)。
25.6 盯市計價
金融機構必須每天對交易賬戶上的產品進行定價,這個過程被交易員稱為盯市計價(marking to market)。這些價值被財會人員用來生成財務季報。財會人員把按盯市計價規則稱為“公允價值會計準則”(fair-value accounting)。
財會人員認識到,有些模型比其他模型給出的價格更可靠。美國財務會計準則委員會(FAS 157)和歐洲國際會計準則委員會(IAS 39)要求銀行將交易賬戶下的產品歸為3類分別估值定價:
·第1類(LevelⅠ)估值定價是對那些從活躍市場可以取得報價的產品的估值;
·第2類(LevelⅡ)估值定價是對那些從活躍市場可以取得與之類似的產品的報價,或從某些不活躍的市場上可以直接取得報價的產品的估值;
·第3類(LevelⅢ)估值定價是必須通過一定的模型(有時被稱為盯住模型(making to model))假設才能得出價格的產品的估值。
我們在第25.4節中討論的定價(該模型被用作複雜的插值工具)將被歸類為第2類估值。如果第25.5節中的校準產品與被評估的產品有些不同,則該估值將歸為第3類估值。
25.7 如何建立成功的定價模型
許多人會認為,當一個模型的參量每天都在變化時,這樣的模型基本沒有什麼用處。對於物理模型而言,這一觀點十分正確。但是正如我們討論的那樣,金融產品的定價模型的應用與物理模型不同。
布萊克-斯科爾斯-默頓模型之所以流行是因為以下幾點。
(1)正如我們討論的那樣,模型可以與對波動率曲面的插值並用,這樣做可以保證模型價格同市場觀察到的價格的一致性。
(2)定價模型通常被用作交易人員之間的交流工具,交易員對於期權價格的報價通常是用隱含波動率的形式而不是期權的實際價格。這樣做的原因是隱含波動率要比期權價格更為穩定,因此報價變化頻率更低。例如,當標的資產價格或利率有所變動時,期權價格會變化,但波動率可能不會變。
(3)模型被充分簡化,交易員可以得出對模型的直觀認識,並由此來建立自己對期權交易市場的理解和觀點。
具有這些特性的其他領域的模型也很受歡迎。模型開發人員和模型驗證小組應清楚,模型的最終目的通常是使模型用戶能夠了解市場並更有效地執行其判斷。在比較替代模型時,這是一個重要的考慮因素,可能會導致更簡單的模型優於更復雜的模型。
25.8 構建模型過程中的誤區
建立模型的精髓是保證模型能夠抓住產品定價和對衝的要點,同時又不能過於複雜。有時,為了抓住產品的重要特性的要求,模型不得不變得複雜,但情況並非總是如此。
模型構建中一個誤區是過度擬合(over-fitting)。考慮表25-1所定義的波動率曲面,我們可以擴展布萊克-斯科爾斯-默頓模型,使波動率成為標的資產價格和期限的某種複雜函數,[1]這對於某些應用程序可能是可取的,但是模型將變得很複雜而難以使用。我們可能會發現與簡單模型相比,擴展模型的其他一些性質不夠合理。特別是,資產價格在多個時間點的聯合概率分佈變得不夠合理,而且在某些情況下,模型給出的未來波動率曲面與今天市場上觀察到的波動率曲面相比,可能變化會非常大。[2]
模型構建中的另一個潛在錯誤是過度參數化(over-parameterization)。我們可以擴展布萊克-斯科爾斯-默頓模型,加入隨機波動率或標的資產價格的跳躍等特性。這樣做不可避免地會引入更多需要估計的參數,使模型更難使用。通常認為,複雜模型中的參數比簡單模型中的參數更穩定,不需要逐日調整。這可能是真的,但是應注意我們不是在處理物理過程。雖然複雜系統的參數在某一個較長的時間會相對穩定,但在一段時間後,參數可能會發生變化,這可能是因為存在經濟學家所說的“常態轉型”(regime shift)的現象。在常態變化發生之前,金融機構可能會認為複雜模型是對簡單模型的改進,但是在變化發生以後,這些複雜的模型可能沒有靈活性來應付不斷變化的市場情況。[3]
正如我們剛剛討論的那樣,簡單模型通常是最成功的。用戶通常對複雜模型持懷疑態度,他們認為這些模型是“黑匣子”(black box),並認為這些模型在直觀上很難理解。在某些情況下,由於以上討論的原因,這種懷疑態度是有根據的。
[1] 這一隱含波動率函數模型在以下論文中被提出:B. Dupire, “Pricing with a Smile,” Risk, 7(February 1994), 18-20; E. Derman and I Kani, “Riding on a Smile,” Risk, 7(February 1994), 32-39; M. Rubinstein, “Implied Binomial Trees,” Journal of Finance 49, 3(July 1994), 771-818。
[2] 如果模型能匹配將來各個時間點的波動率,則對未來收益只依賴即時資產價格的產品,這類模型可以準確地定價。但對障礙期權或複合期權等產品的定價就不那麼準確,這些產品的價格與標的資產在不同時間點的價格的聯合分佈有關。赫爾和索吾林教授發現,隱含波動率函數模型對於複合期權的定價大體上合理,但是對於障礙期權會產生較大的誤差,見J. C. Hull and W. Suo, “A Methodology for the Assessment of Model Risk and its Application to the Implied Volatility Function Model,” Journal of Financial and Quantitative Analysis, 37, 2(June 2002), 297-318。
[3] 經濟學家羅伯特·盧卡斯在1976年提出的著名的盧卡斯評論中討論了這類社會科學問題的性質。參見R. Lucas, “Economic Policy Evaluation: A Critique,” Carnegie-Rochester Conference Series on Public Policy 1(1976):19-46。
小結
模型風險是操作風險的一種形式。現在人們認識到它需要被特別注意。監管機構希望看到金融機構在開發、記錄、驗證和使用模型方面具有全面流程。應該定期檢查模型,以確保它們能夠按預期運行。模型驗證小組應該獨立於模型開發人員和模型用戶。他們應該檢查模型開發人員的工作,並得出應使用模型的情況。
金融模型與物理科學模型存在根本的差別,因為金融模型最終是人類行為的模型,最好也不過是對市場變量的行為的一種近似而已。此外,模型還會碰到不時出現的常態轉型現象,在這一現象中,模型的性能會發生根本轉變。
估值定價模型通常不過是複雜的插值工具,以確保模型價格與其他類似產品的價格一致。隨著被定價產品的標準化程度降低,定價模型的選擇也變得越來越重要。因此,模型驗證組可以通過測試不同模型,獲得實際的價格區間並瞭解隨之而來的模型風險。這些模型應始終根據活躍交易產品的當前價格進行校準。模型的對衝業績和估值定價業績都應該仔細評估。
延伸閱讀
練習題
25.1 解釋(a)盯市計價;(b)按模型定價。
25.2 解釋SR 11-7中確定的兩類模型風險。
25.3 解釋為什麼一個模型必須有完整的文檔記錄。
25.4 “布萊克-斯科爾斯-默頓模型無非是一種較為複雜的插值工具。”討論這一觀點。
25.5 利用表25-1,計算交易員對執行價格為1.04、期限為8個月的期權定價時,使用的波動率。
25.6 物理模型與金融模型的主要區別是什麼?
25.7 對於某一特殊衍生產品,一家金融機構如何判斷其模型有別於競爭對手的模型?
25.8 模型內對衝及模型外對衝的區別是什麼?
25.9 解釋損益分解的含義。
25.10 解釋財會中的“Level Ⅰ”“Level Ⅱ”和“Level Ⅲ”估值的含義?
25.11 構建模型過程中的過度擬合和過度參數化是什麼意思?
25.12 第25.4節使用表25-1中的數據計算執行價格為0.92、到期期限為1.5年的期權的隱含波動率為14.59%。它是這樣做的,首先沿著執行價格維度進行插值,然後沿著時間維度插值。證明:通過先沿著時間維度插值,再沿著期限維度插值,可以得到相同的隱含波動率。
25.13 “對於結構性產品,交易員採用模型來對產品定價,而不是盯市計價。”請解釋這句話的含義。
作業題
25.14 假設所有的期權交易員都決定放棄布萊克-斯科爾斯-默頓模型,並採用另外一個對資產價格有不同假設的模型,這一變化對以下內容會有什麼影響:(a)標準期權定價;(b)標準期權對衝。
25.15 採用表25-1來計算交易員對執行價格為0.98、期限為11個月的期權定價時使用的波動率。
25.16 假設金融機構使用一個不精確的模型來給某種結構化產品定價和對衝,討論該機構會如何(如果會的話)認識到自身的錯誤。
第26章
經濟資本金與RAROC
到目前為止,我們討論的重點是如何建立合理的規程來衡量金融機構面對的不同風險(信用風險、市場風險、操作風險和流動性風險等),現在我們將討論風險是如何被彙集並分配給各個業務部門的。
經濟資本金(economic capital,有時也被稱作風險資本金,risk capital)是金融機構內部評估的為應對本機構持有的風險所需要的資本金數量。經濟資本金和監管資本金不同,對後者,所有的銀行都要遵從巴塞爾委員會制定的統一規則。經濟資本金可以被認為是銀行為了具備承擔一定風險能力而需要的“貨幣”量。一個業務部門只有在具備相應經濟資本金的情況下才能持有某種特定的風險。業務部門的盈利水平應基於為該部門所分配的經濟資本金的數量來衡量。
本章將討論金融機構針對某一特定風險以及某些特定業務部門如何估算經濟資本金,並且說明這些經濟資本金如何彙總來產生對整個機構的經濟資本金的估計。我們將在本章中討論風險調整後的資本回報率,即RAROC。該回報率等於某業務部門的回報除以該部門的資本金配額,RAROC既可以用於評估業務部門在過去某一時間段內的業績,也可以用來預測該業務部門未來的業績表現,從而幫助管理層計劃未來資本金的分配方式,並且為某些業務活動在未來的發展規劃中是應該停止還是擴大提供決策基礎。
26.1 經濟資本金的定義
經濟資本金是指在一定的置信水平下,銀行為了能夠承擔一年內的損失而必須持有的資本金的數量。因此,置信水平等於在一年內銀行的損失不會超過資本金的概率。大型國際性銀行的管理目標通常是保持其AA級的信用等級,具有AA級的公司一年的違約概率小於0.02%,這說明銀行應選擇的經濟資本金置信水平至少應該是99.98%,作為維持AA級的必要指標。由於存在資本金不足以吸收損失的可能性,因此要求違約概率小於0.02%。如果某家銀行想維持的信用等級是BBB,其對應的置信水平也會低一些,一傢俱有BBB信用評級的公司一年的違約概率為0.2%,因此其對應的置信水平應該是99.80%。
資本金的要求必須能覆蓋非預期損失,非預期損失的定義為實際損失與預期損失的差。如第15章所述,預期損失應該已包含在銀行產品的定價之中,因此只有非預期損失才需要資本金。如圖26-1所示,經濟資本金的數量等於損失概率分佈中第X分位數與預期損失的差,其中X%是置信水平。
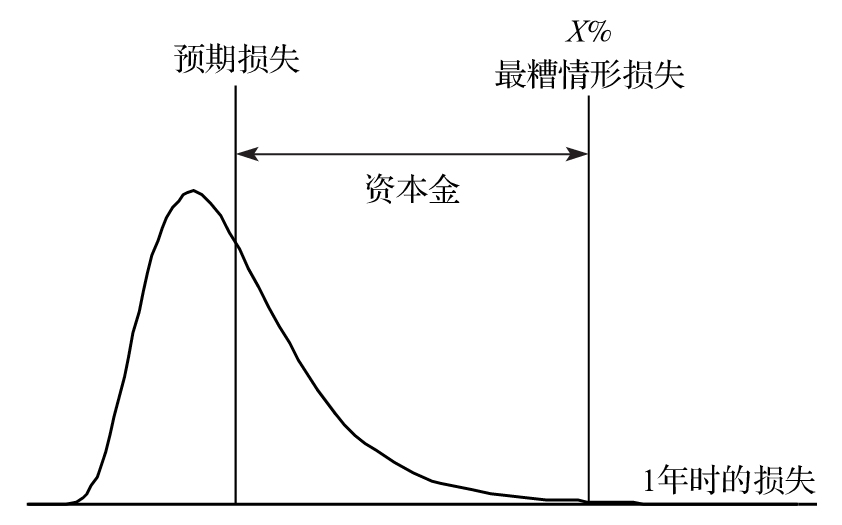
圖26-1 由1年期損失概率分佈來計算經濟資本金,X%為置信水平
【例26-1】 某信用評級為AA的銀行在世界某地區發放貸款。銀行估計平均每年違約的貸款佔未償還本金的1%。在1年展望期、99.98%置信水平下的VaR下估計貸款損失為未償還本金的5%,因此每100美元貸款所需要的資本金為4美元(在99.98%的置信水平下VaR與ES的差)。
測算方法
銀行可以採用兩種方法來計算經濟資本金,它們分別是自上而下法(top-down approach)以及自下而上法(bottom-up approach)。在自上而下法中,我們首先需要估計銀行資產的波動率,然後根據波動率可以得出在一定展望期內銀行資產低於其負債的概率。一種可用於自上而下法的理論框架是默頓模型,在第19.8節中我們曾對默頓模型做過討論。
在實際中採用最多的方法是自下而上法。在這一方法中,我們首先建立各業務部門對不同風險類別的損失分佈,然後進行彙總。彙總過程的第一步是計算各類風險的總損失分佈或各業務部門的總損失分佈,最後一步是求出整個金融機構的整體損失的概率分佈。
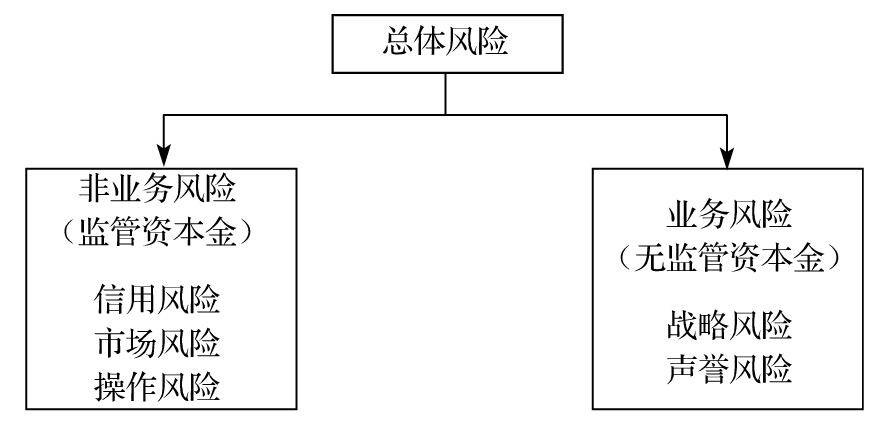
圖26-2 銀行面對的損失種類,以及是否有資本金要求
在圖26-2中,我們對銀行面臨的不同風險進行了總結。像我們在第23章中看到的那樣,監管機構將操作風險定義為“由於內部控制過程、人員及系統不當或失效以及外部事件所造成的損失”。操作風險包括模型風險以及法律風險,但不包括戰略風險以及聲譽風險。這裡不包括的幾項風險被統稱為業務風險。對業務風險沒有監管資本金要求,但有些銀行仍然會評估該風險所需的經濟資本金。
26.2 經濟資本金的構成成分
在前面的幾章中,我們曾經討論了對於不同的風險如何計算損失分佈,接下來我們將對這些方法中的關鍵問題進行簡單總結。
26.2.1 市場風險經濟資本金
在第13章及第14章中,我們討論瞭如何利用歷史模擬法以及模型構建法來估計市場風險損益的概率分佈。如前面討論的,該分佈首先要基於1天展望期計算得出。《巴塞爾協議Ⅰ》和《巴塞爾協議Ⅱ.5》中的市場風險監管資本金基於10天展望期、置信度99%的VaR計算得出,如第18章所述,在FRTB中,確定ES的時間展望期由流動性決定。
在計算經濟資本金時,對於所有的風險類別,我們通常選定同樣的展望期及置信區間,展望期通常為1年,置信區間可能高達99.98%。最簡單的假設是:①在今後一年中每天的損益分佈均相同;②所有的分佈相互獨立,那麼一年內的損益的分佈大致為正態分佈。假定一年有252天,一年損益分佈的標準差等於 乘以一天損益分佈的標準差。如果損失的期望值為0,對應於99.98%置信水平的損失等於3.54乘以損益分佈的標準差,對應於99.8%置信水平的最壞損失等於2.88乘以損益分佈的標準差。請注意,我們並不假設每日損益是正常的。假設每日損益是獨立同分布的,根據統計中心極限定理,大樣本中獨立同分布的和近似於正態分佈。
乘以一天損益分佈的標準差。如果損失的期望值為0,對應於99.98%置信水平的損失等於3.54乘以損益分佈的標準差,對應於99.8%置信水平的最壞損失等於2.88乘以損益分佈的標準差。請注意,我們並不假設每日損益是正常的。假設每日損益是獨立同分布的,根據統計中心極限定理,大樣本中獨立同分布的和近似於正態分佈。
【例26-2】 如果日市場風險損益分佈的標準差為500萬美元,對應於1年展望期,在99.8%置信水平下的VaR等於(以百萬計) ,即2.286億美元。
,即2.286億美元。
在實踐中,每日損益並不是完全彼此獨立並服從相同的分佈。相互獨立的假設可以被放鬆為假設日回報之間的自相關性是個常數。這樣式(12-5)給出的結果就可以使用,而且只要自相關性不是太大,我們仍然可以大致認為一年內的損益為正態分佈。在某些情況下,開發一個更精細的刻畫日損益期望值和方差如何隨時間變化的模型也許更合適。然後我們可以使用蒙特卡羅模擬來彙總每日的損益分佈,這樣得到的結果就不一定再是正態分佈的了。
26.2.2 信用風險經濟資本金
雖然《巴塞爾協議Ⅱ》給予採用內部評級法來計算監管資本金的銀行很大的自由度,但協議仍然不允許銀行採用自己的信用相關模型以及相關性參數。在計算經濟資本金時,銀行有權利根據銀行本身的情況選擇自認為恰當的內部模型。如第21.4節中解釋過,CreditMetrics常常被用來計算信用風險經濟資本金。
另外一種計算經濟資本金的方法是Credit Risk Plus,我們在第21.3節中曾對其做過描述。Credit Risk Plus方法借用了精算的一些方法來計算違約概率分佈。CreditMetrics能夠計算由信用降級及違約所產生的損失,而Credit Risk Plus只計算由違約造成的損失。
在計算信用風險經濟資本金時,金融機構可採用條件模型或非條件模型。在條件模型(與經濟週期有關)中,預期損失及非預期損失均將當前的市場條件考慮在內;在非條件模型(與經濟週期無關)中,計算結果建立在某種跨週期的平均經濟環境條件之下。評級公司給出的評級是非條件化的。再有,當採用內部評級法來計算監管資本金時,對於PD(違約率)以及LGD(違約損失率)的估計應該是無條件性的。很明顯,我們在計算經濟資本金時一定要保持一致性。如果預期損失為條件性的,那麼非預期損失也應該是條件性的;如果預期損失為無條件性的,那麼非預期損失也應該是無條件性的。
無論採用什麼方法,我們往往需要採用蒙特卡羅模擬來計算信用損失的概率分佈。如在第20章和第21章中解釋過的,衍生產品因為在違約或降級時的風險敞口具有不確定性,所以計算時更加複雜。
26.2.3 操作風險經濟資本金
像在第23章中闡述的那樣,銀行監管機構正在從確定操作風險監管資本金的高級計量法(AMA)轉向基於銀行虧損歷史的一種簡化方法。基於圖26-1中的模型,一些老練的銀行可能會繼續使用AMA來計算經濟資本金。
26.2.4 業務風險經濟資本金
在前面我們曾經提到過,業務風險包括策略風險(這與金融機構在進入新市場以及開發新產品等方面的決策有關)及聲譽風險。業務風險比操作風險更難以定量化,因此對業務風險的估測大多是主觀性的。然而,嘗試量化業務風險也很有必要,可以使金融機構的高級風險管理人員對業務風險情況的構成有良好的理解。這可以幫助他們衡量正在醞釀中的新的戰略決策對整體風險的影響。
26.3 損失分佈的形狀
市場風險、信用風險以及操作風險損失的概率分佈各不相同。Rosenberg和Schuermann採用了來自不同方面的數據來估測這些不同損失分佈的形狀,[1]這些分佈分別在圖26-3、圖26-4及圖26-5中給出。市場風險分佈(見圖26-3)形狀對稱,但並不是完全服從正態分佈,一個具有11個自由度的t-分佈與市場損失分佈匹配較好。圖26-4顯示的信用損失分佈具有相當的偏態,這與預期也比較一致。由圖26-5展示的操作風險分佈形狀比較極端,在大多數時候損失不是很大,在某些極端情形損失量巨大。
圖26-3 市場風險損失概率分佈密度函數
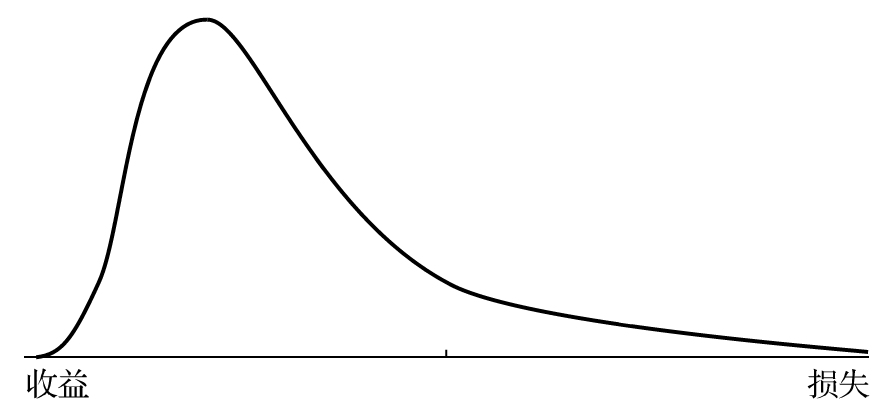
圖26-4 信用風險損失概率分佈密度函數
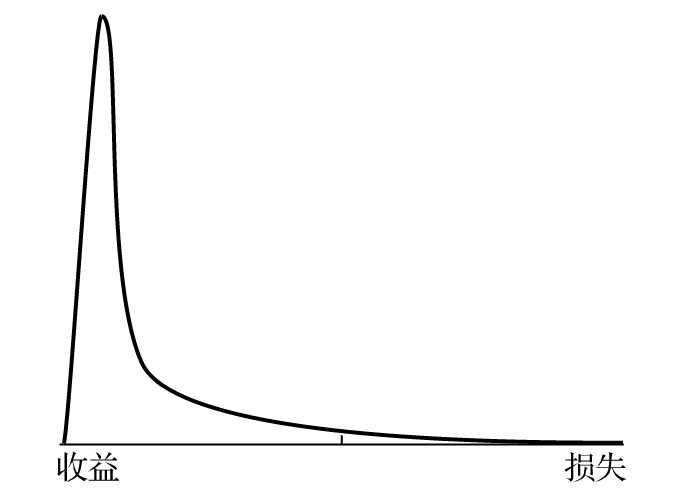
圖26-5 操作風險損失概率分佈密度函數
我們能夠利用損失分佈的二階矩、三階矩以及四階矩來刻畫這些分佈的特徵。不太嚴格地講,二階矩是為了估測標準差(或方差),三階矩是為了估測偏態,四階矩是為了估測峰度(也就是尾部的厚度)。表26-1對於市場、信用以及操作損失分佈的性質進行了總結。
表26-1 不同風險損失分佈的特徵

[1] See J. V. Rosenberg and T. Schuermann, “A General Approach to Integrated Risk Management with Skewed, Fat-Tailed Risks,” Federal Reserve Bank of New York, Staff Report no.185, May 2004.
26.4 風險的相對重要性
風險的相對重要性與業務構成有關。信用風險對金融機構的商業貸款、零售貸款和衍生產品交易非常重要,市場風險對交易以及某些投行業務十分重要。但如在第23章中討論的,操作風險(特別是網絡風險、法律風險以及合規風險)被很多觀察家認為是金融機構目前面臨的最重要的風險。
對於資產管理公司而言,操作風險一直是最大的風險源。如果資產管理經理工作有疏忽,很可能會導致來自投資者的昂貴的法律訴訟。業界事例26-1給出了一個例證。另外一個引人注目的例子來自聯合利華(Unilever)的養老金計劃。美林證券旗下的水星資產管理公司(Mercury Asset Management)曾聲稱自己的投資表現不會比參照指數低超過3%。1997年1月~1998年3月,水星資產管理公司的資產回報比參照指數低了10.5%,聯合利華因此控告了美林證券,並索賠1.85億美元。這個糾紛最後以庭外和解收場。2009年,西班牙的桑坦德銀行(Santander Bank)因將其管理的客戶資金委託給伯納德·麥道夫(Bernard Madoff)而遭受了巨大操作風險損失。麥道夫潛心經營了一個高達500億美元的龐氏騙局。
業界事例26-1
EGT基金
1996年,彼得·揚(Peter Young)是德意志銀行(Deutsche Bank)下屬基金管理公司Deutsche Morgan Grenfell的一個經理,他的責任是管理歐洲增長信託(European Growth Trust,EGT)基金。基金增長的幅度較大,最終彼得·揚所掌管的客戶資產超過了10億英鎊。
對於EGT的投資有一定的規定,其中一條是不能有超過10%的基金投放於非公開發行的證券。彼得·揚違反了這一規定。從某種意義上講,他的投資對於他個人有利。當事實被披露後,他被公司解僱,但德意志銀行必須面對投資者的索賠,最後德意志銀行的總損失超過了2億英鎊。
不同風險之間的相互作用
不同風險之間有一定的相互作用。如果金融機構的對手發生違約,只有在市場變量的變化使衍生產品對於該金融機構有正的價值時,信用風險才會產生。另外一種風險間的相互作用是:交易對手違約概率同金融機構與對手之間的合約價值有關。這就是我們在第20章中討論的錯向風險。如果交易對手是為了對衝才進行交易,這一依賴關係就會比較弱。但是,如果合約的目的是投機,並且這一合約規模對於交易對手而言非常可觀,那麼以上的相互作用關係應該被重視。
長期資本管理基金事件清楚地證明了流動性風險與市場風險(見業界事例22-1)之間存在的相互作用關係。在市場風險與操作風險之間也存在相互作用關係。如果法國興業銀行的傑洛米·科維爾對市場變化趨勢的猜測是正確的,也許我們就不會發現他的違法行為(見業界事例5-5)。同樣,如果基金經理的違規行為帶來的是盈利而非損失,我們也許就不會發現這些違反投資規定的行為了(見業界事例26-1)。
26.5 經濟資本金的彙總
通常來講,金融機構對各業務部門要分別計算市場風險、信用風險、操作風險及(可能的)業務風險損失分佈。完成這些計算以後,金融機構需要將所有的損失分佈進行彙總以產生整個機構所需要的經濟資本金的總量。
最簡單的做法是假定涵蓋n個不同風險的整體經濟資本金等於各項風險資本金的總和,因此

其中Etotal為面臨n種不同風險的金融機構整體資本金的數量,Ei為第i項風險所對應的資本金數量。巴塞爾委員會對於監管資本的做法與上式一致。銀行的整體監管資本金等於信用風險、市場風險及操作風險資本金的總和。
式(26-1)採用了一個非常保守的假設,即假定完美的相關性(完全相關)。假設對於經濟資本金進行計算採用的置信水平為99.9%,這意味著市場風險、信用風險及操作風險各自所對應的99.9%的最壞情形會同時發生。Rosenberg和Schuermann估測市場風險與信用風險的相關性大約是50%,市場風險及信用風險同操作風險的相關性大約都是20%。他們的結果顯示了當採用式(26-1)來對市場風險、信用風險及操作風險進行彙總時會高估整體資本金達40%。
26.5.1 假設正態分佈
一種簡單彙總損失的計算方法是假設損失服從正態分佈,由n個不同種類風險組成的整體風險的標準差為

其中σi為第i項風險的損失分佈的標準差,ρij為第i項風險與第j項風險的相關性。由以上公式可以計算資本金,例如,對應於99.9%置信水平的VaR等於3.09與式(26-2)所得數量的乘積。
以上的方式往往會低估資本金的數量,因為計算沒有考慮分佈的偏態以及峰度。Rosenberg和Schuermann證明採用以上做法對市場風險、信用風險及操作風險進行彙總時會低估整體資本金達40%。
26.5.2 採用Copula函數
一種更為精確的對損失分佈進行彙總的方法是採用Copula函數,在第11章中我們對Copula函數曾做過討論。每種損失分佈均以分位數對分位數的映射形式被映射到某種標準並且性狀良好的分佈上。在這種標準分佈上我們可以定義某種相關性結構,並由此間接地得出原始分佈的相關性結構。
在計算過程中我們可採用不同形式的Copula函數。當採用高斯Copula函數時,標準分佈被假設為多元正態分佈。選擇其他函數時可以得到尾部更肥厚的相關性結構。關於這一點我們在第11.6節中已經進行過討論。
26.5.3 混合型
在第12.9節中,彙總VaR的方法是一種流行的彙總經濟資本金的方法,這種方法被稱為混合型方法(hybrid approach)。在這種方法中整體風險的經濟資本金與各個單項風險的資本金有如下關係

當損益分佈為正態分佈時,以上關係式完全成立;當損失分佈為非正態時,以上關係式近似成立,但這種近似能夠反映單項損益分佈的肥尾特徵。Rosenberg和Schuermann的研究結果證明上式給出的結果同Copula模型的結果十分接近。
【例26-3】 假設兩個業務部門的市場風險、信用風險及操作風險經濟資本金的估計在表26-2中給出,同時表26-3給出了各個業務部門損失的相關性,在每個業務部門中信用風險同市場風險的相關性為0.5,操作風險同市場風險及信用風險的相關性均為0.2(這裡參數的選取同Rosenberg和Schuermann的結果一致)。不同業務部門間不同風險類型的相關性為0,在不同業務類別之間所有市場風險的相關性為0.4,在不同業務類別之間所有信用風險的相關性為0.6,在不同業務類別之間所有操作風險的相關性為0。
表26-2 例26-3中的經濟資本金的估計

表26-3 例26-3中損益分佈的相關性
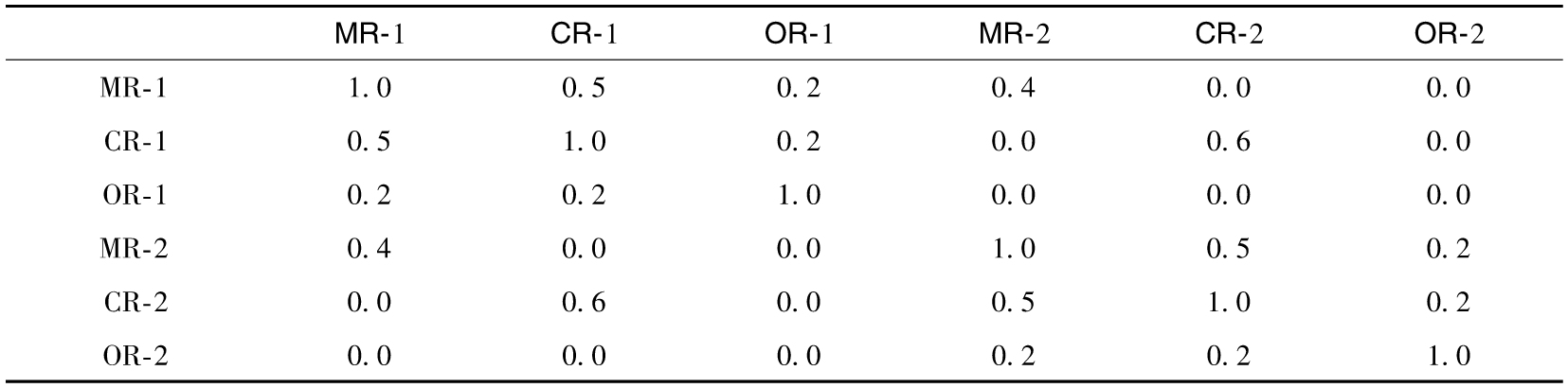
注:MR、CR和OR分別代表市場風險、信用風險和操作風險;數字1和2分別代表業務部門類別。
我們可以將經濟資本金以混合方法進行彙總。整體市場風險經濟資本金為
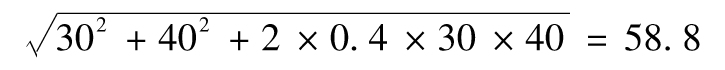
整體信用風險經濟資本金為
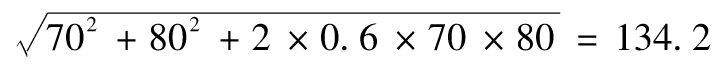
整體操作風險經濟資本金為
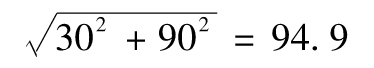
第一個業務部門的整體經濟資本金估計為
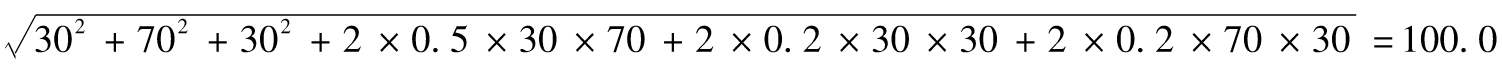
第二個業務部門的整體經濟資本金估計為
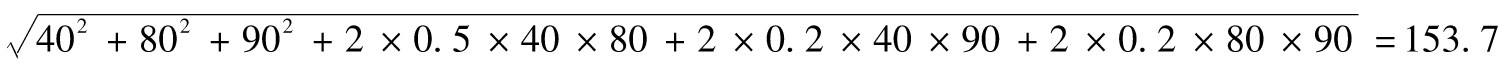
整個企業的經濟資本金是以下數量的平方根
302+402+702+802+302+902+2×0.4×30×40+2×0.5×30×70+
2×0.2×30×30+2×0.5×40×80+2×0.2×40×90+
2×0.6×70×80+2×0.2×70×30+2×0.2×80×90
即203.2。
以上計算在很大程度上顯示了風險分散所帶來的好處。市場風險、信用風險及操作風險經濟資本金的總和為58.8+134.2+94.9=287.9,兩個業務部門的經濟資本金的總和為100+153.7=253.7,以上兩個數值都比實際的經濟資本金估計值203.2要高。
26.6 經濟資本金的分配
假設所有業務部門的經濟資本金的總和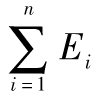 為20億美元,而在考慮了非完全的相關性後,整個銀行實際的經濟資本金為13億美元(實際資本金是各項資本金總和的65%)。這種計算方式給銀行帶來了7億美元的風險分散效益,銀行應如何分配經濟資本金呢?
為20億美元,而在考慮了非完全的相關性後,整個銀行實際的經濟資本金為13億美元(實際資本金是各項資本金總和的65%)。這種計算方式給銀行帶來了7億美元的風險分散效益,銀行應如何分配經濟資本金呢?
一種簡單的方法是將第i個業務部門的經濟資本金分配定為0.65Ei,這種方法可能不是最優的。假如我們總共有50個業務部門,其中兩個業務部門的經濟資本金均為1億美元,如果在計算中不考慮第一個部門,則銀行整體經濟資本金降低6000萬美元;如果在計算中不考慮第二個部門,則銀行整體資本金降低1000萬美元。因此,第一個部門應持有的資本金要高於第二個部門,這是因為這一部門對銀行的整體經濟資本金的遞增效應比第二個部門要更強。
這一問題與在第12.8節中討論的VaR的分配問題類似。一種方法是對每個業務部門計算增量資本金(incremental capital),然後根據增量資本金的比例分配經濟資本金(增量資本金等於包括某業務部門時與不包括該業務部門時的資本金數量的差)。另外一種很流行的方法是採用成分經濟資本金法(component economic capital method),即第i個業務部門所分配的資本金為
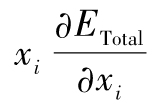
這裡xi為對第i個業務部門的投資額。如第12.8節指出的那樣,歐拉定理保證各個業務部門所分得資本金總和仍然為ETotal。
定義Qi為xi增加Δxi時相應的經濟資本金的增加量,業務部門i的成分資本金的離散估計為

其中yi=Δxi/xi。
【例26-4】 現在我們再一次考慮例26-3,這裡整體經濟資本金為203.2。針對第一個業務部門計算的經濟資本金為100,針對第二個業務部門計算的經濟資本金為153.7。
一種比較簡單的方式是將佔整體資本金100/253.7的部分攤派給部門1,而將佔整體資本金153.7/253.7的部分攤派給部門2,這樣一來部門1分攤的經濟資本金為80.1,部門2分攤的資本金為123.1。
部門1對整體資本金的遞增效應為203.2-153.7=49.5;類似地,部門2對於整體資本金的遞增效應為203.2-100=103.2,兩個遞增效應之和不等於整體資本金(通常是這樣)。我們可以採用遞增數量作為分母來對資本金進行分攤,將整體資本金49.5/(49.5+103.2)分攤給部門1,並將103.2/(49.5+103.2)分攤給部門2。部門1及部門2分攤的資本金數量分別為65.9及137.3。
為了使用式(26-4),並對每個部門計算成分經濟資本金,我們可以對偏導數求得解析解;另外一種做法是求出數值解。如果將部門1的規模增長1%,則由表26-2顯示的市場風險、信用風險及操作風險的經濟資本金分別變為30.3、70.7及30.3。這時整體經濟資本金變為203.906,因而Q1=203.906-203.224=0.682。
如果將部門2的規模增長1%,則由表26-2顯示的市場風險、信用風險及操作風險的經濟資本金分別變為40.4、80.8及90.9,這時整體資本金變為204.577,因而Q2=204.577-203.224=1.353。
在這裡我們考慮的是每個業務部門規模均增長1%,即y1=y2=0.01。由式(26-4)我們可以得出分攤到兩個部門的經濟資本金分別為68.2及135.2(這兩個數量之和與203.2有一些差別,這是由於計算偏導數的誤差所致)。
26.7 德意志銀行的經濟資本金
德意志銀行在其年報上發表其經濟資本金的數量。表26-4是對其2016年監管及經濟資本金的一個總結。德意志銀行計算了市場風險、信用風險、操作風險及業務風險資本金,也計算了市場風險、信用風險及操作風險的分散效應,但沒有考慮業務風險的分散效應。德意志銀行整體經濟資本金為354億歐元。
表26-4 德意志銀行的經濟資本金以及監管資本金 (2016年12月,金額單位:100萬歐元)

德意志銀行實際持有的資本金包括423億歐元的第一類核心資本(即普通股)、46億歐元的附加第一類資本和大約127億歐元的第二類資本。表26-4顯示了這些資本佔風險加權資產的百分比。德意志銀行超過了《巴塞爾協議Ⅲ》的資本要求,包括G-SIB的附加資本,德意志銀行的風險加權資本為2%。
表26-5顯示瞭如何將此資本分配給業務部門。迄今為止,經濟資本金的最大使用者是全球市場部門,德意志銀行表示,全球市場部門以支持自營、代客交易和做市的市場交易為主。該部門的信用風險、市場風險、操作風險和業務風險都是最大的。
表26-5 德意志銀行的經濟資本金分配 (2016年12月,百萬歐元)

26.8 RAROC
經風險調節的績效指標(risk-adjusted performance measurement,RAPM)在近年來已經成為評估銀行業務的重要工具。其測算方式多種多樣,但這些方式的共同點是在對比回報與資本金的關係時都要考慮風險的影響。
在這些方法中,最為流行的方法是將回報與經濟資本金進行比較,這一方法被命名為風險調整後的資本回報率(risk adjusted return on capital,RAROC)。公式為

上式中的分子既可以是稅前收入也可以是稅後收入。有時,由經濟資本金所帶來的無風險利息收入也被包括在分子項中。
【例26-5】 某AA級銀行在某地區發放貸款。每年貸款的平均損失為1%。對應於99.98%置信水平的VaR(即損失超過這一數量的概率僅為0.02%)為未償還本金的5%。如在例26-1中展示的那樣,每100美元貸款所對應的經濟資本金為4美元,這一數量為99.98%置信水平所對應的VaR與ES的差(這裡忽略了實際貸款中的風險分散效應)。資金費用與利息收入的利差為2.5%。將1%的ES從中扣除,我們得出每100美元貸款盈利為1.5美元,假定貸款部門管理費用為整體貸款數額的0.7%,每100美元的預期盈利降為0.8美元,因此RAROC=0.8/4=20%。
另外一種計算方法是將由經濟資本金帶來的利息也考慮在分子中。假設無風險利率為2%,那麼0.02×4=0.08被加到分子上,這時RAROC=0.88/4=22%。
正如Matten(2000)指出的那樣,由式(26-5)計算出的數量應稱為回報與經風險調整的資本比率(return on risk adjusted capital,RORAC),而不是風險調整後的資本回報率,即RAROC。[1]理論上講,在RAROC計算中我們應該對回報(分子項)進行風險調整,而在式(26-5)中我們只對資本金(即分母項)進行了調整。[2]
RAROC的應用有兩種方式,即事前(即在年初)和事後(即在年末)兩種形式。事前形式是基於對將來預期收益的估算,事後形式是基於實際的利潤情況。採用事前形式,我們可以決定在將來哪些部門應該縮減或擴大;採用事後形式,我們可以測算不同部門的表現並決定分紅。
在決定將來哪些部門應該縮減或擴大時,事後形式通常並不適用(雖然我們會傾向於這種做法)。某年的糟糕表現可能是由於信用損失比平均值要高,或者在某年出現了一個較大的操作風險損失,重大業務決策應基於管理人員對業務長期表現的預測。
[1] See C. Matten, Managing Bank Capital: Capital Allocation and Performance Measurement, 2nd ed. (Chichester, UK: John Wiley & Sons, 2000).
[2] 實際上這個問題在將RAROC翻譯成風險調整後的資本回報率時已經陰錯陽差地解決了,也就是說,在中文裡並不存在Matten所說的這個問題。——譯者注
小結
經濟資本金是為了保證銀行或其他金融機構有能力應付自身面對的風險。在計算經濟資本金時,金融機構有權對模型做出選擇,選擇的模型並不一定同監管部門提出的模型一致。一般來講,模型需要計算市場風險、信用風險、操作風險以及(可能的話)業務風險經濟資本金,然後將這些數值進行彙總來產生整個企業的經濟資本金。通常我們假設風險並不是完全相關的,我們對風險分散化的收益要進行估測,並將資本金分配到業務部門。通常計算資本金的方法要反映業務部門對整體資本金的貢獻。
對應於1年展望期的市場風險損失分佈、信用風險損失分佈以及操作風險損失分佈會很不同。市場風險損失分佈比較對稱,信用風險損失分佈具有一定的傾斜度,而操作風險損失分佈具有很高的偏態及肥尾特性。
整體經濟資本金要在整個金融機構的各個部門間進行分攤,然後每個業務部門的風險調整後的資本回報率(RAROC)才可以被計算出來。分攤方式有很多種,但最好的方式應該體現業務部門對金融機構整體資本金的遞增效應。因為風險多元化,分配給每個部門的資本金一般比對這個部門單獨進行計算所得的資本金數量要低。前瞻性的RAROC測算可以幫助管理人員決定在將來哪些部門應該縮減或擴大,實際的RAROC可以用來衡量一個部門的業務表現。
延伸閱讀

練習題
26.1 經濟資本金與監管資本金的區別是什麼?
26.2 一家評級為AA的金融機構經濟資本金置信水平的決定因素是什麼?
26.3 業務風險都包括什麼內容?
26.4 採用內部模型來計算市場風險、信用風險及操作風險經濟資本金與計算監管資本金相比,在哪些方面不同?
26.5 假定信用損失服從對數正態分佈。損失的對數為正態分佈,其期望值為0.5,標準差為4。99.97%的置信水平所對應的經濟資本金為多少?
26.6 假如兩個不同的業務部門所估測的經濟資本金如下表所示。

假定風險之間的相關性如表26-3所示,計算每一個業務部門的經濟資本金。將兩個業務部門合併在一起總的經濟資本金數量為多少?
26.7 在練習題26.6中,每一個業務部門對於整體經濟資本金的遞增效應為多少?並以此來計算每個業務部門的資本金的分攤量。每個業務類別規模分別增長0.5%,對於整體資本金的影響是什麼?請驗證你的結果與歐拉定理的一致性。
26.8 一家銀行在考慮擴大其資產管理業務,這種業務的主要風險是操作風險。經估算得知新業務一年的ES為200萬美元,而99.97%置信水平的VaR為4 000萬美元(來自大客戶的法律訴訟的微小可能性)。每年從客戶收取的資產管理費為1 200萬美元,管理費用預計為300萬美元,這項業務的稅前RAROC為多少?
26.9 RAROC能夠以哪兩種形式得到應用?
作業題
26.10 假定每天的損益為正態分佈,標準差為500萬美元:
(a)估計市場風險最低監管資本金的數量(假定乘積因子為4.0)。
(b)採用1年展望期及99.9%的置信水平,並假設日間損益的相關係數為0.05,根據以上假設計算經濟資本金。
26.11 假如兩個不同業務部門的經濟資本金的估計如下表所示。

同一業務部門的市場風險與信用風險的相關性為0.3,業務部門之間信用風險的相關性為0.7,市場風險的相關性為0.2,其他風險之間的相關性為0。請計算整體經濟資本金,每個業務部門分攤的資本金分別為多少?
26.12 假設某銀行僅有的業務是在世界上的兩個不同地區開展信貸業務。各地區的放貸特徵與第26.8節例26-5中給出的情形相同。在地區A的放貸規模是地區B的3倍,兩個地區貸款損失的相關性為0.4,請估算整體RAROC。
26.13 假如交易的每日損益服從正態分佈並相互獨立,均值為0。計算以下數值(以日損益的標準差為單位):
(a)《巴塞爾協議Ⅰ》規定的監管資本金,即10天展望期、置信度為99%的VaR的3倍;
(b)1年展望期、置信度為99.97%的經濟資本金。
如果日損益的分佈是比正態分佈具有更肥大的尾部的某種分佈,你預計監管資本金和經濟資本金是會彼此接近還是差得更遠?如果日損益之間存在正相關性,那麼情況會怎樣?
第27章
企業風險管理
到目前為止,我們討論的重點是如何建立合理的規程來理解和量化金融機構面對的不同風險(信用風險、市場風險、操作風險和流動性風險等)。確保對風險進行正確的評估是風險管理人員的重要職責之一。同等重要的是,金融機構中的風險管理部門應建立針對風險的統一的、全局性的系統,識別可能出現的不利事件以及它們造成的後果。某一不利事件造成的全局性影響可能比逐個考慮單一風險類別得出的結果更大(或更小)。這種對風險進行整體管理的方法被稱為企業風險管理(enterprise risk management,ERM)。
要理解企業風險管理,需要區分風險管理中的自上而下法與自下而上法。自下而上法關注不同業務類別中不同風險種類的評估和彙總,在前面的章節中我們已經討論過如何完成這項任務。而在自上而下法中,會首先明確整個機構的風險偏好(risk appetite),然後據此制定各個部門風險的容忍度(risk limit)。在實踐中,金融機構需要同時採用這兩種方法。自上而下法用來制定風險偏好,而自下而上法用來評估各部門承擔的風險是否與風險偏好一致。
2004年,全美反舞弊性財務報告委員發起組織(Committee of Sponsoring Organization of the Treadway Commission,COSO)發佈了企業風險管理整合框架(enterprise risk management integrated framework,詳見www.coso.org),其中對企業風險管理進行了如下定義:
企業風險管理是這樣一個過程:它由企業董事會成員、管理層及其他人員把控,在戰略層面橫跨企業各部門實施,用於識別對企業有不利影響的潛在事件,並管理風險使其符合風險偏好,以確保有較大的把握實現企業的既定目標。
以上定義突出了幾點:第一,企業風險管理要有董事會成員的參與;第二,企業風險管理是企業戰略的一部分;第三,涉及對潛在不利事件的識別;第四,作為企業風險管理的一部分,企業必須制定自己的風險偏好,並據此管理自己的風險;第五,企業風險管理應幫助企業達成自己的目標,是戰略規劃和戰略實施過程中的一個核心部分。
傳統上,在自上而下的風險管理中,很多金融機構(以及它們的董事會)普遍存在合規至上的導向,它們的目標僅是讓監管機構滿意並在法律的條文內行事。企業風險管理正在改變金融機構的這種心態,它使風險管理部門具備了戰略導向以及價值提升的作用。一家風險管理更加有效的公司相對其他公司,會擁有競爭優勢。
本章將討論企業風險管理中的核心因素,包括風險偏好、風險文化、如何識別潛在不利事件以及企業風險管理如何與金融機構的戰略進行整合。
27.1 風險偏好
企業風險管理的一個重要部分是明確本企業的風險偏好。為實現企業的既定戰略目標和業務計劃,企業準備承擔多大的風險?要明確金融機構風險偏好,其中的一個問題是在最壞的情況下,機構會承受多大的損失。這一損失可以通過企業整體的在險價值或預期虧空來測算。
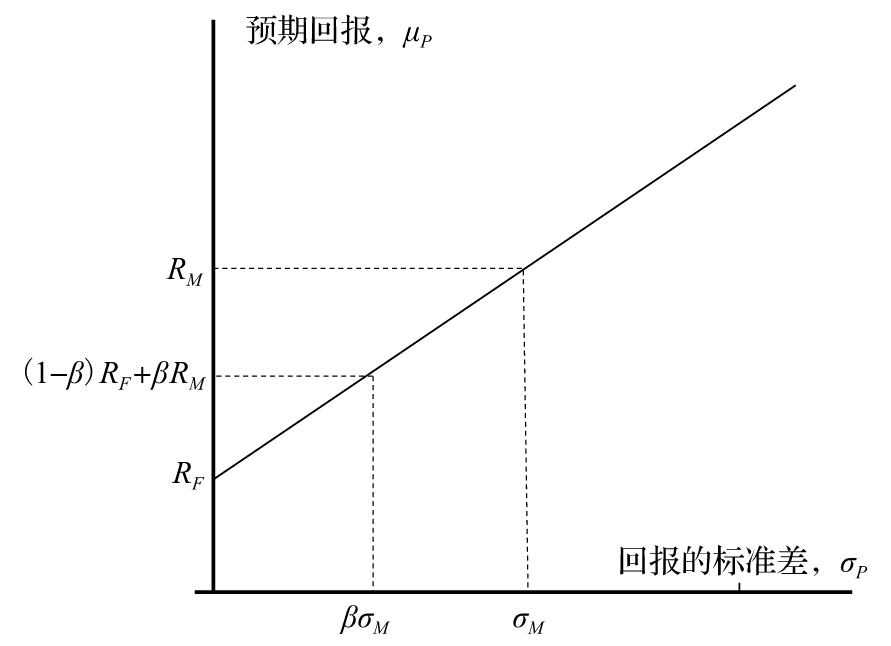
圖27-1 某投資組合中回報的均值和標準差與beta的關係
對一個基金經理來說,這個問題回答起來相對簡單(至少在理論上是這樣的)。第1章解釋了預期回報與風險之間的權衡關係。不同資產的配置會影響組合的beta,而這又在理論上決定了預期的回報和風險。[1]圖27-1與第1章的圖1-4相似,顯示了一個組合預期收益與風險的權衡關係。如在第1.2節中介紹過的,投資組合的beta為β,預期回報μp為
μp=(1-β)RF+βRM
回報率的標準差是
σP=βσM
這裡σM是市場回報率的標準差,RF是無風險回報,RM是市場的預期回報。假設回報服從正態分佈。[2]在一年內,在概率p下會被超出的回報R滿足下式
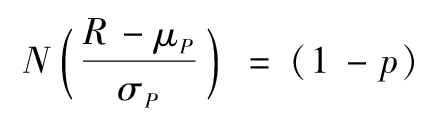
這裡N是累積正態分佈函數。將μP和σP替換後,我們得到
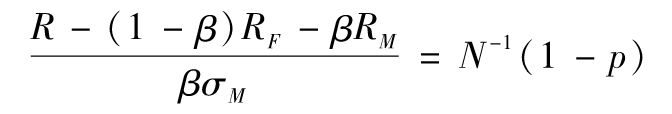
或者

通過上述公式我們可以計算出與特定置信度的VaR相一致的beta。表27-1給出了1970~2016年的47年中,標準普爾500指數的回報(包括股息)。表27-2給出了將最後10年、最後20年以及全部47年的數據使用正態分佈進行擬合後得出的均值和標準差。假設無風險利率是2%(RF=0.02),使用過去10年的數據來計算σM和σM,因此σM=0.1711,RM=0.0875。進一步假設基金的風險偏好是在任一年內,損失不能超過10%的把握是95%。將R=-0.1及p=0.95代入式(27-1),基金經理的beta應該為

表27-1 標準普爾500指數在1970~2016年的年化總收益(包括股息)
表27-2 由表27-1得出的收益統計數據

這意味著要達到VaR目標,風險管理人員需要大致將投資組合的一半投資於市場,剩下的另一半投資於無風險資產。[3]
不幸的是,對銀行或保險公司這類金融機構來說,要對不同的風險-收益折中方案量化,做起來並不像基金經理那樣簡單。在市場有效時,我們可以根據第1章中的論述,認為對股票市場或其他投資,與圖27-1中給出的類似的有效邊界是存在的。但是,對銀行、保險公司和其他金融機構的重大戰略性投資來說,我們沒有理由認為會存在一個能定義收益和風險之間權衡關係的有效邊界。有些戰略投資會位於有效邊界的上方,有些則會位於下方。
對很多公司而言,位於有效邊界上方的戰略性投資通常是那些能充分發揮公司競爭優勢的項目。因此,無論是金融還是非金融企業,都應該明確自己的競爭優勢,並據此來尋找能發揮這些優勢的戰略性投資項目。有證據表明,企業在這方面並不總是成功。鮑曼(Bowman)[4]所做的一項著名的研究顯示,大部分行業中的企業,風險和收益是負相關的。這種現象被稱為鮑曼悖論(Bowman paradox)。在進一步的研究後,鮑曼發現境況越差的公司,承擔的風險越缺乏合理性。[5]對這種現象的一種解釋是,時常陷入困境的公司往往缺乏競爭優勢。這些公司會經營一些成功概率很低的項目,但只要這樣的項目成功,公司就可以生存下去。
金融機構所在的市場是高度競爭的。與其他一些行業相比,競爭優勢往往並不普遍。一般來說,一家金融機構採取的增加收益的措施會涉及系統性風險(beta)的增加,金融機構的股東會也往往會獲得相應的(有些情況下是更好的)風險-收益折中關係。金融機構主要的競爭優勢在於已經建立起來的客戶群體(零售和批發)的信任。給這樣的客戶群體提供服務可以提供令人滿意的風險-收益折中關係。對受監管的金融機構來說,風險-收益折中關係還受到日益嚴格的資本和流動性要求的影響。
如前面所述,金融機構風險偏好有一個維度是關於最壞情況下的損失,或者換一種說法,最壞情況下股本的侵蝕。這個問題可通過特定的展望期和置信度的VaR或ES來表示。風險偏好中的其他維度上的問題就沒有這麼容易被量化。這些問題包括聲譽風險、信用評級風險、監管不合規的風險、法律風險等。這些風險中的一部分適合定性而不是定量表達。例如,銀行可以申明任何戰略性項目,如果預計會降低銀行在核心客戶群體中的聲譽或者其在這些客戶心目中的信任度,則該項目是不可接受的;任何戰略性的舉措,如果在市場看來,會使銀行顯著變得比其主要競爭對手的風險更高,則這樣的項目也是不能被接受的等。此外,銀行還可以採取針對洗錢、行賄、資助恐怖組織等犯罪行為的更加嚴厲的措施。
業界事例27-1描述了富國銀行為了提高銷售額,如何讓員工承受巨大的壓力,以達到不切實際的銷售目標。這種策略導致員工為了達到目標而從事可疑的,有時甚至是欺詐的活動。該策略本應被否決(或至少被更仔細地監控),因為它可能使客戶對銀行產生負面影響,也可能影響銀行與員工的關係。
業界事例27-1
富國銀行交叉銷售
富國銀行是一家在2007~2008年的危機中倖存下來的銀行。它避免了其他銀行在危機爆發前所承擔的風險,並贏得了穩定的聲譽。不幸的是,隨後的事件玷汙了它的聲譽,導致其潛在客戶對它失去了信任。
交叉銷售包括試圖向客戶銷售多種產品。擁有支票賬戶的客戶可能會被鼓勵取出信用卡或開立儲蓄賬戶。富國銀行被認為是最擅長交叉銷售的銀行之一,事實上,交叉銷售並沒有錯,但如果實施得過於激進,可能會損害銀行的聲譽,甚至造成欺詐。
富國銀行認為分行員工是“銷售人員”,而客戶是“客戶”。分行工作人員被給予了非常激進的配額,要求他們完成向客戶銷售產品的數量,並承受著巨大的壓力。結果,他們未經客戶同意就為客戶訂購信用卡。他們還為沒有申請的客戶開設了支票賬戶和儲蓄賬戶。在許多情況下,這些活動導致客戶向銀行支付額外費用。有時甚至通過讓無家可歸者購買收費產品來滿足配額,儘管他們幾乎肯定無法按時付款。
2011年,《華爾街日報》首次報道了富國銀行不正常的銷售文化;2013年,《洛杉磯時報》的一篇文章進一步描述了這種文化。隨後富國銀行進行了一些改革,但該銀行在2016年9月被罰款1.85億美元,原因是它在2011~2016年創建了150多萬個未經授權的存款賬戶和50多萬個未經授權的信用卡賬戶。2017年5月的後期估計顯示,未授權賬戶的數量高於這個數字,總計接近350萬個。
高管聲稱,由於公司高壓的銷售文化,他們不知道發生了什麼。這似乎不太可能,因為員工打了公司的道德熱線電話,而客戶的投訴必須得到處理。2011~2016年,該銀行因欺詐性銷售行為解僱了5 300名員工。首席執行官約翰·斯頓夫(John Stumpf)同意放棄價值4 100萬美元的股票期權,並於2016年10月辭職。後來,他的2 800萬美元收入被追回。其他高管也損失了收益。該銀行向未經許可而開戶的客戶支付了1.1億美元。參議院銀行委員會、美國證券交易委員會和多個司法管轄區的檢察官已展開調查。
顯然,富國銀行激進的銷售文化是被誤導了。它疏遠了員工,他們中的許多人承受著不合理的壓力,而且在被解僱後發現很難找到新工作。它還破壞了富國銀行多年來與客戶建立起來的信任和良好聲譽。如果富國銀行的風險偏好包括希望避免從事可能對其聲譽造成負面影響的活動,它肯定會減少銷售壓力,並強調與客戶建立良好長期關係的重要性。
2016年年底,在新任CEO的領導下,富國銀行採取措施改變銷售文化。它停止了給員工設定銷售配額的做法。一些曾經被解僱的僱員被重新僱用了。銀行與員工和客戶的關係需要一段時間才能恢復,但富國銀行是一家財務實力雄厚的銀行,我們可以預期它最終會恢復元氣。
對風險的量化一直是本書的主題。迄今為止,我們一直在採用自下而上法。我們已經討論了業務部門可採用的計算各種風險指標的不同方法,然後怎樣將這些指標彙總起來,產生整個企業的整體風險指標。例如,在討論經濟資本金時,我們討論瞭如何將不同業務部門承擔的不同類別的風險彙總起來,產生一個整體的經濟資本金指標。風險偏好的制定是一種應由董事會參與的自上而下的行為。風險偏好首先應該針對全機構整體定義,然後再用來制定各業務部門的風險限額。這會涉及一些實驗措施,其中會使用自下而上法來驗證企業的風險偏好是否得到滿足。例如,一家希望維持AA評級的金融機構可能決定,一年內遭受超過500億美元損失的概率不能高於0.03%。接下來,該機構就需要通過不斷的實驗試錯,找出其交易損失、信用損失和其他損失的恰當的VaR限額,使得當這些限額被集中起來時,能夠與其在風險偏好中的相應位置保持一致。風險限額一旦確認,一項重要工作就是監控各個業務部門的決策,以確保風險限額被嚴格遵守。
風險偏好中的一個重要因素是風險集中度。儘管有些事後諸葛亮,但我們還是要說2006年和2007年,很多大型金融機構在次級住房抵押貸款上的集中度太高了。金融機構闡釋的風險偏好會直接或間接地影響到風險集中度。風險偏好中應對以下敞口做出限制:對單一企業的信用風險敞口、對經濟體中某行業的信用風險敞口、對某市場變量變動的敞口等。
很自然地,監管機構會鼓勵銀行建立風險偏好框架。實際上,銀行監管機構必須確保所轄銀行有效地建立和實施了風險偏好闡釋制度。2013年,美國金融穩定委員會發布了一份包含風險偏好框架核心概念和原則的文件。[6]文件中明確了董事會、首席執行官、首席風險官、首席財務官以及業務部門主管各自的職責。
[1] 如在第1章中解釋過的,在實踐中,某一特定beta值對應的理論回報通常被用作基準。能超過基準回報的基金經理被認為取得了超額收益。
[2] 採用這一假設只是為了簡化說明。與正態分佈相比,市場回報的分佈有更肥大的尾部,因此在實踐中,通常會採用其他分佈進行擬合,如有較小自由度的學生t-分佈。
[3] 在實踐中,基金經理在選擇投資組合時,傾向於將自己對收益的判斷納入其中。如何做到這一點。參見F. Black and R. Litterman, “Asset Allocation:Combining Investor Views with Market Equilibrium,” Journal of Fixed Income 1, no.2(September 1991):7-18。
[4] Bowman, E.H., “A Risk-Return Paradox for Strategic Management,” Sloan Management Review 21(1980):17-31.
[5] Bowman, E.H., “Risk Seeking by Troubled Firms,” Sloan Management Review 23(1982):33-42.
[6] See Financial Stability Board, “FSB Principles for an Effective Risk Appetite Framework,” Consultative Document, July 2013.
27.2 風險文化
一家金融機構的風險文化的全部要義在於決策是如何產生的。如果風險文化是良性的,那麼一個決策的制定過程一定有章可循,並仔細考慮各種可能出現的結果,以及風險和收益的權衡。需要強調的是,這樣做不意味著沒有風險,而是說風險要跟可能的收益以及企業的風險偏好結合起來考慮。金融穩定委員會建議銀行監管部門對大型系統重要性銀行的風險文化做出評估。[1]
做出決策時常常要在短期效益以及中長期風險之間做出權衡。一項可以獲得立竿見影的效益的措施可能會在將來造成嚴重的問題。設想這樣一個情景,一家金融機構的銷售人員正在決定是否要賣給客戶一個非常複雜的金融產品,而他知道這個產品並不能真正滿足客戶的需要。如果成交,金融機構會從中獲利,銷售員以及開發該產品的團隊也會得到數額不菲的年終獎金,但這筆交易在將來也許會有不良後果。例如,如果這個產品給客戶造成損失,金融機構的聲譽就會受到影響,隨之而來的可能是昂貴的法律訴訟。
業界事例5-4描述的信孚銀行賣給寶潔公司的產品就是這種情況的一個經典例子。該產品給寶潔公司提供了一個很高的概率,可降低融資利率75個基點,但有一個較小的概率會給寶潔公司造成慘重損失。信孚銀行的銷售人員可能並沒有給寶潔公司解釋過可能會給後者帶來嚴重損失的情景。但是,如果信孚銀行有一個良性的風險文化,管理人員就會從根本上質疑銷售這樣一個產品是不是合理的。實際上,或許從一開始,信孚銀行的量化人員就該被告知不應開發這個產品。
寶潔公司只是眾多與信孚銀行進行了類似交易的公司中的一家。正如我們知道的,小概率事件發生了,與信孚銀行交易的客戶蒙受了重大的損失。這導致了多個法律訴訟,最後都以庭外和解告終。信孚銀行這家在金融市場上顯赫一時的機構變得聲名狼藉,最後被德意志銀行收購。當然,事情也可能是個大圓滿的結局,信孚銀行的客戶會因為信孚銀行給自己節省了75個基點的融資利率而感激它。但很明顯,這筆交易對信孚銀行本身的風險以及因客戶損失導致的聲譽損失明顯太大了。其風險文化表現為員工只注重短期利益而不是長期後果。
還有一個例子是2007年西班牙的桑坦德銀行與葡萄牙國營軌道交通運營商波多捷運之間的一筆交易,業界事例27-2描述了這個例子。在這筆交易中,波多捷運可以在交易的頭兩年降低自己的融資成本,但是作為代價,在此之後的年度中可能會面臨極高的融資成本。從波多捷運的角度看,以長期風險換取短期收益的做法固然是值得推敲的,但對桑坦德銀行來說,這個問題同樣成立。這只是桑坦德銀行賣給很多葡萄牙國有企業的類似產品中的一個。毫無疑問,進行這些交易時,在桑坦德銀行看來可從中獲取可觀的利潤,但後來的法律訴訟包括和解費用以及對桑坦德銀行聲譽的負面影響表明這些交易帶來的損失遠超過短期的利潤。
業界事例27-2
桑坦德軌道交通交易
2007年,葡萄牙軌道交通公司波多捷運(Metro do Porto,MdP)正在尋找途徑,降低自己每年4.76%的融資利率。在諮詢了多家銀行以後,MdP同意與西班牙銀行桑坦德進行一筆14年的互換交易。在這筆互換交易中,桑坦德支付4.76%的融資利率給MdP,而MdP支付給桑坦德1.76%的利率加一個利差。在最初的兩年,利差為0,這樣MdP就節省了3%的融資利率。兩年以後,利差通過下式計算得出
max[0,Previous Spread+2×max(2%-R,0)+2×max(R-6%,0)-D]
其中R為3個月的歐洲銀行間同業拆借利率(Euribor),D被稱作二值息票(DigiCoupon)。如果R為2%~6%,則D=0.5%,否則D=0。
在交易開始時,3個月期限的Euribor大概為4%。如果Euribor在14年內始終停留在2%~6%,那麼在整個期限內,MdP可以每年節省不少於3%的融資成本。但實際情況是,到2009年,當這筆交易滿兩年時,3個月期限的Euribor跌到了2%以下。因此,利差迅速上漲,到2013年9月,竟然達到了40.6%。MdP的問題在於,本季度的利差依賴上一個季度。假設在第二年開始時,3個月的Euribor為0.5%,MdP的利差將每季度上升3%,也就是每年12%。如果後來3個月的Euribor上升,回到2%~6%,利差會下降,但幅度只有每季度0.5%,或者每年2%。
這個交易最後被訴諸法庭(桑坦德與葡萄牙國有企業進行的其他類似交易都以庭外和解告終)。MdP當然應該通過情景測試來理解交易可能帶來的鉅額成本。我們並不清楚它是否進行過這樣的測試以及是否理解交易中利差會遞增這個特性。也許,在開始的兩年中每年能節省3%的融資成本這一條件誘惑力太大。根據2014年Risk雜誌的一篇文章,一家位於倫敦的企業對衝策略諮詢公司將這筆交易描繪成史上最糟糕的交易的有力競爭者之一。
業界事例27-3給出了另一個短期效益和長期風險衝突的例子。在這個例子中,高盛集團與一家客戶進行了一筆被稱為ABACUS[2]的交易,但高盛集團被指控沒有詳盡地披露交易的風險以及交易是如何構建的。這個例子再次顯示了只顧短期效益而不考慮長期聲譽風險和代價的做法。
業界事例27-3
ABACUS
2007年,高盛集團基於合成ABS CDO開發了一種被稱為ABACUS的產品。如第6章介紹過的,合成ABS CDO建立在多個ABS分檔的組合之上(通常是中間檔)。這裡合成(synthetic)的意思是,高盛集團在這裡定義了ABS CDO,但並不真正買入標的ABS的分檔,而是在兩方之間充當中間人的角色。其中A方買入一個信用違約互換,該互換為名義上生成的ABS CDO高級檔的信用損失提供保護;B方賣出這樣一個CDS,並承諾提供信用保護。A方付給B方一個保險費用(即CDS利差)。
看上去萬事大吉。這就是高盛集團一類的投行一直在做的事情——在買家和賣家之間充當中介。在這個具體的案例中,我們所指的A方是約翰·保爾森所掌控的對衝基金。這是少數幾個投下鉅額賭注,押注次級住房抵押貸款以及房市崩盤的對衝基金之一。保爾森的基金付給高盛集團1500萬美元,建立交易結構,而且保爾森的基金有權選擇結構中包含哪些ABS。交易的B方是位於德國杜塞爾多夫(Dusseldorf)的德國工業銀行(IKB Deutsche Industriebank AG,IKB)。這家公司的主要業務是對中小型企業提供貸款。交易組合的管理方是ACA,這在當時也是一家在ABS CDO管理方面聲譽很好的機構。
在該交易中,高盛集團被控對IKB提供不實信息,使其認為ABS CDO是由ACA定義的。但實際情況是,組合中的ABS是由保爾森的對衝基金選取的,而這些ABS發生鉅額損失的可能性非常高。特別是,據說保爾森在構建ABS CDO時,特意選取了那些由來自低FICO分數的貸款者和房價上漲幅度最大的地區的抵押貸款組合構成的ABS分檔。
IKB和ACA都遭受了鉅額損失,而保爾森的對衝基金卻賺得盆滿缽滿(因為在次債危機中損失慘重,IKB不得不接受救助)。SEC對這筆交易進行了調查,結果是高盛集團被罰款5.5億美元,這在當時是SEC史上開出的金額最高的罰單。事後調查發現,負責這筆交易的高盛集團交易員法布里斯·圖爾(Fabrice Tourre)曾給一位朋友寫了一封電子郵件,這封郵件使高盛集團的地位受到了很大的傷害。圖爾在信中說:“系統中的槓桿越來越高,大廈將傾倒……唯一的倖存者將是偉大的法布(指圖爾自己)……矗立在這一堆他自己一手搭建的複雜的、高槓杆的、光怪陸離的交易之間,而連他自己可能也不清楚這些怪物會帶來什麼。”[3]
ABACUS交易以及其他幾起事件促使高盛集團著手改變自己的企業文化。高盛集團的上層一致認為,高盛集團要贏回企業和投資客戶的忠誠,就必須做出改變。CEO勞爾德·貝蘭克梵(Lloyd Blankfein)在18個月內訪問了23個國家,其間他一再強調銀行的道德和聲譽與利潤同等重要(也就是說,如果存在潛在的長期不良後果,則不能以此為代價去換取短期的效益)。加里·科恩(Gary Cohn)[4]被任命執掌全公司客戶及業務標準委員會(The Firmwide Client and Business Standards Committee)。該委員會的一項工作就是評估“我們的客戶是否有足夠的經驗和能力去理解他們將與我們進行的交易所產生的各種結果”。全公司客戶及業務標準委員會採取了一系列步驟確保高盛集團的銀行職員和交易員對客戶坦誠相待,並避免任何可能會產生爭議的舉動。在採取了這些措施後,業界普遍認為高盛集團的聲譽得到了改善。
在金融機構中,薪酬制度在決定短期績效與長期風險的取捨方面扮演著重要角色。傳統上,獎金是根據僱員當年的業績發放的。這意味著僱員在做決定時,考慮的期限僅到下一次發放獎金的日子(總是少於1年)。如果一筆交易會導致不良後果,但是後果不會在年終之前顯現,則這種不良後果往往會被忽視。很多金融機構已經開始採取措施來改變這種只注重短期績效的薪酬制度。現在,某一年度的獎金會在接下來的幾年中分批發放,而且如果後來發現當年的盈利並不如原來設想的那樣好的話,該年度的獎金可以被追回(clawed back,也就是不再繼續發放)。[5]
[1] See Financial Stability Board, “Guidance on Supervisory Interaction with Financial Institutions on Risk Culture: A Framework for Assessing Risk Culture,” April 2014.
[2] 這個詞在中文中的意思是算盤,倒是很符合語境。——譯者注
[3] 圖爾離開高盛集團和華爾街後去芝加哥大學攻讀經濟學博士學位。2014年法庭判SEC對他的欺詐指控成立,他被要求支付82.5萬美元的罰款和其他費用。圖爾本人發表聲明表示不會上訴,並希望這一事件儘快了結,使自己能夠專心學術。——譯者注
[4] 加里·科恩現在擔任特朗普總統的首席經濟顧問和國家經濟委員會主任。——譯者注
[5] 煩瑣的法律問題導致金融機構很難追回已經發放的獎金,因此獎金追回的條款通常需要與獎金的遞延(deferral)發放結合起來。
27.3 識別重大風險
金融機構企業風險管理的一項重要內容是識別已有業務和重大戰略投資計劃的關鍵風險敞口。要識別這些風險敞口在很大程度上與選擇壓力測試的情景類似。歷史可以提供一些指引。例如,金融機構應該考慮,如果類似2007~2009年的衰退再次發生,它應該怎樣應對,對正在發生以及初現端倪的趨勢也應加以仔細分析。為金融機構工作的經濟學家以及高管也可以提供有價值的見解。正如前面章節解釋的,銀行所處的環境在改變。2007年信用危機的後果之一是金融機構受監管的幅度增強了。有些業務,如衍生產品交易的利潤幅度不像危機前那樣大;另一些業務,如自營交易乾脆被禁止(至少在美國是這樣的)。資本金要求以及流動性要求變得更高。一些金融媒介業務由銀行轉移到了影子銀行,如貨幣市場基金、住房抵押貸款公司、證券化機構等。在很多情況下,影子銀行受到的監管比銀行要輕,因此可以提供更有競爭力的服務。
認知偏差
有效識別風險的能力會受到被稱為認知偏差現象的影響。認知偏差(cognitive biases)是指人類思考問題的方式有一定的傾向性而且並不是完全理性的。認知偏差的一個例子是一廂情願。有時我們很難分清什麼是我們想要發生的(如一個項目會成功)以及什麼是我們認為會發生的(作為一個測試,我們不妨問一下曼聯隊的球迷,曼聯下一個年度奪得足總盃的把握有多大)。當希望某件事會發生時,我們往往只考慮能夠促成這件事發生的因素。
心理學家羅列了超過100種認知偏差的表現。很多開創性的工作是由丹尼爾·卡尼曼(Daniel Kahmeman)和阿莫斯·特沃斯基(Amos Tversky)完成的。[1]因為在前景理論(prospect theory)方面與特沃斯基的共同貢獻,卡尼曼獲得了2002年度諾貝爾經濟學獎(特沃斯基不幸在此前去世)。該理論研究的是人們在面臨不同的帶有風險的選項時,是如何做出決策的。
一種重要的偏差被稱作錨定效應(anchoring)。在評估一種可能出現的結果時(例如,一項新的風險投資的收益),我們很可能固守在最初評估得出的結論上。我們會傾向於僅對最初的估計做較小的修正(這種現象被稱為“錨定與調整”現象),而通常不會去考慮更全面的可能性。特別是,重大的不良後果會被有意無意地認作根本不會發生。要說明錨定效應,我們可以做個試驗。詢問一組人一個他們並不知道答案的問題,如冰島的人口數量。先請他們給出自己認為對答案的最好的猜測,然後請他們給出自己主觀認為的人口數量概率分佈的5%和95%分位數之間的範圍。如果他們的估計是好的,則人口的真實數量位於這個區間之外的概率只有10%。但實際上,發生這種情況的頻率遠大於此。錨定效應的存在使人們認為自己瞭解的比實際瞭解得更多。
另外一種認知偏差被稱為可得性啟發(availability)。這是指較新的信息會被賦予過大的權重。不幸的是,企業風險管理(對一般的風險管理也是如此)就是該現象的受害者。在金融危機之前,很多金融機構的風控人員的意見不受重視,因為危機爆發前的情況一直很好。金融危機後,這種情況得到了改善,風控人員有了更大的影響力。但是隨著對危機記憶的消退,“美好的光景可以一直持續下去”這種態度又開始回潮了。
還有一種認知偏差被稱為代表性啟發(representativeness)。這種現象是指一個人會以自己過去在類似背景下的經歷或形成的觀點為模式,對某一件事做出分類。這種現象有助於做出迅速的決策,但是也存在缺陷,因為它會導致思維閉塞和刻板印象。基於過去的經歷,一家金融機構的某位高管可能會認為在某一市場領域,其他任何機構都幾乎不可能具備與本機構競爭的能力。但是,如果這位高管的經歷是有限的,那麼他過去的經歷也許對未來可能會發生的情況缺乏代表性。
人們在估計某一情況可能出現的概率時,有時會犯條件倒置的錯誤。假設有一種特殊的疾病,平均每10 000人中會有1個病例。如果有一個準確率為99%的測試發現你的檢查結果為陽性(陽性表示帶有這種疾病),那麼你得病的概率是多大?你可能馬上會認為這個概率是99%,但正確的答案是1%。我們感興趣的概率是
Prob(D | TP)
其中D為得病的概率,TP為檢查結果呈陽性的概率。
從檢查本身的準確度看,我們有
Prob(TP | D)=0.99
但是
Prob(D | TP)≠Prob(TP | D)
在每10 000個人中,平均有大約100個人的檢查結果呈陽性,但只有1個人是真正的患者。[2]因此,我們真正感興趣的概率只有0.01。這是概率論中的貝葉斯定理的運用。
還有一種偏差被稱作“沉沒成本偏差”(sunk cost bias)。假設有一家金融機構為打開某個新市場已經花費了10億美元,但是情況並不樂觀,成功的希望渺茫,那麼這10億美元的花費會影響這家機構的決策嗎?答案是這10億美元是會計上所稱的沉沒成本。不管現在如何決策,這部分成本都已不能被收回。關鍵的問題是未來的效益是不是足夠高,成為繼續投入的理由。在實踐中,很多人並不情願承認錯誤,而是花費大量時間把明顯已經失敗的項目繼續進行下去。即使明知成功的概率很小,他們還是指望能夠把投入的錢撈回來,這是缺乏理性的。
瞭解這些認知偏差有助於我們做出正確的決策,並識別關鍵風險。但是,我們也應注意,心理學家的實驗表明,偏差是非常難避免的。即便研究人員已經向試驗對象仔細解釋過這些偏差(如錨定效應),並且給予他們經濟上的獎勵,鼓勵他們做出好的估計,偏差還是會出現。
企業風險管理面臨的挑戰是需要識別尾部風險,並儘量準確地估計在尾部風險上升的條件下,各種不良情況發生的概率。我們討論的認知偏差(包括很多沒有在此討論但是已經被心理學家記錄的偏差)表明風險可能被低估。納西姆·塔勒布(Nassim Taleb)在其暢銷書《黑天鵝》中對此做出了論述。[3]在書中他對採用正態分佈來計算風險指標的做法(正如我們在本書中經常做的)提出了尤其嚴厲的批評,並且指出類似1987年的股災以及2007~2009年的信用危機一類的事件發生的可能性遠比我們預想的要大。
通過由高管組成的委員會或經濟學家來定義可能的不良情境是有益的。在討論觀點時,我們還應鼓勵員工充當魔鬼代言人(即充分表達相反甚至極端的意見)。如果CEO獨斷專行,總是相信自己的主要戰略決策是正確的,且不喜歡聽反對的意見,那麼很顯然潛在風險是很難得到充分考慮的。
[1] See, for example, D. Kahneman, P. Slovic, and A. Tversky, Judgment under Uncertainty: Heuristics and Biases (New York: Cambridge University Press, 1982).
[2] 如果有100例檢查結果呈陽性,那麼這個檢查結果對9 901人是準確的,所以準確率是99%。
[3] See N. N. Taleb, The Black Swan: The Impact of the Highly Improbable (New York: Random House, 2007).
27.4 戰略風險管理
一家公司的戰略一旦被制定,戰略風險管理就要考慮已制定的戰略建立在哪些假設的基礎上,以及發生什麼樣的情況會導致這些假設不再成立。競爭者會怎麼樣做?客戶的反饋如何?外部不良事件會怎樣影響到這些戰略?邁克爾·波特(Michael Porter)曾說:“風險實際上就是一個反映在不利的情況發生時,某一戰略表現如何的函數。”[1]
在識別出現有業務或新的戰略性投資中存在特定風險之後,可以採取幾種不同的應對措施:
·規避:退出這項業務或投資;
·降低:採取措施降低不良事件發生的概率或者帶來的影響;
·調整:改變計劃降低風險;
·分擔或保險:將風險轉移出去或者由合作伙伴分擔;
·接受:什麼也不做。
具體應採取哪項措施取決於實際情況,但是正確識別風險以及仔細考慮應對措施始終是關鍵,而不能簡單地忽略。
假設一家成功的加拿大銀行計劃通過併購一家小銀行的辦法擴張在美國的零售業務。銀行已為此制訂了計劃,分析表明這項擴張計劃將提升股東的價值並擴大在美國的客戶群體。同時,有多處風險需要考慮。這家銀行能否在一個競爭更加激烈的市場上覆制它在加拿大的成功?它是否有能力留住美國客戶?能否保持穩定的核心管理團隊?如果在收購完成後,經濟馬上陷入兩年的衰退,將如何應對?這家加拿大銀行要確保收購行為與自己的風險偏好是一致的,而已制定的風險偏好要求在最壞的情況下,銀行要能保證生存而且在加拿大的業務不能受到明顯的影響。因此,銀行要確保新業務的風險是可以監控和管理的,如果結局不妙,要有能夠退出的戰略。
[1] See M. E. Porter, Competitive Advantage (New York: Free Press, 1985), 476.
小結
企業風險管理的目標是從整體上管理風險,而不是逐個應對。其核心理念是,金融機構中的各個業務部門應該是一個統一的、戰略性的和企業全局性管理系統的組成部分。機構的風險偏好應該由頂層制定,並經董事會批准。然後須據此制定相應的規程,保證不同業務部門中不同類型風險的管理實踐與整體的風險偏好框架是一致的。
一家金融機構的風險偏好中應闡明為實現既定目標,其準備承擔多大的風險。風險偏好中的一些層面可以通過定量的方式來表示,例如金融機構可以承受的資本金損失。另外一些層面,例如聲譽風險,可能以定性的方式來描述。明確了風險偏好以後,還必須據此制定業務部門在準備承擔風險時的指導方針,恰當地設定交易風險限額、金融機構投資組合的集中度限制、信用風險限額等。金融機構承擔的風險必須被持續地監控以確保這些風險與整個機構的風險偏好的一致性。
建立一種良性的風險文化是企業風險管理重要的組成部分。風險文化中的一個關鍵因素是在評估能產生短期效益的項目時,應考慮其在中長期的風險。很多金融機構非常激進地追求短期效益,結果導致在幾年後發生嚴重問題,如法律訴訟、罰款以及聲譽損失。這樣的案例不勝枚舉。在過去,金融機構的獎勵機製造成僱員把追求短期效益最大化作為唯一的決策標準。2008年危機以後,金融機構已通過引入獎金延遲發放和追回制度,努力改變這種文化。
金融機構應建立適當的流程來識別極端不利情況造成的後果,這是非常重要的。不幸的是,有很多認知偏差會導致管理人員誤判將來可能發生的情況以及相關的概率。一旦承擔的風險被識別出來,金融機構就應該對其進行積極的管理。有時終止某些業務活動是必要的;有時風險可以被分擔(例如,通過購買保險或成立合資企業);有時可以採取措施來降低風險的影響;當然也可能風險在機構的風險偏好內可以被接受而無須採取額外措施。
延伸閱讀

練習題
27.1 解釋風險管理中自上而下法與自下而上法的區別。為什麼在企業風險管理中二者都需要?
27.2 鮑曼悖論是什麼?
27.3 “銀行的風險文化應將決策的長期影響與短期效益並重。”討論這一觀點。
27.4 銀行可以採取哪些措施鼓勵員工在思考問題時,不拘泥於短期效益的影響?
27.5 企業風險管理與其他傳統的風險管理方法之間的區別是什麼?
27.6 一家基金的風險偏好闡明,基金要有90%的把握在一年內損失不會超過20%。根據表27-2中提供的1970~2016年標準普爾的表現,計算基金應有的beta。計算中假設無風險利率為3%。
27.7 如果Euribor利率從第2年開始為8%,計算業界事例27-2中交易開始後6年MdP支付的利率。
27.8 給出認知偏差的三個例子。
作業題
27.9 假設在業界事例27-2中,3個月的Euribor在每季度中的變化服從正態分佈,其中平均值為0,一個標準差等於x個基點。使用蒙特卡羅試驗(500次)計算MdP在4年中需要支付的平均利息是多少?設x分別等於10、20和50。
27.10 一家基金的風險偏好闡明一年內損失超過25%的概率應低於97.5%。使用表27-2給出的標準普爾500指數在1997~2016年的表現數據,計算基金應有的beta。假設無風險利率為每年2.5%。
第28章
金融創新
20世紀80年代,當預訂從紐約到倫敦的航班時,旅客會聯繫旅行社,旅行社會檢查航班的可預訂性、提供選項、接收指示,然後最終進行預訂。而今天,客戶可能會訪問航空公司的網站,直接向航空公司訂票。我們把這種不再需要旅行社作為中間人所發生的過程叫作一個脫媒(disintermediation)的過程。
這並不意味著在旅遊業務中根本不需要中間商。當客戶不知道該使用哪家航空公司,或者想快速比較不同航空公司提供的價格時,Expedia和Travelocity等在線服務就能提供幫助。但旅遊行業中介機構的性質已經發生了變化,在直接安排航班的過程中,人們的參與基本上已經消失。像Expedia和Travelocity這種基於新技術的中介機構的創建被稱為復媒(reintermediation)。“脫媒後復媒”是一種常見的技術變革的模式。
銀行和其他金融公司是中介機構,就像20世紀80年代的旅行社一樣,它們所提供的服務同樣有被技術衝擊的風險。商業銀行是把錢從存款人轉移到借款人的中介機構,它也是根據客戶的指示結算支票和轉賬資金的支付系統中介機構。投資銀行是促進股票和債券發行的中介機構。銀行和其他金融公司作為中介機構,在為客戶提供理財服務時將客戶的儲蓄投資於合適的產品。
金融科技關注的是技術在金融服務中的應用,如自動取款機、網上銀行和網上交易。本章著眼於未來金融服務可能受到金融科技的何種影響,哪些活動最有可能被數字化,客戶將如何反應,以及金融服務公司如何進行自我調整以適應快速的技術變化。這些都是當今風險管理專業人士面對的重要問題。
28.1 技術的進步
在計算機時代的頭50年裡,計算機處理能力的增長速度確實令人震驚,這使得許多社會科技進步成為可能。1965年,英特爾(Intel)聯合創始人戈登·摩爾(Gordon Moore)正確預測到,計算機的處理能力將每兩年翻一番。現在,一部智能手機的處理能力已經超過了1969年美國宇航局將人類送上月球時的計算機的處理能力。
許多以前人類進行的活動已經被自動化了。機器人流程自動化(robot process automation,RPA)是一個令人感興趣的發展方向。這是一個軟件應用程序,可以複製人類與各種應用系統交互的行為,是一種讓系統實現自動化的方式。軟件機器人是一種虛擬的工作人員,可以通過訓練來執行某些任務,其方法與人類訓練的方法非常相似。例如,這些任務可能與開立新客戶賬戶或僱用新員工有關。通常,數據被髮送到組織內的許多不同系統。
28.1.1 機器學習
計算能力增長的一個重要結果是機器學習的增長。這是人工智能的一個分支,它允許計算機無須顯式編程就能學習。
假設我們想教一臺計算機在英語和日語之間進行翻譯。一種方法是編寫英語字典中包含的所有語法規則和定義,對日語也這樣做,然後提供一個日英詞典。谷歌率先提出的另一種方法是使用機器學習,事實證明這種方法更為成功。計算機被輸入許多由英日雙語者翻譯成日語的英語文本。然後,計算機使用各種工具來搜索模式,並開發自己的複雜翻譯規則。
機器學習在金融領域有許多潛在的應用,如欺詐識別和貸款決策自動化。
機器學習有以下三種類型。
(1)監督學習(supervised learning):向計算機提供由輸入和期望輸出組成的數據,目標是為將輸入映射到輸出制定規則。我們剛才給出的翻譯例子屬於這一類。
(2)無監督學習(unsupervised learning):要求計算機通過查找數據中的結構或隱藏模式來學習。
(3)強化學習(reinforcement learning):計算機程序與動態環境交互,在動態環境中,它必須執行特定的目標,例如駕駛車輛。
在機器學習中,運用多種不同的統計方法和其他工具揭示數據的內在性質與規律。監督學習可以包括線性迴歸和邏輯迴歸。無監督學習可以包括聚類技術,如K-means算法,有時在處理數據前使用降維算法,如主成分分析。
人類非常擅長一些模式識別任務,而這些任務在傳統上是計算機難以完成的,例如,將一個人的臉與另一個人的臉區分開來。一項關於我們如何做到這一點的研究已經在機器學習神經網絡方面取得了一些重要突破。神經網絡是模仿人類識別模式的工具。它們依賴於一種被稱為反向傳播的數學過程來迭代地計算節點上的權重,從而生成所需的輸出。
機器學習算法需要大量的數據進行訓練,所以如果沒有並行處理、雲計算和其他軟硬件方面的進步,今天的應用是不可能實現的。
28.1.2 區塊鏈
在通常情況下,記錄資產所有權的分類賬都涉及欺詐、用戶對其缺乏信任和計算機黑客行為。許多讀者都聽說過所有權欺詐的事例,比如有人宣稱自己擁有房屋所有權,並藉此獲得抵押貸款。有時,記錄相同項目的分類賬由不同組織的人員保管。這樣,記錄中可能會出現不一致的情況,而整理這些問題可能既昂貴又耗時。
區塊鏈是一個分佈式分類賬,用戶可以在其中添加條目,一旦達成一致意見,分佈式分類賬將自動更新。涉及不一致的記錄、欺詐或黑客行為的問題要麼是不可能的,要麼是極其不可能的,因為相同的記錄存在許多不同的計算機上,可以在任何時候進行檢查。區塊鏈最早是在2009年作為與比特幣相關的領域被開發出來的,但目前該技術的許多其他應用正在探索之中。單個分類賬是一個記錄列表,被視為一個區塊。當創建一個新交易塊時(對於比特幣,每10分鐘創建一個),一個新塊就被添加到鏈中。每個參與的人都會得到一個不斷更新的塊列表。
區塊鏈的一個重要方面是哈希。哈希是由64個字符組成的字符串。任何文本都可以轉換為哈希,但是哈希值轉換成文本的反轉進程是不可以的。即使文本中的一個小更改也會完全改變哈希。為了說明這一點,我們可以訪問SHA 256哈希計算器,網址是:
http://www.xorbin.com/tools/sha256-hash-calculator
哈希本書書名,“Risk Management and Financial Institutions”(非斜體),給出:
1dcc48387a27cd95378b08ab26261b161a97c51a7c9146f3d3ff73710d656a3f
添加我們新的版本號後“Risk Management and Financial Institutions 5”(同樣不使用斜體),將生成一個完全不同的哈希值:
117e1e23121f8db4b75d3e2a63d37ef052b11a63cf448721825aadb882492c6b
從理論上講,兩組記錄可以給出相同的哈希,但實際上,這是完全不可能的。我們剛才看到的哈希由數字0~9和字母表的前6個字母組成。這意味著有1664-1個不同的哈希。[1]
區塊鏈的每個塊中的記錄都是密封的,並使用哈希進行防篡改。哈希的一個輸入是緊接前一個塊的哈希,這意味著任何試圖篡改一個塊的操作都會立即被發現,因為它將影響該塊和所有後續塊。
為了使區塊鏈不受人為干預,我們必須激勵參與者檢查新塊並對其進行哈希。比特幣通過邀請參與者(被稱為“礦工”)搜索一種叫作“nonce”的東西來實現這一目的。當nonce被添加到比特幣塊中時,它將導致一個以幾個0開始的哈希。而找到nonce的參與者將獲得預先確定的比特幣數量作為獎勵,同時,也會將新塊哈希並分發到所有參與者的計算機上。
區塊鏈有兩種:需要許可的和無須許可的。比特幣等無須許可的區塊鏈對參與沒有限制,參與者也不需要相互瞭解或信任。需要許可的區塊鏈是私有共享系統,參與者可能彼此瞭解,並且可能(至少在某種程度上)彼此信任。需要許可的區塊鏈是金融機構共享數據以加速交易結算的一種方式。
像區塊鏈這樣的分佈式賬本技術(DLT)現在正受到金融機構、四大會計師事務所以及許多其他大型企業的關注。2016年8月,世界經濟論壇報告了六項進展。[2]
(1)自2013年以來,DLT已有14億美元的風險資本投資。
(2)自2013年以來,共有超過2500項的專利申請,其中許多是由金融機構申請的。
(3)目前有超過24個國家正在投資DLT。
(4)90多家央行參與了DLT的討論。
(5)已有90多家公司加入了DLT協會。
(6)到2017年,約80%的銀行將啟動DLT項目。
區塊鏈和其他DLT的想法是否能達到宣傳的效果還有待觀察。2017年,IBM宣佈正在與7家歐洲銀行合作使用區塊鏈技術,使中小企業之間的貿易更加容易。金融領域的其他潛在應用包括證券交易、結算和其他後臺功能,而DLT有可能加快這些進程。事實上,幾乎實時的貿易結算將成為可能,這同時降低了成本,減少了人為干預的需要。操作風險也應該隨之降低,因為欺詐或網絡攻擊的可能性應該更低。這可能會引起監管資本金的減少。
[1] 這大約等於已知可觀測宇宙中的原子數(在我們的計算中排除了由64個0組成的哈希)。
[2] See World Economic Forum, The Future of Financial Infrastructure: An Ambitious Look at How Blockchain Can Reshape Financial Services, August 2016.
28.2 支付系統
技術已經對支付方式產生了巨大的影響。從現金和支票到信用卡和借記卡,再到移動錢包的使用,支付方式發生了很多變化。發展中國家在某些方面比發達國家取得了更大的進展,部分原因是在這些發展中國家,傳統的支付系統並不完善。許多金融科技初創企業正在提供新的服務,如一些大型、成熟的公司,美國的PayPal、Apple Pay和谷歌錢包,以及中國的支付寶(阿里巴巴旗下)和騰訊。
支付方法的關鍵屬性是速度快、方便、安全、簡單和成本低。許多服務,如PayPal,幾乎可以立即轉賬,它將類似信用卡的信息存儲在iPhone或類似設備中,為許多消費者增加了便利。事實上,考慮到蘋果在智能手機市場的主導地位,蘋果向支付領域擴張是很自然的,一些人猜測,蘋果不久就會提供更廣泛的銀行服務。可以想象,手錶、手鐲,甚至擁有植入物的可穿戴設備,可能都會像智能手機一樣被用來增加支付方式的便利性。
安全是所有支付形式的一個大問題。信用卡詐騙每年造成數百億美元的損失。在卡片中嵌入芯片和磁條並不能消除這個問題。我們很可能會看到未來避免欺詐的方式發生重大變化:數字錢包被認為比信用卡更安全。包括銀行在內的許多支付提供商同時也正在調研生物識別認證的使用情況(生物識別學通常涉及機器學習,這一點我們已經討論過了)。未來,可能會出現這樣的情況:在閱讀器上揮動手掌就可以完成購買。視網膜掃描、面部識別、語音認證,甚至心跳監測都在考慮之中。欺詐的成本通常由支付系統提供商承擔,當然也會以收取費用的形式轉嫁給商家(例如,PayPal在2017年年中對每筆交易收取2.9%的手續費,再加0.30美元),商家又把費用轉嫁給消費者。每個人都希望能減少欺詐,我們剛才討論的提高支付安全性的方法應該受到歡迎。
如果說生物識別認證似乎遙不可及,那麼請記住,印度已經向超過10億人發放了生物識別身份認證(包括指紋和視網膜掃描),為無現金社會打下了基礎。使更多的人成為金融生態系統的一部分是國家發展的重要目標。生物識別技術的優勢還在於,政府的一些有利於民眾的舉措不需要經過太多的中介機構就可以到達民眾的手中。當然,有些人會辯稱,提供生物特徵信息是對個人隱私的不可接受的侵犯,這可能會減緩發達國家對這種行為的接受。
一些支付系統允許用戶借錢。信用卡公司收取的利率非常高,但應該記住,從購買到下一個月的到期日期之間的這段時間內,用戶確實可以獲得免費信貸(PayPal的競爭對手提供14天的免費信貸)。有的支付系統很可能會發展更方便的信貸設施,以滿足用戶的需要。阿里巴巴通過旗下的支付寶(Alipay)和網商銀行(Mybank)等子公司,已經提供了許多與銀行相同的服務。
支付系統還可以提供哪些其他的服務來使自身更具吸引力?許多人定期向居住在另一個國家的家庭成員匯款。與這些交易相關的外匯服務很可能會變得更方便、更具競爭力。企業可能會開發出能與銀行競爭的簡便易用的外匯對衝服務。金融科技公司可能會對銷售數據進行復雜的分析,以幫助公司更好地瞭解客戶或提供會計服務。
當然,還是有喜歡現金的人。有些人有不良的信用記錄,沒有資格使用信用卡,而另一些人則非常厭惡風險,不願將自己的信用卡信息透露給第三方。亞馬遜已經意識到這一點,並允許客戶通過存入現金在精心挑選的零售商處開設賬戶,當客戶購買貨物時,貨款將記入所開設賬戶的借方。
數字化支付使收集個人消費習慣的數據變得容易得多。這可能對銀行做出信貸決策有用(瞭解潛在借款人如何花錢幾乎和了解他賺了多少錢一樣重要)。當然,這也帶來了巨大的隱私問題,比如有時支付系統會出售匿名數據。通常這些支付系統會使用機器學習等技術來分析數據,以便更好地理解消費者的偏好。
28.2.1 加密貨幣
自2009年比特幣首次出現以來,有越來越多的人和機構使用比特幣作為一種支付手段。2014年8月、2015年8月、2016年8月,比特幣日交易量分別為6萬、12萬、22萬。在未來,我們能看到美元、歐元或者日元被比特幣或其他加密貨幣取代嗎?很多人看好比特幣,2017年比特幣的價值增長就表明了這一點(見圖28-1)。
圖28-1 2011年1月~2017年8月用美元表示的比特幣價值
使用比特幣等加密貨幣作為支付手段的優勢是,它不受任何一個政府的控制,因此它的價值不可能受到任何政府的控制,它也不會因為政府的貨幣政策而貶值。[1]這對生活在委內瑞拉或津巴布韋等發展中國家的個人尤其有吸引力,因為這些國家的本幣幣值波動很大。個人在使用加密貨幣時可以保持匿名,而且支付也是安全的、私人的,成本非常低。
加密貨幣的缺點是它的價值比其他法定(傳統)貨幣更不穩定。[2]它不支付利息,而且常常(公平或不公平)與毒品交易等非法活動聯繫在一起。摩根大通的CEO傑米·戴蒙在2017年9月表示:“比特幣是一種欺詐行為,最終會崩塌。”中國在2017年出臺了有關加密貨幣的規定,其他國家的政府可能也會這麼做。加密貨幣的用戶對於加密貨幣的設置方式非常依賴,如果其設置方式發現了缺陷,貨幣就會一文不值。比特幣協議尚未被成功破解,但比特幣交易所已被破解(見業界事例28-1)。
業界事例28-1
Mt.Gox
雖然比特幣是一種安全的支付方式,但一些允許個人用比特幣兌換傳統(法定)貨幣的比特幣交易平臺存在問題。已經有很多關於交易所被黑客入侵的報道,最引人注目的是位於東京澀谷區的Mt.Gox。2014年2月,該公司宣佈價值超過4.5億美元的比特幣丟失,可能被盜,而造成這一損失的原因尚不清楚。看來,糟糕的管理和控制不力的計算機代碼讓黑客得以竊取比特幣。一些人指責CEO挪用了資金,但這一說法遭到了否認。不管是什麼原因,Mt.Gox在2014年4月申請破產。這損害了加密貨幣的形象,但正如圖28-1所示,比特幣的價值在2017年恢復並大幅提升。
怎樣才能避免這類損失?比特幣應不應該存儲在交易所?它們應該轉移到一個值得信賴的只有當你想交易時才存在的在線交易所嗎?
現在有許多可以替代比特幣的加密貨幣。例如litecoin、ripple、dogecoin、nxt、monero、ethereum和zcash。其中,有些貨幣的交易安全程序與比特幣的交易安全程序截然不同。另外還有一些加密貨幣,如以太坊,為智能合約(smart contracts)提供了便利。若滿足了契約中的所有條件,則契約將自動執行,從而消除了對中介的需求。
28.2.2 中央銀行
各國央行正在研究加密貨幣的使用,這其中可能有“如果你不能打敗它們,那就加入它們”的因素,但央行發行的數字貨幣可能會讓央行更容易控制貨幣供應。在目前的體系中,銀行創造貨幣(銀行貸款給實體,該實體將該款項存入銀行,或使用該款項從另一實體處購買東西,另一實體將款項存入銀行,接受資金的銀行轉貸,等等)。在數字貨幣體系中,貨幣總量可以是固定的,除非央行明確決定增加貨幣總量。此外,通過聯邦存款保險公司(Federal Deposit Insurance Corporation)等為銀行存款提供擔保的必要性可能也會降低。像美國這樣擁有許多小銀行的國家的支付系統可以簡化。數字貨幣使用的另一個優勢是普惠金融(尤其是在發展中國家)。無論出於何種原因,沒有銀行賬戶的個人都可能成為金融生態系統的一部分。
可以想象,在一個國家中,所有公民都在央行擁有一個數字貨幣賬戶,私營企業競相提供支付服務。中央銀行可以通過公平的方式增加所有公民的持有量來增加貨幣供應量(這可能會增加總需求)。
當然,這一切行為的潛在風險是不確定的。用數字貨幣取代有形的銀行票據將使一個國家的居民更容易與另一個國家的居民進行數字貨幣的交易。這可能導致不同國家的貨幣之間形成一種新的競爭形式,並可能最終使任何一個國家更難通過控制貨幣供應量來管理其經濟。
[1] 如第28.1.2節所述,比特幣供應量的增加取決於在礦工(參與者)驗證交易時支付給他們的金額。
[2] 根據2006年8月~2007年8月的數據計算,比特幣美元價值的波動率約為每年57%。歐元、英鎊或日元等法定貨幣以美元表示時,其波動率通常每年不到20%。
28.3 貸款
所有學習金融的學生都知道,與貸款相關的C有很多:品德(character)、還款能力(capacity)、資產(capital)、抵押品(collateral)等。科技能使貸款決策自動化嗎?一些銀行認為可以。一些大銀行的信貸員正被能使用機器學習科技的系統所取代。只要提供了足夠的有關銀行貸款經驗的數據,人們認為機器學習算法可以像人類一樣,甚至比人類更好地從不良貸款中分類出好貸款。原則上,機器學習程序可以比人類更客觀,表現出更少的偏差。[1]
28.3.1 P2P貸款
銀行的淨息差由其支付的負債利息與資產利息之間的差額決定的。如果它以每年2%的利率獲得存款,然後以每年5%的利率借出資金,那麼它的淨息差為3%。其中一些(可能高達1%)是為了補償預期的貸款損失,但如果存款人能夠以4%的利率直接貸款給借款人,雙方的情況都有可能變得更好。P2P貸款(peer-to-peer lending)包括脫媒和復媒。銀行不再是中介機構,新成立的中介機構要能夠提供以下服務:
(1)為借款人和貸款人提供相互聯繫的在線平臺;
(2)核實借款人的身份、銀行賬戶、工作情況、收入情況等;
(3)評估借款人的信貸風險,如果借款人的申請獲得批准,確定適當的利率;
(4)處理借款人和貸款人之間的現金流;
(5)嘗試從違約的借款人處收取款項。
許多目前使用P2P平臺的借款人已經被銀行拒絕,因此,與傳統貸款相比,P2P的利率可能相當高(但低於中等至高風險借款人的信用卡餘額和其他信貸來源的利率)。美國兩家著名的P2P貸款平臺是Prosper和Lending Club,它們都位於舊金山。P2P貸款平臺對借款人的信用評級與銀行的做法大致相同。[2]例如,Lending Club通過在A和G之間指定一個字母等級來對借款人進行分類。對信用等級較低的借款人收取的利率高於信用等級為A級的借款人,但違約的預期損失也更高。Lending Club於2017年6月發佈的統計數據彙總如表28-1所示。這表明,其利率和貸款損失都高於銀行發放的大多數貸款。然而,與其他機會相比,投資者平均獲得的淨年回報率相當有吸引力。
表28-1 2017年6月30日Lending Club公佈的借款人支付的利率和貸款人收到的貸款收益

P2P貸款機構的收費可能相當高。例如,在Lending Club,借款人通常要支付貸款金額1%~5%的初始化費用。出借方要對收到的款項支付服務費(通常約為1%),還可能要支付拖欠賬款的催收相關費用。
尋找分散化的貸款來源是有道理的。通常,貸款人可以選擇自己的貸款組合,也可以要求P2P貸款平臺構建一個符合它們風險偏好的投資組合。借款人的風險通常是特殊的,因此不同貸款的表現之間的相關性很低,這使得分散化更加容易。
一些借貸平臺可能會受到批評,因為它們沒有參與其中。如果貸款的表現沒有預期的好,貸款人將承擔全部成本。但是,一個例外是Upstart(由谷歌的前員工在2014年創建)。它有著不同於Lending Club和Prosper的模式。它向借款人收取初始費用,但不向出借方收取費用。在這種貸款中,貸款平臺也參與了對貸款的使用。若貸款獲利,則平臺可獲得貸款的部分績效;若貸款違約,則平臺會用貸款的初始費償還貸款方。它的信用評估著眼於借款人的教育背景、FICO分數和其他數據。事實證明,該公司的信用評估相當準確,業務增長迅速。
P2P貸款也未能倖免於醜聞。Lending Club(2014年通過IPO成為上市公司)創始人因監管不力的醜聞於2016年辭職(但該公司股票似乎已經反彈)。所有的金融創新都有可能在初期遇到類似的麻煩。的確,銀行在其漫長的歷史中也有過不少醜聞。P2P貸款的真正問題在於,它是否會進入傳統的銀行放貸領域?P2P貸款可被用於更大的汽車和房屋貸款市場嗎?企業間的P2P會變得更加普遍嗎?由於P2P平臺形式相對較新,所以觀察它們在經濟低迷時期或利率上升時的表現將是一件有趣的事情。
一些P2P平臺允許出借人在貸款尚未完全償還前出售貸款,但這取決於P2P貸款平臺的另一個客戶是否願意接管貸款。或者我們考慮一個自然的假設,即如果貸款人想出售貸款,那麼貸款就有問題。[3]然而,事實可能只是貸款人遇到了流動性問題,所以他需要現金。為貸款創造一個更好的二級市場是市場發展的一個方向。一個可以用來增加流動性的想法是,按照第6章所描述的,從貸款組合中創建分檔,並將這些貸款組合創建的證券出售給貸款人。
28.3.2 眾籌
眾籌是另一種可能成為金融顛覆力量的活動,它包括從大量不同的人那裡為一個項目籌集資金。據估計,2015年通過這種方式籌集的資金超過340億美元。一些眾籌項目以捐贈為基礎,目的是資助那些捐贈者認同並希望得到資金的項目。Kickstarter是處理此類項目的知名平臺。
其他眾籌平臺旨在為投資者提供回報。Funding Circle是一家成功的英國眾籌平臺,平臺投資者將資金借給小型企業。Companisto也是一個眾籌平臺,旨在為初創企業和高增長公司提供資金,而平臺投資者獲得固定利率或股權投資。SyndicateRoom為初創企業提供股權投資。
與風險投資家和天使投資者相比,眾籌向更多的投資者開放了私募股權投資。公司估值是股權眾籌的重要組成部分。如果一家公司的估值為50萬美元,那麼佔公司1%的股份需要5000美元的投資;如果價值100萬美元,獲得1%的股份則需要投資1萬美元。有時公司會決定估值,有時投資者也會這麼做。在後一種情況下,一些平臺會選擇經驗豐富的專業人士來進行盡職調查,確保投資定價的合理性。理想的情況是,參與這場遊戲的專業人士中有一些是天使投資者。當然,他通常會要求以某種方式獲得補償,而且應該認識到,即使是一位經驗豐富的專業人士,他的估值也是高度主觀的。[4]
由於監管的原因,股權眾籌的增長速度有所放緩。大多數國家對債券和股票的發行都有嚴格的規定。在美國,2012年的《創業企業扶助法案》(Jumpstart Our Business Startups Act,《JOBS法案》)為某些眾籌活動提供了豁免。根據《JOBS法案》,一家公司一年能籌集的資金上限為100萬美元左右,投資者能提供的資金上限取決於投資者的收入。
首次代幣發行(ICO)是一種涉及加密貨幣的眾籌形式。在通常情況下,公司會向投資者發行自己的加密貨幣,以換取比特幣或以太幣等已發行的加密貨幣。投資者對該公司沒有任何權利,但如果該公司表現良好,他們預計該公司發行的加密貨幣將升值,這是因為使用新的加密貨幣對公司的運營是不可或缺的。但是,ICO已經引起了監管部門的注意,有不少國家正在考慮是否應該像IPO一樣對它們進行監管。
[1] 但事實證明,機器學習並非完全沒有偏差。機器學習算法使用的數據可能包含偏差。機器學習程序員可能有意識或無意識地在算法的使用和交易中加入偏差。
[2] 出於監管方面的原因,P2P公司要與一家銀行達成協議,貸款需要通過銀行進行,貸款人需要獲得貸款的擔保。
[3] 經濟學家在喬治·阿克洛夫(George Akerlof)於1970年發表同名論文之後,把這個問題稱為“檸檬市場”問題。
[4] 正如《創智贏家》(Shark Tank)等電視娛樂節目所展示的那樣,在評估初創企業的價值時,專家並不總是意見一致。
28.4 財富管理
傳統上,財富管理對銀行來說是非常有利可圖的。費用通常在每年投資額的1%~1.5%,如果將與共同基金投資和交易成本相關的隱性費用考慮在內,費用可能會高得多。一旦評估了客戶的風險偏好,財富管理就開始為客戶尋找合適的投資。通常,類似的投資被推薦給所有有類似風險偏好的客戶,從而減輕了理財經理的工作負擔。但是,財富管理行業正處於被顛覆的過程中,這並不奇怪。正如在第4章中提到的,約翰·博格在1975年第一個指數基金中邁出了降低投資成本的第一步。從那以後,指數基金變得非常受歡迎,收費低至0.15%,不需要理財經理的人為干預。
機器人投顧(robo-advisers)最早出現在2010年左右。在大多數國家,它們必須向當局登記,並接受監管。它們提供數字平臺,讓投資者表達他們的風險偏好,然後選擇一個投資組合,通常包括跟蹤股票指數和安全投資的ETF,並在必要時自動對該投資組合進行再融資。幾乎沒有人為干預。機器人投顧的收費比傳統的財富管理公司要低,一般為每年投資額的0.50%~0.75%。在這一領域知名的公司包括Wealthfront和Betterment。一些銀行和其他財富管理公司現在正通過提供自己的自動化財富管理服務來應對機器人投顧的競爭。事實上,那些未能做到這一點的企業不太可能生存下來。先鋒等指數共同基金提供商也在這一領域表現活躍。
機器人投顧正將投資建議提供給比以往更廣泛的個人投資者。投資者的最小投資額通常可以是500美元或1000美元,而傳統的財富管理公司的最小投資額可能是5萬美元。機器人投顧讓客戶可以很容易地定期向管理的基金中增加資金。可以說,它們在社會上扮演著重要的角色,鼓勵人們在可能不會儲蓄的時候儲蓄。在早期,機器人投顧往往以小額投資吸引年輕投資者,但現在使用該服務的投資者範圍要廣泛得多,包括那些被列為“高淨值”和“亨利一族”(高收入但還不富裕的人群)的投資者。
到目前為止,機器人投顧的主要創新在於以一種更便宜、更新穎的方式提供服務,同時許多投資者認為這種方式頗具吸引力。所提供的投資策略通常與投資行業多年來使用的策略相似(見第1章)。與稅收相關的策略(如稅收損失獲取)通常被納入所提供的建議中。[1]
這些策略很有可能會變得更加複雜。投資可以更好地實現國際和跨部門的多樣化,更好地針對投資者的目標,考慮到投資者的年齡、退休計劃、子女的高等教育計劃等。
1992年,高盛集團的費希爾·布萊克和羅伯特·利特曼發表了一種廣泛使用的方法,將投資者的觀點納入投資組合的選擇之中。[2]機器人投顧可能會找到方法,擴大使用這項技術的投資者的選擇範圍,或者可以提出具有理論依據的不同意見,請投資者從中做出選擇,甚至有可能讓投資者的意見成為決定投資組合的一種不那麼結構化的直接輸入。
在第27章中,我們提到了在決策過程中存在的一些認知偏差,投資者容易受到這些偏差的影響。例如,他們不願意賣出虧損的股票,他們追逐潮流,他們幻想破滅,在應該長期持有的時候退出股市。專業投資者與業餘投資者的區別,往往在於專業投資者擁有避免這些偏差的能力。而機器人投顧可以開發創新的解決方法,從而試圖阻止投資者成為這種偏差的受害者。最後,機器人投顧可以與其他金融創新相結合,使客戶的資金有一定比例分配給P2P貸款或股權眾籌。
機器人投顧已經成為金融領域的一個重要組成部分,隨著千禧一代逐漸積累財富,它可能會得到更廣泛的應用。對這一代人來說,用iPhone投資比去銀行要酷得多。然而,值得注意的是,自2010年開始提供機器人投顧服務以來,股票市場表現非常好。但是,當經濟低迷、之前從未做過投資的機器人投顧的客戶抱怨虧本時,機器人投顧的吸引力可能會下降。人們同時也希望,這些投顧將能夠教育投資者保持長期關注的重要性。
[1] 稅收損失獲取包括在年底出售出現資本損失的股票,以減少應付的資本利得稅。
[2] See F. Black and R. Litterman, “Global Portfolio Optimization,” Financial Analysts Journal 48, no.5 (1992):28-43。
28.5 保險
技術在保險業中的應用被稱為保險技術。在某些方面,保險公司比銀行更不容易受到技術創新的干擾。這是因為保險的本質是,消費者需要一家經營保守的、穩定的公司。例如,如果房屋有很大可能性被燒燬,保險公司一般不會接受這樣一份保險,所以此時購買住房保險是沒有意義的。監管機構會仔細監控保險公司的財務狀況,一家新公司除非擁有大量資金來支付理賠費用,否則它很難被監管者批准提供保險。然而,一些技術在保險中的應用是直接的,例如,現在很容易在網上比較許多不同保險公司的報價。
通常客戶不會直接與保險公司打交道,而是必須通過經紀人或代理人。這些中介機構有時只與一家保險公司或少數幾家保險公司聯繫在一起,而不是自由地為客戶尋找最佳交易。一個自然的發展將是脫媒,即保險公司創建網站,直接與客戶打交道。然而,這似乎進展相當緩慢。在許多情況下,保險公司不願惹惱與它們密切合作多年的經紀人和代理人。但最終,隨著市場的發展,經紀人和代理商可能要麼消失,要麼成為價格比較的數字化提供者。
一個重要的潛在保險技術應用是由保險公司收集數據,以便更準確地評估風險。汽車保險就是一個很好的例子。通過在汽車上放置一個“黑匣子”,保險公司可以使用telematics(信息技術的一個分支,處理計算機信息的遠程傳輸)來收集客戶的駕駛數據。黑匣子可以記錄行駛速度、行駛距離、晝夜行駛時間、行駛方式(如制動頻率和轉彎速度)以及通常使用的道路類型。這使得保險公司能夠為司機建立精確的費率檔案。如果司機的風險低於平均水平,保險費就會下降;如果司機的風險高於平均水平,保險費就會上升。儘管黑匣子保險已進入英國保險市場,但仍處於起步階段。隨著汽車保險成本的上升,它可能會變得更受歡迎,尤其是在年輕人當中。當駕駛記錄很少甚至沒有時,年輕司機傳統上面臨著非常高的保費。黑匣子可以為他們提供一種更快捷的方式,讓保險公司相信他們是好司機。需要注意的另一點是,黑匣子的成本(通常由驅動程序支付)已經下降了。
同樣,黑匣子可以向駕駛員提供路況信息,它也可以用於司機教育。司機可以訪問一個安全的網站,以瞭解他的表現如何。網站還可以給出改變駕駛風格的建議,並提供降低保險成本的建議。原則上,這可以提高司機的平均駕駛能力,使行車更加安全。當然,並不是每個人都能指望黑匣子會降低保費,一些司機可能認為黑匣子會侵犯隱私。可以推測,隨著黑匣子越來越被廣泛接受,只有優秀的司機才會使用它們,而非用戶的保險費用將會增加。
對於保險公司來說,黑匣子的主要優勢在於它能夠收集數據,從而更準確地評估風險。在一個理想的世界裡,保險費應該能夠反映駕駛里程和駕駛員所承擔的風險。[1]黑匣子對保險公司的另一個潛在優勢是,在發生事故時,它們可能能夠查明責任所在,使索賠變得更簡單。
總的來說,保險公司現在有機會收集比以往任何時候都多的數據來評估它們所承擔的風險。這些數據可以潛在地幫助它們提高對個人預期壽命、一幢小房子被燒燬的可能性的估計,或者提高對世界某一地區發生颶風的可能性的估計,而機器學習為分析這些數據提供了工具。保險業在本質上是保守的(也許是正確的),所以我們很難想象金融科技會徹底改變保險業的結構(在許多情況下,新進入者必須與老牌保險公司合作),但是,成功的公司很可能是那些利用大數據創造出發展機遇的公司。
[1] 舊金山的Metromile公司就是朝這個方向發展的一家保險公司。它使用一個小工具來監測駕駛里程,並向投保人發送每月的保險發票,以反映駕駛里程記錄。這些保單實際上是由一家資金雄厚、監管嚴格的大型保險公司——國家一般保險公司(National General Insurance Company)制定的。
28.6 監管和合規
技術對監管的影響有兩個方面:一個是監管機構應如何處理那些以創新方式使用技術,並有可能成為金融業顛覆力量的公司;另一個被稱為監管科技(RegTech),關注的是監管本身如何使用技術。我們將在本節中同時考慮這兩個問題。
28.6.1 對金融創新者的監管
正如我們在本書中所看到的,金融機構受到高度監管,它們必須與許多不同的監管機構打交道。對於小型金融科技初創企業來說,這是一個進入壁壘。美國的P2P貸款機構必須與銀行達成協議,以遵守監管規定。機器人投顧必須滿足“瞭解你的客戶”(know your customer,KYC)的規則,並向當局登記,儘管它們的服務中人與人之間互動很有限,甚至可能完全沒有。如果一家金融科技公司無視監管規定,它很可能會被監管部門關閉,至少是暫時關閉,並遭受聲譽損失。
監管機構不想扼殺金融創新。的確,正如我們所指出的,金融創新可以通過發展創新的儲蓄、投資和借貸方式給社會帶來許多好處,從而鼓勵更多的人成為金融生態系統的一部分。但監管機構必須小心行事,比如它們不希望影子銀行(shadow bank,即提供與銀行相似業務的非銀行機構)給客戶帶來不合理的風險。
英國金融行為監管局(FCA)開發了一個“沙箱”計劃。[1]它將沙箱定義為一個安全的空間,在這個空間中,企業可以測試創新的產品、服務、業務模型和交付機制,而不會立即引起試點活動的所有正常監管後果。創新者必須填寫一份申請表,解釋他們打算做什麼。FCA鼓勵創新者在使用真實用戶之前進行虛擬測試,並考慮了其他4種保護用戶的方法。
(1)必須在消費者知情同意的情況下才能參與檢測,他們會被告知風險和可能的補償。
(2)根據不同的具體情況,FCA同意適度的信息披露和賠償計劃。
(3)客戶享有與FCA設立並授權的其他公司客戶相同的權利。
(4)進行沙箱試驗的企業必須賠償個人的任何損失,並且必須證明它有能力做到這一點。
FCA似乎更喜歡第二種方法,它可以包含一種或多種其他方法。
儘管面臨來自科技公司和具有前瞻性的成熟金融機構的壓力,但美國並沒有沙箱計劃。一些人認為,這可能使美國處於競爭劣勢。但正如前面所討論的,美國《JOBS法案》減輕了眾籌活動的監管負擔。
監管金融科技公司可能是監管機構未來面臨的一個挑戰。金融科技公司的主要資產通常是其計算機代碼,監管者要像評估銀行風險管理水平一樣評估這些代碼,絕非易事。高頻交易者(HTF)就是最典型的案例。他們的交易活動完全由他們的計算機代碼決定。2010年5月6日,很大程度上由於高頻交易的影響,美國股市發生了一場“閃崩”,道瓊斯工業平均指數在幾分鐘內下跌了約9%,隨後部分回升。2012年8月1日,一家高頻交易公司使用的程序出現軟件錯誤,導致紐約股票交易所148只股票的價格出現重大波動。SEC已經採取了一些措施,以避免未來出現類似的問題,但它很難防範軟件(有意或無意地)對金融市場運行產生不利影響的所有方式。
監管機構面臨的另一個問題是,對一些金融科技公司來說,管轄權可能難以確定。如果它的所有交易都是用數字貨幣進行的,情況可能更為嚴重。
28.6.2 RegTech
監管科技(RegTech)是將技術應用於監管和合規性。有些應用很簡單。監管報告傳統上包括在每個報告期間(例如,每個季度)結束時向監管機構提供大量文件。將這些數據轉移到網上並實時提供數據,有可能簡化監管機構和受監管金融機構的工作,同時有利於監管的及時性,也能夠提高效率。
不遵守監管規定的罰款可能會很高。[2]例如,在第23章中,我們提到一家法國銀行——法國巴黎銀行,因違反美國的監管條例而被處以與其全年利潤相等的罰款。毫無疑問,這是因為少數員工的活動沒有受到銀行合規部門的密切監控。技術可以使銀行更容易地確保自己的業務符合其業務所在國的法規和法律。例如,科技使它能夠實時篩查新客戶和新交易,以識別問題。如果使用由監管機構批准並反映最新規則的實時RegTech應用程序,涉及毒品洗錢、恐怖主義融資和制裁等問題的違規行為可以被有效消除。
防止員工做出有問題的行為對金融機構很重要,因為這種行為可能會被證明在監管罰款、法律成本和聲譽方面代價高昂。一些創新使得公司可以通過多個通信平臺跟蹤員工的對話。例如,總部位於納什維爾,在倫敦、紐約和華盛頓設有辦事處的Digital Reasoning公司,已經開發出一些供大型銀行和資產管理公司使用的監控軟件。它可以監控英語會話(處理6種不同的方言),它可以通過分析數以百萬計的電子郵件、聊天記錄和電話對話來監視員工的行為,從而使用機器檢測可疑或不尋常的活動。如果機器學習檢測到一名員工的行為與通常的模式有很大不同,那就可能需要進行進一步的調查。在一家資產管理公司,這種行為可能會被證明是內幕交易的指示性行為,如果允許這種行為繼續下去,可能會導致鉅額罰款。在一家銀行,這種行為可能會被證明是流氓交易或不尊重下屬的表現。
如第23章所述,網絡風險是銀行最大的經營風險,這也成為一個監管問題。例如,歐洲的《全面數據保護條例》(General Data Protection Regulation)於2018年5月開始實施,如果金融機構丟失了意在保密的數據,將被處以鉅額罰款。一些RegTech應用程序正在幫助銀行保證它們的數據安全,並遵守這樣的規定。
對金融機構來說,僅僅瞭解現有的所有監管規定就是一個重大問題,因為它在全球範圍內運作的監管環境幾乎每天都在發生變化。IBM的Watson監管合規允許相關員工訪問一個法規需求庫,其中可以根據地理位置、業務類型、產品和監管合規性區域對材料進行過濾。此應用程序可以自動突出顯示與特定問題相關的新法規的部分,並將與世界不同地區的特定活動相關的法規進行比較。
正如本書第三部分所解釋的那樣,監管已從單一的形式轉變為多維的形式。監管機構過去只關注單一的資本指標,它們現在有兩個資本指標(一個基於風險加權資產,另一個基於更簡單的槓桿計算)和兩個流動性比率(流動性覆蓋率和淨穩定融資比率)。銀行開展的不同活動對比率有不同的影響,這使得技術公司有可能提出優化銀行戰略的方法,或提供方便的場景分析工具。
[1] See Financial Conduct Authority, “Regulatory Sandbox,” November 2015。
[2] 在2007~2008年金融危機結束至2017年期間,全世界的銀行共支付了約3210億美元的罰款。因此,改善銀行合規性的技術可能會產生鉅額收益。
28.7 金融機構應如何應對
金融科技創新給大型銀行和其他金融機構帶來了戰略風險,它們提供的許多服務將會中斷,應該如何應對?顯然,它們應該接受技術變革,而不是希望技術變革只是曇花一現。它們也應該仔細評估消費者行為如何受到技術變革的影響,並相應地採取措施改變它們的商業模式。
業界事例28-2講述了柯達——一家沒有很好地適應技術變革的公司的案例。關鍵的一點是柯達並沒有意識到其行業正在發生的變化。事實上,第一臺數碼相機是1975年一位為柯達工作的工程師發明的,柯達在這項新技術上投入了數十億美元。那麼柯達是哪裡出問題了呢?其實在當時,很大一部分人(不僅僅是年輕人)開始樂於分享照片並將其存儲在計算機上,他們不再覺得有必要打印照片,這一轉變並沒有花費太長時間。柯達掌握了關鍵技術,卻沒有意識到它可以適應消費者正在改變的行為方式。等柯達意識到這一點時,已為時過晚。
業界事例28-2
柯達和數碼攝影
在20世紀80年代和90年代,伊士曼·柯達公司(Eastman Kodak Company)是一家成功的企業,專注於銷售相機和相機膠捲。它幾乎憑一己之力將美國的攝影從專業攝影師的專屬領域,轉變為幾乎人人都能做的事情。它成功地駕馭了行業的技術變革。它從幹版(dry-plate)電影轉向黑白電影,然後明智地投資於彩色電影,即使彩色電影的收入明顯低於黑白電影。它在1997年的市值約為300億美元。
1975年,柯達工程師史蒂夫·薩森發明了第一臺數碼相機。據薩森說,該公司的迴應是:“這很可愛,但不要告訴任何人。”事實上,柯達並沒有忽視數碼相機的發展趨勢。1995年,公司投入巨資,推出了首款數碼相機DC40。2001年,公司推出了EasyShare傻瓜相機系列。柯達擁有一流的研究能力。它有能力開發出最先進的相機,可以增強色彩、自動調整燈光、實現多種拍攝效果、分享照片、檢測微笑以選出最佳照片,等等。
不幸的是,柯達表現出了一些不願繼續提升產品和創新的態度,這對於身處一個技術變化迅速的行業的柯達是一個錯誤。以進步的名義蠶食現有產品是痛苦的,但也是必要的(即使新產品的利潤低於舊產品)。如果柯達採取不同的戰略,那麼它在智能手機革命中是否能夠生存下來、能夠有怎樣的發展是存在爭議的。我們只能說,富士等競爭對手的表現要好一些。2017年,富士的市值超過150億美元。柯達在2012年年底申請破產,2017年其繼任者公司的市值約為3億美元。
柯達公司創造了“柯達一刻”這個詞,並在其廣告中廣泛使用,以說服人們,他們應該有一個裝有柯達膠捲的柯達相機隨時準備使用。當事後諸葛亮很容易,戰略專業人士會辯稱,該公司本可以從銷售說辭中推斷出自己所從事的業務——成像或瞬間分享業務,而不是電影業務。我們永遠不會知道,如果它在市場初期更熱情地擁抱電子共享和數字圖像存儲,它會生存得有多好(正如業界事例28-2所示,總部位於日本的富士的業績要好於柯達,兩者是類似的公司)。柯達公司深信,對打印照片的需求將持續下去,這最終導致了該公司的倒閉。
大型金融機構的瓦解似乎沒有柯達的瓦解來得那麼快。它們有許多競爭優勢,而且資本充足(蘋果、谷歌和阿里巴巴都是如此)。它們懂得如何應對自己所處的高度監管環境(許多金融科技初創企業發現這很難)。它們有龐大的客戶群而且仍然得到了許多客戶的信任(儘管2007~2008年的金融危機以及此後發生的事件(如業界事例27-1中描述的富國銀行的崩潰)削弱了這種信任)。可以推測,金融機構不像柯達那樣脆弱,因為許多人在選擇管理金錢的方式上要比選擇攝影方式謹慎得多。此外,許多初創企業需要成熟的金融機構來提供產品。
然而,有一些警告跡象表明,銀行應該做出迴應。Millennial Disruption Index調查顯示,71%的千禧一代寧願去看牙醫,也不願聽銀行在說什麼;73%的千禧一代寧願通過谷歌、亞馬遜、蘋果、Paypal或Square來處理他們的金融服務需求。[1]千禧一代是在1981~2000年出生的獨立個體,是未來銀行服務的重要消費者。到2022年,他們將佔勞動力的40%;到2050年,他們將繼承約30萬億美元。隨著年齡的增長,他們對金融服務的興趣可能會減弱,但銀行不應侷限於此。
由於在智能手機中添加了數碼相機的功能,柯達最終變得無足輕重。金融機構自然不想變得同樣無關緊要。它們已經意識到,有必要為支付、財富管理和其他一系列服務提供移動應用程序。但重要的是,它們要能夠真正接受技術的變化,而不只是嘴上說說。金融領域的技術變革將繼續加速。在許多情況下,它將侵蝕銀行以前依賴的利潤(柯達就是一個例子)。最終,能夠實現靈活地調整將是一個持續的挑戰。
銀行開發的新服務需要考慮到方便性和設計性,以便年輕人將其歸類為“酷”,而老年人發現它們易於使用。有許多不同的方法被採用:一些金融機構已經在內部開發了新的服務;一些公司收購了已經開發了這些服務的初創企業;一些公司與初創企業建立了合作關係。第一個替代方案雖然成本最低,對許多在金融服務業工作的人也最有吸引力,但是考慮到大公司往往瀰漫著多少有些沾沾自喜的文化,因此它做起來可能相當困難。第二種和第三種選擇可以作為一種破壞文化和加速變革的方式。一些銀行發現,成立一個組織獨特的部門很有用,這個部門有能力在必要時引入外部人才,並能與初創企業合作。無論採用何種方法,CEO和董事會的大力支持都是成功的必要條件。
發展勢頭良好的金融機構將設法改變它們的文化,使它們能夠以快速、可靠的方式提供對消費者有吸引力的服務。郭士納於20世紀90年代被任命為IBM的CEO,當時該公司正在虧損。他成功地改變了企業文化,將其轉變為一家盈利的公司。他說:“文化不僅僅是比賽的一個方面。它就是比賽。”他成功地將IBM從一家大型計算機供應商轉變為一個業務問題解決者,在那裡,人們可以很好地合作。銀行與IBM的相似之處在於,它們是擁有許多聰明員工的大型組織。CEO的工作是創造一種文化,在這種文化中,個人因接受技術並找到創新方法使他們的服務更方便、更有價值而受到獎勵。
小結
2035年金融服務業將會是什麼樣子的?當然,技術變革的速度如此之快,做出準確的預測是不可能的。然而,提供一些預測是總結本章中一些觀點的一種方便的方法。
支票和信用卡將在很大程度上消失。智能手機和可穿戴設備上的移動錢包將成為常態。生物識別技術將被用來使支付更加安全。一些央行將選擇從紙幣轉向數字貨幣,數字貨幣的交易將變得更加普遍。機器學習將能夠比人類更好地承擔信用評估和欺詐檢測等許多任務。使用區塊鏈和其他DLT,記錄保存將更安全、更快速。
大型保險公司將繼續存在,但經紀人和代理人將不復存在。保險公司將獲得比以往更多的數據,並將使用機器學習和其他技術更精確地評估風險。保險公司和科技公司將結成夥伴關係,以創新的方式提供保險服務。
投資和借貸將發生巨大變化。眾籌和P2P貸款將得到更廣泛的應用。今天的一些大銀行將發現有必要向儲戶和借款人提供這些服務。資金閒置一段時間是不尋常的,借貸和投資的便利將使更多的人成為金融生態系統的一部分。
一些未能積極適應新技術的銀行將會倒閉,並被其他銀行收購(事實上,“大而不倒”可能不再被認為是對超大型銀行的相關描述)。一些大型科技公司將成為銀行,提供全方位的銀行服務。大多數銀行服務將比以前更便宜、更有效,因此銀行將失去一些傳統的利潤來源。倖存下來的銀行將不得不通過大幅削減分支機構數量和員工數量來降低成本。銀行將不得不與許多不同的科技公司建立合作關係,以保證它們提供的服務是最新的。
延伸閱讀

練習題
28.1 解釋“脫媒”和“復媒”。
28.2 解釋如下概念(a)機器學習;(b)分佈式分類賬技術。
28.3 什麼是生物識別認證?給出一些例子。
28.4 為什麼央行會從法定貨幣轉向數字貨幣?
28.5 解釋P2P貸款和股權眾籌是如何運作的。
28.6 “考慮到金融科技的影響,金融機構應該感謝監管。”解釋這句話的含義。
28.7 “指數基金是個好主意,但如果每個人都選擇它們,就不會有價格發現。”你同意這個論點嗎?
28.8 RegTech是什麼意思?給出一些例子。
28.9 “銀行應該像IBM那樣應對變化,而不是像柯達那樣。”討論這個說法。
作業題
28.10 泡沫是什麼意思?考慮一下2017年比特幣價格的上漲是否存在泡沫。
28.11 參考表28-1的數據,Lending Club擅長評估風險嗎?對於貸款人來說,風險和收益之間是否存在合理的平衡?放貸人在承擔什麼樣的風險?
28.12 事後來看,我們可以說柯達從事的是成像和瞬間分享業務。銀行從事什麼業務?
第29章
避免風險管理失誤
自20世紀80年代中期開始,金融市場出現了若干起引人注目的重大損失,本章將要討論我們能夠從中吸取的教訓,並且回顧以前若干章的要點。我們把在本章中將討論的重大損失列舉在業界事例29-1中。
業界事例29-1
重大金融損失
·愛爾蘭聯合銀行
這家銀行因為其外匯交易員約翰·拉斯納克若干年的非授權投機交易而損失了7億美元,拉斯納克以製造虛假期權交易的形式掩蓋了他的損失。
·巴林銀行
這家經營了200年的英國老牌銀行因為其外派新加坡的交易員尼可·利森的行為而毀於一旦。尼可·利森的職責是從新加坡及大阪的日經225期貨指數的報價中進行套利,而實際上他採用了期貨及期權對日經225指數進行了大筆方向性投機。全部損失接近10億美元。
·安然公司的對手方
安然公司精心設計出一些合同,向公司股東隱瞞公司的實際情況。在後來,協助安然公司達到其欺詐目的的許多金融機構因法律糾紛向安然公司股東支付的賠償超過了10億美元。
·哈默史密斯和富勒姆(見業界事例23-1)
這個英國城市的市政當局因為英鎊互換以及期權交易在1988年損失了近6億美元,對這些交易負有直接責任的兩個交易員對產品知識的匱乏令人吃驚。
·基德-皮博迪公司(見業界事例25-2)
公司交易員約瑟夫·杰特的個人行為給這個紐約投資經紀商帶來了3.5億美元的損失。杰特交易的產品主要是美國國債,他的損失由公司計算機系統計算盈利的公式的錯誤而造成。
·長期資本管理公司(LTCM)(見業界事例22-1)
這家對衝基金在1998年進行收斂套利交易時損失了約40億美元,損失的發生是由於在俄羅斯政府違約後市場發生安全投資轉移現象所致。
·國民西敏寺銀行(National Westminster Bank)
這家英國銀行在1997年因使用錯誤的模型來對互換期權定價而損失了1.3億美元。
·奧蘭治縣(Orange County)(見附錄B)
奧蘭治縣的財政官員羅伯特·西特倫(Robert Citron)的行為使這個加州城市在1994損失了近20億美元。這位財政官員利用衍生產品來對利率進行投機,他賭的是利率不會增長。
·寶潔公司(見業界事例5-4)
這家美國公司的財務部與信孚銀行在1994年進行奇異利率衍生產品合約交易時損失了近9000萬美元。後來寶潔公司起訴了信孚銀行,法律糾紛最終庭外和解。
·法國興業銀行(見業界事例5-5)
法國興業銀行的股票交易員傑洛米·科維爾因在2008年1月對股指進行豪賭,損失達70億美元。傑洛米·科維爾被控通過構造虛假交易的方式來掩蓋自己的風險敞口。和巴林銀行的利森一樣,他的職責是進行套利交易。
·次債損失(見第6章)
2007年,投資者對由美國次級住房按揭貸款所生成的結構化產品失去了信心。這引發了市場的信用緊縮和自20世紀30年代以來最大的市場蕭條,在這期間金融機構的損失高達數百億美元。
·瑞銀集團(UBS)
2011年,基庫·阿杜伯利因沒有經過授權而對股票指數投機,損失了23億美元。
業界事例29-1所列舉的事件有一個顯著特點,那就是由單個僱員造成重大損失出現的次數尤為突出。1995年尼可·利森的交易造成一家經營了200年之久的英國老牌銀行巴林銀行的垮臺;1994年羅伯特·西特倫的交易造成加州的奧蘭治縣損失近20億美元;約瑟夫·杰特的交易造成基德-皮博迪公司損失3.5億美元;約翰·拉斯納克給愛爾蘭聯合銀行帶來的7億美元損失在2002年被曝光;2008年傑洛米·科維爾給法國興業銀行造成的損失達70億美元;基庫·阿杜伯利在2011年給瑞銀集團(UBS)帶來23億美元的損失。
從這些損失中得出的教訓是內部控制的重要性。我們將要討論的很多損失之所以發生,就是因為系統不夠完善以至於高風險的交易能大行其道而無人知曉。同樣重要的是,風險管理人員要不落窠臼,發現潛在的危險,並將其消滅在萌芽狀態。
29.1 風險限額
由這些損失我們應吸取的第一個也是最重要的一個教訓是風險限額。所有的公司(金融以及非金融公司)必須對自身所能承擔的風險有一個清晰及含義明確的認識,公司應該設定管理規程來保證限額的貫徹執行。理想地,整體的風險限額應由董事會確立,然後再轉化為各個負責管理特定風險的人員所掌握的額度。每天的風險報告應該闡明某一市場變量的特定變動將會帶來的損益。風險報告所預測的數值要與實際損失進行比較,以保證產生報告的定價流程的準確性。
在涉及衍生產品的使用上,公司應該特別注意監控風險。這是因為衍生產品既可以被用來對衝風險,也可以被用於進行投機及套利。如果不對風險進行嚴格監控,我們幾乎不可能知道交易員是否由一個對衝者變成了投機者,或者從一個套利者變成了一個投機者。巴林銀行、法國興業銀行和瑞銀集團就是這種情況的典型的案例。在每一個事件中,交易員本來的職責都是進行低風險的套利和對衝交易,但是他們從套利者和對衝者變成了投機者,並對市場的變動方向投下了鉅額賭注,而他們的上級還被矇在鼓裡。這說明,銀行的管理系統不夠完善,不能及時發現這種情況。
我們的觀點並不是說我們不能承擔任何形式的風險。一家金融機構的交易員或者基金經理應該擁有對市場變量變動趨勢採取行動的權利,但我們想強調的是這些交易員的交易量一定要受到某種制約,公司必須建立系統以準確地報告有關交易的風險。
29.1.1 進退維谷的處境
如果某個交易員在超過風險限額的情況下獲得了盈利,我們這時應該怎麼辦?對於管理人員來講,這是一個棘手的問題。交易員的盈利會使人們忽略其違反限額的行為,但這是一種短視的做法。因為它會導致一種風險限額不受重視的文化,而這會給將來的失敗埋下伏筆。這裡一個典型的事例發生在奧蘭治縣。奧蘭治縣的羅伯特·西特倫在1991~1993年曾給這個城市帶來了巨大的盈利,城市以他的交易收入作為運轉資金。這時人們因為羅伯特·西特倫的盈利而忽略了他所承擔的風險,不幸的是,1994年羅伯特·西特倫的損失遠超過了他若干年的盈利。
對於違反交易限額的盈利的懲罰與違反交易限額而造成的損失的懲罰應該是一樣的,否則交易員在遭受損失之後很可能會加大賭注來博取盈利,希望扭虧為盈並因此得到豁免。
29.1.2 不要認為你會猜透市場
有些交易員對於市場的預測可能比其他人更為優秀,但是他們的預測也不可能永遠正確。交易員在所有的預測中有60%的正確率就已經相當不錯了。交易員出類拔萃的戰績(像20世紀90年代初的羅伯特·西特倫)往往可能是由於運氣,而並不是因為高超的交易技巧。如我們在第4章中討論的共同基金表現,基金經理所展示的超額回報通常都是因為運氣而非技巧。
假設某金融機構僱用了16名交易員,其中一位交易員在過去一年中的每一個季度都帶來了盈利,這位交易員是否應拿到更多的分紅呢?他的交易限額是否應該增加呢?對第一個問題的答案無疑是肯定的,但對於第二個問題的答案應該是否定的。在4個季度中均盈利的概率為0.54,即1/16,這意味著即使完全出於隨機的概率,每16個交易員中都應該會有一個交易員每個季度“都會盈利”。我們不應該相信交易員的運氣會永遠持續,不應該因為交易員的暫時盈利而給他增加交易限額。
29.1.3 不要低估分散化的好處
如果某個交易員比較擅長預測某些市場變量,公司就會比較願意給該交易員增加限額。我們在前面指出,這麼做可能是一個很糟糕的決策,因為交易員的交易結果可能是出於運氣而並非智慧。即使我們確信某交易員具備某種天賦,我們應該在多大程度上去分散化而更多地依賴這個交易員的天賦來盈利呢?如第1.1節所述,風險分散所帶來的好處是巨大的。我們應該認識到世界上不存在如此出色的交易員以至於我們能為他而忽略風險分散的好處,我們不應該對交易員寄予過分的希望。
接下來我們用一個實例來說明問題。假如我們有20只股票,每隻股票的預期回報均為10%,每隻股票回報率的標準差為30%,股票兩兩之間的相關性為0.2。投資者將資產以均等的形式投入這20只股票,投資者投資組合的預期回報為10%,投資組合標準差為14.7%。分散投資使得投資者的風險降低了一半多。換一種說法就是分散投資將我們每承擔一份風險而獲得的回報加大了一倍。只進行一種股票投資的投資者必須極其“優秀”才能取得比以上更好的風險-回報的替換關係。
29.1.4 進行情景分析以及壓力測試
如第22章所述,在計算諸如VaR一類的風險指標的同時,我們還必須進行情景分析以及壓力測試,這有助於我們進一步理解薄弱環節的風險。如果沒有很嚴格的壓力測試管理流程約束,人類會有一個很不好的傾向,那就是在做出決策時往往過分依賴於一兩個情形。例如在1993年及1994年,寶潔公司在其決策過程中堅信利率會維持在低水平,而完全忽略了利率增長100個基點的可能性。
一旦壓力測試的結果出臺,它們就應成為金融機構制定戰略決策過程中應考慮的一個部分。通常在年景好的時候,壓力測試結果往往會被忽略。在2007年7月以前,一些金融機構就發生了這樣的情況。
29.2 對於交易平臺的管理
在交易部門有一個傾向,那些交易表現出色的交易員往往是不可冒犯的。對於這些交易員的監督要比對於其他交易員的監督鬆散得多。很顯然基德-皮博迪公司的明星交易員約瑟夫·杰特平時可能如此之“忙”,以至於他沒有時間來回答公司風險管理人員的問題並與他們討論自己的頭寸。
所有的交易員,特別是那些盈利高的交易員都應該恪盡職守,做到這一點至關重要。金融機構對某筆獲利很高的交易是不是由於承擔了不合理的高風險所致應該有一個清醒的認識。另外,金融機構還必須檢查自己的計算機系統以及定價模型的準確性,以確保這些工具沒有被濫用。
29.2.1 確保前臺、中臺以及後臺職責的分離
金融機構的前臺主要由交易員組成,這些交易員的職責是進行交易,即對產品進行買賣;中臺(middle office)主要由風險管理人員組成,這些風險管理人員的職責是監控前臺的風險;後臺(back office)的職責主要是記賬以及財會結算。有些金融衍生產品災難的起因就是沒對以上幾個職能部門的職責進行區分。尼克·利森掌管了巴林銀行在新加坡分行的前臺以及後臺,因此他有機會在長時間內掩蓋鉅額交易損失,而遠在倫敦的上級高管對他的行為毫無察覺。
29.2.2 不盲目地相信模型
我們在第25章中對模型風險有過討論。某些金融機構的鉅額損失是由於模型及計算機系統的錯誤造成的。基德-皮博迪公司就是被自己的計算機系統愚弄了。另外一個例子是國民西敏寺銀行,這家銀行因使用了錯誤的互換期權定價模型,使自己蒙受了慘重損失。
如果某家金融機構採用相對簡單的交易策略而獲得大筆盈利,那麼有很大的可能是這家機構計算盈利的模型中存在問題;類似地,如果某家金融機構對某個特定產品的報價一直比其他同業競爭者的報價更具競爭力,那麼有很大的可能這家公司採用的模型同其他市場參與者的模型有所不同。這時這家機構應對自己的模型進行仔細的分析。對於交易大廳的負責人來講,同一種生意做成的太多或這種生意做成的太少,都應令人感到擔憂。
29.2.3 以保守的方式記錄起始盈利
當金融機構向非金融企業出售非常複雜的結構性產品時,產品的價格會與模型有直接的關係。例如,產品中如果包含期限較長的利率期權,這時產品價格會同所採用的利率模型有相當大的關係。這時市場上經常以模型計價的方式來計算產品每天的價格變動,因為在市場上通常找不到類似的產品來作為這些結構性產品的定價參照物。
假定某金融機構出售給客戶的產品的價格比實際價格或者模型價格高出1000萬美元,這裡的1000萬美元被稱為起始盈利(inception profit)。起始盈利應該在什麼時刻被確認呢?不同的衍生產品經紀商會有不同的做法。有些做法是立即將這筆錢計為盈利,而其他更為保守的做法是在合約期限內逐漸地將這筆收入計為盈利。
立即確認起始盈利是一種非常危險的做法。這樣做會鼓勵交易員採用激進的模型,先掙得獎金,然後在模型以及交易價格受到更嚴格的審核之前抽身而去。將起始盈利先計為儲備金,然後逐漸確認為最終盈利的方法明顯更好。這樣做可以鼓勵交易員在進行交易之前,去研究不同模型以及不同假設對於產品價格的影響。
29.2.4 不要向客戶出售不適當的產品
向企業客戶銷售不適當的產品在金融機構中是很容易發生的事情,在客戶對某種風險具有偏好時,這種情況更容易發生,但這麼做是非常沒有遠見的。關於這一點最明顯的例子是信孚銀行在1994年春天之前進行的一些交易行為。許多信孚銀行的客戶,包括寶潔公司,被說服購買了許多風險很高但根本不適當的產品。其中一個典型產品是給客戶提供一個較大的機會節省幾個基點的融資費用,但同時有一個較小的機會給客戶造成嚴重損失。這些產品在1992年及1993年給許多信孚銀行的客戶帶來了收益,但在1994年利率上漲時,這些產品終於出現問題。這些問題公之於世後對信孚銀行的公眾形象產生了很大傷害。信孚銀行長期以來與企業客戶建立的信任以及在衍生產品創新方面積累的聲譽,被幾個激進的銷售員的錯誤行為毀於一旦。信孚銀行不得不向客戶支付大筆賠償以解決法律糾紛。後來它終於在1999年被德意志銀行吞併。
29.2.5 對輕鬆賺大錢的生意要保持警惕
安然公司給我們提供了激進交易員會造成巨大損失的又一實例。曾經有一段時間,許多金融機構認為與安然公司做生意會帶來滾滾財源。因此,許多銀行爭先恐後地與安然公司合作。但我們要注意,即使許多銀行都推崇某種業務,也並不意味著該業務最終一定會盈利。事實上,安然公司與銀行進行的很多業務最終陷入了與股東的昂貴的法律糾紛。一般來說,如果某一業務很輕鬆就能賺得高額利潤,我們就應仔細檢視其潛在的操作、信用及市場風險。
曾經有一段時間,對許多銀行而言,投資由次貸生成的ABS和ABS CDO的AAA級簡直就像打開了一個印鈔機(見第6章)。這些產品所承諾的收益遠高於其他的AAA級債券,而市場上幾乎沒有交易員去質疑這些分級的高收益是不是因為評級機構可能忽視了某些風險。
29.3 流動性風險
我們在第24章中對流動性風險進行了討論。金融工程師在對市場上交易不太活躍的奇異產品或其他一些產品定價時,常常採用市場上交易活躍的產品價格作為基礎,例如:
(1)交易員往往採用市場上交易活躍的政府債券,即被稱為新券(on the run bonds)[1]的債券來建立零息收益曲線,然後將這些曲線用於對交易不頻繁的產品(如舊券,off the run bonds)來進行定價。
(2)交易員經常由交易活躍的期權價格來計算出隱含資產波動率,然後將這些波動率用於市場不活躍的產品定價之中。
(3)交易員經常從交易活躍的利率產品(例如利率上限及利率期權)之中,求得利率變動的信息,然後用這些信息計算複雜的結構性產品的價格。
以上做法並不是不合理。但是,有時假設市場交易不頻繁的產品的交易價格與其理論價格類似的做法可能會非常危險。當金融市場因各種原因出現大的震盪時,市場上可能會出現流動性黑洞(見第24.3節),這時流動性對於投資者來講非常重要,而流動性不好的產品的價格同其理論價格相比會有一個很大的折價。
長期資本管理公司(LTCM)提供了一個流動性風險的實例,這一實例在業界事例22-1中有詳細的描述。LTCM採用的套利策略被稱為收斂套利,在該策略中需要找到兩種證券(或證券的組合),這兩種證券的理論價格應該一致。如果在市場上某種證券的價格較低,這時可以買入價格偏低的證券而賣出價格較高的債券。這種套利的根本假設就是,如果兩個證券的理論價格一致,那麼其市場價格在最終也會一致。
1998年夏天,LTCM蒙受了巨大損失,其損失的根本原因是俄羅斯政府債券的違約造成了市場安全投資轉移現象的發生。LTCM在交易中持有流動性差的產品的多頭並同時持有流動性好的產品的空頭(例如,LTCM同時持有舊券的多頭及新券的空頭)。在俄羅斯國債違約後,流動性好的產品與流動性差的產品的差價急劇增大。LTCM槓桿率很強。在蒙受損失的同時又伴隨著追加保證金的要求,LTCM難以滿足這些要求。
LTCM的故事再一次強調了情景分析以及壓力測試的重要性。通過情景分析及壓力測試,我們可以瞭解極端情況下會發生什麼。如第22章所述,在分析中,我們不但需要考慮即時的損失,同時還要考慮由其他公司損失所帶來的連帶效應。
29.3.1 當所有人都在做同樣的交易時應加倍小心
有時市場上的很多參與者會同時進行相同的交易,這種現象會造成危險的市場環境,這樣的市場會產生大幅度振盪,導致流動性黑洞的出現並使市場參與者蒙受巨大損失。
我們在業界事例24-4中給出了另一個實例。這一實例是關於投資組合保險策略及1987年10月的市場暴跌。在市場暴跌的前一個月,有越來越多的基金經理以合成看跌期權的形式來對他們的投資組合進行保護。他們在市場升值時買入股票或股票指數期貨,而在市場下跌時賣出股票或股票指數期貨。這種策略造成了一個不穩定的市場。市場一個較小的下跌會引發基金經理拋出股票的浪潮,這一浪潮會進一步使得市場下跌,從而進一步促使基金經理拋售股票。毫無疑問,如果沒有投資組合保險策略的存在,1987年10月股票的下跌也不會那麼嚴重。
另外一個實例來自1998年LTCM的經歷。LTCM在遇到麻煩以後,其他採用同樣收斂套利策略的對衝基金使得LTCM的處境雪上加霜。在俄羅斯國債違約造成安全投資轉移現象以後,LTCM曾試圖變賣自己的部分資產以滿足保證金的要求。不幸的是其他對衝基金也面臨類似的問題,這些對衝基金也想進行類似的交易,這進而又使市場狀況進一步惡化,流動性差價變得比原來更大,同時使得安全投資轉移現象更加嚴重。LTCM所持頭寸為美國國債,其交易策略是持有流動性差的國債舊券的多頭以及流動性好的國債新券的空頭。當安全投資轉移現象產生後,兩種債券的收益率差價增大,LTCM只有變賣其部分舊券並且同時買入新券來平倉。其他對衝基金也在進行同樣的交易。所有這些交易促使新券價格相對於舊券價格持續上漲,兩種債券收益率的利差進一步增大。
另外一個實例是關於20世紀90年代英國保險公司的損失,我們曾在業界事例3-1中討論過這一實例。當時所有英國保險公司都決定對自己的利率敞口進行對衝,以應對長期利率下降的風險,而這些對衝行為本身卻造成了長期利率的下降。
從這些故事中我們得到的主要教訓是,對於金融市場的整體狀況要有一個清醒的認識,這一點至關重要。我們要了解,當大量的市場參與者執行相似的交易策略時,市場會蘊含著什麼樣的風險。
29.3.2 不要過分依賴短期負債來支撐長期資產
所有的金融機構都或多或少地依賴短期資金來源來支持長期資金需求,但如果一家機構過分依賴短期資金源,則其遭受不可克服的流動性困難的可能性會增加。
在2007年信用緊縮開始之前,市場上有一種傾向,就是在次級按揭和其他長期資產被打包成結構性產品之前,市場參與者常常利用商業票據來進行融資。管道公司和其他特殊目的實體一直有這樣的運作方式。商業票據每個月都被進行滾轉,例如,買入4月1日發行的商業票據的投資者在5月1日贖回的資金將用於購買5月1日發行的商業票據,買入5月1日發行的商業票據的投資者在6月1日贖回的資金將用於購買6月1日發行的商業票據,並依此類推。當投資者在2007年8月失去對次級貸款的信心時,這些商業票據不再能夠滾轉。在許多情況下,銀行必須為證券化產品提供擔保和融資支持,這造成了流動性短缺。正是由於沒有長期資產融資的安排,信用緊縮才會這麼嚴重。
危機期間很多金融機構難逃厄運(如雷曼兄弟和北巖銀行),都是因為過分地依賴短期資金。一旦市場對金融機構的健康情況產生懷疑,無論這種懷疑是對還是錯,對金融機構短期的融資進行滾轉都很難做到。當我們明白這一點後,就不難理解為什麼監管機構在《巴塞爾協議Ⅲ》中會對銀行引入了流動性要求。
29.3.3 市場透明度非常重要
2007年的信用緊縮給我們的一個教訓是:市場透明度十分重要。在2007年危機以前,投資者熱衷於結構性產品交易,但實際上他們對標的資產並不瞭解,他們僅有的信息是交易產品的信用評級。現在回頭看,投資者應該要求關於標的資產的更多信息,同時應對自身承擔的風險進行謹慎分析。
2007年8月,因為次貸違約,投資者對所有結構化產品失去了信心,並退出了市場。這造成了市場的崩潰。結構化產品的各個分檔只能以遠遠低於其理論價格的價格拋售。市場出現了安全投資轉移現象,信用價差也激增。如果市場具有良好的透明度,投資者確實對自身買入的資產抵押證券有所瞭解,那麼,儘管市場上仍然還會出現次貸損失,但安全投資轉移現象以及市場所受到的衝擊就不會這麼嚴重。
[1] 指最近發行的國債,相對應的、更早發行的、尚未到期的債券就是off-the-run,即舊券。——譯者注
29.4 對於非金融機構的教訓
我們在下面將總結一下這些損失帶給非金融機構的教訓。
29.4.1 理解你的交易目的
企業一定不要去做自己不理解的交易或者使用自己不完全理解的交易策略。這聽起來是十分淺顯的事,但我們會吃驚地發現,仍有如此之多的非金融機構的交易員在遭受了巨大損失之後,才承認自己的無知並且聲稱自己的錯誤是由於投資銀行的誤導。奧蘭治縣的資金主管羅伯特·西特倫就是其中一員,還有哈默史密斯和富勒姆的交易員,雖然他們的交易量巨大,但他們對於利率互換及其他利率衍生產品的知識十分匱乏。
如果一家企業的高管對於下級所提出的交易不理解,那麼這個交易就不應該被批准。一個簡單原則是,如果一個交易的動機是如此複雜以至於管理人員都不能理解,我們基本可以確定該交易對於企業是不適當的。如果採用這一原則,寶潔公司的交易一定會被否決。
一種保證透徹理解某一個金融產品的方法是對該產品進行定價。如果一家企業內部沒有能力去進行產品定價,那麼這家企業就不應該交易這種產品。在實踐中企業常常依賴自己的投資銀行所給出的價格建議,這麼做是很危險的。寶潔公司的教訓就說明了這一點。當寶潔公司想將交易進行平倉時,發現產品的價格是由信孚銀行的特有模型計算得出的,寶潔公司沒有辦法對其進行檢查。
29.4.2 保證對衝者不要成為投機者
生活中有一個不幸的事實,那就是進行對衝相對來講缺乏懸念,而投機行為往往激動人心。當一家公司僱用了一個交易員來管理其外匯、商品以及利率風險時,以下的危險現象可能會產生:在最初時交易員工作勤奮,並贏得了公司高管的信任,這時他會對公司的風險敞口進行評估並採取對衝措施。隨著時間的推移,交易員逐漸確信自己可以把握市場,漸漸地,交易員會變成投機者。在剛剛開始投機時,可能一切順利。但不久產生了交易損失,為了掩蓋損失,交易員會將交易量加倍來進行賭博,進而有可能造成更大的損失,最終結果就是導致災難性的損失。
就像我們先前討論的那樣,風險限額一定要由高管來事先確定,對於限額的實施要設置一定的控制環節。企業在進行交易之前要對自己面臨的外匯、利率、商品等風險做一個分析,交易決策是為了保證將風險控制在一定的可接受範圍內,企業的交易策略與企業的風險敞口脫節是出現問題的明顯前兆。
29.4.3 要警惕將財務部變成盈利中心
在過去的30年有一種將公司的財務部轉換為盈利中心的趨勢。這麼做看來有一定的好處,因為財務部有動力去減小企業融資費用,並且儘可能地以有利可圖的方式管理風險。但問題是,財務部所能取得的盈利是有限的。在進行融資或者將額外資金進行投資時,財務主管面臨的市場是一個有效市場。財務部只有在承擔更大風險的前提下才能給企業帶來利潤。公司的對衝項目給財務主管提供了做出精明的決定來提高盈利的機會。但我們應該記住對衝的目的是降低風險,而不是增加預期利潤。在大概50%的情況下,決定採用對衝造成的後果比不採用對衝還要差。將財務部變為盈利中心的危險是使得財務部(主管)有動機成為投機者,因此像奧蘭治縣及寶潔公司的現象也就容易產生。
29.5 結束語
本書考慮的大部分風險都是已知的,如市場風險和信用風險可以根據歷史數據來定量分析。還有兩類風險對金融機構來說也至關重要:未知風險和不可知風險。
未知風險(unknown risk)是指能夠引發風險的事件已知,但是事件發生的可能性不能輕易確定。操作風險中包含了很多種類的未知風險。由無賴交易員導致損失的概率是多少?重大法律訴訟導致損失的概率是多少?在某新興經濟體中,業務被中斷的概率是多少?這些概率通常不能從歷史數據中得出。如同在第22章中討論的,主觀概率經常會被使用。在一本被廣泛引用的著作中,Knight(1921)使用“風險”來指代已知風險,使用“不確定性”來指代未知風險。[1]
不可知風險(unknowable risk)是指那些我們甚至連能觸發損失的事件都不清楚的風險。從各種角度來講,不可知風險是最險惡的,因為它們總是突然出現並常常導致鉅額損失。不可知風險有時被稱作“黑天鵝”(black swan,黑天鵝過去被認為是不可能存在的,直到它們在澳大利亞被發現)。正如納西姆·塔勒布(2007)指出的,黑天鵝一旦發生,這些事件往往被當作是顯而易見的。[2]在20世紀70年代出版多卷本百科全書的出版商考慮過技術的進步會使他們的產品分文不值嗎?可能不會,但事後我們會覺得這很自然。
公司該如何管理未知風險和不可知風險呢?一個重要工具是靈活性,公司應避免過高的槓桿並儘量保證它們的成本是變化的而不是固定的。對產品和市場進行多元化也有利於增加靈活性。在將來,保險公司可能會開發更多的產品來應對未知風險和不可知風險。如在第23章中討論的,現在市場上已經有產品可對操作風險(未知風險)提供保護。處理不可知風險在合約設計上具有很大挑戰性,但也不是完全不可能。
[1] See F. H. Knight, Risk, Uncertainty and Profit (Boston: Houghton Mifflin Company, 1921).
[2] SeeN. N. Taleb, The Black Swan: The Impact of the Highly Improbable (New York: Random House, 2007).
延伸閱讀


附錄A
利率複利頻率
某銀行聲明1年期儲蓄利率為每年10%,這句話雖然聽起來簡單明瞭,但事實上,其準確的含義依賴利率的計量方式。
假定利率計量方式為每年複利1次,則銀行聲明中給出的10%利率是指100美元的投資在年終會變成
100×1.1=110(美元)
當利率計量方式為每年複利2次時,這意味著每6個月會有5%的利息收入。如果利息也被用於再投資,則100美元的投資在1年後會增長為
100×1.05×1.05=110.25(美元)
當利率計量方式為每年複利4次時,這意味著每3個月會有2.5%的利息收入。假定投資所得利息均用於再投資,100美元的投資在1年後會增長為
100×1.0254=110.38(美元)
表A-1顯示出複利頻率的增長對投資回報的影響。
表A-1 利率為每年10%,複利頻率增加對於100美元投資在1年後的終值的影響
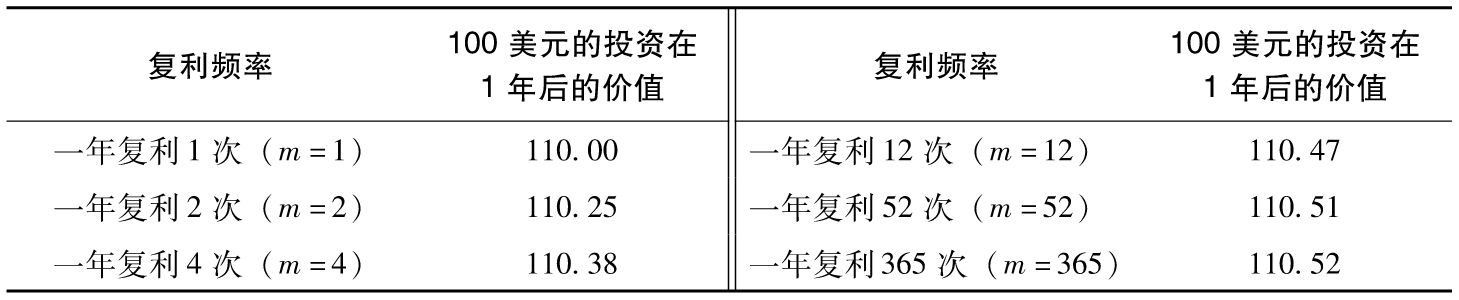
利率複利的頻率定義了利率的計量方式,一個一年複利1次的利率可以被轉換成一個以不同頻率複利的利率。例如,由表A-1我們可以看出,一年複利1次計息利率10.25%與一年複利2次計息利率10%等價。利率在不同計息頻率下的相互關係可類比為公里同英里的關係,它們是兩個不同的計量單位。
為了推廣以上結果,我們假設將A數量資金以一年複利1次利率投資n年,投資的終值為
A(1+R)n
如果利率對應於一年複利m次利息,投資終值為

m=1時所對應的利率有時被稱為年等價利率(equivalent annual interest rate)。
連續複利
複利頻率趨於無窮大時所對應的利率就被稱為連續複利(continuous compounding)利率,[1]在連續複利情況下,我們將A數量資金投資n年,投資的終值為
AeRn
(A-2)
這裡的e=2.71828,在大多數計算器中都有計算函數ex的功能,所以式(A-2)不會產生任何問題。在表A-1的例子中,A=100,n=1,R=0.1,以連續複利計息,A數量資金在投資1年後將增長到
100e0.1=110.52(美元)
這個精確到小數點後兩位的數值與用每天覆利所得的結果一樣,在大多數情況下,我們認為連續複利與每天計算複利等價。對一筆資金以連續複利利率R滾動n年,其效果是相當於乘上eRn項。而對一筆在第n年的資金以連續複利利率R進行貼現,其效果是相當於乘上e-Rn。
假設Rc是某一連續複利利率,Rm是與之等價的每年m次複利利率。由式(A-1)及式(A-2),我們得出
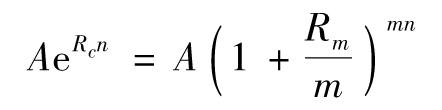
及

這就是說

及
Rm=m(eRc/m-1)
(A-4)
這些公式可將每年m次複利的利率轉換為連續複利的利率,反之亦然。函數ln是大多數計算器設有的自然對數功能。此函數的定義是:如果y=ln(x),則x=ey。
【例A-1】 考慮一個年息為10%的利率,一年複利2次。將m=2及Rm=0.1代入式(A-3)可得出一個等價的連續複利利率
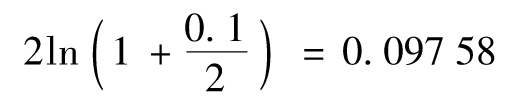
即9.758%。
【例A-2】 假如某債權人給出的每年連續複利利率為8%,而實際利息是每季度支付一次。將m=4及Rc=0.08代入式(A-4),一年複利4次的年等價利率為
4(e0.08/4-1)=0.080 8
即8.08%,這意味著,對於1 000美元的貸款,借款人每季度必須支付20.20美元的利息。
[1] 在精算領域,連續複利利率也被稱為利息力(force of interest)。
附錄B
零息利率、遠期利率及零息收益率曲線
n年的零息利率是指在今天投入資金,連續持有n年後所對應回報的收益率。所有的利息及本金都在n年年末支付給投資者,在n年期滿之前,投資不支付任何利息回報。n年期的零息利率有時也被稱作n年期的即期利率(spot interest rate)、n年期的零利率(zero rate)或者n年期的零率(zero)。作為時間期限的函數,零息利率被稱為零息曲線。假如一個5年期連續複利的零息利率為每年5%(複利頻率見附錄A),這意味著今天100美元的投資在5年後會增長到
100×e0.05×5=128.40
一個遠期利率是由今天零息利率所導出的對應將來某時刻的利率。考慮如表B-1所示的零息利率,6~12個月的遠期利率為6.6%,這是因為將前6個月5%的利率與後6個月6.6%的利率組合在一起會得出一年的平均利率為5.8%。類似地,12~18個月的遠期利率為7.6%,這一利率與今天到12個月5.8%的利率組合在一起所產生的18個月平均利率為6.4%。一般來講,T1~T2的遠期利率F可表達為

其中R1對應於期限為T1的零息利率,而R2對應於期限為T2的零息利率。這一公式在連續複利情形下是個恆等式,而對應於其他計息頻率只是近似式。採用表B-1的數據,應用公式可得出表B-2,例如將T1=1.5、T2=2.0、R1=0.064及R2=0.068代入公式,我們得出F=0.08,這說明18~24個月的遠期利率為8.0%。
表B-1 某零息利率結構

認為將來的實際利率同遠期利率會有很大出入的投資者會很容易地在市場上找到某種交易來反映他們的信念。考慮一個投資者可以由表B-1所示的利率借出或借入資金,假定該投資者認為在今後兩年的利率沒有變化。這個投資者可以借入6個月期的資金,在6個月、12個月及18個月時再進行延展投資,以這種形式可將資金投資兩年,6個月的借款可以在6個月月末、12個月月末和18個月月末再延展,如果利率保持恆定,這種投資決策每年會盈利1.8%,這是因為收入利率為6.8%,而支出利率為5%。這種形式的投資方式被稱為對收益曲線的下注(yield curve play),投資者對將來利率進行投機,認為將來的利率會不同於由表B-2給出的遠期利率。
表B-2 由表B-1(零票息利率)得出的遠期利率(連續複利)
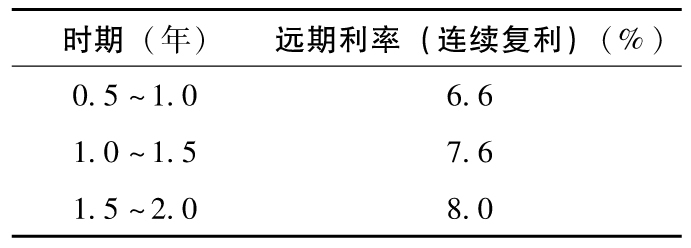
奧蘭治縣的財政官員羅伯特·西特倫在1992年及1993年採用了以上的投資方式,並且在一段時間內獲得了成功。羅伯特·西特倫的盈利在奧蘭治縣的預算中起了很大的作用,因此他也得以連任。1994年羅伯特·西特倫進一步增加了對收益曲線的賭注。如果短期利率恆定或下降,他的投資依然會表現不錯。但在1994年,利率急劇上揚,1994年12月奧蘭治縣宣佈其投資組合損失15億美元。幾天之後,奧蘭治縣宣佈尋求破產保護。
B.1 債券價格
大多數債券提供週期性的券息,債券發行人在債券期滿時將債券的本金(有時也被稱為票面值或面值)償還給投資者。債券的理論價格等於債券將來的現金流貼現後的總和,計算貼現最精確的辦法是對於不同時期的現金流採用不同的零息貼現利率。假定一個2年期的債券的面值為100美元,每年券息利率為6%,半年付息一次。為了計算第一個3美元券息的貼現值,我們採用對應於6個月的貼現率5%;為了計算第二個3美元券息的貼現值,我們採用對應於1年的貼現率5.8%;依此類推,債券的理論價格為
3e-0.05×0.5+3e-0.058×1.0+3e-0.064×1.5+103e-0.068×2.0=98.39(美元)
B.2 債券收益率
一隻債券的收益率是使得債券的貼現的現金流總和等於其市場價格的貼現率,假定一隻債券的理論價格為98.39美元,此價格也等於其市場價格(這裡的債券的市場價格與表B-1的數據完全一致)。如果y對應於連續複利的債券收益率,我們應有等式
3e-y×0.5+3e-y×1.0+3e-y×1.5+103e-y×2.0=98.39(美元)
這一方程式的解可以通過Excel的Solver程序或其他方式得出,其解為y=6.76%。
B.3 國債收益率
國債收益率是投資者投資國庫券或國債時所得的收益率。國庫券及國債是政府借入以本國貨幣為計量單位的資金而發行的金融產品。日元國債收益率是指日本政府借入日元資金的利率,美國國債收益率是指美國政府借入美元的利率,其他國家國債收益率也有類似含義。
B.4 零息收益曲線的確定
一種計算表B-1顯示的零息利率的方法是直接觀測本息分離債券所對應的利率,這些產品是交易員在賣出與本金分離後的票息時人工生成的零息債券。
表B-3 由息票剝離方法計算的2.5年利率
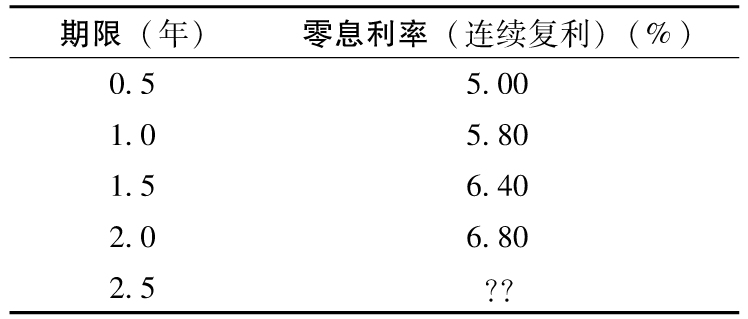
另一種確定零息收益率曲線的方法是從一般的國債及國庫券價格入手來計算零息利率,最流行的方法就是所謂的息票剝離方法(bootstrap method)。這種方法從短期產品入手,然後通過以匹配價格的形式逐漸導出長期利率。假設表B-3是已經確定的零息收益率,我們假設一個息率為8%的債券價格為102美元,債券本金為100美元。我們將2.5年所對應的零息利率計為R,應用表B-3數據,可以給出此債券的正確價格,這一過程會涉及對以下方程求解
4e-0.05×0.5+4e-0.058×1.0+4e-0.064×1.5+4e-0.068×2.0+104e-R×2.5=102
其解R=7.05%。至此我們可以得出一個關於零息利率的表B-3。介於息票剝離節點之間,收益率一般被假設為線性(在我們的例子中,2.25年所對應的零息利率為6.902 5%)。通常的習慣約定是將息票剝離第一節點之前的利率以及最後一個節點之後的利率設定為常數,我們在圖B-1中畫出這裡討論的利率曲線。
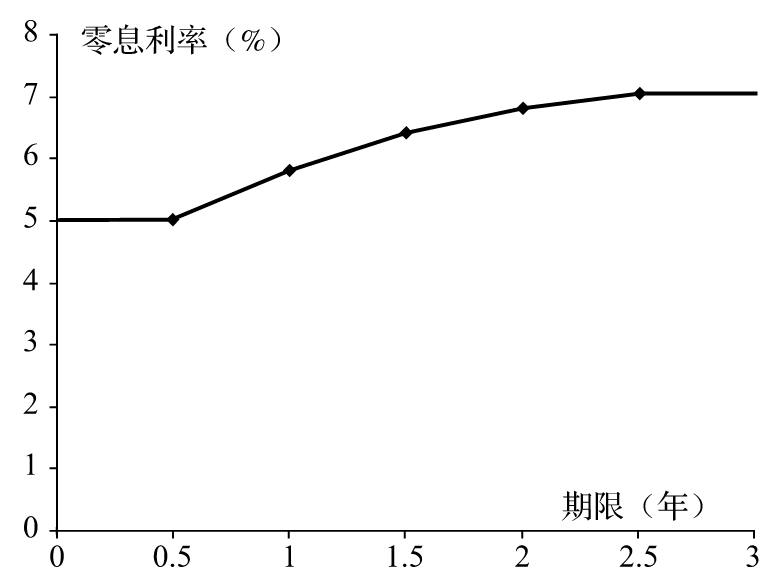
圖B-1 與表B-3對應的零息利率曲線
B.5 OIS零息利率
OIS零息利率曲線的確定方式與確定國債零息曲線的息票剝離法類似。期限為1年的OIS利率適用於1年到期的互換,它們能立即提供有關這些期限的零息利率的信息。期限超過1年的OIS利率通常適用於每3個月交易一次的互換合約,表示按面值出售並按季度支付的債券收益率。
假設3個月、6個月、9個月和12個月的OIS零息利率分別為2%、2.3%、2.5%和2.7%(連續複利)。進一步假設1.25年期的OIS利率為2.8%,一張面值為100美元的1.25年期的債券與每3個月支付0.7利息的債券的價值相等。如果債券收益率R等於1.25年期的OIS零息利率,那麼有
0.7e-0.02×0.25+0.7e-0.023×0.5+0.7e-0.025×0.75+0.7e-0.027×1+100.7e-R×1.25=100
即R=2.794%。
附錄C
遠期合約及期貨合約的定價
一個不提供中間收入的資產的遠期或期貨價值為
F0=S0erT
其中S0為資產今天的現市價格,T為期貨或遠期的到期期限,r為對應於期限T的連續複利無風險利率。如果資產在期限T前提供收入,收入的貼現值為I,則以上表達式變為
F0=(S0-I)erT
如果資產提供收入的收益率為q,資產的遠期或期貨價值為
F0=S0e(r-q)T
外匯可以被看作是提供收入的投資資產,收入的收益率為外匯所對應的無風險利率,所以外匯遠期和期貨的價值為
F0=S0e(r-rf)T
其中rf為外國無風險利率(連續複利),S0為即期匯率。
如果一個遠期合約的持有方能夠以價格K買入資產,那麼這一遠期合約的價格為
(F0-K)e-rT
其中F為遠期價格,如果持有方可以價格K賣出資產,那麼其價格就變為
(K-F0)e-rT
【例C-1】 我們考慮一個6個月期的S&P 500期貨合約,S&P 500股指的當前價格為1 200,6個月期無風險利率為每年5%,S&P 500在今後6個月的預期收益率為每年2%(兩個利率均為連續複利),期貨合約的價格為1 200e(0.05-0.02)×0.5,即1 218.14。
【例C-2】 一個期限為9個月的黃金合約的遠期價格為550美元,某家公司持有遠期合約,公司可以在9個月以每盎司530美元的價格買入1 000盎司黃金,9個月期無風險利率為每年4%(連續複利),遠期合約的價值為1 000×(550-530)e-0.04×9/12,即19 409美元。
在大多數情況下,遠期合約和期貨合約的價格可以假設相等。但是合約的利率除外,歐洲美元期貨合約的報價不能假設為與相應的遠期利率相同,特別是當合約到期時間較長時。
附錄D
互換合約定價
對於利率互換合約定價,我們可以假定在將來某時刻的利率等於今天觀察到的遠期利率。例如,我們考慮某利率互換合約,從現在到利率互換的到期日還有14個月,利率互換合約的本金為1億美元,假定我們在合約中收入的固定利率為5%,付出的浮動利率為LIBOR,資產流互換頻率為每6個月一次。假定:①4個月以前設定的6個月期LIBOR利率為4%;②在今後2個月開始的6個月遠期利率為4.6%;③在將來8個月時的6個月遠期利率為5.2%。所有利率的計算方式為每半年複利一次,假定遠期利率在今後會得以實現,利率互換所對應的現金流在表D-1中有所展示(例如在8個月時收入的固定利率的現金流為0.5×0.05×100,即250萬美元;付出的浮動利率現金流為0.05×0.046×100,即230萬美元),利率互換的價值是表D-1中最後一列淨現金流的貼現值。[1]用於貼現現金流的利率通常是OIS零息利率(計算見附錄B)。
表D-1 在利率互換合約定價中假定遠期利率在將來會得以實現 (百萬美元)

D.1 LIBOR遠期利率
LIBOR遠期利率可以用息票剝離法計算。假設6個月、12個月、18個月和24個月的OIS零息利率分別為3.8%、4.3%、4.6%和4.75%(連續複利)。假設在每6個月交換一次現金流的2年期互換協議中,互換利率為5%。進一步假設0.5年期的LIBOR遠期利率為5.5%(全部以半年複利)。收到LIBOR並支付5%的2年期互換合約的價值為0。第一次互換的價值為
0.5×(0.04-0.05)×100×e-0.038×0.5=-0.490 6
第二次互換的價值為
0.5×(0.05-0.05)×100×e-0.043×1=0
第三次互換的價值為
0.5×(0.055-0.05)×100×e-0.046×1.5=0.233 3
前三次支付的總價值是-0.490 6+0+0.233 3=-0.257 3,假設最後一次支付的遠期利率為F,互換價值為0,有
0.5×(F-0.05)×100×e-0.047 5×2=0.257 3
即F=0.055 65或5.565%。
D.2 貨幣互換
在貨幣互換的定價中,我們可以假設將來的匯率等於今天的遠期匯率。接下來我們考慮一個貨幣互換的實例,這一貨幣互換是以4%的英鎊利率與6%的美元利率每年進行交換。兩種貨幣的面值分別為1 000萬美元以及500萬英鎊,互換交易的期限為3年,互換交易的現金流如表D-2中第2列及第3列所示,遠期匯率(我們假定)如表中第4列所示。我們採用這些匯率將英鎊轉換為美元,最後一列展示了淨現金流,互換的價值等於這些現金流的貼現值。
表D-2 在貨幣互換中假定遠期匯率在將來會得以實現 (百萬美元)

另外一種方式(最終計算價值同以上計算結果相等)是將互換交易作為英鎊債券的多頭與美元債券的空頭進行交換。每一債券均在所對應的貨幣體系下進行定價,最後在計算中,利用當前匯率將英鎊債券的價格轉換為美元價格。
[1] 注意現金流的精確時間取決於天數計算方式和節假日。
附錄E
歐式期權定價
對於一個不提供中間收入的資產的歐式看漲期權及歐式看跌期權,布萊克-斯科爾斯-默頓定價公式為
c=S0N(d1)-Ke-rTN(d2)
及
p=Ke-rTN(-d2)-S0N(-d1)
其中
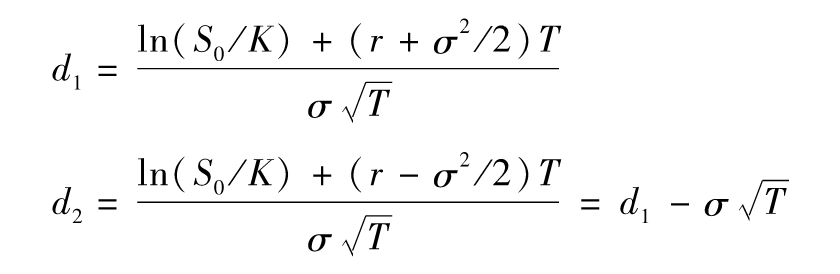
其中N(x)為正態分佈的累積分佈函數(函數表列於本書最後或Excel裡的NORMSDIST功能),變量c及p分別代表歐式看漲期權及歐式看跌期權的價格,S0為在時間0的股票價格,K為執行價格,r為連續複利的無風險利率,σ為股票波動率,T為期權的到期期限。
當資產提供現金收入時,在期權期限內的現金收入的貼現值應該在S0中扣除,當資產提供收入的收益率為q時,以上公式變為
c=S0e-qTN(d1)-Ke-rTN(d2)
及
p=Ke-rTN(-d2)-S0e-qTN(-d1)
其中
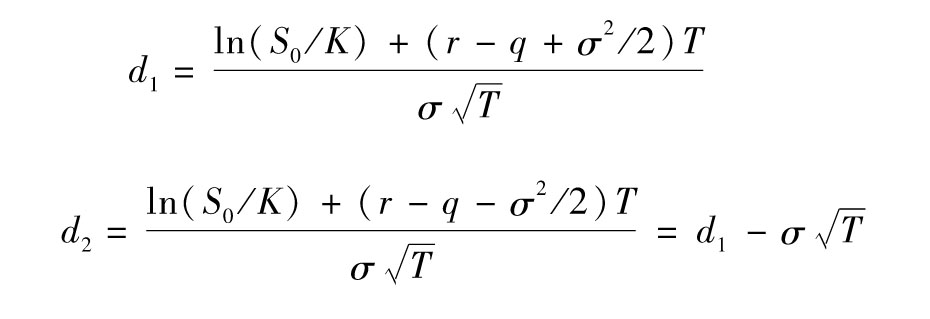
對於匯率期權可以通過設定q等於外匯無風險利率來估值。對於遠期或期貨期權,我們可以採用以上公式,其中,S0等於遠期或期貨的現值,σ是遠期或者期貨價格的波動率。
表E-1給出了期權所對應的希臘值,N′(x)代表正態分佈密度函數,其公式為
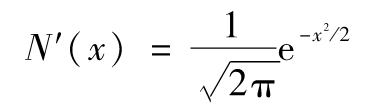
期權的隱含波動率的定義為使得布萊克-斯科爾斯-默頓模型給出的期權價格等於市場價格的波動性(見第10.2節),即σ為隱含波動率。
表E-1 資產的收益率為q的期權的希臘值
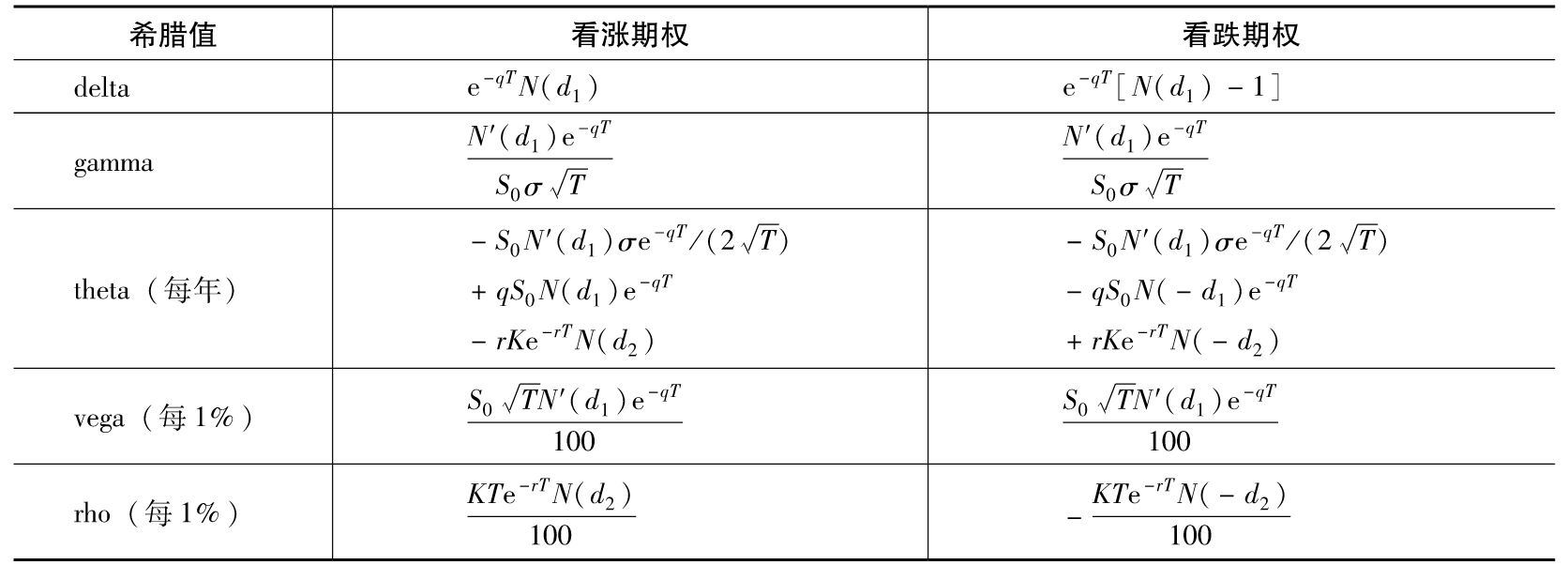
【例E-1】 我們考慮一個6個月期的歐式股指期權,股指的當前價格為1 200,期權執行價格為1 250,無風險利率為5%。股指的股息率為2%,股指的波動率為0.2,這時S0=1 200,K=1 250,r=0.05,q=0.02,σ=0.2,T=0.5,期權價格為53.44,期權的delta為0.45,gamma為0.002 3,theta為-0.22,vega為3.33,rho為2.44,注意表E-1給出的theta的時間單位為每年,我們這裡計算出的theta對應於日曆天。
以上計算可以用RMFI軟件實現,這一軟件可在作者的網頁上下載,在計算中選擇“期權類型:布萊克-斯科爾斯歐式期權”(Option Type:Black-Scholes European),在赫爾(2018)的著作中有關於期權定價更詳細的描述。[1]
[1] See J. C. Hull, Options, Futures, and Other Derivatives, 10th ed. (Upper Saddle River, NJ: Pearson, 2018).
附錄F
美式期權定價
對於美式期權進行定價,我們需要將期權的期限分成n個等份,每一個等份的長度為Δt。假設資產在時間開始的價格為S,在Δt時間後,S上漲為Su的概率為p,S下降為Sd的概率為1-p,對於不提供中間收入的資產,變量u、d及p分別為
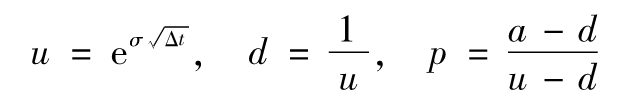
其中
a = erΔt
r為無風險利率,σ為波動率。
圖F-1顯示了一個期限為5個月的美式看跌期權的定價二叉樹,這裡的標的資產為某不付股息的股票,股票的當前價格為50,期權的執行價格為50,無風險利率為10%,波動率為40%,在二叉樹中總共有5步,Δt=0.083 3,u=1.122 4,d=0.890 9,a=1.008 4,p=0.5073,圖中每一個節點上部所對應的數值為股票價格,節點下部所對應的數值為期權價格。
在二叉樹最終端期權價格為期權的內含價格(intrinsic value)。例如,在節點G上,期權價格為50-35.36=14.64。在到期之前的每一個節點,我們假定期權持有者會將期權持有到下一個時間Δt,並且持有者會驗證提早行使期權是否會為最優。首先讓我們考慮節點E,如果期權會被持有到下一個時間段,如價格上漲時(對應概率p),期權價格為0;如價格下跌(對應概率為1-p)時,期權價格為5.45,期權價格的期望為0.507 3×0+0.492 7×5.45,即2.686,利用10%利率進行貼現,對應於節點E的期權期望值的貼現為2.66。因此期權在E點不應該被得以行使,因為這樣做所得回報為0。接下來考慮節點A,假定期權仍然會持有到一個時間段,通過一個類似的計算我們可以得出期權在A點的價格為9.90,如果期權在這一時刻得以行使,回報值為50-39.69=10.31,這時期權在A節點應該被提前行使,因此期權在A節點的價格為10.31。
從二叉樹的最終端開始以後退的形式繼續計算,在到達初始節點D時,我們得出的期權價格為4.49。當我們採用的二叉樹步數增大時,期權價格的精度也增大,利用30、50及100步的二叉樹,我們得出的期權價格分別為4.263、4.272及4.278。
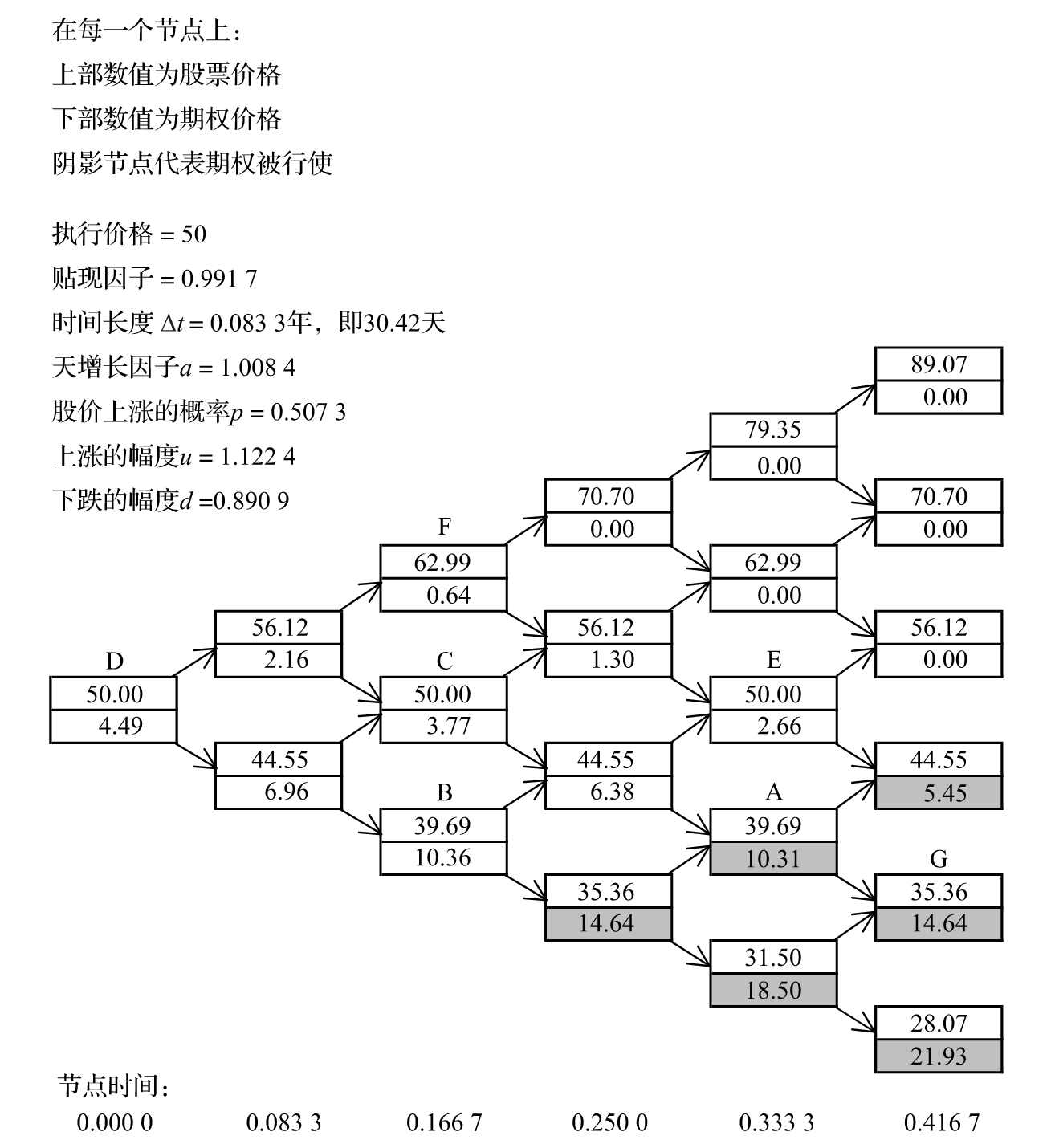
圖F-1 某不付股息的股票的美式看跌期權的定價二叉樹
為了計算delta,我們考慮在Δt時的兩個節點,在我們的例子中,從低位節點轉移到高位節點時,期權價格變化由6.96變為2.16,相應的股票價格由44.55變為56.12,因此delta的近似值為期權價格的變化除以股票價格的變化
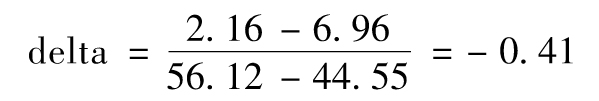
為了計算gamma,我們考慮在2Δt時刻的三個節點,由樹的上半部分兩個節點(C及F)所計算的delta為-0.241,這一delta所對應的股票價格近似為(62.99+50)/2=56.49,由樹的下半部分兩個節點(B及C)所計算出的delta為-0.639,這一delta所對應的股票價格近似為(50+39.69)/2=44.84,因此gamma的近似值為期權delta的變化除以相應股票價格的變化
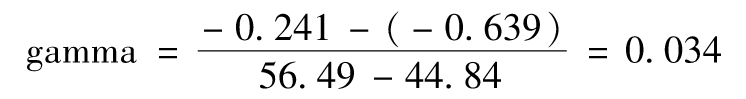
由D及C節點我們可以估計出
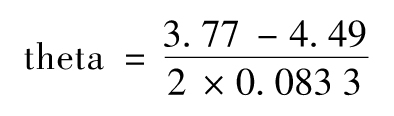
即-4.30(每年)。以上數量對得出每個日曆天所對應的theta為-0.011 8。vega的估計可以通過加大波動率、重新構造新的二叉樹並計算新的期權價格來取得,rho的計算方式和vega類似。
如果標的資產的中間收入的收益率為q,以上計算方式除了a=e(r-q)Δt(而不是erΔt)以外,其他計算過程完全相同(當標的資產是外匯時,q等於外國的無風險利率)。當期權標的資產為期貨或遠期價格時,a設為1,二叉樹各節點可顯示出期貨或遠期的價格。以上我們描述的過程可利用軟件RMFI來實現,這一軟件可在作者的網頁上下載。在軟件中選擇“期權類型:二叉樹美式期權”(Option Type:Binomial American)。在赫爾(2018)關於衍生產品定價的著作中有關於美式期權定價的更詳細描述。[1]
[1] See J. C. Hull, Options, Futures, and Other Derivatives, 10th ed. (Upper Saddle River, NJ: Pearson, 2018).
附錄G
泰勒級數展開
考慮函數z=F(x),假定變量x有一個小的變化,即Δx,變量z隨之也會有一個小的變化,即Δz,Δz和Δx的一階近似關係為

當z=F(x)為線性函數時,以上關係式為恆等式,在其他情形下為近似式。另外一個更為準確的近似式為
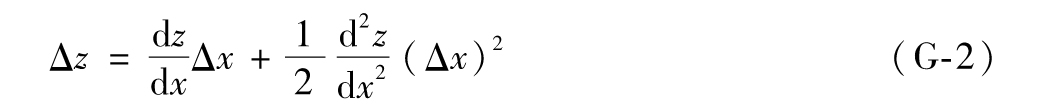
當z=F(x)為二次函數時,以上關係式為恆等式,在其他情形下為近似式。在近似式中加入更多的項,我們可以提高近似精度。泰勒展開的完整表達式為
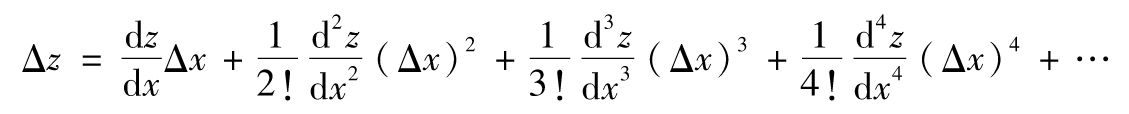
這裡“!”表示階乘函數。2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,依此類推。
【例G-1】 考慮函數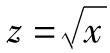 ,因此
,因此
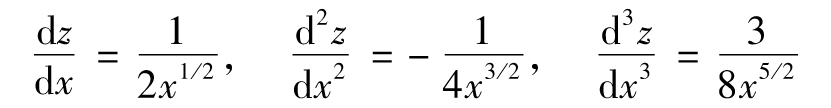
假定x=2以及Δx=0.1,因此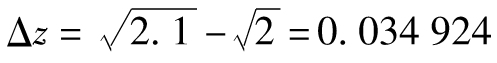 ,當x=2時
,當x=2時
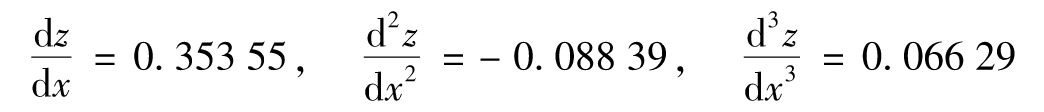
式(G-1)給出Δz的一階近似為
Δz=0.353 55×0.1=0.035 355
式(G-2)給出z=F(x)的二階近似為
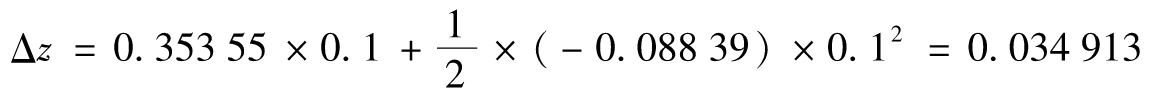
三階近似為

我們可以看出泰勒級數很快就收斂到正確答案0.034 924。
G.1 兩個變量的情形
接下來我們考慮兩個變量的函數z=F(x,y),假定變量x和y分別有小的變化Δx和Δy,變量z隨之也會有一個小的變化,即Δz,這時一階近似關係為

二階近似關係式為
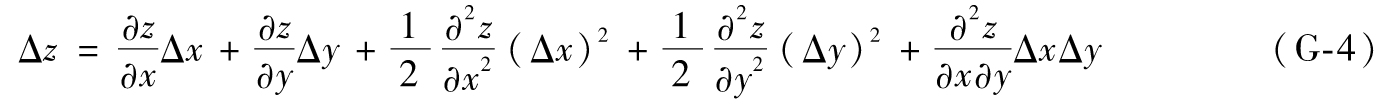
【例G-2】 考慮函數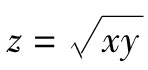 ,因此
,因此
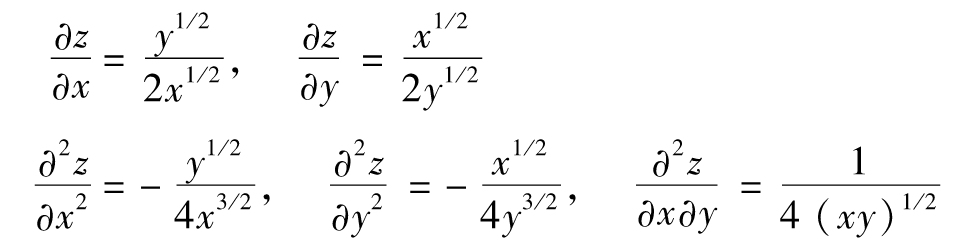
假定x=2,y=1;Δx=0.1,Δy=0.1,因此
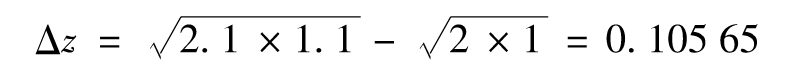
當x=2和y=1時
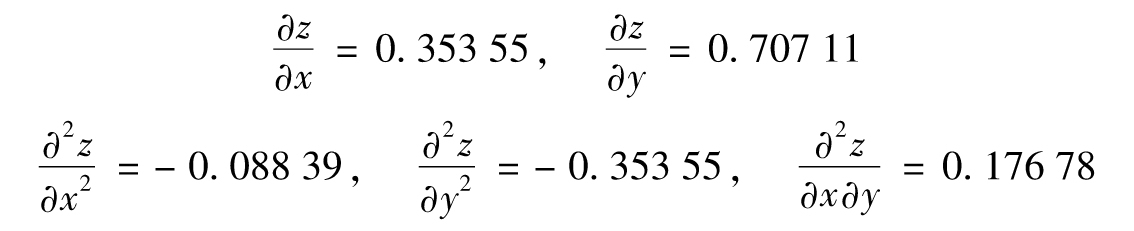
式(G-3)給出Δz的一階近似為
Δz=0.353 55×0.1+0.707 11×0.1=0.106 07
式(G-4)給出的二階近似為
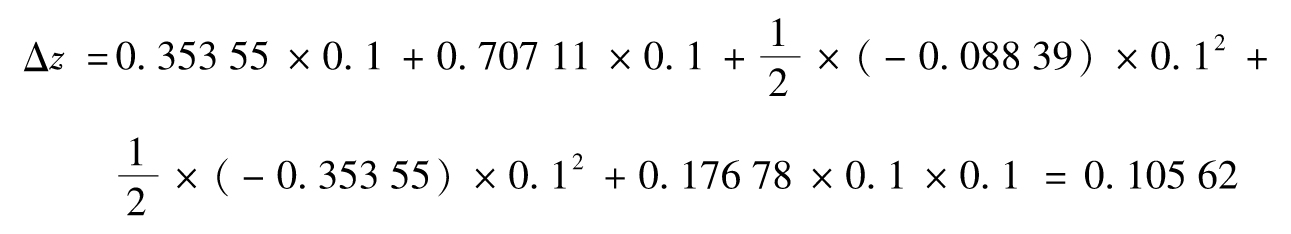
泰勒級數將收斂到0.105 62。[1]
G.2 一般結果
對於一個n個變量x1,x2,…,xn的函數,Δz的泰勒展開式為
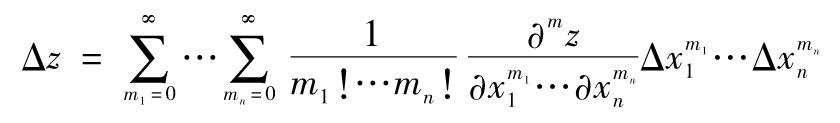
其中m=m1+…+mn,以及對應於所有mi為0的項的取值均為0。
[1] 原書為0.105 65,疑有誤,更正為此。——譯者注
附錄H
特徵向量和特徵值
考慮一個n×n矩陣A,假定x為一個n×1的向量,考慮方程
Ax=λx
(H-1)
以上方程可以寫為
(A-λI)x=0
其中I為n×n單位矩陣(在該n×n矩陣中,對角元素為1,非對角元素均為0)。顯然x=0是式(H-1)的解,但在什麼條件下,以上方程具有非零解呢?線性代數的一個定理保證,如果A-λI的行列式為零,那麼式(H-1)有非零解。滿足以上方程的λ就是滿足令A-λI的行列式為零的一個n次多項式的解,一般來講,這個n次多項式有n個解,這些解被稱為是矩陣A的特徵值,對應於某個特徵值,滿足式(H-1)的向量x為特徵向量。一般來講矩陣A有n個特徵向量,即每一個特徵值會對應一個特徵向量。
作為一個簡單例子,假定
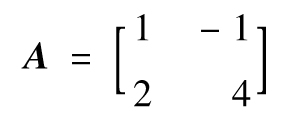
這時

以上矩陣的行列式等於
(1-λ)(4-λ)-(-1)×2=λ2-5λ+6
以上的解為λ=3及λ=2,這兩個值即為矩陣的特徵值。
為了確定對應於λ=3的特徵向量,我們對式(H-1)求解,即
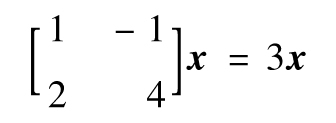
令
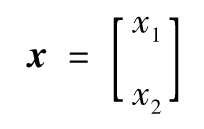
以上方程等價於
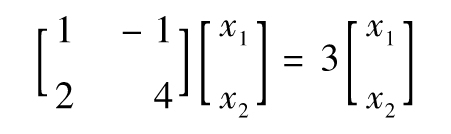
與此相對應的聯立方程為
x1-x2=3x1
及
2x1+4x2=3x2
以上兩個方程均等價於
x2+2x1=0
以上方程說明當λ=3時滿足x2=-2x1的任意x1和x2均滿足以上方程。一種約定是選取x1和x2保證向量x的長度為1,這意味著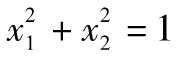 ,這時滿足x的長度為1的解為
,這時滿足x的長度為1的解為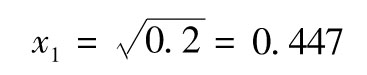 及
及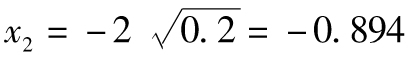 (另外一組解為
(另外一組解為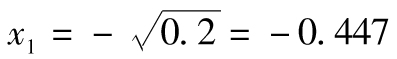 及
及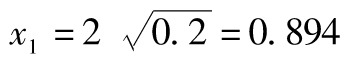 ),向量
),向量
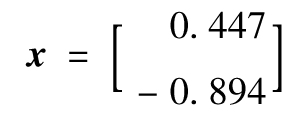
就是對應於特徵值λ=3的特徵向量。
通過一個類似的計算得出,對應於λ=2,式(H-1)為x1+x2=0,滿足以上方程,並且長度為1的向量為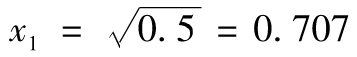 及
及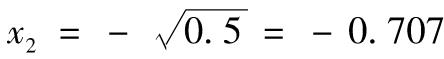 (另外一組解為
(另外一組解為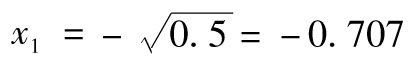 及
及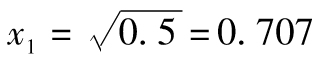 ),向量
),向量
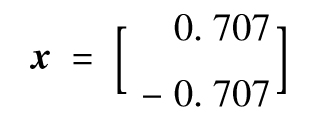
就是對應於特徵值λ=2的特徵向量。對於大型矩陣,我們必須採用數值分析方法來確定特徵值和特徵向量,一種數值方法是由Press等(2007)提供的。[1]
附錄I和附錄J是關於特徵值和特徵向量的應用,計算特徵值和特徵向量的軟件在作者的網站上。
[1] See W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes: The Art of Scientific Computing, 3rd ed. (Cambridge, UK: Cambridge University Press, 2007).
附錄I
主成分分析法
主成分分析法是理解n個相關變量的數據的一種方法,這一分析的目的是用一個小數量不相關的變量取代這裡n個變量。在第9.7節的例子中,總共有8個變量,這些變量是關於1年、2年、3年、4年、5年、7年、10年及30年的互換利率的日變化量。
分析的第一步是計算數據的協方差矩陣。如第11.3節所示,n×n協方差矩陣的第(i,j)個元素為數據中第i個變量與第j個變量的協方差,對角元(即i=j)為方差。
接下來一步是計算以上矩陣的特徵值和特徵向量(見附錄H),特徵向量的長度要等於1(如附錄H所示,這意味著向量的元素的平方之和等於1)。最高特徵值所對應的特徵向量為第一主元素,第二高數量特徵值所對應的特徵向量為第二主元素,等等。第9.7節中的例子所對應的主元素在表9-6中給出了。
第i個主元素的特徵值所佔所有特徵值的和的比率,即為第i個主元素能夠解釋的整體方差的百分比。第i個特徵值的平方根即為第i個因子得分的標準差(見表9-7)。
讀者可在作者的網頁上找到進行主成分分析法的軟件。
附錄J
對信用遷移矩陣的處理
假定一個n×n矩陣A為一年的信用遷移矩陣,這一矩陣就如表21-1所示。假定相連的時間段中,評級的變化是相互獨立的,對應於m年的信用遷移矩陣為Am。如果m為整數,對於Am的計算可以採用常規的矩陣乘法規則。
接下來考慮如何計算當m為整數時,對應於1/m年的遷移矩陣(例如,如果我們想知道一個月的變化,可令m=12)。這個問題要複雜得多,因為我們要計算一個矩陣的m次方根。我們首先需要計算出矩陣的特徵向量x1,x2,…,xn及特徵值λ1,λ2,…,λn,這些特徵值及特徵向量滿足
Axi=λixi
(J-1)
定義一個n×n矩陣X,其第i列為xi,Λ為n×n對角矩陣(即除主對角線以外其他位置都是0的矩陣),第i個對角元為λi,由式(J-1),我們可以給出以下關係式
A·X=X·Λ
即
A=X·Λ·X-1
定義Λ*為對角矩陣,第i個對角元為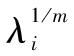 ,因此
,因此
(X·Λ*·X-1)m=(X·Λ*·X-1)(X·Λ*·X-1)…(X·Λ*·X-1)
=X·(Λ*)m·X-1=X·Λ·X-1=A
以上過程說明矩陣A的m次方根為X·Λ*·X-1,我們從而得到了1/m年的遷移矩陣。
有些作者,例如Jarrow、Lando和Turnbull(1997),[1]對於以上計算喜歡採用生成矩陣(generator matrix)的方法。生成矩陣Γ滿足:對應某個較短時間段Δt,遷移矩陣為I+ΓΔt,其中I為單位矩陣;對應於一個較長時間段t,轉移矩陣為
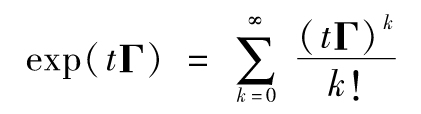
其中I為單位矩陣(對角元為1,其他元素為0)。
進行上述計算的軟件可以從作者的網頁上下載。
[1] See R. A. Jarrow, D. Lando, and S. M. Turnbull, “A Markov Model for the Term Structure of Credit Spreads,” Review of Financial Studies 10(1997):481-523.
附錄K
信用違約互換的定價
我們在第19章中介紹了信用違約互換(CDS),該產品可以通過(風險中性)違約概率來定價。
假設在沒有提前違約發生的條件下,某參照實體在一年內違約的條件概率為2%。表K-1給出了5年中每一年的生存概率和非條件違約概率(即在0時刻看到的違約概率)。由式(19-2),生存到t時刻的概率為e-0.02t。一年內違約的概率為存活到該年年初的概率減去存活到該年年末的概率。例如,存活到第二年年末的概率為e-0.02×2=0.960 8,而存活到第三年年末的概率為e-0.02×0.3=0.941 8。因此在第三年內違約的概率為0.960 8-0.941 8=0.019 0。
表K-1 無條件違約概率和生存概率

我們假設違約總髮生在每一年的年中,一個5年期的信用違約互換每年結束時付款一次。我們還假設連續複利的無風險年利率是5%,回收率是40%。計算分作三個部分,分別顯示在表K-2、表K-3和表K-4中。
表K-2 計算CDS預期付款的貼現值 (每年的數量為s)
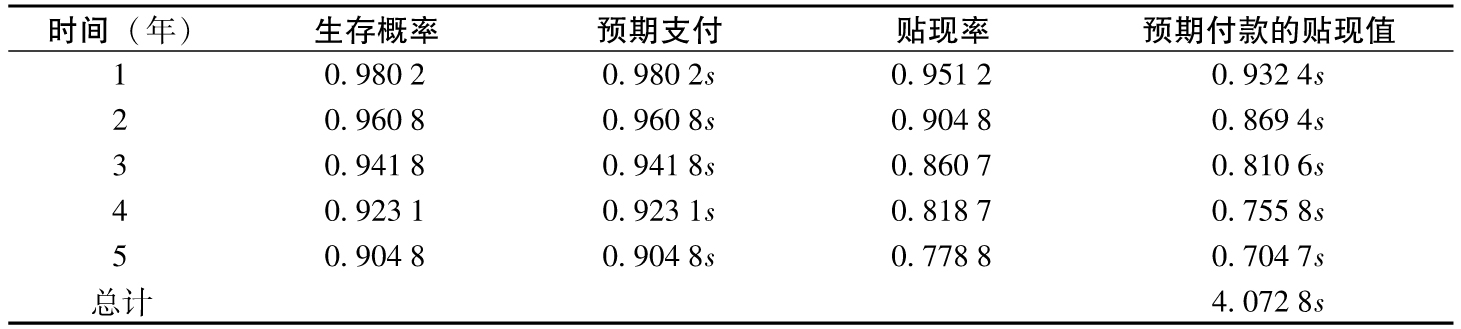
表K-3 計算CDS預期收益的貼現值 (面值1美元)
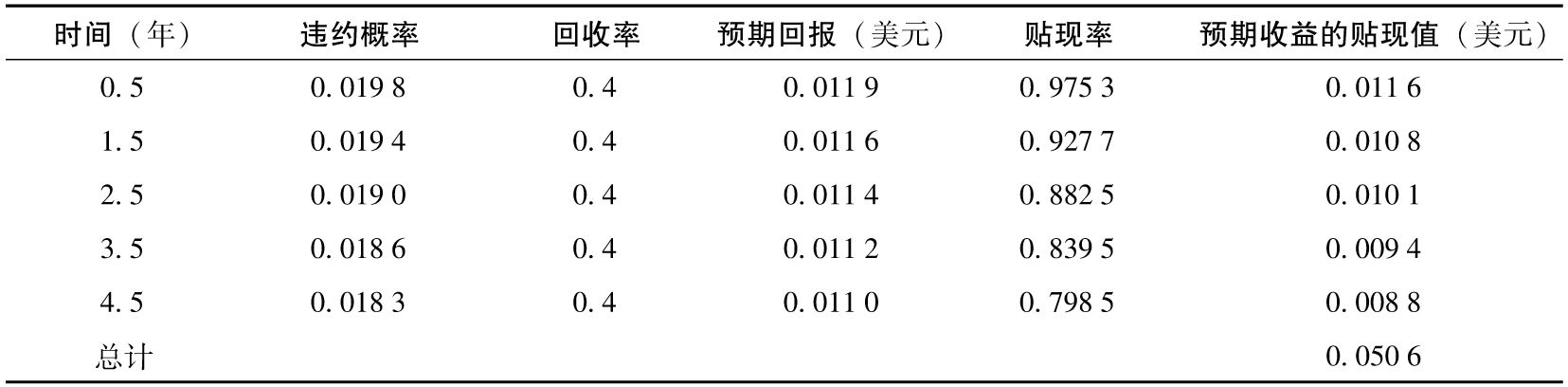
表K-4 計算應計付款的貼現值
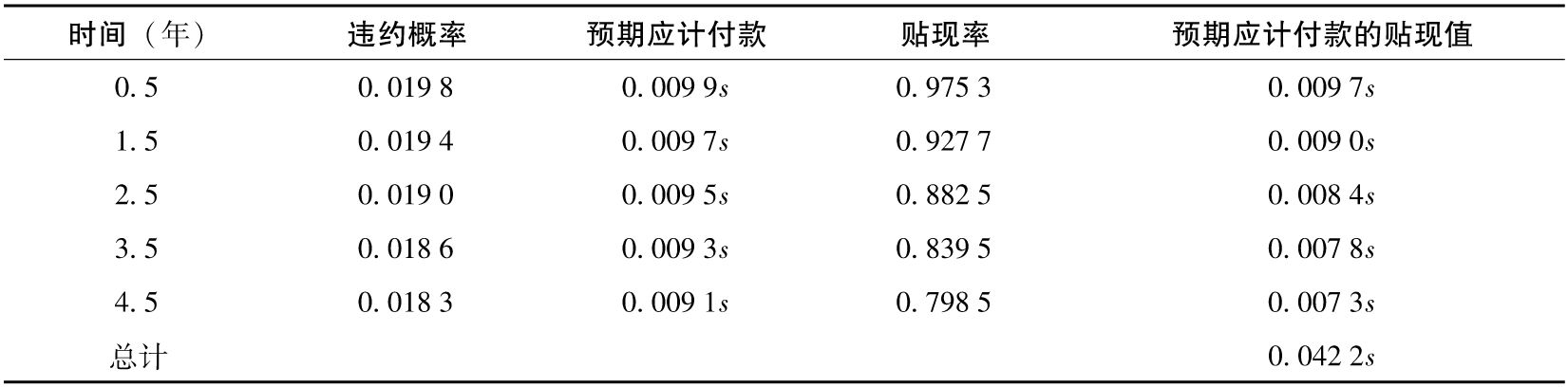
表K-2顯示了計算CDS預期付款的當前價值的過程,其中假設每年的費率(CDS利差)為s,CDS的面值為1美元。例如,有0.941 8的概率第三次付款會發生,因此預期付款是0.941 8s,其貼現值為0.941 8se-0.05×3=0.810 6s。表K-2顯示,預期付款的貼現總值為4.072 8s。
表K-3顯示了CDS預期收益的貼現值的計算過程,其中假設的面值也為1美元。如同前面提到過的,我們假設違約總是發生在年中。例如,有0.019 0的概率CDS在第三年的年中會產生回報。考慮到40%的回收率,這時的預期收益為0.019 0×0.6×1=0.011 4。收益的貼現值為0.011 4e-0.05×2.5=0.010 1。表K-3所示的所有預期收益的貼現值為0.050 6美元。
在最後一步中,我們計算違約發生時的應計付款,如表K-4所示。會產生應計付款是因為CDS利差s是延後支付的,因此當違約發生時,實際已經積累了一部分應該支付的利差。考慮第三年,有0.019 0的概率在這一年的年中會發生違約。到發生違約時,已累積了0.5s的應付款。因此,第三年年中的預期應計付款為0.019 0×0.5s=0.009 5s,其貼現值為0.009 5se-0.05×2.5=0.008 4s。表K-4顯示,所有應計付款的貼現總和為0.042 2s。
由表K-2和表K-4,預期付款的貼現總額為
4.072 8s+0.042 2s=4.115 0s
由表K-3,預期收益的貼現總額為0.050 6。二者應該相等,因此
4.115 0s=0.050 6
由此得出CDS利差s=0.012 3,即CDS的市場中間價應為面值的0.012 3倍,或者每年123個基點(考慮40%的回收率和每年2%的風險率,由式(19-3)給出的關係,我們也可大致估算出這一利差為0.02×0.6=0.012)。
設計這個例子的目的是說明CDS價值的計算方法。在實際中,我們常常會發現需要的計算量比表K-2~表K-4中的大得多,這是因為:第一,CDS付款的支付頻率通常要比每年1次大得多;第二,我們假設違約發生的頻率會比每年1次要高。
對CDS進行盯市計價
在合約談判結束時,CDS的價值和其他大多數衍生產品一樣,幾乎為0。一段時間過後,其價值可能為正或為負。假設我們例子中的CDS合約已經存在了一段時間,合約中的CDS利差為150個基點,買方付款的貼現值為4.115 0×0.015 0=0.061 7,而預期回報為0.050 6。對CDS的賣方,其價值為0.061 7-0.050 6,即0.011 1乘以面值。類似地,合約對信用保護的買方的市場價值為-0.011 1乘以面值。
本書附帶的RMFI軟件可從作者的網頁上下載,其中有一個工作表包含了上述計算。
附錄L
合成CDO及其定價
合成債務抵押債券(CDO)由多個份額構成。在每個份額中,對於特定債券組合在一定範圍內的損失,A方對B方提供補償。相應地,B方同意向A方支付受保護的面值的一定比例,作為買入保護的費用。
假設,對某一特定份額,損失的範圍為從αL到αH。變量αL和αH分別被稱為附著點(attachment point)和分離點(detachement point)。如果αL為8%而αH為18%,則當債券組合的損失介於面值的8%~18%時,A方向B方支付損失的數量。因此,最初8%的損失部分不對該份額產生影響。該份額只承擔接下來10%的損失,而且其面值隨損失的發生而減小(最初為面值的18%-8%=10%)。當損失超過18%時,B方向A方定期支付費用,其數量等於該份額對應的剩餘面值的一定比率。這一比率被稱作份額利差(tranche spread)。
通常,我們假設債券組合中所有債券在違約時間上的分佈是相同的。定義Q(t)為某一債券到t時刻時違約的概率。第11.6節中介紹的單因子高斯Copula違約時間模型是市場上對CDO份額進行定價的標準模型。由式(11-13)
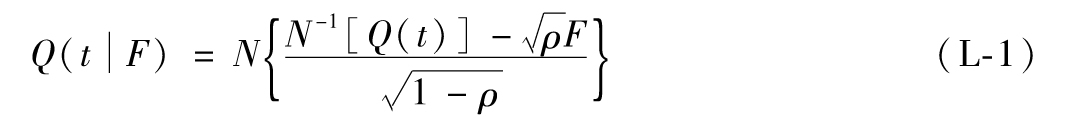
其中,Q(t|F)為基於因子F,第i個實體到t時刻時違約的條件概率。在計算Q(t|F)時,通常假設風險率為常數。當CDS利差或其他信用價差存在時,我們可以採用附錄K中的方法,結合一個搜索過程,來找出風險率。
假設風險率為λ,則
Q(t)=1-e-λt
(L-2)
根據二項分佈的性質,基於因子F,到t時刻,恰好有k個實體違約的條件概率為
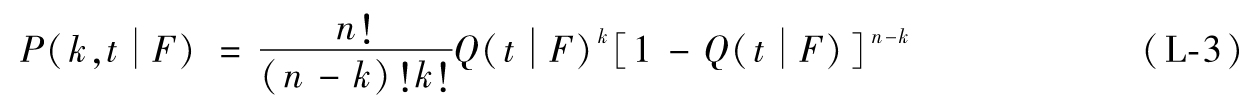
定義

其中R為回收率(假設為常數)。同時,定義m(x)為比x大的最小整數。此份額在違約數k小於m(nL)時不受損失;在k大於或等於m(nH)時,全部損失;在其他情況下,份額在t時刻的面值佔初始面值的比率為
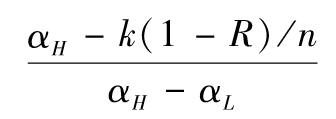
這一結果可以與式(L-1)、式(L-2)和式(L-3)結合起來,計算基於因子F的任意時刻的份額面值的條件期望。然後,我們可以對F積分,以求得份額面值的期望。這一積分通常採用高斯積分(Gaussian quadrature)法來完成(在作者的網頁上提供了在正態分佈上使用高斯積分法進行積分的軟件)。
通常,我們假設違約發生在兩次付款時間間隔的中間點上。與附錄K類似,我們需要知道以下變量:
(1)A方收到的預期付款的貼現值。
(2)A方對份額損失的預期償付的貼現值。
(3)A方收到的應計付款的貼現值。
在某特定時刻,A方收到的付款的數額與份額當時的面額呈線性關係。A方支付的份額損失賠付(假設損失發生在付款間隔的中點)等於該時間段內份額面值的變化值。A方收到的應計付款為份額損失賠付的一定比例。對任意假設的利差,上述3個數值都可由份額面值的期望值求出。然後,採用類似附錄K中求CDS利差的方法,我們可求得使預期付款等於預期份額損失賠付的利差。
由市場對CDO份額的詢價,衍生產品交易商可以計算出隱含Copula相關係數ρ,然後他們會傾向使用ρ來詢價,而不是使用份額利差本身。這和期權市場上,交易商以布萊克-斯科爾斯-默頓模型的隱含波動率,而不是以幣值本身來詢價的做法很相似。因此,CDO市場上也存在相關性微笑現象,這類似於期權市場上的波動率微笑現象。
本書附帶的RMFI軟件中,包含了一個工作表,可進行上述計算。[1]讀者可從作者的網頁上下載該軟件。
[1] 關於計算CDO價值的更多細節,請參閱J. C. Hull, Options, Futures, and Other Derivatives, 10th ed. (Upper Saddle River, NJ: Pearson, 2018)。
練習題答案
第1章
1.1 預期回報為12.5%,回報率的標準差為17.07%。
1.2 由式(1-1)及式(1-2)得出,預期回報為12.5%,回報率的標準差為
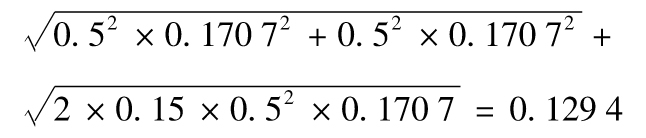
即12.94%。
1.3
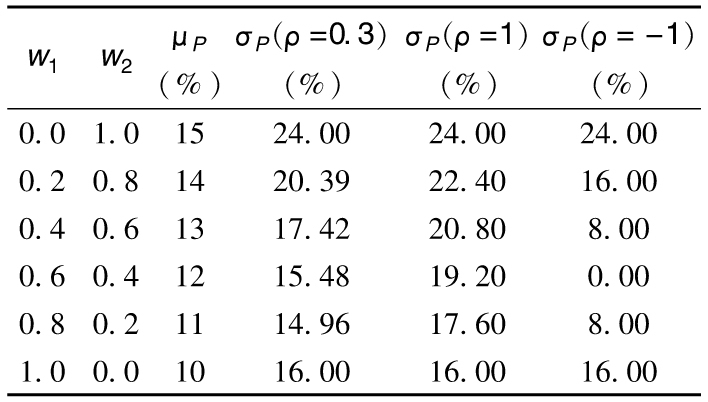
1.4 非系統性風險可以被分散,系統性風險不能被分散。系統性風險對於股票投資者更重要,兩類風險均可以導致企業的破產。
1.5 我們假定投資者在預期回報與風險之間找到平衡,對於一個指定的預期回報,投資者想儘可能使回報率的標準差達到極小,所有人對於特定投資所求得的預期回報、回報率的標準差及回報之間的相關係數的估計均相等。再有,投資者均能夠以無風險利率借入及借出資金,結果是投資者都想在圖1-4所示的“新有效邊界”之上,他們選擇同樣的有風險投資與以無風險利率為利息的借入或借出資金的組合。
1.6 (a)7.2%;(b)9%;(c)14.4%。
1.7 資本資產定價模型假定只有一個單一因子決定回報,套利定價理論假定有多個因子。
1.8 在許多國家和地區,企業債券利息可用於減稅,而股票股息則不行,公司利用債券融資可以節省稅務費用,但是隨著債券發行量的增大,破產概率也會增大。
1.9 風險分解是指將風險逐一處理的過程,而風險聚集是指將風險進行彙總並進行處理的過程。採用風險分解方法,我們需要對每一個風險都有深入瞭解,而採用風險聚集方法,我們需要了解風險間的相關性。
1.10 當潛在損失很大時,我們不能將損失進行聚集並假定損失會被分散,而是有必要將損失單獨進行處理,在處理過程中我們可以利用保險合約以及內控等措施。
1.11 這對應於盈利不小於資產的-4%的概率,該盈利水平為4.6/1.5=3.067倍的標準差,因此銀行股票為正的概率為N(3.067),其中N為標準正態分佈,其解為99.89%。
1.12 銀行有從存款人那裡取得資金的特權,而零售及製造業公司不能做到這一點。
1.13 專業服務費用(每月為1 000萬美元),銷售量下跌(人們不願意同正在重組的公司再打交道),重要高管的辭職(缺乏業務的連續性)。
1.14 alpha為0的對衝基金的回報為0.05+0.6×(0.10-0.05)=0.08,即8%。因為alpha等於4%,對衝基金回報為8%+4%=12%。
第2章
2.1 銀行系統變得更加集中化,大銀行佔有巨大市場份額,銀行數量由14 483家減至5 060家。
2.2 20世紀初,許多州紛紛設定法律禁止銀行開啟多於1家以上的分行,1927年的《麥克法登法案》禁止銀行在不同的州開設分行。
2.3 風險是當利率升高時,如果存款被延期,銀行必須支付更高利率,而收入的貸款利率不變,從而會造成銀行利差收入的降低,同時還有流動性風險。
2.4 DLC的損失超出了其股權資本金,公司可能會解體,次優先級長期債券的500萬美元投資會有損失,存款人會拿回全部資金。
2.5 銀行的淨利息收入等於利息收入減去利息支出。
2.6 信用風險主要影響貸款損失。非利息收入包括交易的盈虧,因此市場風險影響非利息收入,如果資產和負債不匹配,市場風險也會影響淨利息收入;操作風險主要會影響非利息費用。
2.7 私募是指面向少數大型金融機構新發行證券的行為。公募是指面向公眾新發行證券的行為。在非包銷交易中,投資銀行向投資者出售證券,但對證券是否可以售出並不保證;在包銷交易中,投資銀行以某個價格從發行證券的公司買入證券,並隨後在市場上以更高價格出售。
2.8 從高到低,競價排序為H、C、F、A、B、D、E和G。競標人H、C及F的競標數量均為140 000股,A的競標數量為20 000股,競標的清盤價格由A給出,即100美元,H、C和F以這一價格買入100%的競標數量的股票,A以這一價格買入一半的競拍數量的股票。
2.9 荷蘭式拍賣潛在地吸引大批競標者,如果市場上所有感興趣的人均參與競標,成交價格應與剛剛IPO之後的市場價格非常接近。因此在正常的IPO情況中,應避免出現價格遠遠低於市場價格的情形。另外,在荷蘭式拍賣中,投資銀行不能只銷售給自己最好的當前和潛在客戶。谷歌的IPO過程不同於標準荷蘭式拍賣,在其IPO過程中,谷歌對發行股票數量有發言權,並且在看到競標後,可以改變分配給競標人的股票數量。
2.10 毒丸計劃可以給管理人員提供談判的工具,即使是當公司董事會有權推翻毒丸計劃或使之失效時,這一點仍然正確。當管理人員與一個潛在的買方產生對抗時,管理人員可以採用毒丸計劃來爭取時間以得到一個更好的賣出價格,或尋找其他買方。但毒丸計劃的存在,也可能導致其他投資者望而卻步。
2.11 銀行的經紀子公司可能會推薦銀行的投行部賣出的證券,商業銀行子公司可能將一些機密信息傳給投資銀行子公司。當一家銀行與另外一家公司進行業務往來(或者想進行業務往來),銀行可能會說服經紀子公司將這家公司的股票評級為“買入”。商業銀行子公司可能會說服自己的貸款客戶來發行債券,而銀行這麼做的實際動機是因為對客戶貸款的信用產生擔心(同時,銀行可以讓自己的投行部門來說服其客戶買入這些債券,從而承擔信用風險)。以上利益衝突是通過所謂的防火牆來處理的,防火牆可以防止銀行不同部門之間的信息滲透。
2.12 交易賬戶包含那些出於交易目的而持有的項目,這些項目要進行每日的盯市計價。銀行賬戶包括那些預期持有到期滿的項目,例如對公司和個人的貸款。
2.13 根據《國際財務報告準則第9號》(IFR9)和類似美國財務會計準則委員會(FASB)的會計準則,銀行必須在其財務報表中將預計貸款損失從貸款中扣除。
2.14 在發起-分銷模式中,銀行首先發放貸款,然後將貸款打包出售給投資者。在2007年7月以前的7年間,以上經驗模式在市場上盛行。2007年7月,投資者對證券化產品失去了信心,銀行不得不放棄這種經驗模式(至少是暫時)。
第3章
3.1 定期壽險持續一定的期限(例如5年或10年),投保人支付保費,如果投保人在壽險期限內死亡,保險收益人所得賠償就等於保單的面值;終身壽險為投保人終生提供保險,投保人通常每年定期向保險公司支付保費(每年數量為恆定),在投保人死後,保險公司向受益人提供賠償。在終身壽險中,有一定的投資成分,這是因為在保險初期,保費高於預期賠償(在保險後期,保費低於預期賠償),投資所得的稅務可以被延遲到投保人的死亡時刻。
3.2 變額壽險是終身壽險的一種特殊形式,投保人可以指明在保險最初的年份裡的盈餘保費(即保費超出保險精算費用)的投資方式。在投保人死亡時的賠償有一個最低數量保證,但如果投資表現好,賠償數量會遠遠高於最低數量。萬能壽險也是終身壽險的一種形式,在這種保險中,投保人可以將保費減至不造成保險失效的某個最低水平。盈餘保費被保險公司投資(一般是固定收益產品),保險公司將擔保最低回報率,如果投資表現良好,在投保人死亡時投保受益人回報可能高於最低的回報率。
3.3 年金產品對於長壽風險有風險敞口;人壽保險對死亡風險有風險敞口。
3.4 由累計價值所產生的終身年金由以下利率的最大一個來計算:(a)市場利率;(b)實現預定的最低利率。
3.5 女性在第1年死亡的概率為0.003 182,在第2年死亡的概率為0.003 473×(1-0.003 182)=0.003 462,假定持平保費為X,我們有
1 000 000×(0.003 182+0.003 462)=X+(1-0.003 182)X
由此得出X=3 327,持平保費為3 327美元。
3.6 一個男性活到30歲的概率為0.975 19,活到90歲的概率為0.177 35。一個男性在活到30歲的條件下,活到90歲的概率為0.177 35/0.975 19=0.181 86。一個女性在活到30歲的條件下,活到90歲的概率為0.291 04/0.986 35=0.295 07。
3.7 最大的風險來源於類似於地震和颶風的災難,以及一些責任義務(例如,美國關於石棉的索賠),這是因為大數定理不再給保險公司提供任何幫助,這些事件要麼不發生,因此也沒有任何索賠,但事件一旦發生,索賠數量會巨大。
3.8 CAT債券(巨災債券)給承擔災難性風險(例如颶風及地震)的保險公司提供了一種再保險產品,通過這種產品,保險公司可將災難性風險轉嫁,CAT債券由保險公司發行,債券的券息比政府債券券息要高,當保險公司面臨災害索賠時,在實現確定的損失範圍內,CAT債券持有者必須同意放棄將來券息甚至本金。
3.9 CAT債券沒有太多的系統性風險,自然災害的發生與市場回報無關,CAT債券的風險可以由投資組合的其他風險而分解。B級債券具有系統性風險,其系統性風險不可以被分散,因此CAT債券是投資組合的一個更好的附加投資。
3.10 在加拿大和英國,醫療服務由政府來提供;在美國,公共醫療非常有限,大多數人需要從某種類型的私立保險公司買入醫療保險。在英國,私立醫療系統與公共醫療系統並存。
3.11 道德風險和逆向選擇均會產生潛在問題,保險的存在會造成投保人不再努力去保護自己的工作,確實出現過一些投保人故意地失去工作來獲得保險賠償的事件。還有,主動買入保險的投保人往往來自那些有高風險會失去工作的群體。
3.12 對財產險的賠償比對人壽保險的賠償的變動性更大,這是由於類似於地震和颶風的災難,以及一些責任義務(例如,美國關於石棉的索賠)所觸發賠償的變動性而造成。
3.13 賠付率等於1年內賠償數量與保金數量的比;費用比率等於1年內費用數量(如銷售提成和為確認損失而付出的費用)與保金數量的比。以上說法不正確,因為投資收入一般都很大,保費是在年初收入,賠償是在年中的任意時刻,甚至是在年末。
3.14 在一個養老金固定供款計劃中,僱員的供款(包括僱主為僱員的供款)均以僱員的名義存入單獨的賬戶並進行投資。當僱員退休時,累積供款和投資收益一般會轉換為年金產品。在固定收益計劃中,所有僱員的供款被統一在一起來進行投資,僱員收到的養老金數量取決於僱員為公司服務的時間以及僱員的最終工資。在任意一個時刻,固定收益計劃資金均可能會處於資金不足或資金盈餘狀態。
3.15 僱員工資按實值計算為常數,假定工資為每年X(X的單位與我們的計算無關),養老金為0.75X,實際回報為0,因為僱員工作年限為40年,所以僱員的供款的貼現值為40XR,其中R為供款佔工資的比率,僱員所得養老金福利的貼現值為20×0.75X=15X,比率R應保證養老金資金量充足,即
40XR=15X
即R=0.375。因此,僱員和僱主供款總和佔工資的比率至少應為37.5%。
第4章
4.1 開放式基金總數量在有更多的投資者買入基金時會增長,而當有更多的投資者賣出基金時會下降;封閉式基金類似於一家發行固定數量股票的公司。
4.2 共同基金的淨資產價值是在每天下午4點定出,等於基金持有資產價值除以當前共同基金的數量。
4.3 投資者在2018年和2019年分別有300美元和100美元資本收益,在2020年,投資者有200美元的資本虧損。
4.4 指數基金的設計是為了跟蹤特定的股票指數,例如標準普爾500指數。一種構造指數基金的做法是買入指數中的所有(或具有代表性的部分)股票,有時還會採用關於指數的期貨。
4.5 前端收費是投資者首次買入基金份額時支付費用,這個費用按投資數量的比例計算;後端收費是投資者在贖回基金份額時支付的費用,這個費用也是以投資數量的比例為計量。
4.6 跟蹤標準普爾500指數的交易所交易基金(ETF)的過程如下:機構投資者首先將一個用於跟蹤標準普爾500指數的股票交易組合存入基金,作為回報,該機構投資者收到ETF份額。機構投資者可以在任何時候,在ETF份額和構成ETF的股票的份額間進行轉換。與開放式基金相比,ETF的優點在於投資者可以隨時進行基金份額交易,也可以賣空基金,ETF基金管理人並不需要賣出基金資產來應對贖回的基金份額,因此不必刻意保持基金的高流動性;與封閉式基金相比,ETF的優點在於ETF份額價格與每個份額的淨資產價值十分接近。
4.7 n個數字的算術平均值等於這n個數字的和除以n,幾何平均值等於這n個數字的乘積再開n次方,算術平均值永遠大於或等於幾何平均值,將某項投資持有若干年,我們需要使用幾何平均(而不是算術平均值)來計算年回報(過程為首先計算“1加上每年回報”的幾何平均值,然後再減去1)。
4.8 延遲交易是一種違法交易行為,做法是在下午4點以後下單,並以下午4點的價格買入或賣出開放式基金份額;擇時交易是指基金經理允許一些特殊的客戶頻繁地買入或賣出基金的份額來盈利,他們之所以可以這麼做是因為在下午4點計算基金淨資產價值時,有些股票價格沒有被更新;搶先交易是某些人在大型金融機構進行可以影響市場變動的交易之前,搶先交易的行為;定向經紀涉及共同基金與經紀商之間的不當行為,其中經紀商向共同基金推薦客戶,作為回報,共同基金將業務交給該經紀商。
4.9 共同基金必須披露他們的交易策略;共同基金使用槓桿時,會有限制;共同基金不能賣空;他們也不能使用衍生產品。
4.10 如果一個對衝基金通過交易可轉換證券來盈利,則其利益所得一定是建立在其他交易對手損失的基礎上。如果大多數交易員都是對衝基金的話,不可能所有的人都盈利。
4.11 門檻回報率是指只有在業績超出這個最小回報率時,績效費才適用;高潮位標記條款是指前期損失必須在全部補齊的情況下,績效費才適用;分紅追回條款指投資者有權收回以前發出的績效費來彌補將來的損失。
4.12 如果回報率為X(>2%),投資者支付的費用為0.02+0.2(X-0.02),因此
X-0.02-0.2(X-0.02)=0.2
X=0.27,因此回報率在達到27%以上時,才能滿足條件。
4.13 如果對衝基金槓桿很高,短期的收益就變得非常重要,短期損失會引發保證金催付,這可能會摧毀對衝基金。
4.14 機構經紀人對於對衝基金所能夠持有的槓桿有決定權,這從而會影響對衝基金所能持有的風險頭寸。
第5章
5.1 當交易員進入遠期合約的多頭時,他同意在將來一定的時刻以某指定價格買入標的資產;當交易員進入遠期合約的空頭時,他同意在將來一定的時刻以某指定價格賣出標的資產。
5.2 某交易員對某資產有風險敞口,如果他採用衍生產品來減少自己的風險敞口,這時他的行為被稱為是對衝;在投機行為中,交易員最初沒有需要減小的風險敞口,他是在對今後的資產價格變化進行賭博;在套利行為中,交易員進行兩個或更多的市場交易以鎖定盈利。
5.3 在第一種情形中,交易員有義務以50美元的價格買入資產(這時他沒有其他選擇);在第二種情形中,交易員有權利以50美元的價格買入資產(他可以選擇不行使期權)。
5.4 賣給某人看漲期權等於你給了期權持有者在將來以指定價格從你這裡買入某種資產的權利,買入看跌期權給了你在將來以指定價賣給期權出售者某種資產的權利。
5.5 (a)投資者在每英鎊價值為1.290 0美元時,有義務以每英鎊1.300 0美元的價格賣出英鎊,因此收益為(1.300 0-1.290 0)×100 000=100 0美元。(b)投資者在每英鎊價值為1.320 0美元時,有義務以每英鎊1.300 0美元的價格賣出英鎊,損失為(1.320 0-1.300 0)×100 000=2 000美元。
5.6 (a)交易員賣出價格為每磅50美分,資產的實際價格每磅48.20美分,收益=(0.5-0.482)×50 000=900美元。(b)交易員賣出價格為每磅50美分,資產的實際價格為每磅51.30美分,損失為(0.513 0-0.5)×50 000=650美元。
5.7 你賣出了一個看跌期權。當期權持有者決定行使期權時,你必須以每股40美元的價格買入100股,期權持有者只有在股票價格低於40美元的時候才會行使期權,假如在期權到期時股票價格為30美元,你必須以40美元的價格買入實際價格只有30美元的股票,這時你每股損失10美元,整體損失為1 000美元;如果價格為20美元時,期權得以行使,你每股損失20美元,整體損失為2 000美元;損失的最壞情形為在3個月內股票價格幾乎為0,這種不太可能會發生的事件會使你損失4 000美元。作為對將來損失的補償,你會從期權買入方收到期權的買入費。
5.8 場外交易是由電話及計算機將金融機構、基金經理及企業資金管理人結合在一起的網絡系統。在這種網絡系統中,有需求的交易雙方能夠達成令雙方均滿意的協議。場內市場是由交易所組織的市場,在場內市場交易員可以見面或進行電話交流,市場交易的產品由交易所定義。(a)場外交易(OTC);(b)交易所交易;(c)兩者均可;(d)場外交易;(e)場外交易。
5.9 一種策略是買入200股股票,另外一種策略是買入2 000份期權,當股價上漲時,第二種策略會有更大的收益。例如,假如股票價格上漲為40美元,第二種策略的收益為2 000×(40-30)-5 800=14 200美元,而第一種收益僅為200×(40-29)=2 200美元,但是如果股票價格下跌,第二種策略所對應的損失更大,例如,如果股價跌為25美元,第一種策略的損失為200×(29-25)=800美元,第二種策略會失去所有的投資,即5 800美元。這一實例顯示了期權的槓桿效應。
5.10 你可以買入5 000份看跌期權(或者50份合約),期權執行價格為25美元,到期期限為4個月,這種合約提供某種保險,如果在4個月時,股票價格低於25美元,那麼你可以行使期權,這時你以每股25美元的價格賣出股票,這種策略的代價是需要支付買入期權的費用。
5.11 股票期權並不能給發行股票的公司帶來任何資產,這種產品是交易員之間的交易,發行股票的公司並不介入。與此相比,股票在最初發行時要賣給投資者,因此這時會給公司帶來資金。
5.12 忽略貨幣的時間價值,如果在3月時股票價格大於52.50美元,期權持有者會盈利,因為這時的期權回報超過了買入期權所付出的費用,即2.5美元,在期權到期時如果股價大於50美元,期權持有者會行使期權,注意如果股票價格介於50美元與52.50美元之間,期權會被行使,但期權持有者仍會蒙受損失。
5.13 忽略貨幣的時間價值,如果在6月股票價格大於56美元,期權的賣出方會盈利,因為這時向期權持有者支付的費用小於賣出期權所帶來的收入,在到期時如果股價小於60美元,期權會被行使,注意當股票價格介於56美元與60美元之間時,期權的賣出方即使在期權被行使時也會盈利。
5.14 一個4個月期限的看跌期權的多頭給期權持有者提供了保險,這一保險保證外匯的賣出價格不低於執行價格。
5.15 這家公司可以進入在6個月時買入100萬加元的遠期多頭,這樣做可以鎖定將來的外匯利率,並使得其等於現在觀察到的遠期外匯利率。另一種做法是公司可以買入看漲期權,這一看漲期權給公司一個在6個月後以某指定匯率買入100萬加元的權利,如果在6個月時加元強勁,這一權利就給公司提供了保險。如果在6個月時加元疲軟,則公司仍然可以從中謀利。
5.16 ICON的回報是:(a)定期債券;(b)進入一看漲期權空頭,期權面值為169 000日元,執行價格為1/169;(c)進入一看漲期權的多頭,期權面值為169 000日元,執行價格為1/84.5的三種交易組合而成。本頁下面的表格說明了這一點。
5.17 (a)交易員買入180天期限的看漲期權,並且同時進入180天期限的遠期合約的空頭。(b)交易員買入90天期限的看跌期權,並且同時進入90天期限的遠期合約的多頭。
5.18 進入5年期互換合約,在合約中支付3.30%固定利率,並且收入LIBOR利率,投資整體效應為LIBOR-0.30%。
5.19 進入5年期互換合約,在合約中收入3.26%固定利率,並且支付LIBOR利率,借入資金的淨費用為LIBOR+1.74%。
5.20 進入3年期互換合約,在合約中收入LIBOR浮動利率,並且支付3%固定利率,3年借入資金費用為每年4%。
5.21 假定天氣不好,農場主的收成比期望的要差,其他農場主也會受到類似的天氣影響,這時玉米產量整體來講比較低,因此玉米價格會相對較高。同實際產量相比,農場主的對衝可能過了頭。產量低的問題可能會因為期貨空頭而雪上加霜。這一問題強調在進行對衝時,我們一定要有一個宏觀的概念。農場主應該仔細斟酌,只考慮對衝價格的風險而同時忽略其他風險肯定不會是一個好主意。

5.22 公司蒙受損失或取得盈利的概率相等,這意味著用遠期合約來進行投機就像賭硬幣正反面一樣。但是即使這樣,航空公司利用遠期合約來對風險進行對衝,而不對價格進行投機仍然是很有意義的事情,遠期合約有減少風險的效果,在持有對衝合約的情況下,航空公司不會讓股東承擔將來油價所帶來的風險。
5.23 微軟公司選擇交易組合的期權而不是期權的交易組合,交易組合的期權一定會比期權的交易組合價格更加便宜,這是因為某種資產的價格的增長可能會被另外一種資產的價格的下降而中和,現在讓我們比較:(a)一個交易組合的期權,執行價格為20美元,交易組合由兩種資產組成,每個資產的價格均為10美元;(b)兩個期權組成的交易組合,每個期權的執行價格均為10美元,如果兩個資產的價格同時增長或同時下降,(a)和(b)的回報相同,但是如果一個資產價格下降而另一個資產價格上漲,則(a)的回報要比(b)低。亞式及一攬子期權特性均可以幫助微軟減小期權費用,這是因為盈利及虧損有相互抵消的可能。
5.24 這意味著能源價格可升可降,但長期來講,會趨向於長期平均水平,電力迴歸均值的速度最快,石油迴歸速度最慢。
5.25 當我們增大觀察資產價格的頻率時,觀察到的價格達到障礙的概率會增大,敲出期權的價格會減小。
5.26 每一天的平均溫度為華氏75°,每一天CDD為10,月累積CDD為10×31=310,看漲期權的回報為(310-250)×5 000=300 000(美元)。
5.27 一個對於2019年5月的5×8合約是為了保證在一週的5天內非高峰期(晚上11點至早上7點)提供電力,如果合約註明是天行使方式,則期權持有者可以在一週的每一個工作日以某特定價格買入電力;如果合約是月行使方式,則期權持有者只有在月初有一次機會來闡明自己是否會在整個月以某指定價格買入電力,日行使方式顯然價格更高。
5.28 需要進行兩次計算來確定初始保證金。第一次計算:500×(3.5+0.2×57-3)=5 950,第二次計算:500×(3.5+0.1×57)=4 600。初始保證金是其中的較大者,即5 950美元。這其中的一部分可以來自賣出期權提供的500×3.5=1 750美元。
5.29 股票的費用為500×50,即25 000美元。賣空這些股票時,所得資金被用作保證金的一部分。在這個例子中,全部的保證金要求是1.6×25 000,即40 000美元。因此,額外的保證金要求為15000美元。這部分保證金可以現金或滿足保證金要求的證券的形式提供。當股票價格上升到S時,標的股票的價值為500S。如果滿足以下不等式,則會產生保證金催付
40 000 < 1.3 × 500S
即S > 61.54。
5.30 經紀商會設置初始保證金和維持保證金要求。當保證金賬戶的餘額低於維持保證金水平時,經紀商的客戶就需要將保證金餘額恢復到初始保證金的水平。場內清算所在與其會員進行業務時,會將初始保證金和維持保證金要求設置在相同的水平上。客戶每日的保證金餘額必須維持在這個水平上。
第6章
6.1 按揭貸款常常被證券化,在證券化過程中,唯一保存的信息是按揭申請人的FICO分數及按揭的貸款與價值比率。發起人知道這種情況,因此他們只關心這些信息。
6.2 許多人被說服接受了他們並不能夠承擔的按揭,因此供需關係出現了一個短期的失調。
6.3 當按揭損失率為5%時,ABS的中間檔沒有損失,因此ABS CDO的任何分檔都沒有損失;當按揭損失率為12%時,ABS的中間檔損失為7/20,即35%,因此ABS CDO的權益檔和中間檔(夾層檔)的損失為100%,ABS CDO的優先檔的損失為10/75,即13.333%。
6.4 通常ABS分檔比較單薄,其損失的概率分佈和債券有很大不同。如果損失發生,ABS分檔往往會100%損失,而債券全部損失的可能性很低。
6.5 ABS是由貸款、債券、信用卡應收款項所構成投資組合所生成的分檔債券;CDO是由債券等固定收益資產所生成的一種ABS;ABS CDO是以不同ABS的特定分檔(例如,由BBB級分檔)作為資產所生成的ABS。
6.6 投資者低估了在市場受壓情況下,抵押貸款違約相關性會變得非常高,他們也沒有認識到ABS CDO的分檔其實很單薄,因此其損失狀態是要麼不損失,要麼全部損失。另外一個不幸的誤判是,投資者將某一評級的分檔等同於相同評級的債券。根據上面提到的原因,這一假設是不成立的。
6.7 代理成本是指兩方利益不完全一致的情形。交易員、貸款發放者、估價者、結構化產品的創立者和評級機構的不同動機是造成代理成本的原因。
6.8 瀑布式現金流定義了來自標的資產的利息和本金現金流如何在不同的分檔之間進行分配。在典型的合約中,利息收入被優先用於支付承諾給最高級分檔的收益。剩餘的部分(如果有剩餘的話)被用於支付次優先級分檔的收益,依此類推。本金的償還類似,也是以分檔的優先級排序。權益份額只有在其他更高級別的份額收到回報後才會產生利息和本金回報。
6.9 一般ABS CDO是由BBB級的ABS分檔來生成的,這是因為在市場上很難找到願意對ABS的BBB分檔進行投資的投資者。
6.10 Mian和Sufi說明在美國1996年按揭申請遭到拒絕的比率最高的地區也是在2000~2007年,按揭增長速度尤其快的地區。
6.11 ABS或ABS CDO的中間檔是處於分檔優先級排序中中間部分的分檔,它排在優先檔之下、權益檔之上,因此其承擔損失的順序先於優先檔而晚於權益檔。
6.12 當違約相關性增大時,ABS的優先檔風險增大,這是因為優先檔出現損失的機會增大;當違約相關性增大時,權益檔風險變小。為了理解這一點,注意在極限情形下,即完全相關時(同時假定回收率為0),所有的按揭具有相同的損失,因為所有的公司要麼同時違約,要麼沒有任何一家違約。因此,當完全相關時,按揭變得更相似,優先檔的風險更高,權益檔的風險更低。
6.13 年終獎一般僅僅反映一年的表現,交易員和銀行其他僱員常常只關心自己的年終獎(而不是自己所做決策的長期後果),因此他們的決策往往是基於短期目標。目前已有將獎金變為延遲發放並可以收回的趨勢,這有望改變這種局面。
第7章
7.1 由式(7-3),概率等於N(d2),其中

因此,概率等於N(-0.482 5)=0.315。
7.2 由式(7-4)
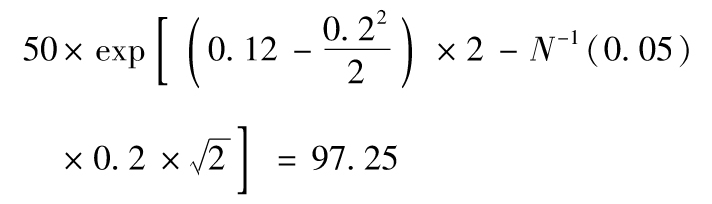
即97.25美元。
7.3 風險中性定價理論認為,當我們對衍生產品定價時,假設投資者是風險中性的(即投資者並不為承擔的風險而索要更高的預期回報),那麼得出的結果對所有的世界都適用(包括真實世界)。
7.4 在真實世界中的價值會更高。更高的價值反映了投資者對承受風險所要求的補償。
7.5 通過購買這兩種衍生產品,一方在98美元的初始投資時能獲得2美元收益。因此,無風險利率為2/98=2.04%(年複利)。違約的風險中性概率為100π/(1+0.020 4)=3,即π=3.061 2%。
7.6 回報的風險中性概率由式(7-3)給出,其中V=30,S0=25,σ=0.3,μ=0.03,以及T=0.25。因此
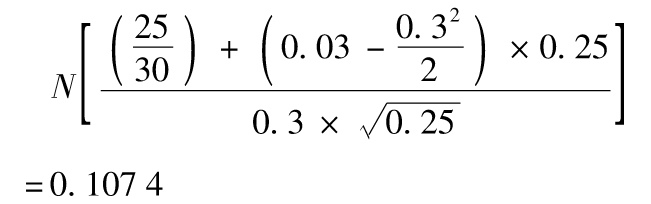
所以,期權的價值為100×0.107 4×e-0.03×0.25=10.66美元。對真實世界中回報的概率,我們設公式中的μ=0.1而不是0.03,得出的值為0.130 5。
7.7 真實世界被用來模擬標的變量一年內可能出現的值。然後使用風險中性世界來計算每一次模擬試驗中,組合在一年後的價值。
7.8 均值迴歸這一術語用來描述一個變量的值,例如利率和商品價格,有趨於一箇中心值的趨勢這樣一種現象。當然,在迴歸均值的過程中會有隨機不確定性。
7.9 哥薩諾夫定理告訴我們,當我們從真實世界變換到風險中性世界時(反之亦然),市場變量的預期變化率會改變,但是波動率保持不變。
第8章
8.1 交易組合價值減少10 500美元。
8.2 交易組合價值增長400美元。
8.3 兩種情形下的增長量均為0.5×30×22=60(美元)。
8.4 delta等於0.7意味著在股票價格上漲一個小的數量的同時,期權價格的上漲大約是股價上漲的70%,同時當股票價格下跌一個小的數量的同時,期權價格的下跌大約是股價下跌量的70%,1 000份期權的空頭的delta等於-700,我們可以通過買入700份股票的形式使交易組合達到delta中性。
8.5 一天的theta等於-100意味著在股價及波動率均沒有變化的情況下,期權價格每天減少100美元,如果一個交易員感覺股價及隱含波動率都不會變化,他就可以賣出期權,這時期權的theta越高越好(在絕對值意義下),相對來講,短期限的平值期權具有最高的theta值。
8.6 期權的gamma是期權的delta同資產價格變化的比率,例如gamma等於0.1意味著當資產價格上漲一定數量時,delta增長的數量是資產價格上漲數量的10%,如果一個期權承約人的gamma絕對值較大,gamma本身為負,並且delta等於0,這時期權承約人會在市場變動較大(或者上漲或者下跌)的情況下有很大的損失。
8.7 為了對衝期權風險,我們有必要構造相反方向的合成期權交易。例如,為了對衝看跌期權多頭,我們應該構造合成看跌期權的空頭,構造人工期權交易的過程也就是對衝期權風險的反過程。
8.8 看漲及看跌期權的多頭都具備正的gamma,由圖8-9我們可以得出,當gamma為正時,對衝者在股票價格變化較大時會有收益,而在股票價格變化較小時會有損失,因此對衝者在(b)情形下收益更好,當交易組合包含期權的空頭時,對衝者在(a)情形下收益會更好。
8.9 delta的數值說明,當歐元匯率增長0.01時,銀行頭寸價格會增長0.01×30 000=300美元;gamma的數值說明,當歐元價格增長0.01美元時,交易組合的delta會下降0.01×80 000=800,為了做到delta中性,我們應賣出30 000歐元。當匯率增長到0.93時,我們期望交易組合的delta下降(0.93-0.90)×80 000=2 400,變為27 600,為了維持delta中性,銀行應該對歐元空頭進行2 400歐元的平倉,這樣可以保證歐元淨空頭量為27 600。如果一個交易組合的delta為中性,同時gamma為負,當資產價格有一個較大變動時會引發損失。因此我們的結論是銀行可能會蒙受損失。
8.10 當採用書中所描述的方式時,我們需要假設波動率為常數。從理論上講,我們可以實施一個靜態期權複製機制,在這一機制下有三個維度:時間、股票價格以及波動率。我們要在這個三維空間中的曲面上進行價格匹配。
8.11 大約需要10個普通期權。對應於邊界上任意一點我們都會有一個方程,總共有10個方程。
8.12 隨著時間的推移,亞式期權的回報會越來越確定,因此在接近到期日時,我們需要對衝的不確定性會越來越小。
8.13 考慮與某單一資產有關的期權組合,無論交易組合的大小我們只需要進行一個交易就可以使得組合變得delta中性。
8.14 期權的價格、delta、gamma、vega、theta及rho分別是0.021 7、-0.396、5.415、0.002 03、-0.000 062 5及-0.001 19,當匯率變化0.001時,delta預測價格下降的數量為0.000 39,這正是我們求得的數值;當匯率增長到0.751時,期權價格下降0.021 3。
第9章
9.1 這時利率不匹配為100億美元,在今後3年,銀行的淨利息收入會每年下降1億美元。
9.2 如果長期利率僅僅反映了將來預期短期利率,我們會看到長期利率小於短期利率的情形與長期利率大於短期利率的情形一樣頻繁(這是基於投資者在一半情況下認為利率會上漲,而在另一半情況下認為利率會下跌的假設)。流動性偏好理論認為長期利率高於將來預期短期利率,這意味著長期利率在多數時間會高於短期利率,當長期利率低於短期利率時,市場會產生利率將急速下滑的預期。
9.3 有兩個原因:①銀行所需的為支持自己所持有的國債的資本金數量要比其他類似的低風險投資產品所需要的資本金數量低;②美國對於國債的稅務處理比其他固定收益產品有利,這是因為持有國債產品無須繳納州稅。
9.4 在隔夜指數互換中,交易的一方支付美聯儲基準利率在某個時間段內(如3個月)的幾何平均值,而收入某一事先確定的固定利率。
9.5 LIBOR-OIS利差可以衡量銀行間相互拆借意願的大小。
9.6 久期信息描述了收益率曲線小的平行移動對於債券價格的影響。交易組合價格減小的百分比等於組合久期乘以利率的小的平行移動的數量。其侷限性是這一方法只適用於利率的小的平行移動。
9.7 (a)債券價格為86.80美元;(b)債券久期為4.256年;(c)久期公式估計當收益率減小0.2%時,債券價格上漲0.74美元;(d)對應10.8%收益率的債券價格為87.54美元,這與(a)及(c)大體一致。
9.8 (a)債券價格為88.91美元;(b)債券修正久期為3.843年;(c)久期公式估計當收益率下降0.2%時,債券價格上漲0.68美元;(d)債券價格對應10.8%收益率(以年複利)的價格為89.60美元,這與(a)及(c)大體一致。
9.9 債券價格為104.80美元,債券久期為5.35年,凸性為30.60,收益率增長1%對於價格的影響可由式(9-4)估算,其對應數值
104.80×(-0.01×5.35+0.5×30.60×0.000 1)=-5.44
變化後的債券價格為99.36美元,這與我們的估算一致。
9.10 我們可以:(a)擾動收益曲線上的每一點(見圖9-5);(b)擾動曲線上的一段(見圖9-7);(c)擾動構造收益曲線產品的報價。
9.11 delta(當因子載荷以基點數衡量時,因子單位造成的投資組合價值變化)分別為-5.64及225.63。
9.12 對於組合的影響(佔組合價值的比例)為
-(2.0×0.001+1.6×0.000 8+0.9×0.000 7+1.6×0.000 6+2.0×0.000 5-2.1×0.000 3-3.0×0.000 1)=-0.002 34
即投資組合減少0.234%。
9.13 絕對額久期等於組合的久期乘以其價格。絕對額凸性等於組合的凸性乘以其價格。
9.14 局部久期的和等於整體久期。DV01等於整體久期乘以組合價值,再乘以0.000 1。
第10章
10.1 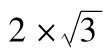 ,即3.46%。
,即3.46%。
10.2 每天百分比變化的標準差為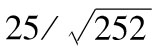 ,即1.57%,在95%置信度下所對應的置信區間為-3.09%~3.09%。
,即1.57%,在95%置信度下所對應的置信區間為-3.09%~3.09%。
10.3 開市時的波動率比閉市時要大很多,交易員在計算波動率時往往採用交易天數而不是日曆天數。
10.4 隱含波動率是使得由布萊克-斯科爾斯-默頓模型所計算出的期權價格等於市價時所對應的波動率,隱含波動率的求解方法通常是採用試錯法的方式。因為不同期權對應於不同的隱含波動率,所以交易員實際上使用了與布萊克-斯科爾斯-默頓模型不同的假設(見第25章有關討論)。
10.5 計算標準差的一般公式所給出的結果為每天0.547%,由式(10-4)的簡單方法得出的結果為每天0.530%。
10.6 由冪律得出0.01=K×500-2,因此K=2 500,(a)2 500×1 000-2=0.002 5或0.25%,(b)2 500×2 000-2=0.062 5%。
10.7 在第n-1天結束時所估計的第n天的方差等於λ乘以在第n-2天所估計的第n-1天的方差加上1-λ乘以第n-1天的回報的平方。
10.8 GARCH(1,1)對EWMA模型進行了改進,對於長期平均方差設定了一定權重。EWMA不具備迴歸均值的特性,而GARCH(1,1)具備方差迴歸均值的特性。
10.9 在這種情形下σn-1=0.015,un-1=0.5/30=0.016 67,由式(10-8)我們可得出
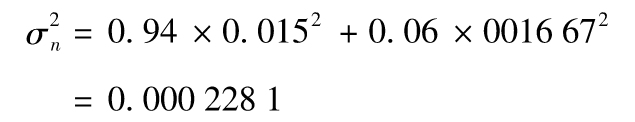
因此在第n天,波動率的估計值為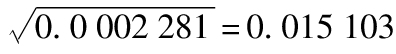 ,即1.510 3%。
,即1.510 3%。
10.10 將λ由0.95減至0.85意味著對於近期的觀察值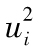 設定更大的權重,而對於更早的數據設定較小的權重。採用λ=0.85所計算出的波動率對最新信息的反映較快,也會比採用λ=0.95時所計算的波動率變動更大。
設定更大的權重,而對於更早的數據設定較小的權重。採用λ=0.85所計算出的波動率對最新信息的反映較快,也會比採用λ=0.95時所計算的波動率變動更大。
10.11 採用通常的符號,un-1=20/104 0=0.019 23,因此
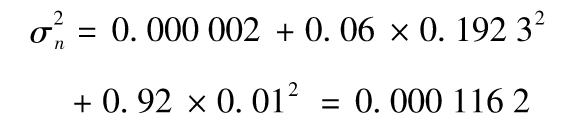
σn=0.010 78,對於最新波動率的估計為每天1.078%。
10.12 價格變化的比率為-0.005/1.500 0=-0.003 333,當前每天的方差估計為0.0062=0.000 036,對於每天方差的新估計為
0.9×0.000 036+0.1×0.003 3332=0.000 033 511
波動率的新的估計值為以上數值的平方根,即0.579%。
10.13 長期平均方差所對應的權重為1-α-β,長期平均方差率為ω/(1-α-β),增大ω會促使長期平均方差的增長。增大α會增大為近期數據所設定的權重,同時減小對長期平均方差所設定的權重,以及增大長期平均方差率。增大β會增大對於前一個方差所設定的權重,減小對於長期平均方差所設定的權重,並且增大長期平均方差的水平。
10.14 長期平均方差率為ω/(1-α-β),即0.000 004/0.03=0.000 133 3,長期平均波動率為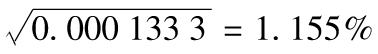 ,描述方差迴歸長期平均的方程式為
,描述方差迴歸長期平均的方程式為
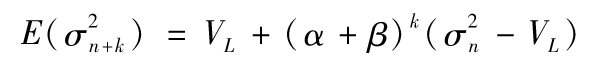
這時
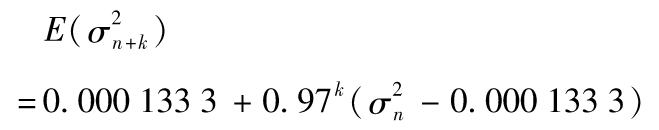
如果當前波動率為每年20%,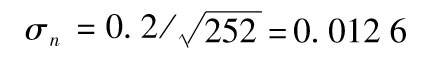 ,在20天后預期方差為
,在20天后預期方差為
0.000 133 3+0.9720(0.012 62-0.000 133 3)=0.000 147 1
因此20天后預期波動率為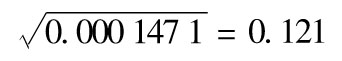 ,即每天1.21%。
,即每天1.21%。
10.15 FTSE用美元表達為XY,X為以英鎊表達的價值,Y為匯率(1英鎊所對應的美元的數量),定義xi為X在第i天的價格百分比變化,yi為Y在第i天的百分比變化,XY的比例變化大約為xi+yi,xi標準差為0.018,yi的標準差為0.009,X及Y變化的相關係數為0.4,因此,xi+yi的方差為
0.0182+0.0092+2×0.018×0.009×0.4=0.000 534 6
因此xi+yi的波動率為0.023 1,即2.31%,這就是以美元為計量的FTSE的波動率。注意,這一波動率比以英鎊為計量的FTSE的波動率更大。這是由於正相關性的影響,當FTSE增長時,英鎊與美元匯率也往往會增長,以美元為計量的FTSE會進一步增加。類似地,我們也可以討論FTSE下降的情形。
10.16 這時VL=0.000 000 3/0.02=0.000 15,式(10-14)給出了30天后的方差期望值為
0.000 15+0.9830×(0.012-0.000 15)=0.000 123
波動率為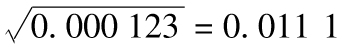 ,即每天1.11%。
,即每天1.11%。
10.17 這時VL=0.000 002/0.02=0.000 1,在式(10-15)中,VL=0.000 1,a=0.020 2,T=20及V(0)=0.000 169,因此波動率為19.88%。
第11章
11.1 你需要兩個變量的標準差。
11.2 不嚴格地講,相關係數是衡量兩個變量的線性關聯性的指標。它並不能反映關聯性。當y=x2時,x及y有一個完美的關聯性(即完全相關),但是E(xy)=E(x3)。當x服從正態分佈(或服從以0點為中心的對稱分佈)時,E(x3)和E(x)均為0,因此x和y的相關係數也為0。
11.3 在因子模型中,兩個變量的相關性完全取決於它們與其他變量的相關性,這些變量被稱為因子,因子模型減少了對大量變量進行相關性分析時所需的計算量。
11.4 一個半正定矩陣對所有的向量w均滿足式(11-4)。如果一個相關矩陣不是半正定的,那麼內部相關性一定不一致。
11.5 (a)由波動率及相關性所計算出的協方差為0.25×0.016×0.025=0.000 1;(b)假如在交易結束時,資產收盤價為20.5美元及40.5美元,資產價格百分比變化分別為0.5/20=0.025及0.5/40=0.012 5,新的協方差估計為
0.95×0.000 1+0.05×0.025×0.012 5=0.000 110 6
資產A的新的方差估計為
0.95×0.0162+0.05×0.0252=0.000 274 45
因此新的波動率為0.016 6。資產B的新的方差估計為
0.95×0.025+0.05×0.012 52=0.00 060 156 2
因此新的波動率為0.024 5,新的相關性估計為

11.6 X和Y的最新回報分別為1/30=0.033 33及1/50=0.02。協方差先前的值為0.01×0.012×0.50=0.000 06,新的估計為
0.000 001+0.04×0.033 33×0.02+0.94×0.000 06=0.000 008 41
X的新的方差估計為
0.000 003+0.04×0.033 3332+0.94×0.012=0.000 141 4
X的新的波動率估計為 ,即1.189%;Y的新的方差估計為
,即1.189%;Y的新的方差估計為
0.000 003+0.04×0.022+0.94×0.0122=0.000 154 4
Y的新的波動率估計為 ,即1.242%;對於資產相關性的估計為
,即1.242%;對於資產相關性的估計為
0.000 084 1/(0.011 89×0.012 42)=0.569
11.7 沿用練習題10.15中的符號,定義zi為標準普爾500指數在第i天的百分比變化,xi與zi之間的協方差為0.7×0.018×0.016=0.000 201 6,yi與zi之間的協方差為0.3×0.009×0.016=0.000 043 2,xi+yi與zi之間的協方差等於xi與zi之間的協方差加上yi與zi之間的協方差,即
0.000 201 6+0.000 043 2=0.000 244 8
由練習題10.15,xi+yi的波動率為2.31%。xi+yi與zi之間的相關係數為
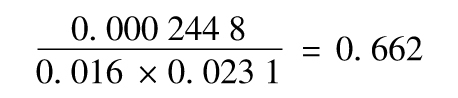
注意,標準普爾500指數的波動率在計算中沒有出現。
11.8
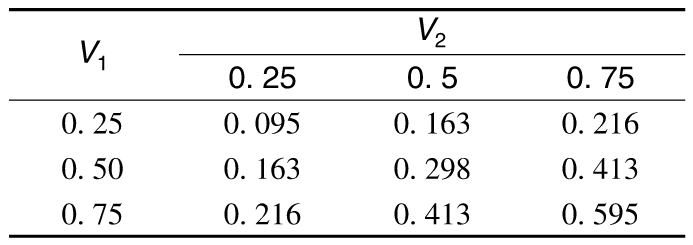
11.9 公式為
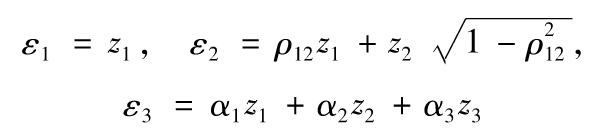
其中

這意味著
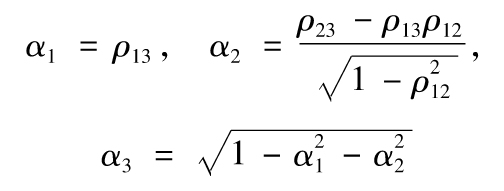
11.10 尾部相關是描述兩個或更多變量同時產生極值的趨勢,Copula的不同選擇會影響尾部相關性,例如學生t-Copula函數給出的尾部相關性比高斯Copula函數要大。
11.11 由二元學生t-分佈得出的抽樣被顯示在圖11-5中,將抽樣以分位數對分位數的形式映射到正態分佈。
11.12 V1<0.1的概率為0.05,在V1<0.1的條件下,V2<0.1的條件概率為0.006/0.05=0.12;在V1<0.1的條件下,V2<0.2的條件概率為0.017/0.05=0.34,等等。
11.13 當V1=0.2時,我們有U1=-0.84,由二元正態分佈的性質得出U2的中值為-0.5×0.841 6=-0.420 8。因此,條件中位數的百分位數為N(-0.420 8)=0.336 9,轉換為x的V2的中值,其中2x2=0.336 9,則對應的V2的中值為0.410 5。
11.14 這時
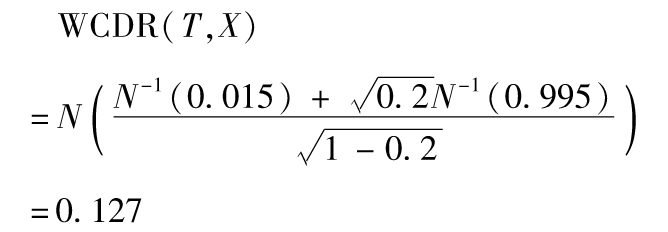
“99.5%最壞情形”的損失絕不會超過12.7%。
11.15 最大似然估計法估算的違約概率和Copula相關係數分別為3.92%和11.18%。
第12章
12.1 VaR是指在一定的置信水平下損失不能超過的數量;ES是在損失超過VaR的條件下損失的期望值。ES永遠滿足次可加性(風險分散總會帶來收益)條件。
12.2 譜函數型風險測度在測算風險時對損失分佈的分位數設定一定的權重,滿足次可加性條件的測度對於第q個分位數設定的權重一定是q的非遞減函數。
12.3 有5%的機會你會在今後一個月損失6000美元或更多。
12.4 在一個“糟糕的月份”,你的預期損失為6000美元。糟糕的月份的定義是,該月的回報小於月回報分佈的5%分位數。
12.5 (a)100萬美元;(b)ES為0.9×10+0.1×1=9.10(百萬美元);(c)有0.0092=0.000 081的概率會損失2 000萬美元,2×0.009×0.991=0.017 838的概率會損失1 100萬美元,有0.9912=0.982 081的概率會損失200萬美元。置信度為99%時的VaR為1 100萬美元;(d)ES為(0.000 081×20+0.009 919×11)/0.01=1 107(萬美元);(e)因為1+1<11,所以VaR不滿足次可加性條件。但是9.2+9.2>11.07,所以ES滿足該條件。
12.6 (a)2×1.96=3.92(百萬美元);(b)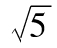 ×2×1.96=8.77(百萬美元);(c)
×2×1.96=8.77(百萬美元);(c) ×2.33=10.40(百萬美元)。
×2.33=10.40(百萬美元)。
12.7 (b)變為996萬美元;(c)變為1 182萬美元。
12.8 邊際VaR是VaR隨第i個資產增加而增長的比率;增量VaR是指第i個資產對於VaR的影響(含有第i個資產VaR與不含有第i個資產VaR的差);成分VaR是指整體VaR對於第i個資產的分配(成分VaR的總和等於整體VaR)。
12.9 總數為17或更多例外發生所對應的概率為
1-BINOMDIST(16,1000,0.01,TRUE)
即2.64%。在5%置信水平下我們應該拒絕這一模型。
12.10 聚束效應是指例外情形會以聚集的形式發生,而不是隨機地分佈在整體時間區間內。
12.11 我們希望計算ΔP1+ΔP2+…+ΔPT的標準差。其數量為

其中σi為ΔPi的標準差,ρij為ΔPi與ΔPj的相關係數。這時對於所有的i,σi=σ,以及當i>j時ρij=ρi-j。進一步進行運算,我們可以得出式(12-5)。
12.12 3個月標準差為 。N-1(0.98)=2.054。3個月展望期、置信度為98%的VaR為3.464×2.054=7.11(百萬美元),相同展望期和置信度下的ES為3.464×
。N-1(0.98)=2.054。3個月展望期、置信度為98%的VaR為3.464×2.054=7.11(百萬美元),相同展望期和置信度下的ES為3.464×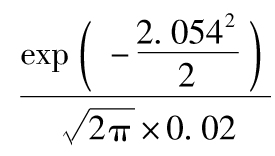 =8.39(百萬美元)。
=8.39(百萬美元)。
第13章
13.1 這裡的假設為:決定明天市場變化的統計過程與決定過去500天市場變化的統計過程相同。
13.2

因此當λ趨近於1時,權重趨向於1/n。
13.3 估算的VaR的標準誤差為
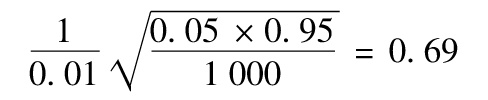
即69萬美元。
13.4 (a)1天展望期、95%置信度的VaR對應於第25大損失的情景,即156511美元;(b)1天展望期、95%置信度的ES為最大的24個損失的平均值,為209310美元;(c)1天展望期、97%置信度的VaR對應於損失中第15大損失的情景,即172 224美元;(d)1天展望期、97%置信度的ES為最大的14個損失的平均值,即240 874美元。
13.5 在表單(名為“Scenarios”)中,交易組合頭寸改變是將單元格L2∶O2中的數據改為2 500,將損失由大到小排序,1天展望期、99%置信度的VaR對應於第5個最大損失,即238 526美元。最大的4個損失的平均值為372 872美元。這是一天99%的ES。
13.6 在表單4(“Scenario with Weights”)中,將單元格F2中的變量λ由0.995變為0.99,將損失由大到小進行排序,最大損失477 841美元(情景494)所對應的累計權重為0.009 48。第二大損失345 435美元(情景339)所對應的累計權重為0.011 47。1天展望期、99%置信度的VaR對應於第二大損失,即345 435美元。一天的ES等於0.948×477 841+0.052×345 435=470 917美元。
13.7 將表單9(“Loss Adjusted for Loss SD”)中單元格K1中的變量λ由0.94變為0.96,將損失由大到小進行排序,第5大損失為541337美元,該量即為1天展望期、99%置信度的VaR。前4大損失的均值為707 146美元。此為1天展望期、99%置信度的ES。
13.8 即為
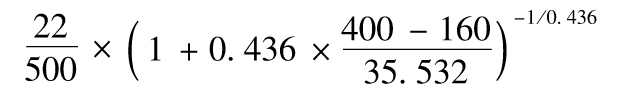
即0.001 623。
13.9 VaR(以千計)等於
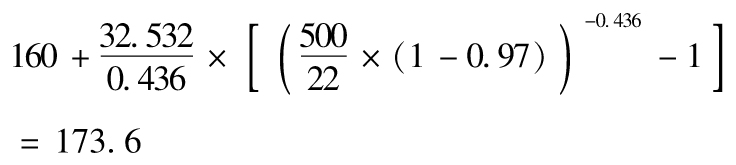
即173 600美元。
13.10 由最大似然估計得出的ξ及β分別為0.353及34.05,1天展望期、99%置信度的VaR為230 725美元,1天展望期、99.9%置信度的VaR為452 831美元。1天展望期、99%置信度的ES為327 336美元,1天展望期、99.9%置信度的ES為670 499美元。
13.11 從波動率更新過程中所得出的損失排序後必須傳到表單11(“Extreme Val Theory”)中。當u=400時,nu=17時,由最大似然估計得出的ξ及β分別為0.438及82.838,1天展望期、99%置信度的VaR為534 100美元。1天展望期、99.9%置信度的VaR為1 096 661美元。1天展望期、99%置信度的ES為785 819美元。1天展望期、99.9%置信度的ES為1 786 335美元。損失大於600 000美元的概率為

第14章
14.1 每一項資產投資的標準差為1 000美元,交易組合每天價格變化的方差為
1 0002+1 0002+2×0.3×1 000×1 000=2 600 000
交易組合的標準差為以上數量的平方根,即1 612.45美元,因此5天展望期、97%置信度的VaR等於
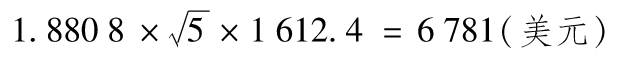
5天展望期、97%置信度的ES為
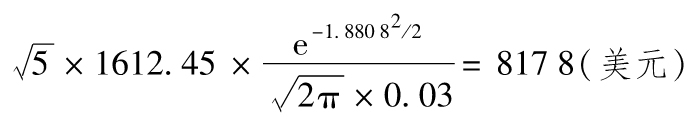
14.2 如本章介紹的,以模型構建法計算VaR時,對利率的三種不同處理方法為:(a)應用久期模型;(b)利用資金流映射的方法;(c)利用主成分分析法。
14.3 10年期頂點的敏感度為30 000美元,因為該比率每增加一個點,12年期頂點的敏感度就會增加0.6個基點。類似地,15年期頂點的敏感度為20 000美元。其他點則沒有敏感度。
14.4 ΔP=3.9Δx,ΔP的標準差為3.9×0.007=0.027。因此交易組合10天展望期、99%置信度的VaR等於0.027×2.326× =0.20。
=0.20。
14.5 關係式為ΔP=3.9Δx+0.5×4.3×Δx2,即ΔP=3.9Δx+2.15Δx2。
14.6 一天內投資組合價值變動的方差為(以千美元計)為
(10×7)2+(8×8)2+2×10×7×8×8×0.8=16 164
由於N-1(0.98)=2.054,ES為

即688 200美元。
14.7 投資組合的風險度量(VaR或ES)等於投資組合的標準差乘以β,風險因子的風險權重是風險因子的標準差乘以β。投資組合的風險敏感度是投資組合因風險因子的1%或1個基點變化而變化的金額。
14.8 交易組合的每天的方差為
62×202+42×82=15 424
每天標準差為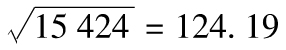 美元,因為N-1(0.9)=1.282,5天展望期、90%置信度的VaR為
美元,因為N-1(0.9)=1.282,5天展望期、90%置信度的VaR為
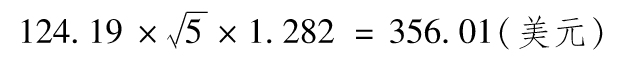
14.9 (a)2.0;(b)43.9。
14.10 期權delta為期權價值變化同標的資產的變化比率。當標的資產上漲一個小數量時,期權價值的下降為標的資產變化的30倍。期權的gamma為期權delta變化同標的資產價格變化的比率,當資產價格增長一個小的數量時,期權的delta的下降為標的資產價格下降數量的5倍。delta和gamma同比例的變化分別為:-30×20=-600和-5×20×20=-2 000。
這時E(ΔP)=-0.10,E(ΔP2)=36.03,E(ΔP3)=-32.415。這意味著交易組合在一天內的變化為-0.1,標準差在一天內的變化為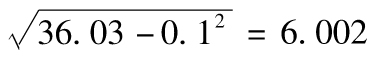 ,偏態為
,偏態為
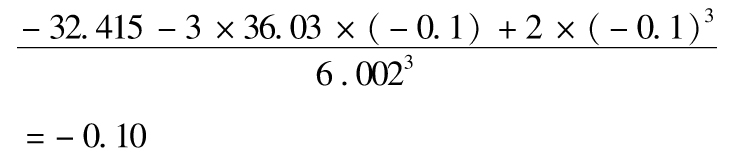
採用前兩階矩,我們得出1天展望期、99%置信度的VaR為14.08美元,當採用三階矩並利用柯尼斯-費希爾展開時,我們求得的VaR為14.53美元。
14.11 定義σ為每年的波動率(百分比),ΔS代表σ的一天變化量,Δσ為σ的一天內波動率的變化量,我們將σ計為1%的倍數,因此當前σ的價值為 。delta-gamma-vega模型為
。delta-gamma-vega模型為
ΔP=-30ΔS-0.5×5(ΔS)2-2Δσ
或
ΔP=-30×20Δx-0.5×5×202(Δx)2-2Δσ
其中Δx=ΔS/S。以上公式可簡化為
ΔP=-600Δx-1 000(Δx)2-2Δσ
交易組合的變化與兩個市場變量有關。
14.12 期權的價值變化與標的資產的價值變化的關係並不是線性的。當標的變量為正態分佈時,期權價格分佈並不是正態的。線性模型假定期權價格服從正態分佈,因此這一模型僅僅是一種近似模型。
14.13 這一合約由一個英鎊債券的多頭與一個美元債券的空頭結合而成。英鎊債券的價格為1.53e-0.05×0.5,即1.492(百萬美元),美元債券價格為1.5e-0.05×0.5,即1.463(百萬美元),合約價值每天變化的方差為
1.4922×0.000 62+1.4632×0.000 52-2×0.8×1.492×0.000 6×1.463×0.000 5=0.000 000 288
相應的標準差為0.000 537(百萬美元),10天展望期、99%置信度的VaR等於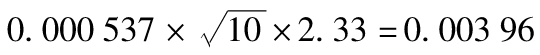 (百萬美元),即3 960美元。
(百萬美元),即3 960美元。
14.14 alpha應變為2 500。當波動率和相關性是由等權重模型估計時,1天展望期、99%置信度的VaR為226 836美元,ES為259 878美元;當採用λ=0.94的EWMA模型時,1天展望期、99%置信度的VaR為487 737美元,ES為558 783美元。
14.15 1天展望期、99%置信度的VaR由471 025美元變為389 290美元,ES由539 637美元變為445 996美元。
14.16 一種方法是假設第一項結構的頂點和第二項結構的頂點之間的相關性相對於所有頂點都是相同的。另一種方法是分別計算各期限結構變化對投資組合的影響,並利用相關性將兩種影響疊加。
第15章
15.1 競爭者的出局可能會對公司(非銀行)有一定好處,但是銀行之間有許多交易。當一家銀行破產時,其他銀行會因與這家破產銀行進行的交易而蒙受損失。另外銀行破產會使公眾對銀行系統失去信心,這也會給銀行系統帶來不利影響。
15.2 不論金融機構承擔什麼樣的風險,存款保險會使存款人的利益得到保護。這會促使金融機構承擔更大的風險,因為這時它們並不會為失去存款客戶而擔心。因此,這樣的措施可能會造成更多的銀行破產,從而使存款保險系統的賠款量加大。監管部門要求銀行必須持有與自己風險相匹配的資本金以避免破產的發生。
15.3 互換中的信用風險是指互換價格對銀行為正價值時,對手違約的風險。
15.4 貨幣互換價值偏離0的趨勢要大於利率互換價值偏離0的趨勢,這一現象是由於貨幣互換中最終本金的交換,因此貨幣互換中因對手違約所造成的潛在損失會更高。
15.5 的確存在某種風險敞口。儘管對手現在違約,不會引發任何損失,但是利率可能會有所變化,因此在將來某時刻,這一互換對於金融機構可能具有正的價值,那時交易對手違約會給金融機構帶來損失。在《巴塞爾協議Ⅰ》的要求下,由表15-2得出的資本金數量為互換面值的0.5%。
15.6 三個交易的風險加權資產分別為:(a)187.5萬美元;(b)200萬美元;(c)300萬美元,整體為687.5萬美元,資本金為0.08×6.875=55萬美元。
15.7 NRR為2.5/4.5=0.556,等價信用量為2.5+(0.4+0.6×0.556)×9.25=928萬美元。風險加權資產為464萬美元,資本金需求為37.1萬美元。
15.8 這時淨額結算不會提供任何價值。
15.9 這可將估算的資本金轉換為風險加權資產,資本金數額為風險加權資產的8%。
15.10 交易賬戶中的資產主要包括市場上交易活躍的並且每天盯市計價的產品。銀行賬戶上的產品主要包括貸款,這些產品並不是每天都要盯市計價。變化的效應是將客戶的貸款由銀行賬戶轉移到交易賬戶,這會減少資本金要求(但是第16章將要討論的《巴塞爾協議Ⅱ.5)中的增量風險資本計提會將資本金要求提升回原有的水平)。
15.11 在《巴塞爾協議Ⅰ》中,企業貸款的資本金要求與企業的信用評級無關,這造成了銀行在給高信用客戶貸款業務的資本金回報相對較低的現象。在《巴塞爾協議Ⅱ》中,資本金的要求與借貸人的信用狀況有緊密關係,因此給高信用客戶貸款又可能成為一個吸引人的業務。
15.12 監管資本金套利會涉及進行一些完全是為了以減少監管資本金為目的的交易,這些交易通常不會對承擔的實際風險產生影響。
15.13 EAD為違約時對風險敞口的估計;LGD為違約損失率的估計,其定義為違約損失與整體風險敞口的比率;WCDR為每千年出現一次的不良年度的違約概率;PD為一般年度的違約概率;MA為期限調節量,其設定是為了考慮產品期限長於一年時,產品在一年內違約或降級可能會引發的損失。
15.14 在簡單法中,對有擔保品掩護的風險敞口部分,交易對手的權重會被擔保品的權重所替代。在綜合法中,敞口大小會被調整,調整時要考慮敞口增大的可能性和擔保品價值減小的可能性。交易對手的風險權重被應用於經調整後的風險敞口與經調整的擔保品的差額。
15.15 標準法採用外部信用評級來確定資本金的數額(但比《巴塞爾協議Ⅰ》更為複雜)。在IRB法中,我們需要採用《巴塞爾協議Ⅱ》的相關性模型來計算資本金,PD參數由銀行提供。在高級IRB法中,我們採用《巴塞爾協議Ⅱ》的相關性模型來計算資本金,其中PD、LGD、EAD及MA均由銀行自己提供。
15.16 在基本指標法中,整體資本金為平均年毛收入的15%。在標準法中,對於不同的業務類別要分別計算毛收入,不同業務類別採用不同的比例從毛收入數量中計算相應的資本金。在高級計量法中,銀行採用內部模型來計算1年展望期、99.9%置信度的VaR。
15.17 ρ=0.121 6,WCDR=0.091 4,資本金(以百萬美元計)為200×0.7×(0.091 4-0.01),即1 139萬美元,這其中至少有一半必須是第一類資本。
15.18 發生5次或更多例外的概率為
1-BINOMDIST(4,250,0.01,TRUE)
即10.8%。我們可以認為監管機構是利用10%置信水平(而不是通常的5%)來選擇是否拒絕模型。
第16章
16.1 《巴塞爾協議Ⅱ.5》的3個主要組成部分是:壓力VaR的計算、增量風險資本計提和對依賴信用相關性的產品的全面風險計量。
16.2 《巴塞爾協議Ⅲ》的6個主要組成部分是:資本金定義及要求、資本金留存緩衝、逆週期緩衝、槓桿率、流動性比率和交易對手信用風險。
16.3 一般定義下的VaR由最近一天一直到過去4年內的日數據計算得出。壓力VaR的計算要選取歷史上使銀行當前投資組合的表現非常差的250天。
16.4 增量風險資本計提由交易賬戶上的信用產品在1年展望期內、99.9%置信度下的VaR求得。計算過程中要考慮信用評級的變化和流動性區間,引入這個概念是因為過去交易賬戶上的產品所需的資本金少於銀行賬戶上相應的產品。
16.5 一個AAA級的ABS的資本金要求是面值的1.6%,而一個AAA級的ABS CDO的資本金要求是面值的3.2%。
16.6 第一類股權資本金的要求由2%增加到7%,而且股權資本的定義更加嚴格。
16.7 (a)40%;(b)20%。
16.8 在槓桿比率中,分母不是風險加權資產,而是資產負債表上無加權的全部資產加上一些表外項目,例如貸款承諾。
16.9 流動性覆蓋比率是在30天承壓期內,高質量流動性資產與淨流出資金的比率。淨穩定資金比率是資產負債表上“負債和淨值”一側項目的加權總和除以“資產”一側的項目的加權總和。
16.10 穩定資金量變為81.6,NSFR變為81.6/74.25=110%。
16.11 CVA是衍生產品交易中,由於交易對手可能違約帶來的預期損失而對收入進行的計提。新的監管規則要求,對信用價差的CVA敞口要被包含在市場風險資本金中。
16.12 CoCo債券在銀行資本金低於預先定義的觸發條件時自動轉換為股權。這類債券對銀行具有吸引力,因為在轉換前,它們對股本回報率不產生影響;這類債券對監管機構也具有吸引力,因為在市場受壓的情況下,它們會成為吸收損失的資本金的來源。
第17章
17.1 當使用ISDA主協議時,場外衍生產品交易的雙方都會承擔對方違約的風險。當使用CCP時,CCP充當雙方的中介,因此雙方都與CCP進行交易。
17.2 金融機構之間的標準交易必須通過CCP清算。對金融機構間雙邊清算的衍生產品,初始保證金和變動保證金都會需要。初始保證金的數額必須能有99%的把握抵禦市場受壓情況下10天內的損失。
17.3 金融機構需要為它們的衍生產品賬戶提供的擔保品的數量(一般來說是現金或國債)會增加。
17.4 用於某金融產品的折減率是該產品用作擔保品時所計的價值與其市場價格相比所減少的百分比。例如,如果某產品的價格為100美元,折減率為10%,那麼該產品用來滿足90美元的擔保品要求。
17.5 如果在衍生產品交易中,簽署了ISDA主協議的雙方中有一方不能繳納擔保品或按照要求付款,那麼我們就認為發生了違約。違約發生後,會接著發生提前終止事件。未違約的一方會終止與違約的一方進行的所有未到期交易。
17.6 A方的風險敞口(包括對CCP的風險敞口)減至70,不包括對CCP的風險敞口保持為0。B方的風險敞口(包括對CCP的風險敞口)減至100,不包括對CCP的風險敞口減小到70。C方的風險敞口不受影響。三方平均的風險敞口,包括對CCP的敞口,由110下降到86.7,不包括CCP的風險敞口由70下降到53.3。
17.7 如果發生以下情況,公司將遭受損失:①CCP違約;②有某一方違約,並且沒有向CCP繳納足夠的保證金和違約基金來抵禦其交易被平倉所造成的損失。
17.8 所需擔保品的數額一般是所有為完結交易的市場價值的淨額。為確定結算額,價值為正的交易會與價值為負的交易淨額結算。
17.9 再抵押的含義是,A方給B方提供的擔保品,被B方用來滿足C方對B方的擔保品要求。
17.10 CCP的業務行為比銀行簡單得多。
17.11 計算方式如下:提前終止時交易對未違約方的市場中間價加上買賣價差的一半。
第18章
18.1 在《巴塞爾協議I》中,市場風險資本金由10天展望期、99%置信度的VaR求出,而該值又通過1天展望期、99%置信度的VaR乘以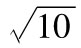 得出。在《巴塞爾協議Ⅱ.5》中,市場風險資本金由兩部分組成,一部分是基於當前99%置信度的VaR(即《巴塞爾協議Ⅰ》),另一部分來自10天展望期、99%置信度的壓力VaR。這兩部分都假設等於相對應的一天VaR的
得出。在《巴塞爾協議Ⅱ.5》中,市場風險資本金由兩部分組成,一部分是基於當前99%置信度的VaR(即《巴塞爾協議Ⅰ》),另一部分來自10天展望期、99%置信度的壓力VaR。這兩部分都假設等於相對應的一天VaR的 倍。在FRTB中,資本金由置信度為97.5%的壓力預期虧空得出,其展望期為一個依賴於投資組合流動性的可變量。
倍。在FRTB中,資本金由置信度為97.5%的壓力預期虧空得出,其展望期為一個依賴於投資組合流動性的可變量。
18.2 97.5%的ES為 。
。
18.3 考慮歷史模擬法是如何實現的。由第0日到第10日的變化有9天與從第1日到第11日的變化重合。因此,它們不是相互獨立的。實際上,我們預期這兩個變量在大部分模擬中會很相近。
18.4 ES與VaR相比,理論上的優點是它能滿足第12.5節中討論的次可加性(分散性);從實用性上講,它能更好地量化尾部風險。
18.5 交易賬戶包含那些出於交易目的而持有的項目,這些項目要進行每日的盯市計價。銀行賬戶包括那些預期持有到期滿的項目。除非遭遇嚴重不良,這些項目會以歷史成本法計價。交易賬戶和銀行賬戶的資本金計算方式有很大不同,而監管機構不希望銀行能夠通過自主決定項目所放賬戶的方式達到減少資本金要求的目的。
18.6 信用價差風險的處理方式和其他市場風險是一致的。突發違約風險的處理與銀行賬戶中項目的信用風險的處理類似。
第19章
19.1 穆迪的10個投資級別為:Aaa,Aa1,Aa2,Aa3,A1,A2,A3,Baa1,Baa2,Baa3。
19.2 標準普爾的10個投資級別為:AAA,AA+,AA,AA-,A+,A,A-,BBB+,BBB,BBB-。
19.3 由式(19-2)得出,平均風險率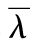 滿足
滿足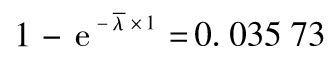 ,這一方程的解為
,這一方程的解為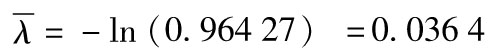 ,平均違約密度為每年3.64%。
,平均違約密度為每年3.64%。
19.4 在前兩年沒有違約情況下,公司在第三年違約的概率為
(0.044 92-0.025 83)/(1-0.025 83)=0.019 60
將第三年平均違約密度記為 ,我們有關係式
,我們有關係式 ,因此
,因此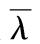 等於每年1.98%。
等於每年1.98%。
19.5 信用保護賣出方在0.5年、1.0年、1.5年、2.0年、2.5年、3.0年、3.5年及4.0年收入300 000 000×0.006 0×0.5=900 000美元,賣出方在違約發生時(4年零2個月)會收到最終付款300 000美元(=300 000 000×0.060×2/12),信用保護賣出方在違約發生時的支付金額為30 000 000×0.6=180 000 000美元。
19.6 有時交易雙方會達成實物交割協議,有時會達成現金交割協議。如果在違約時為實物交割,則信用保護的買入方會以債券票面的價值將違約債券賣給信用保護的賣出方,可賣出債券的總面額等於信用互換的面額。如果在違約時為現金交割,這時會有一個第三方來計算在違約後一定天數之後最便宜可交割債券的價格,信用互換的現金回報等於違約債券的面值減去估算出的債券價格。
19.7 風險中性違約概率由信用互換及債券價格計算得出,真實世界違約概率是從歷史數據中計算得出的。風險中性違約概率被應用於產品定價,真實世界違約概率被應用於情景分析及信用VaR的計算。
19.8 CDS的賠償支付為L(1-R),L為CDS面值,R為回收率。
19.9 由式(19-3),我們得出今後3年的平均違約密度為0.005 0/(1-0.3)=0.007 1,即每年0.71%。
19.10 由式(19-3),我們得出今後5年的平均違約密度為0.008 0/(1-0.4),即每年1.333%。類似地,今後3年的平均違約密度為每年1.166 7%,這意味著4~5年的平均密度為
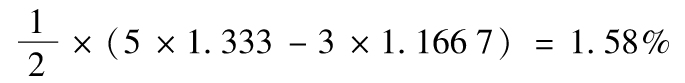
19.11 真實世界違約概率應該用於計算信用風險VaR,風險中性違約概率應該用於對衍生產品價格進行信用風險調節。
19.12 債券的回收率等於在債券發行方違約不久後債券的價格與面值的比率。
19.13 表19-5第2列第1個數字的計算方法為

即每年0.03%。表19-5第2列第2個數字通過類似的方法得出
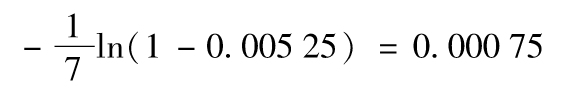
依此類推。最後的數字為
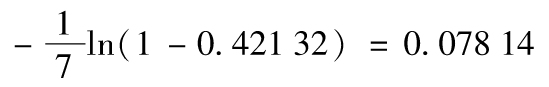
表19-6中第4列等於將表19-5中第2列的風險率(以基點表示)乘以0.6。對Caa級別,結果為781.4×0.6=460。
19.14 債券的無違約價值為
2e-0.03×0.5+2e-0.03×1.0+…+102e-0.03×4.0=103.66
市場價格為96.16。一個類似於表19-3的分析說明,如果Q為每年違約概率,違約損失為272.69Q,隱含違約概率滿足103.66-96.16=272.69Q,因此隱含違約率為每年2.47%。
19.15 如果Q1為在時間0.5年、1.5年及2.5年的違約概率,類似於表19-3的分析顯示第一個債券違約損失的貼現值為每100美元面值178.31Q1。債券的無違約價值為
4×e-0.035×1+4×e-0.035×2+104×e-0.035×3=101.23
市場價格為98.35。因此178.31Q1=101.23-98.35,從而Q1=0.015 7,即1.57%。令Q2為時間3.5年及4.5年違約的概率,類似於表19-3的分析顯示第二個債券違約損失的貼現值為180.56Q1+108.53Q2。這一債券的無違約價值為
4×e-0.035×1+4×e-0.035×2+…+104×e-0.035×5=101.97
債券的市場價格為96.24。因此180.56Q1+108.53Q2=101.97-96.24,代入Q1求得Q2=0.026,即2.60%。
19.16 我們假定在互換到期時有本金交換,這種假設並不會影響互換的價格。如果利差為0,浮動利率支付方對應於1美元本金現金流的貼現值為1美元。因此以LIBOR加利差計息的現金流的貼現值為1+V。1美元單位面值債券產生的現金流的當前價值為B*。對應1美元單位面值,債券現金流支付方的最初付出費用為1-B(如果這一數值為負,那麼浮動利率的支付方必須首先付費B-1),因為資產互換的最初價格為0,我們得出
1+V=B*+(1-B)
因而
V=B*-B
19.17 由默頓模型得出債券價格為V0-E0,即
V0-V0N(d1)+De-rTN(d2)=De-rTN(d2)+V0N(-d1)
令s為信用價差,以上數量等於De-(r+s)T,因此
De-(r+s)T=De-rTN(d2)+V0N(-d1)
代入De-rT=LV0,我們得出
Le-sT=LN(d2)+N(-d1)
因此
s=-ln[N(d2)+N(-d1)/L]/T
19.18 這時,E0=2,σE=0.50,D=5,r=0.04,T=1。對兩個方程求解得出V0=6.80及σV=14.82。違約概率為N(-d2),即1.15%。
19.19 在前四年的每個季度結束時,賣出方收到100萬美元付款。賣出方在4年零2個月之後支付7 000萬美元。賣出方收到最終付款666 667美元。
19.20 信用違約互換提供對參照實體發行的企業債券的信用保護,其大致的作用是將企業債券轉換為無風險債券。因此,信用違約互換的買入方實際上是將一個企業債券與無風險債券做交換。這意味著,買入方持有無風險債券的多頭和企業債券的空頭。
19.21 CDS的回報取決於某公司是否違約,有人認為有些市場參與者對於公司的信用狀態有更多信息(見業界事例19-2)。
19.22 假定面值為100美元。如果債券是無風險的,其貼現值為
2.5e-0.06×0.5+2.5e-0.06×1+…+2.5e-0.06×5+100e-0.06×5=95.357 9
因此,預期違約損失的貼現值為95.357 9-90=5.357 9。構造資產互換時首先保證最初付費為10美元,然後每6個月支付2.5美元。作為交換,收入為LIBOR加上利差,互換的面值為100美元,固定利息付款的貼現值為
10+2.5e-0.06×0.5+2.5e-0.06×1+…+2.5e-0.06×5+100e-0.06×5=105.357 9
因此,高於LIBOR的利差的貼現值為5.357 9。每6個月支付1美元,連續支付5年的當前貼現值為8.510 5。因此,每6個月收入的利差為5.357 9/8.510 5=0.629 6美元,資產互換的利差等於2×0.629 6,即每年1.259 2%,本題為練習題19.16的結果提供了一個說明。
第20章
20.1 一個新的交易在以下兩種情形下會增大銀行對於交易對手的風險敞口:第一種情形為現存的交易對於銀行來講價值為正,新交易價值也為正;第二種情形為現存的交易價值為負,新交易價值也為負。但是當新交易價格同現在交易價值有抵消作用時,新交易附加效應是減小信用風險。
20.2 一家公司本身的股票對這家公司的交易對手來說,不會是好的擔保品。當與該公司的交易違約時,公司股票也可能不會太值錢。
20.3 (a)和(b)均正確,(c)不正確。假定vX及vY分別是對X及Y的風險敞口,vX+vY的期望值等於vX的期望值加上vY的期望值,但對應於95%置信區間的限制,以上結論並不正確。
20.4 假設違約只發生在遠期合約的到期日。在無違約風險的世界,遠期合約是一個歐式看漲期權的多頭與一個歐式看跌期權的空頭的組合,這裡的兩個期權的執行價格均等於遠期合約交割價格,期權的到期日等於遠期合約的到期日。如果無違約遠期合約在到期時價格為正,看漲期權價格為正,看跌期權價值為0,違約對於遠期合約的影響與違約對於看漲期權的影響相同;如果無違約遠期合約在到期時價值為負,看漲期權價值為0,看跌期權價值為正,這時違約不會有任何影響,在這種情況下,違約對於遠期合約的影響也與遠期合約對於看漲期權的影響等同。綜上所述,我們得出遠期合約的價值等價於一個與違約有關的看漲期權的多頭以及與違約無關的看跌期權的空頭。
20.5 布萊克-斯科爾斯-默頓模型得出的價格必須乘以e-0.012×3=0.964,該模型高估價格大概為3.6%。
20.6 當公司X與許多公司簽有的合約中使用了同樣的降級觸發條件時,其效果可能會增加風險。如果公司被降級,降級觸發條款被激活,那麼持有對於X而言價值為負的合約的對手方會向X索取擔保品。其結果是,公司X會面臨流動性困難,甚至會造成公司破產。
20.7 當交易商和交易對手進入一個交易對手賣出信用保護的CDS合約或交易對手進行投機時,交易商容易產生錯向風險。當交易商與交易對手進行的CDS合約中,交易對手從交易商買入了信用保護,或者新交易是為了部分地對衝交易對手的風險敞口時,交易商具有正向風險。
20.8 補救期是指在CVA計算中從違約事件發生到交易被終止的時間。
20.9 如果B方違約,那麼A方與B方之間的所有未清償交易都被當作一個交易來處理。因此,A方在計算損失時,會考慮所有與B方之間未清償交易的價值。
20.10 當銀行遭遇財務危機時,其違約可能性增大。這使得交易對手對銀行違約的預期損失增大。對銀行來說,這就是DVA,DVA會在賬面上增加交易對銀行的價值。
20.11 在《巴塞爾協議Ⅲ》中,與交易對手信用價差變化有關的CVA被包含在市場風險的計算中。
20.12 如果在提前終止事件前15天內,交易商與交易對手之間交易的價值朝向對交易商有利的方向變化500萬美元,交易商的CVA模型會產生損失。假設交易商無法從對手方處獲得額外抵押品,或交易對手無法歸還從交易商處獲得的抵押品。
第21章
21.1 在Vasicek模型及Credit Risk Plus模型中,信用損失在違約發生時發生。在CreditMetrics模型中,信用的降級及違約都會引發損失。Vasicek模型採用了違約時間的高斯Copula模型;Credit Risk Plus模型對每年的違約率的概率分佈採用了某種假設;CreditMetrics模型採用了高斯Copula模型來定義信用評級的變化。
21.2 風險水平恆定假設中假定一段時間t之後,某產品X被另一產品Y替換,其中Y與X的初始評級相同。再經過另一段時間t之後,Y被Z替換,Z也具有和X的初始評級相同的評級,依此類推。
21.3 一家Aaa級的公司在兩年後仍保持Aaa評級的概率為82.77%。其評級變為Aa的概率為15.12%。
21.4 一家Aaa級的公司在6個月後仍保持Aaa評級的概率為95.35%。其評級變為Aa的概率為4.40%。
21.5 所有公司的信用價差在下一天的變化可以被認為是過去500天的日變化中的一個隨機抽樣。該方法的缺點是公司違約的可能性為0,並且並不是所有的公司都有準確的每日信用價差數據。
21.6 使用二項分佈,產生6個或更多損失的概率是0.0005。
21.7 在這種情況下,我們必須求出對應於0.5%損失概率的二項累積分佈和1.5%損失概率的二項累積分佈的均值。有6個或以上違約事件發生的概率為0.0021。這說明,引入相關性會造成尾部風險上升。
21.8 自相關性為0.546。這說明信用VaR的估計應考慮最近的違約記錄。如果去年的違約率較高,則今年的違約率很可能也會較高。
第22章
22.1 我們可以由以下做法來產生情景:(a)對類似利率、股票價格等核心變量進行較大擾動;(b)令所有市場變量的擾動等於歷史上某一天市場變量的劇烈變化;(c)建立一個委員會來產生情形。
22.2 逆向壓力測試是指利用算法來尋求會造成巨大損失的情形。通過這一做法,我們可以確定實施壓力測試的恰當情形。
22.3 金融機構可能會認為如果所考慮的情景會引發巨大損失,則監管機構將提高資本金要求。
22.4 交通燈期權只有在保險業監管機構所規定的情景發生的情況下才產生回報。買入這一產品的危險是,當金融機構買入這種產品時,它們所得到的保護範圍很窄。對某些與保險公司監管機構所考慮的情形相似,但並不完全相同的情形,金融機構並沒有得到保護。
22.5 高管所處的位置對產生壓力測試情景最有利。高管介入壓力測試的產生過程,會使他們更認真地對待壓力測試結果,並將這些結果實施於決策過程。
22.6 優點是不同銀行都會考慮同樣的情形,並且系統性風險也可以被評估。這些情形可能比銀行自己考慮的情景更加惡劣(見練習題22.3)。缺點是在這種做法下,銀行可能不再積極地開發自己的壓力情景。
22.7 客觀概率由數據來產生,主觀概率具有一定的主觀性,它反映了個人的判斷。
22.8 壓力情形的整體概率為1.5%,因此,歷史情形所對應的概率為98.5%,每個歷史情形所對應的概率為0.197。將這些情形及所對應的概率進行排序,在99%置信度下的VaR值為284 204美元(對於340 000美元的損失量,累計概率為0.009 43;對於284 204美元的損失量,累計概率為0.011 41)。
22.9 這時,頭寸價值分別為941.34、-164.39、-1 349.94及-78.36,最糟糕的情形是資產價格為60、波動率為30%的情形,損失量為341.39美元。
第23章
23.1 這一定義包括所有的內部風險及外部風險,但不包括名譽風險及戰略決策風險。
23.2 根據Shih所報告的結果,損失量為100×30.23,即1.287億美元。
23.3 Prob(v>x)=Kx-0.8,當x=20時,概率為0.1,這意味著K=1.098 6。對於特定損失被超出的概率為:(a)5.74%;(b)3.30%;(c)1.58%。
23.4 對於道德風險的處理方式包括設立免賠額度或者將保險費與過去索賠記錄掛鉤。對於逆向選擇的處理是首先在同意承保前儘可能取得關於司機的信息,然後隨著獲得的信息越來越多,再適當對保險費進行調整。
23.5 公司的CEO一定要簽署公司的財務報告來保證財務報表的準確性,如果財務報告出現重大問題並需要改動,CEO必須歸還自己的獎金。
23.6 如果交易員在遵守自己額度的條件下蒙受了交易損失,這種風險屬於市場風險;如果交易員超出額度交易並造成損失,這種風險屬於操作風險。
23.7 (a)即使存在人壽保險,一個人也不太可能不關心自己的健康。不過確曾發生過人壽保險受益人為獲得保金而謀殺投保人的事件。(b)壽命比較短的人往往會比壽命長的人更容易買人壽保險。
23.8 外部數據是與其他銀行損失有關的數據,其取得方式是與其他銀行達成協議來共享數據,或者銀行可以從數據銷售商處獲取數據。外部數據用來決定相對損失程度。這些數據可以用來計算業務部門A的損失平均值同業務部門B的損失平均值的比率,或者計算業務部門A的損失標準差與業務部門B的損失標準差的比率。
23.9 泊松分佈常常被用來描述損失頻率,對數正態分佈常常被用來描述損失程度。
23.10 幾個重要的風險指標的例子包括:僱員的離職率、不成功交易的數量、臨時僱員的數量、管理人員與僱員的比例、空置的職位和過去12個月中未連續休假10天的僱員比例。
23.11 當損失頻率等於3時,整體損失的平均值為3.3,標準差為2.0,當損失頻率增長到4時,整體損失的平均值大約為4.4,標準差為2.4。
23.12 關鍵的投入是業務指標和(對於業務指標超過10億元的銀行)過去10年的損失。業務指標是衡量銀行規模的指標,與操作風險相關。
23.13 A銀行的損失(以百萬歐元計)是7×20+7×20=280,B銀行的損失是7×20+7×20+5×20=380。A銀行的內部損失乘數是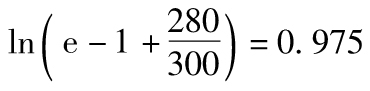 ,B銀行的內部損失乘數是
,B銀行的內部損失乘數是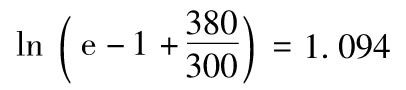 。A銀行的SMA資本要求是110+(300-110)×0.975=295,B銀行的SMA資本要求是110+(300-110)×1.094=318。
。A銀行的SMA資本要求是110+(300-110)×0.975=295,B銀行的SMA資本要求是110+(300-110)×1.094=318。
第24章
24.1 投資者對產生分檔的基礎按揭資產並不瞭解,而且瀑布現金流非常複雜。
24.2 提供報價的公司及個人準備以50美元買入資產,並以55美元賣出資產,市場中間價為52.5美元,買賣價差比率為5/52.5,即0.095 2。
24.3 公司A的股票的買賣價差為0.01×5000=50美元,公司B的股票的買賣價差為0.02×3 000=60美元,對組合進行平倉的費用為(50+60)/2,即55美元。
24.4 對於第一家公司,在95%的置信區間下,買賣價差不會超出5 000×(0.01+1.645×0.01)=132.24美元。對於第二家公司,在95%的置信區間下,買賣價差不會超出3 000×(0.02+1.645×0.03)=204.04美元,在95%的置信區間下,平倉費用不會超出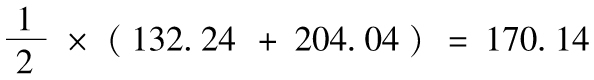 美元。
美元。
24.5 在接下來的幾天中交易數量分別為15.9、12.9、10.0、7.4、5.2、3.4、2.2、1.4、0.9及0.7。買賣價差為13.4美元(單位為百萬),總方差為36.6,因此,在95%的置信區間下的VaR為 美元(目標函數的取值使得以上數量的和達到極小,即23.3美元)。
美元(目標函數的取值使得以上數量的和達到極小,即23.3美元)。
24.6 LCR測試一家銀行是否有足夠的流動性來承受30天的極端壓力(信用降級、存款損失、信貸額度減少等)。NSFR測試資產和負債的到期匹配程度,防止過度依賴短期資金來滿足長期需求。
24.7 在市場受壓的條件下,批發存款更加容易消失。
24.8 它們的對衝交易產生損失,而被對衝的部分會產生盈利。問題在於,對衝交易的損失會引發保證金催付,而被對衝的頭寸雖然價值增加,但這些產品的流動性並不好。
24.9 正反饋是指交易員的交易會加重市場價格的變動,即交易員在價格上漲時買入,在價格下跌時賣出;負反饋是指交易員的交易會減緩市場價格的變動,即交易員在價格下跌時買入,在價格上漲時賣出。正反饋會導致流動性問題。
24.10 這個VaR測度包括在對交易進行平倉時,因買賣價差造成的費用。
24.11 流動性黑洞產生於市場參與者均在市場同一側的情況。監管規則對於流動性黑洞的產生有一定責任。因為金融機構所受的金融監管約束完全類似,所以它們對外部經濟事件的反應也相似。
24.12 流動性黑洞的產生往往是由於眾多的交易員採用同樣的交易策略,當交易員採用不同的交易策略時,流動性黑洞出現的可能性不大。
第25章
25.1 盯市計價涉及利用交易市場上的同類或相似產品的價格來對頭寸定價,按模型定價是指模型在決定價格時起決定性作用。
25.2 模型可能存在基本誤差,或者使用不當。
25.3 模型開發人員可能會離開。此外,金融機構的其他工作人員及其監管者也可以瞭解已完成的工作。
25.4 對簡單看漲期權及看跌期權進行定價時,交易員以布萊克-斯科爾斯-默頓模型作為插值工具。他們利用市場上交易活躍的期權來計算隱含波動率。通過對不同執行價格及期限進行插值,由此他們可以計算出其他期權的隱含波動率,這些波動率又被重新代入布萊克-斯科爾斯-默頓模型來計算這些期權的價格。但是在用於對衝時,布萊克-斯科爾斯-默頓模型就不再只是插值工具。
25.5 13.45%。我們可以採用以下兩種方法得出同樣的答案:(a)先在執行價格介於1.00與1.05之間進行插值,然後在期限介於6個月及1年之間進行插值;(b)先在6個月及1年之間進行插值,然後在執行價格1.00與1.05之間進行插值。
25.6 物理模型用於描述物理現象,而金融模型最終是為了描述人類的行為。
25.7 該機構可能會注意到,其某項業務的業務量很大,因為自己的報價與同業競爭者的報價有差別。另一種找出價格差別的方法是,將交易平倉並因而向同業競爭者詢價。另外我們可以通過訂購報價數據的形式來取得交易商提供的對於某些類別交易的月平均價格。
25.8 模型內對衝是指對模型所包含的隨機變量進行對衝,模型外對衝是指對模型所假設的“常量”進行對衝。
25.9 布萊克-斯科爾斯-默頓模型假定股票在1個月內的價格的概率分佈為對數正態分佈,這裡考慮的股票價格顯然不是對數正態分佈。一個合理的假設是分佈可能是兩個對數分佈的迭加,這時的分佈有兩個峰值,顯然布萊克-斯科爾斯-默頓模型不適用。
25.10 第1類交易是指活躍市場中相同交易中有報價的交易,第2類交易是指活躍市場中類似交易或不活躍市場中相同交易中有報價的交易,第3類交易是指需要模型假設。
25.11 過度擬合是指為了完美地擬合而匹配的東西過多。過度參數化是指通過引入額外的參數使模型變得過於複雜和難以使用。
25.12 執行價格為0.90、期限為1.5年的期權的隱含波動率為14.85%。執行價格為0.95、期限為1.5年的期權的隱含波動率為0.6×14.85%+0.4×14.20%=14.59%。
25.13 盯市計價是指在產品再定價(通常是每天)時,我們要保證產品的價格與市場價格一致,對於市場交易活躍產品計算出的價格通常反映了市場價格信息。這時模型僅僅是一個插值工具,因此盯市計價所得出的價格通常十分準確。而結構性產品價格通常與模型有關,因此這些產品是以模型定價的。
第26章
26.1 經濟資本金是銀行對自身所需要的資本金的一個估計,監管資本金是監管機構要求銀行必須持有的資本金數額。
26.2 AA級公司一年內違約的概率。
26.3 業務風險包括與業務戰略及名譽有關的風險。
26.4 對於市場風險及操作風險,計算經濟資本金的模型與計算監管資本金的模型會比較類似。在計算信用資本金時,銀行可能採用自認為更為合理,但與計算監管資本金不同的相關性模型以及相關性參數。
26.5 99.97%的置信水平所對應的最壞損失的對數為0.5+4×3.43=14.23,因此99.97%置信水平所對應的最壞損失為151萬美元。由於對數正態分佈的性質,我們得出預期損失為exp(0.5+42/2),即4915美元,因此資本金需求大約為150.5萬美元。
26.6 部門1的經濟資本金為96.85,部門2的經濟資本金為63.87,整體資本金為124.66。
26.7 部門1對於整體經濟資本金的遞增效應為60.78,部門2對於整體經濟資本金的遞增效應為27.81,這意味著60.78/(60.78+27.81)=68.61%的經濟資本金應該分攤到部門1及27.81/(60.78+27.81)=31.39%的經濟資本金應該被分攤到部門2。將部門1的規模增大0.5%對於整體資本金的邊際效應為0.4182,將部門2的規模增大0.5%對於整體資本金的邊際效應為0.2056。歐拉定理得以滿足,因為整體資本金大約等於0.4182/0.005與0.205 6/0.005的和。
26.8 資本金為3 800萬美元,稅前收入為700萬美元,稅前RAROC為18.4%(=7/38)。在實踐中,多元化可能會降低資本金數量,並使RAROC有所增加。
26.9 RAROC可以用來比較不同業務部門的表現(績效評估)及用於預測業務部門將來的預期表現(決定資本金分配)。
第27章
27.1 在自上而下法中,整個機構的風險限額由高管或董事會決定。在自下而上法中,風險限額針對各個業務部門來設定。在企業風險管理中,兩種方法都需要,因為我們需要確保各業務部門的風險限額彙總後與整個企業的風險限額保持一致。
27.2 鮑曼悖論來源於對實證數據的觀察,在企業制定重大戰略規劃時,承擔高風險往往會造成更低的回報。
27.3 危險在於決策僅考慮短期效益,但是會導致長期的問題(例如,負面的公眾曝光、聲譽損失和法律訴訟)。業界事例5-4、業界事例27-1、業界事例27-2和業界事例27-3給出了相關實例。
27.4 年度獎金的一部分可以推遲發放,甚至可以被收回。
27.5 企業風險管理採用整體的方法(大圖景)來進行風險管理,而不是單獨考慮不同風險類別的管理(信用風險、市場風險、操作風險等)。
27.6 在式(27-1)中,我們設R=-0.2,RF=0.03,RM=0.117 4,σM=0.188 6及p=0.9。相對應的beta為1.49。
27.7 從第二年後開始的每個季度,利率將增加4%。16個季度後,利息將高達1.76+16×4%=65.76%。
27.8 認知偏差的例子包括:(a)錨定效應(對最初的估計僅進行小的調整);(b)可得性啟發(最近的信息會獲得過高的權重);(c)代表性啟發(過於依賴過去的有限的或對目前形勢沒有代表性的經驗);(d)條件倒置。
第28章
28.1 當先前通過中介相互作用的雙方開始直接相互作用時,就會發生脫媒。當一種新的技術中介(提供與以前中介不同的服務)在非中介化之後進入市場時,就會發生復媒。
28.2 機器學習是人工智能的一個分支,計算機學習時不需要顯示編程。分佈式賬本技術是一種諸如區塊鏈的技術。在該技術中,數據庫可以跨多臺計算機共享和同步。
28.3 生物特徵識別授權使用個人獨特的生物學特徵來驗證他們是誰。指紋、視網膜掃描、面部識別、語音認證和心跳監控就是例子。
28.4 數字貨幣可能更容易控制貨幣供應量和管理通貨膨脹。
28.5 在P2P貸款中,借貸雙方使用技術公司提供的在線平臺直接進行交易。股權眾籌是一種允許廣大投資者通過在線平臺為初創企業提供資金的機制。
28.6 監管是金融科技進入的障礙。為了符合監管,金融科技公司有時不得不通過一家成熟的金融機構提供服務。
28.7 的確,如果每個人僅投資於指數基金,就不會有價格發現。我們需要一些投資者和基金經理關注新聞報道,並積極尋找應該買進或賣出的股票。
28.8 監管科技(RegTech)是指應對法規遵從性挑戰的技術開發。例如,用於在線實時報道的系統,用於篩選客戶和交易以避免合規性問題的系統,以及使金融機構可以輕鬆檢索有關不同國家、不同主題法規信息的在線圖書館。
28.9 IBM意識到不能依靠大型機銷售,因此改變了文化與商業模式以反映市場變化。柯達沒有像攝像市場變化那樣改變其文化和商業模式。為了生存,銀行將需要改變其文化和商業模式。
術語表
A
ABS 見資產支持證券(asset-backed securities)。
ABS CDO 由ABS不同分檔生成的證券。
accrued interest 應計利息 自上一次息票支付日至今為止債券所累積的利息。
additional tier 1 capital 附加第一類資本 不能作為一類股權資本的項目,如非累積優先股。
add-on factor 附加因子 在計算衍生產品交易中的等價信用量時,在當前的風險敞口之上附加的本金比例,其目的是反映衍生產品將來可能的價值變化。
adjoint differentiation 聯合差分 一種高效率的計算希臘字母的求導算法。
advanced measurement approach 高級計量法監管部門所允許的大多數管理成熟的銀行用以計算《巴塞爾協議Ⅱ》操作風險監管資本金的方法。
adverse selection 逆向選擇 這種現象是指如果保險公司以同等的價格向所有人提供保險,其承保的往往是風險最大的客戶。
agency costs 代理成本 描述在某個商業行為中,兩個不同參與者的利益不完全一致的情形。
alpha 投資組合回報高出由資本資產定價模型所預測的那一部分。
alternative investments 另類投資 見對衝基金(hedge funds)。
American option 美式期權 一種在期權期限內可以隨時行使的期權。
analytic result 解析結果 一種被某種方程式所表達的結果。
arbitrage 套利 利用兩種或多種證券定價的相對不一致來獲利的交易策略。
arbitrage pricing theory 套利定價理論 投資回報與若干因子相關的理論。
arbitrageur 套利者 參與套利交易的個體。
ASF factor 可用穩定資金因子 在計算淨穩定資金率時對於資金來源進行加權的因子。
Asian option 亞式期權 回報與一定時間段內標的資產的平均價格有關的期權。
ask price 賣出價 交易商賣出資產的價格,也稱為offer price。
asked price 索要價 見賣出價(ask price)。
asset swap 資產互換 將約定的債券息票與LIBOR加一個利差進行互換。
asset-backed security 資產支持證券 由債券、按揭貸款、信用卡應收款和其他資產的現金流所產生的證券。
at-the-money option 平值期權 執行價格等於標的資產價格的期權。
autocorrelation 自相關 變量本身與變量在k天后取值的相關性(k被稱為時滯)。
average price call option 均價看漲期權 回報等於標的資產平均值超出執行價格之上的數量與0這兩者之間較大值的期權。
average price put option 均價看跌期權 回報等於執行價格超出資產平均值的數量與0這兩者之間較大值的期權。
B
back-end load 後端收費 基金份額被賣出時收取的費用。
back office 後臺 交易記賬的場所。
back testing 回溯測試 利用歷史數據對VaR或其他模型進行檢測。
backwards induction 倒推歸納 一種由二叉樹的底端反向倒推到樹的起始點來對期權進行定價的過程。
banking book 銀行賬戶 銀行投資組合的一部分,這些賬戶中的資產預計會被持有到期滿日。
bankruptcy costs 破產成本(費用) 在宣佈破產後由於銷售的損失、主要管理人員的離職及專業服務費用的增加所帶來的成本,這些成本與引發破產的不利事件無關。
barrier option 障礙期權 回報與標的資產的價格是否達到一定的障礙水平(即事先約定的水平)有關的期權。
Basel Ⅰ 《巴塞爾協議Ⅰ》 1988年頒佈的關於銀行監管的第一個國際協定。
Basel Ⅱ 《巴塞爾協議Ⅱ》 2007年開始實施的計算銀行資本的新國際協定。
Basel Ⅱ.5 《巴塞爾協議Ⅱ.5》 金融危機後,巴塞爾委員會於2010年引入的針對交易賬戶的額外監管資本金要求。
Basel Ⅲ 《巴塞爾協議Ⅲ》 2010年引入的涉及銀行賬戶和流動性比率的國際銀行資本監管規定。
Basel Committee 巴塞爾委員會 由世界各地的銀行監管機構組成的委員會,提出適用於所有國家的銀行的標準。
basic indicator approach 基本指標法 在《巴塞爾協議Ⅱ》中用來計算操作風險監管資本金的最簡單方法。
basis 基差 某種大宗商品現貨價格與期貨價格之間的差距。
basis point 基點 在描述利率時,一個基點等於1%的1%(即0.01%)。
basis risk 基差風險 在進行對衝時,由於基差的不確定性所產生的風險。
basket credit default swap 一攬子信用違約互換 具有若干參考實體的信用違約互換。
basket option 一攬子期權 標的資產為一投資組合的期權。
Bermudan option 百慕大期權 該類期權的持有者在期限中的若干的時間點可以行權。
best efforts 非包銷模式 投行按自身的能力將新發行證券以一個固定價格在投資者中進行銷售,在這種承銷模式中,投行對證券最終是否可以賣出不提供保證。
beta 檢測某項資產的系統性風險的一種測度。
bid-ask spread 買賣價差 賣出價高出買入價的數量。
bid-offer spread 買賣價差 見bid-ask spread。
bid price 買入價 交易商為買入某項資產而準備支付的價格。
bilateral clearing 雙邊清算 場外交易市場的交易雙方對交易進行清算的方式,該方式常常涉及ISDA主協議。
binary credit default swap 二元信用違約互換 當某特定參考公司違約時會引發一個固定數量賠償的信用互換。
binary option 二元期權 具有不連續回報形式的期權。例如,現金或空手期權(cash-or-nothing-option)以及資產或空手期權(asset-or-nothing option)。
binomial model 二項式模型 用於檢測在某一小段時間內資產價格變化的模型,對於任意時間段,其假設價格的變化只有兩個可能。
binomial tree 二叉樹 在二項式模型中描述資產價格變化的樹型結構。
BIS Accord 《巴塞爾協議》 在1988年由世界12個國家的中央銀行所達成關於銀行監管的協議。
bivariate normal distribution 二元正態分佈 用於描述兩個服從正態分佈的相關變量之間關係的分佈。
Black’s model 布萊克模型 用於歐式期貨期權合約定價的模型,這一模型是布萊克-斯科爾斯-默頓模型的擴展。在實際操作中,這一模型被廣泛應用於資產價格在到期日服從對數正態分佈的歐式期權定價中。
Black-Scholes-Merton model 布萊克-斯科爾斯-默頓模型 由布萊克、斯科爾斯及默頓開發的用於歐式股票期權定價的一個模型。
blockchain 區塊鏈 一種分佈式的數據技術,安全數據庫能在多臺計算機上共享和同步。
bond option 債券期權 標的資產為債券的期權。
bond yield 債券收益率 保證債券所有現金流的貼現值總和等於債券市場價格的貼現利率。
bootstrap method 息票剝離方法 通過市場數據來計算零息利率的方法。也是一種通過實證數據確定分佈後,計算置信水平的統計方法。
bunching 聚束效應 超過在險價值的大額損失在時間上聚集在一起的趨勢。
business risk 業務風險 這一術語應用於銀行時是指戰略風險(與銀行進入新市場和開發新產品的決策有關)及聲譽風險。
buy and hold 買入並持有 一種交易策略,建立頭寸後無後續的交易。
C
calendar days 日曆天數 日曆上的每一天。
calibration 校正 通過市場上交易活躍的期權價格來計算隱含的模型參數的方法。
callable bond 可贖回債券 允許發行者在債券期限內的特定時間裡可以按特定價格將債券購回的債券。
call option 看漲期權 在將來某日可以按約定價格買入某種資產的期權。
cancelable swap 可取消互換 交易的一方可以在指定期限取消交易的互換。
cap 上限 見利率上限(interest rate cap)。
capital adequacy 資本充足率 銀行或其他金融機構所持資本金的充足狀態。
capital asset pricing model 資本資產定價模型 關於資產預期回報與資產的beta係數之間關係的模型。
capital conservation buffer 資本留存緩衝 在《巴塞爾協議Ⅲ》下設定的額外的股權資本,為了當市場環境較差時承受額外損失。
caplet 單區間上限 利率上限交易中的一個基礎組成部分。
cap rate 上限利率 決定利率上限回報的利率。
cascade approach 級聯方法 該方法描述了FRTB內部模型方法中的計算方法。
Case-Shiller index 凱斯-希勒指數 美國的住房價格指數。
cash flow mapping 現金流映射 為計算在險價值而將一種產品拆解為一系列零息債券的過程。
cash settlement 現金交割 以現金方式而不是以實物形式對合約進行交割的方式。
CAT bond 巨災債券 一種利息甚至本金可能在特定的災難保險索賠超出一定數額後被減免的債券。
CCP 見中央對手方(central counterparty)。
CDD cooling degree days 製冷天數 日平均溫度超出華氏65°的天數與0之中的較大者,這裡日平均溫度是指最高溫度與最低溫度的平均(子夜到子夜)。
COD 見債務抵押債券(collateralized debt obligation)。
CDO squared CDO平方 在這種產品中一個CDO分檔組合的違約風險以某種形式攤派給新的產品。
CDS 見信用違約互換。
CDS-bond basis CDS債券基差 CDS利差與資產互換利差之差。
CDX 描述由北美125個投資級公司所組成的信用質量指數。
central clearing 中央清算 通過CCP來清算場外衍生產品。
central counterparty 中央對手方 場外衍生產品的清算機構。
central limit theorem 中心極限定理 大量獨立同分布變量的和近似正態分佈。
cheapest-to-deliever bond 最便宜可交割債券 在期貨或信用違約互換中,市場上可買到的最便宜的可用於交割的債券。
Chinese walls 防火牆 這一術語用於描述金融機構內部信息管理政策,當有些信息在金融機構內部傳播會對客戶不利時,金融機構內部的防火牆政策要阻止其傳播。
Cholesky decomposition Cholesky分解 從多元正態分佈中進行抽樣的一種方法。
clawback clause 獎金收回條款 如果是對衝基金,該條款允許收回已發放的獎金的一部分來彌補投資者當前的損失;如果是延遲獎金,該條款可以在財務表現不佳的情況下,取消未發放的獎金。
clean price of bond 債券除息價格(潔淨價) 債券的報價,買入債券的現價(債券帶息價格、髒價)等於這一報價再加上應計利息。
clearing house 清算所 保證場內交易衍生產品的交易雙方履行交易義務的實體(這一機構被稱為清算公司)。
clearing margin 清算保證金 由清算所會員繳納的保證金數量。
closed-end fund 封閉式基金 基金份額為固定的一種共同基金。
CoCo 見未定可轉換債券(contigent convertible bond)。
cognitive bias 認知偏差 一種不合邏輯的判斷模式。
coherent risk measure 一致性風險測度 滿足一定條件的風險測度。
collar 見利率上下限(interest rate collar)。
collateral 抵押品 在一個交易中,為了緩解交易對手對於信用風險的擔憂,而存放於對手處的現金或有價證券。
collateralization 擔保制度 在衍生產品交易中,一方或雙方須支付擔保品的制度。
collateralized debt obligation 債務抵押債券 一種將信用風險打包的方式,由一個債券組合派生出幾種不同的債券(被稱為分檔),各種債券的違約成本攤派服從事先制定的規則。
commercial bank 商業銀行 吸收存款併發放貸款的銀行。
component VaR 成分VaR 與交易組合的某一部分相對應的VaR,成分VaR的定義確保了所有成分VaR的總和等於整個投資組合的VaR。
compounding frequency 複利計息頻率 它定義了計算利息的時間間隔。
compounding swap 複利互換合約 一種利率不是立即交換,而是以複利的形式累積到下一個執行日再行交換的利率互換合約。
compound option 複合期權 期權的期權。
comprehensive risk measure 綜合風險計量 計算依賴於信用相關性的產品的資本金的風險計量手段。
conditional tail exception 條件尾部風險 見預期虧空(expected shortfall)。
conditional value at risk(C-VaR) 條件VaR 見預期虧空(expected shortfall)。
confirmation 交易確認 在場外市場用於確認交易雙方口頭協議的書面合約。
constant level of risk 恆定水平風險 在計算風險度量時的一種假設,即金融機構將定期進行交易,以使其在每個期初的風險都與今天相同(可以與買入並持有策略聯繫)。
consumption asset 消費性資產 用於消費而不是投資的資產。
contagion 見信用連鎖反應(credit contagion)。
contigent convertible bonds(CoCo) 未定可轉換債券 在預先定義的指標表明債券發行方需要更多的股權資本時,會自動轉換成股份的債券。
continuous compounding 連續複利 利率報價的一種方式,當複利報價的時間跨度變得越來越小時,其極限形式就是連續複利。
convenience yield 便利收益率 用於計量擁有某種資產而帶來的便利,這種便利是期貨合約的多頭持有者所不擁有的。
conversion factor 轉換因子 將表外項目轉換為等價信用量時要乘上的因子。
convertible bond 可轉換債券 可以在債券期限內的某個時刻轉換為一定數量股票的公司債券。
convexity 凸性 用來度量債券價格同收益率之間關係的曲線函數的曲率。
convexity adjustment 凸性調整 這一術語的應用之處很多,例如它可以用以描述將期貨利率轉換為遠期利率所需的調節量,它還可以用於描述對某些產品定價時對於遠期利率的調節。
Cooke ratio 庫克比率 在《巴塞爾協議Ⅰ》中定義的資本金與風險加權資產的比率。
cooling degree days 製冷天數 見CDD。
Copula Copula 函數 定義已知分佈的變量之間相關性的一種方式。
core tier 1 capital 核心第一類資本 見第一類股權資本(tier 1 equity capital)。
Cornish-Fisher expansion Cornish-Fisher展開 一種表達概率分佈的分位數與其各階矩之間的近似關係的式子。
correlation 相關性 描述兩個變量的線性關係程度。
correlation matrix 相關矩陣 用矩陣來表達的市場變量之間的相關性。
cost of carry 持有成本 存儲成本加上購買資產所需的融資費用再減去資產的收益率。
countercyclical buffer 逆週期緩衝區 在《巴塞爾協議Ⅲ》中,由各國監管部門決定的一部分額外資本金要求。
counterparty 交易對手 金融交易中的另一方。
coupon 息票 債券所付的利息。
covariance 協方差 描述兩個變量之間的線性關係(等於變量的相關係數乘以它們的標準差)。
covariance rate 協方差率 描述兩個日回報變量之間的協方差。
covered call 備兌看漲期權 賣出看漲期權同時持有資產的多頭的組合。
crashophobia 暴跌恐懼症 人們對於類似1987年股票大跌的恐懼症,有人認為這一現象造成市場參與者提高了深度虛值看跌期權的價值。
credit contagion 信用連鎖反應 某公司的違約會引發其他公司也違約的傾向。
credit default swap,CDS 信用違約互換 買入方有權在債券違約時以面值為價格將債券出售給賣方的一種工具。
credit derivative 信用衍生產品 回報與某家或多家公司或國家的資信(creditworthiness)狀況相關的衍生產品。
credit equivalent amount 等價信用量 在《巴塞爾協議Ⅰ》中與某表外交易等價的貸款數量。
credit event 信用事件 違約或其他可觸發信用違約互換產生收益的事件。
credit indices 信用指數 跟蹤買入針對某組合內所有企業的信用保護所需費用的指數。
CreditMetrics 計算信用VaR的一個過程。
credit migration 信用轉移 公司由某一信用等級變為其他信用等級的事件。
credit rating 信用評級 對債券發行方的資信狀況進行度量的方式。
credit ratings transition matrix 信用遷移矩陣 一種表現公司在一定時間裡由某一信用等級變為其他信用等級概率的表格。
credit risk 信用風險 在衍生產品交易中因為交易對手的違約而造成的風險。
Credit Risk Plus 計算信用在險價值的一種方法。
credit spread 信用價差 買入信用保護的費用,該術語也用於描述可能會違約的債券的收益率與無風險利率之差。
Credit Support Annex 信用支持附件 ISDA主協議的一部分,用於明確擔保品的安排。
credit transition matrix 見信用遷移矩陣(credit ratings transition matrix)。
credit value adjustment 信用價值調整量 衍生產品交易商根據交易對手違約的可能性而對衍生產品交易的價值進行的調整。
credit value at risk 信用在險價值 對應於一定置信水平,信用損失所不會超出的數量。
crowdfunding 眾籌 利用在線平臺為項目或公司提供眾籌資金。
cryptocurrency 加密貨幣 一種被設計用於提供安全交換媒介的加密數字貨幣。
CSA 見信用支持附件(Credit Support Annex)。
cumulative distribution function 累積分佈函數 變量小於x的概率與x(為自變量)的函數關係。
cure period 補救期 在雙邊清算的場外衍生產品交易中,從違約事件發生到將交易平倉所需要的時間。
currency swap 貨幣互換 某種貨幣的本金及利息同另外一種貨幣的本金及利息進行交換的合約。
current exposure method 現期敞口法 一種計算《巴塞爾協議Ⅰ》和《巴塞爾協議Ⅱ》中衍生工具違約風險敞口的方法,它將違約風險敞口設置為等於當前風險敞口加上一個附加數。
current VaR or ES 當前VaR或ES 使用最新數據而不是承壓期數據計算的當前VaR或ES。
curvature gamma。
CVA 見信用價值調整量(credit value adjustment)。
D
day count 計息天數 為了計算利息而設定的用於確定天數的方法。
day trade 日內交易 在某天進入並在同一天進行平倉的交易。
debit value adjustment 債務價值調整量 衍生產品交易商因為自己本身違約的可能性而對衍生產品交易價值進行的調整。
default correlation 違約相關性 用於計量兩個實體同時違約的趨勢。
default intensity 違約密度 見風險率(hazard rate)。
deferred annuity 延遲年金 在該年金合約中,為產生年金而進行付款的時間與年金開始的時間有一段距離。
defined benefit plan 固定收益計劃 在這種養老計劃中,僱員在退休後所得到的養老金數量由該計劃事先定義,通常計算方式是由一個與僱員為公司服務的時間以及僱員的工資有關的公式。
defined contribution plan 固定供款計劃 在這種養老計劃中,僱主及僱員的供款均被存入專一賬戶並進行投資。當僱員退休時,賬戶內的資金數量轉換為年金,有時僱員可以選擇一次性支付。
deleveraging 去槓桿化 個人和公司減少貸款的行為。
delivery price 交割價格 在遠期合約中收到或付出的價格。
delta 衍生產品價格變化同標的資產價格變化的比率。
delta hedging delta對衝 可使衍生產品交易組合價格與標的資產價格變化無關的一種對衝機制。
delta-neutral portfolio delta中性交易組合 delta為0的交易組合,這種交易組合的價格同標的資產價格的微小變化無關。
dependence 相關性 如果已知變量b的取值會對變量a的概率密度產生影響,我們稱變量a與變量b具有相關性。
deposit insurance 存款保險 政府提供的當銀行違約時,對存款人的存款資金提供保障的保險承諾。
DerivaGem 在作者網頁上可以下載的可用於計算期權價值的軟件。
derivative 衍生產品 價格取決於另外一種資產價格的產品。
deterministic variable 確定性(非隨機)變量 將來的值可以確定的變量。
DFAST 《多德-弗蘭克法案》壓力測試 美國對合並資產超過100億美元的銀行進行的壓力測試。
digital currency 數字貨幣 僅以數字形式提供的貨幣類型,不可用作鈔票或硬幣。
directed brokerage 定向經紀 這是一種共同基金與經紀商之間的不當行為,其中經紀商向共同基金推薦客戶,作為回報,共同基金將自己的交易通過該經紀商進行。
dirty price of bond 債券帶息價格(髒價) 債券的現價。
discount bond 折扣債券 見零息債券(zero-coupon bond)。
discount instrument 貼現金融工具 不提供息票的產品,例如短期國債。
discount rate 貼現率 由國庫券或類似工具的價格與面值的比率所得出的年回報率。
disintermediation 脫媒 更少使用媒介的變化。
distance to default 違約距離 會導致違約發生的資產價格的變動量,該量以標準差的倍數表示。
diversification 分散化 將交易組合分散到不同資產所帶來的分散效應。
dividend 股息 向股票持有者支付的現金回報。
dividend yield 股息收益率 股息與股票價格的比率。
Dodd-Frank Act 《多德-弗蘭克法案》 信用危機後美國設立的新法案,其目的是保護消費者和投資者、避免未來對銀行的救助、更加審慎地對金融系統進行監督等。
dollar convexity 絕對額凸性 等於與利率有關的組合的凸性乘以組合的價值。
dollar duration 絕對額久期 等於與利率有關的組合的久期乘以組合的價值。
down-and-in option 下跌敲入期權 標的資產的價格下跌到一定水平之後,這一期權會生效。
down-and-out option 下跌敲出期權 標的資產的價格下跌到一定水平之後,這一期權失效。
downgrade trigger 降級觸發(信用扳機) 當交易對手的信用級別低於一定水平時,交易商可以將現行交易進行平倉的條款。
duration 久期 債券平均壽命的度量值,它也是債券價格變化同債券收益率變化的比率。
duration matching 久期匹配 將資產與負債的久期進行匹配的一種做法。
Dutch auction 荷蘭式拍賣 在這種拍賣過程中,投資者表明希望買入的股票的數量及價格,假設所有被拍賣股票數量為N,將市場清盤的最高價格為P,其中P表示投資者願意以這一價格或更高的價格買入N份股票;在競標時出價高於P的投資者會得到滿足,競標價格等於P的投資者會得到申購股票數量的一部分。
DVA 見債務價值調整量(debit value adjustment)。
DV01 所有期限的利率變動1個基點所帶來的影響。
dynamic hedging 動態對衝 定期調節標的資產的數量以對衝期權頭寸的過程,對衝的目的通常是保證交易組合的頭寸保持風險中性。
dynamic scenarios 動態場景 在考慮市場變量的不利情形時,包括了公司對不利情形的應對措施。
E
EAD 見違約敞口(exposure at default)。
early exercise 提前行權 在到期日之前行使權利。
early termination event 提前終結事件 由於交易對手違約而造成的場外交易的一方提前終止交易合約的事件。
economic capital 經濟資本金 銀行自己計算的對資本金的需求量。
efficient frontier 有效邊界 投資者的預期回報與回報標準差之間的最佳替換關係。
efficient market hypothesis 有效市場假說 該假說認為資產價格反映了有關信息。
electronic trading 電子交易 通過計算機系統來匹配買賣雙方的交易。
embedded option 內含期權 作為其他產品中不可分割的一部分的期權。
empirical research 實證研究 基於市場歷史數據的研究方式。
endowment life insurance 儲蓄壽險 這類保險中的、事先約定的賠償額是在投保人死亡或合同到期二者中較早的一個時間一次性支付。
enterprise risk management,ERM 企業風險管理 從整體上管理企業風險的方法。
equity swap 股票互換 股票組合的回報與固定利率或浮動利率進行交換的合約。
equity tranche 權益檔 標的投資組合派生出的分檔資產中最早承擔損失的一部分。
ERM 見企業風險管理。
ES 見預期虧空。
Eurocurrency 歐洲貨幣 一種脫離貨幣發行國的貨幣當局正式控制的流動性貨幣。
Eurodollar 歐洲美元 美國以外的銀行所持的美元。
Eurodollar futures contract 歐洲美元期貨合約 以歐洲美元利率為標的期貨合約。
Eurodollar interest rate 歐洲美元利率 歐洲美元存款的利率。
European option 歐式期權 只能在期權到期日才能被行使的期權。
event of default 違約事件 類似於破產、不能維持支付義務或不能支付抵押品的事件。
EWMA 指數加權移動平均
exception 異常情況 實際損失超出VaR估計的情況。
excesscost layers 額外損失層 保險公司的某類業務的在一定範圍之內的損失。
excess kurtosis 超額峰度 用以描述與正態分佈相比,某概率分佈的尾部厚薄程度的測度。
excess spread 額外利差 向分檔持有者支付回報的總和小於標的資產收入利息的總和的情況。
exchange-traded fund 交易所交易基金 允許機構投資者隨時將基金份額轉換為標的股票,或將股票轉換為基金份額的基金。
exchange-traded market 場內交易市場(交易所交易市場) 由交易所(例如紐約股票交易所及芝加哥期權交易所)組織的交易市場。
ex-dividend date 除息日 當宣佈股息時,除息日也被確定下來,在除息日之前買入股票的投資者可以得到股息。
exercise price 執行價格 在期權合約中買賣標的資產的價格,也被稱為敲定價格(strike price)。
exotic option 奇異期權 非標準化的期權。
expectations theory 預期理論 該理論認為遠期利率等於預期的未來即時利率。
expected shortfall,ES 預期虧空 在損失分佈的(100-X)%尾部條件下,在N天內的損失期望值,N為展望期,X%為置信水平。
expected tail loss 預期尾部損失 見預期虧空(expected shortfall)。
expected value of a variable 變量的期望值 變量按出現概率為權重得出的加權平均值。
expense ratio 費用比率 基金的費用與所管理的資產的比率。
expiration date 到期日 合約期限的最終日。
exponentially weighted moving average model 指數加權平均移動模型 按時間回溯時,對變量的歷史數據權重以指數下降的方式進行加權平均來產生預測的模型,有時這種模型用來計算VaR求解過程中的方差及協方差。
exponential weighting 指數加權 觀察值的權重與數據的新舊有關的加權方式,對於t期觀察值的權重等於λ乘以t-1時刻的權重,其中的λ<1。
exposure at default 違約敞口 在違約發生時可能損失的最大數量(這裡假設違約資產沒有任何回收價值)。
extreme value theory 極值理論 一種由某些數據來估計分佈尾部形狀的理論。
F
factor 因子 不確定性的來源。
factor analysis 因子分析 一種從描述變化的大量相關變量提取出少量的主要因子的分析方法,這一方法與主成分分析法(principal component analysis)類似。
factor Copula 因子Copula模型 涉及多個變量的Copula,其中以因子模型描述經變換後的變量的相關性結構。
factor loadings 因子載荷 在因子模型中,當只有一個單位的特定因子,而其他因子的單位均為0時,變量的數值。
factor model 因子模型 假定一組相關變量與一組相互獨立變量存在線性關係的模型。
factor scores 因子得分 在因子模型中,觀測到的變量中某一因子的數量。
fair value accounting 公允價值會計準則 以市場價格將資產計入賬戶的做法。
FICO FICO信用得分 由Fair Isaac公司(Fair Isaac Corporation)研發出的信用評分。
financial intermediary 金融中介 促進經濟中不同主體之間的資金流動的銀行或金融機構。
FinTch 金融科技 技術在金融中的應用。
firm commitment 包銷形式 投行對新發行證券的銷售價格進行承諾,如果沒有投資者買入證券,投行就必須自己買入。
fixed annuity 固定年金 年金的支付數額被事先約定。
floor 下限 見利率下限(interest rate floor)。
floor-ceiling agreement 上下限合約 見上下限期權(collar)。
floorlet 單區間下限 利率下限交易中一個組成部分。
floor rate 下限利率 在下限合約中所闡明的利率。
foreign currency option 外匯期權 有關匯率的期權。
forward contract 遠期合約 規定持有者在將來某約定時刻按指定價格買入或賣出某種資產的合約。
forward exchange rate 遠期匯率 一個單位外匯的遠期價格。
forward interest rate 遠期利率 由當前市場利率所得出的將來某時間的利率。
forward price 遠期價格 遠期合約中使得合約價值為0的交割價格。
forward rate 遠期利率 參見遠期利率(forward interest rate)和遠期匯率(forward exchange rate)。
forward rate agreement,FRA 遠期利率協議 交易雙方達成的在將來某時刻按某種利率對一定本金計息的協議。
front-end load 前端收費 投資者首次買入基金份額時支付的費用。
front office 前臺 金融機構中負責進行交易的部門。
front running 搶先交易 在基金進行大筆股票交易之前,提前在個人賬戶進行交易的行為。
FRTB 見交易賬戶基本審查(Fundamental Review of the Trading Book)。
Fundamental Review of the Trading Book 交易賬戶基本審查 巴塞爾委員會提出的新的計算市場風險資本金的方法。
funds of funds 基金的基金 投資於不同的對衝基金的基金。
futures contract 期貨合約 一種規定持有者在將來某時刻按約定價格買賣資產的合約,此合約每天都要進行結算。
futures option 期貨期權 一種關於期貨的期權。
futures price 期貨價格 期貨合約中的當前交割價格。
G
G-30 Policy Recommendations 30人課題組報告 由一組非監管人員在1993年提出的關於衍生產品問題的建議。
gamma 產品的delta變化與資產價格變化的比率。
gamma-neutral portfolio gamma中性交易組合 gamma為0的投資組合。
gap management 缺口管理 保證資產和負債得到匹配的管理過程。
GARCH model GARCH模型 用於預測波動率的模型,此模型的方差具備均值迴歸特性。
Gaussian Copula model 高斯Copula模型 基於多元正態分佈的Copula模型。
Girsanov’s theorem 哥薩諾夫定理 該定理描述了當我們從具有一定風險偏好的世界轉移到另外一個具有一定風險偏好的世界時,隨機變量的漂移項將有所變化,而波動率項保持不變。
Glass-Steagall Act 《格拉斯-斯蒂格爾法案》 美國通過的關於商業銀行與投資行分業經營的法案。
global systematically import bank,G-SIB 全球系統性重要銀行
greek letters 見希臘值(greeks)。
greeks 希臘值 delta、gamma、vega、theta及vega等對衝參數。
gross income 總收入 淨利息收入加上非利息收入。
group life insurance 團體人壽保險 通常由僱主為其僱員安排的團體性人壽保險。
H
haircut 折減 計算擔保品價值時,對用於擔保的資產價格的折扣。
hazard rate 風險率 在沒有前期違約的條件下,對較短一段時期內的違約概率的度量值。
heating degree days,HDD 取暖天數 日平均溫度低於華氏65°的天數與0兩者中的較大者,這裡平均溫度為一天中最高溫度與最低溫度的平均值(子夜到子夜)。
hedge 對衝 用於減小風險的交易。
hedge funds 對衝基金 這類基金所受限制要遠少於共同基金,它們可以利用衍生產品,採用做空交易策略,但是不能向公眾發行證券。
hedger 對衝者 開展對衝交易的個人。
hedge ratio 對衝比率 對衝產品的頭寸與被對衝頭寸的比率。
high-frequency trading(HFI) 高頻交易 使用計算機算法產生的交易。
high water mark clause 高潮位標記條款 該條款闡明前期損失必須在全部補齊的情況下,業績提成才適用。
historical default probabilities 歷史違約概率 由歷史數據估算出的違約概率。
historical simulation 歷史模擬法 基於歷史數據的模擬方式。
historic volatility 歷史波動率 由歷史數據估算出的波動率。
holiday calendar 假期日曆 用於定義哪些天是假期的日曆,這一日曆的目的是確定金融交易的付款日期。
hurdle rate 門檻回報率 只有在業績超出這個最小回報率時,績效費才適用。
hybird approach 混合型方法 將不同類型經濟資本金進行彙總的方法。
I
IFRS 9 國際財務報告準則第9號 一項新的會計準則,要求銀行在考慮預期違約損失的情況下對貸款進行估值。
implied default probability 隱含違約概率 見風險中性違約率(risk-neutral default probability)。
implied volatility 隱含波動率 在布萊克-斯科爾斯-默頓模型(或類似擴展模型)的期權價格中隱含的波動率。
inception profit 起始盈利 由於衍生產品的賣出價格高於理論價值所產生的盈利。
incremental risk charge 增量風險資本計提 《巴塞爾協議Ⅱ.5》中增加的對交易賬戶上對信用敏感的產品的資本金要求。該資本金是為了改變銀行賬戶上的產品需要的資本金數量比交易賬戶上同等風險的產品少的局面。
incremental value at risk 增量VaR 投資組合中包含某頭寸的VaR與不包含某頭寸的VaR之差。
independence 無關 如果已知變量b的取值對變量a的概率密度沒有影響,則稱變量a與變量b無關。
independent amount 獨立金額 在雙邊場外衍生產品交易中,交易商要求的與現有交易價值無關的擔保品的數額。
index fund 指數基金 基金的目的是跟蹤某個股票指數。
initial margin 初始保證金 在最初期貨交易時交易員需要付出的現金保證。
initial public offering,IPO 首次公開募股 指公司第一次面對公眾發行股票。在IPO之前,一般只有公司的創立人、僱員及其他風險投資者(venture capitalist)持有公司的股權。
instantaneous forward rate 即時遠期利率 對應將來某一很短時間段的遠期利率。
interest rate cap 利率上限 在利率高於一定水平時,這種期權會產生回報,這裡對應的利率為需要定期設定的浮動利率。
interest rate collar 利率上下限 一個利率上限及利率下限的組合。
interest rate derivative 利率衍生產品 衍生產品的回報取決於將來的利率。
interest rate floor 利率下限 在利率低於一定水平時,這種期權會產生回報,這裡對應的利率為需要定期設定的浮動利率。
interest rate option 利率期權 回報取決於將來利率水平的期權。
interest rate swap 利率互換 固定利率與浮動利率的互換合約,雙方用於計算利息的本金相同。
internal credit rating 內部信用評級 金融機構本身(而不是穆迪或標準普爾等評級機構)所給出的信用評級。
in-the-money option 實值期權 這種期權可為:①資產價格大於執行價格的看漲期權;②資產價格低於執行價格的看跌期權。
intrinsic value 內在價值 對於看漲期權,此價值等於資產價格超出執行價格的數量與0二者中的較大值;對於看跌期權,此價值等於執行價格超出資產價格的數量與0二者中的較大值。
investment asset 投資資產 出於投資目的而被大量個人擁有的資產。
investment bank 投資銀行 為公司發行證券和股票的銀行。
investment grade 投資級產品 信用級別高於BBB(BAA)的債券及金融工具。
IRB approach 內部評級法 《巴塞爾協議Ⅱ》中規定用於計算信用風險資本金的方法。
IRC 見增量風險資本金(incremental risk charge)。
ISDA 國際互換和衍生產品協會
ISDA Master Agreement ISDA主協議 場外衍生產品交易雙方簽署的規範交易的協議。
Isserlis'theorem Isserlis定理
iTraxx 由歐洲125家投資級公司所組成的信用指數。
J
jump-to-default risk 突發違約風險 某公司違約的風險,該風險與信用價差的變動風險相對,後者指公司在不違約的情況下,信用價差的變動。
junk bond 垃圾債券 非投資級債券。
K
key risk indicators 主要風險指標 跟蹤操作風險水平的指標。
kurtosis 峰度 用於描述分佈尾部肥瘦的度量值。
L
late trading 延遲交易 在下午4點以後下單,並以下午4點的價格買入或賣出基金份額的行為。
leveraging 槓桿化 個人或公司加大借貸力度的行為。
LGD 見違約損失(loss given default)。
liar loan 騙子貸款 這種貸款的申請人在填寫貸款申請表時撒謊。
LIBOR 見倫敦銀行間同業拆借利率(London interbank offer rate)。
LIBOR-in-arrears swap LIBOR後置互換 在該互換交易中,某天支付的利率取決於當日觀察到的利率水平(而不是取決於前一個付款日所觀察到的利率)。
LIBOR-OIS spread LIBOR-OIS利差 特定期限的LIBOR利率與隔夜指數利率之差。
LIBOR/swap zero curve LIBOR/互換零息利率曲線 由LIBOR利率、歐洲貨幣期貨及互換利率所計算出的零息利率曲線,利率為時間的函數。
LIBOR zero curve LIBOR零曲線 見LIBOR/互換零息利率曲線(LABOR/swap zero curve)。
life insurance 人壽保險(壽險) 保險償付取決於某人是否健在。
linear model 線性模型 在線性模型中,投資組合的價格與標的市場變量存在某種線性關係。
linear product 線性產品 價格與一個或多個標的資產變量有著某種線性關係的衍生產品。
liquidity-adjusted VaR 經流動性調節的VaR 包含交易平倉時買賣價差的VaR數額。
liquidity black holes 流動性黑洞 因所有投資者均處於市場同一側所引起的流動性枯竭。
liquidity coverage ratio 流動性覆蓋比率 在受壓情況下30天內,高流動性的資產對流出資金數額的比率。
liquidity funding risk 融資流動性風險 融資來源枯竭的風險。
liquidity preference theory 流動性偏好理論 這一理論的結論是遠期利率會高於預期的將來即期利率。
liquidity premium 流動性利差 遠期利率超出預期的將來即期利率的數量。
liquidity trading risk 交易流動性風險 一個資產的賣出價格不能達到其理論價格的風險。
living will 遺囑 對金融機構進行有序清盤,使其部分得以存續的計劃。
lognormal distribution 對數正態分佈 一個變量服從對數正態分佈是指當這一變量的對數服從正態分佈。
London interbank offered rate 倫敦銀行間同業拆借利率 評級為AA的銀行從同業銀行借款所需支付的利率。
longevity bond 長壽債券 這類債券事先定義一個人群,在某時刻,債券支付的票息與該人群中還健在的人數成正比。
longevity risk 長壽風險 對保險公司而言,一個人活得比預期壽命更長所帶來的風險。
long position 多頭 買入某項資產時所處的頭寸。
long-tail risk 長尾風險 長尾風險是指在財產及意外傷害險合同到期後經過很長時間出現索賠的可能性。
lookback option 回望期權 在到期日的回報和資產價格在一段時間內的最大值或最小值有關的期權。
loss given default 違約損失 在對手違約時的損失與風險敞口的比率。
M
MaCauley’s duration 麥考利久期 等於現金流的收入時間的加權平均,權重等於現金流的貼現值與整體現金流貼現總和的比。
machine learning 機器學習 人工智能的一個分支,允許計算機在沒有明確編程的情況下學習。
maintenance margin 維持保證金 當交易員的保證金低於一定水平時,交易員會被要求增加保證金,以使得保證金恢復到初始保證金水平。
margin 保證金 期貨或期權交易員必須維持的現金(或存入的證券)餘額。
margin call 保證金催付通知 當保證金賬戶內的餘額低於一定水平時,要求增加額外的保證金。
marginal distribution 邊際分佈 隨機變量的非條件分佈。
margin period of risk 見補救期(cure period)。
marginal value at risk 邊際VaR 隨著投資組合中一個組成部分的增加出現的VaR的變動率。
market maker 做市商 對一項資產同時給出買入價與賣出價這兩種報價的交易員。
market model 市場模型 被交易員廣泛採用的模型。
market portfolio 市場投資組合 包含所有可能投資的投資組合。
market risk 市場風險 由市場變量變化所帶來的風險。
market timing 擇時交易 擇時交易是指基金經理允許一些特殊的客戶頻繁交易基金的份額,以從未及時更新的部分資產價格中漁利的行為,或進行延遲交易來牟利。
marking to market 盯市計價(逐市定價) 為反映市場變量的當前市場價格,而對產品重新定價的過程。
marking to model 以模型定價 利用模型來確定當前資產的做法。
maturity date 到期日 合約的最終到期時間。
maximum likelihood method 最大似然估計法 一種計算參數的方法,由這一方法得出的參數可以保證出現觀察值的概率達到極大。
mean reversion 均值迴歸 波動率或利率等市場變量,長期向平均水平迴歸的傾向。
Merton’s model 默頓模型 這一模型利用股票價格來估計違約概率(其他由默頓研發出的模型也被稱為默頓模型)。
mezzanine tranche 中間分檔 損失發生在權益檔之後,但在高級檔之前的分檔。
middle office 中臺 銀行中的市場風險管理部門。
minimum transfer amount 最小轉移數量 抵押協議中規定的最小的擔保品支付數量。
model-building approach 模型構建法 一種計算VaR的方法。
model risk 模型風險 利用模型來對衍生產品定價時所帶來的風險。
modified duration 修正久期 一種對標準久期的修正,其目的是更加準確地描述債券價格變化同收益率實際變化的比率關係,修正久期考慮了收益率報價的計息頻率。
money center banks 貨幣中心銀行 在世界範圍內運營,並且資金主要來自批發市場的銀行。
Monte Carlo simulation 蒙特卡羅模擬 一種對市場變量進行隨機抽樣的過程。
moral hazard 道德風險 某一受保主體因為保險合約的存在而改變自身行為舉止所帶來的風險。
mortality risk 死亡風險 一個人比預期提前死亡而帶來的風險。
multibank holding company 多銀行控股公司 即對多家銀行進行持股的公司,設立控股公司的目的是繞過美國的一些銀行監管規定。
multivariate normal distribution 多元正態分佈 多變量的聯合分佈,其中任意單一變量均服從正態分佈。
mutual fund 共同基金 為眾多小型投資者提供的一種投資形式,在某些國家也被稱為是單位信托(unit trust)。
N
naked position 期權裸空頭 一個不與標的資產多頭相結合的看漲期權空頭。
National Association of Insurance Commissioners,NAIC 美國保險監理官協會 在美國為各州保險行業的監管機構提供服務的組織。
negative feedback trading 負反饋交易 在資產價格上漲時賣出、下跌時買入的交易行為。
net asset value 淨資產價值 基金價值除以基金的份額所得的數量。
net interest income 淨利息收入 銀行的利息收入與利息支出之差。
net replacement ratio 淨替換比率 對當前敞口進行軋差與不進行軋差所得的比率。
net stable funding ratio 淨穩定資金比率 可獲得資金的加權平均與所需要資金加權平均的比率。
netting 軋差 在對手違約時能夠使具有正價值的交易與負價值的交易相互抵消的能力。
neural networks 神經網絡 一種機器學習工具,允許計算機識別模式。
NINJA “忍者” 沒有工作、沒有收入、沒有資產的信用差的貸款群體。
node delta 節點delta 當期限結構為分段線性時,在保持其他點不變的情況下將一個頂點對應的利率改變一個基點對投資組合的影響。
non-investment grade 非投資級 信用級別低於BBB(BAA)的債券或其他產品。
nonlife insurance 非人壽保險 見財產及意外傷害險(property-casualty insurance)。
nonlinear product 非線性產品 產品的價值與標的變量不呈線性關係的衍生產品。
nonperforming loan 不良貸款 利息拖欠已經超過了90天的貸款。
nonsystematic risk 非系統性風險 可以被分散的風險。
normal distribution 正態分佈 統計上標準的鐘形分佈。
normal market 正常市場 期貨價格隨著期限增大而增加的市場。
notional principal 名義本金 用於計算利率互換付款額的本金數額,這裡的本金是一種名義上的形式,因為它有時不被實際支付。
numerical procedure 數值方法 在沒有解析公式時所採用的計算方法。
O
objective probability 客觀概率 基於數據的概率。
offer price 見賣出價(ask price)。
OIS 見隔夜指數互換(overnight indexed swap)。
OIS rate OIS利率 固定利率在OIS互換中轉換為隔夜利率的幾何平均值。
open-end fund 開放式基金 開放式基金的份額數量隨投資者買入或賣出基金份額而變化。
open interest 未平倉合約 期貨市場上存在的多頭總量(等於市場上的空頭總量)。
open outcry 公開喊價 交易員在交易大廳相見並以喊價的形式報價的一種交易方式。
operational risk 操作風險 指不完善或存在問題的內部程序、員工和信息科技系統以及外部事件所造成的風險。
option 期權 買入或賣出資產的權利。
organized trading facility 有序交易設施 標準場外衍生產品的電子交易平臺。
originate-to-distribute model 發起-分銷模式 這一術語是指銀行發行貸款、信用卡應收款等資產,然後將這些資產進行證券化來將信用風險轉移給其他投資者的過程。
OTC market 見場外市場(over-the-counter market)。
OTF 見有序交易設施(organized trading facility)。
out-of-the-money option 虛值期權 這種期權可以是:①資產價格低於執行價格的看漲期權;②資產價格高於執行價格的看跌期權。
outside-model hedging 模型外對衝 對那些在模型中被假設為常數的變量進行對衝(與模型內對衝(within-model hedging)相對)。
overcollateralization 超額抵押 抵押資產的面值比生成的分檔證券的面值更高的情形。
overnight indexed swap 隔夜指數互換 以一段時間內隔夜利率的幾何平均交換某一固定利率的互換協議。
over-the-counter market 場外市場(櫃檯市場) 交易員之間直接交易而不經過交易所的交易市場。交易方通常是為金融機構、企業或基金經理等。
P
P2P Lending P2P貸款 在不涉及銀行或類似中介機構的情況下通過在線平臺向借款人借款。
P&L Attribution 日均損益原因分析 對每天的收益和損失的原因進行的分析。
parallel shift 平行移動 零息利率曲線上每一點移動相同數量的變動形式。
partial duration 局部久期 零息利率曲線上某一點變化所引起的交易組合價值的百分比變化。
partial expected shortfall 局部預期虧空 組合資產的一部分預期虧空。
partial simulation approach 部分模擬法 一種計算VaR的方法,其中通過希臘值和泰勒展開來取得投資組合價值變化的近似值。
par value 面值 債券的本金數量。
par yield 票面收益 使得債券價格等於本金的息票。
payoff 到期收益 期權或其他衍生產品的持有者在產品到期時所收到的付款。
peak exposure 峰值敞口 將來某一時間預期風險敞口分佈上較高分位數(如97.5%)的值。
performing loan 良好貸款 貸款的利息的拖欠時間沒有超出90天。
permanent life insurance 見終身壽險(whole life insurance)。
physical default probability 真實世界違約概率 見歷史違約概率(historical default probability)。
plain vanilla 普通 用於描述標準交易的術語。
poison pill 毒丸 公司採取行動來使其他公司對其兼併變得更加困難的做法。
Poisson distribution 泊松分佈 在泊松過程中,在一定時間內一定數量的事件發生的概率分佈。
Poisson process 泊松過程 描述事件產生次數的一種隨機過程,在任意時間段Δt內,事件產生的概率為λΔt,其中λ為過程的密度。
policyholder 投保人 保險單的持有者。
portfolio immunization 組合免疫 保證投資組合與利率相對不敏感的一種做法。
portfolio insurance 組合資產保險 投資組合經理進行交易以保證組合的價值不會低於一定的水平的做法。
positive feedback trading 正反饋交易 在資產價格下降時賣出,或在資產價格上升時買入的交易。
positive semidefinite 半正定 確保方差-協方差矩陣有效的一個必要條件。
power law 冪律 描述實際中遇到的概率分佈尾部狀態的一種法則。
predatory trading 掠奪性交易 指市場參與者A預計另外一個市場參與者B將進行某一種交易,而這種交易一旦發生,將會對市場走勢產生顯著的影響,因此A決定提前進行與B的交易類似的交易。根據具體的情況,掠奪性交易可能是合法的,也可能是非法的。
premium 收費 一般指買入期權或保險合同需要繳納的金額。
prime broker 機構經紀人 銀行作為機構經紀人是指銀行替對衝基金的交易進行清算、向對衝基金提供貸款及其他服務等。
principal 本金 債務性工具的面額。
principal components analysis 主成分分析法 一種從描述某種變化關係的大量的相關變量中提取少數主要因子的分析方法(與因子分析法類似)。
private placement 私募 不向公眾公開銷售,而僅面對少數金融機構或個人的新發證券銷售過程。
probability of default,PD 違約概率
property-casualty insurance 財產及意外傷害險 財產險為投保人的財產損失提供保險,意外傷害險為投保人的法律責任,以及對於第三者財物或身體的意外傷害提供保險。
proprietary trading 自營交易 金融機構為自身賬戶進行交易,而不是替客戶進行交易的行為。
public offering 公募 向大眾出售證券的過程。
put-call parity 看跌看漲期權平價關係 具有同樣執行價格以及期限的歐式看漲期權和歐式看跌期權所滿足的關係式。
put option 看跌期權 在將來某時刻可以按指定價格賣出某項資產的權利。
puttable bond 可提前退還債券 持有此債券的投資者在將來某時刻以指定價格將債券賣給債券發行人。
puttable swap 可贖回互換 一方有權提前中止的互換協議。
Q
QIS 見定量影響研究(quantitative impact study)。
quadratic model 二次型模型 投資組合價值的變動與市場變量的百分比變化之間存在的二次型關係。
quantitative impact studies 定量影響研究 巴塞爾委員會關於新規定對於銀行資本金的影響的定量研究。
R
RCSA 風險控制和自我評估 一種評估操作風險的方法。
real world 真實世界 我們所生活的世界與風險中性世界相對。後者是我們對衍生產品定價時所用到的虛擬世界。
rebalancing 再平衡 對交易頭寸的調整,其目的是保證delta中性。
recovery rate 回收率 違約時債券收回的價值與面值的比率。
reference entity 參照實體 信用違約互換合約中違約保險所針對的公司或國家。
RegTech 監管科技 金融機構使用技術來提高監管和合規性。
regulatory arbitrage 監管套利 以減少金融機構的監管資本金為目的而進行交易的行為。
regulatory capital 監管資本金 監管機構要求金融機構必須持有的資本金。
rehypothecation 再抵押融資 以某一交易對手提供的擔保品作為擔保品來滿足另外的抵押要求的做法。
reinsurance 再保險 保險公司將風險轉給其他公司的做法;當然,承接風險的公司會得到補償。
reintermediation 復媒 脫媒後新中介體的發展。
repo 回購 回購協議的簡稱,這種協議的一方賣出證券借入資金並約定在今後以稍高價格購回。
repo rate 回購利率 在回購協議中採用的利率。
required stable funding factor,RSF factor 所需穩定資金因子 計算淨穩定資金比率時用到的權重因子。
reserve requirement 準備金要求 即將存款的一定比率存入中央銀行的規定。
reset date 定息日 在互換及上限/下限協議中,一個設定下一時間段內利率的日期。
retail banking 零售銀行 從零售客戶吸收小額存款並向他們發放小額貸款的銀行業務。
reverse stress testing 逆向壓力測試 通過算法來搜索導致重大損失的壓力情形的做法。
reversion level 迴歸水平 市場變量的值(例如波動率)迴歸均值的傾向。
reversion rate 迴歸率 市場變量回歸均值的變化率。
rho 衍生產品價格變化同利率變化的比率。
right-way risk 正向風險 當交易商對某交易對手的風險敞口增大時,交易對手的違約風險反而降低的情況。
risk-adjusted return on capital,RAROC 風險調整後的資本回報率
risk appetite 風險偏好 金融機構關於自身能夠承受的風險水平的聲明。
risk culture 風險文化 某機構中對待風險的態度。風險文化的一個重要方面是關於機構的僱員如何處理短期效益與長期風險之間的矛盾關係。
risk factor 風險因子 隨著時間變化的市場變量,如匯率、商品價格、利率。
risk weight 風險權重 在加權敏感度法中是一個風險因子日標準差波動率的倍數。
risk-free rate 無風險利率 不承擔任何風險就可以得到的利率。
risk-neutral default probability 風險中性違約概率 由信用價差隱含出的違約概率。
risk-neutral valuation 風險中性定價 在期權及其他衍生產品定價中假設世界為風險中性,風險中性定價給出的價格不只是對於風險中性世界而言,在所有世界中均是正確的。
risk-neutral world 風險中性世界 在這一世界中,投資者為所承擔的額外風險不索取額外回報。
risk-weighted amount 風險加權量 見風險加權資產(risk-weighted assets)。
risk-weighted assets 風險加權資產 《巴塞爾協議Ⅰ》和《巴塞爾協議Ⅱ》中的一種計量資產數量的方式,其要求總資本至少是風險加權資產的8%。
robo-advisers 機器人投顧 在線財富管理服務提供商。
robotics process automation 機器人流程自動化 一種軟件應用程序,計算機可以與現有計算機系統交互。
roll back 倒推 倒退歸納法。
S
SA-CCR 一種在使用標準法時計算違約風險敞口的方法。
Sarbanes-Oxley Act 《薩班斯-奧克斯利法案》 美國於2002年通過的法令,其目的是增加上市公司董事、首席執行官及首席財務官的責任。
scenario analysis 情景分析 一種分析市場變量的不同變動對組合價值不同影響的過程,這一術語也用於生成操作風險的損失的不同情形。
scorecard approach 計分卡方式 一種對操作風險的進行自我評估的方法。
SEC 美國證券交易委員會
securitization 證券化 通過將來的現金流來產生證券的過程。
SEF 見互換執行設施(swap execution facility)。
senior tranche 高級分檔 在標的資產違約時,最後承擔損失的分檔。
short position 空頭 交易員賣出自己並不擁有的證券。
short selling 賣空交易 從其他投資者那裡借入資產並在市場上變賣的交易形式。
SIFI 系統性重要金融機構(systemically important financial institution)。
SIMM 見標準初始準備金模型。
simulation 模擬 見蒙特卡羅模擬(Monte Carlo simulation)。
skewness 偏態 用來衡量概率分佈的非對稱性的指標。
Solvency Ⅰ 《償債能力法案Ⅰ》 歐盟從20世紀70年代開始實行的保險公司的監管規定。
Solvency Ⅱ 《償債能力法案Ⅱ》 歐盟設立的關於保險公司監管的新規定,於2016年開始實施。
solvency risk 償還能力風險 負債會大於資產的風險。
sovereign wealth funds 主權財富基金 主權國家設立的投資基金。
specific risk charge 特定風險資本金 對於交易賬戶中特定風險所設定的資本金。
spectral risk measure 光譜型風險測度 對於風險分佈的分位數設定不同權重的風險度量方式。
speculative grade 投機級 見非投資級(non-investment grade)。
speculator 投機者 市場上對資產價格的上漲或下跌下注,並據此開倉的交易者。
spot interest rate 即期利率 見零息利率(zero-coupon interest rate)。
spot price 現貨價格 即期交割的資產價格。
spot volatility 即時波動率 對利率上限定價時,需採用不同波動率對於單一區間上限定價,並以此取得以對整個利率上限定價的波動率曲線。
SR 11-7 美聯儲委員會提供的模型風險管理指南。
standard initial margin model 標準初始保證金模型 由IDSA開發的一個模型,用於計算監管機構對雙邊清算衍生產品組合所需的初始保證金。
standard normal distribution 標準正態分佈 均值為0、標準差為1的正態分佈。
standardized measurement approach 標準計量法 巴塞爾委員會提出的一種計算操作風險資本的方法。
static hedge 靜態對衝 頭寸在設定後無須調整的對衝策略。
static options replication 靜態期權複製 這種對衝方式是找出另一個交易組合使在某個邊界上該交易組合的價值與被對衝產品的價值相等。
stochastic variable 隨機變量 將來取值不確定的變量。
stock index 股票指數 用於跟蹤股票組合的指數。
stock index futures 股指期貨 以股票指數為標的的期貨產品。
stock index option 股指期權 以股票指數為標的的期權。
stock option 股票期權 以單個股票為標的的期權。
stop-loss rule 止損規則 當某頭寸的損失超出一定數量後,必須將頭寸平倉的規定。
storage costs 儲存費用 儲存某種商品的費用。
stressed ES 壓力ES 根據會對金融機構的投資組合價值造成嚴重影響的250天受壓市場條件計算出的ES。
stressed VaR 壓力VaR 根據會對金融機構的投資組合價值造成嚴重影響的250天受壓市場條件計算出的VaR。
stress testing 壓力測試 用於檢驗極端的市場變化對於投資組合價值的影響。
strike price 執行價格(敲定價格) 期權合約中所規定的資產買入或賣出的價格。
structured product 結構性產品 金融機構為了滿足客戶的特殊需求而設計的特殊衍生產品。
student t-Copula 學生t-Copula函數 基於多元t-分佈的Copula函數。
student t-distribution 學生t-分佈 這一分佈比正態分佈有更肥的尾部分佈。
subjective probability 主觀概率 反映了某個人觀點的概率,該概率並不是基於數據得出的。
subprime mortgage 次級按揭貸款 信用質量低於平均質量的按揭貸款。
supplement capital 附加資本金 見第二類資本(tier 2 capital)。
survivor bond 見長壽債券(longevity bond)。
swap 互換協議 以某指定的形式在將來交換現金流的協議。
swap execution facility 互換執行設施 美國用來執行標準場外衍生產品交易的電子化平臺。
swap rate 互換利率 利率互換中保證互換價值為0的固定利率。
swaption 互換期權 一種在將來某時刻可以將固定利率與浮動利率進行互換的期權。
swap zero curve 互換零息利率曲線 見LIBOR/互換零息利率曲線(LIBOR/swap zero curve)。
synthetic CDO 合成CDO 由賣出信用違約互換而創建的CDO。
synthetic option 合成期權 由交易標的資產而創建的期權。
systematic risk 系統性風險 不能被分散的風險。
systemic risk 系統內風險 由一家金融機構違約而引發其他金融機構違約,從而在整個金融體系內形成的風險。
T
tail correlation 尾部相關性 兩個分佈尾部的相關性,用於度量極端事件同時出現的可能性。
tail dependence 尾部相關 檢驗兩個變量在同一時間同時呈現極端取值的頻率。
tail loss 尾部損失 見預期虧空(expected shortfall)。
Taylor series expansion 泰勒級數展開 對於多元變量的函數,在變量變化較小時,這種級數展開將函數價值的變化與變量值的變化聯繫在一起。
teaser rate 前期優惠利率 在按揭的最初2~3年的低利率。
temporary life insurance 見期限壽險(term life insurance)。
terminal value 終端價值 在合約到期時產品的價值。
term life insurance 期限壽險 在這種保險中,如果投保人在一定期限內死亡,保險公司將支付賠償。
term structure of interest rates 利率期限結構 利率與其期限的關係。
theta 隨著時間的推移,期權或其他衍生產品價格的變化率。
threshold 起點金額 在雙邊清算的場外衍生產品交易中,未完結交易的價值超過該額度,交易的一方就需要向另一方提供擔保品。
tier 1 equity capital 第一類股權資本 《巴塞爾協議Ⅲ》中重新定義的股權資本(也被稱為第一類核心資本)。
tier 2 capital 第二類資本 次優先級債務(期限大於5年)及其他類似來源的資本金。
tier 3 capital 第三類資本 短期次優先級債券(期限介於2~5年)。
time decay 時間衰減 見theta。
time value 時間價值 由於當前與到期日之間的時間而產生的期權價值(等於期權價格減去內在價值)。
total expense ratio 總費用比率 財產保險公司的總費用與保費總和的比率。
total return swap 總回報互換 在這一互換協議中,債券等資產的回報與LIBOR加上一個利差進行交換,資產的回報包括息票以及資產價值的變化。
tracking error 跟蹤誤差 以跟蹤股票指數為目標的交易策略產生的誤差。
trading book 交易賬戶 銀行投資組合的一部分,持有這些資產的目的是準備變賣。
trading days 交易日 市場開盤交易的日期。
tranche 分檔 由投資組合產生的證券的一部分,例如ABS的分檔。
transaction costs 交易費用 進行交易而產生的費用(佣金以及取得的價格與產品中間價格的差值,產品中間價格等於買入價與賣出價的平均值)。
treasury bill 短期政府債券 政府發行的用於融資的短期不支付利息的工具。
treasury bond 長期政府債券 政府發行的用於融資的長期帶息工具。
treasury note 中期國債 期限不超過10年的政府債券。
tree 樹 為了給期權及其他衍生產品定價而做出的代表市場變量價值變化的樹形結構。
U
uncleared trades 未清算交易 雙邊清算而不是通過中央對手方清算的交易。
unconditional default probability 無條件違約概率 今天觀測到的,違約發生在將來某時段的概率,該概率可以與條件違約概率進行比較,條件違約概率是指在無前期違約的前提下,違約發生在某個時段的概率。
underlying variable 標的變量 決定期權及其他衍生產品價格的變量。
unit trust 單位信托 見共同基金(mutual fund)。
universal life insurance 萬能壽險 這是終生壽險的一種形式,其中保費數量每年可以有所不同,最終的保險賠償取決於保費、投資表現及費用。
unsystematic risk 非系統性風險 見非系統性風險(nonsystematic risk)。
up-and-in option 上升敲入期權 標的資產的價格上升到一定水平之後,這一期權會生效。
up-and-out option 上升敲出期權 標的資產的價格上升到一定水平之後,這一期權會失效。
V
value at risk,VaR 在險價值 在一定的置信水平之下,損失不會超出的數量。
variable annuity 可變年金 在這種合約中,受益人收到的年金(通常是終身的)數額取決於組合的投資表現。
variable life insurance 變額壽險 這是終生壽險的一種特殊形式,投保人可以指定保費的投資方式。如果投資表現好,投資收入可用來支付保費,在投保人死亡時的賠償有一個最低數量保證,但如果投資表現好,賠償數量會遠遠高於最低數量。
variance-covariance matrix 方差-協方差矩陣 用於表達一系列不同市場變量之間的方差及協方差的矩陣。
variance rate 方差率 波動率的平方。
variation margin 變動保證金 為使得保證金賬戶中的餘額達到一定水平而額外支付的保證金。
Vasicek’s model Vasicek模型 基於高斯Copula函數的違約相關性模型(其他由Vasicek開發出的模型也被稱為Vasicel模型)。
vega 期權或其他衍生產品價格的變化同波動率變化的比率。
vega-neutral portfolio vega中性交易組合 vega為0的投資組合。
VIX index VIX指數 關於標準普爾500指數股指波動率的指數。
volatility 波動率 用於衡量資產所得到回報的不確定性的指標。
volatility skew 波動率傾斜 用於描述非對稱性波動率微笑的術語。
volatility smile 波動率微笑 隱含波動率隨著執行價格的變化。
volatility surface 波動率曲面 揭示隱含波動率隨著執行價格及期限而變的表格。
volatility term structure 波動率期限結構 隱含波動率隨不同期限的變化。
W
waterfall 瀑布現金流 將由標的投資組合所產生的本金現金流和利息現金流進行分配的規則。在一個典型的合約中,利息現金流首先用於兌現對高級分檔收益的承諾,然後剩餘現金流(如果有的話)將按分檔的優先程度依次支付。本金現金流類似,也是高級分檔先收回本金,然後按分檔的優先程度依次贖回。權益分檔總是最後收到本金和利息現金流。
weather derivative 天氣衍生產品 回報取決於天氣的衍生產品。
weighted sensitivity 加權敏感度 用於計算delta的術語。
whole life insurance 終身壽險 這種保險合約為投保人終生提供保險,因此保險一定會支付賠償。
wholesale banking 批發銀行 吸收大額存款併發放大額貸款的銀行業務。
within-model hedging 模型內對衝 對那些在模型中的隨機變量進行對衝(與模型外對衝相對)。
worst case default Rate(WCDR) 最壞違約概率 在某一置信水平下不會超過的違約概率。
writing an option 期權承約 賣出一個期權。
wrong-way risk 錯向風險 對交易對手的風險敞口隨著交易對手違約可能性的增大而增加的情況。
Y
yield 收益率 由產品提供的回報率。
yield curve 收益率曲線 見利率期限結構(term structure of interest rate)。
Z
zero-coupon bond 零息債券 沒有息票的債券。
zero-coupon interest rate 零息利率 無息票債券所對應的收益率。
zero-coupon yield curve 零息利率曲線 零息利率與其期限之間的函數圖。
zero curve 零息曲線 見零息利率曲線(zero-coupon yield curve)。
zero rate 零息利率 見零息利率(zero-coupon interest rate)。
Z-score Z-評分 描述某公司違約可能性的一個數值。
RMFI軟件說明
該軟件可在作者的網站(www-2.rotman.utoronto.ca/~hull/software)上下載。
開始運行軟件
第一次運行一個軟件往往是軟件使用中最困難的一步。下面,我們一步一步介紹如何在RMFI中對一個期權產品定價。
(1)打開Excel文件RMFI.xls。
(2)如果你是Office 2007用戶,單擊屏幕上方的Options(設置)按鈕,然後選擇“Enable this content”。如果你不是Office 2007用戶,你應將Excel Macros(宏)的安全等級設定為Medium(中級)或者Low(低級)。用戶可在Excel中單擊Tools(工具),選擇Macros(宏),再選擇Security(安全),然後選擇適當的安全等級。
(3)在窗口的底部,選擇Equity_FX_Index_Fut_Opts_Calc工作表。
(4)選擇Currency作為標的類型,Binomial American作為期權類型,單擊Put按鈕。不要選擇Imply Volatility選項。
(5)現在,你已經可以對一個外匯的美式看跌期權定價了。輸入參數有7個:匯率、波動率、無風險利率(本幣)、外幣的無風險利率、剩餘期限(以年計)、執行價格和時間步長。將這些參數分別輸入單元格D5、D6、D7、D8、D13、D14、D15,值分別是1.61、12%、8%、9%、1.0、1.60、4。
(6)單擊回車鍵,並單擊Calculate按鈕。你可以看到單元格D20中計算出的期權價格為0.07099。單元格D21~D25顯示了希臘值。
(7)單擊Display Tree 按鈕。我們會看到用於計算期權價值的二叉樹結構。
下一步
現在,你應該可以很容易地在該頁面上對其他期權進行定價。如果要計算隱含波動率,選擇Imply Volatility,然後在單元格D20中輸入期權價格。單擊回車鍵,然後單擊Calculate按鈕。隱含波動率顯示在單元格D6中。
軟件可以顯示各種圖表。要顯示一個圖表,你必須首先指明在縱軸和橫軸上要顯示的變量,以及橫軸的取值範圍。接下來,單擊回車鍵並單擊“Draw Graph”按鈕。
關於這個工作表,其他一些需說明的事項如下:
(1)對股票的歐式期權和美式期權,可以在一個彈出窗口中指定最多10次股息。在第一列中輸入股息的支付日(從今天開始,按年計算),在第二列中輸入股息的數量。股息的輸入必須遵從時間順序。
(2)對美式期權,最多可採用500步二叉樹,但只有10步會被顯示。
(3)除標準看漲期權和看跌期權外,其他期權的希臘值都是通過對輸入參數進行擾動而求得的,而不是通過解析方式求出的。
(4)對亞式期權,Current Average表示從開始到現在的均值。對新的交易(從開始到當前的時間間隔為0),這個值沒有關係。
(5)對回望期權,在計算看漲期權時,使用Minimum to Date的值;在計算看跌期權時,使用Maximum to Date的值。對新的交易,這兩個值都應設為標的資產的當前價格。
(6)利率是連續複利的。
CDS
CDS工作表用來從CDS利差中計算風險率。用戶必須輸入利率的期限結構(連續複利)和CDS期限結構或風險率期限結構二者之一。初始的風險率用在從零時刻起到第一個風險率對應的時刻止的區間,第二個風險率用在從第一個風險率對應的時刻起到第二個風險率對應的時刻止的區間,依此類推。計算中假設違約只發生在兩個付款日期之間的中點。這與附錄K中展示的例子是一致的。
CDO
CDO工作表按照用戶輸入的CDO份額的相關度計算份額的報價(見附錄L)。份額的附著點和分離點由用戶輸入。報價可以是基點數的形式或前端收費的形式。對後一種情況,以基點數計的利差是固定的,前端收費是份額面值的一定比例,來自用戶輸入或隱含地由計算得出(如iTraxx Europe或CDX NA IG股權份額的固定利差為500個基點)。積分點的數量決定了計算的準確度,一般來說10個就可滿足大部分情況的需要(最多為30)。軟件會顯示預期損失佔份額面值的百分比(ExpLoss)和預期收益的貼現值(PVPmts),其中利率為每年10000個基點。利差為ExpLoss×10000/PVPmts。前端費用為ExpLoss-(Spread×PVPmts/10000)。本工作表也可用來隱含地計算份額間的(複合)相關性(compound correlation),或根據用戶輸入的報價計算基礎相關性(base correlation)。為計算基礎相關性,第一個附著點應為0%,而且一個份額的分離點應為下一個份額的附著點。
股票期權功能
Equity Option Functions工作表提供了對一系列不同期權估值的功能。這些函數可以與用戶自己的工作表一起使用,以調查選項的屬性。
VaR
VaR工作表允許使用線性模型(基於初始時刻的模型)來計算單一股票的期權投資組合的在險價值,以及一種生成投資組合可能價值的分析方法。前兩種方法基於第14章的內容。
希臘值
希臘值的定義分別為:
·delta:當標的資產價格增長1美元時,期權價格相應的變化量;
·gamma:當標的資產價格增長1美元時,期權delta相應的變化量;
·rho:當利率增長1%時(例如,利率由5%變為6%),期權價格相應的變化量;
·theta:日曆日往前提進一日時,期權價格的變化量;
·vega:當波動率增長1%時(例如,波動率由20%變為21%),期權價格相應的變化量。
x≥0時N(x)的數表
以下數表列出了對應於x≥0時的N(x)的取值,此數表應該與插值並用。例如:
N(0.627 8)=N(0.62)+0.78[N(0.63)-N(0.62)]
=0.732 4+0.78×(0.735 7-0.732 4)
=0.735 0

x≤0時N(x)的數表
以下數表列出了對應於x≤0時的N(x)的取值,此數表應該與插值並用。例如:
N(-0.123 4)=N(-0.12)-0.34[N(-0.12)-N(-0.13)]
=0.452 2-0.34(0.452 2-0.448 3)
=0.450 9