附錄L
合成CDO及其定價

合成債務抵押債券（CDO）由多個份額構成。在每個份額中，對於特定債券組合在一定範圍內的損失，A方對B方提供補償。相應地，B方同意向A方支付受保護的面值的一定比例，作為買入保護的費用。

假設，對某一特定份額，損失的範圍為從α_L到α_H。變量α_L和α_H分別被稱為附著點（attachment point）和分離點（detachement point）。如果α_L為8%而α_H為18%，則當債券組合的損失介於面值的8%～18%時，A方向B方支付損失的數量。因此，最初8%的損失部分不對該份額產生影響。該份額只承擔接下來10%的損失，而且其面值隨損失的發生而減小（最初為面值的18%-8%=10%）。當損失超過18％時，B方向A方定期支付費用，其數量等於該份額對應的剩餘面值的一定比率。這一比率被稱作份額利差（tranche spread）。

通常，我們假設債券組合中所有債券在違約時間上的分佈是相同的。定義Q（t）為某一債券到t時刻時違約的概率。第11.6節中介紹的單因子高斯Copula違約時間模型是市場上對CDO份額進行定價的標準模型。由式（11-13）

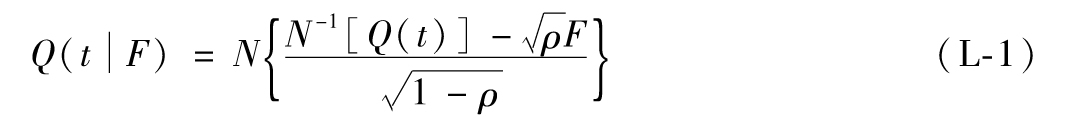
其中，Q（t|F）為基於因子F，第i個實體到t時刻時違約的條件概率。在計算Q（t|F）時，通常假設風險率為常數。當CDS利差或其他信用價差存在時，我們可以採用附錄K中的方法，結合一個搜索過程，來找出風險率。

假設風險率為λ，則

Q（t）=1-e^-λt

（L-2）

根據二項分佈的性質，基於因子F，到t時刻，恰好有k個實體違約的條件概率為

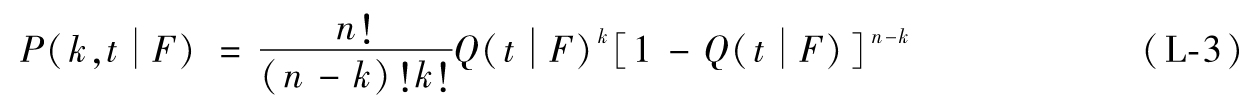
定義

其中R為回收率（假設為常數）。同時，定義m（x）為比x大的最小整數。此份額在違約數k小於m（n_L）時不受損失；在k大於或等於m（n_H）時，全部損失；在其他情況下，份額在t時刻的面值佔初始面值的比率為

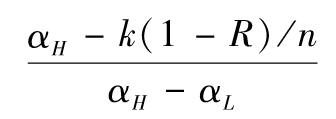
這一結果可以與式（L-1）、式（L-2）和式（L-3）結合起來，計算基於因子F的任意時刻的份額面值的條件期望。然後，我們可以對F積分，以求得份額面值的期望。這一積分通常採用高斯積分（Gaussian quadrature）法來完成（在作者的網頁上提供了在正態分佈上使用高斯積分法進行積分的軟件）。

通常，我們假設違約發生在兩次付款時間間隔的中間點上。與附錄K類似，我們需要知道以下變量：

（1）A方收到的預期付款的貼現值。

（2）A方對份額損失的預期償付的貼現值。

（3）A方收到的應計付款的貼現值。

在某特定時刻，A方收到的付款的數額與份額當時的面額呈線性關係。A方支付的份額損失賠付（假設損失發生在付款間隔的中點）等於該時間段內份額面值的變化值。A方收到的應計付款為份額損失賠付的一定比例。對任意假設的利差，上述3個數值都可由份額面值的期望值求出。然後，採用類似附錄K中求CDS利差的方法，我們可求得使預期付款等於預期份額損失賠付的利差。

由市場對CDO份額的詢價，衍生產品交易商可以計算出隱含Copula相關係數ρ，然後他們會傾向使用ρ來詢價，而不是使用份額利差本身。這和期權市場上，交易商以布萊克-斯科爾斯-默頓模型的隱含波動率，而不是以幣值本身來詢價的做法很相似。因此，CDO市場上也存在相關性微笑現象，這類似於期權市場上的波動率微笑現象。

本書附帶的RMFI軟件中，包含了一個工作表，可進行上述計算。^[1]讀者可從作者的網頁上下載該軟件。

[1] 關於計算CDO價值的更多細節，請參閱J. C. Hull, Options, Futures, and Other Derivatives, 10th ed. (Upper Saddle River, NJ: Pearson, 2018)。