e1 John Hull 風險管理與金融機構 v5
附錄K
信用違約互換的定價
我們在第19章中介紹了信用違約互換(CDS),該產品可以通過(風險中性)違約概率來定價。
假設在沒有提前違約發生的條件下,某參照實體在一年內違約的條件概率為2%。表K-1給出了5年中每一年的生存概率和非條件違約概率(即在0時刻看到的違約概率)。由式(19-2),生存到t時刻的概率為e-0.02t。一年內違約的概率為存活到該年年初的概率減去存活到該年年末的概率。例如,存活到第二年年末的概率為e-0.02×2=0.960 8,而存活到第三年年末的概率為e-0.02×0.3=0.941 8。因此在第三年內違約的概率為0.960 8-0.941 8=0.019 0。
表K-1 無條件違約概率和生存概率

我們假設違約總髮生在每一年的年中,一個5年期的信用違約互換每年結束時付款一次。我們還假設連續複利的無風險年利率是5%,回收率是40%。計算分作三個部分,分別顯示在表K-2、表K-3和表K-4中。
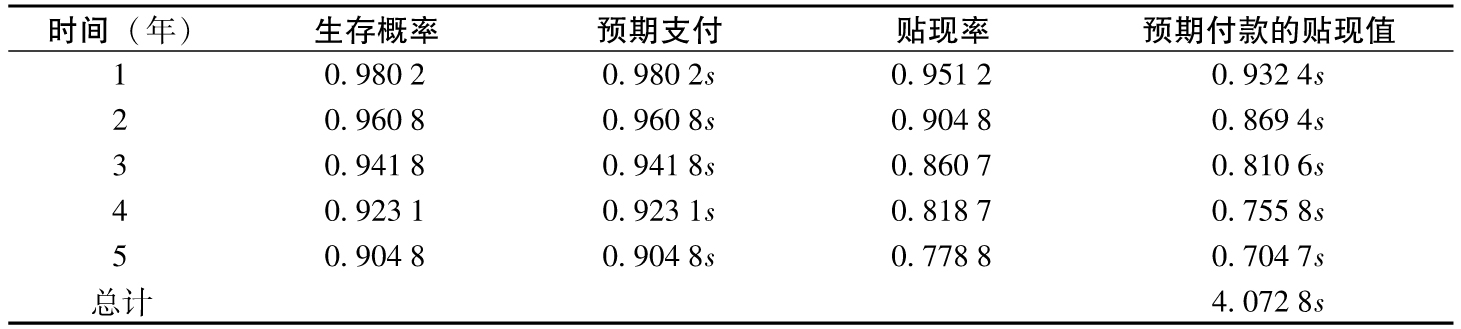
表K-2 計算CDS預期付款的貼現值 (每年的數量為s)
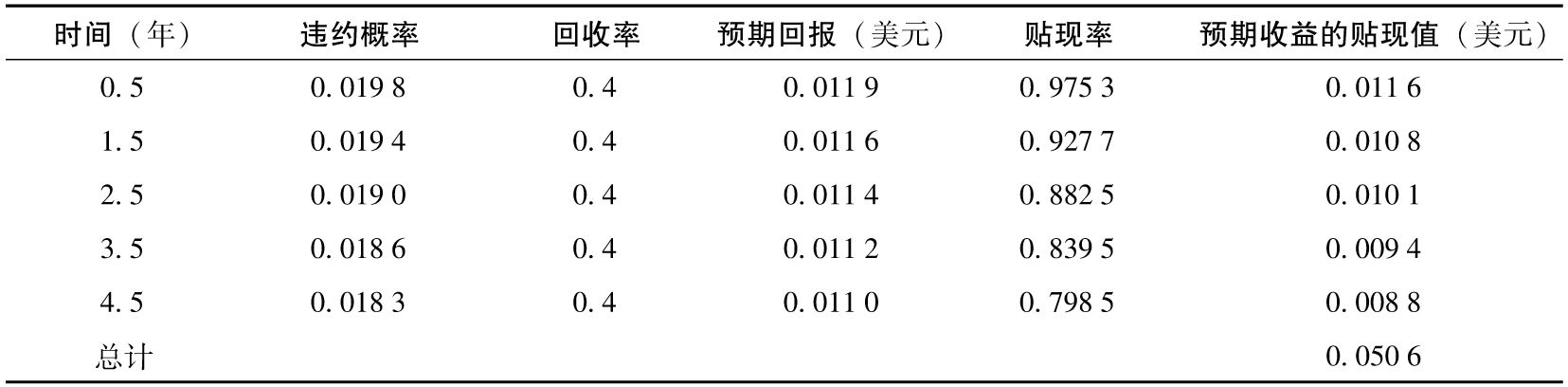
表K-3 計算CDS預期收益的貼現值 (面值1美元)
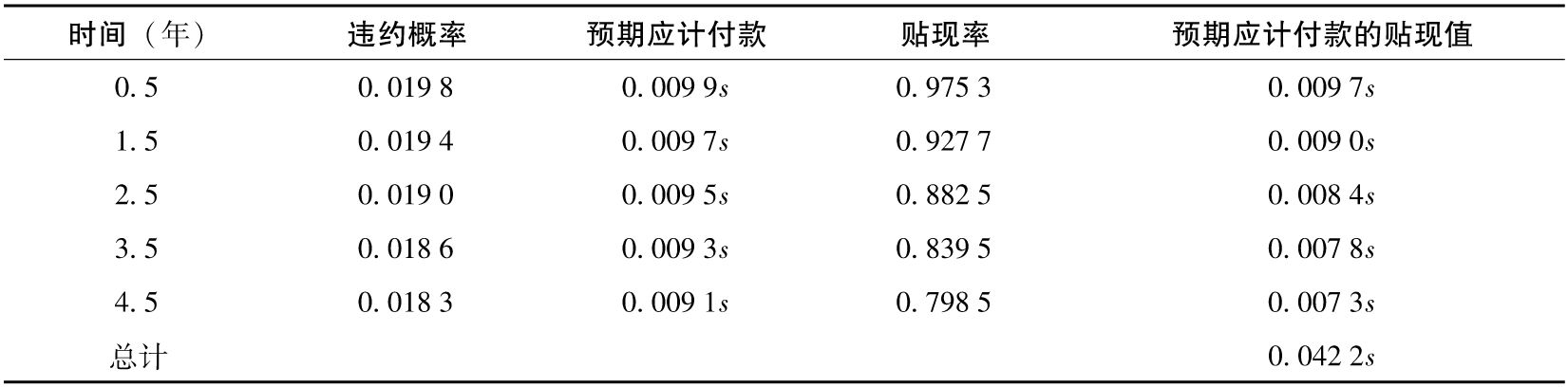
表K-4 計算應計付款的貼現值
表K-2顯示了計算CDS預期付款的當前價值的過程,其中假設每年的費率(CDS利差)為s,CDS的面值為1美元。例如,有0.941 8的概率第三次付款會發生,因此預期付款是0.941 8s,其貼現值為0.941 8se-0.05×3=0.810 6s。表K-2顯示,預期付款的貼現總值為4.072 8s。
表K-3顯示了CDS預期收益的貼現值的計算過程,其中假設的面值也為1美元。如同前面提到過的,我們假設違約總是發生在年中。例如,有0.019 0的概率CDS在第三年的年中會產生回報。考慮到40%的回收率,這時的預期收益為0.019 0×0.6×1=0.011 4。收益的貼現值為0.011 4e-0.05×2.5=0.010 1。表K-3所示的所有預期收益的貼現值為0.050 6美元。
在最後一步中,我們計算違約發生時的應計付款,如表K-4所示。會產生應計付款是因為CDS利差s是延後支付的,因此當違約發生時,實際已經積累了一部分應該支付的利差。考慮第三年,有0.019 0的概率在這一年的年中會發生違約。到發生違約時,已累積了0.5s的應付款。因此,第三年年中的預期應計付款為0.019 0×0.5s=0.009 5s,其貼現值為0.009 5se-0.05×2.5=0.008 4s。表K-4顯示,所有應計付款的貼現總和為0.042 2s。
由表K-2和表K-4,預期付款的貼現總額為
4.072 8s+0.042 2s=4.115 0s
由表K-3,預期收益的貼現總額為0.050 6。二者應該相等,因此
4.115 0s=0.050 6
由此得出CDS利差s=0.012 3,即CDS的市場中間價應為面值的0.012 3倍,或者每年123個基點(考慮40%的回收率和每年2%的風險率,由式(19-3)給出的關係,我們也可大致估算出這一利差為0.02×0.6=0.012)。
設計這個例子的目的是說明CDS價值的計算方法。在實際中,我們常常會發現需要的計算量比表K-2~表K-4中的大得多,這是因為:第一,CDS付款的支付頻率通常要比每年1次大得多;第二,我們假設違約發生的頻率會比每年1次要高。
對CDS進行盯市計價
在合約談判結束時,CDS的價值和其他大多數衍生產品一樣,幾乎為0。一段時間過後,其價值可能為正或為負。假設我們例子中的CDS合約已經存在了一段時間,合約中的CDS利差為150個基點,買方付款的貼現值為4.115 0×0.015 0=0.061 7,而預期回報為0.050 6。對CDS的賣方,其價值為0.061 7-0.050 6,即0.011 1乘以面值。類似地,合約對信用保護的買方的市場價值為-0.011 1乘以面值。
本書附帶的RMFI軟件可從作者的網頁上下載,其中有一個工作表包含了上述計算。