附錄J
對信用遷移矩陣的處理

假定一個n×n矩陣A為一年的信用遷移矩陣，這一矩陣就如表21-1所示。假定相連的時間段中，評級的變化是相互獨立的，對應於m年的信用遷移矩陣為A^m。如果m為整數，對於A^m的計算可以採用常規的矩陣乘法規則。

接下來考慮如何計算當m為整數時，對應於1/m年的遷移矩陣（例如，如果我們想知道一個月的變化，可令m=12）。這個問題要複雜得多，因為我們要計算一個矩陣的m次方根。我們首先需要計算出矩陣的特徵向量x₁，x₂，…，x_n及特徵值λ₁，λ₂，…，λ_n，這些特徵值及特徵向量滿足

Ax_i=λ_ix_i

（J-1）

定義一個n×n矩陣X，其第i列為x_i，Λ為n×n對角矩陣（即除主對角線以外其他位置都是0的矩陣），第i個對角元為λ_i，由式（J-1），我們可以給出以下關係式

A·X=X·Λ

即

A=X·Λ·X^-1

定義Λ^*為對角矩陣，第i個對角元為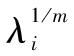，因此

（X·Λ^*·X^-1）^m=（X·Λ^*·X^-1）（X·Λ^*·X^-1）…（X·Λ^*·X^-1）

=X·（Λ^*）^m·X^-1=X·Λ·X^-1=A

以上過程說明矩陣A的m次方根為X·Λ^*·X^-1，我們從而得到了1/m年的遷移矩陣。

有些作者，例如Jarrow、Lando和Turnbull（1997），^[1]對於以上計算喜歡採用生成矩陣（generator matrix）的方法。生成矩陣Γ滿足：對應某個較短時間段Δt，遷移矩陣為I+ΓΔt，其中I為單位矩陣；對應於一個較長時間段t，轉移矩陣為

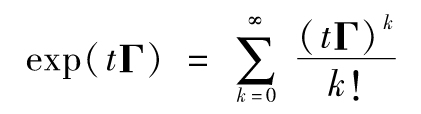
其中I為單位矩陣（對角元為1，其他元素為0）。

進行上述計算的軟件可以從作者的網頁上下載。

[1] See R. A. Jarrow, D. Lando, and S. M. Turnbull, “A Markov Model for the Term Structure of Credit Spreads,” Review of Financial Studies 10(1997):481-523.