e1 John Hull 風險管理與金融機構 v5

附錄G
泰勒級數展開

考慮函數z=F（x），假定變量x有一個小的變化，即Δx，變量z隨之也會有一個小的變化，即Δz，Δz和Δx的一階近似關係為

當z=F（x）為線性函數時，以上關係式為恆等式，在其他情形下為近似式。另外一個更為準確的近似式為

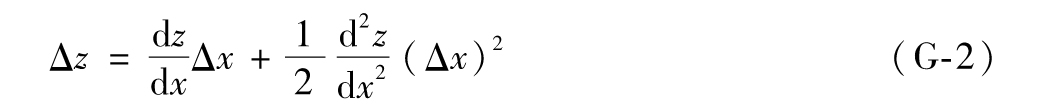
當z=F（x）為二次函數時，以上關係式為恆等式，在其他情形下為近似式。在近似式中加入更多的項，我們可以提高近似精度。泰勒展開的完整表達式為

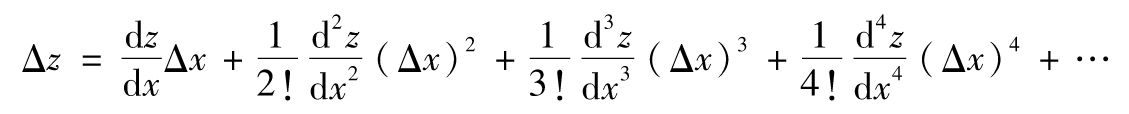
這裡“！”表示階乘函數。2!=2×1=2，3!=3×2×1=6，4!=4×3×2×1=24，依此類推。

【例G-1】　考慮函數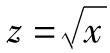，因此

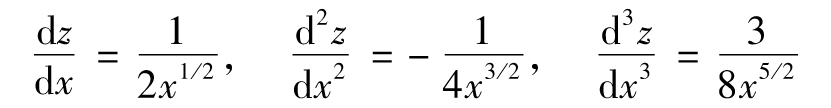
假定x=2以及Δx=0.1，因此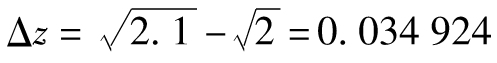，當x=2時

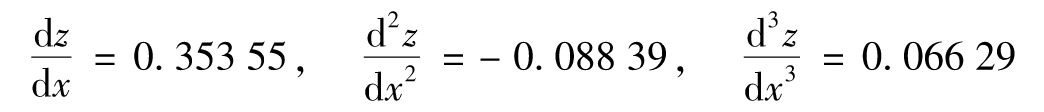
式（G-1）給出Δz的一階近似為

Δz=0.353 55×0.1=0.035 355

式（G-2）給出z=F（x）的二階近似為

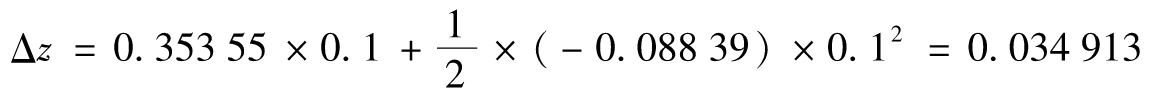
三階近似為

我們可以看出泰勒級數很快就收斂到正確答案0.034 924。

接下來我們考慮兩個變量的函數z=F（x，y），假定變量x和y分別有小的變化Δx和Δy，變量z隨之也會有一個小的變化，即Δz，這時一階近似關係為

二階近似關係式為

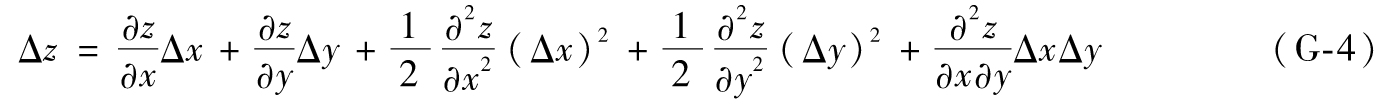
【例G-2】　考慮函數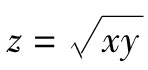，因此

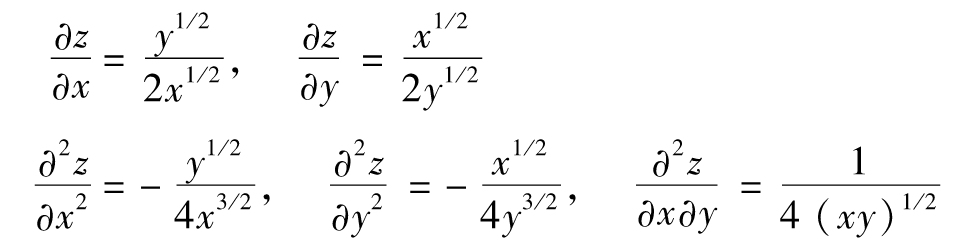
假定x=2，y=1；Δx=0.1，Δy=0.1，因此

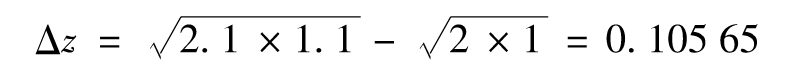
當x=2和y=1時

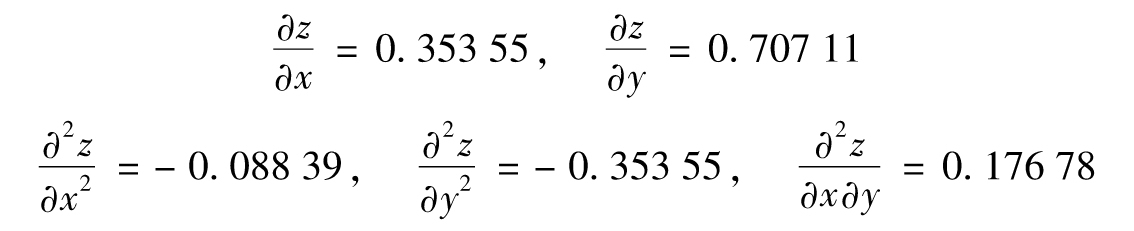
式（G-3）給出Δz的一階近似為

Δz=0.353 55×0.1+0.707 11×0.1=0.106 07

式（G-4）給出的二階近似為

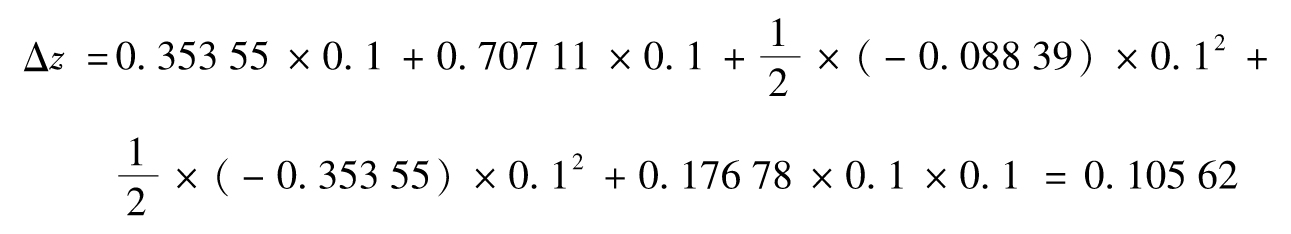
泰勒級數將收斂到0.105 62。^[1]

對於一個n個變量x₁，x₂，…，x_n的函數，Δz的泰勒展開式為

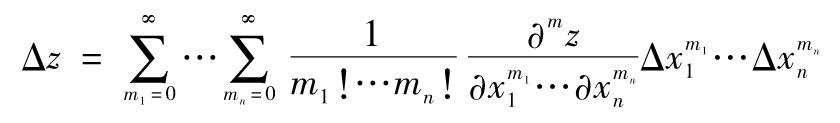
其中m=m₁+…+m_n，以及對應於所有m_i為0的項的取值均為0。

[1] 原書為0.105 65，疑有誤，更正為此。——譯者注