e1 John Hull 風險管理與金融機構 v5
附錄F
美式期權定價
對於美式期權進行定價,我們需要將期權的期限分成n個等份,每一個等份的長度為Δt。假設資產在時間開始的價格為S,在Δt時間後,S上漲為Su的概率為p,S下降為Sd的概率為1-p,對於不提供中間收入的資產,變量u、d及p分別為
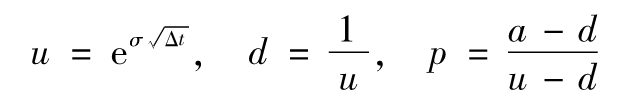
其中
a = erΔt
r為無風險利率,σ為波動率。
圖F-1顯示了一個期限為5個月的美式看跌期權的定價二叉樹,這裡的標的資產為某不付股息的股票,股票的當前價格為50,期權的執行價格為50,無風險利率為10%,波動率為40%,在二叉樹中總共有5步,Δt=0.083 3,u=1.122 4,d=0.890 9,a=1.008 4,p=0.5073,圖中每一個節點上部所對應的數值為股票價格,節點下部所對應的數值為期權價格。
在二叉樹最終端期權價格為期權的內含價格(intrinsic value)。例如,在節點G上,期權價格為50-35.36=14.64。在到期之前的每一個節點,我們假定期權持有者會將期權持有到下一個時間Δt,並且持有者會驗證提早行使期權是否會為最優。首先讓我們考慮節點E,如果期權會被持有到下一個時間段,如價格上漲時(對應概率p),期權價格為0;如價格下跌(對應概率為1-p)時,期權價格為5.45,期權價格的期望為0.507 3×0+0.492 7×5.45,即2.686,利用10%利率進行貼現,對應於節點E的期權期望值的貼現為2.66。因此期權在E點不應該被得以行使,因為這樣做所得回報為0。接下來考慮節點A,假定期權仍然會持有到一個時間段,通過一個類似的計算我們可以得出期權在A點的價格為9.90,如果期權在這一時刻得以行使,回報值為50-39.69=10.31,這時期權在A節點應該被提前行使,因此期權在A節點的價格為10.31。
從二叉樹的最終端開始以後退的形式繼續計算,在到達初始節點D時,我們得出的期權價格為4.49。當我們採用的二叉樹步數增大時,期權價格的精度也增大,利用30、50及100步的二叉樹,我們得出的期權價格分別為4.263、4.272及4.278。
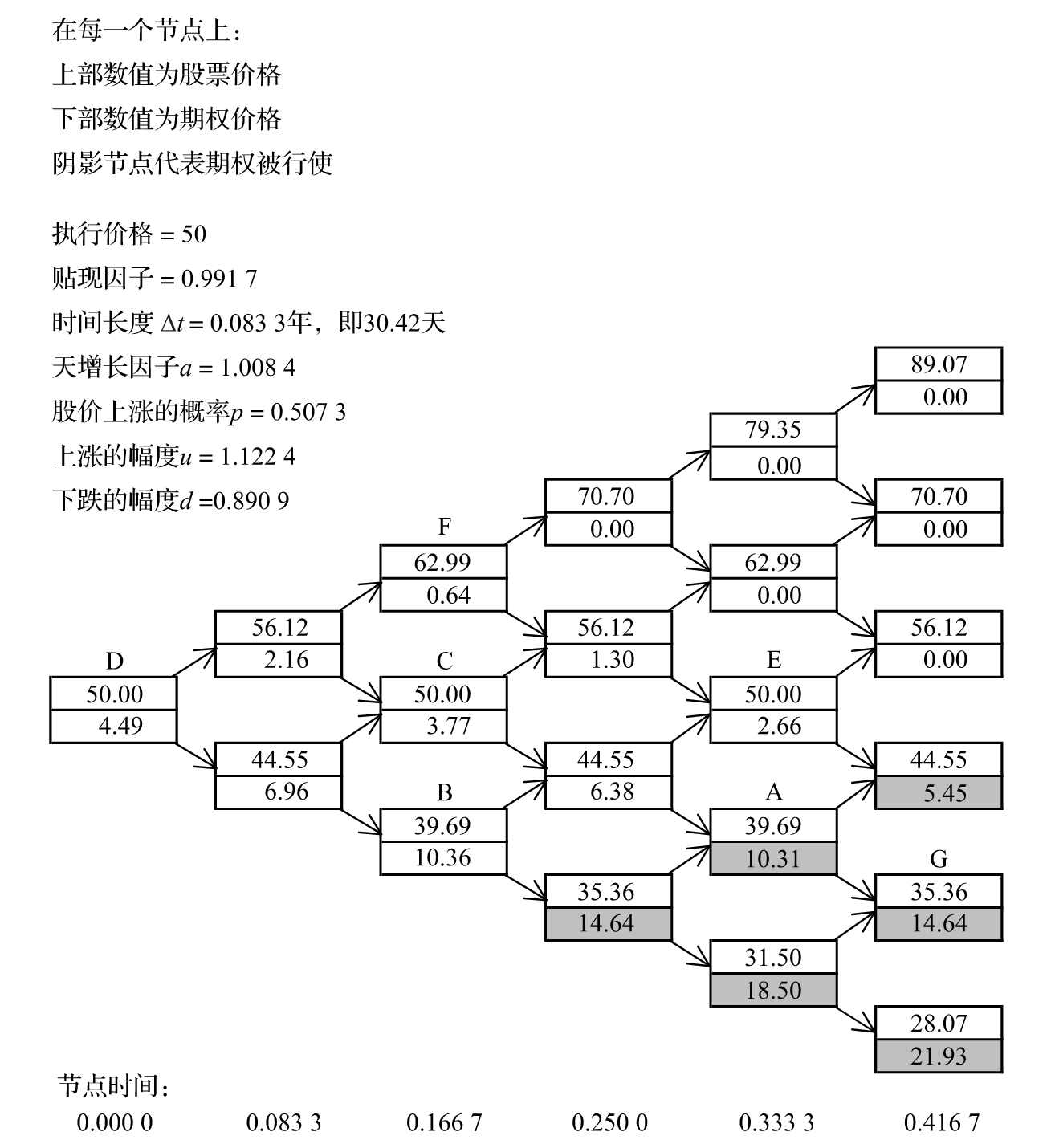
圖F-1 某不付股息的股票的美式看跌期權的定價二叉樹
為了計算delta,我們考慮在Δt時的兩個節點,在我們的例子中,從低位節點轉移到高位節點時,期權價格變化由6.96變為2.16,相應的股票價格由44.55變為56.12,因此delta的近似值為期權價格的變化除以股票價格的變化
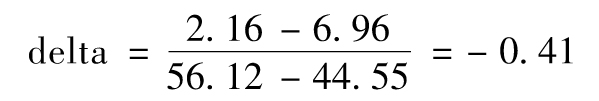
為了計算gamma,我們考慮在2Δt時刻的三個節點,由樹的上半部分兩個節點(C及F)所計算的delta為-0.241,這一delta所對應的股票價格近似為(62.99+50)/2=56.49,由樹的下半部分兩個節點(B及C)所計算出的delta為-0.639,這一delta所對應的股票價格近似為(50+39.69)/2=44.84,因此gamma的近似值為期權delta的變化除以相應股票價格的變化
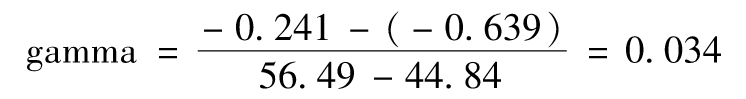
由D及C節點我們可以估計出
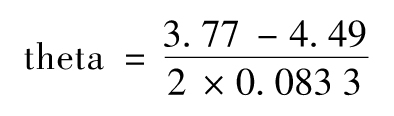
即-4.30(每年)。以上數量對得出每個日曆天所對應的theta為-0.011 8。vega的估計可以通過加大波動率、重新構造新的二叉樹並計算新的期權價格來取得,rho的計算方式和vega類似。
如果標的資產的中間收入的收益率為q,以上計算方式除了a=e(r-q)Δt(而不是erΔt)以外,其他計算過程完全相同(當標的資產是外匯時,q等於外國的無風險利率)。當期權標的資產為期貨或遠期價格時,a設為1,二叉樹各節點可顯示出期貨或遠期的價格。以上我們描述的過程可利用軟件RMFI來實現,這一軟件可在作者的網頁上下載。在軟件中選擇“期權類型:二叉樹美式期權”(Option Type:Binomial American)。在赫爾(2018)關於衍生產品定價的著作中有關於美式期權定價的更詳細描述。[1]
[1] See J. C. Hull, Options, Futures, and Other Derivatives, 10th ed. (Upper Saddle River, NJ: Pearson, 2018).