e1 John Hull 風險管理與金融機構 v5
附錄B
零息利率、遠期利率及零息收益率曲線
n年的零息利率是指在今天投入資金,連續持有n年後所對應回報的收益率。所有的利息及本金都在n年年末支付給投資者,在n年期滿之前,投資不支付任何利息回報。n年期的零息利率有時也被稱作n年期的即期利率(spot interest rate)、n年期的零利率(zero rate)或者n年期的零率(zero)。作為時間期限的函數,零息利率被稱為零息曲線。假如一個5年期連續複利的零息利率為每年5%(複利頻率見附錄A),這意味著今天100美元的投資在5年後會增長到
100×e0.05×5=128.40
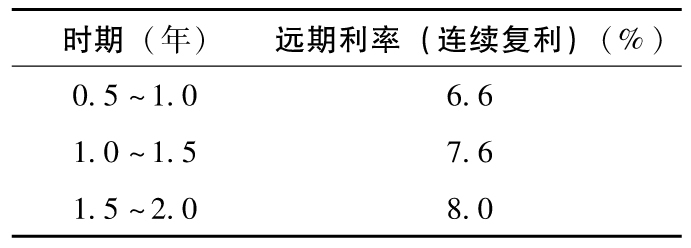
一個遠期利率是由今天零息利率所導出的對應將來某時刻的利率。考慮如表B-1所示的零息利率,6~12個月的遠期利率為6.6%,這是因為將前6個月5%的利率與後6個月6.6%的利率組合在一起會得出一年的平均利率為5.8%。類似地,12~18個月的遠期利率為7.6%,這一利率與今天到12個月5.8%的利率組合在一起所產生的18個月平均利率為6.4%。一般來講,T1~T2的遠期利率F可表達為

其中R1對應於期限為T1的零息利率,而R2對應於期限為T2的零息利率。這一公式在連續複利情形下是個恆等式,而對應於其他計息頻率只是近似式。採用表B-1的數據,應用公式可得出表B-2,例如將T1=1.5、T2=2.0、R1=0.064及R2=0.068代入公式,我們得出F=0.08,這說明18~24個月的遠期利率為8.0%。
表B-1 某零息利率結構

認為將來的實際利率同遠期利率會有很大出入的投資者會很容易地在市場上找到某種交易來反映他們的信念。考慮一個投資者可以由表B-1所示的利率借出或借入資金,假定該投資者認為在今後兩年的利率沒有變化。這個投資者可以借入6個月期的資金,在6個月、12個月及18個月時再進行延展投資,以這種形式可將資金投資兩年,6個月的借款可以在6個月月末、12個月月末和18個月月末再延展,如果利率保持恆定,這種投資決策每年會盈利1.8%,這是因為收入利率為6.8%,而支出利率為5%。這種形式的投資方式被稱為對收益曲線的下注(yield curve play),投資者對將來利率進行投機,認為將來的利率會不同於由表B-2給出的遠期利率。
表B-2 由表B-1(零票息利率)得出的遠期利率(連續複利)
奧蘭治縣的財政官員羅伯特·西特倫在1992年及1993年採用了以上的投資方式,並且在一段時間內獲得了成功。羅伯特·西特倫的盈利在奧蘭治縣的預算中起了很大的作用,因此他也得以連任。1994年羅伯特·西特倫進一步增加了對收益曲線的賭注。如果短期利率恆定或下降,他的投資依然會表現不錯。但在1994年,利率急劇上揚,1994年12月奧蘭治縣宣佈其投資組合損失15億美元。幾天之後,奧蘭治縣宣佈尋求破產保護。
B.1 債券價格
大多數債券提供週期性的券息,債券發行人在債券期滿時將債券的本金(有時也被稱為票面值或面值)償還給投資者。債券的理論價格等於債券將來的現金流貼現後的總和,計算貼現最精確的辦法是對於不同時期的現金流採用不同的零息貼現利率。假定一個2年期的債券的面值為100美元,每年券息利率為6%,半年付息一次。為了計算第一個3美元券息的貼現值,我們採用對應於6個月的貼現率5%;為了計算第二個3美元券息的貼現值,我們採用對應於1年的貼現率5.8%;依此類推,債券的理論價格為
3e-0.05×0.5+3e-0.058×1.0+3e-0.064×1.5+103e-0.068×2.0=98.39(美元)
B.2 債券收益率
一隻債券的收益率是使得債券的貼現的現金流總和等於其市場價格的貼現率,假定一隻債券的理論價格為98.39美元,此價格也等於其市場價格(這裡的債券的市場價格與表B-1的數據完全一致)。如果y對應於連續複利的債券收益率,我們應有等式
3e-y×0.5+3e-y×1.0+3e-y×1.5+103e-y×2.0=98.39(美元)
這一方程式的解可以通過Excel的Solver程序或其他方式得出,其解為y=6.76%。
B.3 國債收益率
國債收益率是投資者投資國庫券或國債時所得的收益率。國庫券及國債是政府借入以本國貨幣為計量單位的資金而發行的金融產品。日元國債收益率是指日本政府借入日元資金的利率,美國國債收益率是指美國政府借入美元的利率,其他國家國債收益率也有類似含義。
B.4 零息收益曲線的確定
一種計算表B-1顯示的零息利率的方法是直接觀測本息分離債券所對應的利率,這些產品是交易員在賣出與本金分離後的票息時人工生成的零息債券。
表B-3 由息票剝離方法計算的2.5年利率
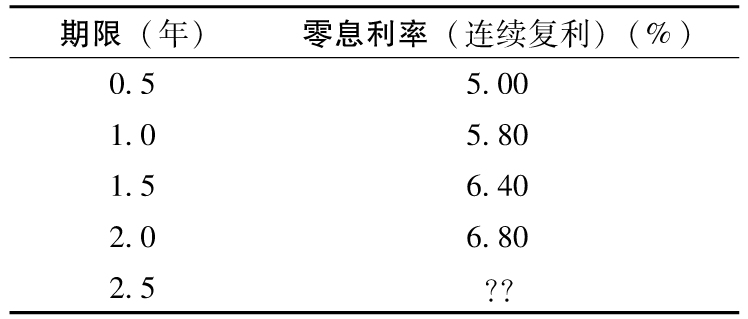
另一種確定零息收益率曲線的方法是從一般的國債及國庫券價格入手來計算零息利率,最流行的方法就是所謂的息票剝離方法(bootstrap method)。這種方法從短期產品入手,然後通過以匹配價格的形式逐漸導出長期利率。假設表B-3是已經確定的零息收益率,我們假設一個息率為8%的債券價格為102美元,債券本金為100美元。我們將2.5年所對應的零息利率計為R,應用表B-3數據,可以給出此債券的正確價格,這一過程會涉及對以下方程求解
4e-0.05×0.5+4e-0.058×1.0+4e-0.064×1.5+4e-0.068×2.0+104e-R×2.5=102
其解R=7.05%。至此我們可以得出一個關於零息利率的表B-3。介於息票剝離節點之間,收益率一般被假設為線性(在我們的例子中,2.25年所對應的零息利率為6.902 5%)。通常的習慣約定是將息票剝離第一節點之前的利率以及最後一個節點之後的利率設定為常數,我們在圖B-1中畫出這裡討論的利率曲線。
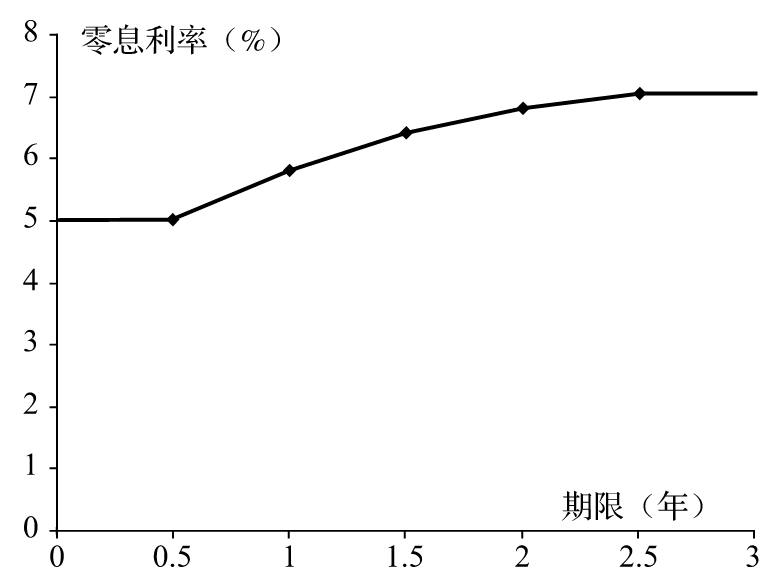
圖B-1 與表B-3對應的零息利率曲線
B.5 OIS零息利率
OIS零息利率曲線的確定方式與確定國債零息曲線的息票剝離法類似。期限為1年的OIS利率適用於1年到期的互換,它們能立即提供有關這些期限的零息利率的信息。期限超過1年的OIS利率通常適用於每3個月交易一次的互換合約,表示按面值出售並按季度支付的債券收益率。
假設3個月、6個月、9個月和12個月的OIS零息利率分別為2%、2.3%、2.5%和2.7%(連續複利)。進一步假設1.25年期的OIS利率為2.8%,一張面值為100美元的1.25年期的債券與每3個月支付0.7利息的債券的價值相等。如果債券收益率R等於1.25年期的OIS零息利率,那麼有
0.7e-0.02×0.25+0.7e-0.023×0.5+0.7e-0.025×0.75+0.7e-0.027×1+100.7e-R×1.25=100
即R=2.794%。