e1 John Hull 風險管理與金融機構 v5
附錄A
利率複利頻率
某銀行聲明1年期儲蓄利率為每年10%,這句話雖然聽起來簡單明瞭,但事實上,其準確的含義依賴利率的計量方式。
假定利率計量方式為每年複利1次,則銀行聲明中給出的10%利率是指100美元的投資在年終會變成
100×1.1=110(美元)
當利率計量方式為每年複利2次時,這意味著每6個月會有5%的利息收入。如果利息也被用於再投資,則100美元的投資在1年後會增長為
100×1.05×1.05=110.25(美元)
當利率計量方式為每年複利4次時,這意味著每3個月會有2.5%的利息收入。假定投資所得利息均用於再投資,100美元的投資在1年後會增長為
100×1.0254=110.38(美元)
表A-1顯示出複利頻率的增長對投資回報的影響。
表A-1 利率為每年10%,複利頻率增加對於100美元投資在1年後的終值的影響
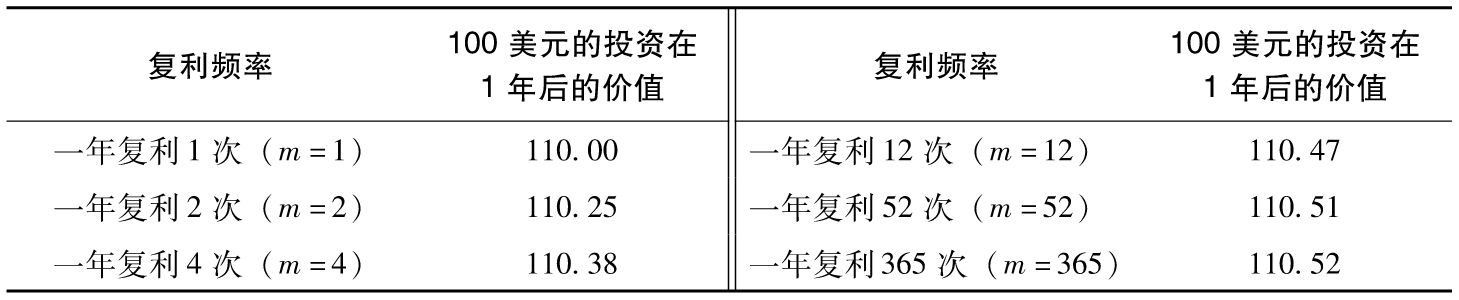
利率複利的頻率定義了利率的計量方式,一個一年複利1次的利率可以被轉換成一個以不同頻率複利的利率。例如,由表A-1我們可以看出,一年複利1次計息利率10.25%與一年複利2次計息利率10%等價。利率在不同計息頻率下的相互關係可類比為公里同英里的關係,它們是兩個不同的計量單位。
為了推廣以上結果,我們假設將A數量資金以一年複利1次利率投資n年,投資的終值為
A(1+R)n
如果利率對應於一年複利m次利息,投資終值為

m=1時所對應的利率有時被稱為年等價利率(equivalent annual interest rate)。
連續複利
複利頻率趨於無窮大時所對應的利率就被稱為連續複利(continuous compounding)利率,[1]在連續複利情況下,我們將A數量資金投資n年,投資的終值為
AeRn
(A-2)
這裡的e=2.71828,在大多數計算器中都有計算函數ex的功能,所以式(A-2)不會產生任何問題。在表A-1的例子中,A=100,n=1,R=0.1,以連續複利計息,A數量資金在投資1年後將增長到
100e0.1=110.52(美元)
這個精確到小數點後兩位的數值與用每天覆利所得的結果一樣,在大多數情況下,我們認為連續複利與每天計算複利等價。對一筆資金以連續複利利率R滾動n年,其效果是相當於乘上eRn項。而對一筆在第n年的資金以連續複利利率R進行貼現,其效果是相當於乘上e-Rn。
假設Rc是某一連續複利利率,Rm是與之等價的每年m次複利利率。由式(A-1)及式(A-2),我們得出
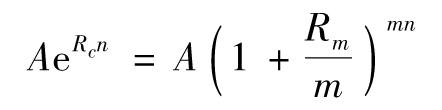
及

這就是說

及
Rm=m(eRc/m-1)
(A-4)
這些公式可將每年m次複利的利率轉換為連續複利的利率,反之亦然。函數ln是大多數計算器設有的自然對數功能。此函數的定義是:如果y=ln(x),則x=ey。
【例A-1】 考慮一個年息為10%的利率,一年複利2次。將m=2及Rm=0.1代入式(A-3)可得出一個等價的連續複利利率
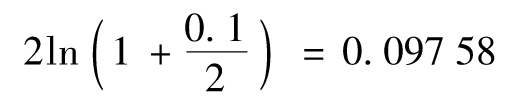
即9.758%。
【例A-2】 假如某債權人給出的每年連續複利利率為8%,而實際利息是每季度支付一次。將m=4及Rc=0.08代入式(A-4),一年複利4次的年等價利率為
4(e0.08/4-1)=0.080 8
即8.08%,這意味著,對於1 000美元的貸款,借款人每季度必須支付20.20美元的利息。
[1] 在精算領域,連續複利利率也被稱為利息力(force of interest)。