e1 John Hull 風險管理與金融機構 v5
26.5 經濟資本金的彙總
通常來講,金融機構對各業務部門要分別計算市場風險、信用風險、操作風險及(可能的)業務風險損失分佈。完成這些計算以後,金融機構需要將所有的損失分佈進行彙總以產生整個機構所需要的經濟資本金的總量。
最簡單的做法是假定涵蓋n個不同風險的整體經濟資本金等於各項風險資本金的總和,因此

其中Etotal為面臨n種不同風險的金融機構整體資本金的數量,Ei為第i項風險所對應的資本金數量。巴塞爾委員會對於監管資本的做法與上式一致。銀行的整體監管資本金等於信用風險、市場風險及操作風險資本金的總和。
式(26-1)採用了一個非常保守的假設,即假定完美的相關性(完全相關)。假設對於經濟資本金進行計算採用的置信水平為99.9%,這意味著市場風險、信用風險及操作風險各自所對應的99.9%的最壞情形會同時發生。Rosenberg和Schuermann估測市場風險與信用風險的相關性大約是50%,市場風險及信用風險同操作風險的相關性大約都是20%。他們的結果顯示了當採用式(26-1)來對市場風險、信用風險及操作風險進行彙總時會高估整體資本金達40%。
26.5.1 假設正態分佈
一種簡單彙總損失的計算方法是假設損失服從正態分佈,由n個不同種類風險組成的整體風險的標準差為

其中σi為第i項風險的損失分佈的標準差,ρij為第i項風險與第j項風險的相關性。由以上公式可以計算資本金,例如,對應於99.9%置信水平的VaR等於3.09與式(26-2)所得數量的乘積。
以上的方式往往會低估資本金的數量,因為計算沒有考慮分佈的偏態以及峰度。Rosenberg和Schuermann證明採用以上做法對市場風險、信用風險及操作風險進行彙總時會低估整體資本金達40%。
26.5.2 採用Copula函數
一種更為精確的對損失分佈進行彙總的方法是採用Copula函數,在第11章中我們對Copula函數曾做過討論。每種損失分佈均以分位數對分位數的映射形式被映射到某種標準並且性狀良好的分佈上。在這種標準分佈上我們可以定義某種相關性結構,並由此間接地得出原始分佈的相關性結構。
在計算過程中我們可採用不同形式的Copula函數。當採用高斯Copula函數時,標準分佈被假設為多元正態分佈。選擇其他函數時可以得到尾部更肥厚的相關性結構。關於這一點我們在第11.6節中已經進行過討論。
26.5.3 混合型
在第12.9節中,彙總VaR的方法是一種流行的彙總經濟資本金的方法,這種方法被稱為混合型方法(hybrid approach)。在這種方法中整體風險的經濟資本金與各個單項風險的資本金有如下關係

當損益分佈為正態分佈時,以上關係式完全成立;當損失分佈為非正態時,以上關係式近似成立,但這種近似能夠反映單項損益分佈的肥尾特徵。Rosenberg和Schuermann的研究結果證明上式給出的結果同Copula模型的結果十分接近。
【例26-3】 假設兩個業務部門的市場風險、信用風險及操作風險經濟資本金的估計在表26-2中給出,同時表26-3給出了各個業務部門損失的相關性,在每個業務部門中信用風險同市場風險的相關性為0.5,操作風險同市場風險及信用風險的相關性均為0.2(這裡參數的選取同Rosenberg和Schuermann的結果一致)。不同業務部門間不同風險類型的相關性為0,在不同業務類別之間所有市場風險的相關性為0.4,在不同業務類別之間所有信用風險的相關性為0.6,在不同業務類別之間所有操作風險的相關性為0。
表26-2 例26-3中的經濟資本金的估計

表26-3 例26-3中損益分佈的相關性
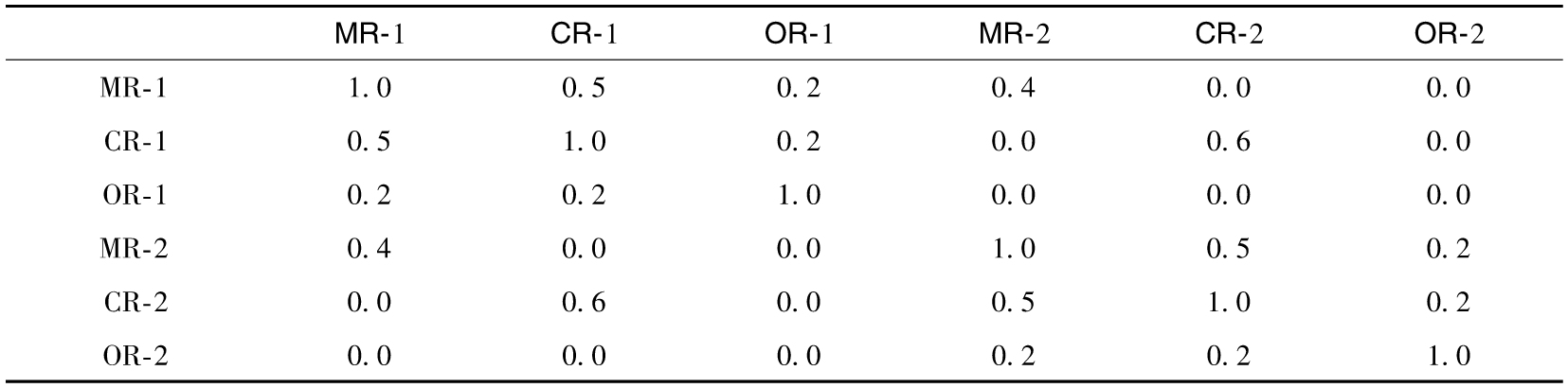
注:MR、CR和OR分別代表市場風險、信用風險和操作風險;數字1和2分別代表業務部門類別。
我們可以將經濟資本金以混合方法進行彙總。整體市場風險經濟資本金為
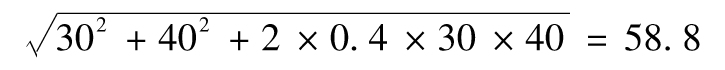
整體信用風險經濟資本金為
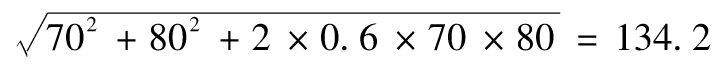
整體操作風險經濟資本金為
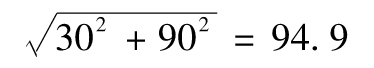
第一個業務部門的整體經濟資本金估計為
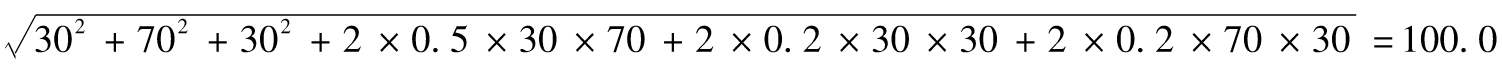
第二個業務部門的整體經濟資本金估計為
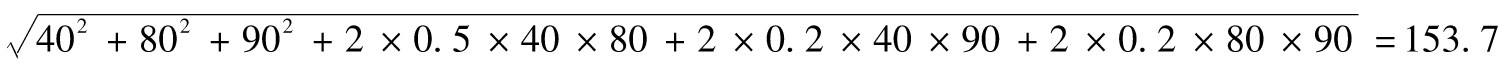
整個企業的經濟資本金是以下數量的平方根
302+402+702+802+302+902+2×0.4×30×40+2×0.5×30×70+
2×0.2×30×30+2×0.5×40×80+2×0.2×40×90+
2×0.6×70×80+2×0.2×70×30+2×0.2×80×90
即203.2。
以上計算在很大程度上顯示了風險分散所帶來的好處。市場風險、信用風險及操作風險經濟資本金的總和為58.8+134.2+94.9=287.9,兩個業務部門的經濟資本金的總和為100+153.7=253.7,以上兩個數值都比實際的經濟資本金估計值203.2要高。