e1 John Hull 風險管理與金融機構 v5
23.3 《巴塞爾協議Ⅱ》下的監管資本
我們現在討論如何通過《巴塞爾協議Ⅱ》來確定監管資本金。正如我們將在第23.4節看到的,巴塞爾委員會已表示,打算完全改變其用以確定操作風險監管資本的程序。它特別指出,將放棄使用高級計量法(AMA),該方法是一種用於確定操作風險損失基於1年展望期和99%置信水平的VaR的複雜程序。然而,許多銀行已經投入了大量資源來實施AMA,這種情況不大可能馬上轉變。實際上,一些國家的監管機構表示,支持它們的銀行繼續使用AMA方法。因此,我們將在本節中回顧AMA方法。
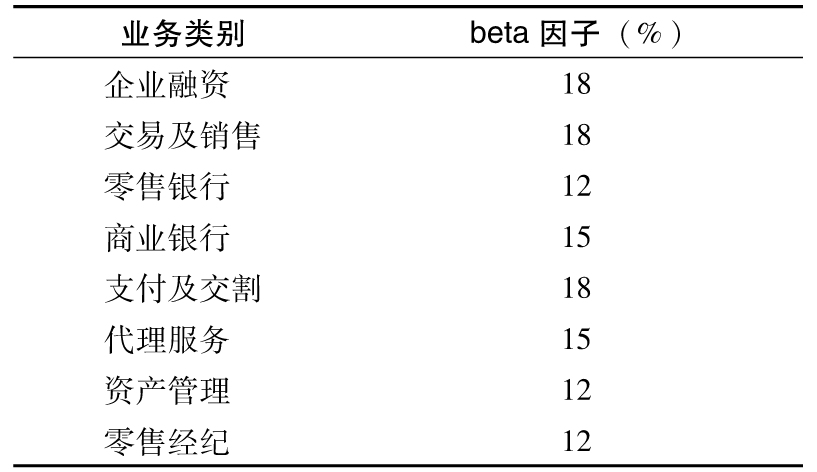
根據《巴塞爾協議Ⅱ》,銀行可以採用三種不同的方法來計算操作風險監管資本金。最簡單的方法被稱為基本指標法(basic indicator approach)。在這種方法中,操作風險資本金等於過去3年毛收入平均值的15%。這裡的毛收入等於淨利息收入與非利息收入的和。[1] [2]另外一種較為複雜的計算操作風險資本金的方法被稱為標準法(standardized approach)。在標準法中銀行業務被分成8個不同業務類別:企業融資、交易及銷售、零售銀行、商業銀行、支付及交割、代理服務、資產管理以及零售經紀。我們首先計算以上列舉的每一業務類別在過去3年中毛收入的平均值與該業務部門相應的“beta因子”乘積,然後我們對以上計算結果求和,最終結果即為操作風險資本金。表23-1展示了不同業務類別所對應的beta因子。計算操作資本金的第三個方法被稱為高級計量法(advanced measurement approach,AMA),在這一方法中銀行可以採用自己設定的定量及定性標準來計算操作風險監管資本金。[3]與信用風險資本金類似,其基於1年展望期、99.9%置信度的VaR。
表23-1 標準法中的beta因子
銀行採用AMA方法來計算操作風險資本金的目的可以與銀行對信用風險進行定量化管理的目的進行類比。其最終的目標是產生一個類似圖23-1中的損失分佈,如果銀行可以使監管人員相信它們計算出的操作風險的預期成本已被包含在產品價格之中,那麼資本金自然也就是用來覆蓋非預期成本的。在計算時所採用的置信水平為99.9%,展望期為1年。非預期損失等於展望期為1年、置信水平為99.9%的VaR與展望期為1年ES的差。
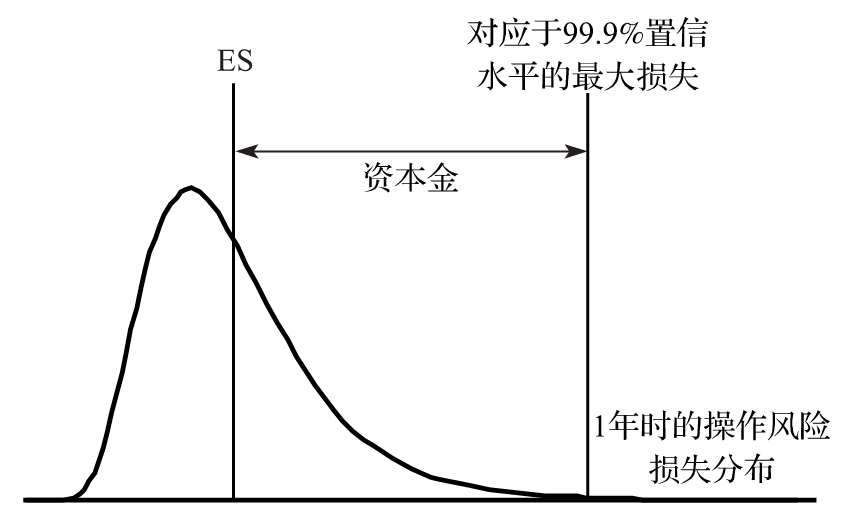
圖23-1 計算操作風險的VaR
如前所述,考慮有8種業務類別,一共有7×8=56(7種風險類別和8種業務類別)種風險與業務類別的不同組合。使用第12.9節描述的方法,對每一個組合,銀行須估計1年期、置信度99%的VaR,然後再將它們彙總起來,以產生一個單一的操作風險VaR測度。
23.3.1 損失程度及損失頻率
有兩個分佈對估計操作風險的損失非常重要:一個是損失頻率分佈,另一個是損失程度分佈。損失頻率分佈(loss frequency distribution)是在某個時間段(通常是一年)內觀察到的損失出現的次數,而損失程度分佈(loss severity distribution)是指在損失事件出現後損失量的大小。通常我們假設損失頻率分佈與損失程度分佈相互獨立。
對於損失頻率,一個比較自然的概率分佈是泊松分佈,在這一分佈中,損失在各個時間段內隨機發生,並且在任意一個Δt的時間段內,損失出現的概率為λΔt。在時間T有n個損失出現的概率為
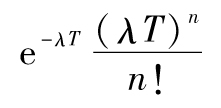
參數λ為每一個單位時間內損失出現的平均次數。例如,假如在10年時內損失出現了12次,對應的λ為每年1.2次,或每個月0.1次。泊松分佈具有一個特性,即損失頻率的期望值等於損失頻率的方差。[4]
我們通常假定損失程度分佈服從對數正態分佈。這一概率分佈中的參數分別為損失的對數的期望值以及方差。
對於每一個業務類別和損失類型的組合,損失頻率分佈與損失程度分佈必須結合在一起以產生整體損失分佈。計算過程可採用蒙特卡羅模擬方法。[5]我們曾提到,通常假定損失程度與損失頻率相互獨立,對於每一次模擬抽樣,我們進行以下計算:
(1)在頻率分佈中進行抽樣,以決定損失事件的數量(=n)。
(2)在損失程度分佈中進行n次抽樣以決定每次損失事件所對應的損失數量(L1,L2,…,Ln)。
(3)計算整體損失(=L1+L2+…+Ln)。
進行多次抽樣後,我們可以得出所考慮的損失類型的整體損失分佈。接下來可以確定分佈的99.9分位數。
圖23-2顯示了這個計算過程。在這一實例中預期損失頻率為每年3次,而損失程度為某種對數正態分佈,每個損失的對數的期望值被假設為0,損失對數的標準差被假設為0.4,這裡的計量單位為百萬美元,讀者可以在作者網頁上下載產生圖23-2的Excel計算表。
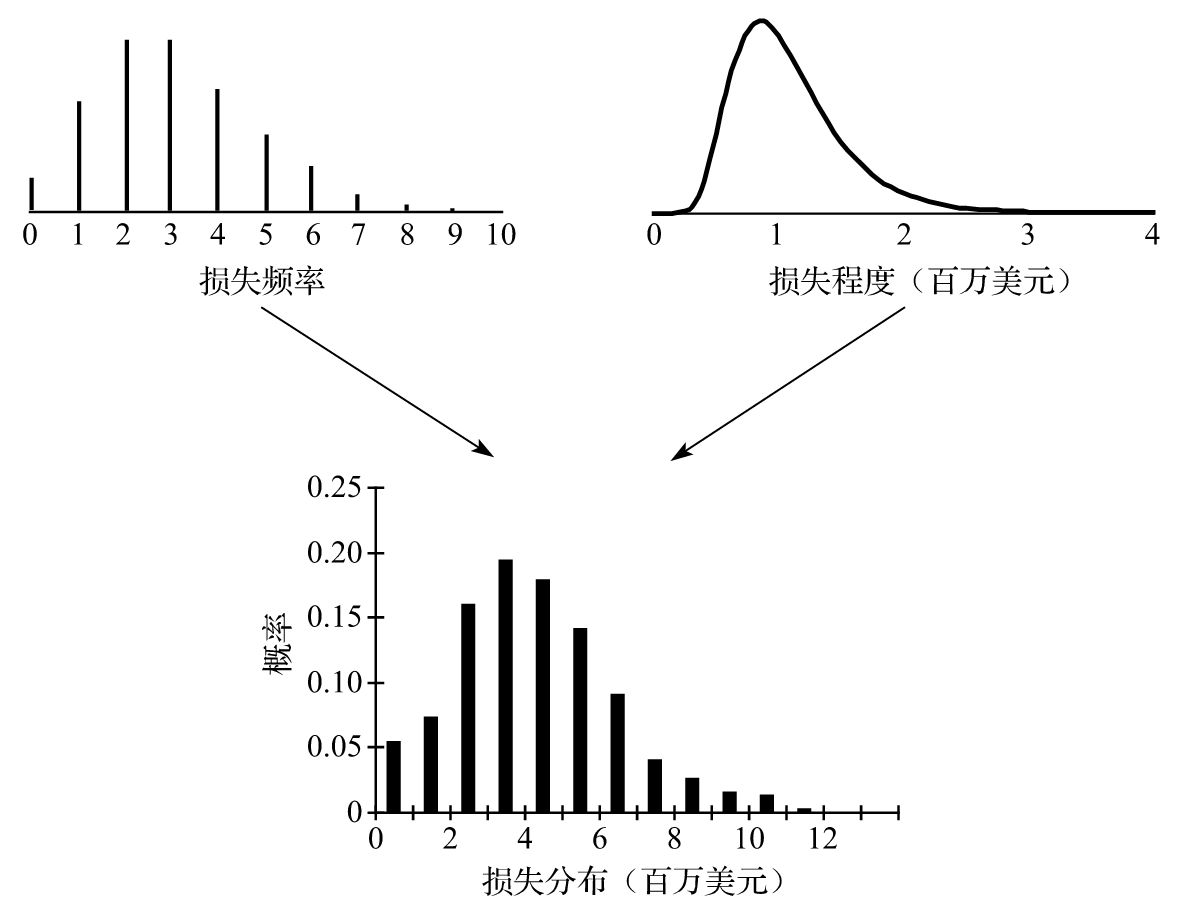
圖23-2 由損失頻率分佈以及損失程度分佈來計算損失分佈
巴塞爾委員會要求AMA的實現中要包含4個要素:內部數據、外部數據、情景分析以及業務環境和內部控制因素。[6]下面我們將對每一個展開詳細討論。
23.3.2 內部數據
不幸的是,銀行內部可以用來估測某一風險種類的損失程度以及損失頻率分佈的歷史數據往往比較少。許多銀行根本就沒有保存自己以往的操作風險損失數據。現在銀行開始收集這些數據,但要採集到合理水平的數據量還需要一些時間。從這個角度,將信用損失數據同操作風險數據進行比較,我們會發現許多有趣的地方。傳統上銀行對於信用風險的記錄要比對操作風險所做的好得多。另外,對於信用風險,銀行可以依賴信用評級公司公佈的大量數據來估測違約概率以及違約損失。銀行對操作風險數據的採集在過去遠沒有像採集信用風險數據那麼系統化。
通常,操作風險損失可以歸為兩類:高頻低額損失(high-frequency low-severity loss,HFLSL)和低頻高額損失(low-frequency high-severity loss,LFHSL)。前一類損失的例子是信用卡詐騙造成的損失,後一類損失的例子是無賴交易員造成的損失。銀行應關注的重點應該是低頻高額損失。這些損失構成了損失分佈的尾部。整體損失分佈的某個分位數可以通過整體低頻高額損失分佈的相應分位數加上整體高頻低額損失的均值來估計。關注低頻高額損失的另一個原因是,高頻低額損失通常已經被考慮在產品定價當中。
按照定義,低頻高額損失發生的頻率低。即使損失數據記錄完整,僅靠內部數據也難以滿足要求,因此需要外部數據和情景分析來彌補。正如我們所講的,外部數據可以用來確定損失嚴重性的分佈。損失頻率分佈僅限於用銀行內部數據和情景分析估算出來。
23.3.3 外部數據
外部數據的來源主要有兩個:一個是數據聯盟,即為銀行提供數據共享服務的公司(保險行業中的數據共享機制由來已久,現在銀行業也開始這麼做);另一個是數據提供商,這些公司採用系統化的手段採集公開發布的數據。外部數據增加了銀行可用來估算損失的數據量,它的另一個好處是,銀行可以藉此將那些沒有發生在自己內部但已經發生在其他銀行中的損失納入考慮範圍。
無論是利用內部數據還是外部數據都要對通貨膨脹進行調節。另外,對於外部數據,銀行還必須進行比例調整。假如一家銀行的銷售額為100億美元,而對應的操作風險損失為800萬美元,這一數據應如何被應用於銷售額僅為50億美元的另一家銀行呢?一個自然假設是當銷售額為50億美元時,操作風險損失就應該是400萬美元。這種估計可能低估了操作風險損失。Shih等(2000)的研究結果顯示公司的規模和損失的規模呈非線性關係。[7]他們估計的模型是
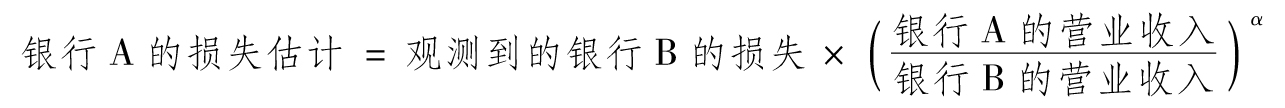
其中α=0.23,這意味著我們例子中銷售額為50億美元的銀行的相應損失估計大約為8×0.50.23=6.82(百萬美元)。在進行恰當的比例調整後,我們可以將其他銀行的共享數據同本銀行的數據進行合併,由此可以得出一個損失程度分佈的更大的數據庫。
數據提供商的數據來自公開發布的數據源,如報紙和交易期刊。數據提供商給出的數據不同於內部數據和銀行業共享數據,因為含有一定的偏差。例如,只有較大的損失才會被披露,而且損失越大,被公開報道的可能性就越高。
外部公開數據對於確定相對損失程度非常有用。假如,一家銀行對本行公司財務部門發生的內部詐騙案所造成損失的期望值及標準差有很好的估計,但是對涉及公司財務的外部詐騙以及發生在交易及銷售部門的內部詐騙所造成的損失沒有太好的數據。如果銀行估計公司財務部門內部詐騙的期望及標準差分別為5 000萬美元及3 000萬美元,進一步假設外部數據顯示公司財務部門外部詐騙損失程度的期望值是內部詐騙損失程度的期望值的兩倍,而外部詐騙損失程度分佈的標準差是內部詐騙的1.5倍。在沒有更好的選擇的情況下,銀行可以假定公司財務部門因為外部詐騙所造成損失程度的期望值為2×5 000=10 000萬美元,標準差為1.5×3 000=4 500萬美元。與此類似,如果外部數據顯示交易及銷售部門內部詐騙損失分佈的期望值及標準差分別是公司財務部門內部詐騙損失分佈的期望值及標準差的2.5倍及2倍,銀行就可以假定本行交易及銷售部門因內部詐騙所造成的損失分佈的期望值為2.5×5 000=12 500萬美元,標準差為2×3 000=6 000萬美元。
23.3.4 情景分析
在AMA中,情景分析是一個評估操作風險的關鍵工具。情景分析的目的是生成能夠全面覆蓋各種可能的低頻高額損失事件的情景。這些情景有可能來自銀行本身的經歷,也可能是基於其他銀行遭受的損失,還有一些可能是諮詢人員建議的,或由風險管理團隊和高管以及業務部門經理一起產生的。巴塞爾委員會估計,在很多銀行內部,經考慮過的可能導致1 000萬歐元以上損失的情景的數量是內部實際發生的、達到這一數字的損失的數量的20倍。
一個由風險管理團隊和公司高管所組成的委員會應該負責估計這些場景中的損失程度和損失頻率的參數。如第23.4節中解釋的,對數正態分佈常常被用來產生損失程度分佈,而泊松分佈常常被用來產生損失頻率分佈。來自其他銀行的數據可能對估計損失程度有幫助。損失頻率應能反映銀行已實施的控制措施的效果和從事的業務類型。它們還應反映操作風險委員會成員的觀點。與第22.3節類似,不同類別的損失頻率可定義如下:
(1)平均千年一遇的情景(λ=0.001);
(2)平均百年一遇的情景(λ=0.01);
(3)平均50年一遇的情景(λ=0.02);
(4)平均10年一遇的情景(λ=0.1);
(5)平均5年一遇的情景(λ=0.2)。
委員會可以將產生的每一個情景劃分給以上任意一個類別。
這裡的情景分析與第22章中的分析有一個差別,我們在這裡並沒有用來確定損失的模型,而且如果無法獲取數據,損失程度分佈的參數應由委員會來估計。一種方法是由委員會來估計平均損失並確定在99%的置信度下,不會被超出的高額損失數量。然後我們可以使用一個對數正態分佈來擬合已有的估計。
幸運的是,操作風險的環境變化不會像市場風險和信用風險環境變化那麼快,因此產生操作風險情景並持續更新的工作量不會像產生市場風險和信用風險情景那麼繁重。但無論如何,高管需要對以上描述的管理過程投入大量的時間。一家銀行採用的情景通常與其他銀行的相關情景類似。行業內的諮詢顧問和行業協會可能會開發出一些標準情景,從某種意義上講,這會減輕操作風險管理委員會的負擔。但是,對損失頻率的估計應該與銀行的特定情況有關,並反映銀行風險控制現狀以及當前的業務狀況。
類似於市場和信用風險壓力測試,基於高管的判斷來產生操作風險壓力情景的優點是,這一方法可以生成金融機構從來沒有經歷過,但可能會出現的損失情景。情景分析可以促使管理人員以更主動和更有創造力的方式來管理將來可能發生的不利事件。這樣做會帶來許多好處。對於有些情景,銀行可以事先制定政策以保證在不利事件發生時如何將損失程度控制到最小,而對於另外一些情景,銀行可以主動提出預防措施來減小不利事件發生的概率。
無論是採用情景分析法還是內部/外部數據法,每個特定損失種類的分佈都必須合併起來以產生最終的整體操作風險損失分佈。各操作風險類別間的相關性假設可能導致算出的1年展望期、99.9%置信度的VaR的結果有很大不同,因此最終的AMA資本金也會不同。基於第12.9節中的材料,第26章給出瞭如何利用相關性來合併包括市場風險、信用風險和操作風險在內的經濟資本金。同樣的方法也可被用來合併不同類型的操作風險資本金要求。人們常常認為操作風險損失之間基本上沒有相關性,而且有實證研究結果支持這一主張。如果假設相關性為0,我們就可以簡單地採用蒙特卡羅模擬的方法,從各個情景的分佈中抽樣來得到整體風險損失的分佈。
23.3.5 業務環境和內部控制因素
在估計損失程度和損失頻率時,業務環境和內部控制因素(business environment and internal control factor,BEICF)應被考慮在內。這些因素包括業務部門的複雜程度、採用的技術的先進程度、變化的快慢、監管的力度、員工更換的頻率等。例如,影響對無賴交易員這一情景的估計的因素可能包括:對交易員的監管力度、對交易的監控程度以及中臺和後臺系統的長處和缺點。
[1] 淨利息收入等於由貸款所帶來利息與支撐貸款的產品的應付利息之差(見第2.2節)。
[2] 如果某年的毛收入為負,則被0取代。——譯者注
[3] 巴塞爾委員會在2016年3月正式公告,將操作風險的AMA從監管資本金體系中刪除。理由是該方法過於複雜,在實踐中缺乏統一標準,容易造成銀行的風險加權資產不合理波動。委員會提出了新的標準計量法(standardized measurement approach,SMA)以取代AMA。——譯者注
[4] 如果期望值大於方差,選擇二項分佈(binomial distribution)可能更為合理。如果期望值小於方差,選擇負二項分佈(negative binomial distribution,也即混合泊松分佈)可能更為合理。
[5] 將損失程度與損失頻率分佈進行結合在保險業中是個十分常見的問題。除了蒙特卡羅法,另外兩個方法也較為流行,一個方法是Panjer算法,另一個方法是快速傅立葉變換(fast Fourier transforms),見H.H. Panjer, “Recursive Evaluation of a Family of Compound Distributions,” ASTIN Bulletin 12(1981):22-29。
[6] See Basel Committee on Banking Supervision, “Operational Risk: Supervisory Guidelines for the Advanced Measurement Approach,” June 2011.
[7] See J. Shih, A. Samad-Khan, and P. Medapa, “Is the Size of an Operational Loss Related to Firm Size?” Operational Risk Magazine 2, no.1(January 2000).Shih的結果是否適應於法律風險非常有爭議,我們常常看到一些大的法律糾紛的賠償數量通常與銀行的承受力有關。