e1 John Hull 風險管理與金融機構 v5

21.5　信用價差風險

交易賬戶上大部分對信用敏感的產品都嚴重依賴信用價差。因此，計算信用風險VaR或ES時需要考慮信用價差的可能變化。一種可能的手段是，類似於市場風險VaR，用歷史模擬法計算出展望期為1天、置信度為99%的信用風險VaR。由1天的VaR，放大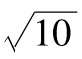倍，可得10天展望期的VaR。為此，需要統計所有相關企業過去500天內（或其他區間）信用價差的變化。第一個歷史模擬場景假設所有公司的信用價差的百分比變化等於第1天的變化，第二個歷史模擬場景假設信用價差的百分比變化等於第2天的變化；依此類推。但是，這個方法有一個顯而易見的問題，如果某家公司在當前還存在，那它過去就沒有違約過，因此該方法實際上假設以後沒有違約的可能性。[1]另一個問題是，並不是所有企業的信用價差都是每天更新的，因此數據的質量可能不高。

另一種辦法是採用CreditMetrics中用到的一種方法。第21.1節給出了計算10天期限的信用評級遷移矩陣的方法。該矩陣給出了一家公司的信用等級在10天內發生各種變化或者違約的概率。信用評級變化的歷史數據定義了與各個信用等級有關的10天后信用價差變化的概率分佈，然後採用蒙特卡羅模擬。在每次模擬中，從遷移矩陣中產生一個抽樣，以決定該公司是維持原評級、遷移到一個新的評級還是發生違約。對信用價差變化的概率分佈同樣進行抽樣，以決定每個信用等級10天后的信用價差，由此我們可得到10天后整個組合的價值並由此進一步得到VaR。

信用相關性可以通過兩種途徑引入。第一種：採用第21.4.1節中介紹的方法，使用高斯Copula模型，將各企業信用評級的變化關聯起來。第二種：各信用等級信用價差的變化可假設為完全（或近似完全）相關，因此當一個評級為A的產品的信用價差上升時，其他信用等級的產品的利差也會上升。

【例21-1】　為說明上述方法，讓我們考慮下面一個簡單例子。假設某公司有一個2年零息債券，面值為1 000美元。無風險利率為3%，當前信用價差為200個基點，因此，債券的收益率為5%（均為年複利）。當前的債券價格為1 000/1.052=907.03美元。假設債券現在的評級為Ba，近似於表21-3中的數據，在下個月，債券評級上升到Baa的可能性為0.6%，有98.5％的可能性評級保持不變，有0.8%的可能性評級會下降到B，還有0.1%的可能性會違約。如果違約，債券的價格將變為400美元。對每一個可能的信用等級，有三個可能性均等的信用價差，按基點計算，這些利差分別為：對Baa級別的80、100和120；對Ba級別的160、200和240；對B級別的400、450和500。

很明顯，最壞的情況是違約。違約發生的可能性為0.1%，將導致的損失為907.03-400=507.3美元。第二壞的情況是評級被降為B，同時利差變為500基點。這種情況發生的可能性為0.8/3=0.267%。因為債券還有1.917年到期，其價格將變為1 000/1.081.917=862.85，損失為907.03-862.85=44.17美元。表21-5顯示了所有可能發生的情況的概率及其帶來的損益。

表21-5　例21-1中的結算結果

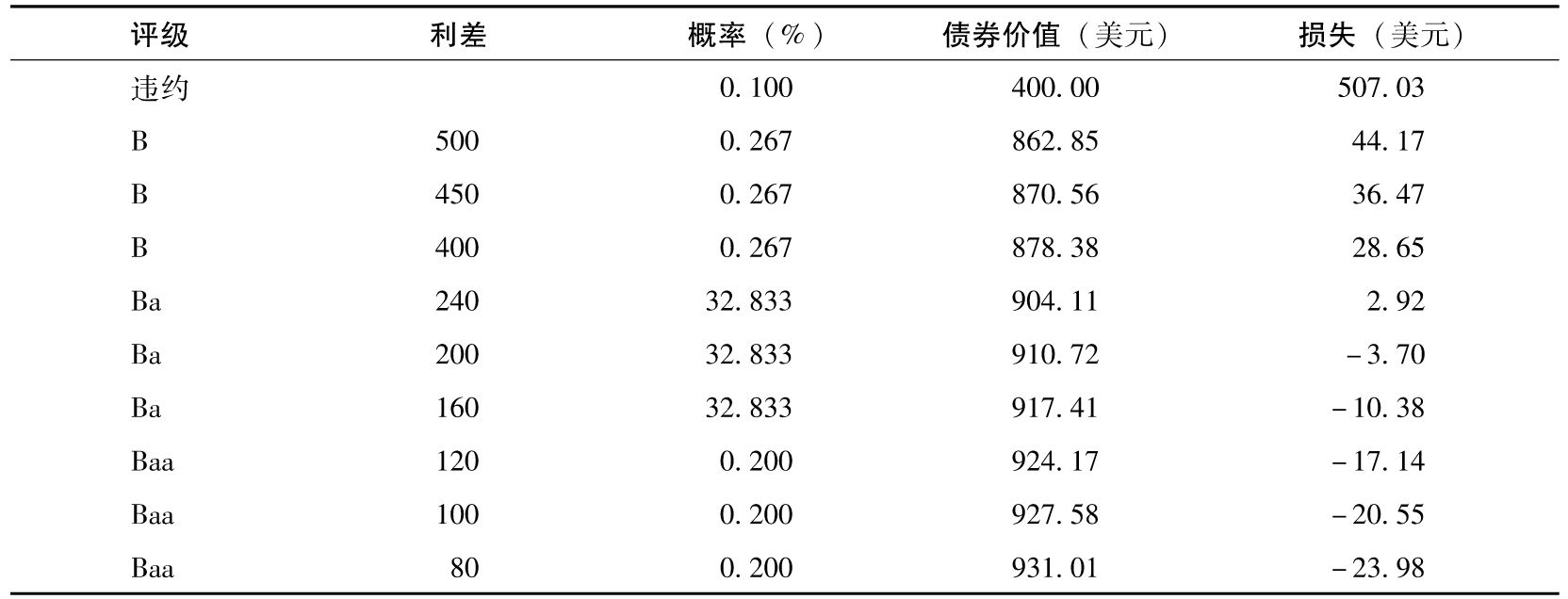
該表表明，如果置信度高於99.9%，得出的VaR為507.03美元；如果置信區間在99.9%和99.633%之間，VaR為44.17美元；依此類推。當置信度為99%時，VaR為2.92美元。

風險水平恆定假設

在計算VaR或ES時，銀行有時會做出一個恆定的風險水平假設，它們假設一個投資組合會週期性地重新平衡，將風險恢復到最初的水平。

例如，假設一家公司投資於Baa級債券，並正在考慮兩種替換交易策略：

（1）持有債券1年，然後賣出債券（“買入並持有”策略）。

（2）在每個月月底進行再平衡，以便如果債券不再是Baa級，它們將被賣出，並被Baa級債券取代（“恆定風險水平”策略）。

表21-1中Baa列的數值是第一種策略的結果，而在第二種策略的情況下，表21-3中Baa列的結果重複12次。

考慮第一次違約的情況，根據表21-1，買入並持有策略下的違約概率為0.001 8。根據表21-3，每月違約概率為0.000 121 5。[2]因此，當使用恆定風險水平策略時，一次違約的概率是

12×0.000 121 5×0.999 878 511=0.001 456

這比買入並持有策略下的違約概率低19%。兩次或兩次以上違約的概率暫不考慮。

接下來考慮債券評級下降至C的概率。根據表21-1，在買入並持有策略下這一概率為0.001 7。而在恆定風險水平策略下，一次降級為C的概率為

12×0.000 127 7×0.999 872 311=0.001 530

這比買入並持有策略下的概率減少了10%。不止一次降級為C的概率暫不考慮。

最後，考慮降級為Ba的概率。根據表21-2，在買入並持有策略下，這一概率為0.040 9。在恆定風險水平策略下，一次降級為Ba的概率為

12×0.003 873 5×0.996 126 511=0.045 505

這比買入並持有策略下降級為Ba的概率增加了10%。恆定風險水平策略下多次降級的概率約為0.001。

計算結果表明，買入並持有策略比恆定風險水平策略將導致更大的違約損失和債券更大幅度的降級，但小幅度評級變動帶來損失的可能性更小。因此，當使用恆定風險水平策略時，VaR和ES通常較小。

[1] 解決這一問題的方法之一是假設當信用價差超過某一水平時，即發生違約。另一種方法是將跳躍式違約（jump-to-default）的風險分開另外處理。

[2] 注意，這些結果是基於比表21-3中小數點後更多的數字得出的，可在作者的網站上看到結果。