BUSINESS BOOKS

21.4　CreditMetrics

Vasicek模型和Credit Risk Plus模型僅估算由違約引起的損失的概率分佈，降級引發的影響沒有被考慮在內。^[1]我們現在討論能處理降級和違約兩種情況的CreditMetrics模型。該模型最先由摩根大通在1997年提出，基於類似於表21-1中所示的某種信用遷移矩陣。評級可由內部產生（由銀行自己的歷史數據）或由評級機構發佈。

計算一個包含有很多對手方的組合1年展望期的信用VaR需要進行蒙特卡羅模擬。在每一條模擬路徑上，每個對手方在一年後的信用等級要被確定下來（我們在稍後會解釋如何做到這一點）。針對每一個交易對手的信用損失由此也可以算出來。如果在一年後某交易對手的信用評級不是違約，那麼我們就要在一年後這個時間點上對與該交易對手進行的所有交易重新定價，然後求出信用損失。如果一年後的信用等級為違約，信用損失等於違約時的敞口乘以1減去回收率。^[2]

計算過程需要用到每個信用等級的信用價差期限結構。一種簡單的假設是，該期限結構與目前市場上觀察到的是一樣的。另外一種假設是存在一個信用價差指數，指數服從某概率分佈，而所有信用價差都與該指數具有某種線性關係。

當與某交易對手的交易中包含衍生產品時，我們需要對第20章中描述的CVA計算進行擴展。回憶一下，對每個交易對手，計算CVA時需要將從目前開始一直到與該對手進行的期限最長的交易結束時為止的這一時間段劃分為n個區間。我們定義q_i為第i個區間內發生違約的概率；v_i為區間i的中點上預期淨敞口的貼現值，其中考慮了擔保品；R為回收率。在當前看來，一年以外違約造成的預期損失為

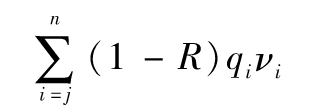
這裡假設第j個區間就是自一年後開始的區間。

在CreditMetrics的每次模擬試驗中，如果在第一年沒有違約，那麼根據式（20-3），一年時的信用價差期限結構會給出一年以後的各區間上的違約概率。假設q_i^*為某次模擬試驗中第i個區間（i≥j）的違約概率。此次試驗中的信用損失為

注意，如果對手的信用評級在年內得到改善（即使保持不變），這一違約損失有可能變成負值。

如果某次模擬試驗中，第一年內發生了違約，會對違約時間進行抽樣，以確定違約時的敞口。該值會被乘以1減去回收率，得出違約損失。

CreditMetrics蒙特卡羅模擬的結果會生成一個包括所有交易對手的違約以及降級造成的總損失的概率分佈。所需的信用VaR可由這個分佈得出來。

相關性模型

在確定信用損失的抽樣過程中，我們不應假設不同交易對手的信用評級變化是相互獨立的。高斯Copula模型可以用來構造信用評級變化的聯合概率分佈（見第11.5節有關Copula模型的討論），兩家公司信用遷移的Copula的相關性一般被設定為等於股票回報的相關性（第1章中介紹的資本資產定價模型提供了一個股票回報的單因子模型。類似第11.4.2節所討論的，此模型可以用來生成具有內部一致性的相關性矩陣）。

假設我們需要對一個A級債券及一個B級債券的信用變化進行模擬。模擬中採用的信用遷移矩陣如表21-1所示。假如兩家公司股票回報的相關性為0.2，在每一個抽樣過程中，我們對兩個服從標準正態分佈的變量x_A及x_B進行抽樣，並保證x_A及x_B的相關性為0.2。變量x_A決定A級公司的新的信用等級，變量x_B決定B級公司的新的信用等級。由表21-1，一家評級為A的公司變為Aaa，Aa，A，…的概率分別是0.000 6，0.026 4，0.909 0，…，因為

N^-1（0.000 6）=-3.238 9

N^-1（0.000 6+0.026 4）=-1.926 8

N^-1（0.000 6+0.026 4+0.909 0）=1.522 0

當x_A<-3.238 9時，A級公司信用級別上升為Aaa級；當-3.238 9<x_A<-1.926 8時，A級公司信用級別變為Aa；當-1.926 8<x_A<1.522 0時，A級公司級別保持不變；依此類推。類似地，表21-1同樣顯示了一家評級為B的公司變為Aaa，Aa，A，…的概率分別是0.000 1，0.000 3，0.001 6，…，因為

N^-1（0.000 1）=-3.719 0

N^-1（0.000 1+0.000 3）=-3.352 8

N^-1（0.000 1+0.000 3+0.001 6）=-2.878 2

當x_B<-3.719 0時，B級公司信用級別上升為Aaa；當-3.719 0<x_B<-3.352 8時，B級公司信用級別變為Aa；當-3.352 8<x_B<-2.878 2時，B級公司信用級別變為A；等等。A級公司在x_A>N^-1（0.999 4）時違約，對應於x_A>3.238 9；B級公司在x_B>N^-1（0.962 1）時違約，對應於x_B>1.775 6。圖21-2是此例的圖形顯示。

注：一家A級公司和一家B級公司在一年後信用轉移的可能，圖中x_A和x_B分別服從標準正態分佈，其相關性等於A級公司及B級公司股票回報的相關性。

有一點值得說明的是，如果CreditMetrics和Credit Risk Plus都使用同樣的一組假設，那麼在理論上它們應產生相同的長期違約損失分佈，主要的區別在於損失發生的時間。例如，假設某組合中包含一筆貸款。在第1年，借貸方的評級從A降到了BBB；在第2年，又從BBB降到了B。我們可以假設在第1年和第2年沒有損失，而在第3年計算損失（Credit Risk Plus的方法）。另外一個方法是，我們可以通過重新定價，分別計算第1年、第2年、第3年的損失（CreditMetrics方法）。第二種方法計算出的各年損失相加後應等於第一種方法計算的損失。

[1] 但是在用於監管資本金的Vasicek模型實現中，期限調整因子可以用來考慮降級。

[2] 回收率通常會從一個經驗數據集中抽樣。