e1 John Hull 風險管理與金融機構 v5
21.3 Credit Risk Plus
1997年,瑞士信貸(Credit Suisse)金融產品小組開發了一個計算信用VaR的模型,這一模型被命名為Credit Risk Plus,[1]該模型使用了保險行業中一種被廣泛採用的解析近似法。
假定一家金融機構有n筆某類型的貸款,每筆貸款在1年時間內違約的概率為q,整個交易組合的違約數量的期望值為qn。假定違約事件之間相互獨立,根據二項分佈可得出有m筆貸款違約的概率是
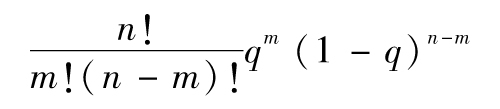
如果q的值較小而n值很大,我們可由泊松分佈(Poisson distribution)給出上式的近似
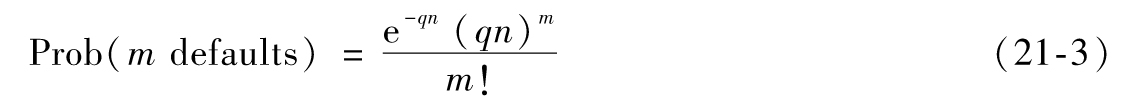
即使各貸款之間的違約概率不相等,上式仍然基本上是正確的,只要所有貸款的違約概率都很小,且q等於未來一年中貸款組合中貸款的平均違約概率。
在實際中,我們並不能確定未來一年內的違約概率q。如表11-6顯示的,不同年份的違約率可能相去甚遠。一個比較方便的假設是預期的違約數量qn服從一個gamma分佈,分佈的均值為μ,標準差為σ。
這樣,式(21-3)中的泊松分佈變成了一個負二項分佈
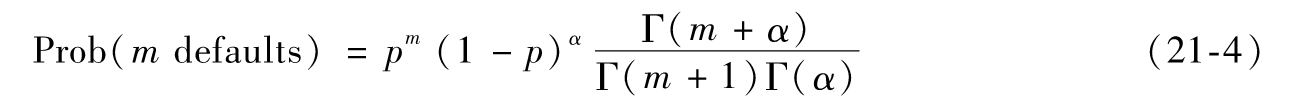
這裡α=μ2/σ2,p=σ2/(μ+σ2),Γ(x)為gamma函數。[2]
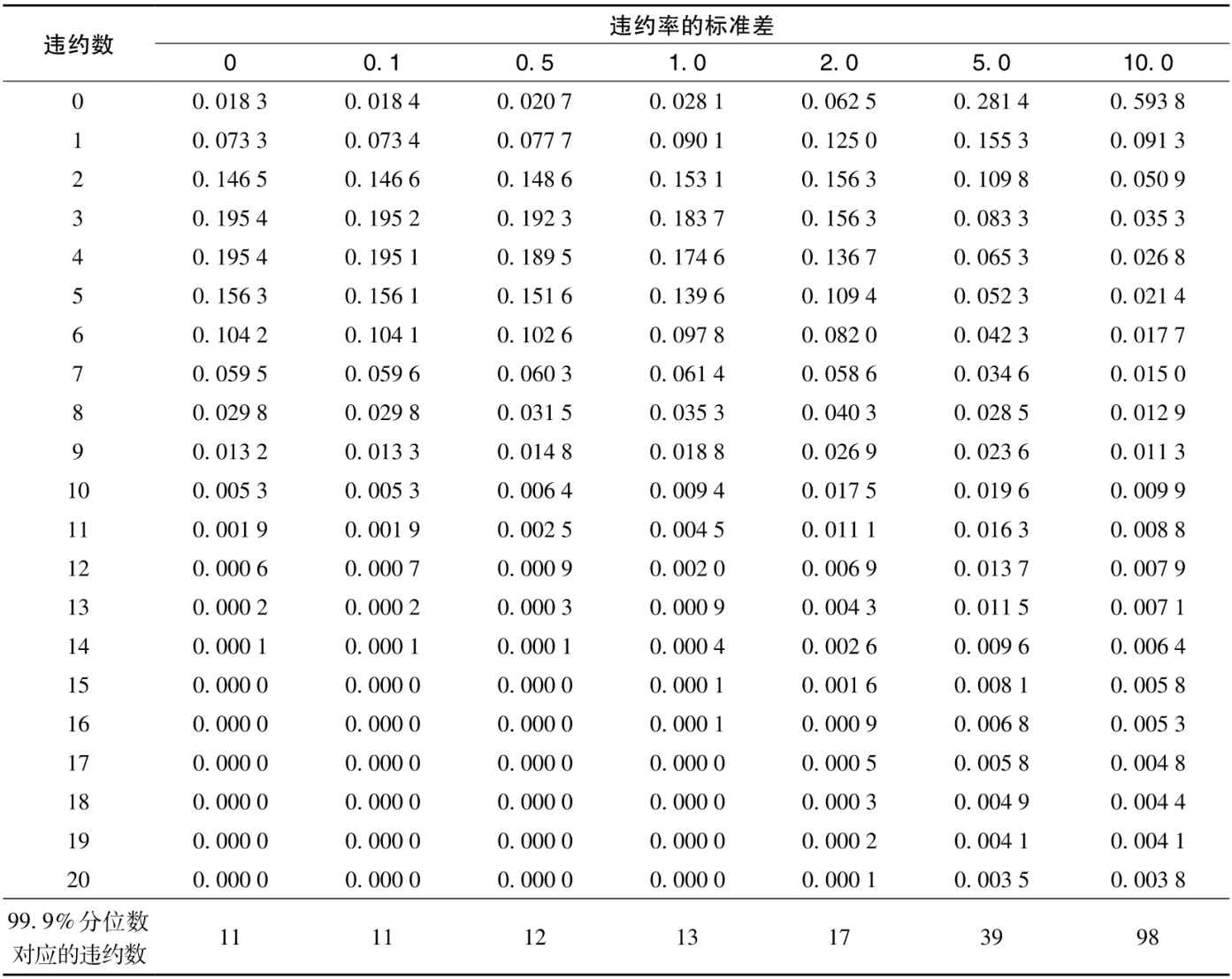
表21-4給出了當μ=4時,不同σ下各違約數的概率分佈。第1列(σ=0)通過式(21-3)得出,其他列由式(21-4)得出。從表中可以看出,當σ趨向於0時,式(21-4)中的負二項分佈得出的各違約數的概率分佈趨向泊松分佈。隨著σ增加,發生極端情況即出現大違約數的概率會增加。假設違約產生的損失是常數,如表中最後一行顯示的,當σ=0時,即違約率不存在不確定性時,99.9%的VaR損失對應11個違約。當σ=10時,即違約率的不確定性很大時,99.9%的VaR變得非常大,其對應發生98個違約時的損失。
表21-4 當預期違約數為4時,違約數的概率分佈
在實際中,違約損失具有不確定性,而且銀行的風險敞口也有很多類別,各類別的違約率也各不相同。我們可以更深入地運用解析方法,但是一種更靈活的方法是使用蒙特卡羅模擬。模擬過程如下:
(1)在整體違約率中進行抽樣。抽樣中使用的數據樣本可以來自類似表11-6的數據源。
(2)開發將各類別的債務人的違約率與整體違約率相關聯起來的模型。一個簡單的做法是建立整體違約率與各類別違約率的迴歸模型。
(3)對各類別的債務人的違約事件進行抽樣。
(4)對各類別的每一違約事件的違約損失進行抽樣。
(5)計算所有違約造成的整體損失。
(6)重複以上(1)~(5)的計算,求得整體損失的概率分佈。
(7)由整體損失概率分佈來計算所要求的VaR。
有多種方法可以進一步改進蒙特卡羅模擬的結果。對錶11-6中的數據的分析表明,某年中的違約概率與前一年的違約概率存在相關性,這說明由表11-6中的數據直接對違約率隨機取樣以決定下一年內的違約率可能不是最好的辦法。開發一個模型,能夠將下一年的違約率與前一年的違約率或其他宏觀經濟因素關聯起來,可能是個不錯的選擇。
需要注意的是,違約率的不確定性在分析中佔有重要地位。如果沒有這個不確定性,就不會有違約相關性,並且如表21-4所顯示的,產生大量違約事件的概率是很小的。隨著違約率不確定性的升高,違約相關性也會增加,大量違約事件出現的概率也會增加。出現違約相關性的原因在於,所有公司都具有相同的違約率,違約率或高或低。沒有違約相關性,損失的概率分佈會很對稱。當存在違約相關性時,損失會呈現正偏態,如圖21-1所示。
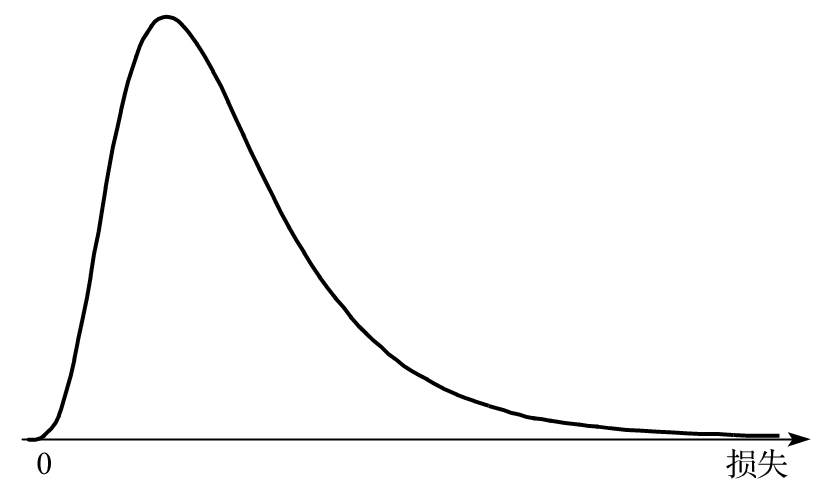
圖21-1 違約損失概率分佈的一般形態
[1] 見瑞士信貸金融產品小組的報告,“Credit Risk Management Framework”,October,1997。
[2] 在Excel中,GAMMALN函數可以返回gamma函數Γ(x)的自然對數。當x為整數時,Γ(x)=(x-1)!。