BUSINESS BOOKS

21.2　Vasicek模型

《巴塞爾協議Ⅱ》中內部評級法（IRB）對銀行賬戶的信用風險資本金要求是基於Vasicek的高斯Copula模型（見第11.6節和第15.8節）。該方法用於計算貸款組合違約率分佈的高分位數。如第11章所示，我們定義WCDR（T，X）為時長為T的區間內，違約率分佈的第X個分位數。注意，WCDR代表最壞違約率。Vasicek模型將WCDR（T，X）與違約概率PD以及用來描述信用相關性的參數ρ建立了聯繫。第11.6節中給出了其公式

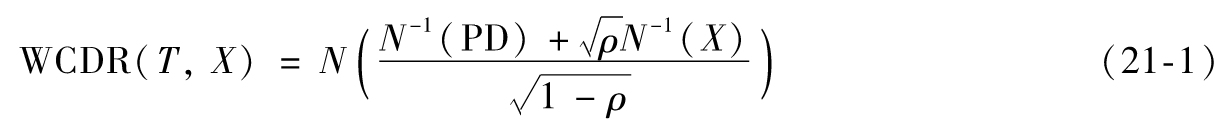
對單筆貸款，令EAD代表違約時的風險敞口，LGD為違約損失，損失分佈的第X個分位數大致為

WCDR（T, X）×EAD×LGD

Gordy的研究結果使我們能夠將上式進行擴展。^[1]假定我們有一個由n筆貸款組成的貸款組合，其中每筆貸款相比整個組合來說都很小。損失分佈的第X個分位數大致為

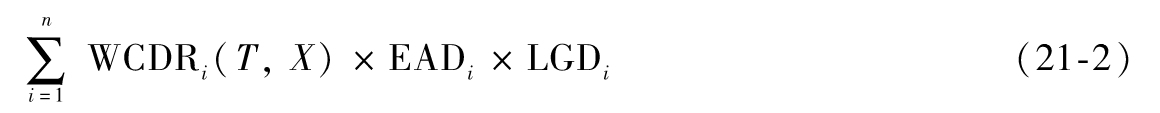
其中，WCDR_i（T，X）、EAD_i和LGD_i分別是組合中第i筆貸款的WCDR、EAD和LGD。

如第15章中討論的那樣，銀行賬戶中的監管資本金等於式（21-2）在展望期T為1年、置信水平X為99.9%時的值。有時式（21-2）中求和的各項需乘以一個期限調整因子MA_i。這是考慮到以下的情況：如果貸款i的期限長於1年，其信用質量可能僅僅是逐漸下降而不是一下違約。在IRB的基礎方法中，銀行估計PD的值，EAD、LGD和MA的值由《巴塞爾協議Ⅱ》的規則設定。在IRB高級方法中，上述各值全部由銀行估計。但在兩種方法中，參數ρ均由《巴塞爾協議Ⅱ》的規則設定。

當Vasicek模型用來確定經濟資本金時，銀行可以自行估計ρ值。第19.8節中討論的結構化模型表明，兩家公司的ρ應該大致等於它們資產回報率之間的相關性。^[2]作為一種近似，這和它們的股票回報率之間的相關性應該是相等的。因此，通過計算一組公司股票回報率之間的相關性，我們可以確定出對這組有公司風險敞口的投資組合的相關性（ρ）。如果這些公司不是上市公司，我們可以使用與之類似的上市公司進行估計。另外一種途徑是第11.6.2節中介紹的最大似然法。

我們在第11章中曾經指出，Vasicek模型的缺點是它對尾部相關性的考慮不夠充分。採用其他Copula模型來取代高斯Copula模型可以對這一點進行修正（其他Copula模型參見第11.6.3節）。

[1] See M.Gordy, “A Risk-Factor Model Foundation for Ratings-Based Capital Rules,” Journal of Financial Intermediation 12, no.3(July 2003):199-233.

[2] See for example, J. Hull, M. Predescu, and A. White, “The Valuation of Correlation Dependent Derivatives Using a Structural Model,” Journal of Credit Risk 6, no.3(Fall 2010):99-132.