e1 John Hull 風險管理與金融機構 v5
20.7 一些簡單例子
為了進一步說明本章的內容,我們在此給出一些簡單例子。
20.7.1 價值為正的單筆交易
首先我們假設某交易商與一個交易對手進行了一筆衍生產品交易,交易對於交易商的價值一直為正,對交易對手的價值一直為負(例如,交易商從對手處買入期權)。我們假設在交易中沒有擔保品,為了簡單起見,我們還假定此衍生產品交易的支付只發生在產品的最終到期日。
在將來任意時刻,交易商對交易對手的風險敞口等於交易的價值。因此,在ti時刻的預期風險敞口的貼現值(被計為vi)等於交易在ti時刻預期價值的貼現值。我們假定在交易期滿之前沒有任何支付,交易在ti時刻預期價值的貼現值總是等於產品的當前價值。
因此,式(20-1)變為
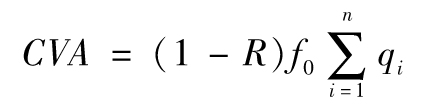
其中f0是在假設交易對手不會違約的情況下的衍生產品價值,假定f0*為將對手違約可能考慮在內的衍生產品價值
f0*=f0-CVA
或者

這意味著在這一情形下,對手違約對於衍生產品的價值的影響是將其價值按一定比率減小,這裡的比率如式(20-6)所示,等於累計風險中性違約概率與1減去回收率的乘積。
我們現在考慮一個由交易對手發行的無抵押零息債券。債券在T時刻支付1 000美元。定義B0為無違約風險時的債券價格,B0*為債券的實際價格。假定在違約時,債券的索償優先權與衍生產品索償的優先權等同。因此,違約時衍生產品的回收率等於債券的回收率,類似於式(20-6),我們可以得出
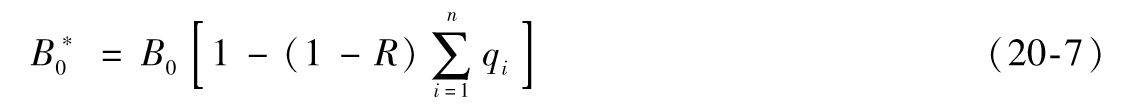
由式(20-6)和式(20-7)得出

如果y為在T時刻到期的無風險零息債券的收益率,y*為在T時刻到期的由衍生產品交易對手發行的零息債券收益率,即B0=e-yT與B0*=e-y*T,由式(20-8)得出
f0*=f0e-(y*-y)T
(20-9)
上式說明,衍生產品的價格等於無風險的衍生產品價格以y*-y進行貼現。
【例20-2】 考慮公司X在場外交易市場賣出的一個2年期的期權,在無違約前提下期權的價值為3美元。假定由公司X發行的2年期零息債券的收益率比相應的無風險利率高1.5%,期權的實際價值為
3e-0.015×2=2.91
即2.91美元。
20.7.2 利率互換與貨幣互換
我們接下來考慮交易商進行了一對與不同交易對手的互換交易,交易之間相互抵消(也被稱作背靠背交易)。圖20-1比較了當互換交易分別為匯率互換和利率互換時,將來的整體預期風險敞口。利率互換的預期風險敞口的起始值為零,然後隨時間變化會增加,最後又會下降;匯率互換的預期風險敞口與之形成對比,隨時間變化會持續增加。利率互換和匯率互換的預期風險敞口不同的主要原因是在匯率互換中,會有最終本金的互換,而進行本金互換時的匯率有很大的不確定性。當利率互換到期時,雙方需要互換的金額很小。因此我們可以得出,匯率互換交易的對手違約風險的影響要遠大於利率互換交易。對兩類互換,式(20-1)中交易商計算的交易對手的違約概率qi是相同的,但是匯率互換的vi一般來說會更大。
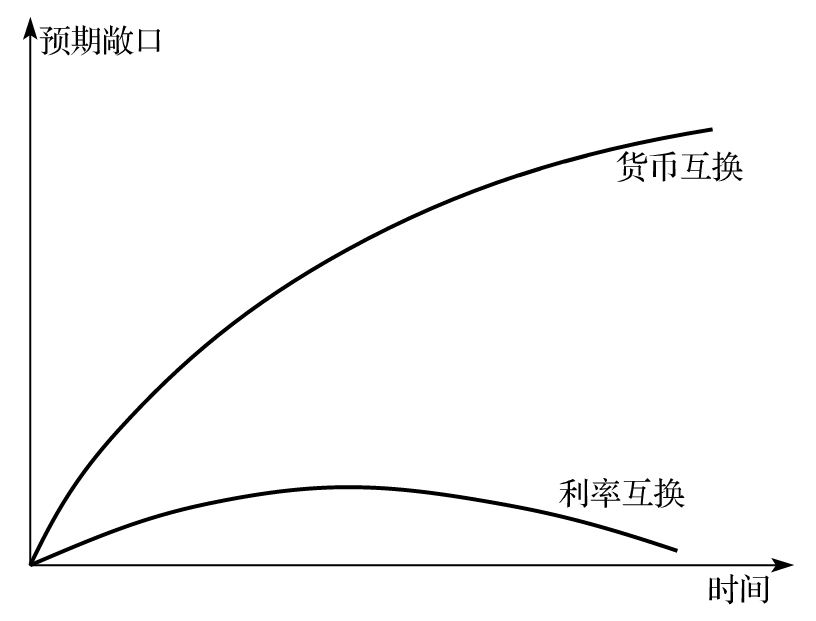
圖20-1 一對背靠背的利率互換和一對背靠背的匯率互換的預期敞口對比
20.7.3 單一遠期交易
下面一個例子是交易商與交易對手之間進行了一筆遠期交易,其中交易商要在將來時間T以特定價格K買入資產。假設在交易中沒有擔保品,資產在今天的遠期價格為F0(在今天為已知),在時間t(t≤T)的遠期價格為Ft(在今天為未知)。如附錄C所示,遠期價格在時間t的價值為
(Ft-K)e-r(T-t)
其中r為無風險利率(假定為常數)。
在時間t的風險敞口為
max[(Ft-K)e-r(T-t),0]=e-r(T-t)max[(Ft-K),0]
(20-10)
風險敞口的當前價值等於在時間t支付回報max[(Ft-K),0]的衍生產品的貼現值,該衍生產品是關於遠期價格的期權,由附錄E的期權公式得出,該衍生產品的價值為
e-rt[F0N(d1)-KN(d2)]
其中
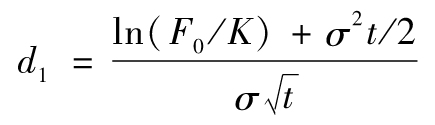
以及

其中σ是資產遠期價格的波動率。由式(20-10)我們可以得出,在時間t的風險敞口的當前值為
e-rt[F0N(d1)-KN(d2)]
因此式(20-1)中的vi滿足
vi=e-rT[F0N(d1,i)-KN(d2,i)]
(20-11)
其中
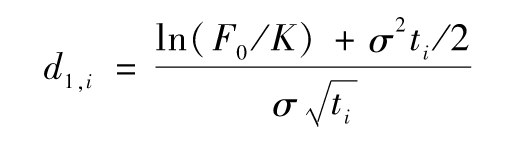
以及
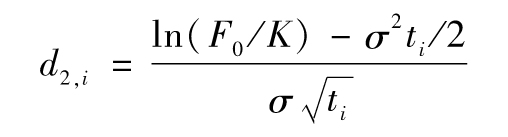
【例20-3】 假定某銀行和一家礦業公司進行了一筆關於黃金的遠期交易,交易規定在兩年後銀行將以每盎司1 500美元的價格買入100萬盎司黃金,黃金的遠期價格為每盎司1 600美元。礦業公司在第1年的違約概率為2%,在第2年的違約概率為3%,假定礦業公司違約的時間發生在每年的年正中,無風險利率為每年5%,金融機構預測礦業公司違約回收率為30%,在黃金遠期合約兩年期滿時,遠期價格的波動率為20%。
在這一情形下,按式(20-11)
v1=e-0.05×2[1600N(d1,1)-1500N(d2,1)]
其中
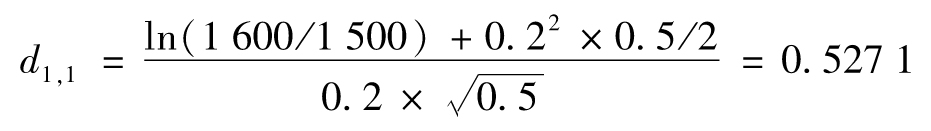
以及

由此得出v1=132.38。同理
v2=e-0.05×2[1600N(d1,2)-1500N(d2,2)]
其中

以及
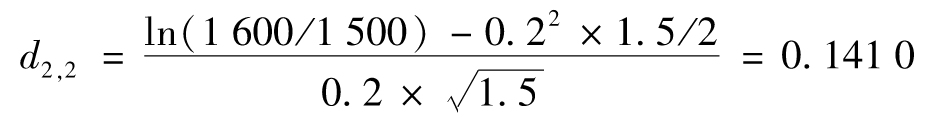
由此得出v2=186.65。
其他變量的取值為q1=0.02、q2=0.03以及R=0.3,因此
CVA=(1-0.3)×(0.02×132.38+0.03×186.65)=5.77
在沒有違約的假設下,遠期合約的價值為(1 600-1 500)e-2×0.05=90.48,將對手違約考慮在內,遠期合約的價值為
90.48-5.77=84.71
我們可以將該例擴展到礦業公司的違約發生時間更為頻繁的情形(見作業題20.13和作業題20.14)。