BUSINESS BOOKS

20.2　CVA

在場外衍生產品交易中，對每一個進行雙邊清算的交易對手，交易商都要計算一個信用價值調整量（CVA）。^[1]這一數量是對交易對手違約所帶來的預期損失的估計。CVA會導致衍生產品的價值下降。在某個時間段內，CVA總值的提高（或降低）會導致同期利潤的降低（或提高）。

假定T代表與某交易對手的所有衍生產品交易中最長的期限，為了計算CVA，我們將0～T的區間化成若干小的時間段（例如，從現在到1個月，從1個月到3個月，等等）。

假定第i個時間區間起始為t_i-1，結束為t_i（t₀=0），假定時間段的數量為n，定義

q_i——交易對手在第i個時間段內的風險中性違約概率；

v_i——如果在第i個時間段內發生違約，在該時間段中點上交易商對交易對手淨預期風險敞口（考慮擔保品以後）的當前價值；

R——交易對手違約時，交易商作為無抵押債權人的回收率。

假定淨風險敞口與對手違約概率無關，對手在第i個時間段違約所產生的預期損失的當前值為

（1-R）q_iv_i

整體預期損失為

變量q_i是風險中性違約概率（這是因為CVA的計算涉及對未來現金流的定價。如第7章所示，在定價時，應使用風險中性違約概率而不是真實世界的違約概率）。q_i的值可以由對手的信用價差來進行估計，如第19.6節所示。假定s_i為交易對手對應於時間t_i的信用價差的估計，根據式（19-3），時間0～t_i的平均風險率（hazard rate）為

時間0～t_i的不違約的概率為

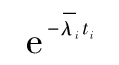
因此

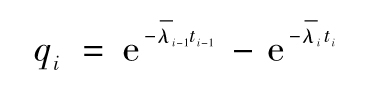
或者

v_i通常是通過蒙特卡羅模擬計算得出的，即在風險中性世界，從時間0到T，我們要對市場變量進行模擬，這些模擬變量決定了交易商與交易對手的交易價值。在每次模擬抽樣中，對於每個小的時間段的中點，我們要計算交易商對於交易對手的風險敞口，然後求得這些敞口的均值，v_i等於對應於第i個區間的均值的貼現。在實踐中，交易商可能與數千個對手存在交易，因此要計算對所有對手的風險敞口v_i對計算量的要求非常大。

20.2.1　擔保品和補救期

在計算v_i的過程中，我們需要考慮擔保品協議。交易雙方達成的擔保品協議通常是信用支持附件（CSA）或ISDA主協議的一部分。協議中會指明交易雙方提交的擔保品計算細節，以及對非現金擔保品價值的折減量。假設違約發生時，交易對手提交的擔保品的價值為C（如果C為負值，則-C為交易商向交易對手提交的擔保品的價值）。在任意情況下，交易商對交易對手的風險敞口為

E=max（V-C, 0）

（20-4）

這裡V是所有現有交易對交易商的市場價值的總和。

式（20-4）說明了一個簡單的事實：當交易的價值-V對交易商來說是正值時，交易對手提供的擔保品可以用來降低（某些情況下甚至消除）由此產生的風險敞口。如果交易商向對手提供了擔保品（C<0的情況），當對手發生違約時，這部分價值不會被返還，而如果-C>-V，則超出的部分也變成了敞口的一部分。前面提到過，在CVA和DVA的計算中，對敞口的考慮一般採用交易的市場中間價（在第17.1.5節中，我們曾展示過一個類似的結果：當違約發生時，需要對市場中間價進行調整，調整幅度為買賣價差的一半，以得出索償的數額）。

在實踐中，從交易對手停止提供擔保品到交易被平倉通常會有一段時間，這段時間被稱為補救期（cure period），也被稱作風險邊際期（margin period of risk）。這段長時間的長度通常介於10到20天之間。補救期的存在意味著當違約發生時，擔保品的價值並不反映違約時刻的交易組合的價值，而是10～20天之前的價值。

假定第i個區間的中間值為t_i^*，即t_i^*=（t_i-1+t_i）/2，c為補救期。在進行蒙特卡羅模擬計算v_i時，計算過程既要考慮到與對手的交易組合在t_i^*的價值，也要考慮到其在t_i^*-c的價值（i=1，2，…，n）。在每次模擬過程中，交易在t_i^*-c的價值與CSA條款結合起來，用來確定在t_i^*時刻持有的擔保品的價值，然後通過式（20-4）得出t_i^*時刻敞口的值。^[2]例20-1對計算過程進行了說明。

20.2.2　峰值敞口

除了計算CVA，交易商通常還會計算在每個時間段中點上風險敞口的峰值（peak exposure）。該峰值對應於蒙特卡羅模擬的高分位數，例如，我們設定了97.5%的分位數，蒙特卡羅模擬的次數為10000次。時刻t_i^*的敞口峰值為在10000個抽樣值中，該時刻對應敞口值按由大到小順序排序的第250個值。最高峰值（maximum peak exposure）對應於所有t_i^*峰值中的最大值。

這裡有一個常常被忽略的理論問題。為了計算CVA，我們要在風險中性世界對市場變量進行模擬，並且在計算中使用的貼現利率為無風險利率（如第7章所述，對衍生產品進行定價時，我們通常這樣做）。但在計算峰值敞口時，我們是在進行情景分析。實際上我們是在問：“將來我們對交易對手的敞口在最壞的情況下有多大？”要回答這個問題，如第7章中討論過的，我們理論上應該是在真實世界而不是風險中性世界中對市場變量進行模擬。^[3]

20.2.3　降級觸發

淨額結算和擔保品協議是雙邊清算的衍生產品交易中降低信用風險的重要手段。有時，ISDA主協議的信用支持附件（CSA）中還會包含降級觸發條款。該條款會申明，如果交易中一方的信用評級下滑到某一級別時，另一方有權索取更多的擔保品或將交易終止。

AIG事件為降級觸發條款的運作提供了一個實例，許多AIG的交易申明，當AIG的信用高於AA級時，AIG無須為交易支付擔保品，而當AIG的信用低於AA時，交易對手就會要求AIG提供擔保品。2008年9月15日，AIG被三家評級公司降級到AA以下，這導致了擔保品的催付而AIG無力支付，AIG最終只有憑藉政府的大規模援助才得以倖存。

其他深陷降級觸發條款困境的公司還有安然（Enron）、施樂（Xerox）和安巴克（Ambac）。如果發生跳躍性降級（例如由AA級直接降至違約），降級觸發條款對被降級公司的交易對手並不能提供保護。另外，某公司的交易對手，只有在有限度的適用針對此公司的降級觸發條款時，才能對自身提供有效的保護。假如一家公司在與許多對手的交易中都設定了信用降級觸發條款，當該公司的信用評級低於一定級別時，會出現類似AIG的情形，造成該公司對現金的需求猛增，如果現金不足，則會迅速導致破產。

[1] 關於CVA的更多內容，可參閱J. Hull and A. White, “CVA and Wrong Way Risk,” Financial Analysts Journal 65, no.5(September/October 2012):5869; E. Canabarro and D. Duffie, “Measuring and Marking Counterparty Risk,” Chapter 9 in Asset/Liability Management for Financial Institutions, ed. L. Tilman (New York: Institutional Investor Books, 2003); E. Picault, “Calculating and Hedging Exposure, CVA, and Economic Capital,” in Counterparty Credit RiskModeling, ed. M. Pykhtin(London: Risk Books, 2005); and J. Gregory, Counterparty Credit Risk: The New Challenge for Financial Markets, 2nd ed. (Hoboken, NJ: John Wiley & Sons, 2012)。

[2] 這裡的結論基於一些簡化假設，即擔保品的支付是一個不間斷的過程，而且沒有最小支付數量的限制，為了反映真實情形，這些假設可以被放鬆。

[3] 當對不遠的將來的峰值敞口進行計算時，使用真實世界進行模擬和使用風險中性世界進行模擬所得的結果差別很小。