e1 John Hull 風險管理與金融機構 v5
19.8 利用股價來估計違約概率
當採用類似表19-1中的數據來估計公司真實世界的違約率時,必須依賴公司的信用評級,不幸的是公司信用評級的更新較慢,因此有些人認為股票價格為估測違約概率提供了更為及時的信息。
1974年,默頓(Merton)提出了一個模型,在模型中公司的股票被當作公司資產的期權。[1]為了便於討論,假設公司僅發行一個零息債券,債券到期時間為T,定義
V0——公司資產的當前價值;
VT——公司資產在時間T的價值;
E0——公司股票的當前價值;
ET——公司股票在時間T的價值;
D——在時間T公司發行債券的本息的總和;
σV——資產波動率(假設為常數);
σE——股票的瞬時波動率。
當VT<D時,公司會對自己發行的債券違約(至少在理論上如此),此時公司的股價為0;當VT>D時,公司會支付自己在時間T的負債,在時間T,股票價值為VT-D。在默頓模型中,公司在時間T的股價為
ET=max(VT-D, 0)
以上公式顯示出公司的股票可以看作是對公司資產的看漲期權,期權的執行價格為債券應償還的本息總量。布萊克-斯科爾斯公式(見本書附錄E)給出了這一期權的當前價格
E0=V0N(d1)-De-rTN(d2)
(19-4)
其中
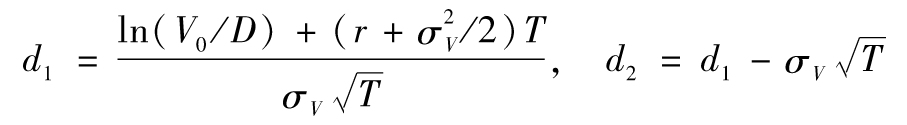
其中N(·)代表累積正態分佈函數。
在默頓模型中,如果期權不被行使,則意味著公司違約。公司在時間T的違約風險中性概率為N(-d2)。為計算這一數量,我們需要V0及σV,這兩個變量都不能在市場上直接觀察。如果公司是一家上市公司,我們可以觀察到E0,這意味著式(19-4)是V0及σV必須遵守的一個等式,我們此時也可以估計σE,由隨機微積分中的伊藤引理(Ito’s Lemma),我們得出
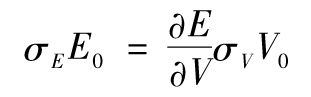
這裡∂E/∂V為股票的delta。由附錄E得出,delta=N(d1),因此
σEE0=N(d1)σVV0
(19-5)
上式是V0及σV必須遵守的另一個等式。式(19-4)及式(19-5)給出了一組關於V0及σV的方程組,由這兩個方程我們可以求得V0及σV的解。[2]
【例19-4】 假如一家公司的股價市值為300萬美元,股價變化的波動率為80%。公司在1年後必須償還的債務為1 000萬美元,無風險利率為每年5%。對應這一情形:E0=3,σE=0.80,r=0.05,T=1及D=10。對式(19-4)及式(19-5)求解,我們得出(以百萬計)V0=12.40及σV=0.212 3,變量d2=1.140 8,公司違約概率為N(-d2)=0.127,即12.7%。債券的當前市價為V0-E0,即9.40。債券預期付款的貼現值為10e-0.05×1=9.51。債券的預期損失為(9.51-9.40)/9.51,為債券不違約時價值的1.2%。
19.8.1 基本模型的擴展
我們接下來將說明基本默頓模型在哪幾個方面可以得到擴展。例如,一種擴展形式是假定每當資產價格低於一定的障礙值時,就會觸發違約;另外一種擴展方式是假定債券可以分期償還。許多研究人員發現公司發行股票的隱含波動率是反映公司違約率的一個很好的指標(隱含波動率越大,違約概率也越高)。赫爾等(2004)的研究證明了這一結果與默頓模型的一致性。[3]這項研究給出了採用兩個股票隱含波動率來實現默頓模型的方法,結果顯示這種擴展的模型與最初的實現方式結果非常接近。
19.8.2 模型的表現
由默頓模型及其擴展形式所產生的違約概率與實際違約概率有多麼接近呢?這一問題的答案是:在風險中性及真實世界中,默頓模型及其擴展形式均對違約概率提供了較好的排序。這意味著通過建立某種單調性關係,我們可以將由默頓模型產生的違約概率映射為真實世界或風險中性世界的違約率。穆迪KMV和Kamakura公司提供一項服務,將默頓模型的違約概率轉換為真實世界的違約概率。CreditGrades採用默頓模型來估計信用價差,這一信用價差與風險中性違約概率密切相關。在理論上,違約概率N(-d2)為風險中性違約概率。這使得穆迪KMV和Kamakura用它來估計真實世界的違約率的做法有些牽強。根據以上描述的校正過程,我們在分析計算中所採用的一個根本假設是:風險中性世界的違約概率、真實世界的違約概率以及由默頓模型估算的違約概率在排序上是一致的。
19.8.3 真實世界與風險中性世界的違約概率的比較
默頓模型有助於我們理解為什麼風險中性世界中的違約概率會高於真實世界。在風險中性世界中,公司資產的預期增長率是無風險利率。在真實世界中,公司資產的預期增長率通常高於無風險利率(反映出市場所要求的風險溢價)。因此,在風險中性世界中,未來資產價值跌到債務價值以下的概率也會比在真實世界中更高。
19.8.4 違約距離
違約距離(distance to default)用來描述默頓模型的輸出結果。這是指要在將來T時刻引發違約所需的、以標準差計算的資產價格的變化量。違約距離的公式為
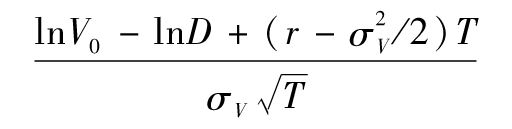
當違約距離降低時,公司違約的可能性會加大。在例19-4中,1年的違約距離為標準差的1.14倍。
[1] See R. Merton, “On the Pricing of Corporate Debt: The Risk Structure of Interest Rates,” Journal of Finance 29(1974):449-470.
[2] 為了對兩個非線性方程F(x,y)=0及G(x,y)=0求解,我們可以採用Excel中的Solver程序,通過求取[F(x,y)]2+[G(x,y)]2的極小值來達到目的。
[3] See J. Hull, I. Nelken, and A. White, “Merton’s Model, Credit Risk, and Volatility Skews,” Journal of Credit Risk 1, no.1(2004):1-27.