e1 John Hull 風險管理與金融機構 v5
19.7 違約概率的比較
現在,我們比較一下由歷史數據得出的違約概率以及由信用價差推算出的違約概率。表19-4顯示了:
·不同信用等級的公司7年的平均累積違約概率,數據由穆迪發佈。與表19-1中7年期違約率所在的列是一致的。
·1996年12月~2007年6月,不同信用等級的公司的平均信用價差。這些數據取自美林發佈的債券收益率數據,其中使用的假設是無風險利率比同期互換利率低10個基點(關於無風險利率的近似見第19.5.2節)。債券的平均期限在7年左右。
表19-4 累積違約概率與信用價差的比較
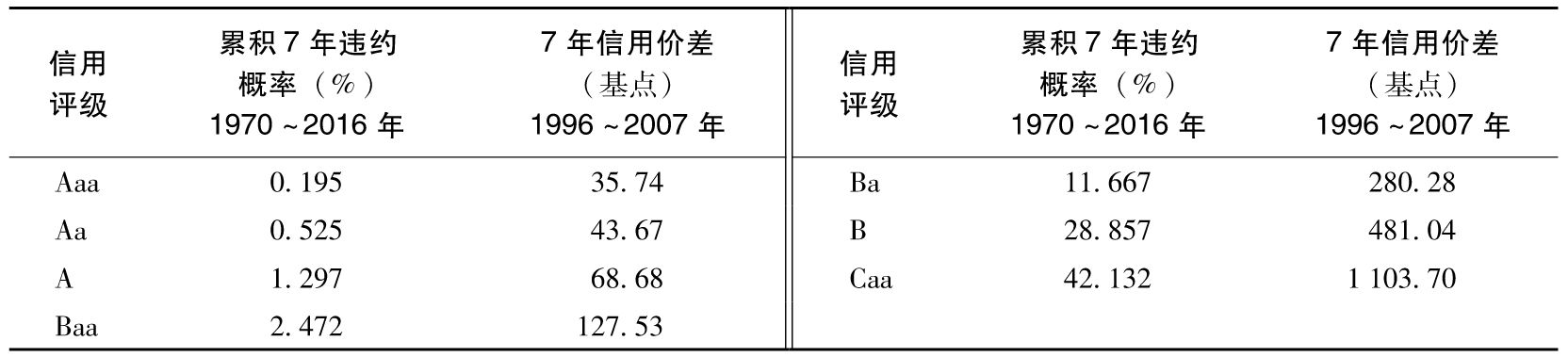
表中考慮的數據截至金融危機爆發之前。在金融危機中,信用價差暴漲。我們會看到由信用價差推算出的違約密度要高於由歷史數據統計得出的違約密度。如果這種非常時期也被包括進來,那麼這一結果會變得更加顯著。
表19-5顯示了7年平均風險率。[1]7年曆史違約密度(風險率)的計算與表19-4中的累積違約率一致。假設Q為7年累積違約概率。由式(19-2)
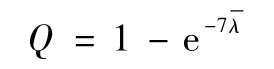
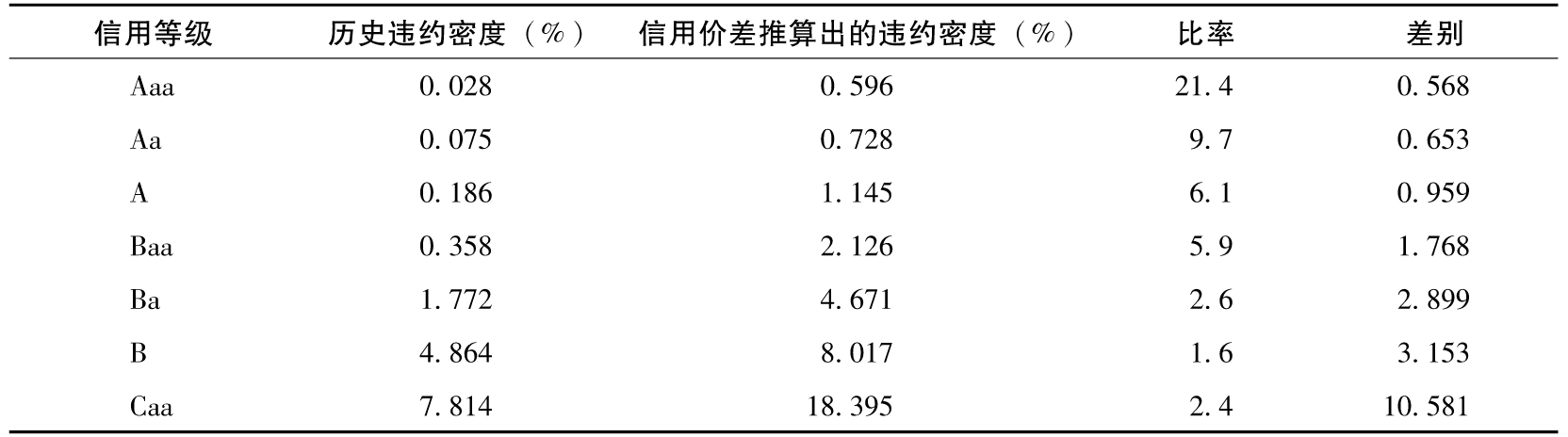
表19-5 7年平均違約密度
其中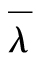 為平均風險率,並且
為平均風險率,並且
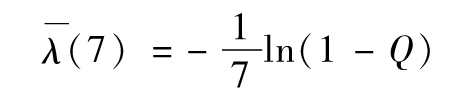
例如,對於信用級別為A的公司,7年累積違約率為1.217%或0.012 17,因此7年違約密度的平均值為
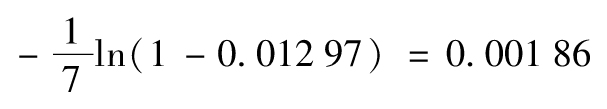
即0.186%。表19-5所示的由信用價差所得出的違約密度基於式(19-3),使用的回收率為40%。再次考慮一個評級為A的債券。表19-4中給出的平均的7年信用價差為68.68基點或0.006 868,因此平均的7年違約密度為
0.006 868/(1-0.4)=0.01145
表19-5顯示,在金融危機前,由信用價差推出的違約密度比通過長期歷史數據得出的要高。債券的信用等級越高,由債券價格倒推出來的違約密度與由歷史數據得出的違約密度之比就越大,隨著信用質量的下降,這個比率也隨之降低。與之相對,兩種違約概率的差隨著信用級別的降低而增加。[2]
表19-6是對這些結果的另一種解釋。此表顯示出投資者從不同信用級別的債券獲得的超出無風險利率之上的投資回報(這裡的無風險利率仍然等於7年互換利率減去10個基點)。我們還是考慮A級債券,這種債券的收益率超過7年國債收益率的平均利差為111個基點,這111個基點中的42個基點是我們選取的無風險利率近似與7年國債收益率的利差。補償預期違約需要11個基點(這一數值等於由表19-5中的歷史違約密度算出的1年違約概率乘以1減去回收率0.4)。最終我們得出額外預期回報(在考慮了預期違約後)為58個基點。[3]
表19-5及表19-6顯示,當兩種違約概率的百分比差距較大時,債券的額外預期回報相對較小。對於Aaa級債券,兩種違約概率的比率為21.4,但額外預期回報只有34個基點。預期額外回報隨著信用級別的降低而有所增加。
表19-6 債券的額外預期回報

表19-6中的額外回報並不總為常數。信用價差(及由此導致的額外回報)在2001年、2002年及2003年的前半年很高,之後一段時間很低,一直到2007年年中信用危機開始後,額外回報和信用價差急劇增加。
19.7.1 真實世界與風險中性概率比較
在第7.2節中,我們解釋了風險中性定價方法。通過這一方法,我們可以假設所有投資者在風險中性的前提下,對現金流進行定價(也就是說,投資者並不因承擔風險而索取超額收益)。採用風險中性定價,我們可以求得產品價格,計算出的價格無論是在真實世界或風險中性世界中均適用。
第7.2節已經解釋了風險中性違約概率的理論基礎。這些違約概率(有時也被稱作隱含違約概率)就是由信用價差推導出的違約概率。與此相對,由歷史數據得到的違約概率為真實世界違約率(有時也被稱作物理違約率)。表19-6中的額外預期回報直接來自真實世界及風險中性世界違約概率的差異,當沒有額外預期回報時,真實世界違約率會等同於風險中性違約率,這一結論反過來也成立。
為什麼真實世界中的違約概率與風險中性世界中的違約概率會相差甚遠呢?就像我們剛剛討論的那樣,這一問題等同於,為什麼企業債券交易員的平均收益要高於無風險利率?
一個原因是企業債券的流動性較差,債券交易員會因此而索求更高的回報,但這隻佔整體額外回報的一小部分。在正常市場情況下,這一說法大概可以解釋表19-6所示的額外回報中的25個基點。另外一個可能的原因是債券交易員的主觀違約率假設可能比表19-1中給出的違約率要高得多。交易員所假想的蕭條情景可能比他們所用的數據中出現的真實情形更差。但是,以上說法很難解釋額外回報中的大部分。[4]
目前為止,造成表19-5及表19-6中結果的最主要原因是債券違約並不是相互獨立的(也就是說,金融市場上的違約是有相關性的)。每年違約率的顯著變化就是證據。穆迪在1970~2016年的統計結果顯示(見表11-6),在對所有被評級的公司中,1979年的違約率最低,僅為0.088%,而2009年的違約率最高達4.996%。這種債券違約率的年度變化會引發系統性風險(即不能通過風險分散而消除的風險)。債券交易員因承擔風險自然會索取回報。從這個角度,債券交易員和股票交易員並沒有什麼不同,後者因承擔系統性風險而每年獲得5%或6%的額外回報。從表19-6中我們可以看到,交易高質量債券的交易員獲得的額外回報遠小於這個數字。但是,隨著債券信用質量的下降,額外回報會增加,接近股票的回報。
是什麼導致了違約的相關性進而引發系統性風險?一個解釋是宏觀經濟。好的宏觀經濟形勢會減少所有公司的違約概率,壞的宏觀經濟形勢會增加所有公司違約的可能(在第11章中討論的Vasicek模型中,可以認為因子F代表了經濟的健康情況)。另一種解釋被稱作“傳染”(contagion)效應。業界事例19-3討論了這一現象。
業界事例19-3
傳染效應
信用危機傳染效應是世界經濟中一個領域的問題引發其他不相關領域的問題的過程。1998年,俄羅斯國債違約引發了安全投資轉移現象,所有債券的信用價差都增大了。在2007年開始的信用危機中,存在類似的安全投資轉移現象,信用價差再次加大。隨之而來的衰退造成了2009年違約公司的數量創下紀錄。2011年,希臘的債務問題使得投資者不願購買其他國家(如西班牙、愛爾蘭、葡萄牙和意大利等)的國債,結果這些國家發行的國債的信用價差大幅增加。
造成信用危機傳染效應的原因在研究人員中存在爭議。系統性風險(見業界事例15-1)可能是傳染的原因之一。也可能是投資者在一個行業遭受損失後,對風險變得更加厭惡。還可能是一個行業出現問題後,導致投資者對其他不相關的行業也變得悲觀。不論原因是什麼,不同行業的實體都會發現為自己的業務活動融資變得更加困難,並因此增加了違約的可能性。
除了我們剛剛討論的系統性風險,每一個債券還會伴有非系統性(或特殊(idiosyncratic))風險。當我們討論股票時,我們認為投資者可以選取一個股票組合,例如,由30個股票構成的股票組合來對非系統性風險進行分散,因此投資者對承擔非系統性風險不應要求額外風險利差(risk premium)。對於債券,我們就沒有這麼清晰的結論。債券收益具有非常大的偏態性(highly skewed),而且上漲的幅度有限(例如,對於單一債券可能在1年內有99.75%的概率收益率為7%,而有0.25%的概率收益率為-60%。第一個情形對應於有沒有違約發生,第二個情形對應於有違約發生)。這類風險難以分散,[5]我們必須持有成千上萬的債券才能將風險分散。在實際中,許多債券組合與完全風險分散相去甚遠。因此,和前面一段提到的因承擔系統性風險而要求額外回報一樣,債券交易員對於自身所承擔的非系統性風險也應要求額外回報。
19.7.2 究竟應該採用哪種估計
到這一步我們自然會問,在信用風險分析中應該採用真實世界的違約率還是風險中性世界的違約率?這個問題在第7章中有更常規的討論。對這一問題的回答取決於分析目的,當對衍生產品定價或者分析違約對產品價格的影響時,應該採用風險中性違約概率,這是因為在分析中會涉及計算將來預期的現金流的貼現值,在計算中會不可避免(有意或無意)地採用風險中性定價理論。當採用情景分析法來估測因違約而觸發的損失時,應該採用真實世界的違約率。例如,在計算監管資本金時採用的違約概率即為真實世界的違約概率。
[1] 這裡分析類似J. Hull, M. Predescu, and A. White, “Bond Prices, Default Probabilities, and Risk Premiums,” Journal of Credit Risk 1, no.2(Spring 2005):53-60。
[2] 其他一些研究也已注意到了兩種方法估算出的違約概率的不同,例如J. S. Fons, “The Default Premium and Corporate Bond Experience,” Journal of Finance 42, no.1(March 1987):81-97, and E.I. Altman, “Measuring Corporate Bond Mortality and Performance,” Journal of Finance 44, no.4(September 1989):909-922。
[3] 為了簡便起見,我們在計算過程中沒有考慮複利頻率對利差、回報和違約密度的影響。
[4] 除了基於1970~2016年時間段的表19-1以外,穆迪也產生了一個基於1920~2016年時間段的數據表。採用這一較長時間段的數據,我們發現對應於表19-5中的投資級債券的歷史違約密度有所增加,但是,非投資等級債券的違約密度有所下降。
[5] See J. D. Amato and E. M. Remolona, “The Credit Spread Puzzle,” BIS Quarterly Review (December 2003):51-63.