BUSINESS BOOKS

19.6　由信用價差來估算違約概率

我們現在討論如何用信用價差來估計違約概率。

19.6.1　近似計算

某個5年期信用價差（CDS利差、債券收益率利差或資產互換利差）為240個基點，預期回收率為40%。這意味著違約帶給企業債券持有者損失的期望值為240個基點（或每年2.4%）。粗略地說，我們可以認為信用價差大致相當於平均損失率。回收率為40%，我們得出在沒有前期違約的條件下，5年內平均每年的條件違約密度為0.024/（1-0.4）=4%，一般來講條件違約概率滿足

其中s（T）是期限為T的信用價差（以連續複利計算），R為回收率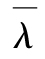，為從時間0到時間T之間的平均違約密度（風險率）。

假定已知若干不同期限的信用價差，我們可以通過利差剝離方法（bootstrap）來求得違約密度的期限結構（至少在近似意義上講），以下我們舉例說明計算過程。

19.6.2　更加準確的計算

以上計算對CDS利差較為適用，當標的債券價格接近於面值時，以上計算對於債券收益率利差和資產互換利差也可以給出比較好的近似。我們接下來給出一個更加準確的計算，這一方法對債券價格不接近於面值時也適用。

假設面值為100美元的某企業5年期債券的息票率為每年6%（每半年付息一次），收益率為每年7%（連續複利）。類似的無風險債券的收益率為5%（連續複利）。由收益率隱含得出的企業債券價格為95.34美元，無風險債券的價格為104.09美元，因此，未來5年內，由違約引發的預期損失為104.09-95.34，即8.75美元。為了簡單起見，假定企業債券每年的違約率為Q，並且違約只會發生在0.5年、1.5年、2.5年、3.5年及4.5年時，即剛好發生在支付息票之前。對所有的期限，假定無風險利率均為5%（連續複利），債券預期回收率為40%（這一分析可以擴展到違約發生更頻繁的情況）。

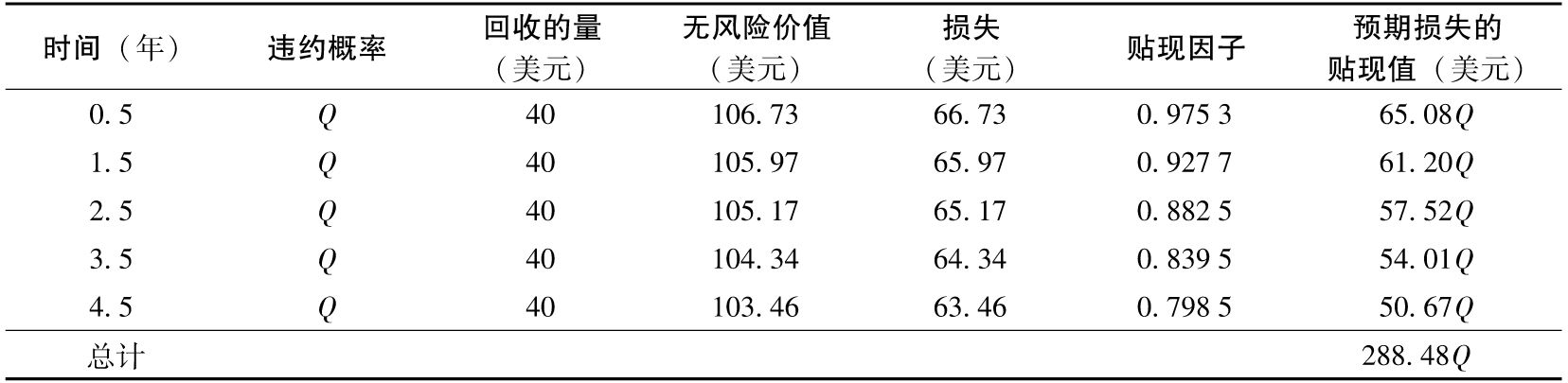
表19-3計算了與違約率Q有關的預期損失。為了說明計算過程，我們考慮表19-3中對應3.5年的一行，在3.5年時，不考慮違約的債券價格的期望值為（在計算中利用遠期無風險利率）

3+3e^-0.05×0.5+3e^-0.05×1.0+103e^-0.05×15=104.34（美元）

注：本金=100美元。

由第19.3節回收率的定義得出，違約發生時債券的回收價值為40美元，因此違約觸發的損失為104.34-40=64.34美元，這一損失所對應的貼現值為54.01美元，因此違約預期損失為54.01Q。

表19-3顯示預期損失的總和為288.48Q，該預期損失等於前面計算出的8.75美元的預期損失，因此Q的值為8.75/288.48，即3.03%。我們在計算中假定每年的違約概率相等，而且每年只能發生一次違約。我們可以把計算擴展到違約發生頻率更高的情況。同時，我們也可以假設違約密度為一個常數，或者違約概率隨時間呈現一定的模式，而不是假定一個不變的無條件違約概率。使用幾隻不同的債券，我們可以估計關於違約概率期限結構的多個參數。例如，假定有期限分別為3年、5年、7年和10年的4只債券，並且違約概率服從一個階躍函數（step function）。我們可以利用第1只債券來估計前3年中每年的違約概率，利用第2只債券來估計第4年和第5年的違約概率，利用第3只債券來估計第6年和第7年的違約概率，利用第4只債券來估計第8年、第9年和第10年的違約概率（見練習題19.15和練習題19.24）。這一方法和附錄B中給出的用券息剝離法計算利率的期限結構的過程很類似。