BUSINESS BOOKS

19.2　歷史違約概率

表19-1是由評級公司公佈的一組典型數據，這些數據顯示了公司的信用隨時間推移而出現的不同變化。例如，表19-1顯示某債券的初始穆迪信用級別為Baa，這家公司有0.177%的概率在1年內違約，並且有0.461%的概率在2年內違約等。債券在一個指定的年份違約的概率可由這一表格計算得出。例如，初始信用級別為Baa的公司在第2年違約的概率為0.461%-0.177%=0.284%。

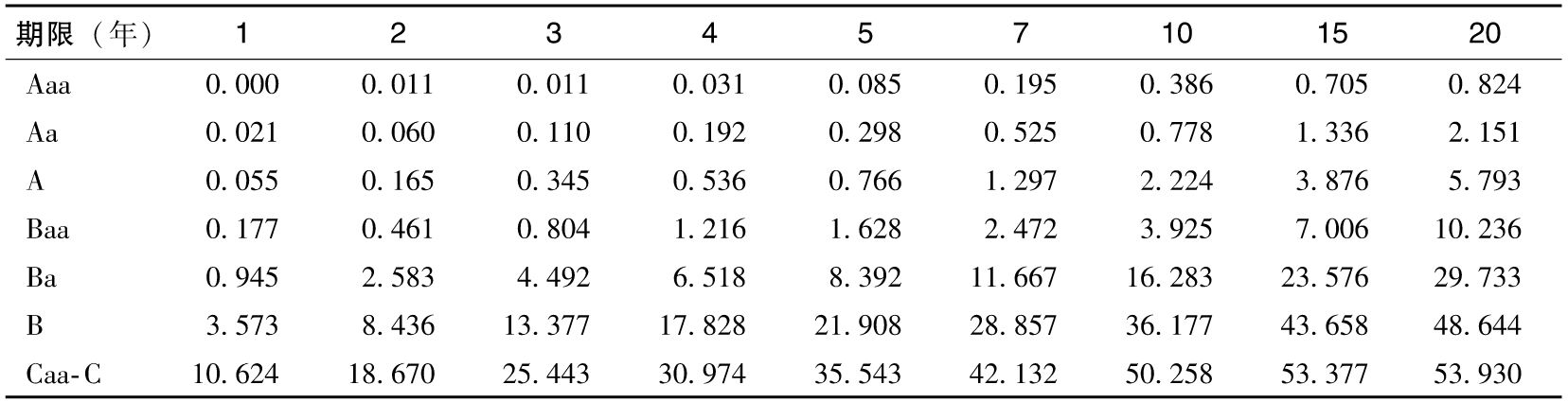
資料來源：穆迪。

表19-1顯示具備投資級別的債券在某年內違約概率隨著期限的增大而有所增大（例如，Aa級債券在第1～5年的違約概率分別為0.021%、0.039%、0.050%、0.082%及0.106%）。這是因為在最初發行時，債券的信用狀況較好，但隨著時間的推移，信用出現問題的可能性也會增大，而對於最初的信用級別較差的債券，每年的違約率常常是時間期限的一個遞減函數（如Caa級別的債券在第1～5年的概率分別為10.624%、8.046%、6.773%、5.531%、4.569%）。產生這一現象的原因是，對信用較差的債券，今後一兩年是企業能否生存下去的關鍵期，如果企業能夠度過這個階段，則說明其財務狀況很可能已得到改善。

違約密度

由表19-1我們可以計算出Caa級別的債券在第3年的違約概率，即25.443％-18.670％=6.773%。這一違約概率被稱為無條件違約概率（unconditional default probability）。此概率是今天，即在0時刻，所看到的第3年的違約概率。Caa債券一直到第2年年底都不會破產的概率為100%-18.670%=81.330%，因此我們得出在前2年沒有違約的條件下，公司在第3年違約的概率為6.773％/81.330％=8.33%。

這裡計算出的違約概率8.33%對應於1年的觀察期。通過考慮在時間t之前沒有違約的條件下，違約發生在t與t+Δt之間的概率，我們可以求得對應於時間t的違約密度（default intensity），這一違約密度也被稱為風險率（hazard rate）。時間t的違約密度λ（t）的含義是指在從0時刻到t時刻違約沒有發生的條件下，違約發生在t與t+Δt之間的概率為λ（t）Δt。如果V（t）是從今天到時間t公司仍然生存的累積概率（就是說直到時間t違約仍沒有發生），那麼t與t+Δt之間的無條件違約概率為V（t）-V（t+Δt），在時間t之前沒有違約的前提下，違約發生在t與t+Δt之間的條件概率為［V（t）-V（t+Δt）］/V（t），因此

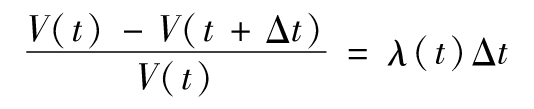
或

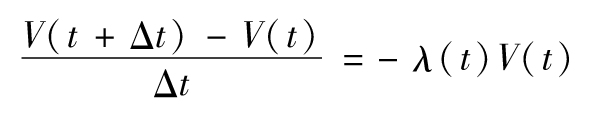
對以上公式求極限得出

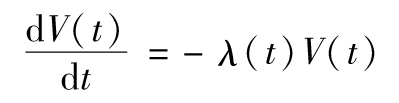
因此

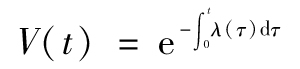
定義Q（t）為時間t之前的違約概率，我們得出

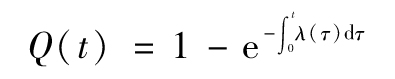
或者

其中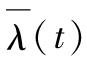為介於0與時間t之間的平均風險率（違約密度）。