e1 John Hull 風險管理與金融機構 v5

17.2　危機後的監管改革

許多人認為，OTC衍生產品市場對2008年信用危機負有部分責任。2008年金融危機爆發後，20國集團（G20）領導人於9月在匹茲堡會晤，他們希望通過監管OTC市場來降低系統性風險。領導人會後發表聲明達成共識：

所有標準化的OTC衍生產品合約應通過交易所或電子交易平臺進行交易，在合適的情況下，應採用中央對手方的方式清算，改革最遲於2012年年底完成。OTC衍生產品應向交易倉庫報告。不採用中央清算的OTC衍生產品交易合同應適用更高的資本要求。我們要求金融穩定委員會及其相關成員評估實施情況及其是否足以提高衍生產品市場的透明度，降低系統性風險，防止市場濫用。

這引起OTC衍生產品的三個主要變化：

（1）要求所有標準化OTC衍生產品通過中央對手方進行清算。標準化衍生產品包括普通利率互換（佔OTC衍生產品交易的絕大部分）和信用指數違約互換。這個要求的目的是降低系統性風險（見業界事例15-1）。它導致衍生產品交易商之間的信用敞口減少，從而降低了金融機構間的內在聯繫導致金融體系崩潰的可能性。

（2）要求標準化的OTC衍生產品合約在電子平臺上交易。這一舉措是為了提高透明度。如果有一個電子平臺來撮合買賣雙方，那麼所有市場參與者都應能隨時獲得產品交易的價格。[1]這些平臺在美國被稱為互換執行設施（SEF），在歐洲被稱為有組織交易設施（OTF）。在實踐上，標準化OTC衍生產品一旦在這些平臺上進行交易，就會被自動轉交給CCP。

（3）要求OTC市場上的所有交易都報告給中央交易數據倉庫。這一要求為監管機構提供了有關OTC交易市場參與者所承擔風險的重要信息。這在一定程度上是對美國國際集團（AIG）慘敗的迴應。在AIG請求紓困之前，監管機構並不知道AIG的一家子公司所承擔的巨大風險。

前兩項規定僅適用於兩家金融機構間的交易（或一家金融機構與一家因OTC衍生產品交易規模而具有系統性重要非金融公司之間的交易）。因此，衍生產品交易商可以繼續以危機前的方式，與許多非金融公司客戶進行交易。

約25%的OTC交易在危機前通過中央交易方清算，其餘75%通過雙邊清算。由於新規定的出現，這些比例發生了反轉，現在約75%的OTC交易通過中央交易方清算，25%的交易通過雙邊清算。

17.2.1　未清算交易

在2011年舉行的另一場G20會議之後，針對非標準OTC衍生產品的監管有所收緊。這些衍生產品不包括在上一節提到的規則中。它們適用於雙邊清算而不是集中清算，被稱為未清算交易（uncleared trade）。監管（在2016～2020年實施）規定兩家金融機構（或一家金融機構與一家被認為具有系統性重要非金融企業）之間的未清算交易必須遵循保證金規定。在此之前，雙邊清算的吸引力之一是，市場參與者可以自由協商其ISDA主協議的任何信用支持附件。

法規規定，對於未清算交易，交易雙方都必須繳納初始保證金和變動保證金。在金融危機前的OTC市場交易中（特別是在衍生產品交易商之間的交易中），變動保證金相當普遍，但很少要求繳納初始保證金。當與信譽不高的交易對手進行交易時，衍生產品交易商可能會堅持要求對手提供初始保證金。但在雙邊清算市場上，需要繳納初始保證金的情況極為鮮見。

變動保證金通常是直接由交易一方轉交給另一方，但初始保證金不能這樣處理。例如，如果A將100萬美元的初始保證金轉給B，B又將100萬美元的初始保證金轉給A，那麼初始保證金就不能達到預期的目的，因為雙方間的保證金會相互抵消。因此，法規要求初始保證金必須轉給第三方，由第三方託管。

17.2.2　初始保證金的確定：SIMM

對於未清算交易的新規定，ISDA主協議的雙方必須就變動保證金和初始保證金達成一致。變動保證金要求就未完成交易的估值達成協議，並已制定解決任何分歧的程序。初始保證金的計算比交易價值的計算更為複雜，不同的模型能給出截然不同的結果。因此，人們一直試圖制定一個行業標準。

在雙方未清算交易組合規則中有明確規定，在壓力市場條件下，初始保證金有99%的概率不會超過10天的價值收益。需要注意的是，初始保證金是在險價值的一個標誌。當計算在險價值時，就是在確定損失分佈的極限百分位數，而當計算初始保證金時，是在確定收益分佈的極限百分位數。這是因為風險敞口隨著投資組合無抵押價值的增加而增加。

巴塞爾委員會提出了一種計算初始保證金的方法，它規定了不同類型交易的初始保證金佔交易額的百分比。這不是一種主流的方法，因為它沒有考慮淨額結算。如果市場參與者在第1天和第5天的兩筆交易幾乎相抵，那麼即使對交易對手的淨風險敞口接近於0，第5天的初始保證金也幾乎是第1天的2倍。ISDA提出了標準初始保證金模型（SIMM）來克服這一問題。這個模型現在已經得到了監管機構的批准。

SIMM使用第14章描述的模型構建法，[2]delta與vega風險使用式（14-8）的加權敏感性和風險權重進行處理

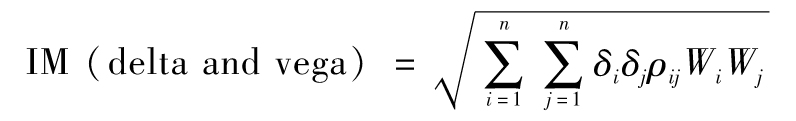
其中Wi為風險因子i的風險權重（由監管機構指定），δi為所持頭寸對風險因子i的敏感性（由銀行決定），ρij為風險因子i與j的相關性（由監管機構規定）。在置信度為99%、10天展望期的情況下，計算Wi的一個公式是

其中σi是在受壓的市場條件下第i個風險因子的每日波動率（或標準差，如利率、信貸息差和波動率）。

為計算初始保證金gamma風險的增量效應，SIMM首先考慮了所有delta為0且沒有交叉gamma的情況。由式（14-11）和式（14-12）可知，1天內投資組合價值變化的均值和標準差分別為

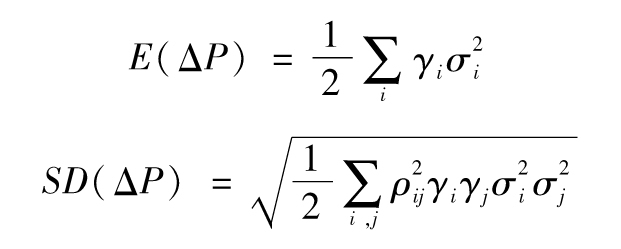
其中γi是對於第i個風險因子的gamma風險。

將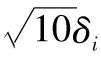代入δi，可以獲得10天內投資組合變化的平均值和標準差的估計值。定義

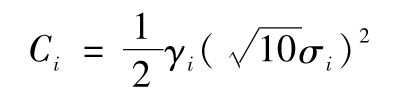
則10天變化中的平均值m，標準差s分別為

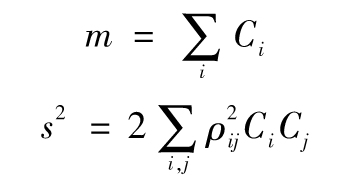
SIMM模型中假設

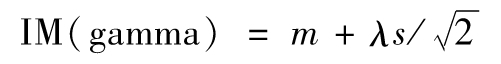
式中參數λ（見作業題17.14）定義為

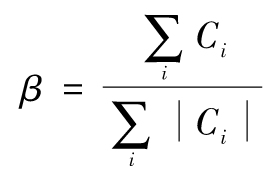
如圖17-3所示。這種關係產生的結果具有正確的性質，並與使用蒙特卡羅模擬進行的測試密切相符。

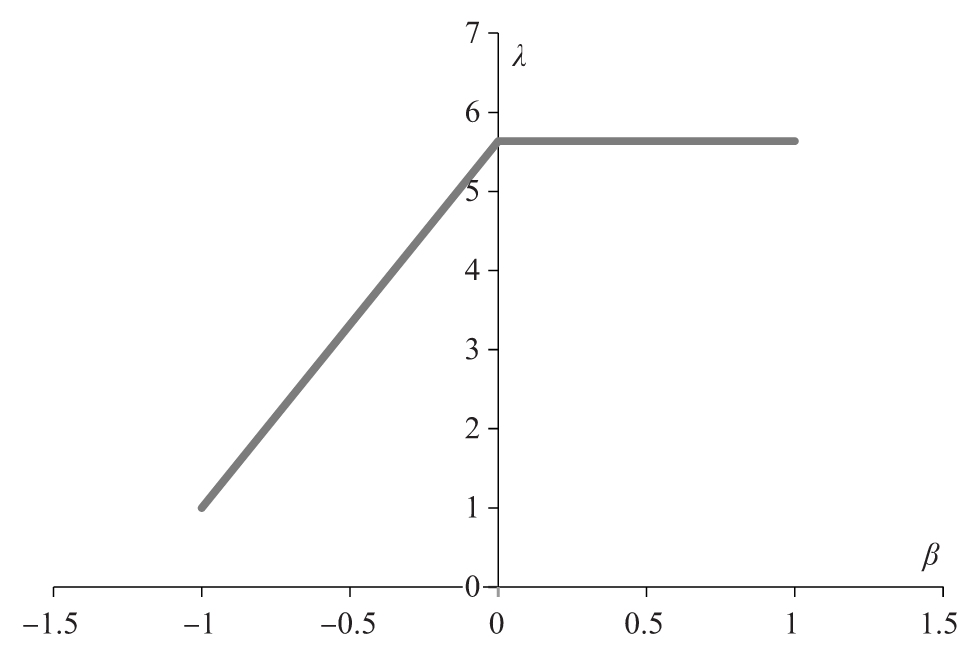
圖17-3　λ和β的關係

SIMM中還有很多其他的細節。為簡化計算，gamma由使用兩種持有歐式期權的vega計算得來。風險因子被分成幾組，一些風險因子涉及帶有頂點的期限結構，按第14章中描述的進行處理。按照規定的規則計算組內與組間的相關性ρij。

[1] 這裡的一個問題是，適用於互換的電子平臺類型可能與交易所使用的電子平臺類型不同。互換交易是間斷性的，有大量的名義本金，而交易所中期貨和期權交易的規模通常要小得多。

[2] See “ISDA SIMM: From Principles to Model Specification,” ISDA, March 3, 2016.