e1 John Hull 風險管理與金融機構 v5
15.8 《巴塞爾協議Ⅱ》中的信用風險資本金
關於信用風險資本金的計算,在《巴塞爾協議Ⅱ》中,銀行有以下三種選擇:
(1)標準法;
(2)基礎內部評級(internal rating based,IRB)法;
(3)高級內部評級法。
但是,美國(如上所述,只對大銀行實行《巴塞爾協議Ⅱ》)決定只採用基礎內部評級法。
15.8.1 標準法
如果某些銀行的管理在監管部門看來還不夠成熟,沒有達到採用內部評級法的程度,這些銀行可以採用標準法來計算資本金。標準法與《巴塞爾協議Ⅰ》類似,其不同之處在於風險權重的不同,[1]表15-4是對某些新規則的一個總結。將表15-4同表15-1進行比較,我們看到一家銀行所在的國家是否擁有OECD身份在《巴塞爾協議Ⅱ》中已經不重要。對於一個主權國家的風險敞口的權重範圍為0~150%,而對於一家銀行或企業的風險敞口的權重範圍為20%~150%。在表15-1中,OECD國家銀行的信用風險被認為小於企業風險,OECD銀行的風險權重為20%,企業的風險權重為100%,而表15-4對於銀行及企業的處理方式較為接近。表15-4有一點非常有趣,如果一個國家、企業或銀行的信用評級很差,其風險權重可能比沒有信用評級的情況還要差,監管機構允許銀行對自己註冊地的國家或國家央行的敞口採用更低的風險權重(20%對應於50%,50%對應於100%,100%對應於150%)。
表15-4 《巴塞爾協議Ⅱ》標準法中關於國家、銀行及企業的風險權重(面額的比率)與信用級別有關

①包括對國家央行的風險敞口。
②國家監管機構有選擇權。
在《巴塞爾協議Ⅱ》的標準法中,住房抵押貸款的風險權重為35%,其他零售貸款的風險權重為75%。如果是針對銀行的風險敞口,那麼計算規則會更加複雜。除了採用由表15-4給出的風險權重,國家監管部門可以選擇根據銀行註冊國的主權評級來確定資本金要求。如果銀行註冊國的評級介於AAA及AA-之間,那麼風險權重為20%;如果註冊國的評級介於A+與A-之間,那麼風險權重為50%;如果註冊國的評級介於BBB+與B-之間,那麼風險權重為100%;如果註冊國的評級低於B-,那麼風險權重為150%;如果註冊國沒有評級,那麼權重為100%。另外一個複雜之處是如果國家監管部門採用表15-4定義的規則,則對於期限小於3個月的貸款處理可能更有利,當借款方信用級別介於AAA與BBB-之間時,權重為20%;當借款方信用級別介於BB+與B-之間時,權重為50%;當借款方信用級別低於B-時,權重為150%;對應於無信用級別的情形,權重為20%。
2017年12月,巴塞爾委員會創建了一個更加細化的標準化方法,用於確定信用風險敞口的風險權重。在某些情況下,它還限制了高級IRB法的使用。如第16.4節所述,修訂後的標準化方法將為確定總資本要求提供依據。
【例15-5】 假定一家銀行資產的構成為貸款方信用評級為A級的1億美元貸款、1 000萬美元信用評級為AAA級的政府債券及5000萬美元房屋貸款。《巴塞爾協議Ⅱ》標準法所計算的風險加權資產總和為(以百萬美元計)
0.5×100+0.0×10+0.35×50=67.5
即6 750萬美元,而《1988年巴塞爾協議》所計算的風險加權資產總和為12 500萬美元(見例15-1)。
15.8.2 對於抵押品的調節
關於抵押品,銀行可以採用兩種辦法來調整其風險權重。第一種方法被稱為簡單法(simple approach),這一方法同《1988年巴塞爾協議》中的方法類似;第二種方法被稱為綜合法(comprehensive approach)。對於銀行賬戶中的資產,銀行有權在兩種方法中任選其一,而對於交易賬戶中的資產,在計算交易對手信用資本金時,銀行只能採用綜合法。
在簡單法中,對應於抵押品所覆蓋的風險敞口部分,交易對手的風險權重被抵押品的風險權重所代替(這裡的敞口是通過淨額結算所得),對於抵押品不覆蓋的部分,仍然採用交易對手所對應的風險權重。抵押品所對應的最小權重為20%,[2]抵押品的價格必須要每6個月重新定價一次,抵押品的期限一定要大於風險敞口的期限。
在綜合法中,銀行要向上調整風險敞口的計算以反映將來市場變化可能造成的風險敞口的增大,同時銀行應減少抵押品的估值以反映市場變化可能造成的抵押品價格的下降[3](具體調整的幅度與敞口及抵押品價格變化的波動率有關)。在進行調節後,新的風險敞口等於調整以後的風險敞口超出調整後的抵押品價值的餘額,然後,我們將交易對手所對應的風險權重用於新的風險敞口得出風險加權資產。對於風險敞口及抵押品價值的調整,銀行可採用《巴塞爾協議Ⅱ》中所設定的規則來進行計算,或者在經過監管部門批准之後,採用內部模型進行計算。當存在淨額結算約定時,風險敞口及抵押品價值的淨額結算要分開進行,各調節量的計算中要進行加權平均。
【例15-6】 假定一家銀行對於某交易對手的風險敞口為8 000萬美元,對應的抵押品的價值為7000萬美元。抵押品由信用評級為A的一家公司的債券組成,交易對手的信用級別為B+。對應於交易對手的權重為150%,而對應於抵押品的權重為50%,在簡單法下銀行的頭寸所對應的風險加權資產為
0.5×7 000+1.5×1 000=5 000(萬美元)
考慮綜合法,假定風險敞口在今後可能會增加10%,而抵押品價值可能會減少15%,因此經過調整後的風險敞口為1.1×8 000-0.85×7 000=2 850萬美元,對應於這一敞口的風險權重為150%,我們得出風險加權資產為4 275萬美元。
15.8.3 內部評級法
圖15-1顯示了內部評級法模型的基本思路。監管機構將資本金建立在在險價值(VaR)的基礎上,而在險價值的計算要選定1年展望期及99.9%的置信區間。它們認識到金融機構在產品定價時往往已經考慮了預期損失(例如,銀行貸款利率的設定要能夠覆蓋貸款預期損失),資本金應等於在險價值減去預期損失。
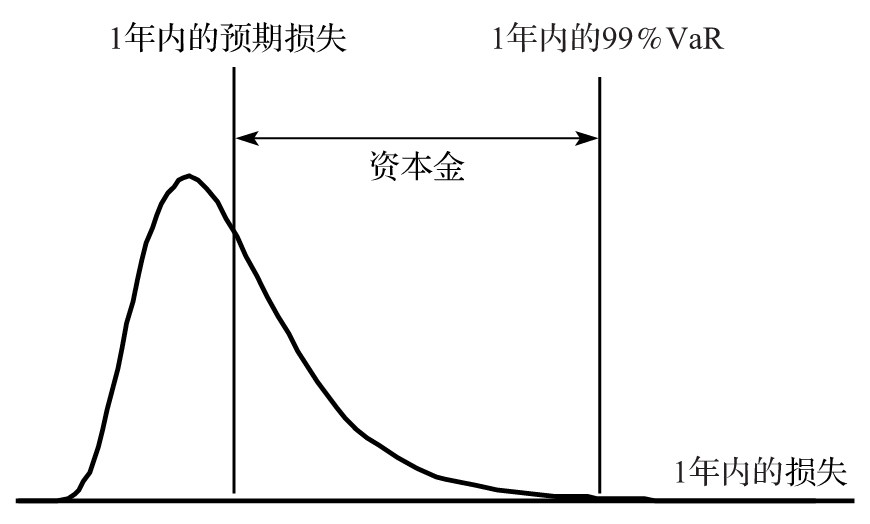
圖15-1 損失概率密度函數以及金融機構所需要的資本金
這裡VaR的計算基於第11.6節中的違約時間單因子高斯Copula模型。假定某銀行的債務人很多,每個債務人在1年內的違約概率均為PD,債務人之間的Copula相關係數均為ρ。[4]如第11.6節所示,我們定義
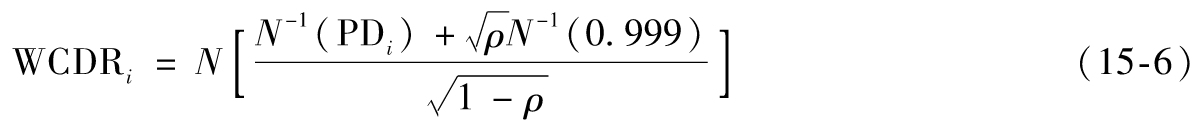
其中WCDRi為“最壞情況下的違約概率”(worst-case default rate),即銀行有99.9%的把握,下一年第i個交易對手的違約可能性不會超過該數。Gordy(2003)[5]的研究表明,對一個大的交易組合(貸款、貸款承諾、衍生產品等),如果相關性ρ相同,則1年展望期、99.9%置信度的VaR近似於
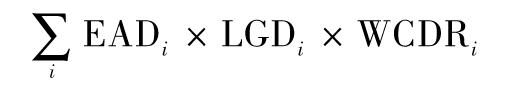
其中EADi為第i個交易對手在違約時的風險敞口,LGDi為第i個交易對手違約的情況下的損失率。變量EADi是一個貨幣量,是指在違約發生時,第i個交易對手欠款的數量。變量LGDi是相對EADi的一個比例值,是指在違約時損失所佔EADi的比率。例如,在債務人違約時,如果一家銀行能收回貸款的30%,則LGDi=0.7。
違約造成的預期損失為
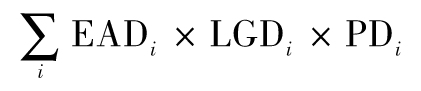
圖15-1所示的資本金等於99.9%置信度所對應的最壞損失減去預期損失,即
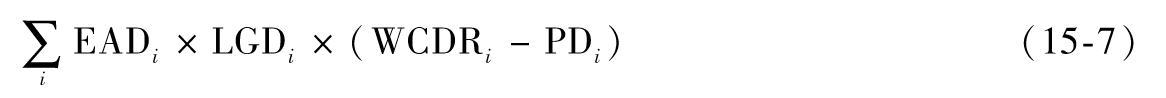
現在我們去掉下標,對一個交易對手,定義:
PD——交易對手在1年內違約的概率(表示為小數);
EAD——違約時的敞口(貨幣值);
LGD——當違約損失率或違約發生時,敞口中損失的比例(表示為小數)。
表15-5顯示了在高斯Copula模型中,WCDR與PD及ρ有關。當ρ=0時,因為資產之間沒有相關性且每一年的違約率相等,所以WCDR=PD;當ρ增加時,WCDR也會隨之增加。
表15-5 1年期、99.9%置信區間的WCDR與PD及ρ的關係

15.8.4 違約風險敞口
在基礎IRB法中,對衍生產品的EAD的計算通常基於《巴塞爾協議Ⅰ》[6]中的CEM方法。在高級IRB法中,銀行可以使用其內部模型來計算EAD。
使用內部模型的第一步是計算未來若干時間內每個交易對手的預期風險敞口(EE,通常涉及蒙特卡羅模擬和第20章討論的方法)。在未來時間t的有效預期風險敞口(有效EE)是時間0到時間t之間的最大EE。EAD設置為有效預期正風險敞口的1.4倍,該值是第一年有效EE的平均值。[7]
15.8.5 對企業、主權國家及銀行的風險敞口
對於企業、主權國家及銀行的風險敞口,《巴塞爾協議Ⅱ》根據實證研究結果,假定相關係數ρ與違約概率之間存在如下關係式[8]
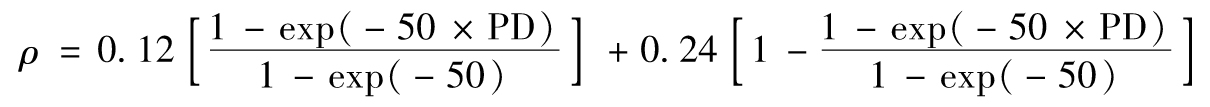
因為數量exp(-50)非常小,所以這一公式實際可以近似為
ρ=0.12(1+e-50×PD)
(15-8)
當PD增加時,ρ會減小。造成這種PD與ρ之間的反向關係的原因如下:當某家企業信用惡化時,企業所對應的PD會增大,此時公司的違約概率會變得更加獨立,市場整體情況對該企業違約概率的影響會變得越來越小。
結合式(15-8)與式(15-6),我們得出表15-6,該表展示了WCDR與PD的關係。如同我們預計的那樣,WCDR是PD的一個遞增函數,但是,如果我們假定ρ與PD無關時,WCDR增長速度並不快。
表15-6 企業、政府和銀行的WCDR與PD的關係

對一個交易對手,資本金的計算公式為
EAD×LGD×(WCDR-PD)×MA
(15-9)
以上公式中前三項的含義已經在關於式(15-7)的討論中解釋過,變量MA是針對期限的調節,這一數量由如下公式決定

其中
b=[0.118 52-0.054 78×ln(PD)]2
M為敞口的期限。針對期限的調整是因為考慮以下情況:當產品的期限大於1年時,1年的信用風險敞口可能會因為對手信用評級降低或違約而增加(當M=1時,MA=1,此時期限調整無任何效果)。如第15.7節所述(見式(15-5)),風險加權資產(RWA)等於12.5乘以資本金
RWA=12.5×EAD×LGD×(WCDR-PD)×MA
因此,資本金等於RWA的8%,其中4%應為第一類資本。
在基礎IRB法中,銀行提供參數PD,而其他參數LGD、EAD及M是由巴塞爾委員會來設定的。針對銀行和企業的風險敞口,需要設置PD的下限0.03%。對於高優先級索賠(senior claims),LGD被設定為45%,而對於次優先級索賠(subordinated claims),LGD被設定為75%。當存在抵押品時,為了應用前述綜合法,我們首先需要將LGD下調,下調的比例等於經調整後的抵押品價值與經調整後的風險敞口的比例。經調整的風險敞口及抵押品的價值都需要以綜合法進行計算。對衍生產品,EAD的計算與《1988年巴塞爾協議》中計算衍生產品等價信用量的方法類似(即當前敞口加附加項),計算中應考慮淨額結算的效應,在大多數情況下M=2.5。
在高級IRB法中,對企業、主權國家及其他銀行的敞口,銀行均提供自己對PD、LGD、EAD及M等參數的估計。信用風險緩釋措施,例如降級觸發,會減小PD的數值(對於PD,有一個與基礎IRB法類似的要求,那就是PD的下限不能低於0.03%)。影響LGD的兩個主要因素為債券的優先級別及抵押品。在計算EAD時,銀行可以在取得監管機構的批准後使用自己的模型。當涉及衍生產品時,模型往往會使用蒙特卡羅模擬來決定在未來1年內,預期敞口(考慮了淨額結算及抵押品以後)會如何變化。
由式(15-9)給出的資本金是用於覆蓋在1年內、99.9%置信度之下非預期損失不會超過的數量(如前面所述,預期損失應該已經包含在銀行對產品的定價中)。WCDR對應於(理論上)千年一遇的違約概率。巴塞爾委員會保留了當由式(15-9)所得出的資本金過高或過低時,對其施加某乘積因子的權利(這裡的乘積因子可能大於1,也可能會小於1),這一因子通常為1.06。
【例15-7】 假定某銀行的資產構成為企業貸款,貸款的總面額為1億美元,借款方的信用等級為A,對於企業的PD的估計為0.1%,LGD為60%,貸款的平均期限為2.5年,這意味著
b=[0.118 52-0.054 78×ln(0.001)]2=0.247
因此

由表15-6,我們得出WCDR為3.4%,在《巴塞爾協議Ⅱ》基礎IRB法中,對於企業貸款的風險加權資產的總量為
12.5×100×0.6×(0.034-0.001)×1.59=39.3(百萬美元)=3 930(萬美元)
《巴塞爾協議Ⅰ》所對應的資本金為1億美元,而由《巴塞爾協議Ⅱ》標準法所計算的數量為5 000萬美元(見例15-1及例15-5,這裡的1億美元貸款只是以上例子中投資組合的一部分)。
15.8.6 零售貸款敞口
零售貸款的資本金計算方法與對企業、政府及銀行敞口的資本金計算方法相似,其不同之處在於這時基礎IRB法與高級IRB法合併成了一個方法。每家銀行都可以對參數PD、EAD及LGD進行估計。在計算中沒有對於期限的調節,計算資本金的公式為
EAD×LGD×(WCDR-PD)
風險加權資產為
RWA=12.5×EAD×LGD×(WCDR-PD)
其中WCDR由式(15-6)計算得出。對於住房抵押貸款,ρ被設定為0.15;[9]對於合格滾動貸款,ρ被設定為0.04;計算其他零售敞口的WCDR所採用的ρ由以下公式得出

因為exp(-35)的數量很小,所以以上公式與以下公式基本等同於
ρ=0.03+0.13e-35×PD
(15-11)
將式(15-11)同式(15-8)進行比較,我們得出對於零售貸款所採用的相關性要比其他貸款低得多。類似於表15-6,表15-7顯示了零售貸款的WCDR與PD的關係。
表15-7 關於零售貸款,1年期、99.9%置信區間的WCDR與PD之間的關係

【例15-8】 假定某銀行資產由5 000萬美元貸款組合構成,其中PD的估計值為0.005,LGD的估計值為20%。對於這一情形,ρ=0.15及
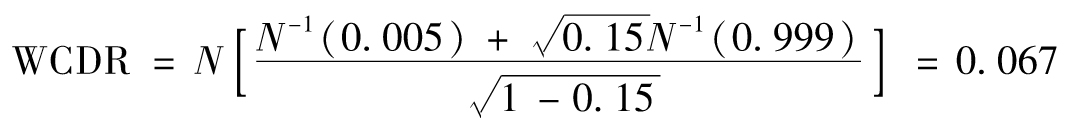
風險加權資產為
12.5×50×0.2×(0.067-0.005)=7.8(百萬美元)
與此相對照,《巴塞爾協議Ⅰ》所對應的風險加權資產為2 500萬美元,《巴塞爾協議Ⅱ》標準法所對應的風險加權資產為1750萬美元(見例15-1及例15-5,這裡討論的5 000萬美元房屋貸款只是投資組合結構的一部分)。
15.8.7 信用擔保以及信用衍生產品
傳統上巴塞爾委員會對於信用擔保和信用衍生產品(如信用互換)所採用的處理方法為信用替換方法。假定一家信用評級為AA級的公司給一個信用評級為BBB級的借款方提供貸款擔保。在計算資本金時,信用擔保方的信用級別(AA級)而不是借款方的信用級別(BBB級)被用於計算資本金,因此,這筆貸款看上去好像是貸給了一家AA級的公司。然而這種計算方式仍然誇大了信用風險,因為只有當擔保方及借貸方同時破產時才會造成貸款損失(而且擔保方要在借款方破產之前就已經破產)。[10]巴塞爾委員會對這一問題做了處理。2005年7月,委員會對《巴塞爾協議Ⅱ》中的雙重破產問題發表了一個報告,這一報告對於雙重破產做了特殊處理。[11]這一方法代替了信用替換方法,銀行首先在風險敞口沒有任何擔保的假設下進行資本金的計算,完成計算後將資本金再乘以0.15+160×PDg,其中PDg 為擔保人的1年期的違約概率,最後的計算結果即為最終的資本金數量。
[1] 採用新權重計算的比率有時被稱為麥克唐納比率,即以巴塞爾委員會主席威廉·麥克唐納(William McDonough)來命名。
[2] 當抵押品為與敞口相同幣種的現金或政府債券時,這一規定並不成立。
[3] 對於貸款,這一調整並不是十分必要的,而對於場外型的衍生產品,就十分有必要,該調整是在附加因子之上的額外調整。
[4] 注意,巴塞爾委員會的文件對Copula相關係數採用的符號為R,而不是ρ。
[5] See M. B. Gordy, “A Risk-Factor Model Foundation for Ratings-Based Bank Capital Ratios,” Journal of Financial Intermediation 12(2003):199-232.
[6] 正如將在16.4節討論的那樣,此規定是根據被稱為SA-CCR的法規變更進行修訂的。
[7] 見巴塞爾銀行監管委員會,“The Application of Basel II to Trading Activities and the Treatment of Double Default Effects,” July 2005。
[8] See J. Lopez, “The Empirical Relationship between Average Asset Correlation, Firm Probabilityof Default, and Asset Size,” Journal of Financial Intermediation 13, no.2(2004):265-283.
[9] 根據我們從金融危機所觀察到的,這個值有可能過低了。
[10] 第19章將要討論的信用違約互換(CDS)為違約提供了保險,對於CDS的處理方式與對信用擔保處理方式類似。
[11] See Bank for International Settlements, “The Application of Basel II to Trading Activities and the Treatment of Double Defaults,” July 2005,這一文獻可在www.bis.org上下載。