e1 John Hull 風險管理與金融機構 v5
14.7 處理非線性情況
現在我們考察投資組合價值的變化與潛在風險因素的變化非線性相關的情況,包含期權的投資組合就是這種情況。非線性投資組合具有vega和gamma風險敞口。大多數投資組合的波動率近似為線性。因此,如前所述,可以考慮波動率期限結構中的潛在變動來考察vega風險敞口。
衡量gamma風險敞口更困難,因為它會產生二次項。考慮一個由單一期權組成的投資組合,投資組合的價值與資產價格S有關。泰勒級數展開式表明
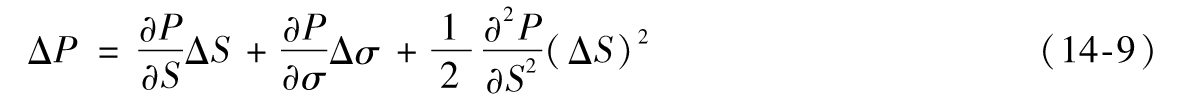
在計算VaR或ES時,不能忽略此擴展中的最後一項。圖14-2顯示了看漲期權多頭的價值同標的資產價格的關係,也能說明這一點。看漲期權多頭是一個具有正gamma產品的例子。如圖所示,當某天標的資產價格的概率分佈為正態分佈時,期權價格的概率分佈具有正偏性。圖14-3顯示了看漲期權空頭價值同標的資產價格的關係。空頭看漲期權的gamma為負。在這種情況下,一天結束時標的資產價格所服從的正態分佈被映射為具有負偏態的期權價值分佈。
一個投資組合的VaR直接取決於投資組合價值概率分佈的左尾。例如,當置信度為99%時,分佈左端小於VaR的數量佔整體分佈的1%。如圖14-2所示,具有正gamma的投資組合與正態分佈相比,左尾分佈較為瘦小,在正態分佈的假設下得出的VaR會偏高。類似地,如圖14-3所示,具有負gamma的投資組合同正態分佈相比,左尾分佈較為肥大,在正態分佈的假設下得出VaR會偏低。
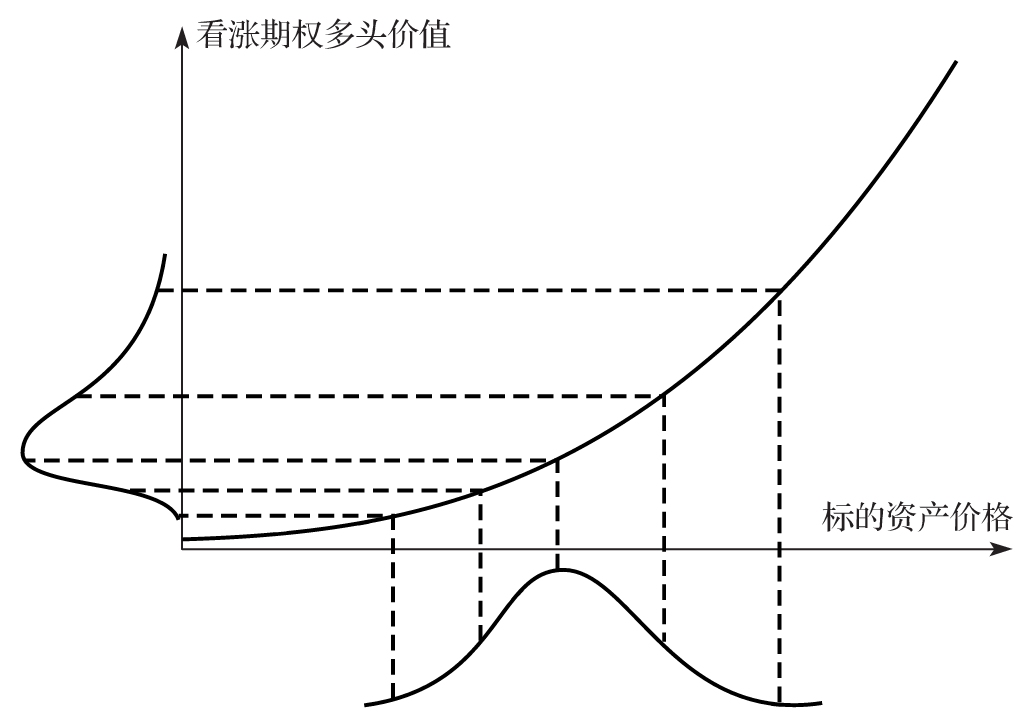
圖14-2 具有正態分佈的標的資產的概率分佈與看漲期權多頭價值的概率分佈的對應關係
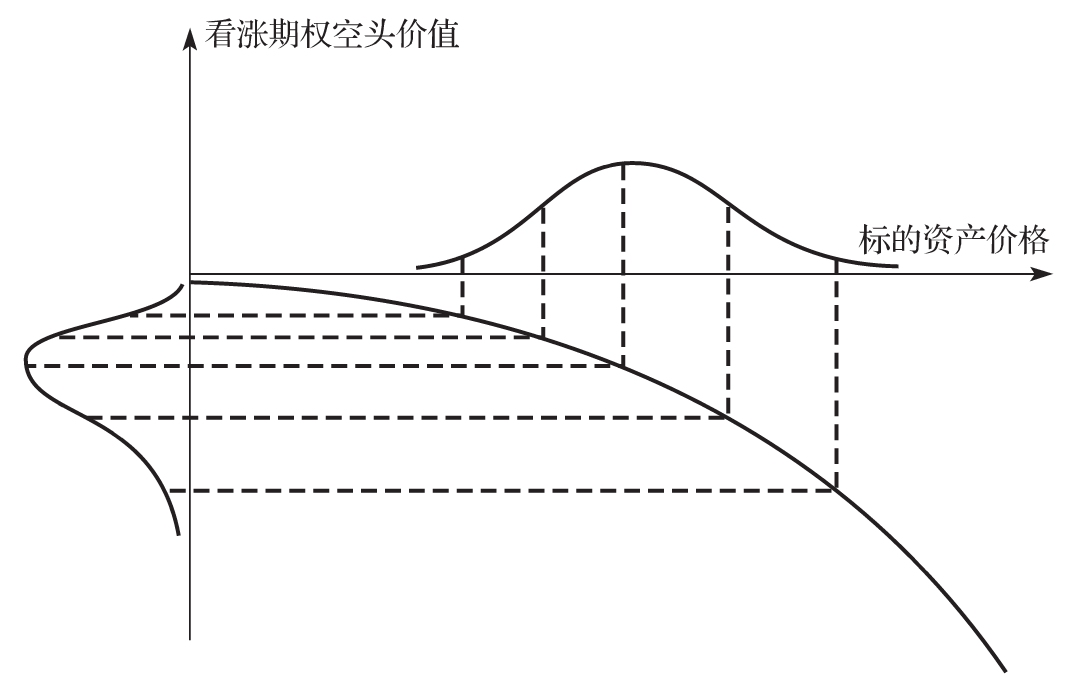
圖14-3 具有正態分佈的標的資產的概率分佈與看漲期權空頭價值的概率分佈的對應關係
如果一個投資組合與n個潛在風險因子相關,式(14-1)變為

γij是交叉gamma,其定義為

如果投資組合中的每一個資產只與一個風險因子有關,則不存在交叉gamma。因此,除了i=j時,γij=0。
14.7.1 蒙特卡羅模擬
作為對以上所討論方法的補充,我們可以在實施模型構建法時採用蒙特卡羅模擬(Monte Carlo simulation)來產生ΔP的概率分佈。假設我們要計算投資組合1天展望期的VaR,過程如下:
(1)利用當前的市場變量對投資組合進行定價。
(2)從Δxi服從的多元正態分佈中進行一次抽樣。[1]
(3)由Δxi的抽樣計算出在交易日末市場變量。
(4)利用新產生的市場變量來對投資組合重新定價。
(5)將第4步產生的數值減去第1步的數值,由此產生了ΔP的一個抽樣。
(6)重複第2步~第5步的計算,建立ΔP的概率分佈。
ΔP的概率分佈中的某個分位數就是我們想要求得的VaR或者ES。例如,假如我們由以上方法計算出ΔP的5 000個不同的抽樣,1天展望期的99%VaR對應於抽樣數值從大到小排序中的第50名;1天展望期的99%ES為排序中的第50名,等等。[2]N天展望期的VaR等於1天展望期的VaR乘以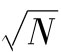 。[3]
。[3]
蒙特卡羅方法的弱點是其計算速度緩慢,計算速度之所以緩慢是因為公司的投資組合(有可能由成百上千的資產所組成)要被定價很多次。一種加速計算的方法是用式(14-10)所描述的ΔP與Δxi的關係,在蒙特卡羅方法中,我們可以由第2步直接跳到第5步,這麼做可以避免投資組合的定價過程,這一技巧被稱為局部模擬方法(partial simulation approach)。
14.7.2 擴展
蒙特卡羅模擬的一個魅力在於,我們不必假設風險因素呈正態分佈。我們可以假設Δxi服從任意的分佈,並使用多元Copula模型定義變量之間的相關性。[4]我們可以採用單因子高斯Copula模型,在以上所描述的5步模擬過程中第2步和第3步之間插入額外的一步,我們可以進行一個新的模擬過程:
(2)由多元概率分佈中提取一次抽樣ui。
(2a)以分位數到分位數的形式將ui映射到Δxi。
14.7.3 柯尼斯-費希爾展開
統計學中柯尼斯-費希爾展開(Cornish-Fisher expansion)由概率分佈的矩入手,來對概率分佈的分位數進行估計。假定μP和σP分別為ΔP的期望值和標準差,即

概率分佈的偏態與第三階矩有關。正偏態性表示概率分佈的右尾比左尾重。負偏態性則相反。ΔP的概率分佈偏態ξP通常定義為
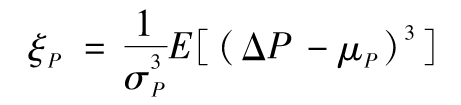
正態分佈的偏態為零。
概率分佈的峰度與第四階矩有關,它衡量分佈尾巴的厚重程度。與偏態相似,ΔP的概率分佈峰度κP通常定義為
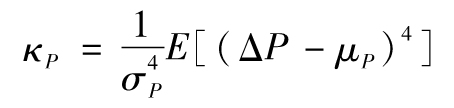
正態分佈的峰度為3。超額峰度(excess kurtosis)衡量的是相對於正態分佈的峰度,定義為峰度減去3。
利用ΔP的前三階矩,柯尼斯-費希爾展開得出的ΔP的第q個分位數為
μP+wqσP
其中
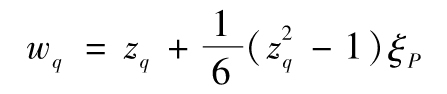
其中zq為標準正態分佈的第q個分位數。當使用更高階矩時,精度會提高。例如,當考慮峰度時,wq的表達式變為
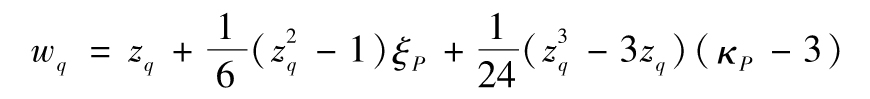
【例14-3】 假定對於某一投資組合我們計算出μP=-0.2,σP=2.2,ξP=-0.4,我們試圖計算分佈1%分位數(q=0.01),對於這一情形,zq=-2.326,假定ΔP的概率分佈為正態,由此得出1%分位數為
-0.2-2.326×2.2=-5.318
換句話講,我們有99%的把握肯定
ΔP>-5.318
對應於q=0.01,採用柯尼斯-費希爾展開並將分佈的偏態考慮在內,我們得出

分佈的1%分位數為
-0.2-2.620×2.2=-5.965
將偏態考慮在內時,投資組合的VaR由5.318變成了5.965。假設我們還知道峰度κP為3.3。對wq的估計改為:
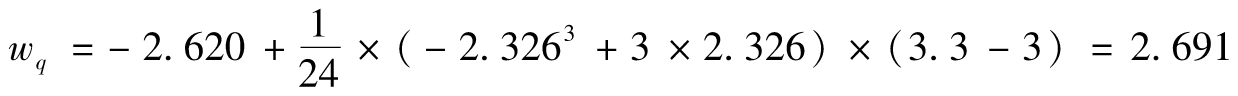
分佈的1%分位數估計為
-0.2-2.691×2.2=6.119
14.7.4 Isserlis定理
為了應用柯尼斯-費希爾展開結果,我們需要計算ΔP的矩。當Δxi服從正態分佈時,原則上可以使用Isserlis定理。定理指出,如果Xi是零均值正態分佈,當n是奇數時
E(X1X2…Xn)=0
當n是偶數時
E(X1X2…Xn)=∑ΠE(XiXj)
∑ΠE(XiXj)的含義為:①列出將X1,X2,…,Xn分成n/2對組合的不同方式;②計算每種方式中每對(XiXj)的期望值E(XiXj),並將它們相乘;③對每組組合的結果求和。
例如
E(X1X2X3X4)=E(X1X2)E(X3X4)+E(X1X3)E(X2X4)+E(X1X4)E(X2X3)
E(X1X2X3X4X5X6)有15種表達形式,其中一種是
E(X1X2)E(X3X4)E(X5X6)
Isserlis定理是一個具有潛在吸引力的結果,因為我們知道一對零均值正態分佈變量的乘積的期望值是標準差σX和σY,它們的協方差為:E(XY)=ρσXσY,其中ρ是σX和σY的相關係數。
當n為奇數時,n個零均值正態分佈變量的乘積為零,因此式(14-10)變為

當只有一個風險因子時,去除下角標σ、ρ、δ和γ,這些等式可簡化為

然而,結構的數量隨著風險因子數量的增加而迅速增加,因此即使風險因子數量並不多,第三階矩的計算也變得非常耗時。
對Isserlis定理的一個變形是(考慮gamma),在計算前二階矩時以VaR或ES為基礎,並且假設沒有交叉gamma。這意味著當i≠j時,γij=0。為簡化公式,我們設γii=γi

由Isserlis定理可得
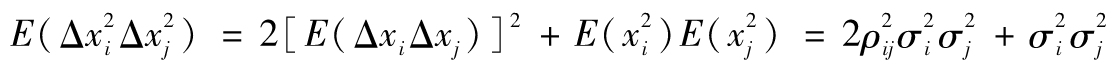
因此可得ΔP的標準差是
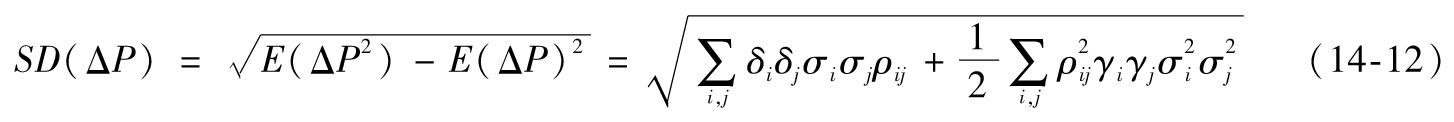
我們在第17章中討論標準初始保證金模型(SIMM)時將應用到這個定理。
[1] 一種做法在第11.4.1節中給出了。
[2] 就像在歷史模擬法中那樣,極值理論可以用來對尾部分佈進行光滑處理,在處理之後我們可以得出極端分位的更好估計。
[3] 當交易組合中包含期權時,這一假設只是一個近似,但這種近似被大多數實際操作採用。
[4] See J. Hull and A. White, “Value at Risk When Daily Changes Are Not Normally Distributed,” Journal of Derivatives 5, no. 3 (Spring 1998): 9-19。