e1 John Hull 風險管理與金融機構 v5
14.3 涉及4個投資的例子
根據式(14-2)或式(14-3),我們現在考慮第13.1節中討論的例子。該例涉及一個在2008年9月25日投資400萬美元於道瓊斯工業平均指數(DJIA)、300萬美元於富時100指數(FTSE 100)、100萬美元於巴黎40指數(CAC 40)和200萬美元於日經225指數(Nikkei 225)的投資組合。為了計算,我們採集了截至2008年9月25日500天的歷史數據,讀者可以在作者的網站www-2.rotman.utoronto.ca/~hull/RMFI/VaRExample上下載這些數據和有關計算表單。
表14-1是利用一般方法,即對500個回報數據採用同等權重的方法求得的相關係數矩陣。結果顯示,FTSE 100與CAC 40具有很高的相關性,DJIA與FTSE 100和CAC 40有一定程度的相關性,Nikkei 225與其他指數的相關性較低(甚至與DJIA呈負相關)。表14-2顯示了協方差矩陣。
表14-1 2008年9月25日,對過去500天所有數據設定同等權重所得出的相關係數矩陣

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
表14-2 2008年9月25日,對過去500天所有數據賦予同等權重所得出的協方差矩陣

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
由式(14-3)以及以上方差-協方差矩陣,我們得出投資組合損失的方差為8 761.833(以千美元計),標準差是以上數量的平方根,即93.60,1天的99%的VaR為
2.326×93.60=217.757(千美元)
即217 757美元。1天的99%的ES為
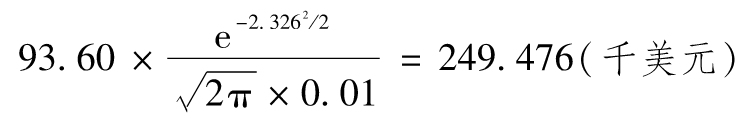
即249 476美元。我們可以將這一結果與由第13章標準歷史模擬法產生的結果(即253 385美元VaR和327 181美元ES)進行比較。
利用EWMA模型
除對所有的市場回報採用同等權重來計算方差-協方差,我們還可以利用指數加權移動平均方法(EWMA),在計算中採用參數λ為0.94。表14-3顯示了通過這種方法得出的方差-協方差矩陣。[1]由式(14-3)以及方差-協方差所給出的組合損失的方差為40 995.765(以千美元計),標準差是以上數量的平方根,即202.474。1天的99%的VaR為
2.326×202.474=471.025
即471 025美元。由式(12-2),1天的ES為539 637美元。以上結果比由等權重所求得結果的兩倍還要高。表14-4和表14-5給出了產生這兩個結果差別的原因。一個由資產多頭頭寸所構成的投資組合的標準差會隨資產回報標準差的增大以及相關係數的增大而增大。表14-4顯示,由EWMA所得出的標準差比由同等權重得出的標準差要高得多。這是因為與緊鄰2008年9月25日前面的一段歷史數據的波動率比500天數據中其他時段的波動率要高得多。比較表14-5和表14-3,我們發現相關係數也比由同等權重得出的相關係數要高得多。[2]
表14-3 利用EWMA模型所求得的2008年9月25日的協方差矩陣,λ=0.94

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
表14-4 利用等權重和EWMA模型所得出的2008年9月25日的波動率(每天%)

表14-5 利用EWMA模型所求得的2008年9月25日的相關係數矩陣

注:變量1為DJIA,變量2為FTSE 100,變量3為CAC 40,變量4為Nikkei 225。
[1] 在EWMA方法中,方差最初可以被設定為所有觀察值的方差,但由任意一個合理的初始方差所得出的最終結果都十分接近,而我們只是關心最終的方差結果。
[2] 在市場承壓時,相關性會增大,這一例子說明了這一點。