e1 John Hull 風險管理與金融機構 v5

14.2　推廣

以上討論的例子是採用線性模型來計算VaR的特例。假定，我們所持有的某投資組合的價值為P，其價值依賴於n個市場變量。根據市場慣例，我們把市場變量稱為風險因子（risk factors），如股票價格、商品價格或匯率（我們會在本章後面考慮利率、信用價差和波動性）。在很大程度上，投資組合的價值變化與風險因子的百分比變化呈線性相關。

其中ΔP為整個投資組合實際的日價值變化，Δxi是一天內第i個風險因子的百分比變化。

參數δi是第8章中解釋的delta風險的變體。持倉頭寸相對於風險因子的delta通常被定義為比率ΔP/ΔS，其中ΔS是風險因子值的微小變化量（所有其他風險因子保持不變），ΔP是投資組合的價值由此產生的變化。我們在這裡使用的參數δi等於ΔP/Δxi，Δxi是第i個風險因子值在百分比上的微小變化（同樣所有其他風險因子保持不變），ΔP是投資組合價值的變化。

如果我們假定式（14-1）中的Δxi服從多元正態分佈，因此ΔP也服從正態分佈。為了計算VaR，我們只需要計算出ΔP的期望值及標準差。基於上一節任意一項Δxi的期望值為0的假設，我們得出ΔP的期望值也為0。

計算ΔP的標準差的方法是前述兩個資產例子的擴展，我們假定σi為第i項資產的日波動率，ρij為資產i及資產j的相關係數，這意味著Δxi的標準差為σi，Δxi和Δxj的相關係數為ρij，將ΔP的方差記為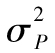（因為我們考慮的展望期為1天，σi是每天的波動率）。ΔP的標準差是

該式也可以寫為

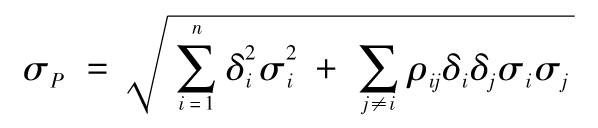
或者

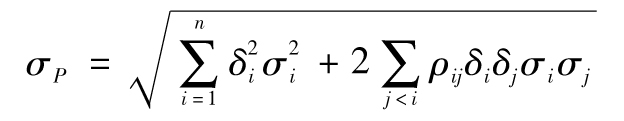
也可以表示為

covij是Δxi和Δxj的協方差，用矩陣形式表示的上式為

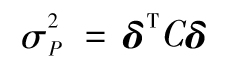
其中，δ是列向量，它的第i個元素是δi，C是方差-協方差矩陣（見第11.3節），δT是δ的轉置。

T天展望期的標準差為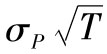，因此展望期為置信水平為X%的VaR等於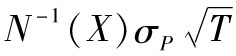。根據式（12-2），T天展望期、置信水平為x%的ES為

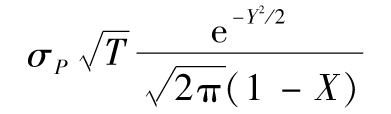
其中Y=N-1（X），且N-1為正態分佈累積函數的反函數（可由Excel中的NORMSINV計算）。

【例14-1】　在前一節所考慮的兩個資產的例子中，投資組合的價值為P，第一個資產（微軟公司）投資了1 000萬美元，第二個資產（AT&T）投資了500萬美元。當以百萬美元計時，δ1=10，δ2=5，並且

ΔP = 10Δx1 + 5Δx2

σ1=0.02，σ2=0.01，ρ12=0.3，則有

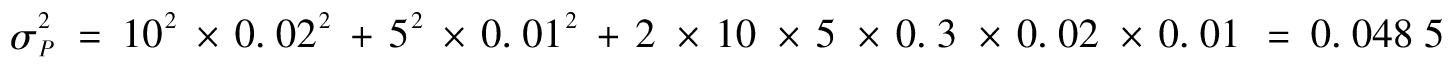
即σP=0.220，這一數量為投資組合每天價值變化的標準差（以百萬美元計），10天展望的99% VaR為，即162萬美元，ES為。

也就是186萬美元。這與上一節所計算的結果完全一致。

與馬科維茨的關係投資組合在1天內的回報為ΔP/P，從式（14-2）中得出，組合的日回報的方差為

其中wi = δi/P。當投資組合由n個資產的多頭和空頭頭寸組成，第i個風險因子為第i個資產的價值時，δi是第i個資產的投資價值（如例14-1所示），wi為組合中第i個投資的權重。式（14-2）由馬科維茨的研究給出，直到今天還經常被投資組合經理使用，以將投資組合收益的標準差與單個資產收益的標準差、單個資產收益之間的相關性聯繫起來（請參閱第1.1節）。