e1 John Hull 風險管理與金融機構 v5
13.6 極值理論的應用
考慮表13-1~表13-4中的數據。當u=160時,nu=22(即有22個情景損失大於160,以千美元計),表13-10顯示了對於β=40和ξ=0.3時的計算。這時,由式(13-7)給出的似然函數的對數為-108.37。
表13-10 對於表13-4的極值理論計算,u=160、β=40及ξ=0.3
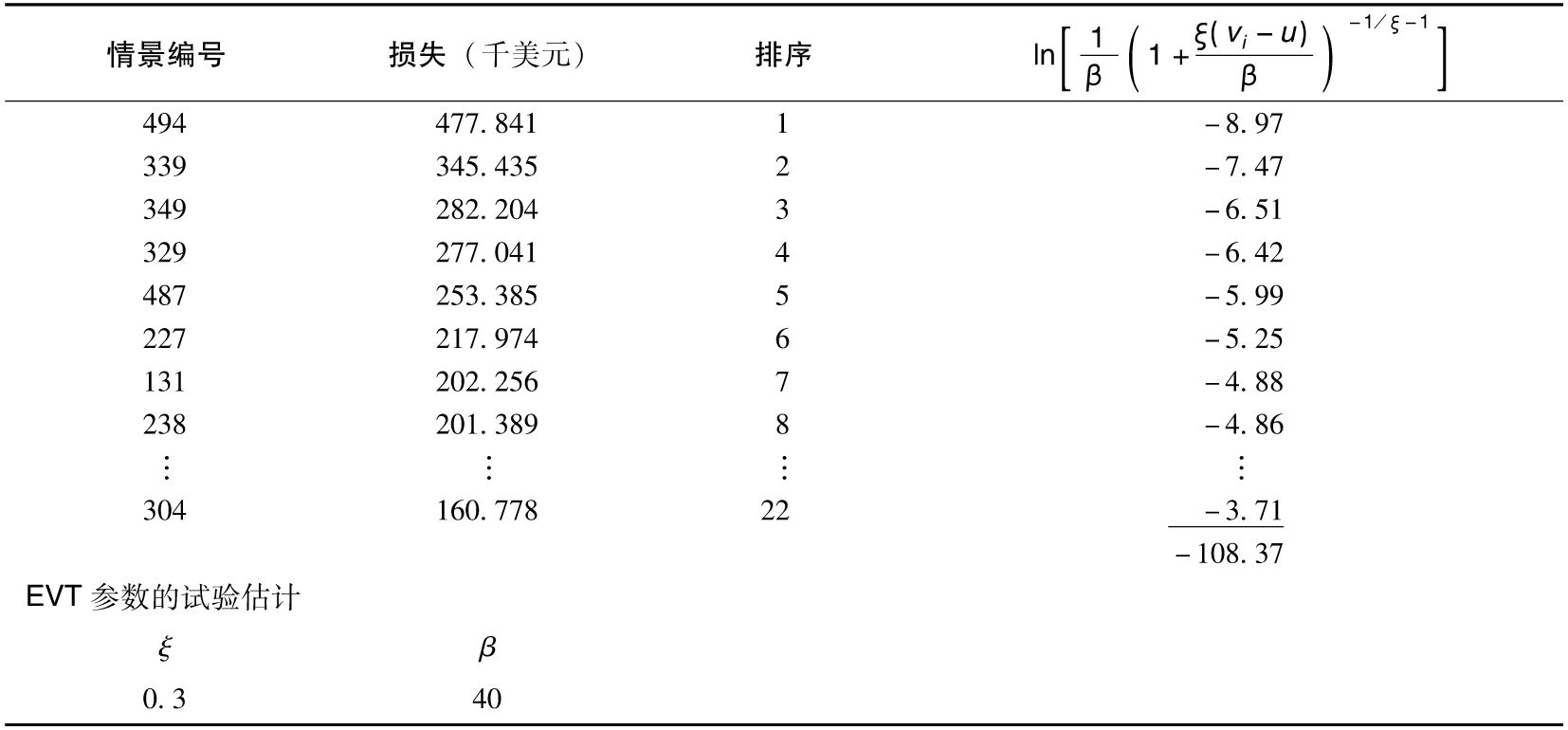
採用Excel計算表中的Solver程序,我們可以求得使得似然函數達到最大值的β和ξ的取值為
β=32.532 ξ=0.436
最大似然函數的對數為-108.21。
假定我們希望估計交易組合在2008年9月25日和9月26日之間,損失大於300 000美元(交易組合價值的3%)的概率,由式(13-8)得出,這一概率為(以下計算式中的金額均以千美元計)
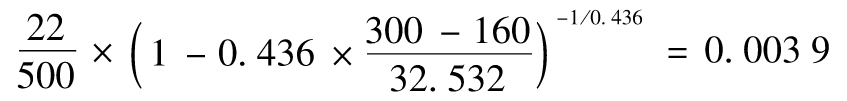
這比從觀察值直接數出來要更為準確。類似地,損失大於500 000美元(交易組合價值的5%)的概率為0.000 86。
由式(13-9)得出,在99%的置信區間下的VaR值為
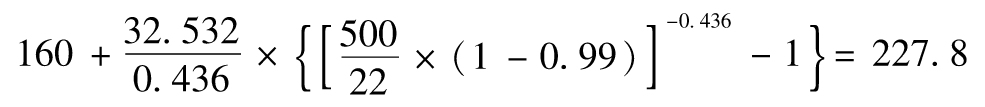
即227 800美元(在本例中,估計的VaR比觀察到的第五大損失少25 000美元)。在99.9%的置信區間下的VaR值為
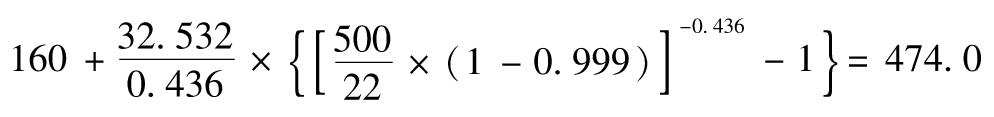
即474 000美元。當置信度進一步增大到99.97%時,VaR值為
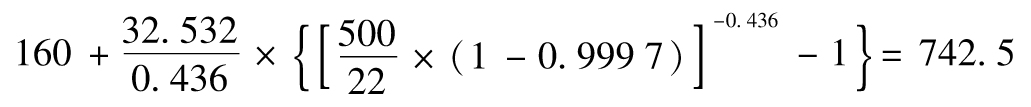
即742 500美元。
式(13-10)可用來提高ES估計的準確度,並可以提升ES估計的置信度。在我們的例子中,當置信水平為99%時,ES為
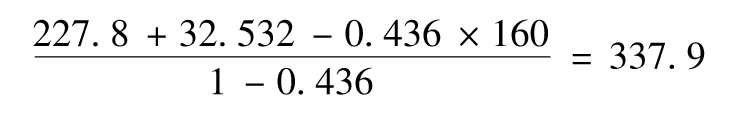
即337 900美元。當置信水平為99.9%時,ES為
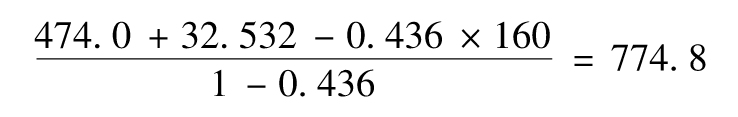
即774 800美元。
極值理論可以用於非壓力或壓力風險測度,也可以比較容易地與第13.3節的波動率調節過程結合起來使用(見練習題13.11)。它還可以與第13.3節討論的數據加權方法結合使用。這時,式(13-7)中的求和部分的每一項必須要乘以賦予不同觀察值的權重。
最後一個應用是對第13.2節中99%置信度的VaR值的置信區間進一步優化。在損失大於160的條件下,取值在VaR水平(227.8)的損失概率分佈的概率密度函數由式(13-6)中的gξ,β(y)給出,其值為
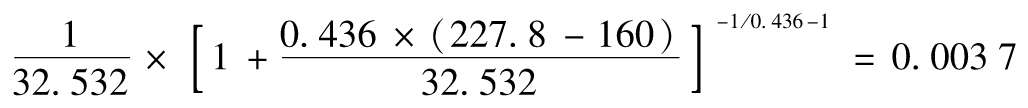
無條件概率密度在VaR水平下的取值為nu/n=22/500與以上數量的乘積,即0.000 16。顯然,這比第13.2節中估計的0.000 284要低,從而使VaR值的置信區間更寬。
有關u的選擇
在計算過程中,我們會遇到一個很自然的問題,那就是如何選定變量u。雖然我們常常發現ξ和β取決於u,但F(x)的估計值大致相同(練習題13.10考慮了我們討論的例子中將u從160變為150的情景),我們希望將u設定為足夠大,來保證確實考慮了尾部分佈的情形,同時我們還希望將u設定為足夠低,來保證使用最大似然估計時的觀測數據不至於太少。在計算中使用更多的數據會提高對於尾部評估的精度,我們在例子的計算過程中應用了500個數據,理想的做法是應用更多的數據。
一個經驗法則是保證u近似等於實證分佈中的95%的分位數(在我們考慮的數據中,實證分佈中的95%的分位數為156.5)。對ξ和β最佳值進行求解時,我們要保證這些參數為正,如果優化程序將ξ設為負值,這可能是由於:①分佈的尾部不比正態分佈更為肥大;②對參數u的選取不當。